随着国内外学者对高性能燃气涡轮叶片复合冷却结构传热机理研究的不断开展,深入研究典型扰流带肋通道的流动和强化换热机理, 对涡轮冷却效率的提高有着重要的意义.数值模拟方法广泛应用于研究肋通道的相关问题,与实验相比,数值模拟能够缩短设计周期.采用的数值模拟算法如能在设计阶段对流动和换热有相当准确地预测能力,将有效提高燃气轮机的设计效率.在肋扰流通道内部流场中,由于剪切层发生分离与再附,以及横向二次流的存在,准确预测肋通道的流动和换热性能是比较困难的.国内外学者已经对肋通道进行了大量的数值和实验研究.如Han等[1]研究了宽高比为1时, 不同结构类型的肋换热性能,结果显示正Ⅴ型肋有更好的换热性能,交叉肋压损最大,换热性能提升最小. Ahn等[2]实验研究了矩形带肋通道的换热情况,结果表明随着带肋壁面数的增加,当地换热系数和摩擦因子将增加. Tanda等[3]与Schüler等[4]采用数值与实验手段分别研究了不同倾角肋片通道对流换热效果,指出在相对的壁面同时存在肋片时,整个壁面换热能力增强,但同时压损也上升.
当前许多研究结果表明,大涡模拟(LES)数值方法对流动的预测能力有了相当大的提高,同时也越来越多地被应用于扰流结构,特别是带肋通道的机理研究与设计分析当中.其中Murata等[5]、Watanabe等[6]、Tafti[7]、Sewall等[8]、Viswanathan等[9]、Liu等[10]的研究中都从不同角度给出了肋通道内的详细的三维流动细节. Lohász等[11-12]采用大涡模拟方法再现了Çakan[13]、Casarsa等[14]的沿流向周期性的肋通道实验结果,提供了细致的流场信息.
本文进一步从机理研究的角度出发,针对典型的肋通道流动和传热性能,分别采用雷诺平均方法和大涡模拟方法进行数值研究,根据不同方法的具体特点,对计算得到的流动与传热结果进行分析,并与文献[15]中的实验数据进行综合比较与评估.本文旨在采用先进的大涡模拟方法,获得不同于雷诺平均方法的多尺度旋涡结构,从机理上揭示其在复杂湍流流动与传热预测方面的优越性,从而为复合冷却结构的机理研究和工程设计提供参考.
1 数值方法及计算模型N-S方程描述了质量、动量和能量的输运,是RANS模型和大涡模拟的起点,方程为
| $ {\rm{d}}\mathit{\boldsymbol{W}}/{\rm{d}}t + {\rm{div}}\;\mathit{\boldsymbol{F}} = 0, $ |
式中:W为主要变量的矢量形式;F为通量张量,F =(f-fv, g-gv, h-hv),其中f、g、h为通量的无黏部分,fv、gv、hv为通量的有黏部分,同时流体满足理想气体状态方程,热通量遵循傅里叶定律.
1.1 大涡模拟方法大涡模拟方法包含空间过滤和建模两个关键步骤.首先对流场空间进行滤波操作:
| $ \widetilde {f\left( {x,t} \right)} = \frac{1}{{\rho \left( {x,t} \right)}}\int_{ - \infty }^{ + \infty } {\rho \left( {x\prime ,t} \right)f\left( {x\prime ,t} \right)G\left( {x\prime - x} \right){\rm{d}}x\prime }. $ |
式中G表示滤波函数.对N-S方程进行滤波操作,引入附加变量亚格子应力张量,并对亚格子应力建模是LES的核心内容.本文采用LES动力学亚格子模型封闭方程组.
1.2 雷诺平均方法雷诺平均方法是工程上常用的数值方法之一,对于可压流动的N-S方程进行Favre平均,将变量分解为平均部分和脉动部分:
| $ F = \widetilde f + f'',\widetilde f = \overline {\rho f} /\overline \rho . $ |
式中波浪线表示雷诺平均量.
Favre平均在动量方程中引入了附加雷诺应力项
本文参考了Casarsa等[14]进行的涡轮叶片冷却流道实验.实验中使用了真实流道的放大模型,同时保证几何与运动的相似条件.通道总长2 800 mm,横截面为100×100 mm2,测试段壁面为15 mm厚的透明有机玻璃.实验中通过PIV测量技术获得流道不同位置的速度;为保证统计参量的收敛,样本点在300左右.在恒定热流密度的条件下,采用液晶测温技术获得壁面温度.
1.4 肋通道几何模型本文的计算模型与参考文献[14]保持一致.通道入口为方形宽、高均为0.10 m,宽高比为1,水力直径Dh=0.1 m,肋片为方形肋片,肋片高度为h=0.3Dh,肋间平板长度p=10 h;基于入口速度和水利直径的入口雷诺数Re=40 000.分别用RANS模型和LES动力学模型对计算域同一工况点进行计算,对比二者在流动和换热方面的预测能力.换热增强效果由努塞尔数体现:
| $ Nu/N{u_0} = ({h_{\rm{a}}}{D_{\rm{h}}}/k)/(0.023 \cdot R{e^{0.8}} \cdot P{r^{0.4}}). $ | (1) |
式中:ha为对流换热系数,Dh为水力直径,k为工质导热系数.
1.5 计算网格及边界条件为了有效减少计算量,假设扰流肋的流动是周期性的,取一个周期性区域为计算域.在周期性计算域,进出口应用平移周期性边界条件,因此设置进出口边界条件时,流向增加一个质量流率来达到Re=40 000的工况,其余边界均设为绝热无滑移壁面.
由于直肋通道中肋的数目有限,冷却流道内流动可能不会达到周期性, 因此另取一个7肋片的全尺寸计算域,验证周期性假设.全肋计算域设置速度进口,静压出口,壁面为热流壁面,热流量为q=650 W/m2.
周期性计算域和7肋计算域均采用结构化网格,如图 1所示.

|
图 1 带肋通道网格示意 Figure 1 Mesh of the ribbed channel |
网格在壁面局部加密,周期性计算域网格M1、M2单元数分别为91万和200万.壁面yplus分别为3和1附近.其中LES在两个计算网格下进行计算以观察yplus对LES计算结果的影响,RANS模型仅采用计算网格M2.数值计算过程在商业软件ANSYS CFX中进行.
2 流动特征 2.1 时均速度图 2为时均流动在对称面上的流谱.可以看到肋的存在使得边界层在肋前发生分离,由于流动方向不能随几何边界突然90o折转,因此流动在肋前发生边界层分离,一部分流体在肋前下角产生一个回流区①;同时分离流动在肋顶再附,形成一个扁平的闭式回流区②; 经过肋片后,由于流面的突然扩张,流动发生第二次大尺度分离,在肋后平板形成一个尺度较大,形状瘦长的回流区③;在肋后下角,由于流体黏性对涡量的输运作用,大尺度的回流将会诱导出一个反向旋转的回流④.理论上,回流区④将继续在肋后下角诱导出与之旋向相反的回流,直至涡量被耗散.边界层在肋后约4.2h处边界层发生再附,并随流动发展变厚,直至遇到下一个肋片,流动将再一次发生上述流动分离.
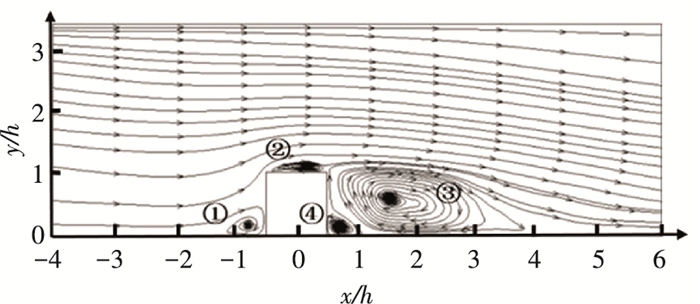
|
图 2 对称面平均流动的流谱 Figure 2 Mean flow topology in the ribbed channel symmetry plane |
图 3为对称面量纲一的流向速度分布云图.结合图 3(e)和图 4中的实验值可以得出,肋的节流效果迫使流动在肋片顶部加速,并且流向速度最大值位置在通道中部,流向速度最大值位于y/h=1.8附近.数值模拟结果显示,不同的湍流模型均能够识别到肋片顶部的流动加速现象;但流向速度的最大值位置有所差异.其中采用k-ε模型和k-ω模型计算相近,最大值位于y/h=3.0附近;采用sst-kω模型,最大值位于y/h=1.3附近;而采用大涡模拟方法,最大值位于y/h=1.8附近,与实验结果吻合最好.
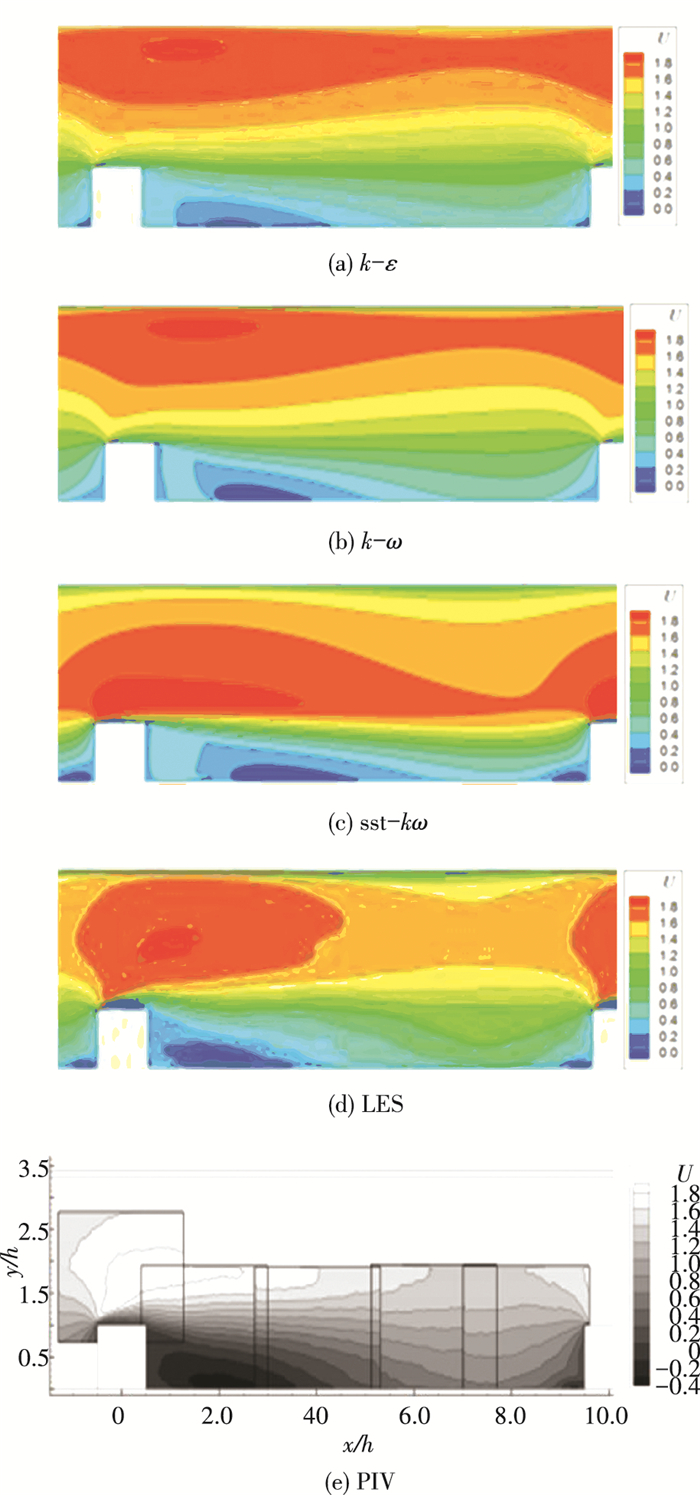
|
图 3 对称面量纲一流向速度分布 Figure 3 The dimensionless streamwise velocity in the ribbed channel symmetry plane |
图 4为对称面平均速度分布随流向变化规律. RANS方法计算结果在肋顶加速流动区域和肋后近壁回流区与实验值有较大差异,大涡模拟的结果与实验结果吻合程度最高,这说明相比RANS方法,大涡模拟对平均流动的预测有着较大的优势.

|
图 4 对称面不同位置的时均速度分布 Figure 4 Streamwise mean velocity at different position in the channel symmetry plane |
图 5为对称面湍流强度的分布规律. 图 5(a)显示了对称面上湍流强度最大值位置随流向的变化.湍流强度的分布一定程度上反映了流场中的湍流结构的分布.实验结果显示,湍流强度最大值位于通道内y/h=1附近.数值模拟结果表明,采用大涡模拟的方法,湍流强度在x/h=6.0~7.5范围内略高于实验值,其他区域吻合度较高;采用sst-kω,SSG湍流模型,在x/h>5.8区域湍流强度低于实验值;采用k-ε模型,在x/h=0.5~2.0时湍流强度最大值位置略高于实验值.因此,数值模拟结果能够对湍流结构的位置给出了很好的预测.
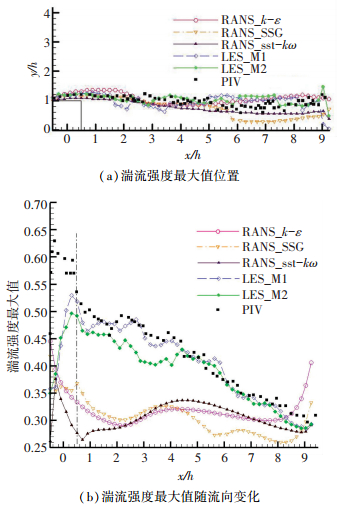
|
图 5 流场湍流强度的分布 Figure 5 The distribution of turbulence intensity |
图 5(b)显示了湍流强度最大值随流向的变化.从实验结果可以看出,湍流强度最大值出现在肋顶靠近前缘区域位置,最大值为0.63.肋顶区域的湍流强度在0.55~0.63之间变化.湍流强度在肋后剧烈下降,直到x/h =1.0和x/h =2.5之间,湍流强度接近0.48.这两个区域与图 4所示②③漩涡结构所产生的剪切层位置一致.之后湍流强度线性下降,直到下一个肋片前降低至0.3左右. RANS模型计算结果与实验结果差别很大,其最大值位于肋前上角,约为0.45,总体趋势为先下降后上升,与实验数据不符;相比之下,大涡模拟计算结果显示湍流强度变化趋势与PIV实验结果一致,但总体水平低于实验结果,而且湍流强度最大值位置位于靠近肋后上角,实验结果则更靠近肋前上角.总体而言,大涡模拟对流场中湍流强度的的预测优于其余湍流模型.
2.3 周期性验证图 6为采用大涡模拟方法计算全肋计算模型得到的时均速度分布.图中以第5肋和第7肋附近流动为例,从图中可以看出,第5肋和第7肋平均速度分布基本重合,并且与PIV实验数据有良好的一致性.即验证了周期性假设的合理性.

|
图 6 Rib_5th和Rib_7th附近平均速度分布 Figure 6 Comparision of mean velocity on Rib_5th and Rib_7th |
本文分别采用RANS模型和大涡模拟的计算结果与实验结果进行对比分析,研究湍流模型在换热预测方面的准确性.采用努塞尔数表征换热增强的效果,计算公式见式(1),其中壁面温度由近壁面流体确定,参考温度取入口流体的温度.
图 7为大涡模拟计算某瞬时温度等值面. 图 8(a)为第一肋附近不同时刻的流场,可以看出漩涡结构A产生自肋顶;随着时间推进,肋顶涡结构破碎,A0脱落,并在原来的位置重新形成漩涡结构A1.周期性脱落的漩涡结构A随主流发展,可以看出脱落涡的轨迹近似在肋顶的高度,与图 5(a)湍流强度最大值位置相符.流体黏性所引起的涡量扩散和耗散使得脱落涡空间尺寸变大,同时强度逐渐减弱,与图 5(b)相符.脱落涡在肋间中部位置,不再保持自身的结构,开始与附近涡结构相互掺混,该位置与边界层的再附位置相符.肋后下角区域不存在明显的漩涡结构.

|
图 7 某瞬时温度等值面(T=298.5 K) Figure 7 Instantaneous isosurface of temperture of constant heat flux LES computation |
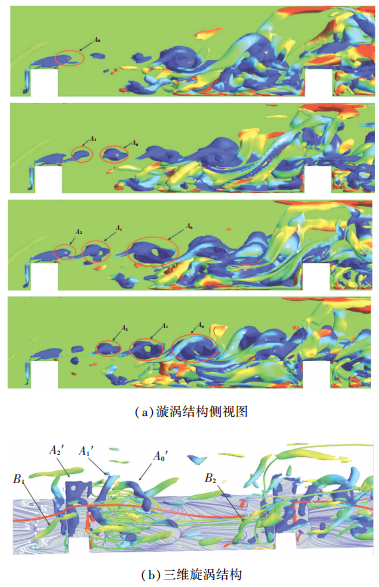
|
图 8 流场中瞬时变量分布 Figure 8 Distribution of instantaneous variable in the ribbed channel |
由图 8(b)可以清晰地看到流动的分离和再附.同时,在肋和侧壁面的作用下,肋前分离流动存在向侧壁偏转的横向二次流动;由壁面流谱可以看出,肋前形成鞍点/螺旋点的分离模式;螺旋点吸收边界层内部分涡量,空间位置抬起并随主流向下游偏转,如图中涡结构B1、B2.而肋后则存在由侧壁面向通道中心靠拢的二次流动,横向二次流对侧壁面的换热增强有重要的作用.肋顶涡结构不断地产生脱落,与图 8(a)一致.肋前的分离流动和大尺度涡结构对质量,动量和能量的输运起主要作用,进而影响局部的换热强度和温度场的分布.
图 9为努塞尔数沿流向的变化规律,可以看出RANS模型计算结果具有相同的变化趋势,最大值位于入口,在第一个肋间存在最低点,在x>0.5 m后,努塞尔数近似沿线性变化.从数值上看,RANS模型计算结果整体高于LES结果.

|
图 9 努塞尔数随流向变化 Figure 9 Enhancement factor on the ribbed wall |
图 10为肋间区域换热增强效果的对比.由图 10(e)可以看出,肋间平板存在两个高努赛尔区域,分别位于肋间平板中部,x/h=3~5,努塞尔数最大值为3左右; 肋前x/h>8区域,努赛尔数最大值为2.19.采用k-ε,SSG模型计算结果显示,肋间平板仅存在一个高努塞尔数区域,均位于x/h>4.5区域,该区域努塞尔数最大值分别为2.24和1.45;k-ω模型计算结果显示,平板中部区域最大值为1.45,肋前区域分裂为两个独立的高努塞尔数区,最大值为1.09. LES的计算结果表明,努塞尔数在平板上的分布规律较好吻合了实验测量结果,即包括肋前和肋中部两个高努塞尔数区域以及此两个区域所在位置.从数值上来看,RANS模型与LES方法低估了肋中部高努塞尔数区域的数值.而在肋前的高努塞尔数区域,LES高估了该区域的努塞尔数,其值高于肋中区域,与实验结果不符.
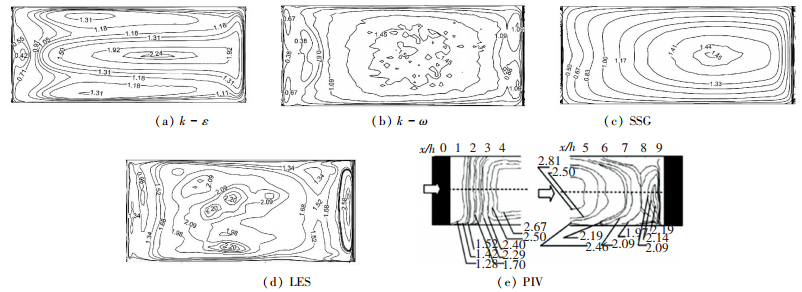
|
图 10 肋间平板换热增强系数分布 Figure 10 Enhancement factor on the wall between ribs |
图 11为肋片3个表面上努塞尔数的分布.从上游表面可以看出,实验结果显示最大值位于肋前上角;同时在通道侧壁的位置等值线出现了凸起. RANS方法和LES方法的计算结果在上游表面有相似的等值线分布,与实验值有差异.
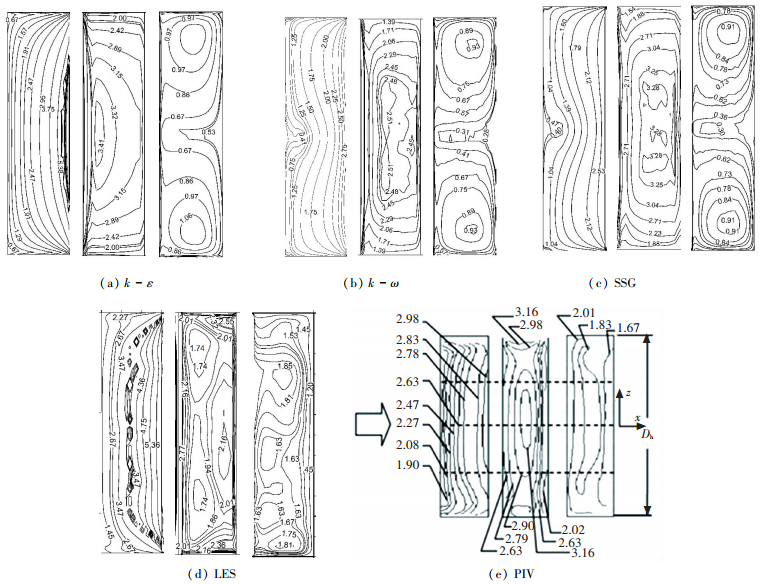
|
图 11 肋片表面换热增强系数的分布 Figure 11 Enhancement factor on the rib wall |
RANS结果在靠近壁面通道并未出现等值线凸起的现象,而LES则在近壁面角区出现了对称分布的两个极小值区域.从数值上来看,上游表面实验测量最大值在3.0左右,LES计算结果高于实验结果,最大值在5.36左右与k-ε结果相当;而采用k-ω和SSG模型低于实验值,最大值在2.6左右.
从肋顶表面可以看出,PIV测量结果显示在肋顶中部出现一个高努塞尔数区域,并向四周递减,且靠近下游表面一侧努塞尔数等值线较密集,即该区域努塞尔数梯度较大;努赛尔数在2.00~3.16范围内变化. LES方法计算结果显示,努塞尔数最大值位于肋顶面靠近展向侧面区域,最大值约为2.55;同时肋顶高努赛尔数区域靠近下游壁面.采用k-ε模型计算结果肋顶高努赛尔数区域靠近上游壁面,数值变化范围在2.00~3.41之间.采用k-ω和SSG模型结果显示,肋顶中部存在高努赛尔数区域,努塞尔数变化范围分别为,1.39~2.51和1.54~3.28.综上,采用SSG模型的计算结果与实验数据最为吻合.
从下游表面可以看出,实验测量结果最大值位于下游平面与肋顶平面的交界处,并向下游递减,其值变化范围在1.5~2.0.数值模拟的结果较实验测量值偏小. RANS模型计算结果可以看出,在平面中部出现对称分布的极值区域,采用k-ε、k-ω、SSG计算值变化范围分别为0.50~0.85、0.31~0.93和0.30~0.91,最大值与实验值相差约56%. LES计算结果,等值线分布接近PIV实验.同时数值变化在1.20~1.85,最大值与实验值相差约8%.
4 结论1) 大涡结构受初边值条件影响表现为各向异性.大涡模拟捕捉到了肋顶扁平涡结构的产生与脱落与过程,指出它在近似肋顶面的高度和下游空间内发展并掺混,强度逐渐衰减,该过程与湍流强度的分布规律一致.同时获得了肋前分离流动中向侧壁面偏转的横向二次流等更加详细的流场结构.
2) 在流动特征方面,大涡模拟准确预测到了平均速度最大值在通道的中心处,并且在速度分布规律上与实验值吻合度较高;雷诺平均方法计算结果显示平均速度的最大值位置及其分布规律与实验值有较大差异.两种方法都预测到了流向湍流强度最大值的空间位置.在数值方面,大涡结果与实验值变化趋势相同,但值略低于实验值;而雷诺平均方法结果变化趋势和数值均与实验不符.
3) 大涡模拟计算结果表明,在肋间平板x/h=3.0~5.0之间和肋前x/h=8.0~9.5存在两个高努塞尔数区域,与实验相符. k-ε和SSG模型计算结果显示高努塞尔数区域在x/h=4.5之后,并且未能显示出肋前第二个高努塞尔数区域;k-ω模型计算结果显示,肋前第二高努赛尔数区一分为二,并且两种方法计算值均低于实验值.对肋顶表面换热,LES计算结果低于实验值,肋顶中部的高努塞尔数区域更靠近下游.但在肋后表面,努塞尔数分布规律上与实验结果吻合最好,最大值的预测误差也比雷诺平均方法要小.
| [1] |
HAN J C, ZHANG Y M, LEE C P. Augmented heat transfer in square channels with parallel, crossed, and v-shaped angled ribs[J].
Journal of Heat Transfer, 1991, 113(3): 590-596.
DOI: 10.1115/1.2910606 |
| [2] |
AHN S W, KANG H K, BAE S T, et al. Heat transfer and friction factor in a square channel with one, two, or four inclined ribbed walls[J].
Journal of Turbomachinery, 2008, 130(3): 538-544.
DOI: 10.1115/1.2775488 |
| [3] |
TANDA G, ABRAM R. Forced convection heat transfer in channels with rib turbulators inclined at 45 deg[J].
Journal of Turbomachi-nery, 2009, 131(2): 021012-021021.
DOI: 10.1115/1.2987241 |
| [4] |
SCHVLER M, ZEHNDER F, WEIGAND B, et al. The effect of side wall mass extraction on pressure loss and heat transfer of a ribbed rectangular two-pass internal cooling channel[C]// ASME Turbo Expo 2009: Power for Land, Sea, and Air. Orlando: the International Gas Turbine Institute, 2009:629-630. DOI: 10.1115/1.4000552.
|
| [5] |
MURATA A, MOCHIZUKI S. Large eddy simulation with a dynamic subgrid-scale model of turbulent heat transfer in an orthogonally rotating rectangular duct with transverse rib turbulators[J].
International Journal of Heat & Mass Transfer, 2000, 43(7): 1243-1259.
DOI: 10.1016/S0017-9310(99)00205-7 |
| [6] |
WATANABE K, TAKAHASHI T. LES simulation and experimental measurement of fully developed ribbed channel flow and heat transfer[C]// ASME Turbo Expo 2002: Power for Land, Sea, and Air. Amsterdam: the International Gas Turbine Institute, 2002:411-417. DOI: 10.1115/GT2002-30203.
|
| [7] |
TAFTI D K. Evaluating the role of subgrid stress modeling in a ribbed duct for the internal cooling of turbine blades[J].
International Journal of Heat & Fluid Flow, 2005, 26(1): 92-104.
DOI: 10.1016/j.ijheatfluidflow.2004.07.002 |
| [8] |
SEWALL E A, TAFTI D K, GRAHAM A B, et al. Experimental validation of large eddy simulations of flow and heat transfer in a stationary ribbed duct[J].
International Journal of Heat & Fluid Flow, 2006, 27(2): 243-258.
DOI: 10.1016/j.ijheatfluidflow.2005.08.010 |
| [9] |
VISWANATHAN A K, TAFTI D K. Detached eddy simulation of flow and heat transfer in fully developed rotating internal cooling channel with normal ribs[J].
International Journal of Heat & Fluid Flow, 2006, 27(3): 351-370.
DOI: 10.1016/j.ijheatfluidflow.2005.12.003 |
| [10] |
LIU H, WANG J. Numerical investigation on synthetical perfor-mances of fluid flow and heat transfer of semi-attached rib-channels[J].
International Journal of Heat & Mass Transfer, 2011, 54(4): 575-583.
DOI: 10.1016/j.ijheatmasstransfer.2010.09.013 |
| [11] |
LOHÁSZ M, RAMBAUD P, BENOCCI C. Flow features in a fully developed ribbed duct flow as a result of LES[J].
Flow Turbulence & Combustion, 2006, 77(1): 59-76.
DOI: 10.1007/s10494-006-9037-3 |
| [12] |
LOHÁSZ M. Large eddy simulation of heat transfer in ribbed ducts[D]. Budapest: Budapest University of Technology and Economics, Faculty of Mechanical Engineering, 2008:12-39.
|
| [13] |
ÇAKAN M. Aero-thermal investigation of fixed Rib-roughened internal cooling passages[D]. Brussels: Von Karman Institute & Université Catholique de Louvain, 2000:35-60.
|
| [14] |
CASARSA L, CÇAKAN M, ARTS T. Characterization of the velocity and heat transfer fields in an internal cooling channel with high blockage ratio[C]//ASME Turbo Expo 2002: Power for Land, Sea, and Air. Amsterdam: American Society of Mechanical Engineers, 2002: 451-458. DOI: 10.1115/GT2002-30207.
|
| [15] |
FRANSEN R, GOURDAIN N, GICQUEL Y M, et al. Steady and unsteady modeling for heat transfer predictions of high pressure turbine blade internal cooling[C]//Proceedings of ASME Turbo Expo 2012. Copenhagen: The International Gas Turbine Institute, 2012 :563-572. DOI: 10.1115/GT2012-69482.
|
 2018, Vol. 50
2018, Vol. 50


