榴弹机枪在现代战争中发展前景广阔,高初速、高精度、威力大、质量轻是未来榴弹机枪的发展趋势[1-2].本文研究的榴弹机枪采用双药室喷管气流反推低后坐发射技术,具有弹丸初速高、威力大、后坐力小的特点.文献[3-4]对采用软后坐技术的大口径枪械进行研究,较常规发射技术,软后坐技术大幅降低了武器的后坐力,但为了得到高效减后坐效率带来首发预压困难、增加武器质量的问题.文献[5-6]提出直接在膛内开孔利用火药燃气减后坐技术降低武器后坐力,但文献[5-6]提出的单药室喷管减后坐技术存在下述问题:获得高效的减后坐效率,喷管导气孔开孔位置必须靠近膛底,这样导致弹丸初速衰减严重;若取喷管导气孔开孔位置靠近膛口,虽然弹丸初速小幅下降,但喷管武器减后坐效果不佳.文献[7-8]建立膨胀波枪炮发射过程的动力学模型,膨胀波减后坐技术有较高的减后坐效率、对弹丸初速影响较小,但结构复杂且膛尾打开时间对弹丸初速较敏感.文献[9]利用制退器降低大口径机枪后坐力,但获得高膛口制退效率必须具有较大装药量,本文研究的榴弹机枪装药量少,无法获得高效的制退效率.
为了克服上述研究不足,提出双药室喷管减后坐技术并应用于高初速榴弹发射器.为了进一步了解火药气流特征量在膛内和喷管内分布状况,建立双药室喷管数学模型.通过调整双药室结构参数,研究其对武器发射性能的影响规律,合理利用火药气体冲量,保证膛口初速几乎不变的前提下使武器获得高减后坐效率,降低武器后坐力.
1 双药室喷管减后坐计算模型 1.1 发射原理基于双药室喷管减后坐技术的高初速榴弹机枪发射原理如图 1所示.喷管为一个可伸缩管,作战时将喷管拉伸至射手身后,携行时将喷管缩回.

|
图 1 双药室喷管减后坐榴弹机枪发射原理 Figure 1 Lauching principle chart of laval nozzles with double chambers for GMGS |
减后坐原理:后药室发射药被点燃,当后药室气体压力达到破膜压力时,一方面火药燃气通过传火孔进入前药室,点燃前药室发射药,另一方面火药燃气通过喷管导气孔进入喷管,经收敛-扩张管道加速后高速冲出喷管尾部,产生喷管反推力.
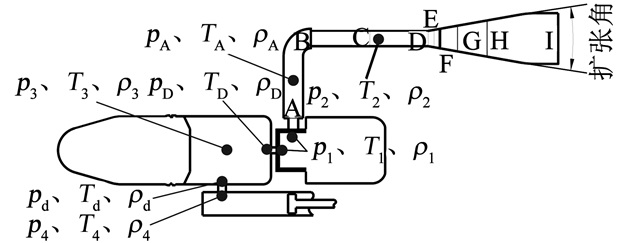
1.2 气体数学模型及基本假设图 2为双药室喷管气流数学计算模型,图中:p1、T1、ρ1分别为后药室气体平均压力、平均温度、平均密度;p2、T2、ρ2分别为收敛管道内气体压力、温度、密度;p3、T3、ρ3分别为膛内气体平均压力、平均温度、平均密度;p4、T4、ρ4分别为导气室内气体平均压力、平均温度、平均密度;pd、Td、ρd分别为膛内导气孔处气体压力、温度、密度;pD、TD、ρD分别为前药室底传火孔处气体压力、温度、密度;pA、TA、ρA分别为喷管气室内气体平均压力、平均温度、平均密度.为了研究喷管内气体特征参数在不同位置处变化规律,截取B~I这8个位置.气体数学模型包括后药室燃烧模型、前药室燃烧的内弹道模型、后药室喷管气流计算模型、导气室计算模型、气室之间流量方程.
|
图 2 双药室喷管气流计算模型 Figure 2 Numerical simulation model of recoilless structures bylaval nozzles with double chambers |
基本假设:
1) 火药燃烧规律按照皮奥伯特定律[10],将实际燃烧过程进行简化,发射过程火药已燃尽,没有固相流动;
2) 内弹道采用修正经典内弹道模型求解,通过次要功系数简化弹丸旋转运动功、弹丸沿膛线运动摩擦功、火药气体运动功等复杂计算;
3) 研究后效期时膛内气流以准定常流处理,膛内任意点气流密度随时间的变化率与该点的密度成正比,膛内气流平均参数按膛轴中点选定;
4) 对于导气装置中气流参数沿空间变化不大的情况,假定气流参数只随时间变化,将导气室内气流参数在空间取平均值[11];
5) 由于喷管装置中具有较长的导气管,管内气体在管壁的摩擦、散热影响下,在管内各种复杂波系的作用下,气流参数沿管轴产生较大差别,喷管装置计算采用准一维非定常数学模型[12].
1.2.1 后药室燃烧模型后药室燃烧模型为
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{Z_1}}}{{{\rm{d}}t}} = \frac{{p_1^n}}{{{I_0}}};\\ \frac{{{\rm{d}}\psi }}{{{\rm{d}}t}} = \left\{ \begin{array}{l} \chi \left( {1 + 2\lambda {Z_1} + 3\mu Z_1^2} \right)\frac{{{\rm{d}}{Z_1}}}{{{\rm{d}}t}},0 \le {\psi _1} \le 1;\\ 0,{\psi _1} > 1; \end{array} \right.\\ \frac{{{\rm{d}}{p_1}}}{{{\rm{d}}t}} = \frac{1}{{{V_1}}}\left( {f{\omega _1}\frac{{{\rm{d}}\psi }}{{{\rm{d}}t}} - {e_{12}}{q_{12}} - {e_{13}}{q_{13}} - \theta \frac{{\delta {Q_1}}}{{{\rm{d}}t}}} \right);\\ {e_{12}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {c_p}{T_1},\\ {c_p}{T_{\rm{A}}}, \end{array}&\begin{array}{l} {p_1} \ge {p_{\rm{A}}};\\ {p_{\rm{A}}} \ge {p_{\rm{1}}}; \end{array} \end{array}} \right.\\ {e_{13}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {c_p}{T_1},\\ {c_p}{T_{\rm{D}}}, \end{array}&\begin{array}{l} {p_1} \ge {p_{\rm{D}}};\\ {p_{\rm{D}}} \ge {p_{\rm{1}}}; \end{array} \end{array}} \right.\\ \frac{{\delta {Q_1}}}{{{\rm{d}}t}} = \varepsilon {\rho _1}\left( {{T_1} - {T_{c0}}} \right){S_1};\\ {\rho _1} = \left\{ \begin{array}{l} \frac{{{\omega _1}{\psi _1} - \int_0^t {{q_{12}}{\rm{d}}t} - \int_0^t {{q_{13}}{\rm{d}}t} }}{{{V_1} - \frac{{{\omega _1}}}{\delta }\left( {1 - {\psi _1}} \right) - \alpha {\omega _1}{\psi _1}}},\;\;\;\;\;\;0 \le {\psi _1} \le 1;\\ \frac{{{\omega _1} - \int_0^t {{q_{12}}{\rm{d}}t} - \int_0^t {{q_{13}}{\rm{d}}t} }}{{{V_1} - \frac{{{\omega _1}}}{\delta }\left( {1 - {\psi _1}} \right) - \alpha {\omega _1}{\psi _1}}},\;\;\;\;\;\;{\psi _1} > 1. \end{array} \right. \end{array} \right. $ |
式中:Z1、ψ1、ω1分别为后药室火药相对厚度、后药室火药燃烧去的百分比、后药室装药量;χ、λ、μ分别为火药药形系数;φ、I0、n分别为计算次要功系数、压力全冲量、多变指数;θ=γ-1、γ分别为绝热指数;f、δ、α、cp分别为火药力、火药密度、气体余容、火药气体比定压热容;V1、S1分别为后药室初始容积与初始表面积;ε=41.9(J·m)/(kg·s·(°));Tc0为后药室壁面温度;e12、q12、e13、q13、δQ1分别为后药室向喷管流入气体比能量、后药室流入喷管流量、后药室向前药室流入的气体比能量、后药室流入前药室流量、后药室对外界散热.
1.2.2 前药室燃烧的内弹道模型前药室燃烧的内弹道模型为
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{Z_3}}}{{{\rm{d}}t}} = \frac{{p_3^n}}{{{I_0}}};\\ \frac{{{\rm{d}}{\psi _3}}}{{{\rm{d}}t}} = \left\{ \begin{array}{l} \chi \left( {1 + 2\lambda {Z_3} + 3\mu Z_3^2} \right)\frac{{{\rm{d}}{Z_3}}}{{{\rm{d}}t}},0 \le {\psi _3} \le 1;\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\psi _3} > 1; \end{array} \right.\\ \frac{{{\rm{d}}l}}{{{\rm{d}}t}} = v;\\ \frac{{{\rm{d}}v}}{{{\rm{d}}t}} = \frac{{{A_3}{p_3}}}{{\varphi m}};\\ \frac{{{\rm{d}}{p_3}}}{{{\rm{d}}t}} = \left\{ \begin{array}{l} \frac{1}{{{A_3}\left( {l + {l_{{\psi _3}}}} \right)}}\left( {f{\omega _3}\frac{{{\rm{d}}{\psi _3}}}{{{\rm{d}}t}} + {e_{13}}{q_{13}} + \cdots } \right.\\ \left. { - {e_{34}}{q_{34}} - v\theta \varphi m\frac{{{\rm{d}}v}}{{{\rm{d}}t}} - \theta \frac{{\delta {Q_3}}}{{{\rm{d}}t}}} \right),0 \le l \le {L_0};\\ - \frac{{\gamma {\mu _{\rm{k}}}{{\left( {A - C} \right)}^{\frac{{n + 1}}{{2\left( {n + 1} \right)}}}}{p_3}^{\frac{{3n - 1}}{{2n}}}}}{{{L_0}}}\sqrt {\frac{{\gamma p_{\rm{k}}^{\frac{1}{n}}}}{{{\rho _{\rm{k}}}}}} ,l > {L_0}; \end{array} \right.\\ {p_{\rm{d}}} = {\left[ {A - C{{\left( {\frac{{{L_{\rm{d}}}}}{{{L_0}}}} \right)}^2}} \right]^{\frac{n}{{n - 1}}}}{p_3};\\ {p_{\rm{d}}} = {\left[ {A - C{{\left( {\frac{{{L_{\rm{d}}}}}{{{L_0}}}} \right)}^2}} \right]^{\frac{1}{{n - 1}}}}{p_3};\\ {p_{\rm{D}}} = {A^{\frac{n}{{n - 1}}}}{p_3};\\ {p_{\rm{D}}} = {A^{\frac{1}{{n - 1}}}}{p_3};\\ {l_{{\psi _3}}} = \frac{1}{{{A_3}}}\left[ {{V_3} - \frac{{{\omega _3}}}{\delta }\left( {1 - {\psi _3}} \right) - \alpha {\omega _3}{\psi _3}} \right];\\ \frac{{\delta {Q_3}}}{{{\rm{d}}t}} = \varepsilon {\rho _3}\left( {{T_3} - {T_{{\rm{b0}}}}} \right)\left( {{S_3} + {\rm{ \mathsf{ π} }}{d_0}l} \right);\\ {\rho _3} = \left\{ \begin{array}{l} \frac{{{\omega _3}{\psi _3} + \int_0^t {{q_{13}}{\rm{d}}t} - \int_0^t {{q_{34}}{\rm{d}}t} }}{{{A_3}\left( {l + {l_{{\psi _3}}}} \right)}},0 \le {\psi _3} \le 1;\\ \frac{{{\omega _3} + \int_0^t {{q_{13}}{\rm{d}}t} - \int_0^t {{q_{34}}{\rm{d}}t} }}{{{A_3}\left( {l + {l_{{\psi _3}}}} \right)}},{\psi _3} > 1. \end{array} \right. \end{array} \right. $ |
式中:Z3、ψ3、ω3分别为前药室火药相对厚度、前药室火药燃烧的百分比、前药室装药量;lψ3、V3、A3、S3、L0、Ld分别为前药室自由容积缩径长、前药室初始容积、线膛横截面积、膛内初始表面积、枪管长度、导气孔距膛底距离;l、v、d0、m分别为弹丸的行程、速度、直径及质量;Td、Tb0分别为膛内导气孔处气流温度、枪管壁面温度;pk、ρk分别为膛口气流压力、膛口气流密度;e34、q34、δQ3、μk分别为枪膛向导气室流入的气体比能量、导气孔处流入导气室的流量、枪管内气流对外界散热、膛口气流流量系数;pk、ρk、A、C计算参考文献[13].
1.2.3 后药室喷管气流计算模型后药室喷管气流计算模型为
| $ \left\{ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{W}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} = \mathit{\boldsymbol{B}},\\ \mathit{\boldsymbol{W}} = \left[ \begin{array}{l} {\rho _2}\\ {\rho _2}{v_2}\\ {\rho _2}\left( {\frac{R}{{\gamma - 1}} + \frac{{v_2^2}}{2}} \right) \end{array} \right],\\ \mathit{\boldsymbol{F}} = \left[ \begin{array}{l} {\rho _2}{v_2}\\ {\rho _2}v_2^2 + {p_2}\\ {\rho _2}\left( {\frac{R}{{\gamma - 1}} + \frac{{v_2^2}}{2}} \right){v_2} + {p_2}{v_2} \end{array} \right],\\ \mathit{\boldsymbol{B}} = \left[ \begin{array}{l} - \frac{{{\rho _2}{v_2}}}{{{A_2}}}\frac{{{\rm{d}}{A_2}}}{{{\rm{d}}x}}\\ - \frac{{{\rho _2}v_2^2}}{{{A_2}}}\frac{{{\rm{d}}{A_2}}}{{{\rm{d}}x}} - {\rho _2}{Z_{\rm{f}}}\\ {\rho _2}\frac{{\delta {Q_2}}}{{{\rm{d}}t}} - \left[ {{\rho _2}\left( {\frac{R}{{\gamma - 1}} + \frac{{v_2^2}}{2}} \right){v_2} + {p_2}{v_2}} \right]\frac{1}{{{A_2}}}\frac{{{\rm{d}}{A_2}}}{{{\rm{d}}x}} \end{array} \right]. \end{array} \right. $ |
式中:v2、A2、Zf分别为喷管内气流速度、管道截面积、表征管壁的摩擦;Dh、λf、Tn0分别为管道内径、气体摩擦系数、喷管管壁温度;δQ2为管壁对管内气体的散热量;Zf、δQ2计算参考文献[14].
1.2.4 导气室计算模型导气室计算模型为
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{\rho _4}}}{{{\rm{d}}t}} = \frac{{{q_{34}} - {q_{40}} - {\rho _4}{A_{\rm{h}}}{v_{\rm{h}}}}}{{{V_4} + {A_{\rm{h}}}{x_{\rm{h}}}}},\\ \frac{{{\rm{d}}{p_4}}}{{{\rm{d}}t}} = \frac{{\gamma - 1}}{{{V_4} + {A_{\rm{h}}}{x_{\rm{h}}}}}\left[ { - \frac{{\delta {Q_4}}}{{{\rm{d}}t}} + {e_{34}}{q_{34}} - {e_{40}}{q_{40}} - \frac{{\gamma {p_4}{A_{\rm{h}}}{v_{\rm{h}}}}}{{\gamma - 1}}} \right],\\ \frac{{\delta {Q_4}}}{{{\rm{d}}t}} = \varepsilon {\rho _4}\left( {{T_4} - {T_{{\rm{q0}}}}} \right)\left( {{S_4} + {\rm{ \mathsf{ π} }}{d_{\rm{h}}}{x_{\rm{h}}}} \right),\\ \frac{{{\rm{d}}{v_h}}}{{{\rm{d}}t}} = \frac{1}{{{m_{\rm{h}}}}}\left( {{p_4} - {p_0}} \right){A_{\rm{h}}} - {K_{\rm{c}}}{x_{\rm{h}}} - {P_{\rm{c}}} - {R_{\rm{c}}},\\ \frac{{{\rm{d}}{x_{\rm{h}}}}}{{{\rm{d}}t}} = {v_{\rm{h}}}. \end{array} \right. $ |
式中:p0为大气压力;Ah、V4、S4、dh分别为活塞横截面积、导气室初始容积、导气室初始表面积、活塞筒名义直径;vh、xh分别为活塞速度、活塞位移;mh、Mc、Kc、Pc、Rc分别为活塞质量、机框组件质量、机框复进簧刚度、机框复进簧预压力、机框与活塞所受摩擦阻力;δQ4、q40、e40分别为导气室气流对外界散热、导气室漏气流量、从导气室间隙漏出的单位质量气体所具有的能量.
1.2.5 气室之间流量方程气室之间流量方程为
| $ {q_{12}} = \left\{ \begin{array}{l} \frac{{{\rm{ \mathsf{ π} }}d_{\rm{p}}^2{\mu _{12}}}}{4}{\left( {\frac{2}{{\gamma + 1}}} \right)^{\frac{{\gamma + 1}}{{2\left( {\gamma - 1} \right)}}}}\sqrt {\gamma {p_1}{\rho _1}} ,{p_{\rm{A}}} \le \zeta {p_1};\\ \frac{{{\rm{ \mathsf{ π} }}d_{\rm{p}}^2{\mu _{12}}}}{4}\sqrt {\frac{{2\gamma }}{{\gamma - 1}}{p_1}{\rho _1}\left[ {{{\left( {\frac{{{p_{\rm{A}}}}}{{{p_{\rm{1}}}}}} \right)}^{\frac{2}{\gamma }}} - {{\left( {\frac{{{p_{\rm{A}}}}}{{{p_{\rm{1}}}}}} \right)}^{\frac{{\gamma + 1}}{\gamma }}}} \right]} ,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\zeta {p_1} < {p_{\rm{A}}} < {p_1};\\ - \frac{{{\rm{ \mathsf{ π} }}d_{\rm{p}}^2{\mu _{12}}}}{4}\sqrt {\frac{{2\gamma }}{{\gamma - 1}}{p_{\rm{A}}}{\rho _{\rm{A}}}\left[ {{{\left( {\frac{{{p_{\rm{1}}}}}{{{p_{\rm{A}}}}}} \right)}^{\frac{2}{\gamma }}} - {{\left( {\frac{{{p_{\rm{1}}}}}{{{p_{\rm{A}}}}}} \right)}^{\frac{{\gamma + 1}}{\gamma }}}} \right]} ,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\zeta {p_{\rm{A}}} < {p_{\rm{1}}} < {p_{\rm{A}}};\\ - \frac{{{\rm{ \mathsf{ π} }}d_{\rm{p}}^2{\mu _{12}}}}{4}{\left( {\frac{2}{{\gamma + 1}}} \right)^{\frac{{\gamma + 1}}{{2\left( {\gamma - 1} \right)}}}}\sqrt {\gamma {p_{\rm{A}}}{\rho _{\rm{A}}}} ,{p_{\rm{1}}} \le \zeta {p_{\rm{A}}}. \end{array} \right. $ |
| $ {q_{13}} = \left\{ \begin{array}{l} \frac{{{\rm{ \mathsf{ π} }}d_{{\rm{13}}}^2{\mu _{13}}}}{4}{\left( {\frac{2}{{\gamma + 1}}} \right)^{\frac{{\gamma + 1}}{{2\left( {\gamma - 1} \right)}}}}\sqrt {\gamma {p_1}{\rho _1}} ,{p_{\rm{D}}} \le \zeta {p_1};\\ \frac{{{\rm{ \mathsf{ π} }}d_{{\rm{13}}}^2{\mu _{13}}}}{4}\sqrt {\frac{{2\gamma }}{{\gamma - 1}}{p_1}{\rho _1}\left[ {{{\left( {\frac{{{p_{\rm{D}}}}}{{{p_{\rm{1}}}}}} \right)}^{\frac{2}{\gamma }}} - {{\left( {\frac{{{p_{\rm{D}}}}}{{{p_{\rm{1}}}}}} \right)}^{\frac{{\gamma + 1}}{\gamma }}}} \right]} ,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\zeta {p_1} < {p_{\rm{D}}} < {p_1};\\ - \frac{{{\rm{ \mathsf{ π} }}d_{{\rm{13}}}^2{\mu _{13}}}}{4}\sqrt {\frac{{2\gamma }}{{\gamma - 1}}{p_{\rm{D}}}{\rho _{\rm{D}}}\left[ {{{\left( {\frac{{{p_{\rm{1}}}}}{{{p_{\rm{D}}}}}} \right)}^{\frac{2}{\gamma }}} - {{\left( {\frac{{{p_{\rm{1}}}}}{{{p_{\rm{D}}}}}} \right)}^{\frac{{\gamma + 1}}{\gamma }}}} \right]} ,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\zeta {p_{\rm{D}}} < {p_{\rm{1}}} < {p_{\rm{D}}};\\ - \frac{{{\rm{ \mathsf{ π} }}d_{{\rm{13}}}^2{\mu _{13}}}}{4}{\left( {\frac{2}{{\gamma + 1}}} \right)^{\frac{{\gamma + 1}}{{2\left( {\gamma - 1} \right)}}}}\sqrt {\gamma {p_{\rm{D}}}{\rho _{\rm{D}}}} ,{p_{\rm{1}}} \le \zeta {p_{\rm{D}}}. \end{array} \right. $ |
式中:ζ为临界压力比;μ12、μ13、μ34、μ40分别为喷管导气孔处流量系数、传火孔处流量系数、导气孔处流量系数、活塞处漏气系数;dp、d13、d分别为喷管导气孔直径、传火孔直径、导气孔直径;q34、q40计算参考文献[15].
1.3 减后坐效率及喷管反推力计算计算武器减后坐效率是评测武器减后坐装置好坏的依据,喷管反推力则反映喷管气流对武器作用效果,是武器系统动力学仿真的基础载荷之一.
通过对比有、无双药室喷管装置的武器后坐动量,可将双药室武器的喷管减后坐效率定义为
| $ \left\{ \begin{array}{l} {\eta _{{\rm{pg}}}} = \frac{{{I_0}\left( p \right) - \left[ {{I_{{\rm{pg}}}}\left( {{p_3}} \right) - {I_{{\rm{pg}}}}\left( {{F_{{\rm{pg}}}}} \right)} \right]}}{{{I_0}\left( p \right)}},\\ {I_0}\left( p \right) = \int_0^{{t_n}} {p\left( {{t_i}} \right){A_3}{\rm{d}}t} ,\\ {I_{{\rm{pg}}}}\left( {{p_3}} \right) = \int_0^{{t_n}} {{p_3}\left( {{t_i}} \right){A_3}{\rm{d}}t} ,\\ {I_{{\rm{pg}}}}\left( {{F_{{\rm{pg}}}}} \right) = \int_0^{{t_n}} {{F_{{\rm{pg}}}}\left( {{t_i}} \right){\rm{d}}t} . \end{array} \right. $ |
式中:I0(p)为无双药室喷管武器膛内平均压力气体冲量;Ipg(p3)为双药室喷管武器膛内平均压力气体冲量;Ipg(Fpg)为双药室喷管武器喷管反推力冲量.
喷管气流反推力随时间变化曲线通过气体数学模型及基本假设编程计算,程序中计算按下式计算:
| $ \begin{array}{l} {F_{{\rm{pg}}}}\left( {{t_{i + 1}}} \right) = {F_{{\rm{pg}}}}\left( {{t_i}} \right) + {p_2}\left( {{t_i},{L_j}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {{A_2}\left( j \right) - {A_2}\left( {j - 1} \right)} \right]. \end{array} $ |
式中:Fpg(ti)为ti时刻喷管气流反推力;p2(ti, Lj)为ti时刻喷管截面位于Lj位置处喷管气流压力;A2(j)为喷管截面位于Lj位置处喷管截面积.
2 模型验证及仿真结果分析 2.1 模型验证表 1为双药室喷管武器预置参数.对气体数学模型及基本假设方程组通过Matlab进行编程计算,得到单发武器系统射击的后药室平均压力曲线、喷管气室压力曲线、膛内平均压力曲线、导气室压力曲线,如图 3所示.
| 表 1 双药室喷管装置预置参数 Table 1 Preset parameters of with laval nozzles double chamber |

|
图 3 双药室喷管气体压力曲线 Figure 3 Curves of gas chamber pressure for laval nozzles with double chambers |
由图 3可知:当t=(0~0.51) ms时后药室火药处于定容燃烧阶段,可看成密闭爆发器模型;当t1=0.51 ms时后药室气体压力达到破膜压力10 MPa,后药室气体分别进入喷管气室、前药室;当t2=1.02 ms时前药室气体压力达到弹丸启动压力30 MPa,弹丸开始挤进膛线,此刻后药室气体压力达到50.8 MPa,而喷管气室压力达到19.9 MPa,武器总体受力方向向后;当t3=1.37 ms时前药室气体压力达到最大膛压79.9 MPa;当t4=1.64 ms时后药室气体达到最大压力138.3 MPa;当t5=1.73 ms时喷管气室达到最大压力71.1 MPa;t6=1.89 ms时弹丸经过导气孔,膛内部分火药气体经导气孔进入导气室;当t7=2.40 ms时导气室内压力达到最大值17.3 MPa;当t8=3.39 ms时内弹道时期结束开始进入后效期,膛内平均压力曲线开始出现拐点,此时弹丸膛口速度为313.6 m/s;当t9=8.50 ms时后药室气体压力降至0.5 MPa.
试验方法:将双药室喷管低后坐武器通过夹具安装于试验滑移架上,滑移架可在试验固定架座沿枪管轴线方向自由移动.试验过程时,枪身后坐带动滑移架尾端挤压电传感器.力传感信号通过DWE-43微型多功能数据采集器采集,由奥地利公司分析软件DEWESoft-DSA得出后坐力测试数据.通过天幕靶测得弹丸初速,膛压传感器测量后药室平均压力、喷管气室压力、前药室平均压力和导气室压力.图 4为天幕靶和高速摄影捕捉榴弹击发瞬间试验图.图 5为试验测得的武器后坐力Fhz曲线.

|
图 4 天幕靶及高速摄影采集武器击发瞬间试验图 Figure 4 Speed-measuring sky screen target and capture screen of firing by high-speed photography |

|
图 5 后坐力曲线 Figure 5 Curves of recoil |
从表 2可以看出压力参数、弹丸初速和后坐力的仿真值与试验值相对误差在10%范围内,表明建立的双药室后喷装置数学模型是可信的,计算的后药室平均压力、喷管气室压力、前药室平均压力及弹丸初速是正确合理的.由图 5可知:B1处波峰为武器射击过程中最大后坐力(1 192.0 N),主要由于弹丸击发后枪身后坐造成的;B2处波峰(533.2 N)主要由于机框后坐到位撞击机匣造成;A1处小波峰测试过程中干扰信号造成;A2、A3处波峰为武器射击过程中滑移架座自身振荡撞击压力传感器所致.
| 表 2 压力参数、弹丸初速和后坐力 Table 2 The pressure parameters, muzzle velocity and recoil |
为了解采取双药室后喷减后坐装置武器与普通武器的发射性能的区别,分别对两种武器的内弹道及后效期进行数值计算,得到膛压曲线、导气室压力曲线和弹丸速度曲线,如图 6、7所示.前药室火药在后药室压力达到破膜压力(t1=0.51 ms)时才开始燃烧,为了更直观区别两种武器压力曲线、速度曲线差别,将普通武器的膛压曲线、导气室压力曲线、速度曲线分别延时Δt=0.51 ms得到对应的压力曲线.

|
图 6 膛压曲线和导气室压力曲线 Figure 6 Bore pressure and gas chamber pressure |

|
图 7 弹丸速度时间曲线 Figure 7 Curves of velocity |
由图 6可知, 延迟普通武器的最大膛压值为76.6 MPa,略小于双药室武器的最大膛压值79.9 MPa,主要由于双药室武器后药室气体压力大于前药室压力,部分后药室火药燃气进入前药室;双药室武器膛压曲线达到最大膛压后衰减更平缓,结合图 3,主要由于在弹丸膛内运动期间后药室压力始终大于前药室压力,气流一直保持向前药室流入状态.双药室武器导气室压力曲线起始时刻早于普通武器的导气室压力曲线起始时刻,由于双药室武器膛内压力对弹丸做功多,弹丸速度大,故到达导气孔时间短.由图 7可知, 双药室武器弹丸膛口速度值为313.6 m/s,略大于普通武器弹丸膛口速度值309 m/s.将图 6中膛压曲线对时间积分,再与枪膛截面积相乘,得I0(p)=67.59 N·s,Ipg(p3)=68.43 N·s;将后药室装药量w1=16 g对应的喷管反推力对时间积分,得Ipg(Fpg)=23.85 N·s.将上述结果代入喷管减后坐效率公式得ηpg=34%.可见采用双药室喷管减后坐技术的武器,对武器弹丸初速影响不大,制退效率高.
2.3 发射过程数值仿真结果及分析 2.3.1 双药室后喷装置气流参数随时间变化曲线图 8为双药室导气管内流场状态参量在不同位置处随时间变化的曲线.整体来说,喷管气流温度、喷管气流速度受压强间断面影响较大,相应的变化曲线出现激增现象,而喷管气流压力曲线、喷管气流密度曲线随时间变化过度较平滑.

|
图 8 喷管气流参数随时间变化曲线 Figure 8 Distribution of gas parameter with time |
由图 8(a)可知,喷管截面距离喷管起始点B越近,喷管截面处达到气流压力峰值越大,气流压力峰值出现在t=(1.73~2.13) ms附近,而后迅速衰减;喷管截面位于最小截面D左侧(靠近喷管起始点)时,喷管截面距离喷管起始点越近,气流压力峰值出现时刻越早,压力波向喷管右侧传播;喷管截面位于最小截面D右侧(靠近喷管出口)时,距离喷管起始点越近,气流压力峰值越滞后,压力波向喷管左侧传播;喷管起始点在整个发射过程中气流压力变化剧烈,而喷管出口处I在整个发射过程中气流压力变化平缓.
由图 8(b)可知,喷管截面位于喷管起始点B时,气流温度变化曲线较平滑,主要在建模时将喷管入口处作为一个有初始容积的气室考虑,将B处气流参数作为喷管计算的初始边界条件,并没有考虑压强间断面的影响;喷管截面位于喷管起始点B与喷管最小截面D之间,越靠近喷管D处喷管气流温度峰值越高;喷管截面位于截面D与喷口I之间,越靠近喷管出口I处喷管气流温度峰值越低.
由图 8(c)可以看出喷管气流密度曲线变化趋势与喷管气流压力曲线变化趋势相同,喷管截面位置越靠近喷管喷口,管内气流密度越小.
由图 8(d)可知,喷管截面越靠近喷管喷口,管内气流速度峰值越大,且峰值出现的时间逐渐滞后,表明管内气流速度一直处于加速状态;在整个射击过程中,管内气流速度激增至最大值而后缓慢衰减.
2.3.2 双药室后喷装置气流参数随位置分布曲线图 9为双药室后喷导气管内流场状态参量在喷管内分布曲线.

|
图 9 喷管气流参数随喷管位置分布曲线 Figure 9 Distribution of gas parameter with position |
由图 9(a)可知,当t=(0.51~1.02) ms时,火药燃气进入喷管,喷管左侧压力高于右侧压力,压力波在喷管内逐渐向喷管口部传播,且随着时间增大,喷管内气体压力逐渐增大,但压力波未完全传至喷管口部;当t=(1.02~1.73) ms时,由于喷管气室气体压力逐渐增大直至达到压力峰值,喷管内呈现喷管两侧压力差增大趋势,当压力波传至喷管喉径D处后,喷管截面开始扩张,管内气流压力迅速衰减;当t=(1.73~3.39) ms时,随着时间增加,由于喷管气室压力降低,喷管两侧压力差逐渐缩小,当弹丸出膛口(t=3.39 ms)时喷管两侧压力差几乎为0;当t=(3.39~8.50) ms时,随着时间增加,喷管内气流压力总体下降.
由图 9(b)可知,当t=(0.51~1.02) ms时,火药燃气刚进入喷管气室,喷管内温度保持常温不变,当喷管气室气体进入喷管,靠近喷管起始位置喷管气流温度迅速升至温度峰值,且随着时间推移喷管内的气流温度逐渐升高;当t=(1.02~1.73) ms时,喷管气流温度在喷管内分布几乎保持不变,靠近喷管左侧的气流温度略高于右侧气流温度,喷管气流经过喷管最小截面D处后气流温度迅速下降,气流经扩张管后气流温度以一恒温向后坐方向喷出;当t=(1.73~8.50) ms时,气流温度在喷管内左侧温度高于右侧温度,且随时间增大喷管内气流温度逐渐降低,喷管两侧温度差变小.
由图 9(c)可以看出,当t=(0.51~1.02) ms时,当火药气体流入喷管,在管内气流密度左侧大于右侧,但压力波未传至处密度保持不变;当t=(1.02~ 1.73) ms时,喷管截面距喷管起始点越近,喷管截面处气流密度越大,当喷管气流经过截面D后密度迅速变小,且随时间增大进入喷管内火药燃气增多,喷管内气流密度增大;当t=(1.73~1.89) ms时,喷管内气流密度在喷管起始点处密度相同,喷管最小截面处气流密度随时间增大而增大;当t=(1.89~ 3.39) ms时,喷管最小截面处气流密度在上述时间段保持不变,喷管在起始点处喷管气流密度随时间增大而减小;当t=(3.39~8.50) ms时,喷管气流密度在最小截面左侧时几乎保持相同,喷管气流密度在最小截面右侧随喷管扩张急剧降低.
由图 9(d)可知,当t=(0.51~1.02) ms时,喷管气流还未冲出导气管,但气流速度随压力波到达喷管位置增大而增大;当t=(1.02~1.73) ms时,喷管气流在最小截面D处左侧时,管内气流速度缓慢增大,但经过D处进入扩张管后,管内气流速度骤增经扩张管加速后以恒速向后喷出;当t=(1.73~ 8.50) ms时,喷管内气流速度任一截面随时间增加而降低,喷管在此时间段内气流加速度减小.
3 双药室喷管参数对发射性能影响喷管减后坐武器利用向后坐方向喷出火药气体动量降低后坐力,提高火药气体流量及增大火药气体速度可以增大喷管气流反推力(Fpg)、提高武器减后坐效率(ηpg).本文将从后药室装药量(ω1)、喷管导气孔直径(dp)、喷管内径(Dh)3个方面研究对武器发射性能的影响.
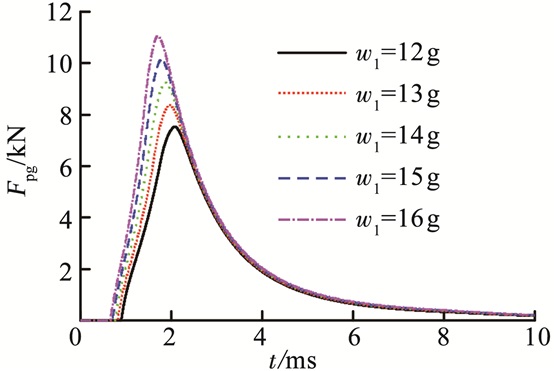
3.1 后药室装药量对发射性能影响分析由图 10可知,随着ω1增大,后药室火药燃气达到破膜压力时间缩短,越早进入喷管及前药室,Fpg作用时间越早;Fpg峰值随着ω1增大而增大,对武器反后坐冲量越大.由表 3可知:增大ω1,故后药室气体压力增大,流入喷管及前药室气体流量增大,Fpg冲量增大,前药室气体压力冲量增大,弹丸出膛口速度增大;ω1=16 g的Fpg峰值是ω1=12 g的1.48倍;ω1由12 g增加至16 g,ηpg提升了32.1%,而v0提升0.8%,可见增加ω1对于前药室内弹道的改变可以忽略不计,但是大大提升了武器的ηpg.
|
图 10 后药室装药量对喷管反推力影响 Figure 10 Impact of back charge mass on thrust of nozzle |
| 表 3 后药室装药量对武器性能参数影响 Table 3 Impact of back charge mass on performance parameters |
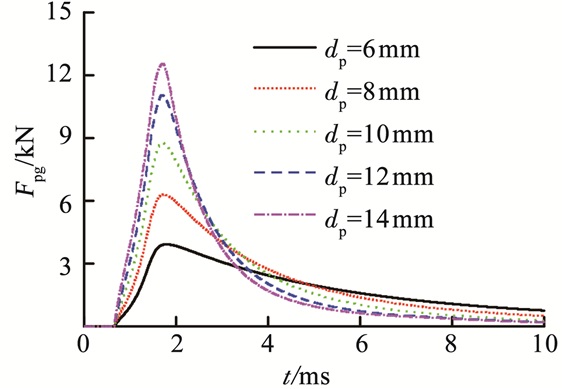
由图 11可知,随着dp由6 mm增大至14 mm,Fpg峰值逐渐增大,结合表 5,Fpg峰值在dp=12 mm时是dp为6 mm时的3.16倍,增加幅度较大.由表 4可知,随着dp增大,后药室火药流入喷管流量增大,Fpg冲量增大;当Fpg达到峰值后开始衰减时,dp越小,后药室火药气体进入喷管流量变小,后药室压力越大,进入前药室气体流量增多,所以前药室气体冲量越大,v0越高;dp由6 mm增加2.3倍至14 mm,武器ηpg提升了42.9%,v0下降了4.2%.
|
图 11 喷管导气孔直径对喷管反推力影响 Figure 11 Impact of gas port diameter on thrust of nozzle |
| 表 4 喷管导气孔直径对武器性能参数影响 Table 4 Impact of gas port diameter on performance parameters |
| 表 5 喷管内径对武器性能参数影响 Table 5 Impact of inside diameter on performance parameters |
由图 12可知,Dh越大,导气管内聚集的火药燃气的能力越大,单位时间内经喷管加速的火药燃气越多,Fpg越大,反后坐冲量越大,且Fpg峰值在Dh=(6~12) mm范围内较敏感.由表 5可知,当Dh由6 mm增加至14 mm,Fpg冲量增加了46%,前药室膛内气体压力冲量减小了2%,v0降低了2.3%,武器ηpg提升了32.1%.

|
图 12 喷管内径对喷管反推力影响 Figure 12 Impact of inside diameter on thrust of nozzle |
1) 利用火药气体能量提出一种新型双药室减后坐装置,对设计的双药室减后坐方案进行实弹射击试验,v0达到316.7 m/s时武器Max(Fpg)仅为1 192 N.
2) 将计算得到双药室喷管低后坐武器的Max(p1)、Max(pA)、Max(p3)、v0、Max(Fpg)与对应的试验结果进行对比,仿真值相对试验值误差在8.6%范围内,表明建立的计算模型是正确合理的.本文采用的双药室减后坐装置传火特性:在0.51 ms前,后药室处于定容燃烧;在0.51 ms时刻,p1达到铝膜破膜压力10 MPa,后药室火药经过传火孔同时进入前药室和喷管气室;在1.02 ms时刻,p3达到弹丸启动压力30 MPa,此时武器总体受力方向向后;在1.64 ms时在后药室位置处武器承受火药最大压力,压力峰值为138.3 MPa;火药燃烧直至后效期结束持续时间为8.5 ms左右.
3) 分析喷管气流参数随时间变化规律:温度、速度受压强间断面影响较大,相应的变化曲线出现激增现象,而压力、密度随时间变化过度较平滑;温度与速度曲线变化趋势相同,而压力与密度曲线变化趋势相同.分析喷管气流参数在喷管内分布状况:当压力波未传至喉径时,气流参数(压力、温度、密度)在喷管左侧时大于右侧,而气流速度在喷管右侧小于左侧;当压力波传至喉径时,喷管气流参数(压力、温度、密度)急剧衰减,而气流被加速从喷管口部高速喷出.
4) 增加ω1、扩大dp和Dh可以增大Fpg、提升ηpg.ω1在(12~16) g范围内增加时,ηpg增幅显著;dp和Dh在(6~14) mm范围内增大时,对提升ηpg越来越不显著.
| [1] |
王晨阳. 春风不度玉门关? -OICW的现状与未来[J]. 军事文摘, 2016(19): 40. WANG Chenyang. The spring breeze is not the yumen pass?-The current situation and future of OICW[J]. Military Digest, 2016(19): 40. |
| [2] |
宋杰.榴弹机枪系统低后坐发射技术研究[D].南京: 南京理工大学, 2017 SONG Jie. Studyon low recoil lauching technology of grenade machine gun system[D]. Nanjing: Nanjing University of Science & Technology, 2017 |
| [3] |
KANG K J, GIMM H I. Numerical and experimental studies on the dynamic behaviors of a gun that uses the soft recoil system[J]. Journal of Mechanical Science and Technology, 2012, 26(7): 2167. DOI:10.1007/s12206-012-0538-9 |
| [4] |
宋杰, 廖振强, 李佳圣, 等. 导气与枪管浮动混合式自动机动力学特性研究[J]. 兵工学报, 2014, 35(6): 753. SONG Jie, LIAO Zhenqiang, LI Jiasheng, et al. Dynamics characteristics of automatic mechanism for gas operated and floating barrel operated automatic action[J]. Acta Armamentaria, 2014, 35(6): 753. DOI:10.3969/j.issn.1000-1093.2014.06.001 |
| [5] |
金永灿.机枪减后坐研究与动力学仿真分析[D].南京: 南京理工大学, 2016 JIN Yongcan. Research on reduce recoil and simulation of dynamics characteristic of machine gun system[D]. Nanjing: Nanjing University of Science & Technology, 2016 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y3046106 |
| [6] |
咸东鹏, 廖振强, 李洪强, 等. 双孔式拉瓦尔喷管减后坐结构效能分析[J]. 弹道学报, 2013, 25(1): 99. XIAN Dongpeng, LIAO Zhenqiang, LI Hongqiang, et al. Performance analysis of two-hole recoilless structure with laval nozzles[J]. Journal of Ballistics, 2013, 25(1): 99. DOI:10.3969/j.issn.1004-499X.2013.01.021 |
| [7] |
张帆, 廖振强, 刘国鑫, 等. 膨胀波枪炮发射性能若干影响因素的研究[J]. 兵工学报, 2008, 29(1): 23. ZHANG Fan, LIAO Zhenqiang, LIU Guoxin, et al. Study of influence factors on launching performance of rarefaction wave gun[J]. Acta Armamentarii, 2008, 29(1): 23. DOI:10.3321/j.issn:1000-1093.2008.01.006 |
| [8] |
王颖泽, 张小兵. 膨胀波火炮发射性能计算分析[J]. 高压物理学报, 2009, 23(6): 433. WANG Yingze, ZHANG Xiaobing. Numerical analysis on launch property of rarefaction wave gun[J]. Chinese Journal of High Pressure Physics, 2009, 23(6): 433. DOI:10.3969/j.issn.1000-5773.2009.06.006 |
| [9] |
陆野, 周克栋, 赫雷, 等. 膛口制退器效率对某新型全枪浮动原理大口径机枪的影响研究[J]. 兵工学报, 2016, 37(9): 1585. LU Ye, ZHOU Kedong, HE Lei, et al. Research on influence of muzzle brake efficiency on a new large caliber machine gun based on floating principle[J]. Acta Armamentaria, 2016, 37(9): 1585. DOI:10.3969/j.issn.1000-1093.2016.09.005 |
| [10] |
张小兵. 枪炮内弹道学[M]. 北京: 北京理工大学出版社, 2014. ZHANG Xiaobing. Interior ballistics of guns[M]. Beijing: Beijing Institute of Technology Press, 2014. |
| [11] |
廖振强, 邱明. 自动武器气体动力学[M]. 北京: 国防工业出版社, 2015. LIAO Zhenqiang, QIU Ming. Gas dynamics of automatic weapons[M]. Beijing: National Defense Industry Press, 2015. |
| [12] |
李玉军, 朱春波, 包钢, 等. 气动系统管路流场计算中边界条件的处理分析[J]. 哈尔滨工业大学学报, 2000, 32(4): 96. LI Yujun, ZHU Chunbo, BAO Gang, et al. Analysis of boundary conditions for calculation of flow field in pneumatic system tubes[J]. Journal of Harbin Institute of Technology, 2000, 32(4): 96. DOI:10.3321/j.issn:0367-6234.2000.04.029 |
| [13] |
廖振强, 王涛, 余世海. 武器气体动力学数值计算方法[M]. 北京: 国防工业出版社, 2005. LIAO Zhenqiang, WAN Tao, YU Shihai. Gas dynamics of automatic weapons[M]. Beijing: National Defense Industry Press, 2005. |
| [14] |
肖俊波, 杨国来, 李洪强, 等. 身管武器时延式喷管减后坐动力学建模仿真[J]. 兵工学报, 2017, 38(10): 1909. XIAO Junbo, YANG Guolai, LI Hongqiang, et al. Dynamics modeling and simulation of recoil reduction of automatic weapon by time-delay nozzle device[J]. Acta Armamentaria, 2017, 38(10): 1909. DOI:10.3969/j.issn.1000-1093.2017.10.005 |
| [15] |
华洪良, 廖振强, 宋杰, 等. 喷管气流反推技术在改善机枪射击精度中的应用[J]. 兵工学报, 2015, 36(12): 2241. HUA Hongliang, LIAO Zhenqiang, SONG Jie, et al. The application of reverse jet gas technology in improving firing accuracy of a machine gun system[J]. Acta Armamentaria, 2015, 36(12): 2241. DOI:10.3969/j.issn.1000-1093.2015.12.005 |
 2018, Vol. 50
2018, Vol. 50


