控制系统的可达集有前向可达集和后向可达集之分，其中前向可达集为系统从初始状态出发，到终止时刻的所有状态的集合；后向可达集为能够到达终止时刻目标状态的所有状态的集合^[1].本文仅研究前向可达集，文中所提到的可达集均指前向可达集.确定可达集的边界对于分析系统的动态性能、设计系统控制器具有重要的实际意义.对于非线性控制理论和动态系统中不定参数的定量研究而言，可达集的数值计算是关键的问题之一.可达集的研究可广泛地应用在众多的学科领域.例如，在飞行器控制领域，可以对飞行器轨道的可达集进行分析，实现良好的变轨过程^[2-3]、确定飞行器着陆区域^[4]、为驾驶员完成标准机动动作提供决策支持^[5]；通过对导弹运动轨迹的可达集研究，可以帮助确定制导导弹的目标命中区域^[6]；通过研究机器人运动轨迹的可达集，可以使其选取最短的行动路径并躲避障碍物^[7].

研究表明, 线性控制系统的可达集是凸集^[8]，而非线性系统的可达集则可能是凸的或非凸的两种.目前针对线性系统，已经提出了很多种近似可达集的理论及算法.文献[9-10]通过构造若干接触可达集边界的外部或内部椭球，来得到可达集的近似估计；文献[11-12]通过将可达集等价描述为有限个最优控制问题，通过直接求解这些最优控制问题来得到可达集的近似；文献[13]将可达集描述为一个Hamilton-Jacobi偏微分方程，并利用水平集方法近似可达集.但对于非线性系统，尤其是具有非凸可达集的系统，计算其可达集目前受到了以下几方面的阻碍：可达集几何复杂度会随着时间间隔增加而增加，非凸性所带来的计算问题以及非线性系统造成的计算不稳定性.为了求解非线性控制系统的可达集，文献[14]分析了非线性离散系统的可达集为凸的充分和必要条件；文献[15]在二维可达集内部布置了若干点，并迭代更新，使这些点的分段线性轮廓线所围成的区域最大，从而近似可达集；文献[16]指出连续系统的可达集可用其相应的离散系统的可达集来近似，近似精度取决于离散化方法和离散化步长；针对离散非线性系统，文献[17]提出了DFOG(distance fields on grids)算法，通过在包含可达集的区域内布置均匀分布的网格点，除去以外部网格点为圆心、该点到可达集的最短距离为半径的开球集，剩余集合即为可达集的近似集合.然而上述方法在可达集近似精度和计算效率方面都有待进一步的提高.

本文在已有的研究中，提出了基于凸优化技术的外部投影法来求解线性离散控制系统的可达集，但该方法不适用于具有非凸可达集的非线性控制系统，且没有给出近似结果的误差分析.本文将继续研究求解离散控制系统的可达集的方法，重点针对具有非凸可达集的非线性控制系统.文中首先对非线性系统及其可达集进行描述，然后介绍离散化后的系统及其相应的离散可达集，进一步地提出了近似离散系统可达集的网格投影法，并给出了近似误差的理论分析，最后将该方法与文献[17]中的DFOG方法进行数值仿真对比，给出了仿真和分析结果.

1 控制系统及其可达集

考虑非线性动态系统为

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}}\left( t \right) = f\left( {t,\mathit{\boldsymbol{x}}\left( t \right),\mathit{\boldsymbol{u}}\left( t \right)} \right),\\ \mathit{\boldsymbol{x}}\left( {{t_0}} \right) = {\mathit{\boldsymbol{x}}_0},\\ \mathit{\boldsymbol{u}}\left( t \right) \in \mathit{\boldsymbol{U}}. \end{array} \right. $

(1)

式中：x ∈ Rⁿ为系统的状态向量；x₀∈ Rⁿ为系统的初始状态；U⊂ R^m是一个非空凸紧集；t∈[t₀, t_f]，其中t₀、t_f分别为动态系统的初始时刻和终点时刻，且t₀ < t_f.

定义1    系统(1)从初始条件(t₀, x₀)出发，在t_f时刻的前向可达集可定义如下

$ \Re \left( {{t_{\rm{f}}},{t_0},{\mathit{\boldsymbol{x}}_0}} \right): = \left\{ {\mathit{\boldsymbol{y}} \in {{\bf{R}}^n}:\exists \mathit{\boldsymbol{u}}\left( \cdot \right){\rm{s}}.\;{\rm{t}}.\;\mathit{\boldsymbol{x}}\left( {{t_{\rm{f}}}} \right) \in \mathit{\boldsymbol{y}}} \right\}. $

(2)

对于连续系统，可以用数值方法如欧拉法、龙格-库塔法、线性多步法等^[18]对其离散化得到离散系统.以欧拉法为例, 在[t₀, t_f]时间内，取等间隔时间t_i=t₀+ih，h=(t_f－t₀)/N，i=0, …, N.假定控制函数u(t)在[t_i, t_i+1]间隔内恒定为$\mathit{\boldsymbol{\tilde u}}\left( {{t_i}} \right)$，则采用欧拉法对系统(1)离散化, 可得离散系统为

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{\tilde x}}\left( {{t_{i + 1}}} \right) = \mathit{\boldsymbol{\tilde x}}\left( {{t_i}} \right) + hf\left( {{t_i},\mathit{\boldsymbol{\tilde x}}\left( {{t_i}} \right),\mathit{\boldsymbol{\tilde u}}\left( {{t_i}} \right)} \right),\\ \mathit{\boldsymbol{\tilde u}}\left( {{t_i}} \right) \in \mathit{\boldsymbol{U}},\\ \mathit{\boldsymbol{\tilde x}}\left( {{t_0}} \right) = {\mathit{\boldsymbol{x}}_0}, \end{array} \right. $

(3)

式中i=0, …, N－1.

定义2    对于离散系统(3)，从初始条件(t₀, x₀)出发，在t_N时刻的可达集可定义如下

$ {\tilde \Re } \left( {{t_N},{t_0},{\mathit{\boldsymbol{x}}_0}} \right): = \left\{ {\mathit{\boldsymbol{y}} \in {{\bf{R}}^n}:\exists \mathit{\boldsymbol{\tilde u}}\left( \cdot \right){\rm{s}}.\;{\rm{t}}.\;\mathit{\boldsymbol{\tilde x}}\left( {{t_N}} \right) \in \mathit{\boldsymbol{y}}} \right\}. $

(4)

用离散系统的可达集(4)对连续系统的可达集(2)进行近似，其近似精度可以利用豪斯多夫距离(Hausdorff distance)来衡量.

定义3    设集合C, D ⊂ Rⁿ为两个非空紧集，则C与D之间的豪斯多夫距离为

$ {d_{\rm{H}}}\left( {\mathit{\boldsymbol{C}},\mathit{\boldsymbol{D}}} \right): = \max \left\{ {d\left( {\mathit{\boldsymbol{C}},\mathit{\boldsymbol{D}}} \right),d\left( {\mathit{\boldsymbol{D}},\mathit{\boldsymbol{C}}} \right)} \right\}, $

式中$d(\mathit{\boldsymbol{C}},\mathit{\boldsymbol{D}}) = \mathop {{\rm{max}}}\limits_{\mathit{\boldsymbol{c}} \in \mathit{\boldsymbol{C}}} \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{d}} \in \mathit{\boldsymbol{D}}} {\left\| {\mathit{\boldsymbol{c}} - \mathit{\boldsymbol{d}}} \right\|_2}$.

文献[16]指出，连续系统的可达集$\Re $(t_f, t₀, x₀)可以用其离散系统的可达集${\tilde \Re }$ (t_N, t₀, x₀)来近似，近似精度取决于离散步长h.

定理1    设系统(1)中的f满足利普希茨(Lipschitz)条件，取正整数N为离散步数，h=(t_f－t₀)/N为离散步长.利用欧拉方法对系统(1)进行离散化处理得到系统(3)，则存在一常数M>0使得连续系统可达集$\Re $(t_f, t₀, x₀)与离散系统可达集${\tilde \Re }$(t_N, t₀, x₀)有如下关系：

$ {d_{\rm{H}}}\left( {\Re \left( {{t_{\rm{f}}},{t_0},{\mathit{\boldsymbol{x}}_0}} \right),\tilde \Re \left( {{t_N},{t_0},{\mathit{\boldsymbol{x}}_0}} \right)} \right) \le Mh. $

本文用离散控制系统可达集近似连续控制系统可达集，重点研究离散控制系统可达集的数值求解方法.根据定义2，离散控制系统的可达集问题可以归结为如下求集合Y的问题：

$ \begin{array}{l} {\rm{Find}}\;\mathit{\boldsymbol{Y}}: = \left\{ {\mathit{\boldsymbol{y}} \in {{\bf{R}}^n}:\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\tilde x}}\left( {{t_N}} \right)} \right\},\\ {\rm{s}}.\;{\rm{t}}.\;\;\mathit{\boldsymbol{\tilde x}}\left( {{t_0}} \right) = {\mathit{\boldsymbol{x}}_0},\\ \;\;\;\;\;\;\mathit{\boldsymbol{\tilde x}}\left( {{t_{i + 1}}} \right) = \mathit{\boldsymbol{\tilde x}}\left( {{t_i}} \right) + hf\left( {{t_i},\mathit{\boldsymbol{\tilde x}}\left( {{t_i}} \right),\mathit{\boldsymbol{\tilde u}}\left( {{t_i}} \right)} \right),\\ \;\;\;\;\;\;\mathit{\boldsymbol{\tilde u}}\left( {{t_i}} \right) \in \mathit{\boldsymbol{U}},\\ \;\;\;\;\;\;i = 0, \cdots ,N - 1. \end{array} $

(5)

进一步地，将式(5)中的每个约束都转化为g_i(x)≤0的形式，则上述问题描述为

$ \begin{array}{l} {\rm{Find}}\;\mathit{\boldsymbol{Y}}: = \left\{ {\mathit{\boldsymbol{Px}}:\mathit{\boldsymbol{x}} \in \mathit{\boldsymbol{X}}} \right\},\\ {\rm{s}}.\;{\rm{t}}.\;\;\mathit{\boldsymbol{X}} = \left\{ {\mathit{\boldsymbol{x}} \in {{\bf{R}}^n}:{g_i}\left( \mathit{\boldsymbol{x}} \right) \le 0,i = 1, \cdots ,l} \right\}. \end{array} $

(6)

式中：x=(${\mathit{\boldsymbol{\tilde u}}}$(t₀)^T, …, ${\mathit{\boldsymbol{\tilde u}}}$(t_N-1)^T, ${\mathit{\boldsymbol{\tilde x}}}$(t₀)^T, …, ${\mathit{\boldsymbol{\tilde x}}}$(t_N-1)^T, ${\mathit{\boldsymbol{\tilde x}}}$(t_N)^T)^T为变量；P为一个最后n列为单位阵而其他元素为0的矩阵.

2 网格投影法

网格投影法是一种求解式(6)中Y的方法.该方法从集合某个内部点出发，沿着坐标轴的正负方向，逐渐构造一系列等间距的网格，并将这些网格点沿着各个坐标轴方向向集合边界进行投影以得到边界点.

2.1 网格点生成与投影点计算

设集合Y⊆Rⁿ为一非空紧集, 用intY表示集合Y内部，而bdY表示集合Y边界.取任意一点a∈intY.将点a沿坐标轴i的正、反方向向集合Y的边界进行投影，可以分别通过解决以下最优化问题来求得相应的投影边界点：

$ P_{\max }^{i + }\left( \mathit{\boldsymbol{a}} \right)\max {d_{i + }}\;{\rm{s}}.\;{\rm{t}}.\;\mathit{\boldsymbol{a}} + {d_{i + }}{\mathit{\boldsymbol{e}}_i} = \mathit{\boldsymbol{y}},\mathit{\boldsymbol{y}} \in \mathit{\boldsymbol{Y}}; $

$ P_{\max }^{i - }\left( \mathit{\boldsymbol{a}} \right)\max {d_{i - }}\;{\rm{s}}.\;{\rm{t}}.\;\mathit{\boldsymbol{a}} - {d_{i - }}{\mathit{\boldsymbol{e}}_i} = \mathit{\boldsymbol{y}},\mathit{\boldsymbol{y}} \in \mathit{\boldsymbol{Y}}. $

式中e_i为第i个元素值为1，其余元素均为0的n维向量.设d_i+^*、d*_i－分别为求解P_maxⁱ⁺(a)、P_max^i－(a)得到的最优目标函数值，则从a点出发沿着坐标轴i正、负方向向Y投影得到的边界点分别为：

$ {\mathit{\boldsymbol{p}}_{i + }} = \mathit{\boldsymbol{a}} + d_{i + }^ * {\mathit{\boldsymbol{e}}_i},{\mathit{\boldsymbol{p}}_{i - }} = \mathit{\boldsymbol{a}} - d_{i - }^ * {\mathit{\boldsymbol{e}}_i}. $

以a点为起点，在p_i+、p_i－之间，可沿坐标轴i的正、反方向布置间隔为d_s>0的均匀分布的参考点.进一步将这些参考点沿着其它的坐标轴上投影，生成新的参考点，所有的参考点形成了网格点.

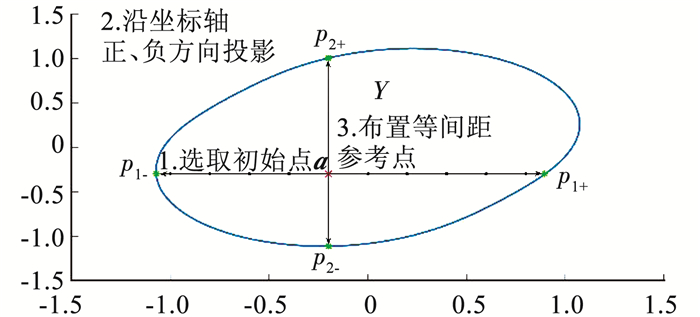
图 1展示了投影及网格点的生成过程.图中二维平面内的闭合实线围成的区域为所求集合Y，内部两条带箭头实线的交点为任意选取的初始点a，箭头分别表示4个投影方向，边界线上有4个投影边界点p_1－、p₁₊、p_2－、p₂₊，线上的每个点表示由a生成的等间隔的网格点.

2.2 算法描述

网格投影法的算法流程如图 2所示.

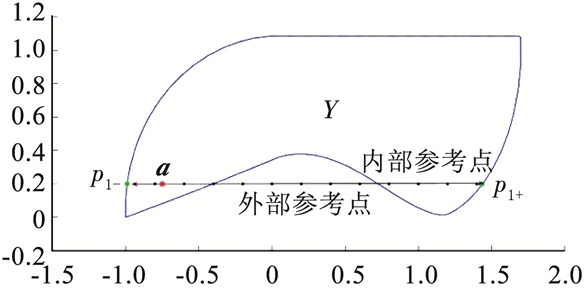
算法1的输出结果B为Y的边界点集，将B中的相邻点依次连接，围成的内部区域记作clB，clB即为Y的近似集.算法1可以有效地解决具有凸可达集的控制系统问题，如线性系统的可达集.但是对于非凸可达集，如图 3所示，二维平面内的实现围成的闭合区域为集合Y，a为初始点，闭合区域的边界上p_1－, p₁₊为投影点，两投影点间的圆点为参考点，出现了参考点位于Y外部的情况.这是由于求解P_maxⁱ⁺(a)、P_max^i－(a)，内部点的投影会跨过可达集非凸部分的边界线，而得到最远投影距离的投影点p₁₊，致使生成的内部网格点实际落在了集合Y的外部，如图中标注的6个外部参考点.若对外部的参考点继续按照算法1的流程生成网格点，将无法求得正确的边界点，且导致算法无法停止.

鉴于实际问题中，大多数可达集Y具有如下特点：对于任意一点y∉Y，将该点沿每个坐标轴的正、负方向Y做投影，至少有一个方向的投影不存在.因此对于这种类型的非凸可达集，可通过在网格投影法中添加额外的判断条件以区分外部投影点.对某个参考点a′沿所有坐标轴求解P_maxⁱ⁺(a′)、P_max^i－(a′)，若出现沿某个方向的解不存在时，则认为a′∉Y.这时，可计算如下的优化问题得到a′沿坐标轴在Y上的投影，进而修正投影边界点.

$ P_{\min }^{i + }\left( {\mathit{\boldsymbol{a'}}} \right)\min {d_{i + }}\;{\rm{s}}.\;{\rm{t}}.\;\mathit{\boldsymbol{a'}} + {d_{i + }}{\mathit{\boldsymbol{e}}_i} = \mathit{\boldsymbol{y}},\mathit{\boldsymbol{y}} \in \mathit{\boldsymbol{Y}}; $

$ P_{\max }^{i - }\left( {\mathit{\boldsymbol{a'}}} \right)\min {d_{i - }}\;{\rm{s}}.\;{\rm{t}}.\;\mathit{\boldsymbol{a'}} - {d_{i - }}{\mathit{\boldsymbol{e}}_i} = \mathit{\boldsymbol{y}},\mathit{\boldsymbol{y}} \in \mathit{\boldsymbol{Y}}. $

具体修正过程如下：当a′沿坐标轴i投影时，若P_maxⁱ⁺(a′)的解存在而P_max^i－(a′)的解不存在，则求解P_minⁱ⁺(a′)得到投影点p′_i+= a′+d_i+^*e_i，并在p_i+、p′_i+之间布置网格点；同理，若P_maxⁱ⁺(a′)的解不存在而P_max^i－(a′)的解存在，则求解P_min^i－(a′)，得到投影点p′_i－= a′－d_i－^*e_i，并在p_i－、p′_i－之间布置网格点；对该点的其他坐标轴方向，需要求解P_minⁱ⁺(a′)、P_min^i－(a′)得到p′_i+、p′_i－来补全边界投影点, 且这两个边界投影点之间的网格点均被判断为外部网格点.修正后的网格投影法算法如图 4所示.

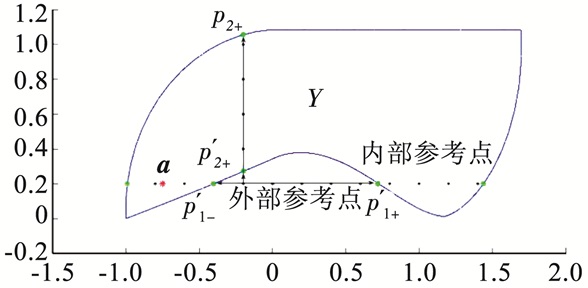
算法2在处理外部参考点时如图 5所示，图 5中二维平面内的实线围成的闭合区域为所求集合Y，a为初始点，图中有6个外部网格点位于集合Y外部，它们沿纵坐标轴负方向的投影点不存在，其中带有箭头实线的交点为计算投影的网格点g，闭合区域的边界上p′₁₊、p′_1－为对g求解P_min¹⁺(g)、P_min^1－(g)得到的投影点，p₂₊、p′₂₊为对g求解P_max²⁺(g)、P_min²⁺(g)得到的投影点，圆点为网格点.

2.3 算法近似误差分析

本文把由算法2得到的边界点集B相邻点依次连接，所围成的区域记作clB.clB与真实集合Y间存在如下关系.

定理2    对于一个非空闭集Y⊆Rⁿ，假定选取参考点间隔为d_s>0，且Y与内部参考点集G_int⊂Y满足d_H(Y, G_int)，利用算法2近似Y，记所得投影边界点集合为B，则Y与B满足如下关系：

$ {d_{\rm{H}}}\left( {\mathit{\boldsymbol{Y}},{\rm{cl}}\mathit{\boldsymbol{B}}} \right) \le \sqrt n {d_{\rm{s}}}. $

证明    根据定义3，有d_H(Y, clB)= max{d(Y, clB), d(clB, Y)}，其中：

$ d\left( {\mathit{\boldsymbol{Y}},{\rm{cl}}\mathit{\boldsymbol{B}}} \right) = \mathop {\max }\limits_{\mathit{\boldsymbol{y}} \in \mathit{\boldsymbol{Y}}} d\left( {\mathit{\boldsymbol{y}},{\rm{cl}}\mathit{\boldsymbol{B}}} \right), $

(7)

$ d\left( {{\rm{cl}}\mathit{\boldsymbol{B}},\mathit{\boldsymbol{Y}}} \right) = \mathop {\max }\limits_{\mathit{\boldsymbol{b}} \in {\rm{cl}}\mathit{\boldsymbol{B}}} d\left( {\mathit{\boldsymbol{b}},\mathit{\boldsymbol{Y}}} \right). $

(8)

对于式(7)，取任意一点y∈Y，若同时y∈clB，则d(y, clB)=0；若y∉clB，由于离散点集G_int⊂clB和定理2的假定条件，有$d(\mathit{\boldsymbol{y}},{\rm{cl}}\mathit{\boldsymbol{B}}) \le d(\mathit{\boldsymbol{y}},{\mathit{\boldsymbol{G}}_{{\rm{int}}}}) = \mathop {{\rm{max}}}\limits_{\mathit{\boldsymbol{y}} \in \mathit{\boldsymbol{Y}}} \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{g}} \in {\mathit{\boldsymbol{G}}_{{\rm{int}}}}} d(\mathit{\boldsymbol{y}},\mathit{\boldsymbol{g}}) \le \sqrt n {d_{\rm{s}}}$，式(7)得证.

对于式(8)，取任意一点b∈clB，若b∈Y，则d(b, Y)=0；若b∉Y, 则有d(b, Y)≤d(b, G_int)≤max{d(F¹, G_int), …, d(F^k, G_int)}，其中Fⁱ(i=1, …, k)为clB的外围边界面, 且有∪_i=1^kFⁱ= bd{clB}.n维空间内每个F^k可由相邻的投影边界点b_i^k(i=1, …, n)的凸包来表示.对于每个F^k及其对应的b_i^k而言，假定b₁^k、b₂^k为相邻的投影点，与它们对应的最近的网格点为g₁^k、g₂^k，如果生成b₁^k、b₂^k的两个投影方向相同，则d(g₁^k, g₂^k)=d_s，否则g₁^k、g₂^k为同一点.若对每个g_i^k以其自身为起点沿g_i^kb_i^k方向生成新的参考点g_i^k′∉Y，有d(g_i^k, g_i^k′)=d_s.将g_i^k、g_i^k′作为顶点可以构建一个超立方体，该立方体的最长对角线距离为$\sqrt n {d_{\rm{s}}}$.由立方体的构建方式可知b_i^k位于该立方体的边界面上，F^k位于该立方体内.因此有$d({\mathit{\boldsymbol{F}}^k},{\mathit{\boldsymbol{G}}_{{\rm{int}}}}) = \mathop {{\rm{max}}}\limits_{\mathit{\boldsymbol{b}} \in {\mathit{\boldsymbol{F}}^k}} d(\mathit{\boldsymbol{b}},\mathit{\boldsymbol{g}}_i^k) \le \sqrt n {d_{\rm{s}}}$，则式(8)得证，因此定理2成立.

定理2    表明了网格投影法的近似误差与d_s有关，d_s越小，布置的网格点密度越大，得到的投影边界点数量越多，近似误差越小.

3 数值仿真

本文将网格投影法和文献[17]中的DFOG方法进行对比.实验采用MATLAB 2016a仿真了两种算法，选取了同样的可达集内部网格点，利用求解器IPOPT^[19]对投影时的非线性优化问题进行求解.将上述程序用于求解以下3个控制系统问题.对于所有的例子，均采用带有分段恒定控制量的欧拉法来离散化.

首先考虑两个二维系统的例子.

例1    考虑如下一个二维双线性系统：

$ \left\{ \begin{array}{l} {{\dot x}_1}\left( t \right) = {\rm{ \mathsf{ π} }}{x_2}\left( t \right),\\ {{\dot x}_2}\left( t \right) = - {\rm{ \mathsf{ π} }}u\left( t \right){x_1}\left( t \right),\\ {x_1}\left( 0 \right) = - 1,\\ {x_2}\left( 0 \right) = 0,\\ u\left( t \right) \in U = \left[ {0,1} \right], \end{array} \right. $

式中初始时刻t₀=0，终点时刻t_f=1，取欧拉法的步长h=1/30.

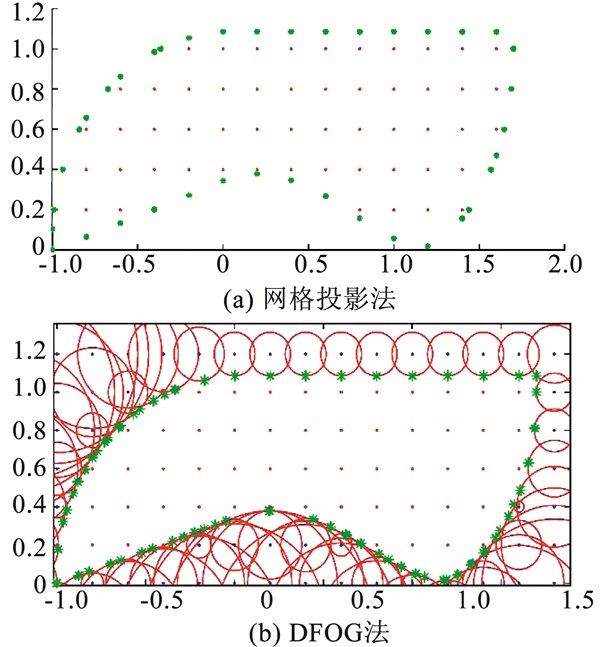
图 6(a)、(b)分别显示了网格投影法和DFOG法的结果.图中圆点为网格点，星点为求得的可达集边界点，图 6(b)中的大圆(不含边界线)展示了DFOG方法计算得到的开球集，DFOG法得到的可达集为圆圈集围成的内部区域.可以看出，两种方法的得到的可达集类似，但网格投影法求得的边界点疏密更为均匀.

例2    考虑如下一个二维非线性系统：

$ \left\{ \begin{array}{l} {{\dot x}_1}\left( t \right) = x_2^2\left( t \right) + {x_1}\left( t \right) + u\left( t \right),\\ {{\dot x}_2}\left( t \right) = {x_2}\left( t \right) + 5\sin \left( {{x_1}\left( t \right)} \right) + u\left( t \right),\\ {x_1}\left( 0 \right) = 0,\\ {x_2}\left( 0 \right) = 0,\\ \left| {u\left( t \right)} \right| \le 1, \end{array} \right. $

式中:初始时刻t₀=0，终点时刻t_f=1，取欧拉法的步长h=0.01.

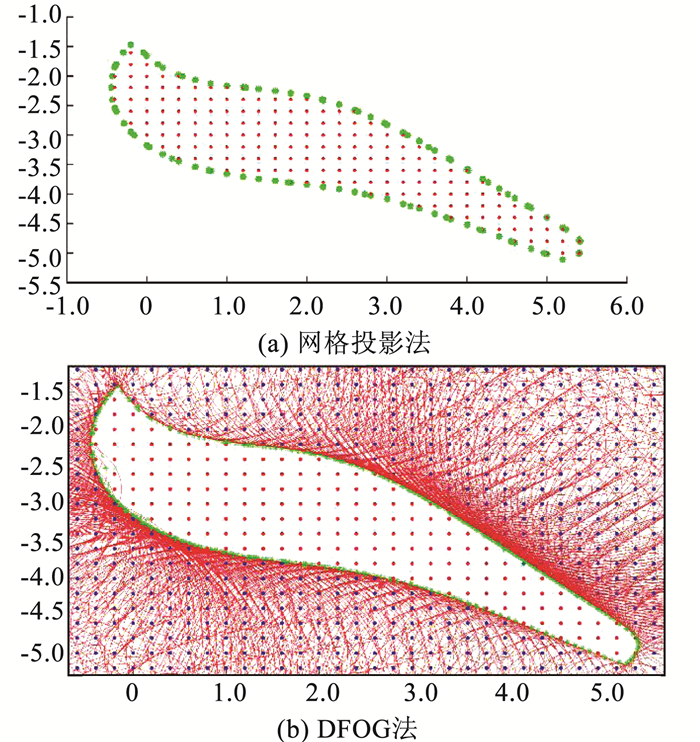
图 7(a)、(b)分别显示了网格投影法和DFOG法的结果.由于本系统的可达集在坐标轴上跨度较大，DFOG算法在可达集外部布置的网格点较多；此外也有部分网格点的优化问题没有求得全局最优值，使得相应的开球集半径过大，导致所求可达集比实际可达集小.而网格投影法并不需要求解如此多的优化问题，耗时较短.

例3    考虑如下的一个三维线性时不变系统.系统矩阵和控制矩阵分别为：

$ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - 1}&1&0\\ 0&{ - 1}&0\\ 0&0&{ - 2} \end{array}} \right],\mathit{\boldsymbol{B = }}\left[ {\begin{array}{*{20}{c}} 0&0&0\\ 0&2&0\\ 0&0&1 \end{array}} \right]. $

式中：控制约束为U={u∈R³:‖u‖₂≤1}，初始状态x₀=(0, 0, 0)^T，初始时刻t₀=0，终点时刻t_f=1，取欧拉步长h=0.02.

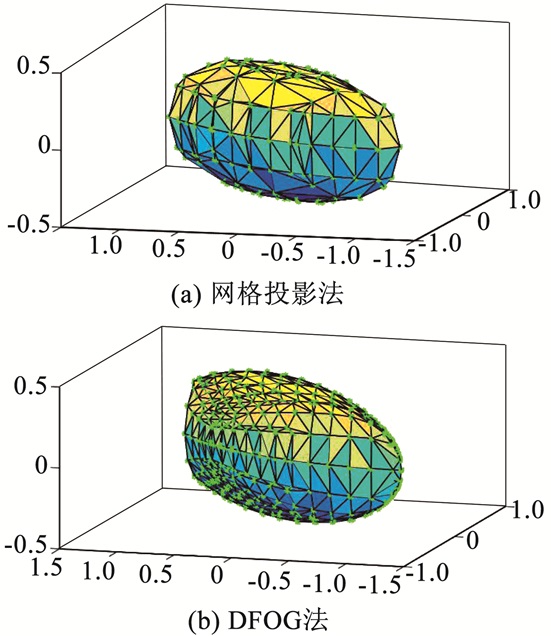
图 8(a)、(b)分别显示了网格投影法和DFOG法求得的边界点凸包.图中可以看出DFOG法左侧某些边界点落在了网格投影法得到的可达集内部，表明了DFOG法中某些外部网格点的优化问题没有求得全局最优值，使计算得到的边界点位于真实可达集的内部.

表 1进一步总结了用网格投影法和DFOG法计算例1~3得到的结果，表中列出两种方法的计算时间，计算非线性优化问题的个数(NPs)，最终得到的边界点的个数(BPs).如对于问题例1，表 1记录了网格投影法的耗时/s、NPs、BPs分别为22.81、54.00、46.00；而DFOG法的相应数据分别为28.97、128、72.这是由于DFOG法需要布置大量外部网格点，且每个网格点都需要求解一个优化问题；而网格投影法中，仅对于非凸集才需要布置外部网格点，且沿每个投影方向只需要计算一次投影.可以说明，在同样内部网格点的情况下，相较于DFOG方法，网格投影法所需的计算时间短，求解优化问题的个数少.进一步地，仿真结果图也显示了网格投影法得到的可达集边界点分布更加均匀.与DFOG法相比，得到的可达集描述更接近真实的可达集.

4 结论

1) 网格投影法在可达集内部布置均匀分布的网格点，将网格点向可达集边界投影，每个投影点都是可达集的边界点，这些投影点围城的区域即为可达集的近似描述.

2) 网格投影法的近似误差与布置网格点的间隔相关，网格点间隔越小，则近似误差越小，需要求解优化问题个数越多.

3) 相较于DFOG算法，网格投影法具有近似误差小、边界点分布均匀、速度快的优点；当DFOG方法出现优化问题无法求得全局最优时，会使求得的可达集比真实的可达集小，实验结果显示本方法可靠性较高.

4) 提出了网格投影法直接近似离散系统的可达集.该方法简单，易于实施，可以有效地解决可达集为非凸的情况.