2. 哈尔滨工业大学 航天学院, 哈尔滨 150001
2. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China
随着反导体系的日益完善,单枚导弹突破反导体系实现打击任务的难度越来越大,这催生了多导弹协同攻击体系的出现.通过对早期的导弹进行改进并加装通信装置,将携带不同传感器的导弹进行编组,利用通信网络将不同导弹获得的信息收集处理并用以控制整个弹群的制导飞行,不仅能够充分利用早期将退役导弹的潜能,发挥最大的作战效果,还能够显著提高弹群的突防效率,同时也能够显著降低经济成本[1-5].
传统关于多导弹协同攻击的研究,在导弹自身运动模型上,通常考虑巡航导弹、反舰导弹、空空导弹等大气层内飞行导弹[6-9],对弹道导弹的研究鲜有出现,对弹道导弹特定飞行阶段的研究更是鲜有出现;多数将导弹运动模型视作线性时不变系统模型,未考虑实际情况的非线性情形[10-12];为简化分析,往往将导弹看作一阶或者二阶系统,仅考虑二维平面运动,不能反映真实情况[13-15].针对主弹-从弹的协同攻击体系,一般仅考虑二维平面内的导引,三维平面内的导引模型鲜有出现[10, 16];对目标的设定方面,多数假设目标为固定目标或水平运动目标[17-18],难以体现代表性;由于存在主弹,多数文献并未考虑主弹发生故障无法给出指令信号时从弹如何导引,从弹与目标间的导引关系同样重要;当以状态一直性或输出一致性作为协同攻击效果的衡量指标时,从弹与主弹很可能最终会趋于同一条弹道,这会造成弹与弹之间的碰撞,影响协同攻击的效果[19-20].
基于上述文献中存在的问题,针对弹道导弹自由飞行段弹头飞行的特殊环境,本文基于主-从式多弹头协同攻击体系,给出了多弹头协同攻击的状态空间模型,对此模型的特点以及模型非线性动态对多弹头协同攻击带来的挑战进行了详细分析,以主-从式多弹头协同攻击体系的输出一致性作为多弹头协同攻击效果的衡量指标,应用输入输出反馈线性化方法,给出了从弹弹头(下文称从弹头)协同加速度指令信号(下文称指令信号)的设计方法,为进一步开展自由飞行段多弹头协同攻击提供了模型基础及设计基础.
1 多弹头三维空间运动建模及分析 1.1 多弹头三维空间运动状态空间模型针对主-从式多弹头自由飞行段协同攻击,本文假设主弹弹头(下文称主弹头)在此阶段为无控自由运动,且其运动状态独立于从弹头的运动状态.即考虑主弹头不受指令信号的控制,仅从弹头接收来自于主弹头的指令信号的控制;在主弹弹头的发射坐标系下考虑所有弹头的状态量及所有参数,下述发射坐标系即为主弹的发射坐标系.
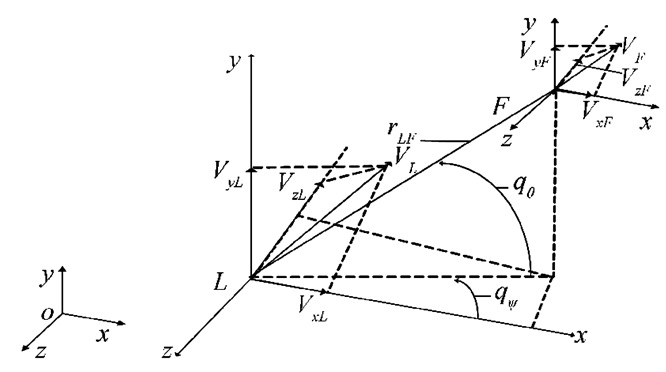
基于上述假设,本文考虑如图 1所示的主-从式多弹头自由飞行段协同攻击体系.图中Oxyz为主弹的发射坐标系,Lxyz与Fxyz分别为平移到主弹头和从弹头质心的发射坐标系,VF为从弹头的速度值,VxF、VyF、VzF分别为从弹头速度在发射坐标系各轴上的分量;VL为主弹头的速度值,VxL、VyL、VzL分别为主弹头速度在发射坐标系各轴上的分量.
|
图 1 主-从式多弹头协同攻击相对运动关系 Figure 1 Relative motion of leader-followers multiple warheads cooperative attack |
自由飞行段的弹道导弹,由于相对转动着的地球有相对运动,因此其主要受到地球引力、牵连惯性力,柯氏惯性力以及空气阻力作用.但由于其处于稀薄大气中,其受到的空气阻力可以忽略不计.因此,根据质点动力学理论,考虑多弹头间的协同,本文在发射坐标系上建立如下形式的从弹头运动方程[21]:
| $ \left[ {\begin{array}{*{20}{c}} {{{\dot V}_{xF}}}\\ {{{\dot V}_{yF}}}\\ {{{\dot V}_{zF}}}\\ {{{\dot x}_F}}\\ {{{\dot y}_F}}\\ {{{\dot z}_F}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{g_{xF}} + {{\dot V}_{exF}} + {{\dot V}_{cxF}} + {a_x}}\\ {{g_{yF}} + {{\dot V}_{eyF}} + {{\dot V}_{cyF}} + {a_y}}\\ {{g_{zF}} + {{\dot V}_{exF}} + {{\dot V}_{cxF}} + {a_z}}\\ {{V_{xF}}}\\ {{V_{yF}}}\\ {{V_{zF}}} \end{array}} \right], $ |
| $ {V_F} = \sqrt {V_{xF}^2 + V_{yF}^2 + V_{zF}^2} , $ |
式中:xF、yF、zF分别为从弹头位置在发射坐标系各轴上的分量;gxF、gyF、gzF分别为从弹头位置处引力加速度g在发射坐标系各轴上的分量;
上述模型中,引力加速度分量具有如下形式:
| $ \left[ {\begin{array}{*{20}{c}} {{g_{xF}}}\\ {{g_{yF}}}\\ {{g_{zF}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{g_{rF}}\frac{{{x_F} + {R_{0xF}}}}{{{r_F}}} + {g_{\omega F}}\frac{{{\omega _x}}}{\omega }}\\ {{g_{rF}}\frac{{{y_F} + {R_{0yF}}}}{{{r_F}}} + {g_{\omega F}}\frac{{{\omega _y}}}{\omega }}\\ {{g_{rF}}\frac{{{z_F} + {R_{0zF}}}}{{{r_F}}} + {g_{\omega F}}\frac{{{\omega _z}}}{\omega }} \end{array}} \right], $ |
| $ \left[ {\begin{array}{*{20}{c}} {{g_{rF}}}\\ {{g_{\omega F}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{ - fM}}{{r_F^2}} + \frac{\mu }{{r_F^4}}\left( {5{{\sin }^2}{\varphi _{sF}} - 1} \right)}\\ { - \frac{{2\mu }}{{r_F^4}}\sin {\varphi _{sF}}} \end{array}} \right]. $ |
式中:grF、gωF分别为从弹头位置处引力加速度在地心矢径及地球自转轴方向上的分量;地球平均半径
| $ {r_F} = \sqrt {{{\left( {{x_F} + {R_{0xF}}} \right)}^2} + {{\left( {{y_F} + {R_{0yF}}} \right)}^2} + {{\left( {{z_F} + {R_{0zF}}} \right)}^2}} , $ |
| $ \mu = fM{R^2}J = 26.332\;81 \times 1\;024, $ |
而fM=3.986 005×1 014 m3/s2为地心引力常数,R为地球赤道半径,J为地球一阶扁率系数;ω=7.292 115×10-5 rad/s为地球自转角速度的大小,ωx、ωy、ωz分别为地球自转角速度在发射坐标系各轴上的分量.
牵连加速度分量具有如下形式:
| $ \left[ {\begin{array}{*{20}{c}} {{{\dot V}_{exF}}}\\ {{{\dot V}_{eyF}}}\\ {{{\dot V}_{ezF}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{d_{11}}}&{{d_{12}}}&{{d_{13}}}\\ {{d_{21}}}&{{d_{22}}}&{{d_{23}}}\\ {{d_{31}}}&{{d_{32}}}&{{d_{33}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_F} + {R_{0xF}}}\\ {{y_F} + {R_{0yF}}}\\ {{z_F} + {R_{0zF}}} \end{array}} \right], $ |
其中:
| $ {d_{11}} = {\omega ^2} - \omega _x^2,{d_{12}} = {d_{21}} = - {\omega _x}{\omega _y}, $ |
| $ {d_{22}} = {\omega ^2} - \omega _y^2,{d_{23}} = {d_{32}} = - {\omega _y}{\omega _z}, $ |
| $ {d_{33}} = {\omega ^2} - \omega _z^2,{d_{13}} = {d_{31}} = - {\omega _x}{\omega _z}. $ |
柯氏加速度分量具有如下形式:
| $ \left[ {\begin{array}{*{20}{c}} {{{\dot V}_{cxF}}}\\ {{{\dot V}_{cyF}}}\\ {{{\dot V}_{czF}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{{e_{12}}}&{{e_{13}}}\\ {{e_{21}}}&0&{{e_{23}}}\\ {{e_{31}}}&{{e_{32}}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{V_{xF}}}\\ {{V_{yF}}}\\ {{V_{zF}}} \end{array}} \right], $ |
其中:
| $ {e_{12}} = - {e_{21}} = 2{\omega _x}, $ |
| $ {e_{31}} = - {e_{13}} = 2{\omega _y}, $ |
| $ {e_{23}} = - {e_{32}} = 2{\omega _z}, $ |
为便于分析,选取以下运动参数作为状态为
| $ {\mathit{\boldsymbol{\eta }}_F} = \left[ {\begin{array}{*{20}{c}} {{x_F}}&{{V_{xF}}}&{{y_F}}&{{V_{yF}}}&{{z_F}}&{{V_{zF}}} \end{array}} \right]. $ | (1) |
选取下述指令信号为协同控制输入
| $ {\mathit{\boldsymbol{u}}_F} = \left[ {\begin{array}{*{20}{c}} {{a_x}}&{{a_y}}&{{a_z}} \end{array}} \right], $ |
则从弹头三维空间运动状态空间模型为:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot \eta }}}_F} = {\mathit{\boldsymbol{A}}_F}{\mathit{\boldsymbol{\eta }}_F} + {\mathit{\boldsymbol{B}}_F}{\mathit{\boldsymbol{u}}_F} + {\mathit{\boldsymbol{\alpha }}_F},\\ {\mathit{\boldsymbol{y}}_\mathit{\boldsymbol{F}}} = {\mathit{\boldsymbol{C}}_F}{\mathit{\boldsymbol{\eta }}_F}. \end{array} $ | (2) |
式中:AF=[aij] ∈ R6×6, i=1, 2, …, 6, j=1, 2, …, 6为系统矩阵;BF=[bik] ∈ R6×3, i=1, 2, …, 6, k= 1, 2, 3为输入矩阵;CF=[cki] ∈ R3×6, k=1, 2, 3, i=1, 2, …, 6为输出矩阵;yF为输出.定义式(2)中的αF为初始发射矩阵,且αF=[αi1] ∈ R6×1, i= 1, 2, …, 6.
故系统矩阵AF中的元素分别为:a24=-a42=2ωx,a26=-a62=-2ωy,a46=-a64=2ωz,a23=a41=-ωxωy,a25=a61=-ωxωz,a45=a63=-ωyωz,a12=1, a1i=0, i=1, 3, 4, 5, 6,a34=1, a3i=0, i=1, 2, 3, 5, 6,a56=1, a5i=0, i=1, 2, 3, 4, 5,aii=0, i=1, 2, …, 6,a21=[
输入矩阵BF中的元素分别为
| $ {b_{21}} = {b_{42}} = {b_{63}} = 1, $ |
其余元素为零.
初始发射矩阵αF中的元素分别为:
| $ {\alpha _2} = {a_{21}}{R_{0xF}} - {\omega _x}{\omega _y}{R_{0yF}} - {\omega _x}{\omega _z}{R_{0zF}} - \frac{{2\mu {\omega _x}\sin {\varphi _{sF}}}}{{r_F^4\omega }}, $ |
| $ {\alpha _4} = {a_{43}}{R_{0yF}} - {\omega _x}{\omega _y}{R_{0xF}} - {\omega _y}{\omega _z}{R_{0zF}} - \frac{{2\mu {\omega _y}\sin {\varphi _{sF}}}}{{r_F^4\omega }}, $ |
| $ {\alpha _6} = {a_{65}}{R_{0zF}} - {\omega _x}{\omega _z}{R_{0xF}} - {\omega _y}{\omega _z}{R_{0yF}} - \frac{{2\mu {\omega _z}\sin {\varphi _{sF}}}}{{r_F^4\omega }}, $ |
其余元素为零.
输出矩阵CF中的元素分别为
| $ {c_{12}} = {c_{24}} = {c_{36}} = 1, $ |
其余元素为零.
对于主弹头而言,由于其为无控自由运动,故其三维空间运动状态空间模型为:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot \eta }}}_L} = {\mathit{\boldsymbol{A}}_L}{\mathit{\boldsymbol{\eta }}_L} + {\mathit{\boldsymbol{\alpha }}_L},\\ {\mathit{\boldsymbol{y}}_L} = {\mathit{\boldsymbol{C}}_L}{\mathit{\boldsymbol{\eta }}_L}. \end{array} $ |
式中:AL ∈ R6×6为系统矩阵;CL ∈ R3×6为输出矩阵;yL为输出;αL ∈ R6×1为初始发射矩阵.
上述主弹头中矩阵的定义以及矩阵中元素值的大小和定义类似于从弹头中矩阵的定义以及矩阵中元素值的大小和定义,下标体现了二者的不同.
由此,多弹头三维空间运动状态空间模型如下式所示:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot \eta }}}_L} = {\mathit{\boldsymbol{A}}_L}{\mathit{\boldsymbol{\eta }}_L} + {\mathit{\boldsymbol{\alpha }}_L},\\ {\mathit{\boldsymbol{y}}_L} = {\mathit{\boldsymbol{C}}_L}{\mathit{\boldsymbol{\eta }}_L}.\\ {{\mathit{\boldsymbol{\dot \eta }}}_F} = {\mathit{\boldsymbol{A}}_F}{\mathit{\boldsymbol{\eta }}_F} + {B_F}{\mathit{\boldsymbol{u}}_F} + {\mathit{\boldsymbol{\alpha }}_F},\\ {\mathit{\boldsymbol{y}}_\mathit{\boldsymbol{F}}} = {\mathit{\boldsymbol{C}}_F}{\mathit{\boldsymbol{\eta }}_F}. \end{array} $ | (3) |
注释1 上述多弹头三维空间运动状态空间模型(3)中,仅存在一个主弹头的状态空间模型及一个从弹头的状态空间模型.但很显然,多弹头协同攻击可存在多个弹头为主弹头,多个弹头为从弹头,而所有主弹头的状态空间模型一致,所有从弹头的状态空间模型一致.因此式(3)代表了一般情况.
1.2 模型分析从式(2)可以发现,由于主弹头或者从弹头的运动,系统矩阵中a21、a43、a65元素和初始发射矩阵中的α2、α4、α6会随着弹头与地心间距离的变化以及弹头位置处地心纬度的变化而呈非线性变化.因此,自由飞行段的多弹头三维空间运动状态空间模型为非线性、时变系数的.
很显然,由于上述状态空间模型的非线性、时变系数性,虽然主弹头在自由飞行段为无控自由运动,但上述状态空间方程模型的解析解仍然无法根据初始条件获得,只能利用数值积分获得弹头运动参数的数值及弹头运动规律.而数值积分所得到的运动规律的可靠性显然难以保证.这对多弹头协同攻击的实现带来了严峻的挑战.
对于从弹头而言,其状态空间模型同样是非线性、时变系数的.而由于其为受控运动,因而其运动参数的数值以及运动规律不但无法通过解微分方程的方式得到,甚至于通过数值积分也无法得到,这同样为多弹头协同攻击的实现带来了严峻的挑战.
然而,上述状态空间模型虽然是非线性、时变系数的,但当主弹头以及从弹头运动的初始运动参数相对精确已知时,便可以在此基础上通过设计合适的指令信号,使之作为从弹头的控制输入而将非线性状态空间模型(3)变换为等价的线性系统模型,实现主-从式多弹头协同攻击的输出一致性.
2 从弹头指令信号设计由于输入输出反馈线性化能够通过输入变换和输出反馈将非线性系统代数的转化为一个线性系统,因此其在具有状态耦合的非线性系统中具有广泛应用.本文将对该方法中的系数设置进行改进以实现主-从式多弹头协同攻击体系的输出一致性.
基于主-从式多弹头协同攻击体系,本文以输出一致性作为衡量指标,利用输入输出反馈线性化方法[22],由以下定理给出指令信号的设计方法.
定理1 考虑图 1所示的主-从式多弹头协同攻击体系.定义:
| $ {e_x} = {V_{xF}} - {V_{xL}},{e_y} = {V_{yF}} - {V_{yL}},{e_z} = {V_{zF}} - {V_{zL}}, $ |
分别为从弹头在发射坐标系各轴上的速度跟踪误差.若从弹头接收到的指令信号满足如下条件:
| $ {a_x} = - \sum\limits_{i = 1}^6 {{a_{2i}}{\eta _{Fi}}} + \frac{{2\mu {\omega _x}\sin {\varphi _{sF}}}}{{r_F^4\omega }} - {a_{21}}{R_{0xF}} + {v_1}, $ |
| $ {a_y} = - \sum\limits_{i = 1}^6 {{a_{4i}}{\eta _{Fi}}} + \frac{{2\mu {\omega _y}\sin {\varphi _{sF}}}}{{r_F^4\omega }} - {a_{43}}{R_{0yF}} + {v_2}, $ |
| $ {a_z} = - \sum\limits_{i = 1}^6 {{a_{6i}}{\eta _{Fi}}} + \frac{{2\mu {\omega _z}\sin {\varphi _{sF}}}}{{r_F^4\omega }} - {a_{65}}{R_{0zF}} + {v_3}. $ |
式中:ηFi为状态ηF的第i个分量,vi, i=1, 2, 3具有如下形式:
| $ {v_1} = {{\dot V}_{xF}} + {\lambda _x}\left| {{V_{xF}}\left( 0 \right) - {V_{xL}}\left( 0 \right)} \right|{e_x}, $ |
| $ {v_2} = {{\dot V}_{yF}} + {\lambda _y}\left| {{V_{yF}}\left( 0 \right) - {V_{yL}}\left( 0 \right)} \right|{e_y}, $ |
| $ {v_3} = {{\dot V}_{zF}} + {\lambda _z}\left| {{V_{zF}}\left( 0 \right) - {V_{zL}}\left( 0 \right)} \right|{e_z}, $ |
则主-从式多弹头协同攻击体系能够实现从弹头对主弹头输出的快速跟踪,实现主-从式多弹头协同攻击体系的输出一致性.式中:λx、λy、λz为具有负实部的复数,定义为收敛系数;|VxF(0)-VxL(0)|、|VyF(0)-VyL(0)|、|VzF(0)-VzL(0)|分别为初始时刻速度跟踪误差的绝对值.
证明 不失一般性,此处仅考虑x轴方向,y轴与z轴方向与x轴方向类似.将上述指令信号带入系统状态空间模型可得
| $ \begin{array}{l} {{\dot V}_{xF}} = \sum\limits_{i = 1}^6 {{a_{2i}}{\eta _{Fi}}} + \sum\limits_{i = 1}^6 {{b_{2i}}{u_{Fi}}} + {\alpha _2} = \\ \;\;\;\;\;\;\;\;\sum\limits_{i = 1}^6 {{a_{2i}}{\eta _{Fi}}} + {a_x} + {a_{21}}{R_{0xF}} - {\omega _x}{\omega _y}{R_{0yF}} - \\ \;\;\;\;\;\;\;\;{\omega _x}{\omega _z}{R_{0zF}} - \frac{{2\mu {\omega _x}\sin {\varphi _{sF}}}}{{r_F^4\omega }} = - {\omega _x}{\omega _y}{R_{0yF}} - \\ \;\;\;\;\;\;\;\;{\omega _x}{\omega _z}{R_{0zF}} + {v_1} = {{\dot V}_{xL}} + {\lambda _x}\left| {{V_{xF}}\left( 0 \right) - {V_{xL}}\left( 0 \right)} \right|{e_x} - \\ \;\;\;\;\;\;\;\;{\omega _x}{\omega _y}{R_{0yF}} - {\omega _x}{\omega _z}{R_{0zF}}, \end{array} $ |
整理后可得
| $ \begin{array}{*{20}{c}} {{{\dot V}_{xF}} - {{\dot V}_{xL}} = {{\dot e}_x} = {\lambda _x}\left| {{V_{xF}}\left( 0 \right) - {V_{xL}}\left( 0 \right)} \right|{e_x} - }\\ {{\omega _x}{\omega _y}{R_{0yF}} - {\omega _x}{\omega _z}{R_{0zF}},} \end{array} $ |
即
| $ \begin{array}{*{20}{c}} {{{\dot e}_x} - {\lambda _x}\left| {{V_{xF}}\left( 0 \right) - {V_{xL}}\left( 0 \right)} \right|{e_x} = }\\ { - {\omega _x}{\omega _y}{R_{0yF}} - {\omega _x}{\omega _z}{R_{0zF}}.} \end{array} $ | (4) |
式(4)实则为一阶非齐次常系数微分方程.显然,若λx为具有负实部的复数,则跟踪误差最终将会以指数趋势收敛到零,也即从弹头实现了对主弹头沿发射坐标系x轴方向速度的无误差跟踪.发射坐标系y轴和z轴方向的证明与此类似.因此,上述设计的从弹头指令信号能够实现主-从式多弹头协同攻击体系的输出一致性.证毕
注释2 上述设计的指令信号中的复数λi, i=x, y, z,实则部分代表了误差收敛的速度.复数λi实部的模值越大,误差收敛速度越快.但显然,弹头推进机构的能力是有限的,复数λi实部的模值不可能取得无限大.
注释3 |VxF(0)-VxL(0)|实则为代表误差收敛速度的另一部分,这一部分体现了输入输出反馈线性化后的等价线性系统能够根据初始速度跟踪误差实时调整收敛速度,且初始速度跟踪误差越大,收敛速度越快.这即是对经典输入输出反馈线性化中的系数设置在跟踪控制中的改进.
注释4 上述分析及设计,实则为基于主-从式多弹头协同攻击体系,考虑从弹头的非线性状态空间模型在发射坐标系各轴上的形式,利用输入输出反馈线性化设计了合适的指令信号,将非线性的从弹头状态空间模型等价变换为了发射坐标系各轴上的一阶线性系统.可以证明,上述状态空间模型的内动态是稳定的.
3 结果及分析针对主-从式多弹头协同攻击体系的输出一致性,本文进行仿真研究.
考虑一个主弹头及一个从弹头的攻击体系,导弹射程为1 000 km;主弹头发射坐标系位于天文经度东经105°,天文纬度北纬38°,从弹头发射坐标系位于天文经度东经104.9°,天文纬度北纬38°,且两个发射坐标系的的天文瞄准方位角均为90°;主弹头的指令周期为ΔT=0.1 s,定义指令周期数为k=[t/ΔT],[·]为向下取整函数;从弹头的指令周期为ΔT1=0.1 s,速度跟踪的计算周期为ΔT2=0.01 s.
以当前时刻为时间零点,多弹头已经飞过弹道顶点,进入加速阶段,取仿真时间为2 s.主弹头初始速度大小为2.525 62×103 m/s,其中沿发射坐标系x轴和y轴方向初始速度分量分别为:
| $ {V_{xL}}\left( 0 \right) = 1.653\;4 \times {10^3}\;{\rm{m/s,}} $ |
| $ {V_{yL}}\left( 0 \right) = - 1.909\;2 \times {10^3}\;{\rm{m/s}}{\rm{.}} $ |
沿发射坐标系x轴和y轴方向速度增量随指令周期数的变化规律为ΔV0i(k|k-1)=(k2/2) m/s,i=x,y;从弹头初始速度大小为2.521 79×103 m/s,其中沿发射坐标系各轴的初始速度分量分别为:
| $ {V_{xF}}\left( 0 \right) = 1.651\;0 \times {10^3}\;{\rm{m/s,}} $ |
| $ {V_{yF}}\left( 0 \right) = - 1.906\;2 \times {10^3}\;{\rm{m/s,}} $ |
| $ {V_{zF}}\left( 0 \right) = - 0.502\;7\;{\rm{m/s}}. $ |
从弹头高度为230 km,沿发射坐标系x轴方向已飞行300 km,沿z轴方向已飞行0 km.
一般而言,弹道导弹的弹道是位于射面内的,至多会因为随机扰动而小幅度偏离射面;又由于从弹头沿发射坐标系z轴方向已飞行0 km,故假设主弹头沿发射坐标系z轴方向的速度分量为服从标准正态分布的随机变量,本文所取的一组样本值随指令周期数的变化关系见表 1.
| 表 1 主弹头沿发射坐标系z轴方向速度分量值 Table 1 Velocity component value along the z axis of launch coordinate system of the leader's warhead |
忽略发射点的垂线偏差,故发射点的天文经纬度即为发射点的地理经纬度,而地心纬度φ与地理纬度α的换算公式为[23]
| $ \varphi = \alpha - 11.545\;44\sin 2\alpha , $ |
故主弹发射坐标系的地心经度为东经105°,地心纬度为北纬26.80°,从弹发射坐标系的地心经度为东经104.9°,地心纬度为北纬26.80°.
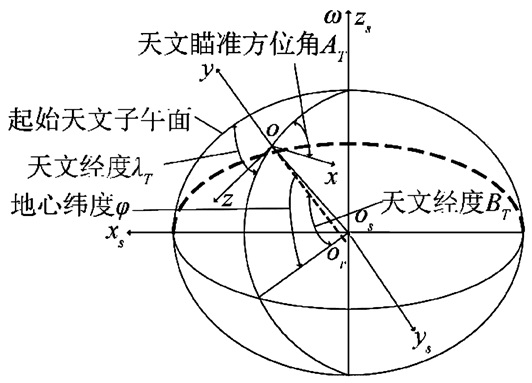
如图 2所示,根据地心大地直角坐标系Oexsyszs的定义,考虑从弹发射点处的地心矢径长度为地球平均半径
| $ {x_0} = - 1.462\;23 \times {10^3}\;{\rm{km,}} $ |
| $ {y_0} = 5.495\;45 \times {10^3}\;{\rm{km,}} $ |
| $ {z_0} = 2.872\;54 \times {10^3}\;{\rm{km}}{\rm{.}} $ |
|
图 2 地心大地直角坐标系与发射坐标系转换关系 Figure 2 Transformation relationship between the earth-rectangular coordinate system and the launch coordinate system |
由地心大地直角坐标系Oexsyszs与发射坐标系Oxyz之间的关系可得从弹发射点处的地心矢径在发射坐标系各轴上的投影分别为:
| $ {R_{0xF}} = - 3.86\;{\rm{km,}} $ |
| $ {R_{0yF}} = 6.249\;96 \times {10^3}\;{\rm{km,}} $ |
| $ {R_{0zF}} = 5.800\;53 \times {10^3}\;{\rm{km,}} $ |
而从弹头距离地心的距离为
| $ \begin{array}{l} {r_F} = \sqrt {{{\left( {{x_F} + {R_{0xF}}} \right)}^2} + {{\left( {{y_F} + {R_{0yF}}} \right)}^2} + {{\left( {{z_F} + {R_{0zF}}} \right)}^2}} = \\ \;\;\;\;\;8.701\;738\;25 \times {10^3}\;{\rm{km}}. \end{array} $ |
引力加速度沿地心矢径及地球自转轴方向的分量分别为:
| $ {g_r} = \frac{{ - fM}}{{{r^2}}} + \frac{\mu }{{{r^4}}}\left( {5{{\sin }^2}{\varphi _s} - 1} \right) = - 6.92\;{\rm{m/}}{{\rm{s}}^2}, $ |
| $ {g_w} = - \frac{{2\mu }}{{{r^4}}}\sin {\varphi _s} = - 0.41 \times {10^{ - 2}}\;{\rm{m/}}{{\rm{s}}^2}. $ |
地球自转角速度沿发射坐标系各轴的分量分别为:
| $ {\omega _x} = 0\;{\rm{rad/s,}} $ |
| $ {\omega _y} = \omega \sin {\varphi _s} = 4.52 \times {10^{ - 5}}\;{\rm{rad/s,}} $ |
| $ {\omega _z} = - \omega \cos {\varphi _s} = - 5.76 \times {10^{ - 5}}\;{\rm{rad/s}}{\rm{.}} $ |
根据实际情况,当速度跟踪误差小于0.01 m/s时,再提高跟踪精度必然会花费较大代价,且实际意义不大.因此,以首次速度跟踪误差小于0.01 m/s的指令时刻作为评价所设计指令信号能否使主-从式多弹头攻击体系尽快实现输出一致性的标准.
由于z轴方向速度变化规律与x轴及y轴方向速度变化规律不同,因此令λx=λy=-2, λz=-5,结果如图 3~8所示.
|
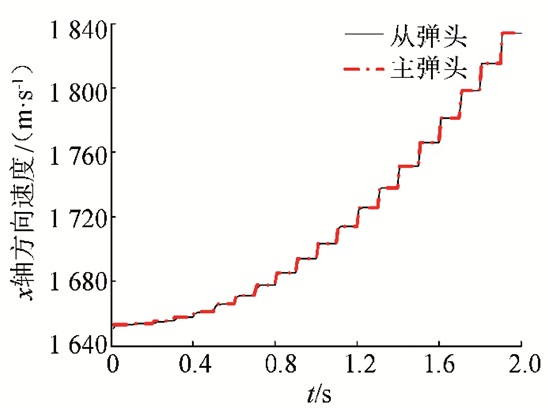
图 3 x轴方向主-从弹头速度(λx=-2) Figure 3 Speed of leader-followers in the x-axis direction (λx=-2) |
|
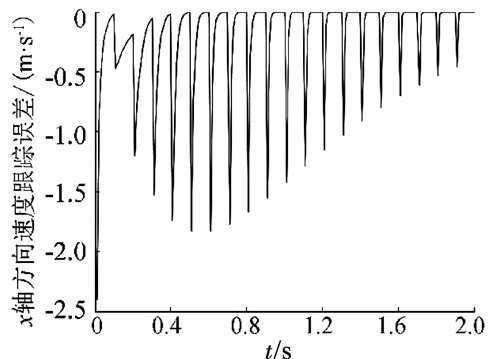
图 4 x轴方向速度跟踪误差(λx=-2) Figure 4 Tracking error of speed in the x-axis direction(λx=-2) |

|
图 5 x轴方向速度跟踪误差(λx=-5) Figure 5 Tracking error of speed in the x-axis direction (λx=-5) |
|
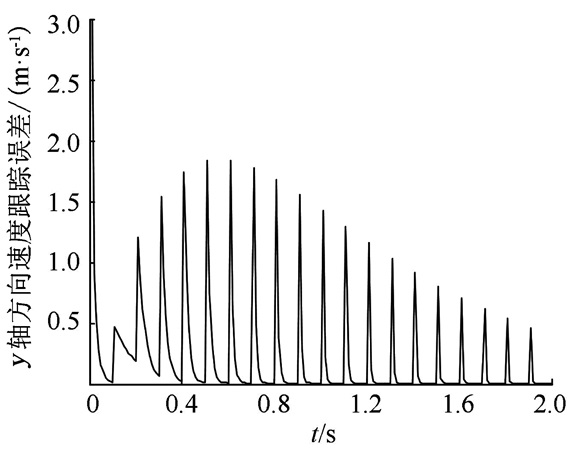
图 6 y轴方向速度跟踪误差(λy=-2) Figure 6 Tracking error of speed in the y-axis direction (λy=-2) |
|
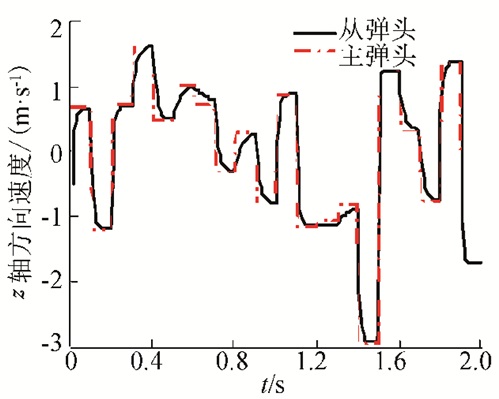
图 7 z轴方向主-从弹头速度(λz=-5) Figure 7 Speed of leader-followers in the z-axis direction (λz=-5) |
|
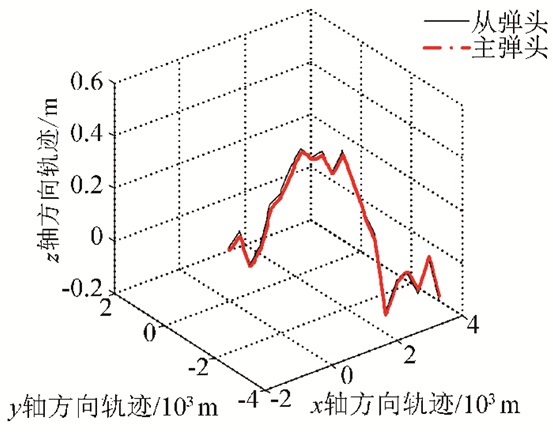
图 8 主-从弹头弹道轨迹 Figure 8 Trajectories of leader-followers |
图 3为x轴方向主-从弹头速度曲线.图中,从弹头x轴方向的速度信号对主弹头x轴方向整体上实现了良好跟踪.0.5 s之前,跟踪速度较慢且跟踪误差较大,0.5 s之后,跟踪速度逐渐加快,跟踪误差也相应减小,到最后已接近零误差跟踪,实现了主-从弹头的速度输出一致性.
图 4为x轴方向从弹头速度跟踪误差曲线.从图中可以发现,每个指令周期内的误差均呈指数形式收敛,且收敛速率越来越快;每一个指令周期时刻(下称指令时刻)的跟踪误差的整体趋势是先增大后减小,在0.6 s时达到最大.
图 5为λx=-5时x轴方向从弹头速度跟踪误差曲线.其反映了收敛系数的选择对收敛速度的影响.通过对比图 4、5可以发现,当λx的实部模值较大时,收敛速度显著提高,到1.5 s之后几乎仅用一步便跟踪上了快速变化的主弹头速度,充分体现了本文理论分析的正确性及所设计指令信号的有效性.
图 6为y轴方向从弹头速度跟踪误差曲线.对比图 4、6,若将图 6曲线沿时间轴对称处理,可以发现图 6曲线与图 4曲线趋势相同.这是由于x轴方向与y轴方向速度增量的变化趋势相同,故误差变化趋势也大致相同.
图 7为z轴方向主-从弹头速度曲线,其反映了从弹头对主弹头速度实现了较好的跟踪,但与x轴方向以及y轴方向相比,跟踪速度及精度较差,部分时刻跟踪误差非常大.
对于x轴方向,表 2数据显示0.4 s之前,最小速度跟踪误差均未达到跟踪误差要求,这也反映了图 3的分析结果.但对于协同攻击而言,0.4 s即可达到输出的一致性,这为进行其他方向的协同提供了基础.
| 表 2 各轴向各指令时刻最小速度跟踪误差 Table 2 Minimum velocity tracking error of each instruction moment in each axis |
对比表 2、3的数据,可以发现x轴方向的最小速度跟踪误差与终态跟踪误差是一致的.这是由于理论推导的结论是,跟踪误差单调且式(4)为一阶齐次微分方程,故跟踪误差的符号是确定的.因此最小跟踪误差与终态跟踪误差是相同的.
| 表 3 各轴向各指令时刻终态速度跟踪误差 Table 3 Final velocity tracking error of each instruction moment in each axis |
对于y轴方向,表 2数据显示0.5 s之前最小速度跟踪误差均未达到跟踪误差要求.而对于自由飞行段较长的飞行时间而言,0.5 s便可以实现良好跟踪是较良好的性能.由于式(4)为一阶非齐次常系数微分方程,故表 3中相应数据与x轴方向差别较大,但最小速度跟踪误差与终态跟踪误差还是一致的.
对于z轴方向,表 2数据反映当λz=-5时,在将近1/2指令时刻上,跟踪性能未达到要求;而当λz=-10时,除了0、0.7、1.3 s这3个指令时刻外,其余所有指令时刻的跟踪误差均达到了性能要求.因此,当跟踪误差达不到要求的时候,可以通过在适当范围内进一步增大λz实部模值来加快收敛速度,减小跟踪误差.
观察表 3数据并与表 2数据对比可以发现,x轴与y轴方向的最小跟踪误差与终态误差分别相同,但z轴方向的最小跟踪误差与终态误差则不同.因此,在指令周期内,应仅计算到最小跟踪误差所在的步数,否则跟踪误差反而会变大.表 3同样反映了λz=-5时z轴方向1/2以上的指令时刻的跟踪误差未达到要求,需要进一步改变λz以增大其实部模值.
图 8为主-从弹头的弹道轨迹曲线.从图 8中可以看出,从弹头实现了对主弹头的良好跟踪.由于z轴方向的速度设置为随机变化,导致轨迹沿z轴方向急速切换,出现弹道轨迹不够平滑,而这在实际情况中几乎不会出现.
综合上述分析,可得出:1)本文所设计的指令信号使得沿发射坐标系x轴及y轴方向,从弹头对主弹头的速度实现了整体上的有效跟踪,跟踪误差满足条件;而对于z轴方向,由于所取随机量样本值的原因,使得部分指令时刻的跟踪误差未能达到要求,这可以通过进一步增大λz实部模值的方式使跟踪误差达到要求.2)λi, i=x, y, z值的实部模值显著影响跟踪误差的收敛速率,合理设计λi能够有效兼顾收敛速率与推进机构能力.3)上一指令时刻末的从弹头速度与下一指令时刻的主弹头速度差值越大,最小跟踪误差与终态跟踪误差也越小,主-从弹头的弹道轨迹贴合度也更好.4)当上一指令时刻末的从弹头速度与下一指令时刻的主弹头速度差值较大时,可以仅计算数步,到达允许的跟踪误差范围即可.5)当式(4)为一阶非齐次常系数微分方程时,虽然跟踪误差仍呈指数形式单调收敛,但其模值可能会在指令周期内出现先减小后增大的情况,因此当需要达到最小跟踪误差时,应当判断最小跟踪误差点的出现时间并仅计算到该点,以获得最小跟踪误差.
4 结论1) 通过详细推导,给出了弹道导弹自由飞行段的多弹头三维空间运动状态空间模型,并通过对该状态空间模型的详细分析,指出其非线性本质对多弹头协同攻击形成的挑战,为后续进行多弹头协同攻击提供了模型基础.
2) 对输入输出反馈线性化控制方法中经典的系数设置进行了改进,使之更加适应于速度快速变化的弹道导弹自由飞行段多弹头的飞行特点.在此基础上,以主-从弹头的输出一致性为协同攻击的性能指标,设计了从弹头的指令信号并进行了理论证明.
3) 通过数值仿真,对沿发射坐标系各个轴向的速度跟踪问题进行了仿真研究,并进行了详细分析,验证了所设计指令信号的合理性.
| [1] |
胡建平, 杨峻巍. 弹群组网应用与关键技术[J]. 电讯技术, 2014, 54(3): 251. HU Jianping, YANG Junwei. Application and key technology of missiles network[J]. Telecommunication Engineering, 2014, 54(3): 251. DOI:10.3969/j.issn.1001-893x.2014.03.002 |
| [2] |
王昊宇, 徐学强, 房玉军. 网络化协同打击弹药技术[J]. 兵工学报, 2010, 31(S2): 136. WANG Haoyu, XU Xueqiang, FANG Yujun. Networked cooperative attack ammunition technology[J]. Acta Armamentarii, 2010, 31(S2): 136. |
| [3] |
肖增博, 雷虎民, 滕江川, 等. 多导弹协同制导规律研究现状及展望[J]. 航空兵器, 2011(6): 18. XIAO Zengbo, LEI Humin, TENG Jiangchuan, et al. The present status and prospect of multi-missile cooperative guidance law[J]. Aero Weaponry, 2011(6): 18. DOI:10.3969/j.issn.1673-5048.2011.06.006 |
| [4] |
梁海朝, 王剑颖, 孙兆伟, 等. 多小型飞行器自主编队姿态协同控制方法[J]. 哈尔滨工业大学学报, 2016, 48(4): 13. LIANG Haizhao, WANG Jianying, SUN Zhaowei, et al. Decentralized attitude synchronization of spacecraft formation under disturbances[J]. Journal of Harbin Institute of Technology, 2016, 48(4): 13. DOI:10.11918/j.issn.0367-6234.2016.04.002 |
| [5] |
邵光远.面向多弹协同的导弹建模与姿态控制研究[D].北京: 北京理工大学, 2016 SHAO Guangyuan. Research of missile modeling and attitude control for multi-missile cooperation[D]. Beijing: Beijing Institute of Technology, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10007-1016717771.htm |
| [6] |
吴蔚楠.巡飞弹协同攻击任务规划问题建模与方法研究[D].哈尔滨: 哈尔滨工业大学, 2013 WU Weinan.Research on modeling and method for cooperative combat task planning of multiple cruise flight missiles[D]. Harbin: Harbin Institute of Technology, 2013 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D416822 |
| [7] |
赵雪峰.反舰导弹协同攻击制导方法研究[D].哈尔滨: 哈尔滨工业大学, 2012 ZHAO Xuefeng. Research on guidance laws for cooperative attack of multiple anti-ship missiles[D]. Harbin: Harbin Institute of Technology, 2012 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D240884 |
| [8] |
王君, 芮同林, 李进, 等. 空空导弹网络化协同制导作战模式[J]. 航空兵器, 2015(5): 32. WANG Jun, RUI Tonglin, LI Jin, et al. The networking cooperative guidance combat pattern for air-to-air missile[J]. Aero Weaponry, 2015(5): 32. DOI:10.3969/j.issn.1673-5048.2015.05.006 |
| [9] |
雷宇曜, 姜文志, 顾佼佼, 等. 防空导弹协同制导交接班模型研究[J]. 战术导弹技术, 2015(3): 74. LEI Yuyao, JIANG Wenzhi, GU Jiaojiao, et al. Cooperative guidance handover model of anti-aircraft missile[J]. Tactical Missile Technology, 2015(3): 74. DOI:10.16358/j.issn.1009-1300.2015.03.14 |
| [10] |
SUN X, ZHOU R, HOU D, et al. Consensus of leader-followers system of multi-missile with time-delays and switching topologies[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(3): 1202. DOI:10.1016/j.ijleo.2013.07.159 |
| [11] |
SONG Lei, ZHANG Youan, HUANG Dan, et al. Cooperative simultaneous attack of multi-missiles under unreliable and noisy communication network: A consensus scheme of impact time[J]. Aerospace Science and Technology, 2015, 47: 31. DOI:10.1016/j.ast.2015.09.015 |
| [12] |
MING C, SUN R, SUN C. Optimal guidance law to maximize terminal velocity for missiles with impact angle constraint[J]. Journal of Harbin Institute of Technology (New Series), 2016, 23(2): 72. DOI:10.11916/j.issn.1005-9113.2016.02.011 |
| [13] |
彭琛, 刘星, 吴森堂, 等. 多弹分布式协同末制导时间一致性研究[J]. 控制与决策, 2010, 25(10): 1557. PENG Chen, LIU Xing, WU Sentang, et al. consensus problems in distributed cooperative terminal guidance time of multi-missiles[J]. Control and Decision, 2010, 25(10): 1557. DOI:10.13195/j.cd.2010.10.120.pengch.017 |
| [14] |
QU Pingping, ZHOU Di. Observer-based guidance law accounting for second-order dynamics of missile autopilots[J]. Journal of Harbin Institute of Technology (New Series), 2013, 20(1): 17. DOI:10.3969/j.issn.1005-9113.2013.01.004 |
| [15] |
PAN Huan, NIAN Xiaohong, GUO Ling. Consensus analysis and formation control of second-order multiagent systems via nonlinear protocol[J]. Journal of Computational and Nonlinear Dynamics, 2013, 8(3): 034502. DOI:10.1115/1.4023353 |
| [16] |
刘冬责.多导弹协同制导与控制技术研究[D].北京: 北京理工大学, 2016 LIU Dongze. Research on multi-missile cooperative guidance and control technology[D]. Beijing: Beijing Institute of Technology, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10007-1016716797.htm |
| [17] |
LI Bin, LIN Defu, WANG Hui. Finite time convergence cooperative guidance law based on graph theory[J]. Optik-international Journal for Light and Electron Optics, 2016, 127(21): 10180. DOI:10.1016/j.ijleo.2016.08.035 |
| [18] |
HOU Mingzhe, DUAN Guangren. Integrated guidance and control of homing missiles against ground fixed targets[J]. Chinese Journal of Aeronautics, 2008, 21(2): 162. DOI:10.1016/S1000-9361(08)60021-7 |
| [19] |
LU Maobin, HUANG Jie. Cooperative output regulation problem for linear time-delay multi-agent systems under switching network[J]. Neurocomputing, 2016, 190: 132. DOI:10.1016/j.neucom.2016.01.025 |
| [20] |
WANG Xiangyu, LI Shihua, LAM J. Distributed active anti-disturbance output consensus algorithms for higher-order multi-agent systems with mismatched disturbances[J]. Automatica, 2016, 74(C): 30. DOI:10.1016/j.automatica.2016.07.010 |
| [21] |
张毅, 杨辉耀, 李俊莉. 弹道导弹弹道学[M]. 长沙: 国防科技大学出版社, 1999. ZHANG Yi, YANG Huiyao, LI Junli. Ballistic missile ballistics[M]. Changsha: National Defense Science and Technology University Press, 1999. |
| [22] |
SLOTINE J-J E, Li Weiping. Applied nonlinear control[M]. Englewood Cliffs, New Jersey: Prentice-Hall, 1991
|
| [23] |
张少泉. 有关地理纬度和地心纬度的换算问题[J]. 西北地震学报, 1985, 7(1): 39. ZHANG Shaoquan. The conversion of geographic latitude and geocentric latitude[J]. Northwestern Seismological Journal, 1985, 7(1): 39. |
 2018, Vol. 50
2018, Vol. 50


