2. 上海市空间智能控制技术重点实验室(上海航天控制技术研究所),上海 201109;
3. 上海航天技术研究院,上海 201109;
4. 西北工业大学 航天学院,西安 710005;
5. 华域汽车电动系统有限公司,上海 201109
2. Shanghai key Laboratory of Space Intelligent Control Technology (Shanghai Aerospace Control Technology Institute), Shanghai 201109, China;
3. Shanghai Academy of Spacecraft Technology, Shanghai 201109, China;
4. School of Astronautics, Northwestern Polytechnical University, Xi'an 710005, China;
5. Huayu Automotive Electric Drive System Co., Ltd, Shanghai 201109, China
近年来,随着航天器在轨服务技术的发展以及机械臂动力学和运动学研究的进步,利用空间机械臂进行空间碎片清除等在轨服务技术成为研究的热点[1-3].服务航天器利用机械臂实现对空间碎片的捕获之后,由于空间碎片属于非合作目标[4-6],其质量、转动惯量的数值未知,导致服务航天器与空间碎片形成的组合体航天器的质量特性未知,无法建立精确的动力学模型,对组合体航天器的控制提出了挑战.
面向质量特性参数未知的组合体航天器,传统的解决方法为参数辨识方法,通过参数辨识技术得到组合体关键质量特性参数,然后再建立精确的组合体动力学模型的基础上实现组合体控制[7-9].这种方法需要设计组合体参数辨识算法,在组合体控制之前进行参数辨识,效率不高,并且对于复杂的系统,比如质量特性参数变化的系统,无法实现精确的参数辨识[10-12].
针对该问题,本文将无模型数据驱动控制方法引入到航天器姿态控制中,该方法不依赖于航天器的精确动力学模型,依靠系统的在线输入和输出数据,实现系统基于数据的预报和控制.自上世纪90年代数据驱动控制理论被提出以来,截止目前为止已应用于化工、冶金、机械、电力和交通运输等多个领域并且取得了良好的控制效果.无模型数据驱动控制作为数据驱动控制方法的一种,由侯忠生等[13-16]学者于1994年提出,利用被控系统的输入输出数据在线估计动态线性化模型中的伪偏导数,进而实现系统的无模型控制,目前该控制方法的有效性已经在实际应用中得到验证.
1 无模型自适应控制器简介本文主要介绍无模型自适应控制算法在单输入单输出离散时间系统的控制器方程推导过程,并且根据航天器输入输出的实际情况,对控制器方程进行拓展,得到适用于航天器姿态控制系统的无模型自适应控制器方程.
对于服务航天器与空间非合作目标形成的组合体,服务航天器与空间非合作目标之间形成了稳定的固连,因此对组合体航天器施加一个典型力矩输入,必定可以得到唯一的姿态响应输出.可以将输入与输出数据之间的关系简化为一类如下式所示的单输入单输出的离散时间非线性函数:
| $ \begin{array}{l} y\left( {k + 1} \right) = f\left( {y\left( k \right), \cdots ,y\left( {k - {n_y}} \right),} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {u\left( k \right), \cdots ,u\left( {k - {n_u}} \right)} \right). \end{array} $ | (1) |
式中:y(k)∈ℝ、u(k)∈ℝ分别为函数在k时刻的输出和输入;ny、nu分别为两个未知的正整数;f(…)为未知的非线性函数.
约束条件1 除有限时刻点之外,函数f(…)关于第(ny+2)个变量的偏导数是连续的.
约束条件2 除有限时刻点之外,函数(1)满足广义Lipschitz条件,即对任意的k1≠k2,k1, k2≥0和u(k1)≠u(k2)有
| $ \left| {y\left( {{k_1} + 1} \right) - y\left( {{k_2} + 1} \right)} \right| \le b\left| {u\left( {{k_1}} \right) - u\left( {{k_2}} \right)} \right|, $ |
式中,b>0是一个常数.
对于满足上述两条约束条件的如式(1)所示的非线性函数,当|Δu(k)| ≠0时,一定存在一个被称为伪偏导数的时变参数ϕc(k)∈ℝ,可以使函数(1)转化为如下的动态线性化数据模型为
| $ \Delta y\left( {k + 1} \right) = {\phi _c}\left( k \right)\Delta u\left( k \right), $ | (2) |
式中,ϕc(k)为函数(1)的伪偏导数.式(2)的具体证明过程可参考文献[8].
对于式(1)所示的离散时间函数,考虑如下的输入准则函数:
| $ \begin{array}{l} J\left( {u\left( k \right)} \right) = {\left| {{y^ * }\left( {k + 1} \right) - y\left( {k + 1} \right)} \right|^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda {\left| {u\left( k \right) - u\left( {k - 1} \right)} \right|^2}. \end{array} $ | (3) |
式中:λ>0是一个权重因子,用来限制控制输入量的变化,y*(k+1)为期望值.
将式(2)带入准则函数(3)中,对u(k)求导数,并令其等于零,可以得到如下控制算法:
| $ \begin{array}{l} u\left( k \right) = u\left( {k - 1} \right) + \frac{1}{{\lambda + {{\left| {{\phi _c}\left( k \right)} \right|}^2}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\left[ {\rho {\phi _c}\left( k \right)\left( {{y^ * }\left( {k + 1} \right) - y\left( k \right)} \right)} \right], \end{array} $ | (4) |
式中,ρ∈(0, 1]为步长因子,它加入的目的是使控制算法更加具有一般性.
由式(4)可知,控制器u(k)的求解需要已知的伪偏导数值,考虑伪偏导数估计准则函数为
| $ \begin{array}{l} J\left( {{\phi _c}\left( k \right)} \right) = {\left| {y\left( k \right) - y\left( {k - 1} \right) - {\phi _c}\left( k \right)\Delta u\left( {k - 1} \right)} \right|^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mu {\left| {{\phi _c}\left( k \right) - {{\hat \phi }_c}\left( {k - 1} \right)} \right|^2}, \end{array} $ | (5) |
式中,μ>0为权重因子.
对式(5)关于φc(k)求极值,可以得到伪偏导数的估计算法为
| $ \begin{array}{l} {{\hat \phi }_c}\left( k \right) = {{\hat \phi }_c}\left( {k - 1} \right) + \frac{{\eta \Delta u\left( {k - 1} \right)}}{{\mu + {{\left| {\Delta u\left( {k - 1} \right)} \right|}^2}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\left[ {\Delta y\left( k \right) - {{\hat \phi }_c}\left( {k - 1} \right)\Delta u\left( {k - 1} \right)} \right], \end{array} $ | (6) |
式中:η∈(0, 1]为加入的步长因子,目的是使得该算法具有更强的灵活性和一般性;
式(4)、(6)即为无模型自适应控制器的求解方程.
2 组合体航天器无模型自适应设计本文将推导得出的无模型自适应控制器引入到航天器姿态控制领域,并且根据航天器系统输入输出数据的实际情况,对无模型控制器进行拓展.
由无模型自适应控制推导可以得出,式(4)、(6)所描述的单输入单输出离散时间系统的无模型控制器方程中,输入数据u(k)和输出数据y(k)属于实数域,但是在航天器姿态控制系统中,输入数据为航天器三轴方向的控制力矩,输出数据为三轴方向的角加速度,输入和输出数据是3×1的向量,下面根据航天器姿态控制系统的实际情况,对式(4)、(6)进行拓展.
对于航天器运动,其经典的姿态动力学方程为
| $ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{\dot J\omega }} + \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{J\omega }}. $ | (7) |
式中:u ∈ ℝ3×1为作用在航天器上的控制力矩;ω ∈ ℝ3×1为航天器的姿态角速度;
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {{j_{11}}}&{{j_{12}}}&{{j_{13}}}\\ {{j_{21}}}&{{j_{22}}}&{{j_{23}}}\\ {{j_{31}}}&{{j_{32}}}&{{j_{33}}} \end{array}} \right]. $ |
将式(7)表示为三轴方向的运动为
| $ \left\{ \begin{array}{l} {u_x} = {\mathit{\boldsymbol{J}}_1}\mathit{\boldsymbol{\dot \omega }} + {\psi _1}\left( {{\mathit{\boldsymbol{\omega }}^2}} \right),\\ {u_y} = {\mathit{\boldsymbol{J}}_2}\mathit{\boldsymbol{\dot \omega }} + {\psi _2}\left( {{\mathit{\boldsymbol{\omega }}^2}} \right),\\ {u_z} = {\mathit{\boldsymbol{J}}_3}\mathit{\boldsymbol{\dot \omega }} + {\psi _3}\left( {{\mathit{\boldsymbol{\omega }}^2}} \right), \end{array} \right. $ | (8) |
其中:
| $ \mathit{\boldsymbol{\dot \omega }} = {\left[ {\begin{array}{*{20}{c}} {{{\dot \omega }_x}}&{{{\dot \omega }_y}}&{{{\dot \omega }_z}} \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{J}}_1} = \left[ {\begin{array}{*{20}{c}} {{j_{11}}}&{{j_{12}}}&{{j_{13}}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{J}}_2} = \left[ {\begin{array}{*{20}{c}} {{j_{21}}}&{{j_{21}}}&{{j_{23}}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{J}}_3} = \left[ {\begin{array}{*{20}{c}} {{j_{31}}}&{{j_{32}}}&{{j_{33}}} \end{array}} \right], $ |
| $ \begin{array}{l} {\psi _1}\left( {{\mathit{\boldsymbol{\omega }}^2}} \right) = - {j_{21}}{\omega _x}{\omega _z} - {j_{22}}{\omega _y}{\omega _z} - {j_{23}}\omega _z^2 + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{j_{31}}{\omega _x}{\omega _y} + {j_{32}}\omega _y^2 + {j_{33}}{\omega _y}{\omega _z}, \end{array} $ |
| $ \begin{array}{l} {\psi _2}\left( {{\mathit{\boldsymbol{\omega }}^2}} \right) = {j_{11}}{\omega _x}{\omega _z} + {j_{12}}{\omega _y}{\omega _z} + {j_{13}}\omega _z^2 - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{j_{31}}\omega _x^2 - {j_{32}}{\omega _x}{\omega _y} - {j_{33}}{\omega _x}{\omega _z}, \end{array} $ |
| $ \begin{array}{l} {\psi _3}\left( {{\mathit{\boldsymbol{\omega }}^2}} \right) = - {j_{11}}{\omega _x}{\omega _y} - {j_{12}}\omega _y^2 - {j_{13}}{\omega _y}{\omega _z} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{j_{21}}\omega _x^2 + {j_{22}}{\omega _x}{\omega _y} + {j_{23}}{\omega _x}{\omega _z}. \end{array} $ |
式中:ux、uy、uz分别为航天器三轴方向的控制力矩.
根据式(8)中所描述的航天器任意旋转轴方向的输入数据与输出数据之间的关系,由于航天器的三轴姿态角速度ω、航天器转动惯量J的值有界,因此可以得出航天器任意旋转轴方向的输入数据与输出数据满足约束条件1和约束条件2,因此输入和输出之间的关系可以动态线性化为
| $ \left\{ \begin{array}{l} \Delta {{\dot \omega }_x}\left( {k + 1} \right) = {\phi _x}\left( k \right)\Delta {u_x}\left( k \right),\\ \Delta {{\dot \omega }_y}\left( {k + 1} \right) = {\phi _y}\left( k \right)\Delta {u_y}\left( k \right),\\ \Delta {{\dot \omega }_z}\left( {k + 1} \right) = {\phi _z}\left( k \right)\Delta {u_z}\left( k \right). \end{array} \right. $ | (9) |
式中:Δ
式(9)也可以表示为
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\Delta {{\dot \omega }_x}\left( {k + 1} \right)}\\ {\Delta {{\dot \omega }_y}\left( {k + 1} \right)}\\ {\Delta {{\dot \omega }_z}\left( {k + 1} \right)} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {{\phi _x}\left( k \right)}&0&0\\ 0&{{\phi _y}\left( k \right)}&0\\ 0&0&{{\phi _z}\left( k \right)} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {\Delta {u_x}\left( k \right)}\\ {\Delta {u_y}\left( k \right)}\\ {\Delta {u_z}\left( k \right)} \end{array}} \right], \end{array} $ |
即
| $ \Delta \dot \omega \left( {k + 1} \right) = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c}\left( k \right)\Delta \mathit{\boldsymbol{u}}\left( k \right). $ | (10) |
式中,Δ
对式(10)采用式(3)和式(5)所示的准则函数,得到:
| $ \begin{array}{l} \mathit{\boldsymbol{u}}\left( k \right) = \mathit{\boldsymbol{u}}\left( {k - 1} \right) + \frac{1}{{\lambda + {{\left| {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c}\left( k \right)} \right|}^2}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\left[ {\mathit{\boldsymbol{\rho }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c}\left( k \right)\left( {{y^ * }\left( {k + 1} \right) - y\left( k \right)} \right)} \right]. \end{array} $ | (11) |
式中:λ>0为一个权重因子,用来限制控制输入量的变化;ρ∈ℝ3×3为步长因子,使控制算法更具有一般性.
| $ \begin{array}{l} {{\mathit{\boldsymbol{ \boldsymbol{\hat \varPhi} }}}_c}\left( k \right) = {{\mathit{\boldsymbol{ \boldsymbol{\hat \varPhi} }}}_c}\left( {k - 1} \right) + \frac{{\mathit{\boldsymbol{\eta }}\Delta \mathit{\boldsymbol{u'}}\left( {k - 1} \right)}}{{\mu + {{\left| {\Delta \mathit{\boldsymbol{u}}\left( {k - 1} \right)} \right|}^2}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;{\left[ {\Delta y\left( k \right) - {{\mathit{\boldsymbol{ \boldsymbol{\hat \varPhi} }}}_c}\left( {k - 1} \right)\Delta \mathit{\boldsymbol{u}}\left( {k - 1} \right)} \right]^\prime }, \end{array} $ | (12) |
其中
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{u'}}\left( {k - 1} \right) = \\ \left[ {\begin{array}{*{20}{c}} {\Delta {u_x}\left( {k - 1} \right)}&0&0\\ 0&{\Delta {u_y}\left( {k - 1} \right)}&0\\ 0&0&{\Delta {u_z}\left( {k - 1} \right)} \end{array}} \right]. \end{array} $ |
式中:[Δy(k)-
对于式(11)、(12)所描述的航天器姿态无模型自适应控制器方程,其表现形式为离散递推关系方程,伪偏导数Φc(k)的选取影响系统的收敛时间.应航天器有限时间控制要求及燃料消耗最优原则,对伪偏导数Φc(k)值的优化选取是必要的.
本文对于伪偏导数的初值选取提供一个合理的优化值,从而实现控制过程快速收敛的目的.
式(7)所示的航天器姿态动力学方程,ω×Jω表示航天器姿态三轴转动之间的耦合作用影响,在Φc(k)初值的选取计算中,可忽略其对系统运动的影响,式(7)可表示为
| $ \Delta \mathit{\boldsymbol{\dot \omega }} = {\mathit{\boldsymbol{J}}^{ - 1}}{\mathit{\Delta}} \mathit{\boldsymbol{u}}. $ | (13) |
由式(13)可以得到,无模型自适应控制器中伪偏导数Φc(k)可以取为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c}\left( k \right) = {\mathit{\boldsymbol{J}}^{ - 1}}. $ | (14) |
本文所设计的无模型自适应控制器作用于质量特性未知的航天器,即航天器转动惯量J的值是未知的.本文将介绍一种利用航天器在线输入/输出数据值估算航天器转动惯量J的算法,作为航天器无模型自适应控制器的控制过程优化算法.
如式(8)所示的三轴方向的姿态运动,每个方向都包含线性部分Ji
| $ \left\{ \begin{array}{l} {u_x} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_1}}&{{{\mathit{\boldsymbol{f'}}}_1}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot \omega }}}\\ {{\mathit{\boldsymbol{g}}_x}\left( \mathit{\boldsymbol{\omega }} \right)} \end{array}} \right],\\ {u_y} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_2}}&{{{\mathit{\boldsymbol{f'}}}_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot \omega }}}\\ {{\mathit{\boldsymbol{g}}_y}\left( \mathit{\boldsymbol{\omega }} \right)} \end{array}} \right],\\ {u_z} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_3}}&{{{\mathit{\boldsymbol{f'}}}_3}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot \omega }}}\\ {{\mathit{\boldsymbol{g}}_z}\left( \mathit{\boldsymbol{\omega }} \right)} \end{array}} \right], \end{array} \right. $ | (15) |
其中:
| $ {{\mathit{\boldsymbol{f'}}}_1} = \left[ {\begin{array}{*{20}{c}} {{j_{31}}}&{2{j_{32}}}&{{j_{33}}}&{ - {j_{21}}}&{ - {j_{22}}}&{ - 2{j_{23}}} \end{array}} \right], $ |
| $ {{\mathit{\boldsymbol{f'}}}_2} = \left[ {\begin{array}{*{20}{c}} {{j_{11}}}&{{j_{12}}}&{2{j_{13}}}&{ - 2{j_{21}}}&{ - {j_{32}}}&{ - {j_{33}}} \end{array}} \right], $ |
| $ {{\mathit{\boldsymbol{f'}}}_1} = \left[ {\begin{array}{*{20}{c}} {{j_{31}}}&{2{j_{32}}}&{{j_{33}}}&{ - {j_{21}}}&{ - {j_{22}}}&{ - 2{j_{23}}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{g}}_x}\left( \mathit{\boldsymbol{\omega }} \right) = {\left[ {\begin{array}{*{20}{c}} {{\omega _x}{\omega _y}}&{{\omega _y}}&{{\omega _y}{\omega _z}}&{{\omega _x}{\omega _z}}&{{\omega _y}{\omega _z}}&{{\omega _z}} \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{g}}_y}\left( \mathit{\boldsymbol{\omega }} \right) = {\left[ {\begin{array}{*{20}{c}} {{\omega _x}{\omega _z}}&{{\omega _y}{\omega _z}}&{{\omega _z}}&{{\omega _x}}&{{\omega _x}{\omega _y}}&{{\omega _x}{\omega _z}} \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{g}}_z}\left( \mathit{\boldsymbol{\omega }} \right) = {\left[ {\begin{array}{*{20}{c}} {{\omega _x}}&{{\omega _x}{\omega _y}}&{{\omega _x}{\omega _z}}&{{\omega _x}{\omega _y}}&{{\omega _y}}&{{\omega _y}{\omega _z}} \end{array}} \right]^{\rm{T}}}. $ |
根据式(15)所描述的方程,求逆运算得到转动惯量参数的值为
| $ \left\{ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_1}}&{{{\mathit{\boldsymbol{f'}}}_1}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot \omega }}}\\ {{\mathit{\boldsymbol{g}}_x}\left( \mathit{\boldsymbol{\omega }} \right)} \end{array}} \right]^{ - 1}} \cdot {u_x},\\ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_2}}&{{{\mathit{\boldsymbol{f'}}}_2}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot \omega }}}\\ {{\mathit{\boldsymbol{g}}_y}\left( \mathit{\boldsymbol{\omega }} \right)} \end{array}} \right]^{ - 1}} \cdot {u_y},\\ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}_3}}&{{{\mathit{\boldsymbol{f'}}}_3}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot \omega }}}\\ {{\mathit{\boldsymbol{g}}_z}\left( \mathit{\boldsymbol{\omega }} \right)} \end{array}} \right]^{ - 1}} \cdot {u_z}. \end{array} \right. $ | (16) |
根据式(16),利用系统的输入值和输出值以及测量得到的姿态角速度的值,可以在线估算航天器转动惯量参数值,将计算得到的参数值带入式(14),得到伪偏导数初始时间的赋值.
4 仿真验证本文对于组合体航天器的姿态运动,采用组合体航天器无模型自适应设计所设计的无模型自适应控制方法,验证其在航天器姿态控制的可行性及控制精度,之后采用控制过程优化设计所描述的控制过程优化设计算法,验证并分析其对控制结果的影响.
针对具有如下质量特性参数的空间组合体航天器:
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {668.5}&{4.56}&{ - 7.76}\\ {4.56}&{585.3}&{ - 3.87}\\ { - 7.76}&{ - 3.87}&{271.7} \end{array}} \right]. $ |
伪偏导数Φc(k)初值设定为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c}\left( 0 \right) = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right]. $ |
参数初值设定为
| $ \mathit{\boldsymbol{\eta }} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right],\mathit{\boldsymbol{\rho }} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right], $ |
| $ \mu = {10^{ - 7}},\lambda = {10^{ - 7}}. $ |
航天器初始时刻的控制力矩输入为
| $ \mathit{\boldsymbol{u}} = {\left[ {\begin{array}{*{20}{c}} {0.01}&{ - 0.05}&{0.02} \end{array}} \right]^{\rm{T}}}. $ |
航天器运动状态的期望值为
| $ \mathit{\boldsymbol{\dot \omega }} = {\left[ {\begin{array}{*{20}{c}} {0.001}&{0.001}&{0.001} \end{array}} \right]^{\rm{T}}}. $ |
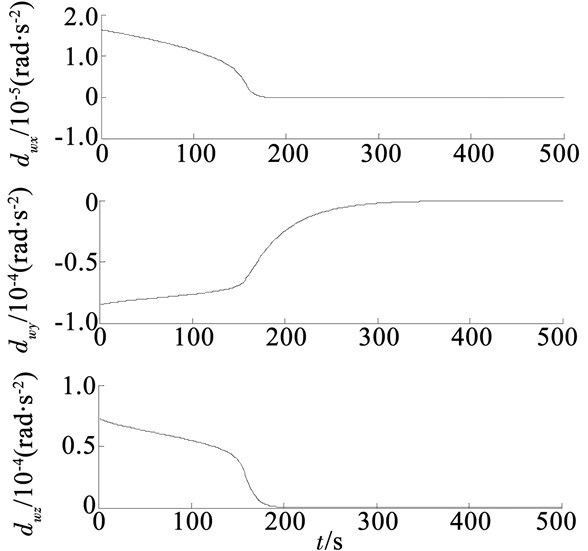
将上述初始参数带入空间组合体航天器姿态无模型自适应控制器中,作用于具有上述质量特性的组合体航天器,采用经典姿态动力学模型,分别得到空间组合体系统的角加速度输出曲线、控制力矩输入曲线以及角加速度误差曲线如图 1~3所示.
|
图 1 角加速度输出曲线 Figure 1 Output of angular acceleration |
|
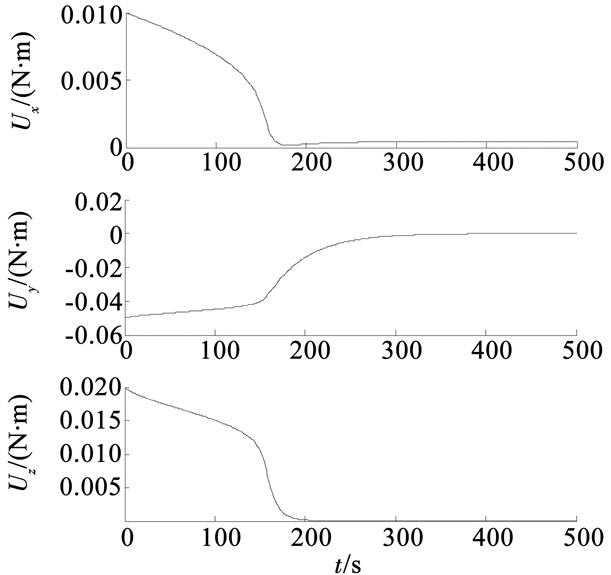
图 2 控制力矩输出曲线 Figure 2 Change of control torque |
|
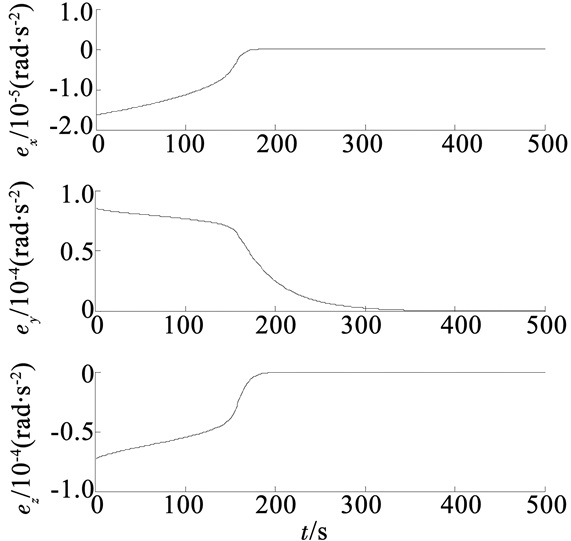
图 3 角加速度误差曲线 Figure 3 Change of the error of angular acceleration |
由图 1可以得出空间组合体航天器的角加速度值在300 s左右收敛于期望角加速度值,由图 3可以得出角加速度相对于期望值的误差在2.2×10-8rad/s2,证明本文所设计的姿态无模型自适应控制器的有效性,并且控制精度满足空间组合体姿态控制精度要求.
下面采用控制过程优化算法,令伪偏导数Φc(k)的值为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c}\left( 1 \right) = {\mathit{\boldsymbol{J}}^{ - 1}}, $ |

|
图 4 角加速度变化曲线 Figure 4 Change of angular acceleration |
|
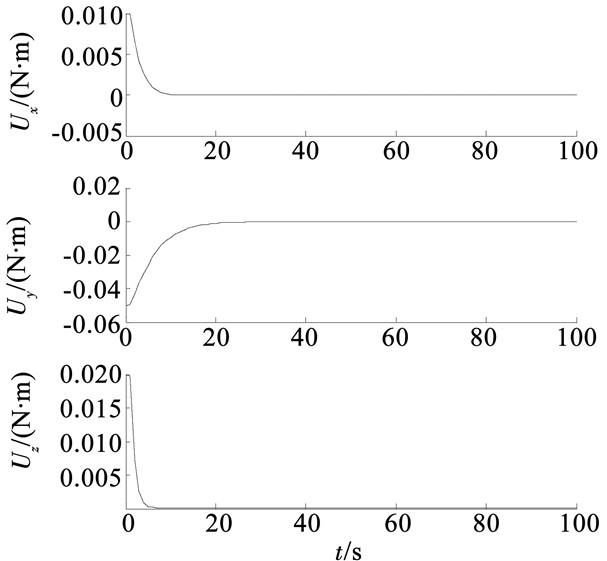
图 5 控制力矩变化曲线 Figure 5 Change of control torque |
|
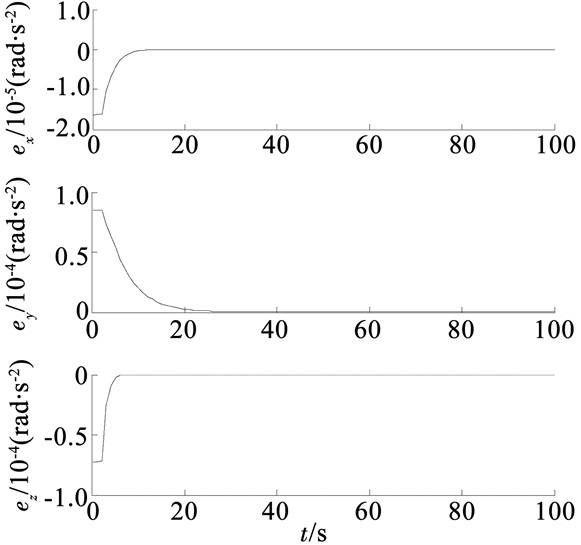
图 6 角加速度误差变化曲线 Figure 6 Change of the error of angular acceleration |
由图 4所示,采用控制过程优化算法之后,在同样的推力器作用下,空间组合体航天器的姿态角加速度收敛于期望角加速的时间为30 s,相比于未使用优化算法时的收敛时间300 s时间缩短了10倍,可以实现快速收敛并且节省航天器燃料消耗的目的.
5 结论1) 针对由于非合作目标惯性参数未知,而无法建立组合体航天器精确动力学模型,导致姿态无法精确控制的问题,设计一种基于无模型自适应控制理论的组合体航天器姿态控制算法.
2) 针对控制过程,考虑收敛时间和燃料消耗设计了控制过程优化算法.本文所设计的基于无模型自适应控制算法能够实现惯性参数未知的组合体航天器姿态精确控制,通过控制过程优化能够保证组合体航天器姿态控制具有较快的收敛速率和较高的控制精度,对工程实际具有一定的指导意义.
| [1] |
崔乃刚, 王平, 郭继峰, 等. 空间在轨服务技术发展综述[J]. 宇航学报, 2007, 28(4): 805. CUI Naigang, WANG Ping, GUO Jifeng, et al. A review of on-orbit servicing[J]. Journal of Astronautics, 2007, 28(4): 805. DOI:10.3321/j.issn:1000-1328.2007.04.005 |
| [2] |
REYNERSON C M.Spacecraft modular architecture design for on-orbit servicing[C]// Proceedings of the 2000 IEEE Aerospace Conference. Big Sky, MT: IEEE, 2000, 4: 227. DOI: 10.1109/aero.2000.878426
|
| [3] |
林来兴. 空间碎片现状与清理[J]. 航天器工程, 2012, 21(3): 1. LIN Laixing. Status and removal of space debris[J]. Spacecraft Engineering, 2012, 21(3): 1. DOI:10.3969/j.issn.1673-8748.2012.03.001 |
| [4] |
韦文书, 荆武兴, 高长生. 捕获非合作目标后航天器的自主稳定技术研究[J]. 航空学报, 2013, 34(7): 1520. WEI Wenshu, JING Wuxing, GAO Changsheng. Research automatic stability technology of spacecraft assembly with captured non-cooperative targets on orbit[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(7): 1520. DOI:10.7527/S1000-6893.2013.0114 |
| [5] |
都亨, 张文祥, 庞宝君, 等. 空间碎片[M]. 北京: 中国宇航出版社, 2007. DU Heng, ZHANG Wenxiang, PANG Baojun, et al. Space debris[M]. Beijing: China Aerospace Press, 2007. |
| [6] |
戴崇, 徐振海, 肖顺平. 非合作目标动态RCS仿真方法[J]. 航空学报, 2014, 35(5): 1374. DAI Chong, XU Zhenhai, XIAO Shunping. Simulation method of dynamics RCS for non-cooperative targets[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1374. DOI:10.7527/S1000-6893.2013.0411 |
| [7] |
FUJIMOTO K, SATOH A, FUKUNAGA S. System identification based on variational bayes method and the invariance under coordinate[C]// Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference. Orlando, FL: IEEE, 2011: 3882. DOI: 10.1109/cdc.2011.6160563
|
| [8] |
LUIZ C G D. Inertia parameter experimental estimation of a satellite simulator[J]. Advances in the Astronautical Sciences, 2008, 130(1): 969. |
| [9] |
王明, 黄攀峰, 常海涛. 非合作目标航天器质量特性参数辨识[J]. 飞行力学, 2014, 32(6): 536. WANG Ming, HUANG Panfeng, CHANG Haitao. Identification of mass characteristic parameters for non-cooperative target spacecraft[J]. Flight Dynamics, 2014, 32(6): 536. DOI:10.13645/j.cnki.f.d.20140917.008 |
| [10] |
韦文书.质量体附着航天器模型参数辨识及姿态跟踪耦合控制研究[D].哈尔滨: 哈尔滨工业大学, 2013 WEI Wenshu. Research on the parameters identification and attitude tracking coupling control for the mass body attached spacecraft[D]. Harbin: Harbin Institute of Technology, 2013 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D422565 |
| [11] |
WILSON E, LAGES C, MAH R. On-line, gyro-based mass property identification for thruster controlled spacecraft using recur-sive least squres[C]//Proceedings of the 45th IEEE International Midwest Symposium on Circuits and Systems. Tulsa, Oklahoma: IEEE, 2002. DOI: 10.1109/mwscas.2002.1186866
|
| [12] |
WILSON E, SUTTER D W, MAH R W. Motion-based mass and thruster property identification for thruster controlled spacecraft[C]//Proceedings of the 2005 AIAA Infotech@ Aerospace Conference. Arlington, Virginia: AIAA, 2005. DOI: 10.2514/6.2005-6907
|
| [13] |
侯忠生, 许建新. 数据驱动控制理论及方法的回顾和展望[J]. 自动化学报, 2009, 35(6): 650. HOU Zhongsheng, XU Jianxin. On data-driven control theory and method: the state of the art and perspective[J]. Acta Automat Sinica, 2009, 35(6): 650. DOI:10.3724/SP.J.1004.2009.00650 |
| [14] |
侯忠生, 金尚泰. 无模型自适应控制理论与应用[M]. 北京: 科学出版社, 2013.
|
| [15] |
侯忠生, 晏静文. 带有迭代学习前馈的快速路无模型自适应入口匝道控制[J]. 自动化学报, 2009, 35(5): 588. HOU Zhongsheng, YAN Jingwen. Model free adaptive control based freeway ramp metering with feedforward iterative learning controller[J]. Acta Automatica Sinica, 2009, 35(5): 588. DOI:10.3724/SP.J.1004.2008.00588SP.J.1004.2008.00588 |
| [16] |
梁佳, 刘劲松, 顾苗. MFA控制在热流模拟中的应用[J]. 航天器环境工程, 2009, 26(5): 431. LIANG Jia, LIU Jinsong, GU Miao. Application of model-free control in heat flow simulation[J]. Spacecraft Environment Engineering, 2009, 26(5): 431. DOI:10.3969/j.issn.1673-1379.2009.05.007 |
 2018, Vol. 50
2018, Vol. 50


