无人水面艇(unmanned surface vehicle, USV)作为一种小型水面智能任务平台,在海洋环境监测、海洋资源勘探以及现代化军事作战、维护海域安全等方面具有广阔的应用前景[1-2],已成为国内外无人装备领域研究的热点.目前,国外已有较多无人艇的实际应用,美国海军已装备包括近海港口级、远海舰队级以及多用途无人艇,以色列海军舰队也装备有不同作战用途的无人艇.相比国外,中国无人艇的研究开展较晚,应用实例较少.中国针对无人艇总体设计和智能控制开展相关研究的单位主要有海军工程大学、江苏科技大学、上海大学等院校和一些舰船研究所.航迹跟踪作为USV安全航行和完成各项使命任务的前提,同时也是USV智能控制的关键技术之一[3-4].不具有侧向推进器或侧向推进器在高速航行时失效的USV是一类典型的欠驱动系统,由于控制输入个数少于其所需控制的自由度个数,故该类系统存在不可积的加速度约束,具有一定的复杂性[5-6].
视线导引(line-of-sight, LOS)算法[7]作为一种经典有效的导引策略,其原理独立于动力学控制,不依赖于任何模型,对高频白噪声敏感度低,且需要设计的参数少,期望航向的获取只与船舶的实时位置和给定的期望航线有关,能够实时高效地计算期望航向并传递给控制层,因而被广泛应用于船舶的航迹跟踪控制.田勇等[8]利用视线导引算法和抗饱和PID控制算法实现了直线航迹跟踪控制器的设计,通过湖上试验验证了算法的有效性,但并未考虑外界扰动的影响.Oh等[9]将LOS导引策略与模型预测控制算法相结合,设计了一种无人艇航迹跟踪控制算法,并通过仿真实验证明了算法的有效性.Fossen等[10]提出了一种自适应积分LOS制导算法,与PID航向控制器共同作用,实现了水面船舶航迹跟踪控制系统的设计,并证明了在平衡点处,控制系统是一致半全局指数稳定的.Caharija等[11]提出了一种基于ILOS导引算法和动态反馈控制的航迹跟踪算法,证明了控制系统是全局k-指数稳定的,并通过直线航迹跟踪仿真试验验证了算法的有效性.此外,鲁棒自适应控制[12]、模糊神经网络控制[13]以及非线性控制[14]等为航迹跟踪控制算法的研究提供了参考.
虽然目前国内外对于欠驱动USV航迹跟踪控制取得了一定的研究成果,但大多仍处于仿真验证或实验室半物理仿真阶段,实际应用的实例比较少见.因此,本文针对真实海洋环境下无人艇的航迹跟踪问题,采用理论研究、仿真分析和试验验证相结合的方法,首先以“海鲟03号”无人艇操纵运动模型和辨识得到的参数为基础,提出了一种基于改进视线导引算法与自适应滑模航向控制算法级联形式的欠驱动无人艇航迹跟踪控制算法,并基于李雅普诺夫理论证明了当所有控制目标实现时,控制系统为一致全局渐近稳定的.同时,航迹跟踪对比仿真实验,验证了算法的有效性和先进性.最后,利用“海鲟03号”无人艇对所提出的控制算法进行了海上试验,验证了该算法在实际工程应用中的正确性和有效性.
1 问题描述 1.1 USV数学模型“海鲟”号系列无人艇是海军工程大学自主研制的一款具有遥控、半自主和全自主控制的多功能智能无人水面航行器,如图 1所示.“海鲟03”号无人艇长7.0 m,宽2.05 m,喷水推进、最高航速35节,采用模块化设计思想,可搭载有效载荷900 kg,续航能力为15 h(15节),搭载有姿态方位组合导航、光电设备、无线通信设备、先进的雷达及武器系统等,配备自主开发的无人艇载中央控制系统和地面站遥测控系统等,可与地面站(母舰)指挥控制中心协同配合,通过搭载不同的任务模块满足不同的任务需求.

|
图 1 “海鲟03”号无人艇 Figure 1 "Sturgeon 03" USV |
“海鲟03”号USV的运动学模型如下:
| $ \begin{array}{l} \dot x = u\cos \left( \psi \right) - v\sin \left( \psi \right),\\ \dot y = u\sin \left( \psi \right) + v\cos \left( \psi \right),\\ \dot \psi = r. \end{array} $ | (1) |
式中:x、y、ψ分别为惯性坐标系{i}下USV在水平面的位置和艏向角;u、v、r分别为USV在船体坐标系{b}中的纵向、横向线速度及艏向角速度.
“海鲟03”号USV的动力学模型如下
| $ \mathit{\boldsymbol{M\dot v}} + \mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} + \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{v}} \right) = \mathit{\boldsymbol{Bf}}. $ |
式中:v=[u, v, r]T,M为欠驱动USV的惯性参数矩阵;C(υ)为科里奥利/向心力矩阵;D(υ)为阻尼参数矩阵,D(υ) ≠ DT(υ),D(υ)>0;f=[Tu, Tr]T为控制输入矩阵,其中Tu为前进推力,Tr为偏航力矩;矢量矩阵B为控制输入配置矩阵,作用是将控制输入映射成作用到艇体上相应的力及力矩.通常,矩阵M、D(υ)、C(υ)、B有如下结构:
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {{m_{11}}}&0&0\\ 0&{{m_{22}}}&0\\ 0&0&{{m_{33}}} \end{array}} \right].\;\;\;\mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{v}} \right) = \left[ {\begin{array}{*{20}{c}} {{d_{11}}}&0&0\\ 0&{{d_{22}}}&0\\ 0&0&{{d_{33}}} \end{array}} \right]. $ |
| $ \mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{v}} \right) = \left[ {\begin{array}{*{20}{c}} 0&0&{ - {m_{22}}v}\\ 0&0&{{m_{11}}u}\\ {{m_{22}}v}&{ - {m_{11}}u}&0 \end{array}} \right].\;\;\;\;\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{b_{11}}}&0\\ 0&{{b_{22}}}\\ 0&{{b_{32}}} \end{array}} \right]. $ |
欠驱动USV水平面的航迹跟踪问题可分为两个子问题[15]:1)动力学问题,即设计纵向控制律Tu使得USV保持期望的纵向速度;2)几何学问题,即设计艏向控制律Tr使得USV的位置收敛到参考路径上.因此,本文所研究的航迹跟踪问题可描述为:在海流等外界扰动存在的情况下,设计导引策略和航向控制算法,使得从任意初始位置和任意初始状态下出发的USV以期望纵向速度ud前进,最终使USV能够沿期望的航迹航行,此时其横向误差收敛到0.因此控制目标可表示为:
| $ \mathop {\lim }\limits_{t \to \infty } {y_{\rm{e}}} = \left( {y - {y_{\rm{d}}}} \right) = 0, $ |
| $ \mathop {\lim }\limits_{t \to \infty } {u_{\rm{e}}} = \left( {u - {u_{\rm{d}}}} \right) = 0. $ |
本文设计的航迹跟踪控制系统采用LOS导引子系统与航向控制子系统级联的形式.导引子系统根据USV实时的位置、姿态以及期望航线的信息,求解出期望的USV航向,而航向控制子系统则根据导引子系统给定的期望信号和USV当前的运动信息求解出期望的舵机操纵信号,以此使得USV航迹跟踪的位置和航向能够渐进收敛到平衡位置,同时航速控制子系统作为一个单独的负反馈回路实现USV对期望速度的跟踪.
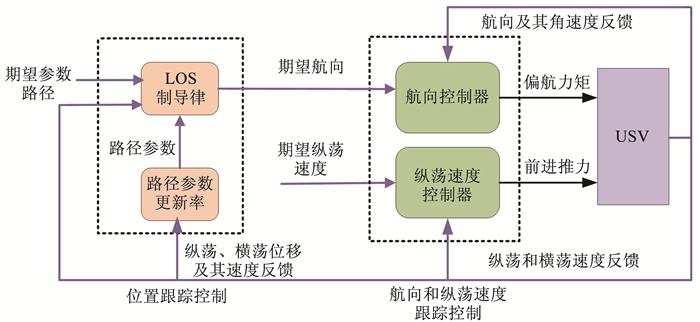
2.1 航迹跟踪控制系统设计航迹跟踪控制系统设计框图如图 2所示,LOS导引算法利用从导航系统获取的无人艇当前位置信息(x(t), y(t))和期望路径点(xd, yd)信息,实时计算USV当前位置与期望航迹之间的横向误差ye(t),并将其映射到指令艏向角ψd,然后设计航向控制器跟踪ψd,在航向控制子系统的作用下最终间接消除USV与参考航迹之间的横向误差,实现对期望航线的跟踪.可以看出,级联的设计方法使得航迹跟踪控制系统的结构清晰,物理意义明确,便于控制器设计和稳定性分析.
|
图 2 航迹跟踪控制系统设计框图 Figure 2 Design block diagram of the path tracking control system |
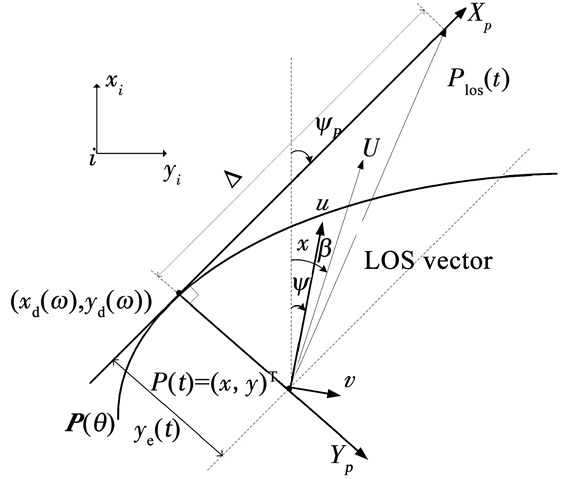
LOS导引算法是一种经典有效的导航算法,文献[7]中给出了船舶运动控制领域中LOS导引算法的定义:LOS矢量是船舶当前位置在期望航路投影点的切线上一点与当前船舶位置的连线.通过控制船舶合速度的方向始终对准LOS矢量,引导船舶逼近期望航路.LOS导引原理独立于动力学控制,不依赖于任何数学模型,需要设计的参数少,且对高频白噪声不敏感,期望航向的获取只与给定的期望航路和船舶的实时位置有关,能够实时高效地计算期望航向并传递给控制层.LOS导引算法可分为基于前视距离和包围圈两种,本文采用基于前视距离的LOS导引算法,如图 3所示,以USV当前位置(x(t), y(t))在参考路径上的投影点(xd(ω), yd(ω))为原点建立Serret-Frenet坐标系,其中ω为路径参数变量.该坐标系的纵轴Xp沿参考路径的切线方向,横轴Yp沿参考路径的法线方向并指向右侧,且纵轴Xp与惯性坐标系纵轴间的夹角记为路径方位角为
| $ {\psi _p}\left( \omega \right) = \arctan \left( {\frac{{{{y'}_{\rm{d}}}\left( \omega \right)}}{{{{x'}_{\rm{d}}}\left( \omega \right)}}} \right) \in \left[ { - {\rm{ \mathsf{ π} }},{\rm{ \mathsf{ π} }}} \right]. $ | (2) |
|
图 3 基于前视距离的LOS导引策略原理图 Figure 3 LOS guidance based on lookahead distance |
式中:
路径参数变量的变化率满足:
| $ \dot \omega = \frac{U}{{\sqrt {{{x'}_{\rm{d}}}^2\left( \omega \right) + {{y'}_{\rm{d}}}^2\left( \omega \right)} }} > 0, $ |
式中,
传统的LOS导引算法[7]如下
| $ {\chi _{{\rm{los}}}} = {\psi _p}\left( \omega \right) + \arctan \left( { - \frac{{{y_{\rm{e}}}\left( t \right)}}{{\mathit{\Delta}} }} \right), $ |
式中,χlos为期望的航迹角.故期望艏向角为
| $ {\psi _{\rm{d}}} = {\chi _{{\rm{los}}}} - \beta = {\psi _p}\left( \omega \right) + \arctan \left( { - \frac{{{y_{\rm{e}}}\left( t \right)}}{{\mathit{\Delta}} }} \right) - \beta , $ |
式中,β为由于无人艇在真实海洋环境中航行时,其实际航迹跟踪过程中会受到海流等外界干扰的影响,从而会导致无人艇的航迹角χ与其艏向角ψ之间存在夹角,即漂角.
本文基于自适应观测技术,设计自适应观测器来估计缓慢变化的漂角β,再选择恰当的虚拟控制输入yint对漂角进行补偿,最终实现对期望航迹的精确跟踪.同时,考虑到当无人艇距离期望航线较远时,首要任务是快速逼近期望航线,减小横向误差;当无人艇在期望航线附近时,首要任务是精确跟踪期望航迹,避免位置超调和震荡行为,因此时变的前视距离会使无人艇的操纵更加灵活.基于上述思想,提出一种新的LOS导引算法,设计如下:
| $ {\psi _{\rm{d}}} = {\psi _p}\left( \omega \right) - \arctan \left( {\frac{{{y_{\rm{e}}}\left( t \right)}}{\Delta } + {y_{{\rm{int}}}}} \right), $ | (3) |
| $ {{\dot y}_{{\rm{int}}}} = k\frac{{\Delta U{y_{\rm{e}}}\left( t \right)}}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + \Delta {y_{{\rm{int}}}}} \right)}^2}} }}, $ | (4) |
| $ k = {k_i}{{\rm{e}}^{ - \rho {y_{\rm{e}}}{{\left( t \right)}^2}}}, $ | (5) |
| $ \Delta = \left( {{\Delta _{\max }} - {\Delta _{\min }}} \right){{\rm{e}}^{ - \lambda {y_{\rm{e}}}{{\left( t \right)}^2}}} + {\Delta _{\min }}. $ | (6) |
式中,ki、ρ、λ分别为要设计的严格大于零的常值参数;yint为所要设计的虚拟控制输入;Δmax、Δmin分别为前视距离Δ的最大和最小值.记
下面给出以上导引子系统的稳定性分析.
由图 3的几何关系可得
| $ \begin{array}{l} {y_{\rm{e}}}\left( t \right) = - \left( {x\left( t \right) - {x_{\rm{d}}}\left( \omega \right)} \right)\sin {\psi _p}\left( \omega \right) + \\ \;\;\;\;\;\;\;\;\;\;\left( {y\left( t \right) - {y_{\rm{d}}}\left( \omega \right)} \right)\cos {\psi _p}\left( \omega \right), \end{array} $ | (7) |
对ye(t)求导可得
| $ \begin{array}{l} {{\dot y}_{\rm{e}}}\left( t \right) = - \left( {\dot x\left( t \right) - {{\dot x}_{\rm{d}}}\left( \omega \right)} \right)\sin {\psi _p}\left( \omega \right) - \\ \;\;\;\;\;\;\;\;\;{{\dot \psi }_p}\left( \omega \right)\left( \theta \right)\left( {x\left( t \right) - {x_{\rm{d}}}\left( \omega \right)} \right)\cos {\psi _p}\left( \omega \right) + \\ \;\;\;\;\;\;\;\;\;\left( {\dot y\left( t \right) - {{\dot y}_{\rm{d}}}\left( \omega \right)} \right)\cos {\psi _p}\left( \omega \right) - \\ \;\;\;\;\;\;\;\;\;{{\dot \psi }_p}\left( \omega \right)\left( {y\left( t \right) - {y_{\rm{d}}}\left( \omega \right)} \right)\sin {\psi _p}\left( \omega \right). \end{array} $ | (8) |
由式(2)可得
| $ {{\dot x}_{\rm{d}}}\left( \omega \right)\sin {\psi _p}\left( \omega \right) - {{\dot y}_{\rm{d}}}\left( \omega \right)\cos {\psi _p}\left( \omega \right) = 0. $ | (9) |
且由图 3所示的几何关系得到:
| $ \begin{array}{l} {{\dot \psi }_p}\left( \omega \right)\left[ {\left( {x\left( t \right) - {x_{\rm{d}}}\left( \omega \right)} \right)\cos {\psi _p}\left( \omega \right) + } \right.\\ \left. {\left( {y\left( t \right) - {y_{\rm{d}}}\left( \omega \right)} \right)\sin {\psi _p}\left( \omega \right)} \right] = 0. \end{array} $ | (10) |
将式(1)、(9)、(10)代入式(8)中可得
| $ {{\dot y}_{\rm{e}}}\left( t \right) = U\sin \left( {\psi + \beta - {\psi _p}\left( \omega \right)} \right). $ | (11) |
式中:
条件1 漂角β很小(一般β < 5°)且为缓慢变化.即存在βmax>0,使得|β| ≤βmax,且
那么,式(11)等价于:
| $ {{\dot y}_{\rm{e}}}\left( t \right) = U\sin \left( {\psi - {\psi _p}\left( \omega \right)} \right) + U\cos \left( {\psi - {\psi _p}\left( \omega \right)} \right)\beta . $ |
令
| $ \begin{array}{l} {{\dot y}_{\rm{e}}}\left( t \right) = U\sin \left( {\tilde \psi + {\psi _{\rm{d}}} - {\psi _p}\left( \omega \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;U\cos \left( {\tilde \psi + {\psi _{\rm{d}}} - {\psi _p}\left( \omega \right)} \right)\beta , \end{array} $ | (12) |
又因为
| $ \begin{array}{l} \sin \left( { - \arctan \left( {\frac{1}{\Delta }{y_{\rm{e}}}\left( t \right) + {y_{{\mathop{\rm int}} }}} \right)} \right) = \\ \frac{{{y_{\rm{e}}}\left( t \right) + {\Delta y_{{\mathop{\rm int}} }}}}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + {\Delta y_{{\mathop{\rm int}} }}} \right)}^2}} }}, \end{array} $ | (13) |
| $ \begin{array}{l} \cos \left( { - \arctan \left( {\frac{1}{\Delta }{y_{\rm{e}}}\left( t \right) + {y_{{\mathop{\rm int}} }}} \right)} \right) = \\ \frac{\Delta }{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + {\Delta y_{{\mathop{\rm int}} }}} \right)}^2}} }}. \end{array} $ | (14) |
将式(13)、(14)代入式(12)可得
| $ \begin{array}{l} {{\dot y}_{\rm{e}}}\left( t \right) = - \frac{{U\left( {{y_{\rm{e}}}\left( t \right) + {\Delta y_{{\mathop{\rm int}} }}} \right)}}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + {\Delta y_{{\mathop{\rm int}} }}} \right)}^2}} }} + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{U\Delta }}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + {\Delta y_{{\mathop{\rm int}} }}} \right)}^2}} }}\beta + \\ \;\;\;\;\;\;\;\;\;\;\;U\left[ {{\varphi _1}\left( {{y_{\rm{e}}}\left( t \right) + \tilde \psi } \right) + \beta {\varphi _2}\left( {{y_{\rm{e}}}\left( t \right) + \tilde \psi } \right)} \right]\tilde \psi , \end{array} $ | (15) |
其中:
| $ \begin{array}{l} {\varphi _1}\left( {{y_{\rm{e}}}\left( t \right) + \tilde \psi } \right) = \frac{{\sin \tilde \psi }}{{\tilde \psi }}\cos \left( {{\psi _{\rm{d}}} - {\psi _p}\left( \omega \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\cos \tilde \psi - 1}}{{\tilde \psi }}\sin \left( {{\psi _{\rm{d}}} - {\psi _p}\left( \omega \right)} \right), \end{array} $ |
| $ \begin{array}{l} {\varphi _2}\left( {{y_{\rm{e}}}\left( t \right) + \tilde \psi } \right) = - \frac{{\sin \tilde \psi }}{{\tilde \psi }}\sin \left( {{\psi _{\rm{d}}} - {\psi _p}\left( \omega \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\cos \tilde \psi - 1}}{{\tilde \psi }}\cos \left( {{\psi _{\rm{d}}} - {\psi _p}\left( \omega \right)} \right). \end{array} $ |
由高等数学知识可知,|(cos
| $ \left| {{\varphi _1}\left( {{y_{\rm{e}}}\left( t \right),\tilde \psi } \right)} \right| \le 1.73,\left| {{\varphi _2}\left( {{y_{\rm{e}}}\left( t \right),\tilde \psi } \right)} \right| \le 1.73. $ |
假定航向控制子系统能够准确地跟踪期望航向角ψd,取虚拟控制输入yint=
| $ \begin{array}{l} {{\dot y}_{\rm{e}}}\left( t \right) = - \frac{{U{y_{\rm{e}}}\left( t \right)}}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + \Delta \hat \beta } \right)}^2}} }} + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{U\Delta }}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + \Delta \hat \beta } \right)}^2}} }}\tilde \beta . \end{array} $ |
取正定且径向无界的李雅普诺夫函数V1为
| $ {V_1}\left( {{y_{\rm{e}}}\left( t \right),t,\tilde \beta } \right) = \frac{1}{2}{y_{\rm{e}}}{\left( t \right)^2} + \frac{1}{{2k}}{{\tilde \beta }^2} > 0. $ | (16) |
式中:ye(t)≠0,
对式(16)微分可得
| $ \begin{array}{l} {{\dot V}_1}\left( {{y_{\rm{e}}}\left( t \right),t,\tilde \beta } \right) = {y_{\rm{e}}}\left( t \right){{\dot y}_{\rm{e}}}\left( t \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{k}\tilde \beta \dot {\tilde \beta} = - \frac{{U{{\rm{y}}_e}{{\left( t \right)}^2}}}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + \Delta \hat \beta } \right)}^2}} }} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\frac{{U\Delta {y_e}\left( t \right)}}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + \Delta \hat \beta } \right)}^2}} }} + \frac{1}{k}\dot {\tilde \beta} } \right). \end{array} $ | (17) |
由于
| $ {{\dot V}_1}\left( {{y_{\rm{e}}}\left( t \right),t,\tilde \beta } \right) = - \frac{{U{y_{\rm{e}}}{{\left( t \right)}^2}}}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + \Delta \hat \beta } \right)}^2}} }} \le 0. $ |
因此,在平衡点ye(t)=0处,导引子系统是一致全局渐近稳定的(uniform global asymptotic stability,UGAS).
2.3 航向控制子系统通常情况下,设计航向控制器时,船舶水平面内的运动数学模型通常采用Nomoto模型,但是该模型是在低频小舵角的假设条件下进行推导的,而无人艇有着更快的航速和更好的机动性,通常需要高频操舵,因此Nomoto模型不适用于无人艇.本文在考虑无人艇特性以及模型非线性的基础上,采用Norrbin模型来进行航向控制器的设计:
| $ \begin{array}{*{20}{c}} {T\dot \psi = {H_N}\left( \psi \right) = K\delta ,}\\ {{H_N}\left( \psi \right) = {n_3}{{\dot \psi }^3} + {n_2}{{\dot \psi }^2} + {n_1}\dot \psi + {n_0}.} \end{array} $ | (18) |
式中:ψ为航向角;δ为舵角输入;T为时间常数;K为增益;HN(ψ)为非线性项,用于描述USV的操纵性能;n0、n1、n2、n3分别为Norrbin系数,当USV具有对称结构时,n0=n2≈0;当USV具有直行特性时,n1=1,否则n1=-1.故式(18)可简化为
| $ T\ddot \psi + {n_3}{{\dot \psi }^3} + \dot \psi = K\delta . $ |
因此航向控制子系统∑2为:
| $ \dot r = - \frac{{{n_3}}}{T}{r^3} - \frac{1}{T}\dot \psi + \frac{K}{T}\delta , $ |
| $ \dot \psi = r. $ |
无人艇艏向控制目标为
| $ \psi = {\psi _{\rm{d}}} = {\psi _p}\left( \omega \right) - \arctan \left( {\frac{{{y_{\rm{e}}}\left( t \right)}}{\Delta } + {y_{{\mathop{\rm int}} }}} \right), $ | (19) |
因此,
| $ {r_{\rm{d}}} = {{\dot \psi }_{\rm{d}}} = {{\dot \psi }_p}\left( \omega \right) - \frac{{{{\left( {\frac{{{y_{\rm{e}}}\left( t \right) + \Delta {y_{{\mathop{\rm int}} }}}}{\Delta }} \right)}^\prime }{\Delta ^2}}}{{{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + \Delta {y_{{\mathop{\rm int}} }}} \right)}^2}}}. $ |
定义一阶滑膜面为
| $ s: = \bar r + \gamma \bar \psi . $ |
式中: ψ =ψ-ψd,r=r-rd.
选取李雅普诺夫函数V2=
| $ {{\dot V}_2} = s\left( { - \frac{{{n_3}}}{T}{r^3} - \frac{1}{T}r + \frac{K}{T}\delta - {{\dot r}_d} + \gamma \bar r} \right). $ | (20) |
因此艏向控制律为
| $ {T_r} = \delta = \frac{T}{K}\left( {\frac{{{n_3}}}{T}{r^3} + \frac{1}{T}r + {{\dot r}_{\rm{d}}} - \gamma \bar r - {k_{\rm{d}}}s} \right), $ | (21) |
式中,kd>0为常值参数,将式(20)代入式(21)可得
| $ {{\dot V}_2} = - {k_{\rm{d}}}{s^2} < 0. $ |
因此,s=0(或r=0且ψ=0)为航向控制子系统的平衡点且在该处系统∑2是一致全局渐近稳定的(uniform global asymptotic stability,UGAS).
3 系统的稳定性分析导引子系统与航向控制子系统一起构成无人艇航迹跟踪控制系统,使无人艇从任意初始状态出发,沿期望航迹运动,横向误差ye(t)全局渐近收敛,从而完成对期望航线的跟踪.航向控制子系统通过航向跟踪误差ψ =φ-ψd影响导引子系统,而导引子系统则通过参考信号ψd和出现在参考信号rd中的ye(t)扰动航向控制子系统,下面给出整个控制系统的稳定性分析.无人艇航迹控制系统可表述为
| $ \left\{ \begin{array}{l} {{\dot y}_{\rm{e}}}\left( t \right) = U\sin \left( {\psi + \beta - {\psi _p}\left( \omega \right)} \right),\\ \dot \psi = r,\\ \dot r = - \frac{{{n_3}}}{T}{r^3} - \frac{1}{T}\dot \psi + \frac{K}{T}\delta . \end{array} \right. $ | (22) |
定理1 当无人艇能够准确地跟踪导引子系统给出的期望艏向角即满足式(19)且控制输入满足式(21)时,系统(22)是全局渐近稳定的.
证明 选取正定且径向无界的李雅普诺夫函数为V3=
| $ \begin{array}{l} {{\dot V}_3} = {y_{\rm{e}}}\left( t \right){{\dot y}_{\rm{e}}}\left( t \right) + s\dot s = \\ \;\;\;\;\;\;\;{y_{\rm{e}}}\left( t \right)U\sin \left( {\psi + \beta - {\psi _p}\left( \omega \right)} \right) + \\ \;\;\;\;\;\;\;s\left( { - \frac{{{n_3}}}{T}{r^3} - \frac{1}{T}r + \frac{K}{T}\delta - {{\dot r}_{\rm{d}}} + \gamma \bar r} \right). \end{array} $ | (23) |
将式(19)、(21)代入式(23)可得
| $ \begin{array}{l} {{\dot V}_3} = {y_{\rm{e}}}\left( t \right)U\sin \left( {\beta - \arctan \left( {\frac{{{y_{\rm{e}}}\left( t \right)}}{\Delta } + {y_{{\mathop{\rm int}} }}} \right)} \right) + \\ \;\;\;\;\;\;s\left( { - \frac{{{n_3}}}{T}{r^3} - \frac{1}{T}r + \frac{K}{T}\frac{T}{K}\left( {\frac{{{n_3}}}{T}{r^3} + \frac{1}{T}r + } \right.} \right.\\ \;\;\;\;\;\;\left. {\left. {{{\dot r}_{\rm{d}}} - \gamma \bar r - {k_{\rm{d}}}s} \right) - {{\dot r}_{\rm{d}}} + \gamma \bar r} \right) = \\ \;\;\;\;\;\;{y_{\rm{e}}}\left( t \right)U\left( {\frac{{\sin \beta \Delta }}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + \Delta {y_{{\mathop{\rm int}} }}} \right)}^2}} }} - } \right.\\ \;\;\;\;\;\;\left. {\frac{{\cos \beta \left( {{y_{\rm{e}}}\left( t \right) + \Delta {y_{{\mathop{\rm int}} }}} \right)}}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + \Delta {y_{{\mathop{\rm int}} }}} \right)}^2}} }}} \right) - {k_{\rm{d}}}{s^2}. \end{array} $ | (24) |
由条件1可知,漂角β很小(一般β < 5°),即满足sin β≈β,cos β≈1,且假定自适应观测器(4)可较为准确估计缓慢变化的漂角β,即yint=
| $ \begin{array}{l} {{\dot V}_3} = {y_{\rm{e}}}\left( t \right)U\left( {\frac{{\beta \Delta }}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + \Delta \beta } \right)}^2}} }} - } \right.\\ \;\;\;\;\;\;\;\left. {\frac{{\left( {{y_{\rm{e}}}\left( t \right) + \Delta \beta } \right)}}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + \Delta \beta } \right)}^2}} }}} \right) - {k_{\rm{d}}}{s^2} = \\ \;\;\;\;\;\;\; - \frac{{U{y_{\rm{e}}}{{\left( t \right)}^2}}}{{\sqrt {{\Delta ^2} + {{\left( {{y_{\rm{e}}}\left( t \right) + \Delta \beta } \right)}^2}} }} - {k_{\rm{d}}}{s^2} < 0. \end{array} $ |
因此控制系统(22)在其平衡点(ye(t), s)=(0, 0)处是一致全局渐近稳定的.
4 仿真验证及结果分析为了验证算法的先进性和普适性,选择期望航迹为常见的曲线路径,在MATLAB平台下将本文所设计的航迹跟踪控制算法(算法1)和传统LOS导引策略下的航迹跟踪算法(算法2)进行仿真实验对比.USV在海上航行时,风、浪的干扰作用最终将作用到对无人艇舵角控制的干扰,即对其航向控制子系统的干扰,因此本文通过在航向控制中添加功率谱密度为0.1的白噪声来进行模拟.仿真过程中海流设置为:Uc=0.2 m/s,ψc=30°;USV的初始状态位置为x=0 m,y=-15 m,初始航向设置为ψ=90°,航速设定为10节.
算法1中的参数设定如下:λ=4,ki=0.03,ρ=5,γ=4.2,Δmin=6,Δmax=16;算法2中的参数设定为:Δ=6,γ=5.仿真结果如图 4~7所示.
|
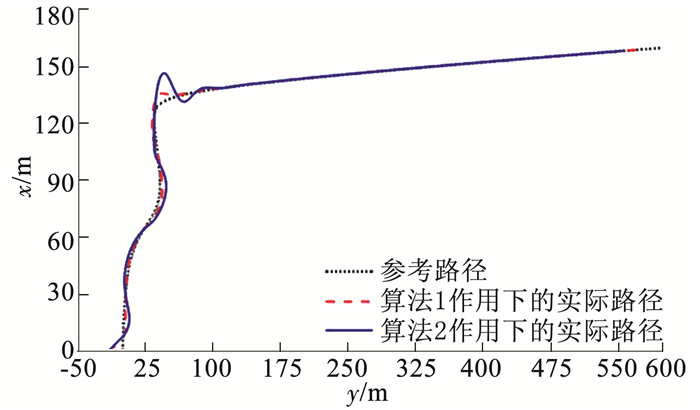
图 4 USV曲线路径跟踪轨迹 Figure 4 Curve path tracking of USV |

|
图 5 横向误差的变化 Figure 5 Variation of cross-track error |
|
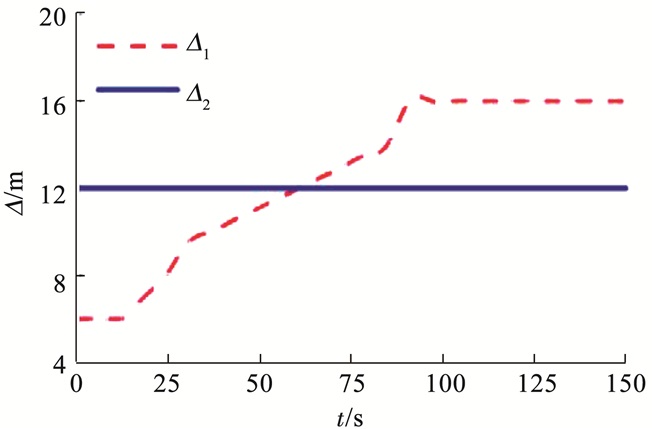
图 6 前视距离的变化 Figure 6 Variation of lookahead distance |
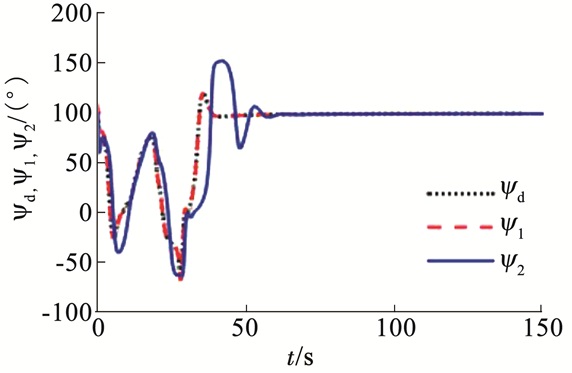
|
图 7 期望艏向角及艏向角的变化 Figure 7 Variation of expected heading angle and actual heading angles |
由图 4可以看出,在算法1和算法2的单独作用下,USV都能较为准确地跟踪给定的期望航迹,且在期望航迹为曲线段时,算法1的跟踪效果要明显优于算法2;从图 5可得,在算法1和算法2的单独作用下,USV分别能够在40、60 s时收敛到期望航迹,在算法1的作用下,USV航迹跟踪过程中超调较小(最大为10 m),且运动轨迹相对平滑,而算法2存在较大超调行为(最大达20 m),这是由于算法1中设计的时变前视距离能够使无人艇在距离期望航迹较远时,自适应选择较小的前视距离,从而快速逼近计划航线,而在距离期望航迹较近时,自适应选择较大的前视距离,从而能够控制无人艇平缓地靠近计划航线,这与图 6中算法1的前视距离变化情况是一致的,因此时变前视距离的设计能够使USV的操纵性更加灵活.图 7给出了航迹跟踪过程中无人艇的期望艏向角、算法1和算法2作用下USV艏向角的变化情况,可以看出,算法1的跟踪效果要明显优于算法2,且艏向角跟踪曲线更为平滑.
5 实艇验证及结果分析 5.1 试验描述海上实艇试验的任务区域为青岛至连云港之间某一海域,试验时,该海域的海洋环境条件为海况2级,风力3级,实艇试验过程如图 8所示.试验中设定的期望航线为一平行四边形,航线总长度为2 km,期望航速设定为10节,航迹中包括锐角和钝角转角,可检验无人艇控制算法在转弯处的跟踪性能.跟踪过程中,艇载控制子系统实时记录无人艇的位置、航向、风向风速、机舱温度、发动机状态、视频等实时信息,并通过无线通信信道实时发送给岸基(母舰)控制子系统,在显示设备上进行实时显示.

|
图 8 航迹跟踪实艇试验过程 Figure 8 The real ship test process of path tracking |
根据航迹跟踪过程中数据库记录的试验数据,以经度为横坐标,以纬度为纵坐标,将USV的实际航行航迹与设定的跟踪期望航迹进行对比,如图 9所示,start和end分别为USV起点和终点,USV逆时针航行.
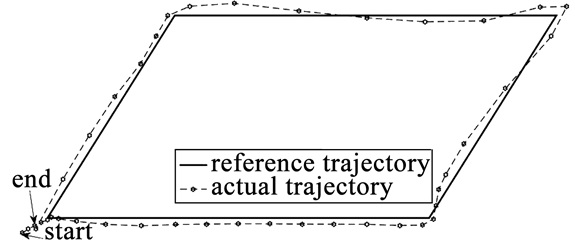
|
图 9 “海鲟03”试验的航迹跟踪结果 Figure 9 Test result of path tracking of "sturgeon 03" USV |
从图 9可以看出,在本文设计的航迹跟踪控制算法的作用下,无人艇能较为准确地跟踪预先设定的期望航迹,且在整个航迹跟踪过程中,航迹误差相对较小;由图 10中横向误差曲线的变化情况可以看出,当无人艇航行至期望航迹的拐点处时,尤其是航向变化率较大的锐角拐点处,由于期望航迹的航向变化较为“猛烈”,导致无人艇的航迹跟踪误差较大,误差最大处约为20 m,但是在本文航迹跟踪控制算法的作用下,能够使得无人艇较快地向着减小航迹误差的方向运动,并在短时间内使得无人艇的实际航迹收敛到期望航迹附近,从而保证了航迹跟踪控制的精度,同时也证明了该控制算法在实际工程应用中的有效性.
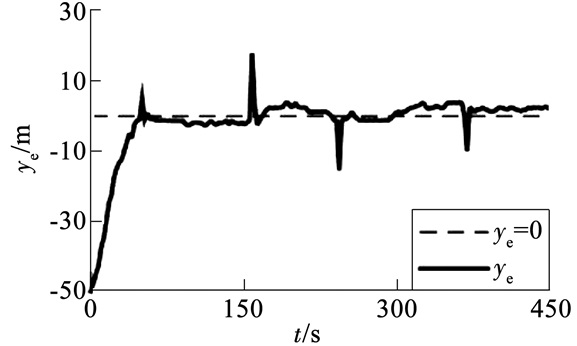
|
图 10 横向误差的变化 Figure 10 Varying of cross-track error |
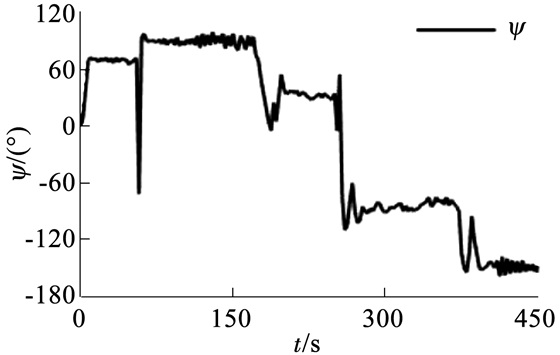
|
图 11 航向角的变化 Figure 11 Varying of course degree |
1) 研究真实海洋环境下一类欠驱动无人艇的航迹跟踪控制问题,提出了一种基于改进视线导引算法与自适应滑模航向控制算法级联形式的欠驱动无人艇航迹跟踪控制算法.
2) 基于李雅普诺夫理论和级联系统理论证明了当所有控制目标实现时,本文所提出的控制系统为一致全局渐近稳定的.
3) 以“海鲟03”号无人艇操纵运动模型及辨识的参数为基础,通过与传统基于视线导引的航迹跟踪算法进行仿真实验对比分析,表明了文中所提出的控制算法具有更好的航迹跟踪效果和动态性能,具有一定的先进性.
4) 在青岛至连云港之间某海域,利用“海鲟03号”无人艇对所提出的控制算法进行了海上试验,验证了该算法在实际工程应用中的有效性.
| [1] |
张树凯, 刘正江, 张显库, 等. 无人船艇的发展及展望[J]. 世界海运, 2015, 38(9): 29. ZHANG Shukai, LIU Zhengjiang, ZHANG Xianku, et al. The development and outlook of unmanned vessel[J]. World Shipping, 2015, 38(9): 29. DOI:10.16176/jcnki2l-1284.2015.09.008 |
| [2] |
薛春祥, 黄孝鹏, 朱咸军, 等. 外军无人系统现状与发展趋势[J]. 雷达与对抗, 2016, 36(1): 1. XUE Chunxiang, HUANG Xiaopeng, ZHU Xianjun, et al. Status quo and development trends of foreign military's unmanned systems[J]. Radar & ECM, 2016, 36(1): 1. DOI:10.19341/j.cnki.issn.1009-0401.2016.01.001 |
| [3] |
王浩铎, 王钦若, 吴小泽. 船舶全局一致渐进路径跟踪变积分增益导航策略[J]. 控制理论与应用, 2015, 32(3): 849. WANG Haoduo, WANG Qinruo, WU Xiaoze. Uniformly globally asymptotically stable path following with integral gain-variable guidance law for ships[J]. Control Theory & Applications, 2015, 32(3): 849. DOI:10.7641/CTA.2015.14067 |
| [4] |
王常顺, 肖海荣. 基于自抗扰控制的水面无人艇路径跟踪控制器[J]. 山东大学学报(工学版), 2016, 46(4): 54. WANG Changshun, XIAO Hairong. Path following controller for unmanned surface vessels based on ADRC[J]. Journal of Shandong University (Engineering Science), 2016, 46(4): 54. DOI:10.6040/j.issn.1672-3961.0.2016.010 |
| [5] |
FOSSEN T I, PETTERSEN K Y. On uniform semiglobal exponential stability (USGES) of proportional line-of-sight guidance laws[J]. Automatica, 2014, 50(11): 2912. DOI:10.1016/j.automatica.2014.10.018 |
| [6] |
FOSSEN T I, LEKKAS A M. Direct and indirect adaptive integral line-of-sight path-following controllers for marine craft exposed to ocean currents[J]. International Journal of Adaptive Control and Signal Processing, 2015, 28(3): 20. DOI:10.1002/acs.2550 |
| [7] |
BORHAUG E, PAVLOV A, PETTERSEN K Y. Integral LOS control for path following of underactuated marine surface vessels in the presence of constant ocean currents[J]. Proceedings of the 47th IEEE Conference on Decision and Control. Cancun, Mexico: IEEE, 2008, 4984. |
| [8] |
田勇, 王丹, 彭周华, 等. 无人水面艇直线航迹跟踪控制器的设计与验证[J]. 大连海事大学学报, 2015, 41(4): 14. TIAN Yong, WANG Dan, PENG Zhouhua, et al. Design and validation of path tracking controller for USV along straight-lines[J]. Journal of Dalian Maritime University, 2015, 41(4): 14. DOI:10.16411/j.cnki.issn1006-7736.2015.04.017 |
| [9] |
OH S R, SUN Jing. Path following of underactuated marine surface vessels using line-of-sight based model predictive control[J]. Ocean Engineering, 2010, 37(2): 289. DOI:10.1016/j.oceaneng.2009.10.004 |
| [10] |
FOSSEN T I, PETTERSEN K Y, GALEAZZI R. Line-of-sight path following for dubins paths with adaptive sideslip compensation of drift forces[J]. IEEE Transactions on Control Systems Technology, 2015, 23(2): 820. DOI:10.1109/TCST.2014.2338354 |
| [11] |
CAHARIJA W, PETTERSEN KY, SORENSEN A J, et al. Relative velocity control and integral LOS for path following of autonomous surface vessels: Merging intuition with theory[J]. Engineering for the Marine Environment, 2014, 228(2): 180. DOI:10.1177/1476-090213512293 |
| [12] |
DO K D. Global robust adaptive path-tracking control of underactuated ships under stochastic disturbances[J]. Ocean Engineering, 2016, 111: 267. DOI:10.1016/j.oceaneng.2015.10.038 |
| [13] |
董早鹏, 刘涛, 万磊, 等. 基于Takagi-Sugeno模糊神经网络的欠驱动无人艇直线航迹跟踪控制[J]. 仪器仪表学报, 2015, 36(4): 863. DONG Zaopeng, LIU Tao, WAN Lei, et al. Straight-path tracking control of underactuated USV based on Takagi-Sugeno fuzzy neural network[J]. Chinese Journal of Scientific Instrument, 2015, 36(4): 863. DOI:10.16322/j.cnki.issn123-7687.2015.04.014 |
| [14] |
ZHANG Tianhong, ZHANG Jun, LIU Zhilin, et al. Finite time control line path following of underactuated surface vessels[C]//Proceedings of the 34th Chinese control conference. Hangzhou: IEEE, 2015: 5084. DOI: 10.1109/ChiCC.2015.7260432
|
| [15] |
WIIG M S, PETTERSEN K Y, KROGSTAD T R. Uniform semiglobal exponential stability of integral line-of-sight guidance laws[J]. IFAC-PapersOnLine, 2015, 48(16): 61. DOI:10.1016/j.ifacol.2015.10.259 |
 2018, Vol. 50
2018, Vol. 50


