近年来,很多研究人员对运动体入水问题进行了广泛研究.运动体入水涉及到运动体从空气介质到水介质的过渡,经历了运动介质密度的突然变化,在航天器的海上回收以及空投鱼雷等方面的应用具有重大价值.运动体入水往往伴随着空泡的生成和液体表面的射流现象等复杂现象.May[1]对运动体入水过程所经历的入水冲击、入水空泡形状、空泡内压力和入水后运动体的弹道轨迹进行了讨论并总结了研究成果.Lee[2]基于能量方程的方法建立了空泡动力学行为的数学模型,并与数值仿真的结果进行相互验证,显示出该模型具有一定的精度,由于泡内压力的计算对入水空泡形态影响非常大,文献[2]对泡内压力进行了估算.Abelson[3]实验测量了运动体不同速度和入水角度入水时的空泡压力,运动体头型不同时空泡内的压降不同,当空泡表面闭合后空泡内的压强和体积满足等熵关系.Duclaux等[4]基于求解Besant-Rayleigh问题的方法建立了空泡形态的动力学模型.Aristoff等[5]用实验研究了低密度球体入水的问题,并结合球体动力学和空泡动力学建立了理论模型,结果表明通过改变球体的密度对可以改变球体入水空泡的动力学特性.何春涛等[6]基于VOF方法用数值模拟了头部带锥角回转体入水的空泡动力学行为,研究了空泡壁面运动和表面闭合特性.王聪等[7]用数值模拟方法研究了空气压强对回转体入水空泡的影响.He等[8]分析了运动体垂直入水时空泡内部的压力分布.Wei等[9-10]用实验的方法研究了圆柱体以不同的姿态入水时空泡的行为特性以及圆柱体的运动特性.施红辉等[11]实验研究了细长体入水时的空泡特征以及入水后细长体的运动稳定性.Guo等[12]用实验和Duclaux的理论模型研究了不同头型的射弹高速水平入水形成的空泡并研究了阻力系数与射弹头型的关系.Lee等[13-14]采用基于能量方程用理论模型和数值模拟的方法研究了球体高速入水时的空泡行为.本文基于独立膨胀原理对空泡形态建立了理论模型,采用高速相机对不同速度的球体入水过程进行研究,观察球体入水空泡的发展过程,研究空泡的形成对射流的影响以及入水时球体的速度、加速度和阻力系数的变化规律,分析了空泡的动态特性.
1 理论模型在小球入水速度较低时,在小球后方难以形成空泡,在小球入水速度较高时,在小球后方形成稳定的入水空泡.在形成较为稳定的空泡后,由小球入水传递给液体的动能一定,液体与气体界面的扩张可以由液体运动时动能和势能的和守恒来确定.近年来很多理论被用来描述小球入水的空泡形态,为了描述超空泡的动力学特性,Vasin[15]建立了独立膨胀原理,独立膨胀原理揭示了空泡在垂直于小球路径的截面径向扩张,与小球经过该截面时的运动状态、小球的形状和尺寸、以及该截面处空泡内外的压差有关,与小球经过该截面前后的运动状态无关.在本文中将基于独立膨胀原理建立球体入水空泡形态的动力学方程.
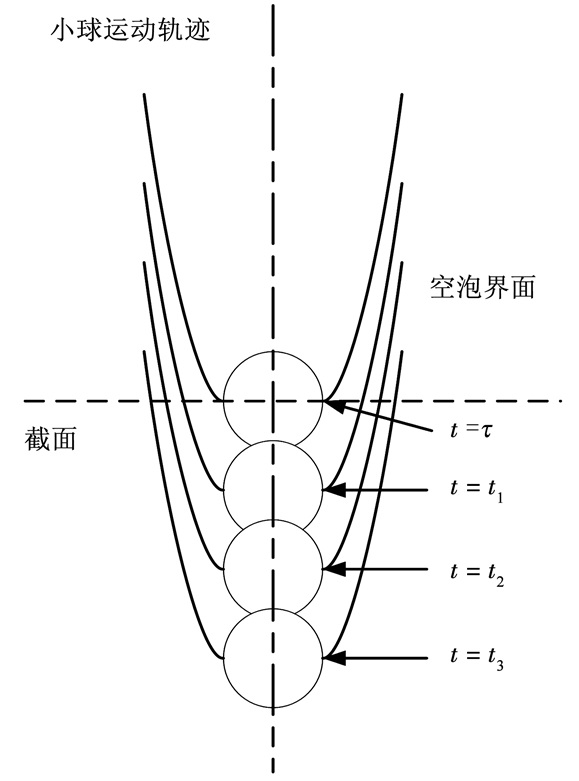
设小球的半径为Rn,直径为Dn,小球的质量为m,水的密度为ρ.小球入水时,空泡发展过程示意图如图 1所示.小球刚入水时,记入水深度为h=0,时间为初始时刻t=0,小球经过轨迹中某一点h时,过该点做出垂直于小球轨迹的截面,此时刻为该截面处空泡开始发展的初始时刻t=τ,随后小球继续下潜到t1、t2和t3时刻时该截面处的空泡状态.
设小球在经过点h时,速度为vp,vp = dh/dt.小球在运动过程中主要受到重力mg和阻力W的作用,小球受到的阻力W为
| $ W = 0.5{C_{\rm{d}}}{\rm{ \mathsf{ π} }}R_{\rm{n}}^2\rho v_{\rm{p}}^2, $ |
|
图 1 空泡发展示意 Figure 1 Schematic of cavity formation |
式中,Cd为阻力系数,与小球的速度相关.根据牛顿第二定律,小球入水时的动力学方程为
| $ m\frac{{{{\rm{d}}^2}h}}{{{\rm{d}}{t^2}}} = mg - 0.5{C_d}{\rm{ \mathsf{ π} }}R_{\rm{n}}^2\rho v_{\rm{p}}^2. $ | (1) |
由式(1),得到小球的阻力系数Cd为
| $ {C_d} = \frac{{2m\left( {g - {{\rm{d}}^2}h/{\rm{d}}{t^2}} \right)}}{{{\rm{ \mathsf{ π} }}R_{\rm{n}}^2\rho {{\left( {{\rm{d}}h/{\rm{d}}t} \right)}^2}}}. $ |
设在过点h的截面上的空泡在t时刻的半径为Rc(h, t-τ),截面积为Sc(h, t-τ),在该截面内空泡内的压强为Pc(h, t-τ),无穷远处的环境压强为P∞(h, t-τ),空泡内外压强差为ΔP(h, t-τ),ΔP=P∞-Pc.对于入水速度小于20 m/s,空泡内的压强为Pc=Pair-0.5Caρavi2,其中Pair为空气压强,ρa为空气密度,vi为小球入水速度,Ca为气流压力降系数.
小球运动dh距离时,小球受到的阻力做功为Wdh,假设阻力做的功全部转化为dh段液体的动能Tdh和势能Edh,得到:
| $ T\left( {h,t - \tau } \right) + E\left( {h,t - \tau } \right) = W\left( {h,\tau } \right). $ | (2) |
假设φ为空泡边界的绝对速度势,则有液体的动能为
| $ T = - 0.5\rho \varphi 2{\rm{ \mathsf{ π} }}{R_{\rm{c}}}{{\dot R}_{\rm{c}}}, $ | (3) |
液体的动能可以表示为
| $ E = \int_\tau ^t {\Delta P\left( {h,t - \tau } \right)2{\rm{ \mathsf{ π} }}{R_{\rm{c}}}{{\dot R}_{\rm{c}}}{\rm{d}}t} . $ | (4) |
在τ时刻,小球边缘处的液体的速度势为φn,φn=-0.5aRnvp,其中a为某一常数.在τ时刻,将式(3)、(4)代入式(2)可得
| $ {{\dot R}_{{\rm{c0}}}} = \frac{{{C_d}}}{a}{v_{\rm{p}}}, $ | (5) |
式中,Ṙc0为深度h处空泡半径的初始扩张速率,设深度h处空泡面积的初始扩张速率为Ṡc0,则Ṡc0=2πRnṘc0.假设深度h处空泡半径的初始扩张速率Ṙc0与球体经过该处时的速度成正比,即Ṙc0=γvp.其中γ为比例系数,反映了小球经过深度点h时,小球速率对空泡半径初始扩展速率影响程度,文献[4]建议γ为0.01,文献[12]用能量守恒的方法得到了γ的表达式,即
独立膨胀原理描述了空泡截面积的扩张过程,空泡截面积满足的方程为
| $ {{\ddot S}_{\rm{c}}}\left( {h,t - \tau } \right) = - k\frac{{\Delta P\left( {h,t - \tau } \right)}}{\rho }, $ | (6) |
式中,k= 4πCd/a2,将前文得到的a的表达式代入该式,得到k=2π/N.将式(6)积分一次,得到空泡截面积的扩张速率的表达式为
| $ {{\dot S}_{\rm{c}}}\left( {h,t - \tau } \right) = {{\dot S}_{{\rm{c0}}}} - k\int_\tau ^t {\frac{{\Delta P\left( {h,t - \tau } \right)}}{\rho }{\rm{d}}t} , $ | (7) |
将式(7)积分一次得到空泡截面积的表达式为
| $ \begin{array}{l} {S_{\rm{c}}}\left( {h,t - \tau } \right) = {S_0} + {{\dot S}_{{\rm{c0}}}}\left( {t - \tau } \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k\int_\tau ^t {\int_\tau ^t {\frac{{\Delta P\left( {h,t - \tau } \right)}}{\rho }{\rm{d}}t} } , \end{array} $ | (8) |
式中, S0为空泡扩张的初始截面积,S0=πRn2.
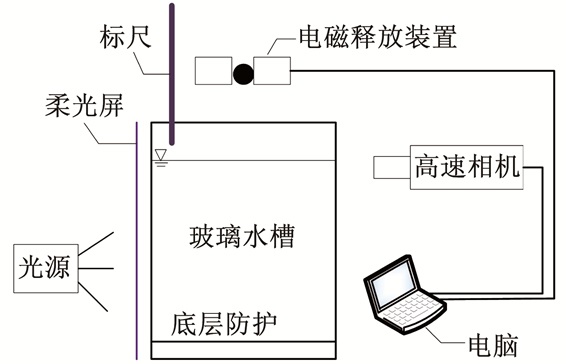
2 实验方案实验方案示意图如图 2所示,实验装置主要由玻璃水槽、防护装置、电磁释放装置和摄像装置组成.水槽由钢化玻璃制作而成,其中4个侧面钢化玻璃为10 mm厚,底面钢化玻璃为15 mm厚,具有较高的强度,满足球体入水对水槽的强度需求,每两面钢化玻璃之间用酸性硅酮玻璃胶粘合,防止实验过程中漏水.玻璃水槽尺寸为1.5 m × 0.8 m × 0.9 m,相对球体具有较大尺寸,水槽四周的玻璃边界对球体入水空泡形态的影响可以忽略.玻璃水槽四面透明,为高速相机拍摄和补充光源提供便利.玻璃水槽底部铺有4层10 mm厚的橡胶垫作为防护装置,防止球体撞击底面钢化玻璃造成的损坏.电磁释放装置固定在可调节高度的支架上,控制球体的释放,支架上固定具有刻度的标尺,实现对小球释放高度的控制,从而控制小球入水的速度.电磁释放装置通过电脑控制,工作时由电磁铁夹紧小球,开始释放时由电脑控制触发器输出高电平信号,控制电磁铁释放小球.摄像装置由光源和高速相机组成,光源采用8盏500 W的钨丝灯组成点阵光源,通过柔光屏照射在玻璃水槽中的流场中,为拍摄提供清晰的视场,2盏1 000 W钨丝灯放置在玻璃水槽的两侧补充光照.实验采用Photron FASTCAM SA-X型号的高速相机,并采用Nikon AF Nikkor 28-85 mm的镜头,对球体进行拍摄帧率为5000 fps的高速拍摄.高速相机和电磁释放装置由电脑控制,同时触发.
|
图 2 实验方案示意 Figure 2 Experiment schematic |
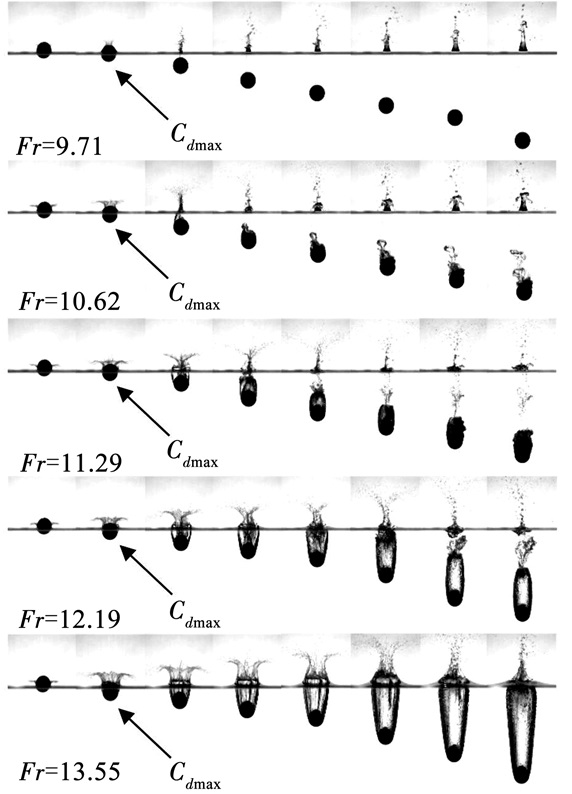
实验中采用表面未经特殊处理的钢球体,密度为7 810 kg/m3,直径为20 mm,质量为0.032 7 kg,实验中水的密度为1 000 kg/m3.为了研究不同入水速度对球体入水空泡形态的影响,使钢球体从不同高度落下,用高速相机拍下钢球体在不同速度下的入水空泡形态如图 3所示.在实验过程中对同一高度进行多次实验以实现实验结果的可重复性.
|
图 3 不同入水速度情况下球体入水空泡形态 Figure 3 Cavity shapes at different water entry velocities |
不同的高度落下时,球体的入水速度分别为4.3、4.7、5.0、5.4、6.0 m/s.不同入水速度vi时,定义
从图 3中可以看出,在Fr为9.71时,球体入水时没有形成空泡.在球体没有完全进入水中时,水流沿球体表面向上形成一层水膜,随后水膜向四周溅射.在球体完全进入水中后,在球体上面有一股向上的射流,射流形成水柱并随着小球下落而逐渐升高.当Fr为10.62时,在入水初期液体和球体在球体的上半部分分离,球体的上半部分有一个微小的空泡,随后空泡溃灭,并在球体的后方形成云状空泡.在随球体的空泡距离液体表面较近时,球体上方的射流在液体表面主要以喷溅的形式射出,在随球体的空泡距离液体表面较远时,射流在液体表面形成水柱.当Fr为11.29时,液体与球体在球体中间分离,在球体后方形成微小空泡,空泡随着球体向下移动,并以气泡的形式向后方泄气.液面上方的射流受到空泡泄气的影响,以喷溅的形式射出.随着球体速度的降低,空泡形态难以维持,逐渐溃灭并在球体后方形成云状空泡.当Fr为12.19时,液体与球体在球体中间分离,在球体后方形成较为清晰的空泡轮廓.相比Fr为11.29时形成的空泡,此时的空泡长度和直径都相对较大.随着球体下落,空泡在表面闭合,在球体后方形成一个近似椭圆型的空泡.在空泡闭合前,液面上方的射流向四周喷溅,在空泡闭合后,液面上方的射流主要向上喷溅,由于空泡泄气的影响没有形成水柱.在Fr为13.55时,液体与球体在球体中间分离,在球体后方形成更加清晰的空泡形态,随着小球下落,空泡在表面闭合.在空泡闭合前液面上方的射流以向四周喷溅的形式射出,在空泡闭合后射流主要向上喷溅.对比不同入水速度时小球入水形成的空泡形态,本文发现随着入水速度的增加,小球入水形成的空泡直径和长度逐渐增加,在Fr>12.19时,在球体后已经能够形成清晰稳定的空泡形态.
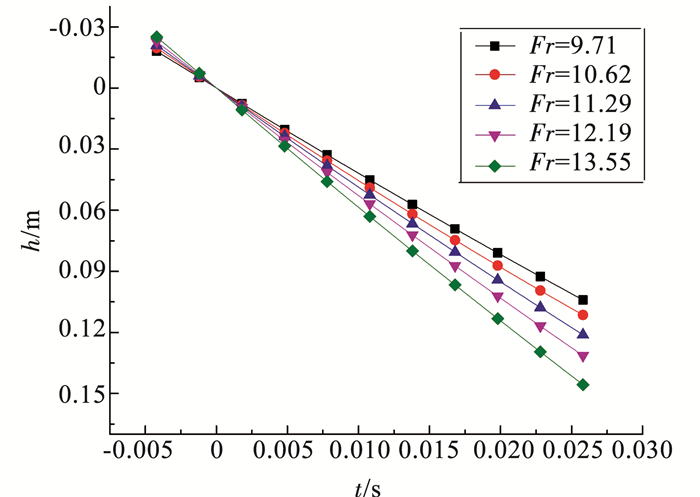
3.2 球体运动参数以入水点为坐标原点和初始时刻,球体入水深度、速度和加速度以向下为正.在球体入水初期,不同入水速度情况下球体的入水深度、速度和加速度随时间变化的关系分别如图 4~6所示.
|
图 4 球体入水深度随时间变化曲线 Figure 4 Change of ball depth |
|
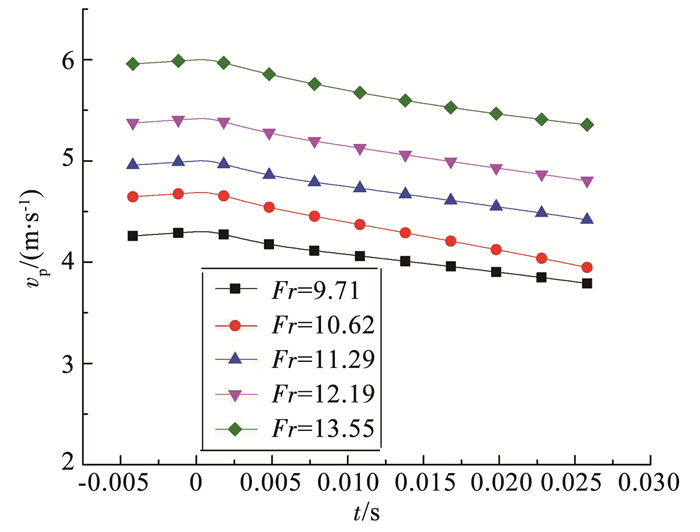
图 5 球体速度随时间变化曲线 Figure 5 Change of ball velocity |
|
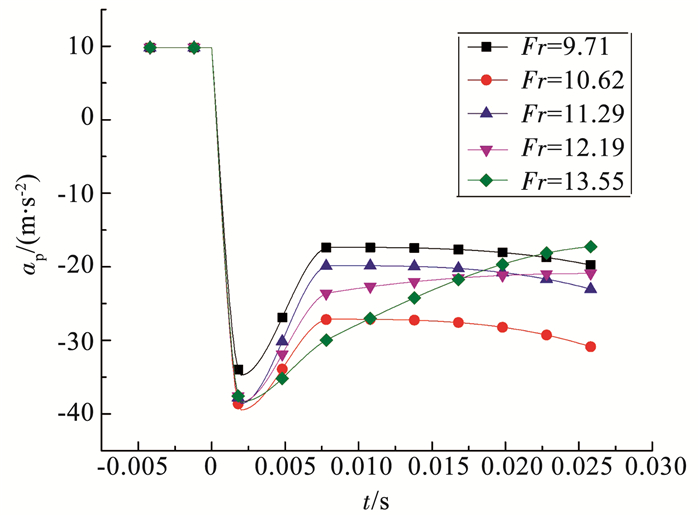
图 6 球体加速度随时间变化曲线 Figure 6 Change of ball acceleration |
从图 4中,可以看出入水速度大的情况球体下潜更快,但由于高速相机拍摄的入水初期的情况,时间在0~30 ms之间,所以入水深度随时间变化的关系中没有明显地显示出不同入水速度情况下变化趋势的差别.从图 5中,可以看出在球体入水前,球体速度逐渐增加,球体入水后,入水速度逐渐减小.不同入水速度情况下,球体速度减小的快慢不同,一方面是由于球体入水速度增加时,球体受到更加大的阻力,另一方面球体入水速度增加,入水空泡逐渐形成,由于球体的部分处在空泡中,减小了球体入水的阻力.
为了更清晰地看出球体入水速度变化的情况,图 6显示了不同入水速度情况下球体的加速度随时间的变化关系.由于球体入水速度的变化、入水空泡的形成以及入水撞击时冲击力的影响,球体的加速度变化比较复杂.从图中可以看出在入水空泡未完全形成的时候,球体的加速度先减小后增大再减小,在入水空泡完全形成后加速度先减小后增大.
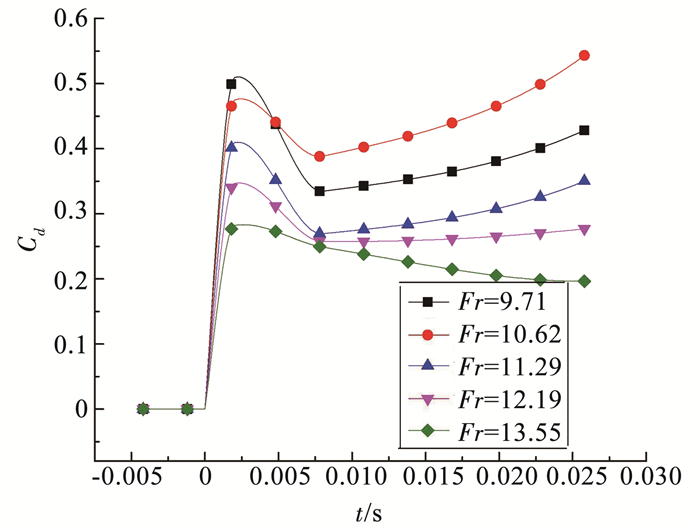
球体的阻力系数随时间变化的关系如图 7所示.从图中可以看出,入水空泡未充分形成时,阻力系数先增大后减小再增大,这是由于在球体刚与液面撞击时,球体受到较大的冲击力,之后由于时间在0~30 ms,球体的速度未明显变化,速度的变化对球体阻力的影响较小,但是球体已经逐渐与水充分接触,受到较大的压差阻力和黏性阻力.当入水空泡充分形成后,阻力系数线增大后逐渐减小,由图 7可见空泡的形成减小了球体与水接触的面积,使球体受到了较小的阻力.由图 7可以看出在球体刚入水阶段,球体最大阻力系数在入水时间为2.2 ~ 2.6 ms之间,球体所受的阻力主要为入水撞击所引起的,此时球体的位置以及相应的空泡形态如图 3所示,在图 3中由箭头指出.
|
图 7 球体阻力系数随时间变化曲线 Figure 7 Change of ball drag coefficient |
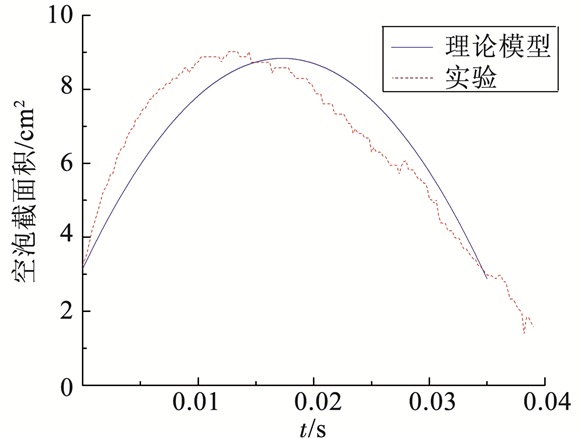
在Fr为13.55时,空泡完全发展,本文取深度为6倍的球体直径,即h=6Dn,以球体经过该深度处时为初始时刻,观察此处空泡截面积随时间的变化,实验测得的空泡截面积随时间变化关系与式(8)得到的结果如图 8所示.
|
图 8 实验和理论空泡截面积对比 Figure 8 Cavity section area comparison of theoretical model and experiment |
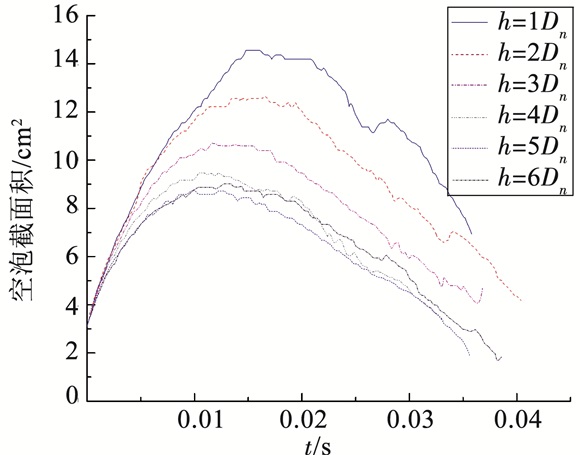
从图 8中可以看出理论模型在计算低速入水的空泡形态时具有一定的精度,但是与实际测得空泡截面积有一定差别,这是由于在实际中空泡内的压强并非统一,它在空泡内沿深度方向有一定的梯度分布,但是在实际计算中为了计算模型的简便往往忽略了泡内压强沿深度方向的变化.为了观察入水深度不同时空泡截面积的变化规律,对于Fr为13.55时,在不同的入水深度处测得的空泡截面积随时间变化的规律如图 9所示,图中均以相应深度处空泡开始发展的时刻为初始时刻.
|
图 9 不同深度处空泡截面积随时间变化曲线 Figure 9 Change of cavity section area at different depths |
从图中可以看出在距离水面较近时,空泡的最大截面积最大,这是由于此时小球传递给液体的能量较多,而且该深度处的静水压强较低.从图中还可以看出不同深度处空泡从发展到破灭的时间大致相同.
对应图 3中Fr为13.55时小球典型时刻的空泡形态,本文发现在小球入水过程中,不同深度处空泡截面面积逐渐增大,即对应于图 9中空泡发展的前半段,而之后小球超出相机视野,空泡逐渐缩小并溃灭.空泡截面发展的能量主要来自于球体动能的减少,由图 8、9可以看出,不同深度处空泡截面发展过程中的最大截面积不同,深度较小处空泡发展过程中的最大截面积较大,这说明球体在处于深度较小处时有较多的动能转变为空泡发展的能量.图 7中Fr为13.55时,在经历入水撞击后,球体的阻力系数逐渐减小,即球体入水深度较小时,阻力系数较大,球体有较多的动能转换为空泡发展的能量,所以空泡发展过程中的最大截面积较大.
4 结论1) 在球体入水速度较低时,没有形成空泡,球体后方的射流以水柱的形式向上溅射;随着入水速度的增加,球体入水形成稳定的空泡,在空泡表面闭合前,射流向四周溅射,在空泡表面闭合后,射流主要向上溅射.
2) 受到球体入水速度变化、入水空泡形成以及入水撞击时冲击力的影响,球体的加速度变化比较复杂,但是球体的阻力系数由于空泡的形成而明显减小.
3) 基于独立膨胀原理建立了空泡形态的数学模型,并与实验结果进行了对比,对比结果显示出该理论模型具有一定的精度,同时还得到了不同深度处空泡截面积的变化规律.
| [1] |
MAY A. Review of water-entry theory and data[J]. Journal of Hydronautics, 1970, 4(4): 140. DOI:10.2514/3.62851 |
| [2] |
LEE M. Influence of cavity pressure on the dynamics of water-entry cavity[C]//Proceedings of the 1997 ASME Fluids Engineering Division Summer Meeting: FEDSM'97. Vancouver: ASME, 1997
|
| [3] |
ABELSON HI. Pressure measurements in the water-entry cavity[J]. Journal of Fluid Mechanics, 1970, 44(1): 129. DOI:10.1017/s0022112070001738 |
| [4] |
DUCLAUX V, CAILLE F, DUEZ C, et al. Dynamics of transient cavities[J]. Journal of Fluid Mechanics, 2007, 591: 1. DOI:10.1017/s0022112007007343 |
| [5] |
ARISTOFF J M, TRUSCOTT T T, TECHET A H, et al. The water entry of decelerating spheres[J]. Physics of Fluids, 2010, 22(3): 1. DOI:10.1063/1.3309454 |
| [6] |
何春涛, 王聪, 闵景新, 等. 回转体匀速垂直入水早期空泡数值模拟研究[J]. 工程力学, 2012, 29(4): 237. HE Chuntao, WANG Cong, MIN Jingxin, et al. Numerical simulation of early air-cavity of cylinder cone with vertical water-entry[J]. Engineering Mechanics, 2012, 29(4): 237. |
| [7] |
王聪, 何春涛, 权晓波, 等. 空气压强对垂直入水空泡影响的数值研究[J]. 哈尔滨工业大学学报, 2012, 44(5): 14. WANG Cong, HE Chuntao, QUAN Xiaobo, et al. Numerical simulation of the influence of atmospheric pressure on water-cavity formed by cylinder with vertical water-entry[J]. Journal of Harbin Institute of Technology, 2012, 44(5): 14. |
| [8] |
HE Chuntao, WANG Cong, WEI Yingjie, et al. Numerical simulation of pressure distribution in vertical water-entry cavity[J]. Journal of Ship Mechanics, 2011, 15(9): 960. |
| [9] |
WEI Zhaoyu, HU Changhong. Experimental study on water entry of circular cylinders with inclined angles[J]. Journal of Marine Science and Technology, 2015, 20(4): 722. DOI:10.1007/s00773-015-0326-1 |
| [10] |
WEI Zhaoyu, HU Changhong. An experimental study on water entry of horizontal cylinders[J]. Journal of Marine Science and Technology, 2014, 19(3): 338. DOI:10.1007/s00773-013-0252-z |
| [11] |
施红辉, 周浩磊, 吴岩, 等. 伴随超空泡产生的高速细长体入水实验研究[J]. 力学学报, 2012, 44(1): 49. SHI Honghui, ZHOU Haolei, WU Yan, et al. Experiments on water entry of high-speed slender body and the resulting supercavitation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(1): 49. |
| [12] |
GUO Zitao, ZHANG Wei, XIAO Xinke, et al. An investigation into horizontal water entry behaviors of projectiles with different nose shapes[J]. International Journal of Impact Engineering, 2012, 49: 43. DOI:10.1016/j.ijimpeng.2012.04.004 |
| [13] |
LEE M, LONGORIA R G, WILSON D E. Cavity dynamics in high-speed water entry[J]. Physics of Fluids, 1997, 9(3): 540. DOI:10.1063/1.869472 |
| [14] |
LEE M. Water-entry induced cavity pressure[J]. Journal of Mechanical Science and Technology, 2000, 14(5): 562. DOI:10.1007/bf03185659 |
| [15] |
VASIN A D. The principle of independence of the cavity sections expansion (logvinovich's principle) as the basis for investigation on cavitation flows[C]//VKI Special Course on Supercavitating Flows. Brussels: RTO-AVT and VKI, 2001, RTO-EN-010(8)
|
 2018, Vol. 50
2018, Vol. 50


