利用超空泡减阻技术提高水下航行体的速度已成为国内外学者研究的焦点问题,但受实验条件和相关技术的限制,大多数研究都是围绕直线运动展开[1-2].如果超空泡航行体只做直线定深航行运动,其实际应用将受很大限制.欧、美等国对超空泡航行体的机动性进行了大量研究,最具代表性的当属德国的BARRACUDA超空泡高速水下导弹[3],该导弹利用火箭发动机和超空泡减阻技术使其水下时速可以达到370 km,并且依靠可以偏转的空化器实现转弯半径小于60 m的转弯运动,利用这种导弹的高机动性可以保护舰艇和潜艇免遭鱼雷的攻击.
近年来中国对超空泡航行体的机动运动也开展了一些研究,Feng等[4]采用独立膨胀原理的方法在考虑空化器攻角以及重力的作用下,对水下航行体的加速过程进行了动力学仿真.周景军等[5]研究了不同锥角空化器在偏转角发生变化时流体动力的变化情况,指出在相同条件下圆盘空化器具有较好的空化特性并且其升力系数对偏转角的变化敏感.张广等[6-7]利用非惯性圆柱坐标系并根据达朗贝尔原理,在动量方程中增加运动源项ρVθ2/r的方法预测了通气圆盘空化器转弯运动条件下生成的空泡形态;研究了通气超空泡航行体转弯运动流体动力特性.黄小腾[8]利用动态网格的方法研究了自然空化条件下的航行体在水平面内摆动的流体动力变化规律.李振旺[9]研究了通气航行体转弯运动中转弯半径对航行体流体动力的影响.
目前对于超空泡航行体机动运动研究多是采用相对运动定常计算的方法,这种方法虽然可以得出空泡形态及流体动力,但是往往忽略了航行体质心位置的影响.本文利用CFD动态网格非定常计算的方法,得到了航行体转弯运动中绕质心转动情况的空泡形态,进而比较了该情况下超空泡航行体在不同转弯半径条件下的空泡形态及流体动力特性.
1 数值计算模型 1.1 控制方程本文的航行体模型运动速度不高,自然空化空化较弱,并且采用主动通气的方式,所以空泡内部主要被通入的空气充满[10],所以本文数值仿真采用气-液两相流模拟.参照文献[11]对通气超空泡形态研究的方法,本文使用VOF多相流模型,该模型预测空泡形态界面更为清晰.
1.1.1 连续性方程连续性方程为
| $ \frac{{\partial {\rho _m}}}{{\partial t}} + \frac{{\partial ({\rho _m}{u_i})}}{{\partial {x_i}}} = 0. $ |
式中:混合介质的密度
动量方程为
| $ \frac{{\partial ({\rho _m}{u_i})}}{{\partial t}} + \frac{{\partial ({\rho _m}{u_i}{u_j})}}{{\partial {x_j}}} = {\rho _m}{g_i} - \frac{{\partial p}}{{\partial {x_i}}} + \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}}. $ |
式中:黏性应力
根据陈鑫[12]对通气空泡流的研究,本文选择RNG k-ε湍流模型对通气空泡流进行研究,该模型由Launder等[13]提出,该模型适合的流动类型广泛,对研究边界层流动和分离流动等有效,可以很好地处理高应变率及弯曲程度较大的流动.关于k和ε的输运方程如下:
| $ \begin{array}{l} \frac{{\partial ({\rho _m}k)}}{{\partial t}} + \frac{{\partial ({\rho _m}k{u_i})}}{{\partial {x_i}}} = \\ \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _k}{\mu _t}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} + {G_b} - {\rho _m}\varepsilon - {Y_M} + {S_k},\\ \frac{{\partial ({\rho _m}\varepsilon )}}{{\partial t}} + \frac{{\partial ({\rho _m}\varepsilon {u_i})}}{{\partial {x_i}}} = \\ \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _\varepsilon }{\mu _t}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right) + {C_{1\varepsilon }}\frac{\varepsilon }{k}\left( {{G_k} + {C_{3\varepsilon }}{G_b}} \right) - \\ {C_{2\varepsilon }}{\rho _m}\frac{{{\varepsilon ^2}}}{k} - {R_\varepsilon } + {S_\varepsilon }. \end{array} $ |
式中:Gk由平均速度梯度引起的湍动能产生;Gb由浮力影响引起的湍动能产生;YM为可压缩湍流脉动膨胀对总的耗散率的影响;αk、αε分别为k和ε的负向效应对应的普朗特数,αk=αε≈1.393;C1ε、C2ε、C3ε分别为常数.
1.2 量纲一的数的定义本文计算中气体流速较低,暂不考虑气体的可压缩性,文中涉及量纲一的通气率系数Q、弗劳德数Fr、空化数σ分别定义如下:
| $ \bar Q = \frac{Q}{{{V_\infty }D_n^2}},Fr = \frac{{{v_\infty }}}{{\sqrt {g{D_n}} }},\sigma = \frac{{{p_\infty } - {p_c}}}{{\frac{1}{2}\rho v_\infty ^2}}. $ |
式中:Q为气体体积流量;v∞为航行体运动速度;Dn为空化器直径;g为重力加速度;p∞为远场压力;pc为空泡内压力;ρ为流体密度.
1.3 动态网格的运动方式本文利用动态网格技术,令整个计算网络区域在zox平面上作刚体运动,区域节点之间没有相对位移,航行体的运动方式如图 1所示,航行体先进行直线运动,待航行体空泡形态相对稳定后,令航行体以R为半径进行转弯运动.

|
图 1 航行体运动方式 Figure 1 The movement of vehicle |
Logvinovich空泡截面独立膨胀原理是研究超空泡形态的一种简单有效的方法[14-15].为了使验证结果更为直观,本文针对直径Dn=12 mm的圆盘空化器模型做转弯运动的条件下,采用CFD动态网格方法和独立膨胀原理方法计算得出的空泡形态对比结果如图 2所示.

|
图 2 基于两种方法得到的空泡形态结果对比 Figure 2 Comparison of cavity shape based on two methods |
图 2为Q=0.51、Fr=58.32时,在相同空化数σ条件下,采用上述两种方法得出的空泡形态对比,两者空泡尺度相差不大,其中Logvinovich独立膨胀原理得到的空化器运动轨迹也代表了空泡的轴线,而本文运用CFD动网格方法得到的空泡轴线基本也和运动轨迹一致,这说明了本文采用的方法所得计算结果可以很好的说明超空泡航行体非定常转弯运动的空泡形态特点.
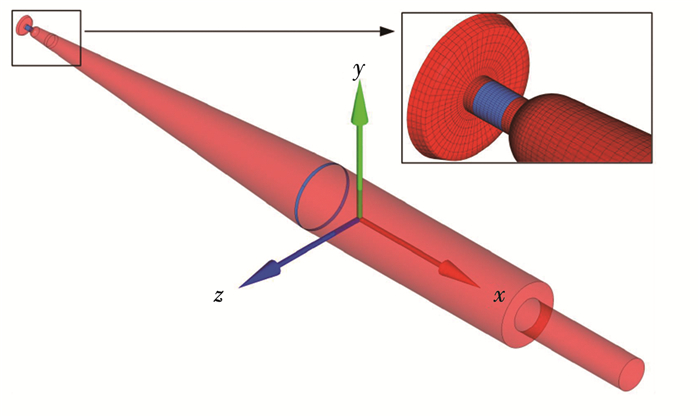
2.2 流域边界设置航行体模型由圆盘空化器、锥柱段弹身、圆柱形尾喷管组成,如图 3所示.图 3中航行体模型全长L=467 mm,柱段直径D=40 mm,其中圆盘空化器直径Dn=12 mm,坐标系的原点建立在航行体的质心上.
|
图 3 计算模型 Figure 3 Computation model |
计算域为圆柱形,边界条件设定如图 4所示,直径为34Dn,长度为160Dn,各边界面都采用压力出口条件,重力方向沿y轴负向,流场初始压力依照航行体所处的5 m水深位置按重力方向线性分布.整个计算域采用六面体结构化网格划分,如图 5所示,数值计算后航行体表面的y+值在10~22之间,符合本文计算要求.

|
图 4 计算域及边界条件 Figure 4 Computational region and boundary conditions |

|
图 5 计算域网格 Figure 5 Computational domain grid |
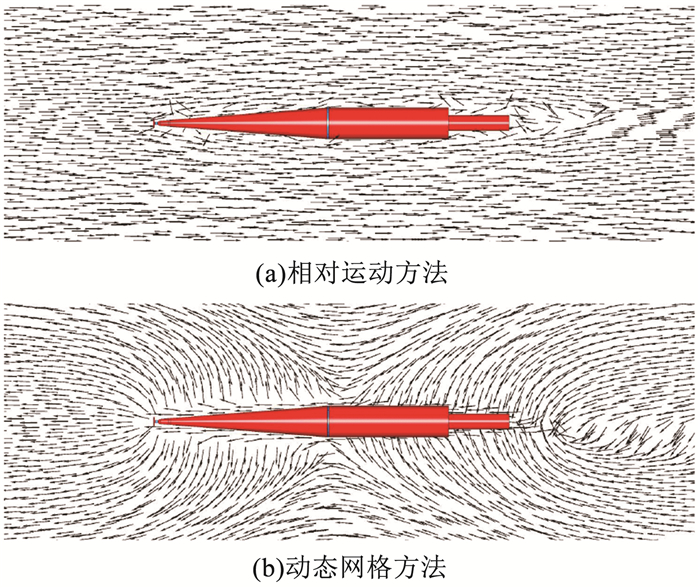
航行体模型直航时采用相对运动的方法和动网格的方法得到的其流场的速度矢量分布情况如图 6所示,采用动网格方法令航行体在静水中航行的计算条件设定方式更加符合航行体的实际工作情况.
|
图 6 航行体周围流场的速度矢量图 Figure 6 The velocity vector of flow field around the vehicle |
航行体直航时形成了轴线是直线超空泡,然后利用动态网格的方法,令航行体的转动中心位于空化器中心和航行体质心分别进行计算,保持转弯半径R=10 m,Q=1.42、σ=0.035、偏转角θ=ω(t-t1),航行体不同偏转角下的空泡形态俯视如图 7、8所示.

|
图 7 航行体绕空化器中心转动俯视图 Figure 7 Vertical view of vehicle turning motion around the center ofcavitator |

|
图 8 航行体绕质心转动俯视图 Figure 8 Vertical view of vehicle turning motion around the center of mass |
通过图 7看出,当航行体绕空化器中心转动时,空泡略微产生弯曲变形并同航行体相交,使得航行体靠近转弯半径外侧表面最先处于沾湿状态.随着偏转角度的增加,沾湿表面逐渐增大,而航行体靠近转弯半径内侧表面被空泡包裹,空泡内部大部分气体通过这一侧向后排出,此结果与文献[7, 9]的研究结果相同.
通过图 8看出,当航行体绕质心转动时,随着航行体偏转角度的增加,空泡弯曲变形的弧度增大,空泡轴线弯曲程度比图 7更为明显,航行体转弯运动的空泡轴线和航行体运动轨迹线都以相同方向弯曲,航行体的在靠近转弯半径内侧最先接近沾湿状态.按着绕质心转动的方法,在不同转弯半径R下,航行体空泡形态侧视如图 9所示.

|
图 9 不同转弯半径下的空泡形态侧视图 Figure 9 Profile of cavity shape of different turning radiuses |
从图 9可以看出,转弯半径处于5~6 m时,航行体内侧出现沾湿区,转弯半径越小,航行体的沾湿区就越大;转弯半径处于7~10 m时,空泡虽然非常接近航行体转弯半径内侧,但并未出现沾湿区.
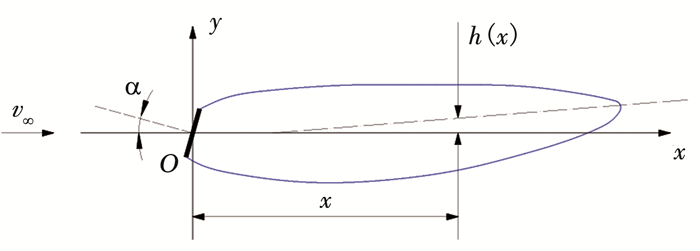
3.1.2 空化器对空泡轴线的定向效应具有一定攻角的空化器产生的横向作用力将导致空泡轴线的变形,空泡轴线的偏移方向和空化器所受的横向外力方向相反[16],如图 10所示,空泡轴线的偏转方向和空化器中心线偏转方向相同.本文中假设空化器与航行体同轴,空化器附近的流场速度方向如图 11所示,按照文献[16]的结论,文中这一时刻航行体的空化器中心线与水流方向存在夹角α,则相应空泡的轴线就有偏向转弯半径外侧的趋势,再加上转弯运动产生的空泡轴线弧形弯曲,产生了航行体靠近转弯半径内侧表面最先出现沾湿区的现象.
|
图 10 空化器定向效应示意 Figure 10 The sketch of cavitator orientation effect |

|
图 11 空化器附近的流速方向 Figure 11 Flow direction near the cavitator |
通气空泡自由闭合时存在两种泄气模式,一种是重力对通气空泡流动的影响较弱时,通气空泡呈现回注射流的模式;另一种是重力效应显著,即弗劳德数Fr和空化数σ较小时,通气空泡呈现双涡管模式[17].
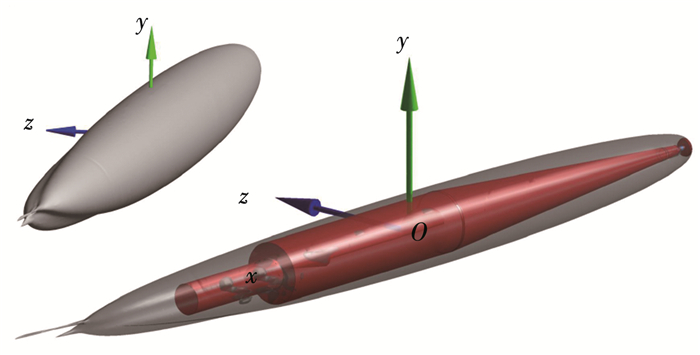
本文采用动态网格方法得到了超空泡航行体转弯运动时的空泡尾部形态如图 12所示,其中zox平面是航行体运动平面,航行体坐标系的z轴与转弯半径重合并指向运动轨迹的圆心.可以发现空泡尾部的双涡管形态是呈倾斜排布的,因为重力沿y轴负向,使得空泡尾部下界面向y轴正向凹陷;同时航行体的转弯运动产生的惯性力沿z轴负向,使得空泡尾部右界面向z轴正向凹陷,在这样的综合作用下,空泡尾部的双涡管就形成了倾斜的排布方式.
|
图 12 超空泡航行体尾部空泡形态 Figure 12 The cavity shape at the tail of the supercavitating vehicle |
统计图 9中不同转弯半径工况下的航行体流体动力进行比较,结果如图 13所示.
|
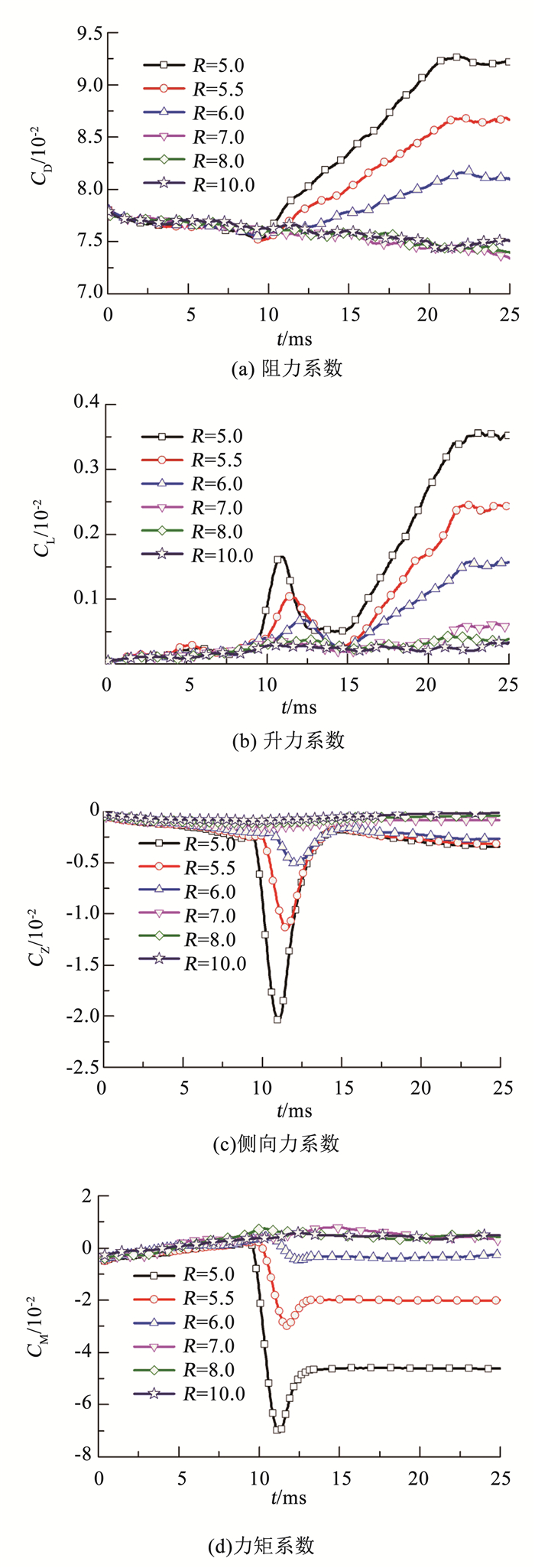
图 13 流体动力随时间变化 Figure 13 Hydrodynamic varying with time |
从图 13(a)中可以看出,转弯半径R处于5.0~6.0 m区间时,航行体出现沾湿区域引起阻力系数发生变化,转弯半径越小、沾湿区越大,阻力系数增加越快;R处于7.0~10.0 m区间时,由于没有出现沾湿区,阻力系数变化不大.从图 13(b)、(c)中可以看出,在航行体出现沾湿区时,升力系数和侧向力系数都有一个波动变化,这个波动是出现沾湿区时产生的回射流使航行体局部压力升高所致,通过表 1中可以看出,随着航行体转弯角度的增加,沾湿面积虽不断增大,但沾湿区的高压区范围却不断缩小,且高压区最大压力值也在不断的降低,压力分布云图随着沾湿区域面积的稳定而逐渐趋于稳定.航行体沾湿区在重力作用下,其位置略微偏下,从而使航行体产生一些较小的升力,转弯半径越小,升力和侧向力系数越大.从图 13(d)中可以看出,在转弯半径R处于5.0~6.0 m区间时,力矩系数先随着沾湿区的增大而增大,但因侧向力作用的位置不断的移近质心,从而使力矩系数有一段回复的过程,力矩系数随沾湿区面积稳定而稳定.转弯半径越小,力矩系数越大,力矩系数为负值,说明流体动力有使航行体保持原直线轨迹的趋势.而转弯半径R处于7.0~10.0 m区间时,由于没有出现沾湿区,力矩系数几乎不受转弯半径影响.
| 表 1 航行体表面压力分布 Table 1 Vehicle surface pressure distribution |
1) 使用CFD动态网格的方法计算超空泡航行体转弯运动,可以得到弯曲形状的空泡外形,转弯半径越小,空泡弯曲变形越大;航行体转弯运动时,由于空泡轴线的向外偏移使航行体转弯半径内侧表面最先出现沾湿区.
2) 航行体直线运动时,重力作用使得空泡尾部形态呈现水平的双涡管泄气排布,超空泡航行体在转弯运动时,空泡尾部的形态还会受到惯性力的影响而发生改变,在重力和惯性力的共同作用下,空泡尾部呈现倾斜的双涡管排布.
3) 航行体表面开始出现沾湿区时,沾湿区附近因回射流影响出现高压区,航行体的流体动力会出现波动,转弯半径越小,沾湿区越大,流体动力波动越大.
| [1] |
SAVCHENKO Y N. Experimental investigation of supercavitating motion of bodies[R].Brussels: VKI Special Course on Supercavitating Flows, 2001
|
| [2] |
YU Kaiping, ZHOU Jingjun, MIN Jingxin, et al. A contribution to study on the lift of ventilated supercavitating vehicle with low froude number[J]. Journal of Fluids Engineering, 2010, 132(11): 111303-1. DOI:10.1115/1.4002873 |
| [3] |
丛敏, 刘乐华. 德国BARRACUDA超空泡高速水下导弹的制导与控制[J]. 飞航导弹, 2007, 37(5): 38. CONG Min, LIU Yuehua. Guidance and control of high-speed supercavitation underwater missile of Germany[J]. Winged Missiles Journal, 2007, 37(5): 38. DOI:10.3969/j.issn.1009-1319.2007.05.013 |
| [4] |
FENG Guang, CHEN Weizheng, CHU Xuesen, et al. Simulation of unsteady artificial supercavities[J]. Journal of Hydrodynamics, Ser. B, 2010, 22(5): 905. DOI:10.1016/S1001-6058(10)60050-9 |
| [5] |
周景军, 于开平. 空化器倾斜角对超空泡流影响的三维数值仿真研究[J]. 船舶力学, 2011, 15(1/2): 74. ZHOU Jingjun, YU Kaiping. Three dimensional simulation on the influence of cavitator inclination angle to supercavity flow[J]. Journal of Ship Mechanics, 2011, 15(1/2): 74. DOI:10.3969/j.issn.1007-7294.2011.01.010 |
| [6] |
ZHANG Guang, YU Kaiping, ZHOU Jingjun. Numerical research on ventilated supercavity shape and flow structure in the turning motion[J]. Journal of Ship Mechanics, 2011, 15(12): 1335. DOI:10.1016/S1001-6058(11)60323-5 |
| [7] |
张广, 于开平, 周景军, 等. 超空泡航行体转弯运动流体动力特性的数值研究[J]. 应用力学学报, 2012, 29(3): 278. ZHANG Guang, YU Kaiping, ZHOU Jingjun, et al. Numerical research on hydrodynamic characteristics of supercavitating vehicle in the turning motion[J]. Chinese Journal of Applied Mechanics, 2012, 29(3): 278. |
| [8] |
黄小腾.锥形空化器航行体非定常流体动力特性研究[D].哈尔滨: 哈尔滨工业大学, 2012 HUANG Xiaoteng. Research on unsteady hydrodynamics of supercaviting vehicle with conical cavitator[D]. Harbin: Harbin Institute of Technology, 2012 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D240968 |
| [9] |
李振旺.水下高速航行体机动运动非定常超空泡数值模拟[D].哈尔滨: 哈尔滨工业大学, 2013 LI Zhenwang. Transient numerical study on maneuverable motion of high speed supercavitating vehicles[D]. Harbin: Harbin Institute of Technology, 2013 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D416996 |
| [10] |
周景军.通气超空泡流动及航行体流体动力数值模拟研究[D].哈尔滨: 哈尔滨工业大学, 2011 ZHOU Jingjun. Numerical simulation study on the ventilated supercavitating flow and hydrodynamics of vehicle[D]. Harbin: Harbin Institute of Technology, 2011 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D263907 |
| [11] |
陈鑫, 鲁传敬, 吴磊. 通气超空泡的形态特性研究[J]. 弹道学报, 2005, 17(1): 1. CHEN Xin, LU Chuanjing, WU Lei. The investigation on morphology of ventilated supercavity[J]. Journal of Ballistics, 2005, 17(1): 1. DOI:10.3969/j.issn.1004-499X.2005.01.001 |
| [12] |
陈鑫.通气空泡流研究[D].上海: 上海交通大学, 2006 CHEN Xin. An investigation of the ventilated cavitating flow[D]. Shanghai: Shanghai Jiaotong University, 2006 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1052925 |
| [13] |
LAUNDER B E, SPALDING D B. Lectures in mathematical models of turbulence[M]. London: Academic Press, 1972.
|
| [14] |
CHEN Yongliang, HEISTER S D. Modeling hydrodynamic nonequilibrium in cavitating flows[J]. Journal of Fluid Engineer, 1996, 118(1): 172. DOI:10.1115/1.2817497 |
| [15] |
VASIN A D. The principle of independence of the cavity sections expansion(Logvinovich's principle) as the basis for investigation on cavitation flows[C]//VKI/RTO Special Course on Supercavitating flows. Brussels: Von Karman Institute for Fluid Dynamics, 2001: 105
|
| [16] |
SEMENENKO V N. Artificial supercavitation physics and calculation[J]. Materials Research, 2001, 1(3): 1. |
| [17] |
EPSHTEIN L A. Methods of theory of dimensionality and similarity in problems of ship hydrodynamics[M]. Leningrad: Sudostroenie Publishing House, 1970.
|
 2018, Vol. 50
2018, Vol. 50



