回转体在入水过程中由于经历了气、水两相介质的改变,其运动环境的物理性质发生了突变,该过程中伴随有入水空泡的形成与演化、湍动涡等复杂物理现象.Lee等[1]基于能量守恒定律,对独立膨胀原理的进行改进与修正,提出了可用于高速入水空泡计算的理论模型.Tabuteau等[2]对球体垂直入水问题进行了研究,分析了空泡尺寸和入水喷溅高度与入水速度的关系.Lee等[3]在Lundstrom基础上提出了空泡形态发展的理论方法,分析了球体以不同速度入水过程中空泡发展过程.Yan等[4]基于细长体理论,对低雷诺数条件下的入水空泡流体动力特性进行数值计算.Aristoff等[5]基于Rayleigh-Besant理论,对不同入水速度的憎水球体垂直入水空泡形态进行了数值计算.Sun等[6]基于边界元法及时间步法,针对锥体的倾斜入水过程中的拍击问题展开研究,分析了拍击过程中液体喷溅形态演化特性及压力分布特征.叶取源等[7]利用欧拉-拉格朗日混合边界元法对锥头和平头圆柱体垂直入水过程其进行了研究,获得了运动体入水空泡的生成和发展规律.温俊生等[8]基于Fluent流体计算平台,研究了回转体头型对垂直入水过程中入水空泡演化特性的影响规律.魏卓慧等[9]利用附加质量法,分析了截锥形弹体垂直入水过程中入水速度及弹体头部锥角对冲击载荷的影响规律.王聪等[10-11]通过求解雷诺时均的Navier-stokes方程,分析了小型回转体低速垂直入水过程中入水空泡的发展规律,并研究了大气压力对入水空泡面闭合的影响研究.杨衡等[12]利用不同头型圆柱体开展低速垂直和倾斜弹体低速入水过程研究,并定性分析了回转体入水过程中入水速度和入水角度对入水空泡的影响规律.黄志刚等[13]分析了平头锥形回转体高速入水过程中,回转体所受冲击载荷及强度特性.
关于入水问题学者们开展了很多的试验和数值模拟工作,并且取得了很多成果,但这些成果大多关注于垂直入水问题[14].在运动体倾斜入水过程中,空泡的演化受到重力影响更加显著,且由于重力方向与回转体运动方向不一致,使得空泡呈现出非对称特性,这种非对称特性对运动体入水过程的流体动力影响规律与垂直入水具有较大差异.本文基于数值模拟方法,分析回转体在低速倾斜入水过程中入水速度和入水角度对入水空泡形态演化过程及流体动力特性的影响规律.
1 控制方程混合介质的连续性方程为
| $ \frac{{\partial {\rho _m}}}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {{\rho _m}{u_i}} \right) = 0. $ | (1) |
混合介质的动量守恒方程为
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {{\rho _m}{u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {{\rho _m}{u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \\ \;\;\;\frac{\partial }{{\partial {x_i}}}\left[ {\left( {{\mu _m} + {\mu _t}} \right)\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right]. \end{array} $ | (2) |
式中:i=1, 2, 3;ρm=αlρl+αgρg+αvρv为混合介质的密度;μm=αlμl+αgμg+αvμv为动力黏度;ui为速度分量.
湍流模型采用Realizable k-ε湍流模型[15],湍动能k和湍能耗散率ε的输运方程分别为:
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \\ \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon , \end{array} $ | (3) |
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \varepsilon {u_i}} \right) = \\ \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}S\varepsilon - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }}. \end{array} $ | (4) |
式中:σk、σε分别为k和ε的Prandtl数,取值分别为σk=1.0,σε=1.2;
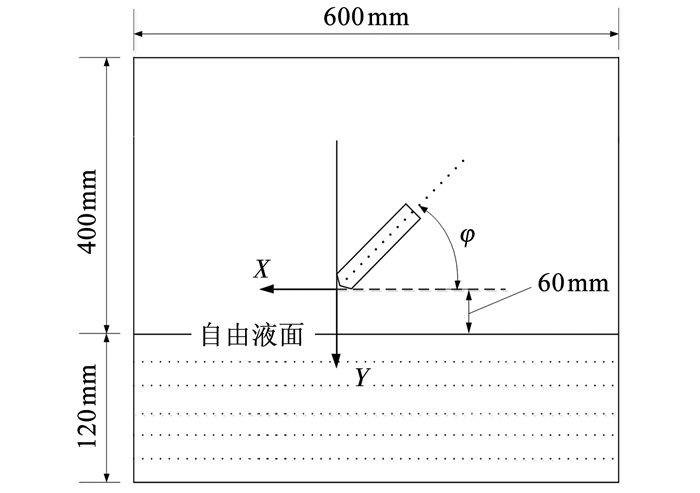
本文采用的计算域示意图如图 1所示.对于低速倾斜入水过程,可认为运动体作平面运动,即在运动平面的法线方向上没有速度分量且运动过程中回转体不绕其轴线旋转.因此为减少网格量以提高计算效率,本文采用1/2模型进行计算.图 1中XY平面为计算域的对称面,其直径为600 mm,高度为520 mm.初始状态下,回转体头部取在坐标原点处,其轴线与X轴夹角为φ;自由液面取在坐标原点下方60 mm处,空气域高度为400 mm,水域深度为120 mm.运动开始后,回转体在初始给定的入水速度和入水角度条件下进行三自由度运动.
|
图 1 回转体倾斜入水计算域示意 Figure 1 Schematic layout of revolution body oblique water-entry |
图 2给出了本文采用的计算模型.计算模型为1/2的锥头圆柱体,对称面参数如图 3所示.模型密度ρ=7.85 g/cm3,柱段L0=40 mm,直径D0=9 mm,θ为圆锥体锥角.

|
图 2 回转体计算模型 Figure 2 Calculation model of revolution body |

|
图 3 数值计算模型对称面结构示意 Figure 3 Schematic layout of revolution body's symmetry plane |
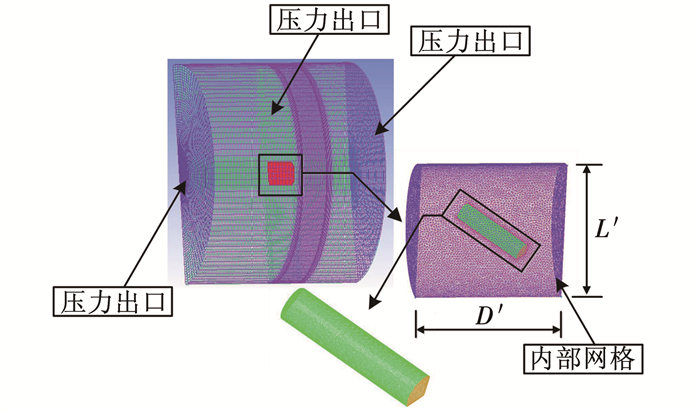
图 4给出了回转体倾斜入水计算域及边界条件.本文中流域边界均采用压力出口边界条件,并利用UDF对整个入水过程中边界上的压力定义.计算域外形为1/2圆柱,基于计算效率的考虑,回转体附近流域采用四面体网格,并对回转体周围1/2圆柱体范围的计算区域进行局部加密(D′=75 mm、高度L′=75 mm);远离回转体区域采用六面体网格.
|
图 4 回转体计算域及边界条件示意 Figure 4 Computational domain and the boundary conditions of revolution body |
基于Fluent流体计算平台,结合动网格技术,对回转体低速倾斜入水过程进行数值模拟研究.空间离散采用二阶迎风格式,时间离散采用一阶隐式格式,速度压力耦合采用PISO算法,压力项离散采用Body Force Weighted离散格式;基于用户自定义函数(UDF)定义入水运动体惯性矩及边界压力.
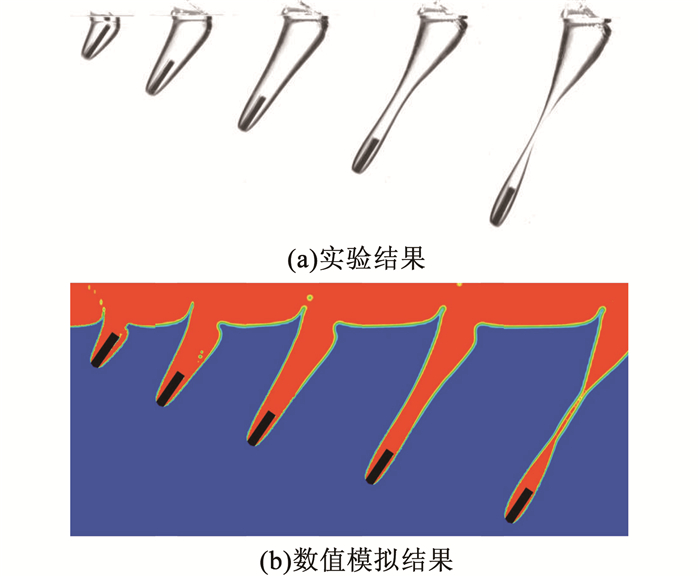
为检验数值模拟结果的可靠性,对文献[16]中的实验进行了数值模拟.图 5分别给出了140°锥角回转体v0=4.1 m/s、入水角度φ0=55°条件下,入水深度分别为4D0~20D0时,本文数值模拟方法与文献[16]实验方法所获得的空泡形态对比图片,图 6定量对比了不同入水深度条件下空泡轮廓及速度变化规律的数值结果与实验数据(其中空泡形态提取了水相体积分数为0.8的界面[17]).从图 6中可以看出,在入水空泡形态方面,除喷溅现象有所偏差外,数值结果与试验数据吻合度较好,速度变化规律亦基本一致,数值计算结果可以较好地反映入水过程中各阶段空泡形态变化过程.
|
图 5 回转体入水空泡形态 Figure 5 Cavities of revolution body water-entry |

|
图 6 入水深度空泡轮廓及速度对比 Figure 6 Comparison between cavities and velocities of revolution bodies with experiment and simulation method |
基于上述数值模拟方法,开展了不同入水速度下,回转体倾斜入水过程空泡演化特性及流体动力特性的数值研究.计算模型采用140°锥角头型回转体,入水角度φ0=55°,入水速度分别取v0=5、10、15、20 m/s.
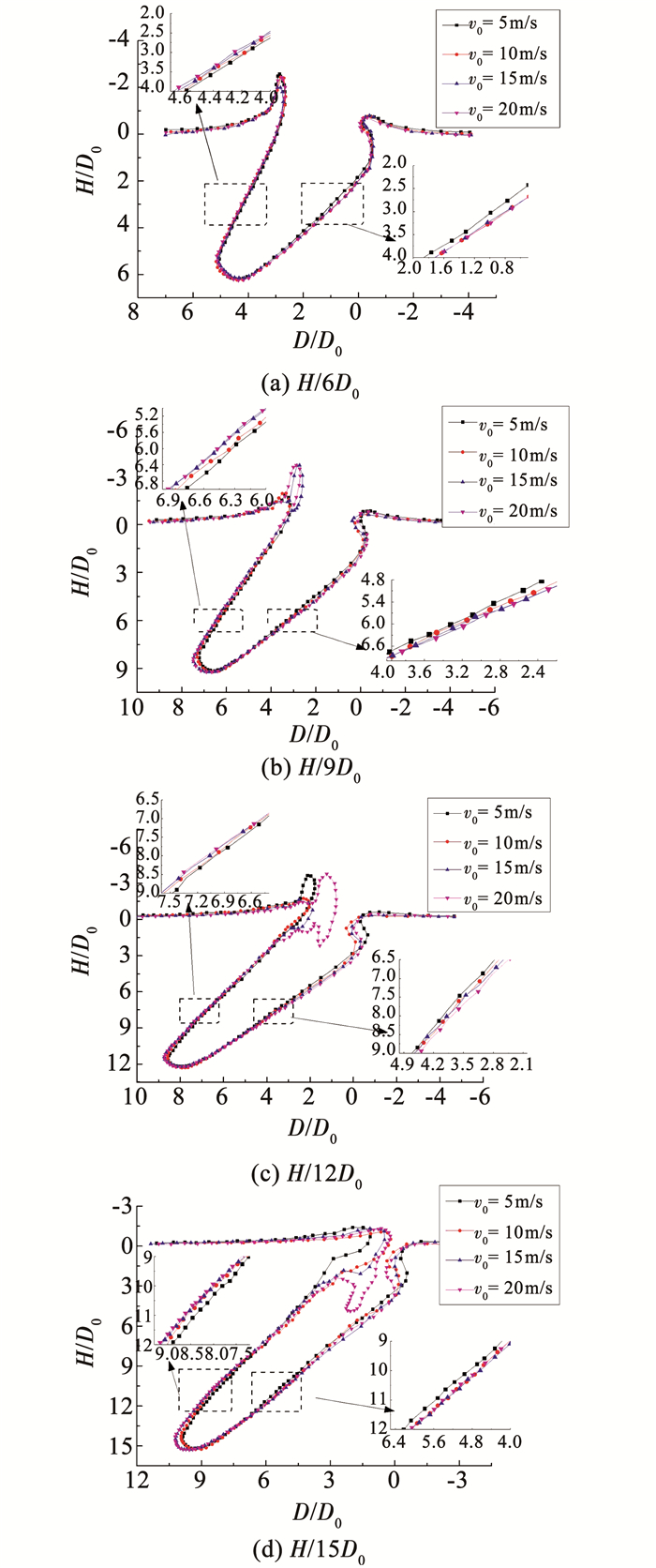
3.1 入水速度对空泡影响图 7给出了4种入水速度条件下不同入水深度回转体入水空泡形态对比.从图 7中可以看出,在相同入水深度,不同入水速度回转体其头部和中间部分空泡轮廓极其相似,自由液面处空泡轮廓随着入水深度的增加而逐渐产生差异;在空泡扩张阶段,回转体空泡直径随着入水速度的增加而小幅增大.该现象可从能量守恒角度进行分析,即小型回转体撞击自由液面后,自身动能以阻力形式传递给撞击点附近水域,使得水域质点从静止状态开始运动,形成包裹回转体的空泡.回转体入水速度越高,在同一入水深度其损失的动能值就越大,撞击点附近的水域质点获得的运动速度就越高,所以在相同入水深度空泡直径随着入水速度的增加而增大.
|
图 7 不同入水深度回转体入水空泡形态对比 Figure 7 Cavities comparison of revolution bodies with different velocities |
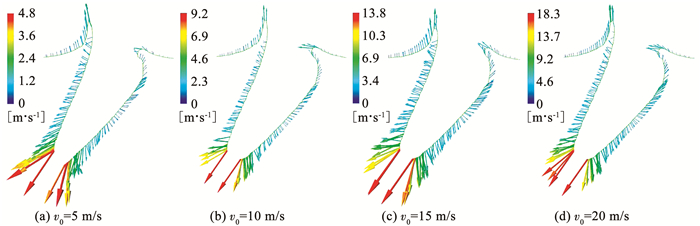
图 8为回转体入水深度H=6D0时,不同入水速度下入水空泡壁面速度矢量分布特征.可以清楚的知道,在相同入水深度处,回转体肩部附近的流域,入水空泡壁面扩张速度较高;在入水空泡上部,即随着与自由液面距离的减小,入水空泡壁面扩张速度逐渐减小,并且同一位置处空泡壁面扩张速度随着回转体入水速度的增加而增大,这也解释了在空泡扩张阶段,回转体空泡直径随着入水速度的增加而小幅增大的原因;不同入水速度回转体空泡扩张速度最高点出现在与回转体的分离点位置,且最高速度随着回转体入水速度增加而增大.
|
图 8 入水深度H=6D0入水速度空泡壁面速度矢量分布 Figure 8 Velocity vector distribution of cavity wall for H=6D0 |
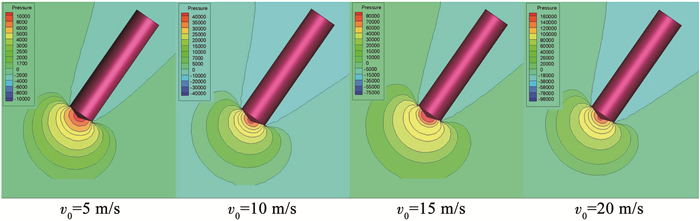
图 9为倾斜入水过程中回转体入水深度H=6D0时,入水空泡附近压力特征分布.从图中可以知道,当回转体入水深度相同时,不同入水速度致使流场中最高压力随着入水速度的增加而增大;流场的最小压力与入水速度直接相关,随着回转体入水速度增加而减小.
|
图 9 入水深度H=6D0时流场压力等值线云图 Figure 9 Pressure contour of flow field for H=6D0 |
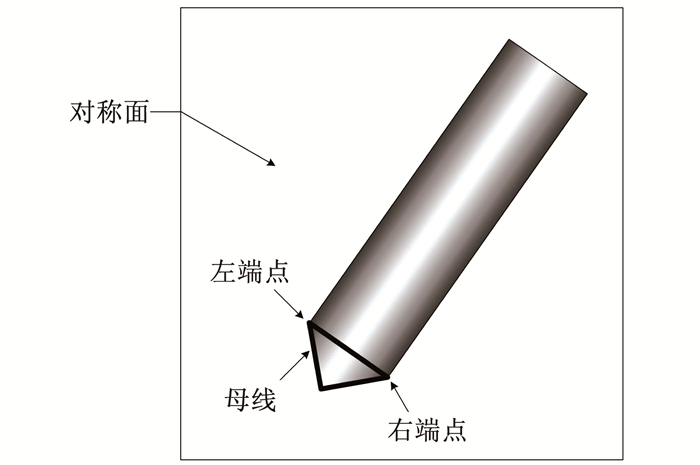
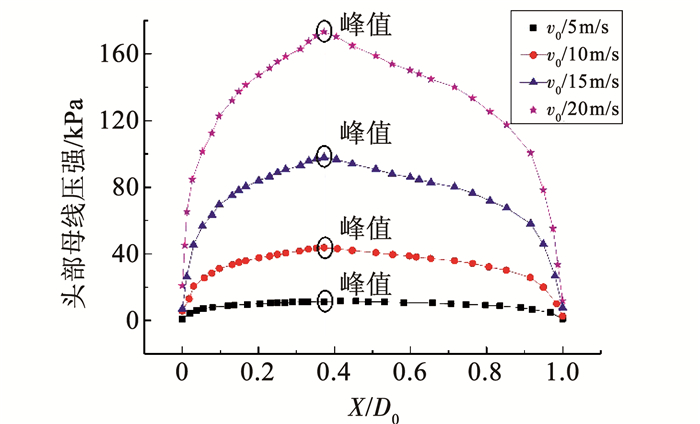
图 10为回转体锥头母线示意图,母线为回转体头部与计算对称面的交线.图 11为倾斜入水过程中回转体入水深度H=6D0时,回转体锥头母线压力分布特征.从图中可以知道,回转体以不同入水速度倾斜入水,其锥头母线上压力最高点均位于锥头顶点处;同一入水深度母线上相同位置处回转体压力随着入水速度的增加而增大.
|
图 10 锥头母线示意 Figure 10 Schematic layout taper generatrix |
|
图 11 入水深度H=6D0时锥头母线压力分布 Figure 11 Pressure of taper generatrix with H=6D0 |
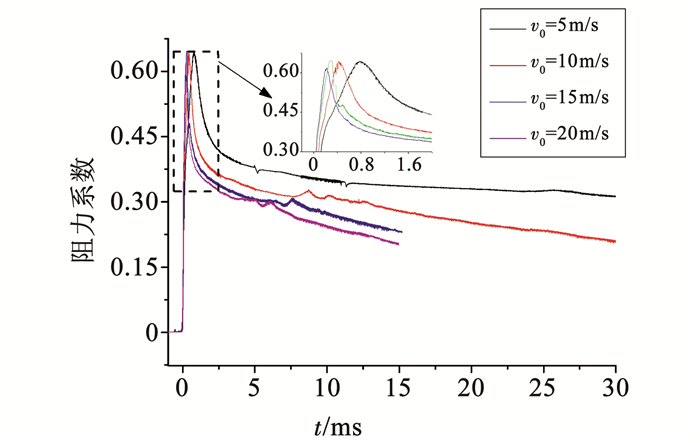
图 12为回转体低速倾斜入水过程中阻力系数随入水速度变化对比.从图中可以知道,对于不同速度入水的回转体,其阻力系数变化趋势近似性很强:在回转体入水之前,由于空气密度远小于水密度,所以其阻力系数很小,接近于零;当回转体头部触水之后,其阻力系数在很短时间内急剧增大,进而产生一个峰值,此峰值是由于入水冲击载荷形成的;随着回转体距离自由液面距离的增大,冲击载荷的影响逐渐减弱,阻力系数逐渐减小,并最终稳定,但稳定后的阻力系数随着回转体初始入水速度的增加而减小.从阻力系数峰值局部放大图可以看出,在本文速度研究范围内,不同入水速度回转体其阻力系数峰值差别不大.
|
图 12 阻力系数变化曲线 Figure 12 Drag coefficients of the revolution body with different velocities |
为分析入水角度对回转体低速倾斜入水过程中入水空泡及流体动力特性的影响规律,开展不同入水角度回转体低速倾斜入水过程数值仿真研究.计算过程中,回转体模型采用140°锥角头型,入水速度v0=10.0 m/s,入水角度为φ0=45°、φ0=55°、φ0=65°.
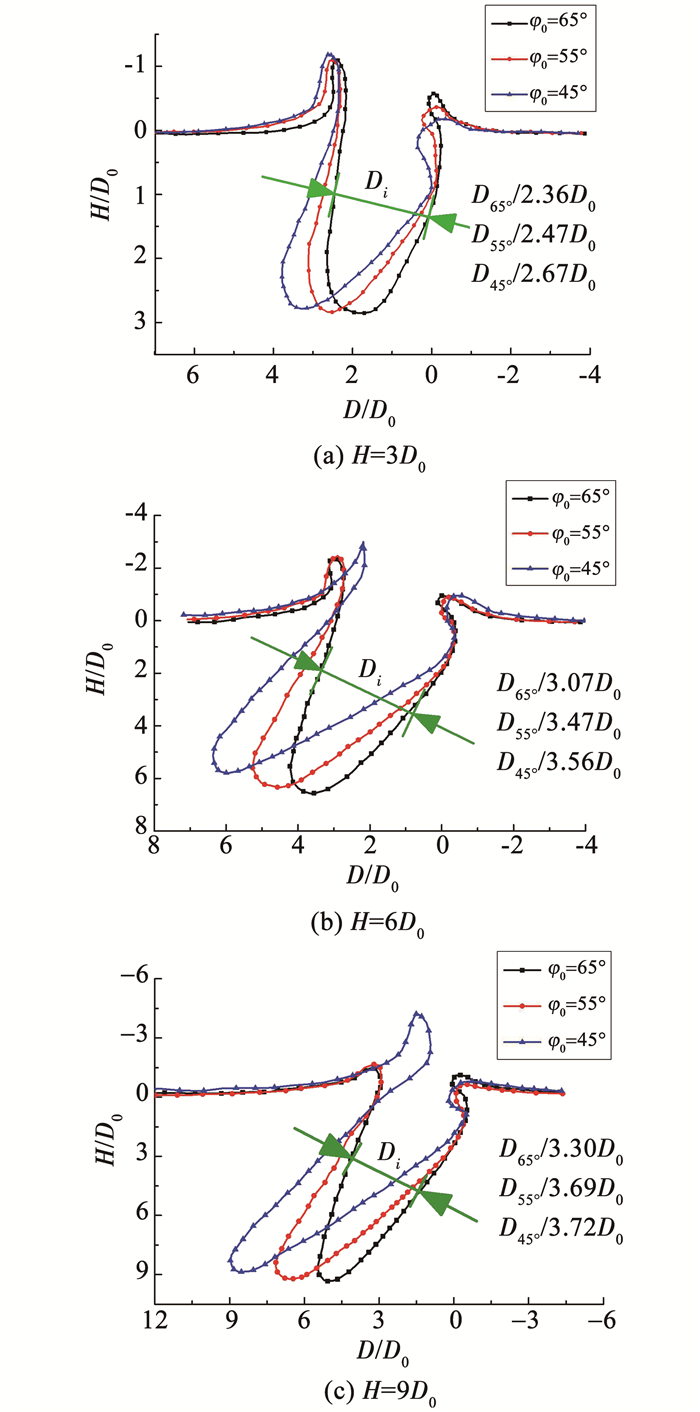
4.1 入水角度对空泡影响图 13为回转体低速倾斜入水过程中,不同入水角度下所形成的入水空泡形态对比.从图中可以知道,当回转体入水深度较小时,不同入水角度回转体所产生的入水空泡在自由液面处差异较小,空泡轮廓近似重合;随着入水深度的增加,自由液面附近的空泡轮廓差异越来越大.入水深度H=6D0时刻,入水角度φ0=45°回转体入水所引起的空泡即将出现表面闭合现象,另两种角度入水所引起的入水空泡仍处于扩张阶段,由此可以得出,在同一入水速度下,回转体入水空泡闭合时间随着入水角度φ0的减小而减小.图 13中给出了不同入水角度空泡中段相同入水深度处空泡直径,从图 13中可以看出,在入水前期,同一入水空泡中段处其直径随着入水深度的增加而增大;在同一入水深度,入水空泡的直径随着入水角度的增加而减小.
|
图 13 不同入水深度空泡形态对比 Figure 13 Water-entry cavities of the revolution body |
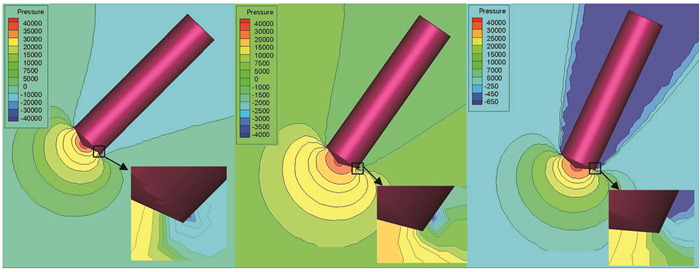
图 14为回转体以不同角度入水过程中,流场压力特征分布.从图中可以知道,对于低速倾斜入水的回转体,当入水深度相同时,不同入水角度回转体入水过程中流场的最高压力差别较小,均为40 kPa左右;但回转体附近流场的由于入水过程造成的最小压力差别较大,其值随着回转体入水角度的增加而显著增大.
|
图 14 H=6D0时流场压力等值线云图 Figure 14 Pressure contour for H=6D0 |
图 15为低速倾斜入水过程中入水深度H=6D0,回转体锥头母线压力分布随入水角度变化规律.从图中可以知道,当入水深度相同时,在回转体肩部左端点附近,由于不同角度入水造成的回转体母线压力差别较小;但是随着距离回转体头部左端点距离的增大,入水角度对回转体母线压力形成的差异逐渐显现,且随着入水角度的增加而增大;不同入水角度的回转体锥头母线上压力最高点均位于母线中点偏左处,且其位置逐渐随着入水角度的增加而向母线右端点偏移,但其值差别较小.

|
图 15 入水深度H=6D0锥头母线压力分布 Figure 15 Pressure of taper generatrix for H=6D0 |
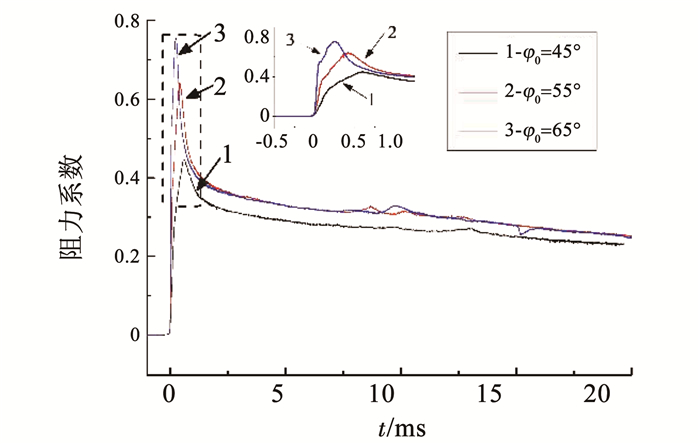
图 16给出了不同入水角度回转体阻力系数变化规律对比.从图 16中可以看出,在入水之前,回转体阻力系数近似为零,且保持恒定;在撞击自由液面后回转体阻力系数在极短时间内出现峰值,且不同入水角度阻力系数峰值随着入水角度的增加而增大;随着距离自由液面的深度增加,阻力系数值缓慢减小,并逐渐达到稳定值,其中入水角度φ0=45°回转体其阻力系数稳定值较小,入水角度φ0=55°和φ0=65°回转体阻力系数稳定值差别很小,阻力系数曲线基本重合.
|
图 16 阻力系数变化曲线 Figure 16 Drag coefficients of the revolution body |
1) 对于低速倾斜入水过程,当回转体入水深度相同时,回转体入水所形成空泡直径随其入水速度的增加而小幅增大,随着入水角度的增加而减小.
2) 入水速度对流场中压力分布规律有较大影响,在同一入水深度处不同入水速度回转体入水过程中流场的最大压力随着入水速度的增加而增大;入水角度对回转体附近流域的最大压力影响较小,但最小压力随着回转体入水角度的增加而增大.
3) 同一入水深度母线上相同位置处,回转体压力随着入水速度的增加而增大,回转体锥头母线上压力最高点位于其母线中点偏左处,且位置相同;对于不同入水角度回转体,母线压力峰值位置随着入水角度的而逐渐向母线右端点偏移,但峰值差别较小.
4) 不同入水速度回转体阻力系数峰值差别不大,但稳定后的阻力系数值随着入水速度的增加而减小;不同入水角度阻力系数峰值随着入水角度的增加而增大.
| [1] |
LEE M, LONGORIA R G, WILSON D E. Cavity dynamics in high-speed water entry[J]. Physics of Fluids, 1997, 9(3): 540. DOI:10.1063/1.869472 |
| [2] |
TABUTEAU H, SIKORSKI D, De VET S J, et al. Impact of spherical projectiles into a viscoplastic fluid[J]. Physical Review E, 2011, 84(3): 031403. DOI:10.1103/PhysRevE.84.031403 |
| [3] |
LEE M. Water-entry induced cavity pressure[J]. KSME International Journal, 2000, 14(5): 562. DOI:10.1007/BF03185659 |
| [4] |
YAN Hongmei, LIU Yuming, KOMINIARCZUK J, et al. Cavity dynamics in water entry at low Froude numbers[J]. Journal of Fluid Mechanics, 2009, 641: 441. DOI:10.1017/S0022112009991558 |
| [5] |
ARISTOFF J M, BUSH J W M. Water entry of small hydrophobic spheres[J]. Journal of Fluid Mechanics, 2009, 619: 45. DOI:10.1017/S0022112008004382 |
| [6] |
SUN S L, WU G X. Oblique water entry of a cone by a fully three-dimensional nonlinear method[J]. Journal of Fluids and Structures, 2013, 42: 313. DOI:10.1016/j.jfluidstructs.2013.05.012 |
| [7] |
叶取源. 锥头物体垂直入水空泡的发展和闭合[J]. 水动力学研究与进展, 1989, 4(2): 33. YE Quyuan. Evolution and closure of cavity after vertieal water entry of cone-head bodies[J]. Journal of Hydrodynamics, 1989, 4(2): 33. DOI:10.16076/j.cnki.cjhd.1989.02.005cnki.cjhd.1989.02.005 |
| [8] |
温俊生, 施红辉, 徐胜利, 等. 头型对回转体垂直入水时空泡面闭合影响的数值模拟[J]. 浙江理工大学学报(自然科学版), 39(5): 573. WEN Junsheng, SHI Honghui, XU Shengli, et al. Numerical simulation of the effects of different heads on surface closure of the water entry supercavity[J]. Journal of Zhejiang Sci-Tech University(Natural Sciences Edition), 39(5): 573. DOI:10.3969/j.issn1673-3851(n).2018.05.009 |
| [9] |
魏卓慧, 王树山, 马峰. 刚性截锥形弹体入水冲击载荷[J]. 兵工学报, 2010, 31(Z1): 118. WEI Zhuohui, WANG Shushan, MA Feng. Diving impact load of rigid truncated conical projectile[J]. ACTA Armamentarii, 2010, 31(Z1): 118. |
| [10] |
王聪, 何春涛, 权晓波, 等. 空气压力对垂直入水空泡影响的数值研究[J]. 哈尔滨工业大学学报, 2012, 44(5): 14. WANG Cong, He Chuntao, QUAN Xiaobo, et al. Numerical simulation of the influence of atmospheric pressure on water-cavity formed by cylinder with vertical water-entry[J]. Journal of Harbin Institute of Technology, 2012, 44(5): 14. |
| [11] |
何春涛, 王聪, 闵景新, 等. 回转体匀速垂直入水早期空泡数值模拟研究[J]. 工程力学, 2012, 29(4): 237. HE Chuntao, WANG Cong, MIN Jingxin, et al. Numerical simulation of early air-cavity of cylinder cone with vertical water-entry[J]. Engineering Mechanics, 2012, 29(4): 237. |
| [12] |
杨衡, 张阿漫, 龚小超, 等. 不同头型弹体低速入水空泡试验研究[J]. 哈尔滨工程大学学报, 2014, 35(9): 1060. YANG Heng, ZHANG Aman, GONG Xiaochao, et al. Experimental study of the cavity of low speed water entry of different head shape projectiles[J]. Journal of Harbin Engineering University, 2014, 35(9): 1060. DOI:10.3969/j.issn.1006-7043.2013 |
| [13] |
黄志刚, 孙铁志, 杨碧野, 等.平头锥型回转体高速入水结构强度数值分析[J].爆炸与冲击[2018-05-23].http://kns.cnki.net/kcms/detail/51.1148.O3.20180124.1638.004.html HUANG Zhigang, SUN Tiezhi, YANG Biye, et al. Numerical analysis of structural strength of high speed water entry for a cone-shaped flatted revolutionbody[J]. Explosion and Shock Waves[2018-05-23]. http://kns.cnki.net/kcms/detail/51.1148.O3.20180124.1638.004.html |
| [14] |
宋武超, 王聪, 魏英杰, 等. 不同头型回转体低速倾斜入水过程流场特性数值模拟[J]. 北京理工大学学报, 2017, 37(7): 661. SONG Wuchao, WANG Cong, WEI Yingjie, et al. Numerical simulation of the flow field characteristics of low speed oblique water entry of revolution body[J]. Transactions of Beijing Institute of Technology, 2017, 37(7): 661. DOI:10.15918/j.tbit1001-0645.2017.07.001 |
| [15] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201. DOI:10.1016/0021-9991(81)90145-5 |
| [16] |
宋武超.小型回转体低速倾斜入水过程流场特性研究[D].哈尔滨: 哈尔滨工业大学, 2015 SONG Wuchao. Study on flow field characteristics of small-scale revolution body during water entry[D]. Harbin: Harbin Institute of Technology, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10213-1015981316.htm |
| [17] |
马庆鹏.高速射弹入水过程多相流程特性研究[D].哈尔滨: 哈尔滨工业大学, 2014 MA Qingpeng. Investigation of multiphase flow characteristics induced by water entry of high-speed projectiles[D]. Harbin: Harbin Institute of Technology, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10213-1014085234.htm |
 2018, Vol. 50
2018, Vol. 50


