2. 北京宇航系统工程研究所,北京 100076;
3. 哈尔滨工业大学 航天学院,哈尔滨 150001
2. Beijing Institute of Aerospace System Engineering, Beijing 100076, China;
3. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China
功能梯度材料(functionally graded materials, FGMs)是一种非均匀的新型复合材料,其成分、密度等物理属性沿某一方向呈现连续梯度变化,因其物理性能没有突变,所以可以较好的避免或降低应力集中现象,这是与传统复合材料的不同之处[1-2].由于其具有特殊的性能,如高刚度和热抗性;同时具有很好的可设计性,可以有针对性地改变各组分材料体积分数的空间分布规律,从而达到优化结构内部应力分布的目的[3].所以这种材料在航空航天、汽车船舶、核反应堆、能源动力等工程领域具有十分广阔的应用前景.因此引起国内外大量学者的广泛关注和研究.
功能梯度材料可以按所设计的方向进行材料属性变化,其中材料属性梯度变化规律最常见的为指数函数型[4]和幂函数型[5].对于功能梯度梁,其材料属性通常沿厚度方向或轴向变化.在对材料属性沿厚度方向变化的功能梯度梁动力学特性分析中,姚晓莎等[6]采用微分求积法,分析了轴向运动速度对功能梯度Euler-Bernoulli梁的横向振动特性以及失稳形式的影响. Pradhan等[7]利用Rayleigh-Ritz法分析了功能梯度Timoshenko和Euler-Bernoulli梁动力学特性,给出了材料属性、梁长细比对梁固有频率的影响.对于材料属性沿轴向变化的功能梯度梁,由于其控制方程是变系数的,因此处理起来更为复杂. Shahba等[8-9]通过有限元方法和微分变化单元法(differential transform element method)对变截面轴向功能梯度Euler-Bernoulli和Timoshenko梁的自由振动和轴向稳定性进行了研究,分析了不同材料属性和截面变化率对固有频率和临界屈曲载荷的影响. Rajasekaran[10-11]利用差分变换方法和低阶微分求积单元法对旋转的轴向梯度楔形Euler-Bernoulli和Timoshenko梁分别进行了自由振动分析.黄意新等[12-14]提出了一种改进的Chebyshev谱方法,并将其应用于均匀与变截面轴向功能梯度Euler-Bernoulli梁和Timoshenko梁的动力学分析,该方法具有近似指数收敛特性且计算精度与效率较有限元等数值计算方法更具优势.
但上述研究均是对经典边界条件下的功能梯度Euler-Bernoulli梁或Timoshenko梁进行动力学分析,而对于弹性连接边界、集中质量等因素考虑较少,而实际工程中边界条件对系统固有频率、模态振型等动力学特性的影响往往不可忽略.因此,本文将基于Timoshenko梁理论,利用改进型的Chebyshev谱方法对复杂边界条件下的变截面轴向功能梯度梁动力学特性进行研究.其中复杂边界条件问题将通过投影矩阵法进行处理,以便在不需重新推导系统动力学方程的前提下计算不同边界条件下系统的固有频率数值解,进而对材料梯度指数、截面变化率、集中质量等参数效应进行分析研究.
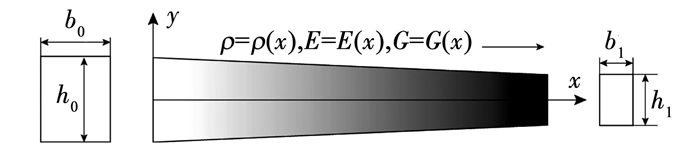
1 动力学建模 1.1 系统动能与势能考虑如图 1所示的长为l的变截面轴向功能梯度梁,其材料属性沿梁的轴向连续变化,材料属性如剪切模量G、弹性模量E、密度ρ,以及截面积A均为轴向坐标x的函数.
|
图 1 变截面轴向功能梯度梁 Figure 1 An axially FGM beam with non-uniform cross-section |
基于Timoshenko梁理论,考虑剪切变形和转动惯量的影响,根据文献[15]可得Timoshenko梁的动能为
| $ T = {T_{{\rm{trans}}}} + {T_{{\rm{rot}}}}, $ | (1) |
其中:
| $ {T_{{\rm{trans}}}} = \frac{1}{2}\int_0^l {\rho \left( x \right)A\left( x \right){{\left( {\frac{{\partial w\left( {x,t} \right)}}{{\partial t}}} \right)}^2}{\rm{d}}x} , $ |
| $ {T_{{\rm{rot}}}} = \frac{1}{2}\int_0^l {\rho \left( x \right)I\left( x \right){{\left( {\frac{{\partial \alpha \left( {x,t} \right)}}{{\partial t}}} \right)}^2}{\rm{d}}x} . $ |
势能为
| $ U = {U_{{\rm{bending}}}} + {U_{{\rm{shear}}}}, $ | (2) |
其中:
| $ {U_{{\rm{bending}}}} = \frac{1}{2}\int_0^l {E\left( x \right)I\left( x \right){{\left( {\frac{{\partial \alpha \left( {x,t} \right)}}{{\partial x}}} \right)}^2}{\rm{d}}x} , $ |
| $ {U_{{\rm{shear}}}} = \frac{1}{2}\int_0^l {\kappa G\left( x \right)A\left( x \right){{\left( {\frac{{\partial w\left( {x,t} \right)}}{{\partial x}} - \alpha \left( {x,t} \right)} \right)}^2}{\rm{d}}x} . $ |
式中:w(x, t)为梁的横向振动位移; α(x, t)为由于弯曲引起的转动角度; κ为梁的截面剪切系数.由上述各式可得系统Lagrangian函数L=T-U.
1.2 离散动力学方程利用文献[12]中所提出的改进型Chebyshev谱方法对轴向功能梯度梁的变形场进行离散,然后根据第2类Largrange方程推导系统动力学方程.
根据Chebyshev谱方法,对于任意在定义域x∈[-1, 1]上连续可导且平方可积的函数y(x)可采用Chebyshev多项式进行逼近:
| $ {y_N}\left( x \right) \approx \sum\limits_{k = 0}^{N - 1} {{a_k}{T_k}\left( x \right)} . $ |
式中:N为采用的多项式项数,Tk(x)为第k项Chebyshev多项式.基于文献[12]中的函数逼近方法,在已知函数y(x)在N个Gauss-Lobatto节点上的值时,可以得到其n阶导数的逼近[13]
| $ {\mathit{\boldsymbol{y}}^{\left( n \right)}} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{\rm{B}}}{\mathit{\boldsymbol{D}}^{\left( n \right)}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{\rm{B}}^{ - 1}\mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{Q}}_n}\mathit{\boldsymbol{y}}, $ | (3) |
式中, Qn为n阶Chebyshev微分矩阵.此外,对于在定义域[l1, l2]上连续可导且平方可积的两个函数f(x)、g(x),其内积可表示为
| $ \int_{{l_1}}^{{l_2}} {f\left( x \right)g\left( x \right){\rm{d}}x} = {\mathit{\boldsymbol{f}}^{\rm{T}}}\mathit{\boldsymbol{Vg}}. $ |
式中: V为N×N阶Chebyshev内积矩阵; f、g分别为函数f(x)、g(x)的Gauss-Lobatto节点值列向量.此外,函数f(x)、g(x)关于函数h(x)的加权内积可表示为
| $ \int_{{l_1}}^{{l_2}} {f\left( x \right)g\left( x \right)h\left( x \right){\rm{d}}x} = {\mathit{\boldsymbol{f}}^{\rm{T}}}{\mathit{\boldsymbol{V}}_h}\mathit{\boldsymbol{g}}, $ | (4) |
式中Vh是关于函数h(x)的N×N Chebyshev加权内积对角阵.与文献[13]不同的是文献[12]对函数的内积矩阵和加权内积矩阵进行了重新推导,新推导出的加权内积矩阵为对角阵,大大减小了运算量.
令:
| $ f\left( x \right) = E\left( x \right)I\left( x \right),\;\;\;g\left( x \right) = \kappa G\left( x \right)A\left( x \right), $ |
| $ m\left( x \right) = \rho \left( x \right)A\left( x \right),\;\;\;s\left( x \right) = \rho \left( x \right)I\left( x \right). $ |
根据式(3)、(4)可将式(1)中动能和式(2)中势能表示为:
| $ \begin{array}{l} U = \frac{1}{2}{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{Q}}_1^{\rm{T}}{\mathit{\boldsymbol{V}}_f}{\mathit{\boldsymbol{Q}}_1}\mathit{\boldsymbol{\alpha }} + \frac{1}{2}\left( {{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{Q}}_1^{\rm{T}}{\mathit{\boldsymbol{V}}_g}{\mathit{\boldsymbol{Q}}_1}\mathit{\boldsymbol{w}} - } \right.\\ \;\;\;\;\;\;\left. {2{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{Q}}_1^{\rm{T}}{\mathit{\boldsymbol{V}}_g}{\mathit{\boldsymbol{Q}}_1}\mathit{\boldsymbol{\alpha }} + {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\mathit{\boldsymbol{V}}_g}\mathit{\boldsymbol{\alpha }}} \right), \end{array} $ | (5) |
| $ T = \frac{1}{2}\left( {{{\mathit{\boldsymbol{\dot w}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}_1^{\rm{T}}{\mathit{\boldsymbol{V}}_m}\mathit{\boldsymbol{\dot w}} + {{\mathit{\boldsymbol{\dot \alpha }}}^{\rm{T}}}{\mathit{\boldsymbol{V}}_s}\mathit{\boldsymbol{\dot \alpha }}} \right). $ | (6) |
式中:w、α分别为位移w和转角α在N个Gauss-Lobatto节点上的值向量;Vf、Vg、Vm、Vs分别为关于函数f(x)、g(x)、m(x)和s(x)的加权内积矩阵.考虑式(5)、(6),利用Lagrange方程:
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial {{\dot q}_j}}}} \right) - \frac{{\partial L}}{{\partial {{\dot q}_j}}} = 0, $ |
可以得到未考虑边界条件时的变截面轴向功能梯度Timoshenko梁自由振动的离散控制方程为
| $ \mathit{\boldsymbol{M\ddot q}} + \mathit{\boldsymbol{Kq}} = \mathit{\boldsymbol{F}}, $ | (7) |
其中:
| $ \mathit{\boldsymbol{q}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{w}}\\ \mathit{\boldsymbol{\alpha }} \end{array}} \right],\mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_m}}&{}\\ {}&{{\mathit{\boldsymbol{V}}_s}} \end{array}} \right],\mathit{\boldsymbol{F}} = 0, $ |
| $ \mathit{\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{Q}}_1^{\rm{T}}{\mathit{\boldsymbol{V}}_g}{\mathit{\boldsymbol{Q}}_1}}&{ - \mathit{\boldsymbol{Q}}_1^{\rm{T}}{\mathit{\boldsymbol{V}}_g}}\\ { - \mathit{\boldsymbol{Q}}_1^{\rm{T}}{\mathit{\boldsymbol{V}}_g}}&{\mathit{\boldsymbol{Q}}_1^{\rm{T}}{\mathit{\boldsymbol{V}}_f}{\mathit{\boldsymbol{Q}}_1} + {\mathit{\boldsymbol{V}}_g}} \end{array}} \right]. $ |
为了方便地处理各类经典与复杂边界条件问题,本文采用投影矩阵法向式(7)所描述的离散系统施加各类边界条件.
表 1给出了各类边界条件的数学表达式,其中上标“′”为对变量x的偏导数,ei为第i个元素为1其余元素均为0的N维行向量.对于表中各类线性边界条件可以表示成如下形式:
| $ \mathit{\boldsymbol{Bq}} = \mathit{\boldsymbol{0}}, $ | (8) |
| 表 1 各类边界条件及其数学表达式 Table 1 Formulas of boundary conditions |
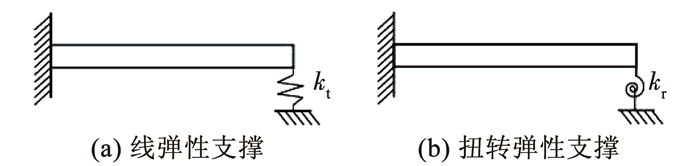
式中矩阵B的行数M代表了边界条件的个数,例如,对于图 2 (a)中的线弹性支撑梁则有4个边界条件,即
| $ \left[ {\begin{array}{*{20}{c}} \begin{array}{l} {\mathit{\boldsymbol{e}}_N}\\ \mathit{\boldsymbol{0}}\\ {\mathit{\boldsymbol{e}}_1}\left( {\kappa GA{\mathit{\boldsymbol{Q}}_1} - {k_{\rm{t}}}\mathit{\boldsymbol{I}}} \right)\\ \mathit{\boldsymbol{0}} \end{array}&\begin{array}{l} \mathit{\boldsymbol{0}}\\ {\mathit{\boldsymbol{e}}_N}\\ - {\mathit{\boldsymbol{e}}_1}\kappa GA\\ {\mathit{\boldsymbol{e}}_1}EI{\mathit{\boldsymbol{Q}}_1} \end{array} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{w}}\\ \mathit{\boldsymbol{\alpha }} \end{array}} \right] = \mathit{\boldsymbol{Bq}} = \mathit{\boldsymbol{0}}, $ |
|
图 2 弹性支撑边界条件 Figure 2 elastic supports |
式中I为N×N单位矩阵.同样,对于扭转弹性支撑边界条件则有
| $ \left[ {\begin{array}{*{20}{c}} \begin{array}{l} {\mathit{\boldsymbol{e}}_N}\\ \mathit{\boldsymbol{0}}\\ \mathit{\boldsymbol{0}}\\ {\mathit{\boldsymbol{e}}_1}\kappa GA{\mathit{\boldsymbol{Q}}_1} \end{array}&\begin{array}{l} \mathit{\boldsymbol{0}}\\ {\mathit{\boldsymbol{e}}_N}\\ {\mathit{\boldsymbol{e}}_1}\left( {EI{\mathit{\boldsymbol{Q}}_1} - {k_{\rm{r}}}\mathit{\boldsymbol{I}}} \right)\\ - {\mathit{\boldsymbol{e}}_1}\kappa GA \end{array} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{w}}\\ \mathit{\boldsymbol{\alpha }} \end{array}} \right] = \mathit{\boldsymbol{0}}. $ |
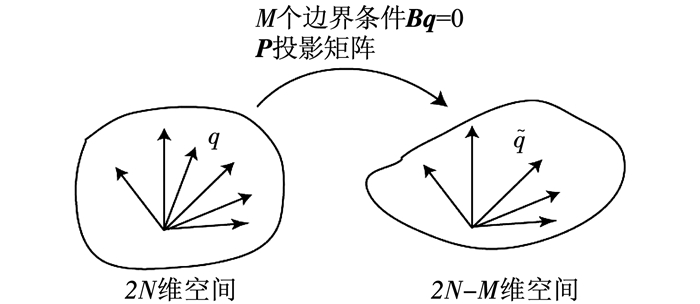
对于满足式(8)中M个约束条件的方程(7)的解(2N维向量)将是2N-M维空间中的向量且可以表示为
| $ \mathit{\boldsymbol{q}} = \mathit{\boldsymbol{P\tilde q}}, $ | (9) |
式中:
|
图 3 投影矩阵 Figure 3 Projection matrix |
将式(9)代入式(7)即可得到施加边界条件后的系统离散形式控制方程为
| $ \mathit{\boldsymbol{\tilde M \ddot {\tilde q}}} + \mathit{\boldsymbol{\tilde K\tilde q}} = \mathit{\boldsymbol{0}}, $ |
其中:
| $ \mathit{\boldsymbol{\tilde M}} = {\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{MP}},\;\;\;\mathit{\boldsymbol{\tilde K}} = {\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{KP}}, $ |
分别为系统质量阵与刚度阵,且
首先通过数值算例验证本文方法的正确性,在此基础上进一步分析截面变化率、材料属性和复杂边界条件等因素对系统动力学特性的影响.
假定功能梯度材料由ZrO2和Al两种材料成分构成,其属性沿轴向呈指数变化规律为:
| $ T\left( x \right) = {T_{\rm{z}}} + \left( {{T_{\rm{a}}} - {T_{\rm{z}}}} \right){\left( {\frac{x}{l}} \right)^n}, $ |
| $ A\left( x \right) = {A_0}\left( {1 - c\frac{x}{l}} \right),\;\;\;\;I\left( x \right) = {I_0}{\left( {1 - c\frac{x}{l}} \right)^3}. $ |
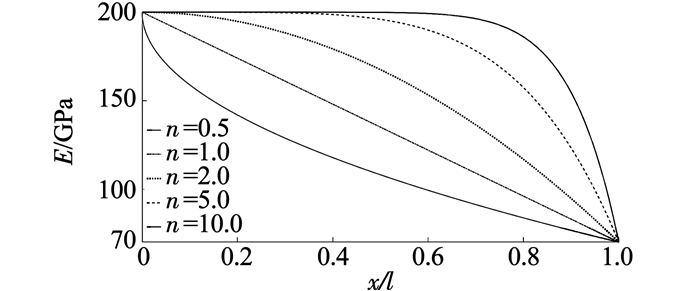
式中:T为材料属性ρ、E、G等,下标z、a分别为材料ZrO2和Al;A为截面面积;I为截面惯性矩,下标0代表x=0处(即梁的左端);c为截面变化率;n为材料梯度指数.取Ez=200 GPa,ρz=5 700 kg/m3,Ea=70 GPa,ρa=2 702 kg/m3,不同梯度指数下弹性模量沿轴向变化规律如图 4所示.
|
图 4 不同材料梯度指数时弹性模量沿轴向变化规律 Figure 4 Young's modulus with respect to different n |
为方便与文献[8]对比,定义量纲一的参数:
| $ r = \frac{{{I_0}}}{{{A_0}{l^2}}},\varpi = \omega \sqrt {\frac{{{\rho _0}{A_z}{l^4}}}{{{E_z}{I_0}}}} , $ |
式中:r为梁的细长比,ϖ为量纲一的固有频率.取r=0.01,截面剪切系数κ=5/6,泊松比ν=0.3,材料梯度指数n=2.0.计算不同截面变化率、不同边界条件下梁的固有频率,结果如图 5与表 2所示.
|
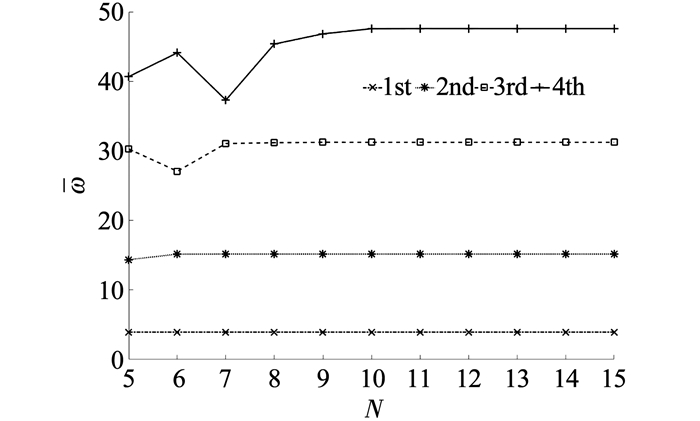
图 5 量纲一的固有频率计算结果收敛性 Figure 5 The convergence of dimensionless natural frequencies |
| 表 2 不同边界条件和截面变化率下前四阶量纲一的固有频率 Table 2 The first four dimensionless natural frequencies with different boundary conditions (n=2.0) |
图 5为固支-自由(C-F)边界条件、截面变化率c=0.1时Chebyshev谱方法计算结果的收敛性,从中可以看出随着采用的Chebyshev多项式项数N的增大,各阶固有频率将收敛于稳定值,对于前四阶频率计算,取N=12即可满足计算精度要求.从表 2中可以看出,采用12阶Chebyshev多项式时,其计算精度与文献[8]中采用30个单元时的结果吻合很好,验证了本文方法的正确性.
3.1 截面与材料属性影响从表 2可以发现悬臂梁的前一阶量纲一的固有频率随着截面变化率的增大而增大,如表中粗体数字所示,而其他阶量纲一的固有频率均表现出减小趋势.对于两端简支(H-H)和两端固支(C-C)边界条件,各阶量纲一的固有频率均随着截面变化率的增大而减小.
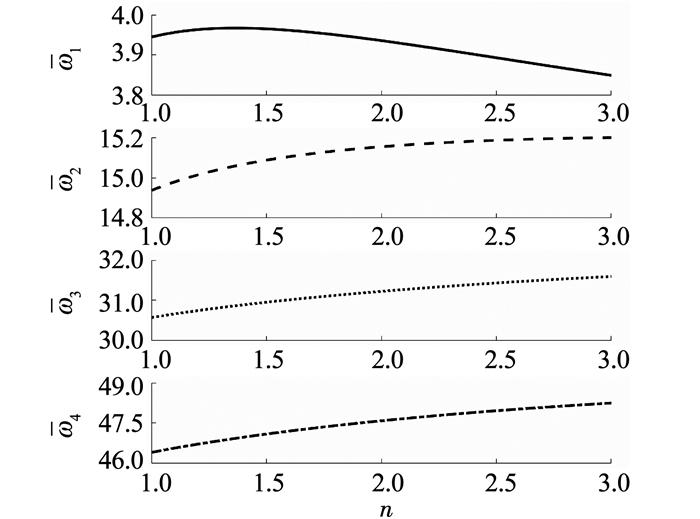
为了解材料非均质性对梁动力学特性的影响,采用12阶Chebyshev多项式,在截面变化率c=0.1的情况下,图 6~8给出了不同边界条件下,材料梯度指数n对前四阶量纲一的固有频率的影响.从中可以看出,对于不同的边界条件,随着n的增加,对前四阶量纲一的固有频率有不同的影响.从图 6中可以发现,悬臂梁的一阶固有频率在n=1.35时,量纲一的固有频率增加到ϖ=3.966 93,然后开始有下降的趋势.但其他各阶频率则均呈现单调增加的趋势.这说明对于悬臂梁,存在着一个最优的材料梯度指数n使其一阶固有频率取得最大值.从图 7中可以看到,两端简支梁的前四阶量纲一的固有频率均随着n值的增加而增加.从图 8中可以发现,随着n的增加,两端固支梁的前两阶量纲一的固有频率呈现下降趋势,而三、四阶量纲一的固有频率则呈现增加的趋势.
|
图 6 悬臂梁量纲一的固有频率随n的变化 Figure 6 Dimensionless natural frequencies of the cantilever beam |
|
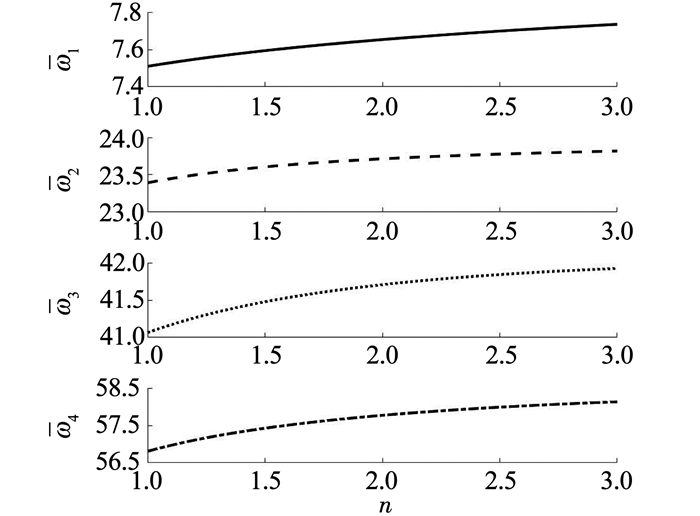
图 7 两端简支梁量纲一的固有频率随n的变化 Figure 7 Dimensionless natural frequencies of the hinged-hinged beam |
|
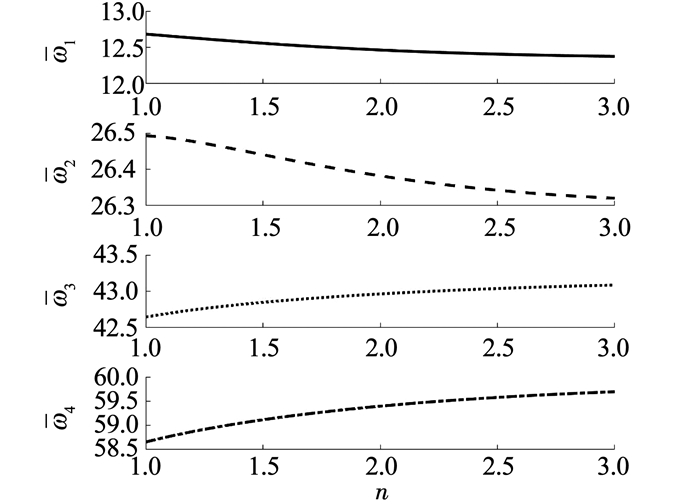
图 8 两端固支梁量纲一的固有频率随n的变化 Figure 8 Dimensionless natural frequencies of the clamped-clamped beam |
考虑如图 9所示的弹性连接变截面轴向功能梯度Timoshenko梁,其一端为固定端,另一端为弹性约束.定义量纲一的参数:
| $ {K_{\rm{t}}} = \frac{{{k_t}{l^3}}}{{{E_0}{I_0}}},{K_{\rm{r}}} = \frac{{{k_r}l}}{{{E_0}{I_0}}}. $ |

|
图 9 变截面轴向功能梯度Timoshenko梁的弹性约束模型 Figure 9 An elastically restrained axially FGM beam with non-uniform cross-section |
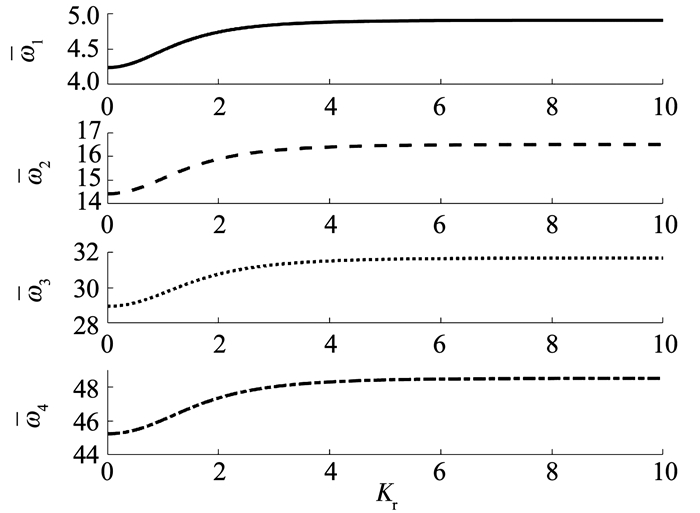
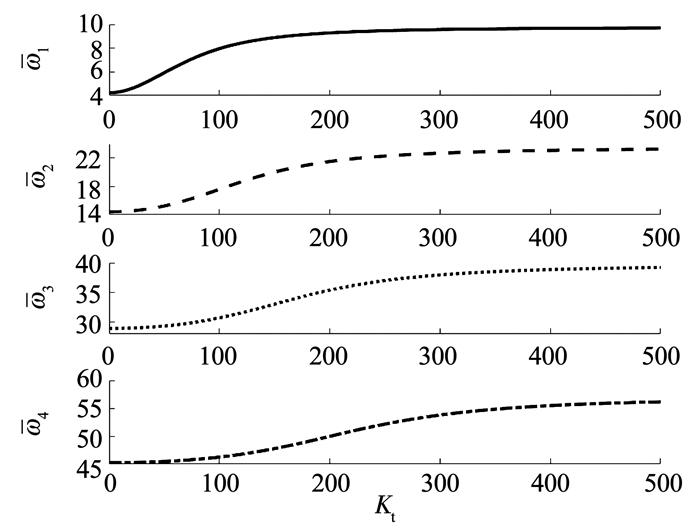
图 10、11显示了线性弹簧参数Kt和旋转弹簧参数Kr在材料梯度指数n=2.0,截面变化率c=0.5时对量纲一的固有频率的影响.从中可以发现,各阶量纲一的固有频率随弹簧刚度增加呈阶梯状变化,最终收敛至常值,且低阶模态收敛速度比高阶模态更快;从图 10、11对比中可以发现,旋转弹簧和线性弹簧随着刚度的增加均使前四阶量纲一的固有频率有增大的趋势,且旋转弹簧较线性弹簧在低刚度时对量纲一的固有频率的影响更大.从表 3中可以看出,当旋转弹簧和线性弹簧同时较小时,量纲一的固有频率将趋于悬臂梁梁的值,当弹簧刚度无限大时,量纲一的固有频率将趋于两端固支梁的值.
|
图 10 旋转弹簧约束条件下固有频率的变化 Figure 10 The variation of dimensionless natural frequencies vs. rotational spring restrained |
|
图 11 线性弹簧约束条件下固有频率的变化 Figure 11 The variation of dimensionless natural frequencies vs. translational spring restrained |
| 表 3 弹性约束下的前四阶量纲一的固有频率 Table 3 The first four dimensionless natural frequencies with an elastically restraint |
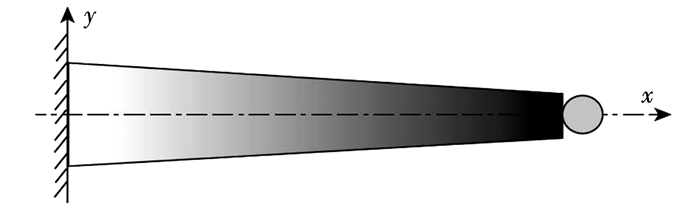
对于一端固定,一端附加质量块的轴向楔形功能梯度Timoshenko梁悬臂梁模型如图 12所示,定义量纲一的参数:
| $ \alpha = \frac{{{I_m}}}{{{\rho _0}{A_0}{l^3}}},\beta = \frac{{{M_m}}}{{{\rho _0}{A_0}l}}, $ |
|
图 12 轴向功能楔形Timoshenko梁附加质量块模型 Figure 12 Schematic of an axially FGM beam with tip mass |
式中Im、Mm分别为质量块的转动惯量与质量.
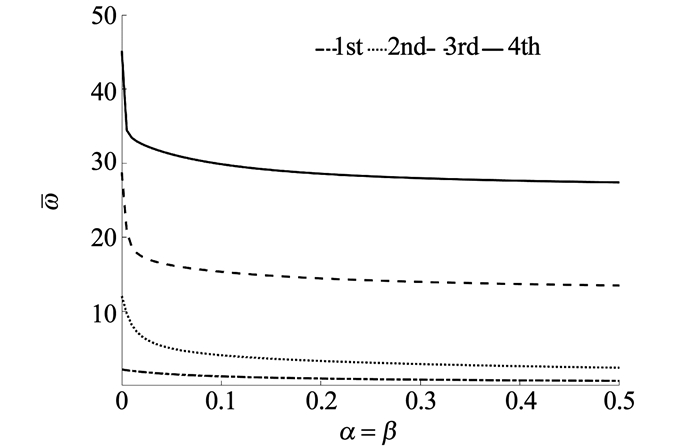
在材料属性n=2.0、截面变化率c=0.1、量纲一的参数α=β的条件下,图 13显示了前四阶量纲一的固有频率的变化.可以看出,附加集中质量块可以使前四阶量纲一的固有频率减小,并且附加质量块对高阶固有频率的影响更大.
|
图 13 集中质量对悬臂梁量纲一的固有频率的影响 Figure 13 Effect of the attached tip mass on the natural frequencies of a cantilever axially FGM beam |
1) 随着截面变化率的增大,悬臂梁一阶频率随之增大且其他阶频率随之减小,两端简支梁与两端固支梁的各阶频率均随之减小.
2) 材料梯度指数对系统固有频率的影响因边界条件而不同;对于悬臂梁,其一阶量纲一的固有频率随材料属性n的增大呈先增大后减小的趋势;两端简支梁的前四阶量纲一的固有频率随着n值的增加而增加;两端固支梁的前两阶量纲一的固有频率随着n的增加呈现下降趋势,而三、四阶量纲一的频率呈增大趋势.
3) 弹性支撑刚度的增大使量纲一的固有频率呈现阶梯状增大趋势,最终收敛至一常值;在刚度值较小时,旋转弹簧相较线性弹簧对量纲一的固有频率的影响更大.
4) 附加集中质量使前四阶量纲一的固有频率减小,且对高阶量纲一的固有频率的影响更大.
| [1] |
韩杰才, 徐丽, 王保林, 等. 梯度功能材料的研究进展及展望[J]. 固体火箭技术, 2004, 27(3): 207. HAN Jiecai, XU Li, WANG Baolin, et al. Progress and prospects of functional gradient materials[J]. Journal of Solid Rocket Technology, 2004, 27(3): 207. DOI:10.3969/j.issn.1006-2793.2004.03.012 |
| [2] |
仲政, 吴林志, 陈伟球. 功能梯度材料与结构的若干力学问题研究进展[J]. 力学进展, 2010, 40(5): 528. ZHONG Zheng, WU Linzhi, CHEN Weiqiu. Progress in the study on mechanics problems of functionally graded materials and structures[J]. Advances in Mechanics, 2010, 40(5): 528. |
| [3] |
徐刚年.功能梯度梁的力学行为研究[D].兰州: 兰州理工大学, 2010 XU Gangnian. Research on mechanical behavior functionally graded beam[D]. Lanzhou: Lanzhou University of Technology, 2010 http://cdmd.cnki.com.cn/Article/CDMD-10731-2010181221.htm |
| [4] |
KIM J H, PAULINO G H. Finite element evaluation of mixed mode stress intensity factors in functionally graded materials[J]. International Journal for Numerical Methods in Engineering, 2002, 53(8): 1903. DOI:10.1002/nme.364 |
| [5] |
GUPTA A, TALHA M. Recent development in modeling and analysis of functionally graded materials and structures[J]. Progress in Aerospace Sciences, 2015, 79: 1. DOI:10.1016/j.paerosci.2015.07.001 |
| [6] |
姚晓莎, 王忠民, 赵凤群. 轴向运动功能梯度梁的横向振动[J]. 机械工程学报, 2013, 49(23): 117. YAO Xiaosha, WANG Zhongmin, ZHAO Fengqun. Transverse vibration of axially moving beam made of functionally graded materials[J]. Journal of Mechanical Engineering, 2013, 49(23): 117. DOI:10.3901/JME.2013.23.117 |
| [7] |
PRADHAN K K, CHAKRAVERTY S. Free vibration of Euler and Timoshenko functionally graded beams by Rayleigh-Ritz method[J]. Composites Part B: Engineering, 2013, 51(4): 175. DOI:10.1016/j.compositesb.2013.02.027 |
| [8] |
SHAHBA A, ATTARNEJAD R, MARVI M T, et al. Free vibration and stability analysis of axially functionally graded tapered Timoshenko beams with classical and non-classical boundary conditions[J]. Composites Part B: Engineering, 2011, 42(4): 801. DOI:10.1016/j.compositesb.2011.01.017 |
| [9] |
SHAHBA A, RAJASEKARAN S. Free vibration and stability of tapered Euler-Bernoulli beams made of axially functionally graded materials[J]. Applied Mathematical Modelling, 2012, 36(7): 3094. DOI:10.1016/j.apm.2011.09.073 |
| [10] |
RAJASEKARAN S. Differential transformation and differential quadrature methods for centrifugally stiffened axially functionally graded tapered beams[J]. International Journal of Mechanical Sciences, 2013, 74: 15. DOI:10.1016/j.ijmecsci.2013.04.004 |
| [11] |
RAJASEKARAN S. Free vibration of centrifugally stiffened axially functionally graded tapered Timoshenko beams using differential transformation and quadrature methods[J]. Applied Mathematical Modelling, 2013, 37(6): 4440. DOI:10.1016/j.apm.2012.09.024 |
| [12] |
ZHAO Yang, HUANG Yixin, GUO Mingquan. A novel approach for free vibration of axially functionally graded beams with non-uniform cross-section based on Chebyshev polynomials theory[J]. Composite Structures, 2017, 168: 277. DOI:10.1016/j.compstruct.2017.02.012 |
| [13] |
黄意新, 田浩, 赵阳. 弹性连接旋转柔性梁动力学分析[J]. 力学学报, 2016, 48(4): 963. HUANG Yixin, TIAN Hao, ZHAO Yang. Dynamic analysis of a rotating flexible beam with elastic boundary conditions[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(4): 963. DOI:10.6052/0459-1879-16-083 |
| [14] |
黄意新, 赵阳, 田浩, 等. 弹性支撑旋转Timoshenko梁动力学特性[J]. 噪声与振动控制, 2016, 36(3): 6. HUANG Yixin, ZHAO Yang, TIAN Hao, et al. Dynamic characteristics of a spinning Timoshenko Beam with elastic supports[J]. Noise and Vibration Control, 2016, 36(3): 6. DOI:10.3969/j.issn.1006-1335.2016.03.002 |
| [15] |
HAN S M, BENAROYA H, WEI T. Dynamics of transversely vibrating beams using four engineering theories[J]. Journal of Sound and Vibration, 1999, 225(5): 935. DOI:10.1006/jsvi.1999.2257 |
| [16] |
LEUNG A Y T, ZHOU W E, LIM C W, et al. Dynamic stiffness for piecewise non-uniform Timoshenko column by power series—part Ⅰ: Conservative axial force[J]. International Journal for Numerical Methods in Engineering, 2001, 51(5): 505. DOI:10.1002/nme.159.abs |
 2018, Vol. 50
2018, Vol. 50


