能源问题与环境问题是当今社会上受到普遍关注的两大问题.随着经济和科技的发展,人类对能源的需求日益增长,而目前全球消耗量最大的化石能源正面临着枯竭的危机.日益增长的能源需求与有限的化石能源之间的矛盾将导致围绕能源的争夺越发紧迫[1].美国太空安全办公室发表报告认为,能源的短缺与人口的增长成为21世纪世界局部冲突与矛盾的潜在根源,因而能源短缺成为国家安全的重要威胁[2].另一方面,大量化石能源的开采和使用造成了许多环境污染与破坏问题,如城市大气污染、温室效应、全球变暖等,因此能源问题与环境问题之间有着紧密的联系.为了应对将来可能出现的能源危机和目前的环境污染问题,许多国家高度重视清洁新能源的研发和利用.太阳能是无污染、可再生的绿色能源,对缓解世界的能源与环境问题有着重要的作用.尽管太阳能是丰富的可再生能源,但其利用却受到多种因素的制约[3-4],如:发电效率受昼夜、天气、季节等因素的影响较大,因而发电效率不稳定且难以预测;地面的太阳能能量密度低,因此需要占用大量陆地面积才能实现大规模发电;太阳能电池板上的灰尘、积雪等需要定期清理,还需要考虑冰雹、狂风等天气造成的破坏.
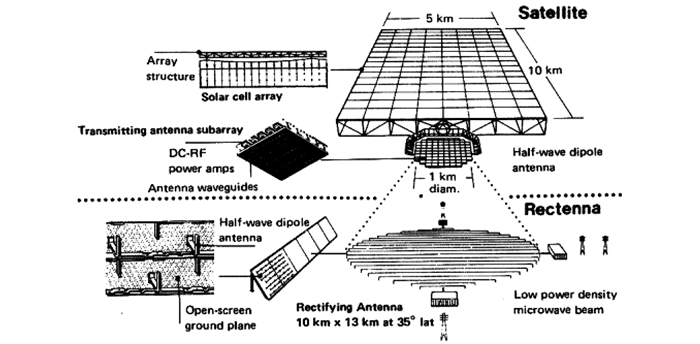
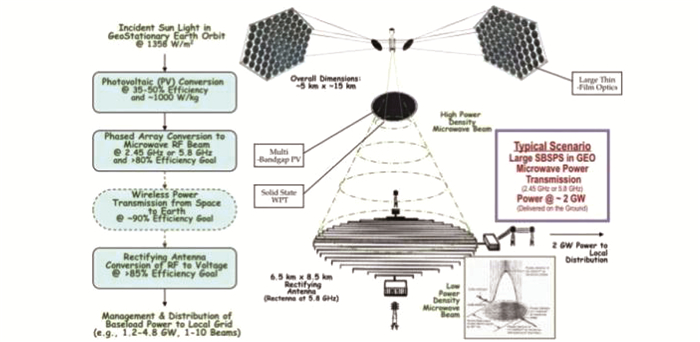
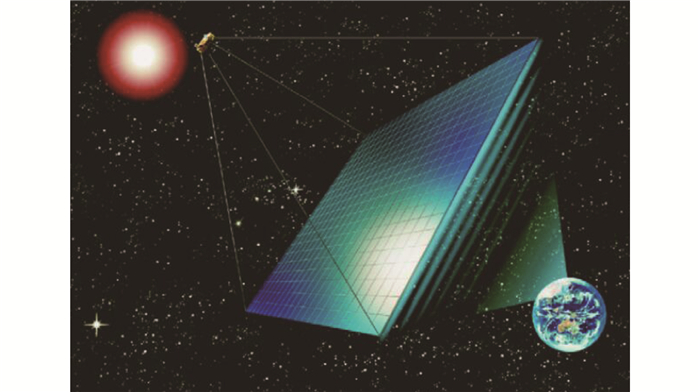
为了实现高效、持续的太阳能发电,美国学者Glaser[5]于1968年在《Science》上发表论文,首次提出了建立空间太阳能电站的设想.Glaser[5]认为太阳能是人类赖以生存的重要能源,但是目前还没有得到充分的利用,因此提出了通过超大的空间太阳能电站为地球提供源源不断的电能的想法.空间太阳能电站的发电过程主要包括3个部分:首先通过大型太阳能电池阵列在太空中将太阳能转化成电能;再将电能转换为微波,通过微波发射天线将能量传输到地面的接收天线;最后地面接收天线将接收到的微波转化为电能,输入电网供用户使用.Glaser[5]设想的太阳能电池阵列、微波发射天线和地面接收天线的直径分别为6、2、3 km,系统运行的轨道可能是地球同步轨道.1973年,Glaser[6]给出了一个地面接收功率为5 GW的空间太阳能电站构型,巨大的太阳能电池阵列对称分布在微波发射天线的南北两侧,系统运行在地球同步轨道,如图 1所示.由于微波能量传输基本不受天气的影响,即使在大雨天也能保证94%的能量传输效率,所以空间太阳能电站可以实现持续向地面供电.
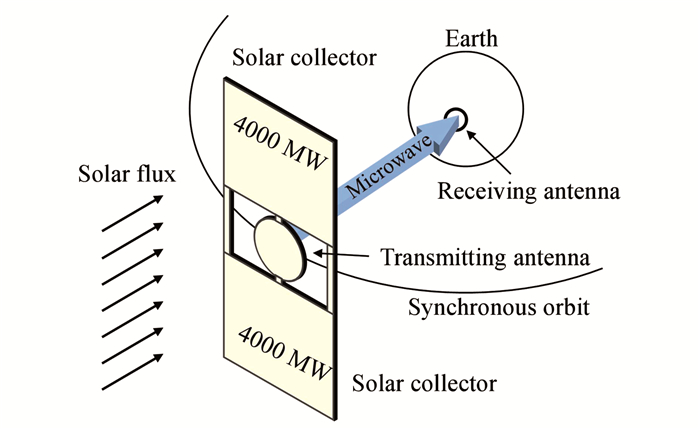
|
图 1 1个5 GW的空间太阳能电站概念 Figure 1 A concept of 5-GW SSPS |
Glaser[5-6]提出空间太阳能电站时正值苏、美两国太空竞赛期间,苏、美两国先后掌握了发射人造地球卫星、载人航天、空间交会对接、太空行走等技术,美国也已经启动了阿波罗载人登月计划.另一方面,20世纪50、60年代欧、美等发达国家化石燃料消耗量持续上升,世界范围内也广泛地出现了环境污染问题如伦敦烟雾事件[7]、洛杉矶光化学烟雾事件等[8-9],给人们的健康带来了严重威胁,使得人们对清洁环境呼声不断.航天技术的飞速发展、化石能源的大量消耗与环境的恶化,使得Glaser[6]提出的空间太阳能发电的构想在国际上引起了广泛的关注.美国、日本、中国和欧洲国家纷纷投入到空间太阳能电站的研究中.
经过半个世纪的发展,人们对空间太阳能电站的概念设计方案已经有了大量的研究,但是很多关键技术仍不成熟,其中包括空间太阳能电站的动力学与控制技术.在空间太阳能电站概念设计方案方面已经有综述文献,如文献[10-14],但尚未发现空间太阳能电站动力学与控制方面的综述文献.本文旨在回顾和总结空间太阳能电站的概念设计方案和其在轨服役过程的动力学与控制研究工作,为空间太阳能电站动力学与控制的研究者们提供方便的参考资料.与文献[10-14]不同的是,本文在总结空间太阳能电站概念设计方案时,更偏向于介绍其与动力学与控制方面相关的特性.空间太阳能电站在很多文献里也被称为太阳能发电卫星(Solar power satellite, SPS), 为了不引起歧义,本文统一称为空间太阳能电站(Space solar power station, SSPS).
1 空间太阳能电站设计方案回顾本文对美国、日本、欧洲和中国对空间太阳能电站的研究历史和提出的概念设计方案进行回顾.
1.1 美国20世纪60年代末到70年代初,美国的大型国防合约商雷神公司、格鲁门飞机工程公司、美国国家航空航天局(NASA)等研究机构对空间太阳能电站作了大量的系统分析与相关技术研究.随后波音公司于1976年12月到1977年12月、罗克韦尔国际公司于1977年3月到1978年3月,独立地进行了详细的空间太阳能电站概念设计研究.1977年7月NASA与能源部(DOE)联合启动并资助了空间太阳能电站概念开发与评估项目,这个项目一直持续到1980年7月,结合波音公司和罗克韦尔国际公司等的概念设计方案的优点,提出了一个新的空间太阳能电站设计方案,称为1979 SSPS基准系统[15],如图 2所示.除了提出1979 SSPS基准系统的设计方案外,这个项目在技术、安全、经济、制度等方面作了详细的分析.在1980年4月DOE和NASA共同举办的空间太阳能电站项目研讨会上,约235名专家围绕空间太阳能电站作了约180个报告,围绕空间太阳能电站概念设计、空间太阳能电站对环境、经济以及社会的影响等主题展开了深入的讨论[16].
1979 SSPS基准系统是空间太阳能电站概念开发与评估项目的产物,是一个非常完善的空间太阳能电站设计方案.1979 SSPS基准系统的太阳能电池阵列长度和宽度分别约为10 km和5 km,由厚度约为500 m的桁架支撑,最终输入电网的功率为5 GW,系统质量为3.4×104~5.0×104 t.直径为1 km的微波发射天线通过大功率导电旋转关节与太阳能电池阵列的一端相连,相应的地面接收站的大小为10 km× 13 km.1979 SSPS基准系统原计划2000年开始建造,每一个的建造周期为0.5 a,30 a总共建造60个空间太阳能电站为地面提供能量.如果采用硅材料的太阳能电池板方案,建造过程需要480人在地球静止轨道进行组装、维护等工作,另外需要75人在近地轨道工作.尽管DOE和NASA对1979 SSPS基准系统方案作了非常详细的设计和计划,但是由于所需人力、物力、财力过高,所以没有获得最终立项,因而也就停止了对空间太阳能电站研究的资助[17].
后来,由于世界能源消耗量持续增加、温室气体的大量排放、科学技术的进步与冷战结束后国际合作的发展,空间太阳能电站的研究热潮再一次被掀起.1995—1997年间,NASA组织了近百位来自各个学科的专家进行了为期两年的“Fresh Look”研究项目,目的是研究空间太阳能电站新的技术发展、经济可行性及其可能带来的环境效应[17].这个项目分析了将空间太阳能电站或能量中继卫星放置在太阳同步轨道、近地轨道、中地球轨道、地球同步轨道上的可行性;提出了模块化的思想,采用了机器人技术和自动化技术,降低了对人为操作的依赖;将30余个空间太阳能电站方案进行了对比,最终挑选出4个方案进行了深入分析,其中包括太阳塔方案和太阳盘方案.
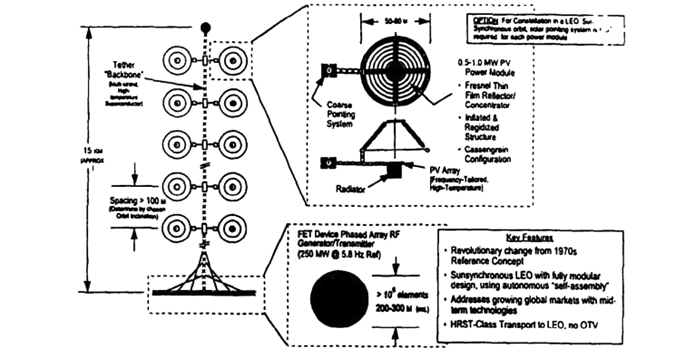
太阳塔方案[17-18]由微波发射天线、中央缆绳和两排聚光器和太阳能电池板构成,发电功率约为200 MW,如图 3所示[17].系统运行在轨道高度为1 000 km的太阳同步轨道,采取万有引力梯度稳定方式,通过若干个太阳塔来实现持续供电.聚光器通过充气的方式展开并获得一定的刚度,太阳能电池板背面安装散热器.中央缆绳长度约为15 km,微波发射天线的直径约为260 m,厚度约为1 m,聚光器的直径约为50~100 m.
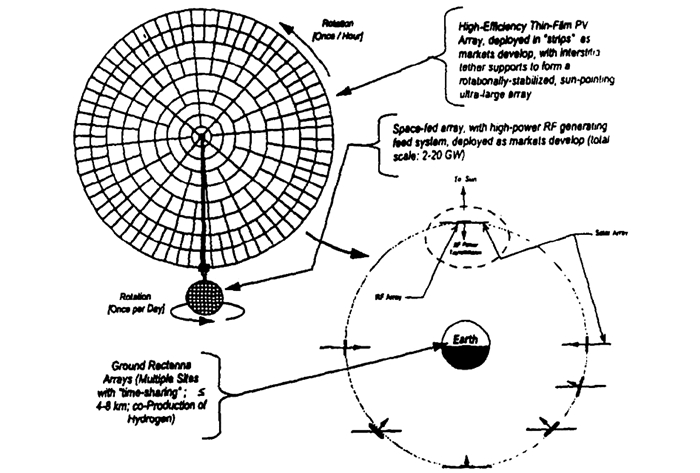
太阳盘方案由圆形的太阳能电池阵列、桁架结构和微波发射天线组成,如图 4所示[17],系统运行在地球静止轨道.太阳能电池阵列的直径为3~6 km,通过自旋的方式保持对日指向,约1 h旋转1周.桁架结构的一端连接在太阳能电池阵列的中心,另一端连接直径为1 000 m的微波发射天线,桁架保持固定的指向.太阳能电池阵列产生的能量通过大功率的导电旋转关节和桁架传输到微波发射天线.微波发射天线保持指向地球,因此相对于桁架每天旋转1周.
1999—2000年,NASA又资助了“空间太阳能电站探索研究与技术(SERT)”项目,对空间太阳能电站的技术发展路线、概念设计、技术标准和地面试验进行了详细的分析,把实现商业级空间太阳能电站的过程分成了4个阶段.针对初始阶段提出了多种100 kW和10 MW的空间太阳能电站实验方案,针对商业阶段提出了集成对称聚光系统和Abacus/Reflector两个具有代表性的设计方案[19].
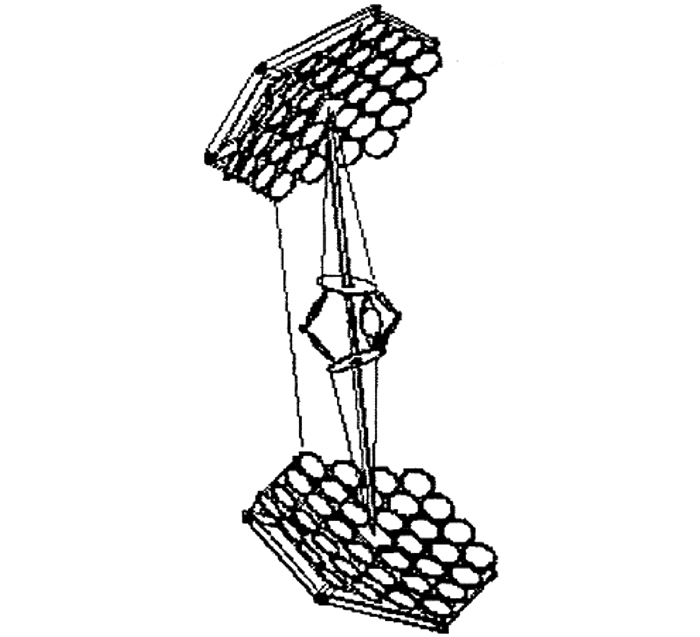
在上述的空间太阳能电站设计方案中,由于需要长距离电力传输,电力管理系统的质量都非常大,而且大功率的导电旋转关节始终是一个关键的技术难点.集成对称聚光系统方案正是为了解决这两个问题而提出的,如图 5所示.这个方案是典型的聚光型空间太阳能电站方案,通过位于桅杆两端的大型聚光镜将太阳光反射至桅杆中央的两个太阳能电池板上,再通过较短的电缆将能量传输到微波发射天线上,从而避免了长距离电力传输和对大功率导电旋转关节的使用.桅杆、太阳能电池板、微波发射天线作为一个整体保持相对静止,桅杆保持与轨道法线平行,微波发射天线指向地面接收站,桅杆与聚光镜之间通过旋转关节相连.系统运行在地球静止轨道,系统总重量约为1.7×104 t,发电功率为1.2 GW.桅杆长度为6 373 m,聚光镜大小约为3 559 m×3 642 m,太阳能电池板的直径为1 000 m,微波发射天线直径为500 m.后来基于集成对称聚光系统,“SERT”项目又提出了“三明治”型空间太阳能电站,也被称为对称二次聚光系统,如图 6所示[20].该系统的关键技术是采用了“三明治”结构,厚度约为10 m,上层为太阳能电池板,中间层为微波转换器,下层为微波发射天线,系统安排得更加紧凑.太阳光经过一级聚光镜反射到位于系统中间的二级聚光镜,经过再次反射后到达“三明治”结构的上层太阳能电池板.这个方案的缺点是紧凑的三明治结构会带来严峻的散热问题,而过高的温度会影响系统的正常工作.
“SERT”项目提出的另一个空间太阳能电站方案是Abacus/Reflector方案,如图 7所示.微波发射天线与大型桁架相连,桁架表面铺设菲涅尔透光镜,微波发射天线指向轨道法线方向.反射镜将微波发射天线的能量反射到地球上,从而用较轻的反射镜的精确指向控制代替了微波发射天线的指向控制,同时也避免了大功率导电旋转关节的使用.但是这样会同时引起新的问题,如反射镜的高精度指向、型面保持、热变形等.Abacus/Reflector的总质量为2.2×104 t,供电功率和微波发射天线的尺寸均与集成对称聚光系统相同.
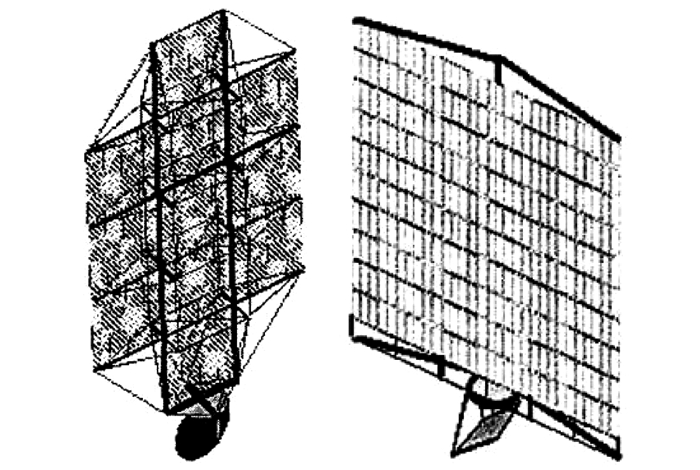
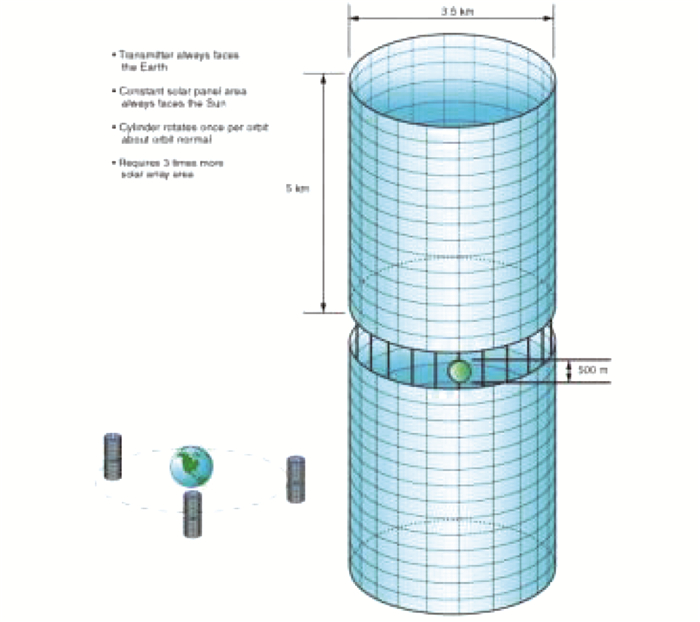
由于Abacus/Reflector方案的巨型太阳能电池阵列需要保持对日指向,其俯仰姿态受万有引力梯度力矩的影响较大,给姿态控制系统设计带来了困难,因此NASA又提出了圆柱型空间太阳能电站方案,如图 8所示[22].此方案在轨运行时保持圆柱的母线垂直于轨道平面,从而不受万有引力梯度力矩的影响.
2007年3月,美国国防部意识到空间太阳能电站不仅可以解决能源问题,而且对空间技术、经济、环境和国家安全都有着重要的意义.于是美国太空安全办公室通过网络公开互动合作论坛的方式收集到170名专家的意见.该论坛的主题分为通用主题、科学与技术、法律与政策、基础设施与后勤和商业案例五方面,经过了半年时间的讨论,最终形成了“空间太阳能电站作为战略安全的机遇”的报告[2].该报告认为,要想在21世纪的上半世纪内建造出空间太阳能电站,美国政府必须要在3个方面作出努力:1)资助解决关键技术问题;2)在政策、管理、法律、组织等方面引导政府间、政府与商业界、商业界之间的合作;3)成为空间太阳能电站的采用者并以资鼓励其他早期的采用者.
2011—2012年,在NASA创新先进概念项目的支持下,Mankins等[23]提出了任意相控阵空间太阳能电站方案,如图 9所示.这个概念的运行轨道为地球静止轨道,采用万有引力梯度稳定的姿态,框架整体不需要调整,固定在框架上的每个薄膜反射镜单独调整方向,保证太阳光反射到太阳能电池板上.采用三明治结构,从而避免了长距离电力传输.该系统还采用了很多先进的技术,如实现高精度传播方向控制的波束方向控制系统、集成了散热管理系统的高效光伏太阳能电池等.系统总质量约为1×104 t,发电功率为2 GW.
1.2 日本日本从20世纪80年代开始了对空间太阳能电站的研究,开创性地提出了多个空间太阳能电站设计方案,并研究了微波和激光两种能量传播方式[24].
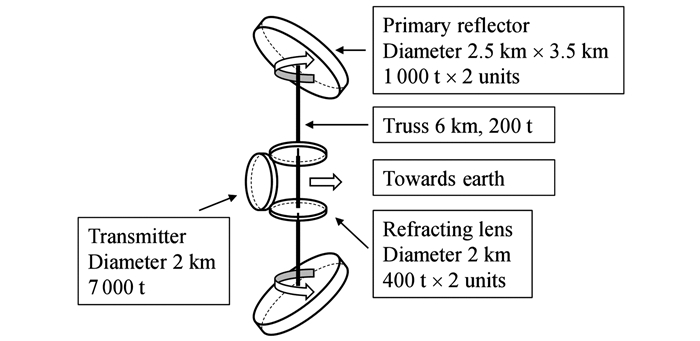
日本宇宙航空研究开发机构(JAXA)基于集成对称聚光系统和“三明治”型空间太阳能电站,提出了SSPS 2001方案,如图 10所示.这个概念也采用二级反射镜和“三明治”结构,所有的组件通过桁架结构相连.一级反射镜的尺寸约为6 km×4 km,三明治结构的直径约为2.6 km,发电功率为1 GW.这个方案不足之处有两点,一是“三明治”结构的散热问题难以解决,二是需要大型的桁架结构提供支撑.为了解决“三明治”结构的散热问题,JAXA于2002年对SSPS 2001方案进行了改进,提出了SSPS 2002方案,如图 11所示.SSPS 2002方案不再采用三明治结构,而是把太阳能电池板和微波发射天线放置在同一平面,从而背面可以用于散热.尺寸上比SSPS 2001方案小,一级反射镜的尺寸为3.5 km×2.5 km,天线的直径为2 km.这个方案虽然解决了散热问题,但同时也带来了新的问题:由于微波发射天线占用了部分面积而导致了能量转化效率降低、模块与模块之间的电力传输成为困难等.因此这种方案在后续的空间太阳能电站研究中也没有被采用.
|
图 11 日本的SSPS 2002方案 Figure 11 SSPS 2002 concept by JAXA |
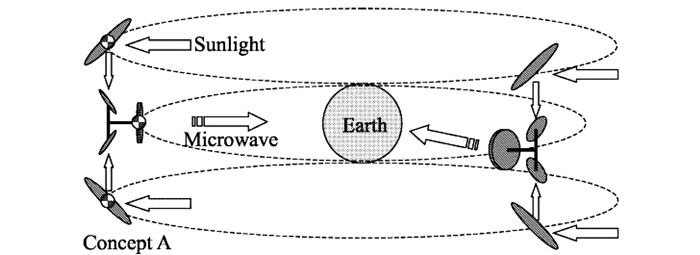
2003年JAXA的Takeichi等[25-27]在研究中发现,SSPS 2001方案以及美国的集成对称聚光系统都需要非常大的桁架结构作为支撑,即使桁架的直径达到300 m,整个结构的最低阶扭转固有频率也只有5.7×10-4 Hz.同时为了满足一级聚光镜对日指向、微波发射天线对地指向,需要设计超大型的旋转关节.这两方面都成为了巨大的技术难点.为了解决这两个问题,他们提出了编队飞行空间太阳能电站的方案,如图 12所示.这个方案由南、北两个聚光器和中间的发电-传输装置组成,其中发电-传输装置由太阳能电池板与微波发射天线或激光发射器组成.在这个方案中,两个聚光镜将单独地运行在自己的轨道,通过编队飞行技术保持与发电-传输装置的相对位置固定,并保持对日指向.聚光镜的轨道和姿态将通过太阳光压力在南北方向的分量和太阳光压力矩来维持.因此编队飞行方案不需要大型的桁架结构和大型的旋转关节,并且成功避免了超柔的桁架结构振动给精确姿态指向控制带来的影响.编队飞行方案的发电功率与反射镜尺寸均与SSPS 2002方案相同.在2003年提出的方案中,采用了三明治结构,2004年为了解决散热问题又提出了将太阳能电池板和微波发射天线分开的方案[28].
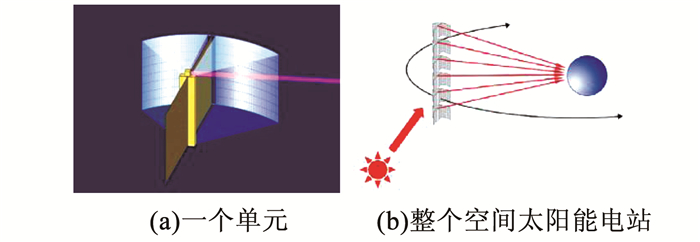
微波能量传输和激光能量传输是两种最可能的能量传输方式,日本提出微波型空间太阳能电站的同时,也提出了很多激光型的空间太阳能电站方案,基本上是在平行地进行研究.文献[28]提出了多种激光型的空间太阳能电站方案,其中最具有代表性的是2004年JAXA提出的激光空间太阳能电站,如图 13所示.其中图 13(a)是激光太阳能电站的一个基本单元,由两个反射(或透射)聚光镜、激光发射器和两块散热板组成.基本单元的聚光镜和散热板的大小均为100 m× 100 m,输出功率为10 MW.由于系统的聚光比大于100,所以需要采用冷却液的主动散热技术维持激光发射器合适的工作温度.图 13(b)是由100个基本单元沿南北方向排列而成的激光空间太阳能电站,其输出功率为1 GW.
除了JAXA以外,日本另一个研究空间太阳能电站的机构是无人太空实验自由飞行物研究所(Institute for unmanned space experiment free flyer),他们通过研究发现以往的空间太阳能电站都过于复杂,需要取得挑战性的技术突破,并且系统鲁棒性不高.于是Sasaki等[29]于2001年提出了一种新的空间太阳能电站概念:绳系空间太阳能电站,如图 14所示.这个电站由1.9 km×2.0 km的发电-传输面板、卫星平台系统和多根系绳组成.面板的上表面是太阳能电池板,下表面合理布置太阳能电池板和微波发射天线.系统运行在地球静止轨道,采用万有引力梯度保持面板的下表面指向地球,因而发电功率会随时间波动,地面接收的平均发电功率约为0.75 GW.卫星平台系统到面板的距离为10 km,面板由400个95 m×100 m的子面板组成,通过机器人在轨组装形成最终的系统.这个方案的显著优势为:系统比较简单,避免了单点失效问题,不需要旋转机构,也不需要主动的姿态控制.因此,绳系空间太阳能电站方案受到了广泛的关注[30-34].
1.3 欧洲1998年,欧洲航天局(ESA)与德国宇航中心(DLR)联合进行了一项“空间探索与利用中的系统概念、体系结构与技术”研究,并提出了太阳帆塔空间太阳能电站的方案[35],如图 15所示. 2003年,ESA的先进概念团队对多种空间太阳能电站方案综合可行性进行了分析,他们认为大规模的空间太阳能电站跟地面太阳能电站相比有明显的优势,是解决未来能源问题的重要途径[24].
太阳帆塔方案的灵感来源于美国提出的太阳塔空间太阳能电站,并结合了ESA与DLR所掌握的太阳帆技术,对太阳塔方案进行了改进.太阳帆塔由微波发射天线、中央缆绳和缆绳两边的太阳能电池板组成.缆绳长度为15 km,太阳能电池板的尺寸为150 m×150 m,微波发射天线直径为1 000 m,系统总质量为2.1×103 t,发电功率为450 MW.采用厚度仅为12 um薄膜太阳能电池以降低系统的质量,每个太阳能电池板由自主展开的十字型桁架支撑,并连接于中央缆绳上.每个太阳能电池模块还集成了自主展开系统、散热系统、姿态和轨道控制系统等,包括离子推进器和燃料箱.每个模块从地面发射至近地轨道,自主展开后通过自身的推进系统转移至地球静止轨道.太阳帆塔的中央缆绳采用万有引力梯度保持姿态稳定,另一方面,太阳能电池板通过导电旋转关节保持对日指向.虽然有时会出现互相遮挡的情况,但总体上太阳能电池板的太阳光照射率能达到88%.与其他空间太阳能电站方案相比,太阳帆塔具有面质比大、功率质量比高的特点.
1.4 中国中国对空间太阳能电站的关注和研究开始于20世纪末. 1998年,李国欣等[11, 36-37]根据1997年在加拿大举办的“空间太阳能电站国际研讨会”的会议资料,对空间太阳能电站在国际上的发展状况作了详细的总结,对空间太阳能电站的技术可行性作了分析,最后对中国发展空间太阳能电站的必要性进行了讨论.他们认为,空间太阳能电站是解决中国能源需求、优化能源结构的重要途径,在中国的航天技术基础上,需要加快对关键技术的攻关.“两弹一星”元勋王希季院士[4]指出,空间太阳能电站的发展将引发新的技术产业革命,将从根本上改变人类获取能源、传输能源和利用能源的方式.王立等[10, 12]对2006年以来中国空间太阳能电站的研究进展作了总结,结合国际空间太阳能电站的发展状况,对中国空间太阳能电站的关键技术提出了许多发展建议[38].2010、2017年中国空间技术研究院主办了两届空间太阳能电站发展技术研讨会,规模上从2010年有近百名专家发展到2017年有近两百名专家参与了会议[39];在王希季院士、孙家栋院士等多位院士的带领和指导下,空间太阳能电站的研究得到了越来越多的关注.该研讨会的专家组提出了“2030年建设兆瓦级空间太阳能试验电站,2050年前具备建设百万千瓦级商业空间太阳能电站的能力”的目标[39].中国空间技术研究院、西安电子科技大学、西北工业大学、大连理工大学、哈尔滨工业大学等单位的研究团队从不同的角度对空间太阳能电站进行了深入研究.当前,国内提出的最具代表性的方案为多旋转关节空间太阳能电站方案和SSPS-OMEGA方案.
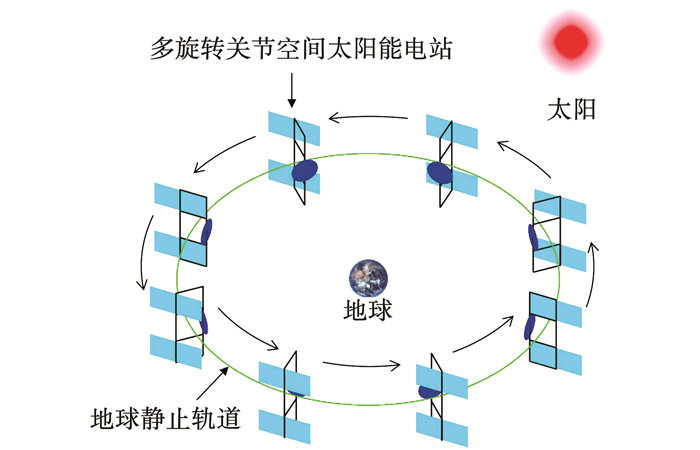
2015年钱学森空间技术实验室提出了多旋转关节空间太阳能电站的方案,如图 16所示[40-41].该方案开创性地将大型的太阳能电池阵列分成50个太阳能电池子阵,从而降低了导电旋转关节的技术难点,并避免了导电旋转关节的单点失效问题,提高了系统的鲁棒性.每个太阳能电池子阵的尺寸为200 m×600 m,通过中等功率的导电旋转关节和导线将能量传输至直径为1 km的微波发射天线.系统主结构的长度为10 800 m,总质量为10 000 t,发电功率为1 GW.每个太阳能电池子阵由12块100 m×100 m的薄膜太阳能电池组成,薄膜太阳能电池、主结构、微波发射天线都通过在轨展开和在轨组装形成整体构型.系统运行在地球静止轨道,太阳能电池子阵沿南北方向排列,微波发射天线保持对地指向,太阳能电池子阵通过旋转关节保持对日指向.
|
图 16 多旋转关节空间太阳能电站 Figure 16 Multi-rotary joints SSPS |
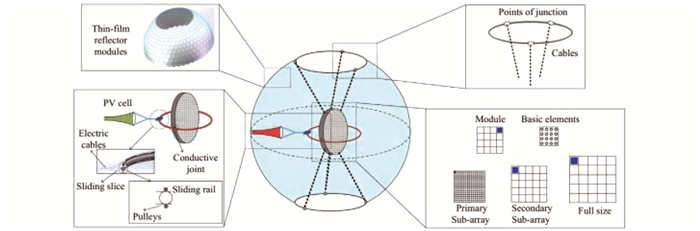
西安电子科技大学段宝岩院士的研究团队分析了SSPS-ALPHA方案的不足之处,并提出了SSPS-OMEGA方案,如图 17所示[42-43].SSPS-OMEGA方案采用球形反射镜,使太阳光聚焦在柱状体太阳能电池表面,从而避免了单个反射镜模块自身的旋转,因此也避免了SSPS-ALPHA的漏光现象.聚光镜需要采用单向透光材料,即正面透光、反面反光的材料.直径约为1 km的微波发射天线通过缆绳与球形框架相连,并可以通过调节缆绳的长度来控制发射天线的姿态指向.SSPS-OMEGA的运行轨道为地球静止轨道,反射镜与微波发射天线保持相对静止,微波发射天线对地指向,太阳能电池的两端沿着滑轨滑动以保持在聚光位置.太阳能电池与微波发射天线之间通过电缆、滑轨、滑片、滑轮、导电关节相连,电缆长度小于750 m.由于球形反射镜具有对称性,所以发电功率稳定.与SSPS-ALPHA相比,SSPS-OMEGA的质量降低了15.71%,功率质量比提升了31.68%.后来该团队基于SSPS-OMEGA方案和透射聚光技术,提出了该方案的另一种形式[44].
|
图 17 SSPS-OMEGA方案 Figure 17 The concept of SSPS-OMEGA |
虽然世界各国对空间太阳能电站进行了半个世纪的研究,先后提出了多种设计方案,但是目前很多关键技术仍未实现.空间太阳能电站的关键技术包括空间超大型结构动力学与控制技术、无线能量传输技术、大型运载器及高密度发射技术、高效率太阳能转换技术等[3, 38].空间太阳能电站的发射、展开、组装、服役、回收等过程都会面临许多动力学与控制问题,其中服役过程是空间太阳能电站最重要的过程,一般历时30~50 a.本文主要针对空间太阳能电站服役过程的动力学与控制问题进行回顾.
空间太阳能电站是超大尺度的空间柔性系统,无论是尺寸还是质量都比当今最大的国际空间站大1~2个数量级.因此空间太阳能电站在太空飞行时将表现出与普通小卫星不同的动力学行为,因而其动力学建模与分析受到了学术界的广泛关注.虽然研究者们都希望能充分考虑复杂的太空环境,建立能描述空间太阳能电站轨道-姿态-结构振动耦合的动力学模型,但如此复杂的动力学模型将使动力学分析成为困难.目前文献中的动力学分析方法是针对具体的问题进行模型简化,考虑主要影响因素,从而对空间太阳能电站进行动力学分析.因此,轨道、姿态或结构振动之间的耦合动力学模型(本文统称为轨道-姿态-结构振动耦合动力学模型)、空间摄动力/力矩的影响分析、太空热环境的影响分析成为3个主要的研究课题.
2.1 轨道-姿态-结构振动耦合模型目前的空间太阳能电站的轨道-姿态-结构振动耦合模型包括哑铃模型、柔性梁模型、柔性板模型和多体模型等。柔性梁、柔性板模型的建模方法可分为浮动坐标法和绝对节点坐标法.
哑铃模型多用于描述绳系卫星系统的动力学,将卫星看作质点,不考虑系绳的质量.哑铃模型又分为刚性哑铃模型和柔性哑铃模型,其不同之处是前者不考虑系绳的弹性,后者考虑系绳的轴向变形.柔性哑铃模型能同时描述系统的质心轨道、俯仰姿态和轴向振动,因此被学者们广泛用于大型空间结构的轨道-姿态-结构振动耦合动力学分析.Malla等[45-46]讨论了将大型空间结构简化为柔性哑铃模型的可行性,并分析了轨道高度、轨道离心率、姿态运动和结构柔性对系统动力学响应的影响.Ishimura等[47]将绳系空间太阳能电站简化为柔性哑铃模型,研究了系统不同的端部质量比、绳子固有频率与轨道运动角频率之比、绳长与轨道半径之比对系统动力学响应的影响,他们发现频率比对系统的耦合效应影响最大,并且得到频率比小于10 h系统的姿态、轨道和结构振动出现明显耦合的结论.魏乙等[48]考虑了地球非球形摄动对柔性哑铃模型的影响,发现地球非球形摄动对系统的轨道影响较大,而对轴向振动的影响最小.穆瑞楠等[49]通过理论公式和数值实验分析了柔性哑铃模型的轨道、姿态与结构振动三者之间的相互影响,他们发现结构振动对姿态和轨道的影响与结构尺寸的平方成正比,且结构的柔性使姿态角更易于翻滚.然而上述文献中,柔性哑铃模型采用的万有引力梯度力矩公式是通过Taylor级数得到的近似公式,谭述君等[50]发现该近似公式在空间结构的尺寸较大、质量分布不均匀或初始姿态角位于不稳定平衡点时会导致较大误差;为此,他们通过保留Taylor级数的高阶项,推导了万有引力梯度力矩的修正近似公式.Xu等[51]推导了刚性哑铃模型的精确万有引力势能和万有引力梯度力矩表达式,并通过变量变换避免了精确表达式中出现的奇点,他们发现近似模型的万有引力势能误差随结构尺寸的平方增长.然而,柔性哑铃模型由于无法描述结构的弯曲、剪切或扭转变形,在空间太阳能电站耦合动力学分析应用中受到限制.
在刚柔耦合建模方法方面,浮动坐标法是最常用的方法,通过浮动坐标系与全局坐标系能方便地研究描述柔性体的平动、转动和结构振动[52].Liu等[53]采用浮动坐标法建立了集成对称聚光系统姿态-结构振动耦合的参数激励模型,将太阳能电池阵列与微波发射天线看作刚体、桅杆看作欧拉梁、一级聚光镜看作质点;然而在文中没有考虑轴向变形、万有引力和系统轨道的影响.他们在文献[54]中假设系统运行在圆形轨道,进一步考虑了万有引力梯度的影响,他们发现当系统的最低固有频率小于2倍的轨道角频率时,系统会出现屈曲不稳定现象;为了让系统获得足够的刚度,系统的最低固有频率应大于10倍的轨道角频率.Zhao等[55]基于浮动坐标法推导了太空中的大型柔性板的高阶万有引力和高阶万有引力梯度力矩的表达式.穆瑞楠等[56]基于能量等效原理将多旋转关节空间太阳能电站等效成太空中的一根柔性梁,采用浮动坐标法建立了系统的动力学模型,并研究了系统的轨道、姿态和结构振动之间的耦合现象.他们在文献[57]中进一步研究了该模型,发现随着姿态运动频率降低,结构振动的稳定区域减小.
然而浮动坐标法是基于小变形假设而提出的建模方法,在求解大变形、大转动问题上求解精度和效率都有所下降[58].空间太阳能电站在轨运行时超柔的结构可能会出现大变形,此时可采用绝对节点坐标法[52].采用绝对节点坐标法建立的多柔体系统动力学方程具有常数质量矩阵、不存在科氏力和离心力项等特点,比传统浮动坐标法、大转动矢量法等更能精确地描述柔性多体系统的动力学特性[59-61].正是由于这些优点,绝对节点坐标法已经被用于大柔性空间结构的动力学与控制研究中[62-65].魏乙等[32]采用绝对节点坐标法建立了绳系空间太阳能电站的轨道-姿态-结构振动耦合动力学模型,将卫星平台系统简化为质点,发电-传输面板简化为欧拉梁,忽略系绳的质量和弹性,分析了系绳长度、轨道半径和卫星平台的质量对梁振动特性的影响.徐方暖等[66]在该模型的基础上考虑了系绳的弹性,并研究了太阳光压作用下系统姿态和结构振动的相互影响;他们发现,柔性梁的振动和太阳光压都对系统的姿态角产生重要影响,而且在不同的梁刚度条件下太阳光压对姿态角产生的影响明显不同,而太阳光压引起的结构振动跟万有引力梯度引起的结构振动相比可以忽略不计.然而,文献[62-63]由于研究的是短时间的动力学行为而没有考虑万有引力的影响,文献[32, 66]以体积积分的形式给出了万有引力势能,文献[64-65]以体积积分的形式给出了万有引力的广义力向量,但是都没有给出具体的计算方法.Sun等[67]发现在动力学仿真过程中处理体积积分比较耗时,于是他们提出将梁分成若干段,每一段的万有引力看作是集中于质心,再对所有段进行叠加得到近似的万有引力;然而这种方法需要取较多的段才能达到较高的精度.Li等[68]提出了一种适用于所有绝对节点坐标法单元的万有引力计算方法(已经考虑了万有引力梯度力矩),且利用该方法可以方便地计算出单元的万有引力势能和万有引力的雅克比矩阵;他们将这种方法用于多旋转关节空间太阳能电站的太阳能电池子阵姿态控制仿真,发现保持对日指向的太阳能电池子阵在近地轨道会产生大幅度的振动,姿态控制误差和所需的控制力矩都比刚体模型显著增大,从而得到结构柔性在动力学分析和控制器设计中必须予以考虑的结论.
对于空间太阳能电站多体模型,如果考虑结构柔性,则可能需要采用很小的步长进行数值仿真,不利于进行长达几十年的动力学分析;而如果建立多刚体模型,则可以研究在太空环境下系统的长时间动力学行为.欧拉角、四元数等方法适用于单个刚体系统,对于空间太阳能电站这类复杂的多体系统难以应用.自然坐标法与欧拉角方法相比有很多优势[69],例如完全采用笛卡尔坐标、方程与系统约束形式简单、质量矩阵为常数、可以方便地描述多体系统等.自然坐标法也多次被用于建立空间多刚体系统动力学模型[70-71],但是均没有考虑万有引力.Li等[72]推导了自然坐标法的万有引力表达式(已经考虑了万有引力梯度力矩),并建立了JAXA SSPS 2002方案的姿轨耦合多刚体模型,研究了在太阳光压作用下运行一年的动力学响应,发现在太阳光压的作用下,系统的姿态对轨道产生重要的影响.后来,Li等[73]还用这种方法建立了多旋转关节空间太阳能电站的包含51个刚体的动力学模型,用于高精度姿态控制系统的设计与仿真.用于描述刚体的自然坐标法和用于描述柔性体的绝对节点坐标法有很多相似之处,其最终的动力学方程也有相似的特点,所以这两种方法通常应用于刚柔耦合多体系统的建模,被称为绝对坐标法[71, 74].浮动坐标法与绝对节点坐标法各有所长,浮动坐标法可用于动力学行为的理论分析、基于模型的控制器设计等,绝对节点坐标法可用于精确动力学数值仿真、无模型控制器设计与仿真等.
除此之外,空间太阳能电站的多体模型可以用质点、弹簧、阻尼、刚体、柔性体等基本构件组合建立,如文献[31-32, 66]等.李学府等[75]将卫星平台看作质点、将发电-传输面板看作刚体、将系绳看作柔性体,建立了绳系空间太阳能电站的耦合模型,并分析了发电-传输面板初始姿态误差的演化特性以及对系统运动的影响.邓子辰等[76]以太阳帆塔的两个邻近太阳帆为研究对象,建立了刚体-弹簧的简化动力学模型,得到了系统的平衡点,并通过线性化方程的系数矩阵特征值分析了平衡点的稳定性.
2.2 空间摄动力/力矩影响分析空间太阳能电站在太空中会受到多种摄动力和摄动力矩的影响[77],由于质量和尺寸比常规的卫星大2~3个数量级,导致空间摄动对空间太阳能电站的影响比常规的卫星更加显著[78-79].因此,如何精确地计算空间太阳能电站在空间摄动作用下的动力学响应、如何实现空间摄动下高精度的的轨道和姿态保持、如何根据空间摄动的特点进行空间太阳能电站的设计、如何利用空间摄动进行轨道和姿态控制等,都是值得关注的问题.其中轨道和姿态保持控制将在后面进行介绍.
关于航天器受到的空间摄动力和摄动力矩的计算,在很多文献中已有详细的介绍,如文献[77-79],但由于空间太阳能电站的特殊性,仍然需要对其进行摄动影响分析和解决方法研究.Wie等[22, 80-81]针对Abacus空间太阳能电站建立了轨道和姿态动力学模型,分析了空间主要的摄动力和摄动力矩的影响.他们发现空间太阳能电站的面质比比常规的通讯卫星大20倍左右,给空间太阳能电站的轨道保持带来很大困难;在姿态方面,万有引力梯度力矩的影响非常大,需要采用10万个控制力矩陀螺才能提供如此大的角动量;为了解决这两个困难,他们采用500个离子推进器进行轨道-姿态保持控制,研究发现轨道保持所消耗的燃料质量约为每年85 000 kg,而姿态保持不需要消耗额外的燃料.Liu等[82-83]建立了地球同步拉普拉斯轨道上的空间太阳能电站动力学模型,他们在推导过程中发现,结构振动不会改变万有引力对轨道和姿态的作用;通过数值仿真发现,高阶地球万有引力对轨道产生显著的影响,而高阶地球万有引力梯度力矩以及日月引力梯度力矩对姿态产生的影响可以忽略不计.刘玉亮等[84]研究了在轨道平面内运动的欧拉梁,得到了结构出现屈曲不稳定现象的条件,并发现结构振动对姿态运动的影响只存在于三阶及以上的重力和重力梯度力矩项中,其影响可以忽略不计.魏乙等[85]发现对于太阳能电池阵列采用重力梯度稳定方式的空间太阳能电站,地球阴影和空间太阳能电站的姿态对轨道有重要的影响,且姿态的影响大于地球阴影的影响,因此在轨道动力学分析中应予以考虑.
由于空间太阳能电站的质量和尺寸都超大,轨道和姿态控制都需要消耗大量的燃料.因此,一些学者们致力于寻找消耗燃料更少的空间太阳能电站构型、轨道和姿态.在轨道方面,对于运行在地球同步拉普拉斯轨道上的航天器,地球的非球形摄动和日月引力摄动带来的长期影响基本上相互抵消了,从而使航天器的轨道漂移较小.McNally等[86-87]对比了地球静止轨道上和地球同步拉普拉斯轨道上的空间太阳能电站在空间摄动力作用下的动力学响应;他们发现地球同步拉普拉斯轨道上的空间太阳能电站在长时间运行过程中,轨道漂移较小,从而每年节省105 kg数量级的燃料,并能维持平稳的电力无线传输效率、节省宝贵的地球静止轨道资源、降低空间太阳能电站与太空垃圾碰撞的风险.刘玉亮等[88]对拉普拉斯轨道作了进一步分析,发现轨道倾角为7.9°时轨道倾角在30年内的振动幅值比7.5°时小,因而更加适合作为空间太阳能电站的运行轨道;同时他们还提出了评判空间太阳能电站轨道的3个标准:接收功率、轨道适用性和安全性.McNally等[89]针对Abacus空间太阳能电站,从轨道和姿态耦合控制系统的燃料消耗的角度进一步对比了地球同步拉普拉斯轨道和地球静止轨道;他们发现考虑轨道和姿态耦合控制后,地球同步拉普拉斯轨道比地球静止轨道每年节省约17 000 kg控制燃料;而拉普拉斯轨道上的燃料消耗主要用于姿态控制,因此通过改进系统的质量分布、姿态指向方案等措施有望进一步节省空间太阳能电站的控制燃料.
在姿态方面,最初提出的1979 SSPS基准系统采取的姿态方案是对日定向姿态,因此需要巨大的姿态控制力矩来抵消万有引力梯度力矩的影响.而如果采用万有引力梯度稳定的姿态方案,则巨型的太阳能电池阵列无法保持对日指向,从而降低了系统的发电效率,且无法实现持续供电.为了解决这个矛盾,Elrod[90]提出了航天器的准惯性定向姿态,巨型太阳能电池阵列可以在某一固定指向附近作小幅度振动(<18.8°),且几乎不需要姿态控制力矩来维持;这种姿态方案能使空间太阳能电站保持较高的发电效率,同时节省了用于抵消万有引力梯度力矩所需的燃料.但是Elrod[90]提出的准惯性定向姿态没有考虑太阳的方向随时间改变的情形.Sincarsin等[91]将太阳的长期、缓慢的方向改变过程引入到准惯性定向姿态中,提出航天器的准对日定向姿态,因此空间太阳能电站采取准对日定向后可以始终在指向太阳的方向附近波动,且能跟随太阳的长期运动过程;他们发现准对日定向的振动幅值与准惯性定向的振动幅值基本相同,而空间太阳能电站的高阶惯性矩只对准对日定向姿态产生很小的影响.然而,航天器的结构振动以及其他摄动力和摄动力矩对准对日定向姿态的影响、地球同步拉普拉斯轨道上的准对日定向姿态、准对日定向姿态的控制等问题仍需进一步的研究.
2.3 空间热环境影响分析由于受太阳光照射不均匀、发热器件散热不及时、进出地球阴影等原因,空间太阳能电站会出现温度分布不均匀和随时间变化的情况,从而可能引起结构振动甚至影响系统工作.因此空间太阳能电站的热环境影响分析也是受到广泛关注的课题.
针对柔性哑铃模型,Malla等[92]研究了其在太阳热辐射、地球热辐射和地球热反射作用下的动力学响应,他们发现太空热环境对哑铃模型的轨道影响较小,对姿态运动和结构振动的影响较大,另外,在地球同步轨道则可以忽略地球热辐射和地球热反射的影响.Lin等[93]进一步考虑了柔性哑铃模型的热环境与结构振动的耦合动力学,发现热环境的变化和结构上的非均匀温度分布会引起结构发生弯曲变形,并且影响结构的姿态.
Ishimura等[30]用有限元方法建立了考虑系绳和面板柔性的绳系空间太阳能电站的动力学模型,考虑了发电-传输面板的热致变形;他们发现:绳子的低刚度是系统姿态和结构振动耦合的重要原因;面板的热变形可能会导致部分绳子发生松弛,从而降低了系统的固有频率,使系统的姿态和结构振动耦合效应更加明显;系统的滚转运动和偏航运动在面板热变形作用下出现发散的趋势;最后他们对系统结构进行了改进以降低面板热变形带来的影响.Sato等[94]将绳系空间太阳能电站的发电-传输面板设计成由太阳能电池、微波发射机和微波发射天线组成的面板,每两层之间用蜂窝结构相隔,通过实验测试了面板的温度特性,并用于分析绳系空间太阳能电站在轨飞行过程的温度变化情况;他们考虑了太阳直接辐射、地球红外辐射、地球反射和面板工作产生的热量,发现在一天的时间内面板的最低温度约为-80℃,此温度已经低于空间太阳能电站的工作温度范围.Yang等[95]对3种空间太阳能电站的构型进行了热分析,通过对比发现,多旋转关节空间太阳能电站的中等功率导电旋转关节的温度比其他空间太阳能电站的大功率导电旋转关节的温度低60℃左右;聚光型空间太阳能电站的三明治结构的温度比非聚光型空间太阳能电站的太阳能电池阵列高55℃;为了降低三明治结构的温度,他们分析了阶梯型方案和分离方案,发现这两种方案都能明显降低系统的温度.赵利军[96]将绳系空间太阳能电站的发电-传输面板当作单层蜂窝结构,研究了其在轨运行过程的温度变化情况、温度分布不均匀而引起的热变形和面板的热致振动现象.
3 长时间数值仿真算法由于空间太阳能电站的复杂性,其动力学方程也通常表现为复杂的非线性微分方程组,因此目前对空间太阳能电站动力学问题的分析大多采用数值仿真手段.空间太阳能电站的数值仿真面临着以下3个方面的困难.首先,系统的轨道运动、姿态运动和结构振动的耦合造成了空间上的多尺度,结构振动的快变量和姿态、轨道运动的慢变量造成了时间上的多尺度,因此耦合动力学方程的高精度、高效率求解成为困难.其次,柔性多体系统往往存在机械铰、系绳等约束,因此系统的动力学方程为高维非线性的微分-代数方程组,传统的数值方法求解效率低,且可能会出现约束违约问题.最后,空间太阳能电站需要在轨服役30~50 a,因此需要对空间太阳能电站进行长时间的数值仿真,而许多常用的数值算法都含有算法内在的阻尼,使得系统的固有特性无法在长时间数值仿真中得到保持.这些问题是计算力学和计算数学领域的研究者们共同关注的问题.近年来,在空间太阳能电站动力学数值仿真过程中使用的辛算法、保能量保约束算法等为解决长时间数值仿真问题提供了新的思路.
3.1 辛算法对于非线性常微分方程的求解,常用的方法包括Euler方法、Runge-Kutta方法、Adams方法等.但是这些方法都具有算法内在阻尼,在Hamilton系统的长时间数值仿真中无法保持系统的固有性质,如能量守恒、角动量守恒等,导致系统出现错误的定性性质.冯康等[97]提出了能保持Hamilton系统的时间演化为辛变换的数值仿真算法,并将其称为辛算法;他们发现辛算法在整体性、结构性以及长期稳健的跟踪能力方面比非辛算法有明显的优越性.钟万勰等[98-101]将辛几何算法引入到应用力学领域,发现了计算结构力学与最优控制之间的模拟关系,并提出了辛弹性力学理论.辛算法已经成功用于天体动力学与航天器轨道动力学的长时间数值仿真分析中[102-104].
中国的研究者们首先展开了辛算法在空间太阳能电站动力学分析中的应用探索.邓子辰等[76]推导了太阳帆塔简化模型的Hamilton动力学方程,采用辛算法和非辛的Runge-Kutta算法进行了长时间数值仿真;通过对比发现,非辛的Runge-Kutta算法在小步长时能量误差呈线性增长,但是取大步长时能量误差增长加快,且结构振动经过数值耗散最终停止了,在辛空间中对偶变量最终收缩成一点;而辛算法不管在大步长还是小步长,均能保持系统长时间数值仿真的能量守恒,保持系统固有的振动特性,保持辛空间图形的面积;最后他们采用辛算法研究了系统在平衡点附近的振动特性,得到了与理论分析一致的结果.这说明在长时间数值仿真中,辛算法能保持系统的固有性质,从而能使系统的定性性质得到体现.魏乙等[48]推导了柔性哑铃模型的Hamilton方程,发现Hamilton方程中的角动量变量的导数为零,即角动量是自动守恒的;他们采用辛Runge-Kutta算法进行了数值仿真,发现采用辛算法进行数值仿真中保持了系统的总能量守恒.Xu等[51]推导了刚性哑铃模型的Lagrange方程和Hamilton方程,每一组方程都用辛Runge-Kutta算法和Runge-Kutta算法进行数值仿真;他们发现Hamilton系统下采用辛Runge-Kutta算法的能量误差最小,且不随时间增长;Lagrange系统下采用辛Runge-Kutta算法的能量误差很小,但是随时间增长;而两种系统下Runge-Kutta算法的能量误差都较大,且随时间增长明显.魏乙等[85]在分析太阳光压对空间太阳能电站轨道的影响时也采用了辛Runge-Kutta算法,他们发现该算法可以采用大步长进行数值计算,从而可以对系统进行长时间的数值仿真分析.徐方暖等[66]在研究绳系空间太阳能电站动力学行为时也发现辛算法能准确计算弹簧的振动,而非辛算法由于算法的耗散性质导致系统的固有振动特性出现错误.吴志刚等[105]提出了一种轨道预报的乘法保辛摄动方法,考虑地球非球形引力、日月引力、太阳光压和潮汐摄动,将卫星运动方程分解为二体问题和摄动部分,其中二体问题部分采用解析解,摄动部分采用保辛的区段矩阵方法,从而实现整个轨道预报过程的保辛.
上述研究都是基于保守的Hamilton系统进行的,对于非保守的Hamilton系统,徐斌等[106]提出了分离变换原理,可以将经典阻尼系统变换成无阻尼系统,从而可以用辛方法进行求解.Yin等[107]针对空间太阳能电站太阳能接收器展开过程,采用经典阻尼模型,建立了简化的动力学方程;基于分离变换原理,将系统的动力学方程变换到Hamilton体系下保守动力学方程,从而采用辛算法对动力学过程进行仿真.
3.2 微分-代数方程的数值算法对于微分-代数方程的求解,积分过程中约束方程的违约是造成微分-代数方程数值积分困难的原因之一[108].常用的微分-代数方程数值算法包括:Newmark方法[109]、广义α方法[110]、投影方法[111]、差分方法等[112].然而,上述方法引入了算法内在的阻尼特性,从而不能保持约束Hamilton系统的固有性质,如保辛性、能量和动量守恒性等.为了同时实现约束Hamilton系统在数值仿真中保辛和保约束,钟万勰等[113]提出了一种分析结构力学积分法:首先保证约束在时间节点处严格满足,采用时间有限元离散,从而实现了保约束.由于提出了“约束不必处处满足,只需在节点处满足即可”的思想,与祖冲之计算圆周率的思想类似,因此这种方法在文献[100]中被命名为祖冲之类算法,吴锋等[114]证明了此算法是保辛的.文献[108]将祖冲之类算法的思想与辛Euler格式结合,得到求解约束Hamilton系统微分-代数方程的保能量保约束积分方法.Wei等[115]基于祖冲之类方法的思想,提出了保能量保约束的Verlet算法,并从理论上证明了该方法能保持约束Hamilton系统的总能量.Wei等[116]提出了能量投影方法,将系统状态同时向约束流形和能量流形投影,使系统状态在时间节点处满足能量守恒,且避免了约束违约现象.徐方暖等[117]在研究绳系空间机器人的姿态运动时提出了一种单位四元数的显式投影保范数算法,这种方法在数值仿真中能保持单位四元数的范数约束,且效率比普通的隐式投影方法高.
目前对空间太阳能电站的动力学研究中,采用无约束系统的文献较多,而采用约束动力学系统的较少.王新栋等[118]用辛分离Runge-Kutta方法对空间太阳能电站太阳能接收器展开过程进行了数值模拟,发现采用辛分离Runge-Kutta方法计算的结果能保持系统的能量守恒,同时在时间节点处严格满足约束条件.Li等[72]结合祖冲之类算法的思想,提出了基于一般Runge-Kutta格式的保能量保约束方法;通过卫星姿轨耦合动力学仿真的例子,将辛Runge-Kutta格式的保能量保约束算法与广义α方法进行了对比,发现在长时间数值仿真中保能量保约束算法的精度较高,且能保持系统的总能量守恒;最后采用了辛Runge-Kutta格式对聚光式的空间太阳能电站进行了一年的数值仿真,并分析了系统轨道和姿态的长期演化规律.文奋强等[119]将文献[76]中的弹簧简化为等距约束,建立了简化的太阳帆塔动力学模型,并采用文献[72]中的方法求解,发现基于辛Runge-Kutta格式的保能量保约束算法比基于非辛的Runge-Kutta格式的保能量保约束算法相对能量误差更小,且不随时间增长.魏乙等[32]也采用基于辛Runge-Kutta格式的保能量保约束算法对绳系空间太阳能电站轨道、姿态以及结构振动耦合动力学进行了数值仿真,发现系统的总能量和约束都能在数值仿真中得到保持.
除了辛算法和保能量保约束算法外,还有文献采用广义多辛算法进行空间太阳能电站的动力学仿真.Hu等[120]采用Hamilton原理建立了空间阻尼梁的动力学方程,将系统分解为大范围平面运动和梁的结构振动两个子系统,采用广义多辛算法的思想构造了与Preissmann方法等效的15点数值格式,从而分析了阻尼对空间梁的影响.此后,他们在文献[121]中建立了绳系空间太阳能电站的动力学模型,将发电-传输面板看作阻尼梁,分析了系统构件间的能量传输和耗散行为.
4 轨道、姿态与结构振动控制空间太阳能电站在轨服役时存在大量的控制问题,目前的研究主要集中于轨道保持、姿态控制和结构振动抑制等方面.
4.1 轨道保持与姿态控制由于太空中存在的多种摄动力和摄动力矩会使空间太阳能电站出现轨道和姿态偏差,影响其正常工作,所以必须对空间太阳能电站的轨道和姿态进行控制.Donatiello等[122]发现如果不对地球静止轨道上的空间太阳能电站进行控制,在4 d以后轨道误差就超出了所要求的误差范围,甚至可能与静止轨道上的其他卫星发生碰撞.由于空间太阳能电站面质比超大,所以受太阳光压的影响比当前的小卫星大得多,再加上其超大的质量,导致轨道保持需要消耗大量的燃料.在姿态方面,空间太阳能电站的姿态控制又分为发射天线的对地指向控制和太阳能电池阵列或聚光镜的对日指向控制.文献[80]认为,对地指向的精度要求为0.1°,而对日指向要求为0.5°.空间太阳能电站中的超大型结构具有非常低的固有频率,在空间摄动力和摄动力矩的作用下可能出现结构振动与姿态运动的耦合,从而加大了精确姿态指向控制的难度.
Glaese等[123]借助计算机建模软件建立了集成对称聚光系统的多体动力学模型,考虑了桅杆的柔性,而将一次反射镜、太阳能电池阵列、微波发射天线都看作刚体;他们研究了春分、夏至、秋分和冬至时系统的姿态控制问题,考虑了万有引力摄动、太阳光压摄动以及地球阴影的影响;他们发现姿态控制系统能达到预期的精度要求,但最大的问题是生产出足够大的离子推进器和获得足够多的推进燃料.Wie等[22, 80]针对Abacus空间太阳能电站的单刚体模型设计了姿态控制器,他们发现结构振动的最低固有频率为0.002 Hz,通过采用带宽小于10-5 Hz的前馈-反馈姿态控制器避免激起结构的振动,从而避免结构振动与姿态控制发生耦合;另外,他们还设计了合理的离子推进器布局,从而可以利用轨道控制力来产生足够的力矩用于太阳能电池阵列的对日指向控制.Wu等[124]针对同一模型进行了对日指向控制,将内模控制原理与最优控制技术相结合,提出了时变鲁棒最优控制器;他们考虑了万有引力梯度力矩摄动和10%的转动惯量不确定性,通过数值仿真发现所提出的控制算法与PID控制技术相比收敛更快,并且稳态误差更小.刘明洋等[125]在考虑空间摄动的作用下建立了空间太阳能电站的轨道动力学方程,并采用最优控制的方法实现空间太阳能电站的轨道保持.Li等[72]采用PD控制律对聚光型空间太阳能电站进行了对日指向和对地指向控制,发现控制误差和控制力矩都呈现出明显的周期性.对于周期性的姿态保持任务,迭代学习控制方法是一种有效的控制方法,通过对以往周期的学习可以达到提高控制精度的目的[126-127].迭代学习控制是一种无模型的控制方法,对于系统参数不确定、存在周期性外界干扰、周期性轨迹跟踪等问题都能很好地解决[128-130].因此,Li等[73]提出了采用迭代学习控制方法进行姿态跟踪,并基于双曲正切切换函数和Fourier级数设计了高阶的迭代学习控制器;通过对多旋转关节空间太阳能电站对日指向和对地指向的同时控制仿真,他们发现在考虑系统不确定性、传感器噪声、空间摄动力矩和控制目标慢时变的情况下,所设计的迭代学习控制器提高系统控制精度的同时还降低了控制系统对传感器噪声的敏感性.
空间摄动力和摄动力矩一般情况下对航天器产生不利的影响,但是在某些情况下可以对空间摄动因素的特点进行研究,使其对航天器产生有利的影响.Senda等[131]针对绳系空间太阳能电站的单刚体模型,研究了利用地磁力矩进行姿态稳定控制的可行性;研究发现,通过控制线圈上的电流强度可以消除姿态误差,但是缺点是需要消耗一定的电量,并且线圈增加了系统的质量.然而Senda等[131]只研究了绳系空间太阳能电站的其中一个小模块,而不是整个空间太阳能电站.Takeichi等[25-27]提出了编队飞行空间太阳能电站方案,他们研究主反射镜的轨道保持问题时,发现利用太阳光压力的分量可以用于轨道保持,从而节省轨道保持的控制燃料.
4.2 结构振动控制空间太阳能电站在空间摄动力、摄动力矩、控制力、控制力矩和空间交变热环境的作用下会发生结构振动,这些结构振动可能会引起推进器发生运动,从而引起轨道和姿态控制出现误差,同时还可能影响微波发射天线的指向精度.而如此大型的空间结构一般固有频率为10-3 Hz量级,可能会与姿态运动、姿态控制系统发生耦合.因此,空间超大型航天器的结构振动必须予以重视.Li等[68]发现,系统的柔性会造成更大的对日指向姿态控制误差,同时也需要消耗更多的姿态控制能量.目前很多研究者建立空间太阳能电站柔性体模型的目的是用于动力学分析,进行结构振动控制研究的较少.
Donatiello等[122]针对Abacus空间太阳能电站分别建立了质点的轨道模型、单刚体的姿态动力学模型和有限元的结构振动模型,研究了地球静止轨道上的姿轨保持控制系统与结构振动之间的耦合;他们发现在姿轨耦合控制的作用下,结构会出现低频与高频的结构振动,其中低频振动的频率与轨道角频率或万有引力梯度力矩的频率一致,而高频振动与结构的固有频率一致;他们还采用传感器/作动器共位布置的方式设计了结构振动控制系统,通过数值仿真发现结构振动控制系统能有效地抑制结构的高频振动,且只对系统的轨道和姿态产生轻微的影响.然而在他们的研究中没有考虑空间摄动因素、系统的姿轨运动引起的结构振动,也没有考虑结构振动所引起的姿轨传感器/作动器的运动.刘宇飞等[132]将主次桁架等效为简单的梁、柱和支撑结构,得到了空间太阳能电站的柔性太阳能电池阵的振动频率和模态;设计了轨道、姿态控制器和传感器、作动器的布局,并估计了所需的燃料消耗量;他们发现结构振动对轨道控制系统或姿态控制系统的影响并不显著.Fujii等[133]将绳系空间太阳能电站的发电-传输面板看做刚体,将卫星平台看做质点,忽略绳子的质量和弹性,建立了系统的动力学模型,并研究了通过调整系绳长度来控制附加质量块相对于太阳帆板的位置,从而实现系统的姿态稳定控制;最后他们将太阳帆板看作欧拉梁,建立了梁的动力学方程,通过调节系绳的张力,抑制了结构的振动.Zhou等[134]研究了绳系空间太阳能电站的大角度姿态机动和结构振动抑制问题:将太阳能电池板简化为欧拉梁,研究了卫星的单轴回转,采用主动姿态调整和主动振动抑制相结合的复合控制方法,实现了系统姿态的快速大角度机动.他们在文献[33-34]中将绳系空间太阳能电站的发电-传输面板看作Kirchhoff板,建立了系统的动力学模型,同样也研究了系统单轴大角度机动过程中的姿态控制和通过绳子张力进行结构振动抑制的问题.Fujii等[135]将绳系空间太阳能电站的发电-传输面板简化为欧拉梁,进一步通过地面实验验证了采用调整绳子张力的方式进行太阳能电池板主动振动控制的可行性,并研究了面板刚度对控制性能的影响.晋冰冰[31]以绳系空间太阳能电站的一个宽度为100 m的柔性板单元为研究对象,建立了动力学模型,采用压电材料作为传感器和作动器,通过模糊PID的方法进行发电-传输面板的振动控制.
5 结论1) 本文对空间太阳能电站的概念设计方案及其服役阶段的动力学与控制研究现状进行了总结.自从空间太阳能电站提出的半个世纪以来,以美国、日本为首的航天大国提出了数十种空间太阳能电站概念设计方案,并对许多关键技术进行了研究.在动力学与控制领域,研究者们主要关注空间超大尺度结构的建模、复杂太空环境的影响、长时间数值仿真算法、高精度姿轨控制以及结构振动抑制等几方面的问题.目前对空间太阳能电站动力学与控制的研究尚处于起步阶段,有很多动力学与控制问题仍未得到解决,同时也有很多新的动力学与控制问题等着研究者们去发现.
2) 兼顾精确和高效的刚柔耦合系统长时间动力学仿真方法仍是未来重要的发展方向之一.目前的研究主要针对非常简化的空间太阳能电站动力学模型进行研究,且考虑的空间摄动不够全面.为了精确分析空间太阳能电站在复杂太空环境下的动力学行为,需要建立更加精确的轨道-姿态-结构振动耦合多体模型,考虑更全面的空间环境的影响.另一方面,由于刚柔耦合系统的动力学方程通常表现为刚性方程,而且通常需要对空间太阳能电站进行长时间的数值仿真,所以数值仿真通常消耗大量的时间,因此也需要发展更高效的长时间数值积分算法.
3) 对于空间太阳能电站的动力学建模,需要进一步研究复杂桁架、框架和旋转机构的动力学行为.以往的文献建立刚柔耦合模型时,都需要把空间太阳能电站的超大尺度桁架结构和框架结构等效成梁、板、壳和刚体等的组合形式,但是对于不同的材料和结构形式等效方法和等效精度有待进一步分析.另外,空间超大结构可能是通过在轨组装或在轨展开的方式构建的,其中的关节间隙对等效后的结构动力学行为的影响也是未知的.空间太阳能电站上大型的旋转机构设计和动力学分析方面也有大量的问题需要解决.
4) 空间太阳能电站的轨道、姿态和结构振动三者的协调控制仍需进一步研究.由于空间太阳能电站的结构振动频率超低,在控制系统的作用下可能会出现与姿态运动的耦合,所以在控制器设计的时候必须要考虑结构柔性的影响,而现有文献中进行控制器设计时很少考虑结构的柔性.由于发射天线的对地指向精度要求较高,所以大型结构的振动必须予以抑制和隔离,防止引起发射天线对地指向抖动.另外,如此复杂的空间系统的在轨参数辨识也是值得研究的问题.
5) 空间太阳能电站是非常复杂的超大型空间系统,其设计、建造与维护过程涉及光学、力学、材料、机械、通信、控制等多个学科的问题,多学科分析、设计与优化是未来发展的必然趋势.
| [1] |
董秀成, 高建, 张海霞. 能源战略与政策[M]. 北京: 科学出版社, 2016.
|
| [2] |
Rouge J D. Space-based solar power as an opportunity for strategic security: Phase 0 architecture feasibility study[R]. [S.l]: National Security Space Office, 2007
|
| [3] |
侯欣宾. 不同空间太阳能电站概念方案的比较研究[J]. 太阳能学报, 2012, 33(S): 63. HOU Xinbin. Analysis and comparison of various SPS concepts[J]. Acta Energiae Solaris Sinica, 2012, 33(S): 63. |
| [4] |
王希季, 闵桂荣. 发展空间太阳能电站引发新技术产业革命[J]. 能源与节能, 2011, 5: 1. WANG Xiji, MIN Guirong. New technology industrial revolution triggered by the development of space solar power station[J]. Energy and Energy Conservation, 2011, 5: 1. |
| [5] |
GLASER P E. Power from the sun: Its future[J]. Science, 1968, 162(3856): 857. DOI:10.1126/science.162.3856.857 |
| [6] |
GLASER P E. The satellite solar power station[C]//1973 IEEE G-MTT International Microwave Symposium. Boulder, CO: IEEE, 1973. DOI: 10.1109/GMTT.1973.1123143
|
| [7] |
杨拓, 张德辉. 英国伦敦雾霾治理经验及启示[J]. 当代经济管理, 2014, 36(4): 93. Yang Tuo, Zhang Dehui. Haze governance experience of London and the enlightenments[J]. Contemporary Economic Management, 2014, 36(4): 93. DOI:10.13253/j.cnki.ddjjgl.2014.04.016 |
| [8] |
梅雪芹. 工业革命以来西方主要国家环境污染与治理的历史考察[J]. 世界历史, 2000(6): 20. Mei Xueqin. A historical study on the environmental pollution and prevention of the western countries since the Industrial Revolution[J]. World History, 2000(6): 20. |
| [9] |
张虹萍. 二战后美国非政府组织开展城市环境运动及启示[J]. 学术交流, 2014(9): 202. DOI:10.3969/j.issn.1000-8284.2014.09.038 |
| [10] |
侯欣宾, 王立. 空间太阳能电站技术发展现状及展望[J]. 中国航天, 2015(2): 12. |
| [11] |
李国欣, 徐传继. 国际空间太阳能电站的发展现状[J]. 电源技术, 1998, 22(3): 38. LI Guoxin, XU Chuanji. Review on the development status of space power system in the world[J]. Chinese Journal of Power Sources, 1998, 22(3): 38. |
| [12] |
王立, 成正爱, 张兴华, 等. 空间太阳能电站发展展望[J]. 国际太空, 2017(10): 14. DOI:10.3969/j.issn.1009-2366.2017.10.005 |
| [13] |
FEINGOLD H, CARRINGTON C. Evaluation and comparison of space solar power concepts[J]. Acta Astronautica, 2003, 53(4/5/6/7/8/9/10): 547. DOI:10.1016/S0094-5765(3):80016-4 |
| [14] |
Glaser P E. An overview of the solar power satellite option[J]. IEEE Transactions on Microwave Theory and Techniques, 1992, 40(6): 1230. DOI:10.1109/22.141356 |
| [15] |
DOE/NASA. Satellite power system: Concept development and evaluation program: DOE/ER-0023[R]. Washington DC: Nasa Sti/recon Technical Report N, NASA, Department of Energy, 1979
|
| [16] |
DOE/NASA. The final proceedings of the solar power satellite program review[R]. Lincoln, Nebraska: The Solar Power Satellite Program Review, 1980 http://adsabs.harvard.edu/abs/1980spsp.nasa......
|
| [17] |
MANKINS J C. A fresh look at space solar power: New architectures, concepts and technologies[J]. Acta Astronautica, 1997, 41(4/5/6/7/8/9/10): 347. DOI:10.1016/S0094-5765(98)00075-7 |
| [18] |
MANKINS J C. A technical overview of the "SunTower" solar power satellite concept[J]. Acta Astronautica, 2002, 50(6): 369. DOI:10.1016/S0094-5765(01)00167-9 |
| [19] |
CARRINGTON C, FIKES J, GERRY M, et al. The Abacus/Reflector and integrated symmetrical concentrator-concepts for space solar power collection and transmission[C]//Proceedings of the 35th Intersociety Energy Conversion Engineering Conference and Exhibit. Las Vegas, NV: NASA Technical Reports Server, 2000: 3067 http://arc.aiaa.org/doi/abs/10.2514/6.2000-3067
|
| [20] |
MANKINS J C, NOBUYUKI K. Space solar power: The first international assessment of space solar power: Opportunities, issues and potential pathways forward[R]. Paris France: International Academy of Astronautics (IAA), 2011
|
| [21] |
MANKINS J C, O'NEIL D A. New concepts and technologies from NASA's space solar power exploratory research and technology program[C]//Laying the Foundation for Space Solar Power: An Assessment of NASA's Space Solar Power Investment Strategy.[S.l.]: National Research Council of the National Academy of Sciences, 2001: 78
|
| [22] |
WIE B, ROITHMAYR C M. Integrated orbit, attitude, and structural control systems design for space solar power satellites: AIAA 2001-4273[R]. Hampton, VA: National Aeronautics and Space Administration, Langley Research Center, 2001. DOI: 10.2514/6.2001-4273
|
| [23] |
MANKINS J, KAYA N, VASILEM. SPS-ALPHA: The first practical solar power satellite via arbitrarily large phased array: AIAA-2012-3978[R]. Reston, VA: AIAA, 2012 http://arc.aiaa.org/doi/abs/10.2514/6.2012-3978
|
| [24] |
MATSUMOTO H, HASHIMOTO K. Report of the URSI Inter-Commission Working Group on SPS[R]. Ghent: URSI, 2007
|
| [25] |
TAKEICHI N, UENO H, ODA M. Feasibility study of a solar power satellite system configured by formation flying[C]//Proceedings of the 54th International Astronautical Congress of the International Astronautical Federation (IAF), the International Academy of Astronautics and the International Institute of Space Law. Bremen, Germany: AIAA, 2003: 35 http://www.sciencedirect.com/science/article/pii/S0094576505001323
|
| [26] |
TAKEICHI N, UENO H, ODA M. Solar power satellite system configured by formation flying[C]//Proceedings of the 4th International Conference on Solar Power from Space, SPS'04-Together with The 5th International Conference on Wireless Power Transmission. Granada, Spain: ESA, 2004: 37
|
| [27] |
TAKEICHI N, UENO H, ODA M. Feasibility study of a solar power satellite system configured by formation flying[J]. Acta Astronautica, 2005, 57(9): 698. DOI:10.1016/j.actaastro.2005.02.006 |
| [28] |
MORI M, KAGAWA H, SAITO Y. Summary of studies on space solar power systems of Japan Aerospace Exploration Agency (JAXA)[J]. Acta Astronautica, 2006, 59(1/2/3/4/5): 132. DOI:10.1016/j.actaastro.2006.02.033 |
| [29] |
SASAKI S, TANAKA K, HIGUCHI K, et al. A new concept of solar power satellite: Tethered-SPS[J]. Acta Astronautica, 2007, 60(3): 153. DOI:10.1016/j.actaastro.2006.07.010 |
| [30] |
ISHIMURA K, HIGUCHI K. Coupling between structural deformation and attitude motion of large planar space structures suspended by multi-tethers[J]. Acta Astronautica, 2007, 60(8/9): 691. DOI:10.1016/j.actaastro.2006.10.002 |
| [31] |
晋冰冰.地球同步轨道分布式绳系太阳能电站柔性板振动控制研究[D].大连: 大连理工大学, 2017 JIN Bingbing. Research on vibration control of flexible plate of the distributed tethered solar power satellite system on the geo-synchronous orbit[D]. Dalian: Dalian University of Technology, 2017 |
| [32] |
魏乙, 邓子辰, 李庆军, 等. 绳系空间太阳能电站动力学响应分析[J]. 宇航学报, 2016, 37(9): 1041. WEI Yi, DENG Zichen, LI Qingjun, et al. Analysis of dynamic response of tethered space solar power station[J]. Journal of Astronautics, 2016, 37(9): 1041. DOI:10.3873/j.issn.1000-1328.2016.09.002 |
| [33] |
周荻, 范继祥. 绳系太阳能发电卫星姿态机动的主动振动控制[J]. 宇航学报, 2012, 33(5): 605. ZHOU Di, FAN Jixiang. Active vibration control of tethered solar power satellite during attitude maneuvering[J]. Journal of Astronautics, 2012, 33(5): 605. DOI:10.3873/j.issn |
| [34] |
周荻, 范继祥. 绳系太阳能发电卫星姿态机动的边界控制[J]. 振动工程学报, 2013, 26(1): 41. ZHOU Di, FAN Jixiang. Boundary control in the attitude maneuvering of tethered space solar power satellite[J]. Journal of Vibration Engineering, 2013, 26(1): 41. DOI:10.16385/j.cnki.issn.1004-4523.2013.01.016 |
| [35] |
Seboldt W, Klimke M, Leipold M, et al. European sail tower SPS concept[J]. Acta Astronautica, 2001, 48(5/6/7/8/9/10/11/12): 785. DOI:10.1016/S0094-5765(01)00046-7 |
| [36] |
李国欣, 徐传继. 我国发展空间太阳能电站的必要性和相关技术基础分析[J]. 太阳能学报, 1998, 19(4): 101. LI Guoxin, XU Chuanji. Analysis on the necessity of developing space solar power plant in China[J]. Acta Energiae Solaris Sinica, 1998, 19(4): 101. |
| [37] |
李国欣, 徐传继, 黄秉琰, 等. 空间太阳能电站技术的可行性研究[J]. 上海航天, 1998(2): 13. LI Guoxin, XU Chuanji, HUANG Bingyan, et al. The technology feasibility study on space solar power system in the world[J]. Aerospace Shanghai, 1998(2): 13. DOI:10.19328/j.cnki.1006-1630.1998.02.003 |
| [38] |
王立, 侯欣宾. 空间太阳能电站的关键技术及发展建议[J]. 航天器环境工程, 2014, 31(4): 343. WANG Li, HOU Xinbin. Key technologies and some suggestions for the development of space solar power station[J]. Spacecraft Environment Engineering, 2014, 31(4): 343. DOI:10.3969/j.issn.1673-1379.2014.04.001 |
| [39] |
陆征. 中国航天和能源领域"创新旗舰"扬帆远航——第二届空间太阳能电站发展技术研讨会在京召开[J]. 国际太空, 2017(11): 74. DOI:10.3969/j.issn.1009-2366.2017.11.017 |
| [40] |
侯欣宾, 王立, 张兴华, 等. 多旋转关节空间太阳能电站概念方案设计[J]. 宇航学报, 2015, 36(11): 1332. HOU Xinbin, WANG Li, ZHANG Xinghua, et al. Concept design on Multi-Rotary joints SPS[J]. Journal of Astronautics, 2015, 36(11): 1332. DOI:10.3873/j.issn.1000-1328.2015.11.016 |
| [41] |
HOU Xinbin, LI Meng, NIU Lili, et al. Multi-rotary joints SPS[J]. Online Journal of Space Communication, 2016(18): 1. |
| [42] |
YANG Yang, ZHANG Yiqun, DUAN Baoyan, et al. A novel design project for space solar power station (SSPS-OMEGA)[J]. Acta Astronautica, 2016, 121: 51. DOI:10.1016/j.actaastro.2015.12.029 |
| [43] |
杨阳, 段宝岩, 黄进, 等. OMEGA型空间太阳能电站聚光系统设计[J]. 中国空间科学技术, 2014(5): 18. YANG Yang, DUAN Baoyan, HUANG Jin, et al. SSPS-OMEGA: A new concentrator system for SSPS[J]. Chinese Space Science and Technology, 2014(5): 18. DOI:10.3780/j.issn.1000-758X.2014.05.003 |
| [44] |
LI Xun, DUAN Baoyan, SONG Liwei, et al. A new concept of space solar power satellite[J]. Acta Astronautica, 2017, 136: 182. DOI:10.1016/j.actaastro.2017.03.017 |
| [45] |
MALLA R B. Structural and orbital conditions on response of large space structures[J]. Journal of Aerospace Engineering, 1993, 6(2): 115. DOI:10.1061/(ASCE)0893-1321(1993)6:2(115) |
| [46] |
MALLA R B, NASH W A, LARDNER T J. Motion and deformation of very large space structures[J]. AIAA Journal, 1989, 27(6): 374. DOI:10.2514/3.48822 |
| [47] |
ISHIMURA K, HIGUCHI K. Coupling among pitch motion, axial vibration, and orbital motion of large space structures[J]. Journal of Aerospace Engineering, 2008, 21(2): 61. DOI:10.1061/(ASCE)0893-1321(2008)21:2(61) |
| [48] |
魏乙, 邓子辰, 李庆军, 等. 空间太阳能电站的轨道、姿态和结构振动的耦合动力学建模及辛求解[J]. 动力学与控制学报, 2016, 14(6): 513. WEI Yi, DENG Zichen, LI Qingjun, et al. Coupling dynamic modeling among orbital motion, attitude motion and structural vibration and symplectic solution of SPS[J]. Journal of Dynamics and Control, 2016, 14(6): 513. DOI:10.6052/1672-6553-2016-021 |
| [49] |
穆瑞楠, 谭述君, 吴志刚. 重力梯度对超大柔性空间结构在轨动力学特性的影响[J]. 国防科技大学学报, 2017, 39(3): 7. MU Ruinan, TAN Shujun, WU Zhigang. Effect of gravity gradient on dynamical characteristics of very large flexible space structures in orbit[J]. Journal of National University of Defense Technolgy, 2017, 39(3): 7. DOI:10.11887/j.cn.201703002 |
| [50] |
谭述君, 殷伟栋, 穆瑞楠. 重力梯度力矩近似公式适用条件的探讨[J]. 力学与实践, 2017, 39(5): 496. DOI:10.6052/1000-0879-17-063 |
| [51] |
XU Nuanfang, DENG Zichen, WANG Yan, et al. A symplectic Runge-Kutta method for analysis of the tethered satellite system[J]. Multidiscipline Modeling in Materials & Structures, 2017, 13(1): 16. DOI:10.1108/MMMS-11-2016-0060 |
| [52] |
SHABANA A A. Flexible multibody dynamics: Review of past and recent developments[J]. Multibody System Dynamics, 1997, 1(2): 189. DOI:10.1023/A:1009773505418 |
| [53] |
LIU Yuliang, WU Shunan, ZHANG Kaiming, et al. Parametrical excitation model for rigid-flexible coupling system of solar power satellite[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(10): 1. DOI:10.2514/1.g002739 |
| [54] |
LIU Yuliang, WU Shunan, RADICE G, et al. Gravity-gradient effects on flexible solar power satellites[J]. Journal of Guidance Control & Dynamics, 2017, 41(11): 1. DOI:10.2514/1.G003104 |
| [55] |
ZHAO Yi, ZHANG Jingrui, ZHANG Yao, et al. Gravitational force and torque on a solar power satellite considering the structural flexibility[J]. Acta Astronautica, 2017, 140: 322. DOI:10.1016/j.actaastro.2017.08.029 |
| [56] |
穆瑞楠, 王艺睿, 谭述君, 等. 空间太阳能电站姿态运动-结构振动耦合建模与分析[J]. 宇航学报, 2018, 39(6): 615. MU Ruinan, WANG Yirui, TAN Shujun, et al. Attitude-structure coupled modeling and dynamics of space solar power station[J]. Journal of Astronautics, 2018, 39(6): 615. DOI:10.3873/j.issn.1000-1328.2018.06.003 |
| [57] |
穆瑞楠, 谭述君, 吴志刚, 等. 超大柔性空间结构姿态振动耦合稳定性分析[J]. 宇航学报, 2018, 39(7): 709. MU Ruinan, TAN Shujun, WU Zhigang, et al. Coupling stability of very large flexible space structures[J]. Journal of Astronautics, 2018, 39(7): 709. DOI:10.3873/j.issn.1000-1328.2018.07.001 |
| [58] |
SHABANA A A, HUSSIEN H A, ESCALONA J L. Application of the absolute nodal coordinate formulation to large rotation and large deformation problems[J]. Journal of Mechanical Design, Transactions of the ASME, 1998, 120(2): 188. DOI:10.1115/1.2826958 |
| [59] |
胡海岩, 田强, 张伟, 等. 大型网架式可展开空间结构的非线性动力学与控制[J]. 力学进展, 2013, 43(4): 390. HU Haiyan, TIAN Qiang, ZHANG Wei, et al. Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes[J]. Advances in Mechanics, 2013, 43(4): 390. DOI:10.6052/1000-0992-13-045 |
| [60] |
GERSTMAYR J, SUGIYAMA H, MIKKOLA A. Review on the absolute nodal coordinate formulation for large deformation analysis of multibody systems[J]. Journal of Computational and Nonlinear Dynamics, 2013, 8(3): 031016. DOI:10.1115/1.4023487 |
| [61] |
NACHBAGAUER K. State of the art of ANCF elements regarding geometric description, interpolation strategies, definition of elastic forces, validation and the locking phenomenon in comparison with proposed beam finite elements[J]. Archives of Computational Methods in Engineering, 2014, 21(3): 293. DOI:10.1007/s11831-014-9117-9 |
| [62] |
ZHAO Jiang, TIAN Qiang, HU Haiyan. Deployment dynamics of a simplified spinning IKAROS solar sail via absolute coordinate based method[J]. Acta Mechanica Sinica, 2013, 29(1): 132. DOI:10.1007/s10409-013-0002-9 |
| [63] |
LIU Cheng, TIAN Qiang, YAN Dong, et al. Dynamic analysis of membrane systems undergoing overall motions, large deformations and wrinkles via thin shell elements of ANC[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 258: 81. DOI:10.1016/j.cma.2013.02.006 |
| [64] |
MALLA R B, LIN Chijie. Dynamics of flexible structures in orbit under jet impingement loading[C]//Proceedings of the 43th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Denver, CO: AIAA, 2002. DOI: 10.2514/6.2002-1507
|
| [65] |
LIN Chijie, MALLA R B. Dynamic response of a flexible structure under jet plume loading in a planar orbit[C]//Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Norfolk, Virginia: AIAA, 2003. DOI: 10.2514/6.2003-1592
|
| [66] |
徐方暖, 邓子辰, 王博, 等. 太阳光压作用下空间太阳能电站的动力学响应[J]. 西北工业大学学报, 2018, 36(3): 590. XU Fangnuan, Deng Zichen, WANG Bo, et al. Dynamic response of solar power satellite considering solar radiation pressure[J]. Journal of Northwestern Polytechnical University, 2018, 36(3): 590. DOI:10.3969/j.issn.1000-2758.2018.03.027 |
| [67] |
SUN Xin, XU Ming, ZHONG Rui. Dynamic analysis of the tether transportation system using absolute nodal coordinate formulation[J]. Acta Astronautica, 2017, 139: 266. DOI:10.1016/j.actaastro.2017.07.020 |
| [68] |
LI Qingjun, DENG Zichen, ZHANG Kai, et al. Unified modelling method for large space structures using absolute nodal coordinate[J]. AIAA Journal, 2018. DOI:10.2514/1.J057117 |
| [69] |
De JALÓN J G. Twenty-five years of natural coordinates[J]. Multibody System Dynamics, 2007, 18(1): 15. DOI:10.1007/s11044-007-9068-0 |
| [70] |
LIU Cheng, TIAN Qiang, HU Haiyan. Dynamics and control of a spatial rigid-flexible multibody system with multiple cylindrical clearance joints[J]. Mechanism and Machine Theory, 2012, 52: 106. DOI:10.1016/j.mechmachtheory.2012.01.016 |
| [71] |
ZHAO Jiang, TIAN Qiang, HU Haiyan. Deployment dynamics of a simplified spinning IKAROS solar sail via absolute coordinate based method[J]. Acta Mechanica Sinica, 2013, 29(1): 132. DOI:10.1007/s10409-013-0002-9 |
| [72] |
LI Qingjun, WANG Bo, DENG Zichen, et al. A simple orbit-attitude coupled modelling method for large solar power satellites[J]. Acta Astronautica, 2018, 145: 83. DOI:10.1016/j.actaastro.2017.12.037 |
| [73] |
LI Qingjun, DENG Zichen, ZHANG Kai, et al. Precise attitude control of multirotary-joint solar-power satellite[J]. Journal of Guidance, Control, and Dynamics, 2018, 41(6): 1431. DOI:10.2514/1.G003309 |
| [74] |
GARCÍA-VALLEJO D, ESCALONA J L, MAYO J, ET AL. Describing rigid-flexible multibody systems using absolute coordinates[J]. Nonlinear Dynamics, 2003, 34(1/2): 75. DOI:10.1023/B:NODY.0000014553.98731.8d |
| [75] |
李学府, 蔡志勤. 空间绳系太阳能电站初始姿态误差影响分析[J]. 应用力学学报, 2014, 34(5): 821. LI Xuefu, CAI Zhiqin. Attitude error influence analysis of a space tethered solar power station[J]. Chinese Journal of Applied Mechanics, 2014, 34(5): 821. DOI:10.11776/cjam.34.05.D061 |
| [76] |
邓子辰, 曹珊珊, 李庆军, 等. 基于辛Runge-Kutta方法的太阳帆塔动力学特性研究[J]. 中国科学:技术科学, 2016, 46(12): 1242. DENG Zichen, CAO Shanshan, LI Qingjun, et al. Dynamic behavior of sail tower SPS based on the symplectic Runge-Kutta method[J]. Scientia Sinica Technologica, 2016, 46(12): 1242. DOI:10.1360/N092016-00163 |
| [77] |
肖峰. 人造地球卫星轨道摄动理论[M]. 长沙: 国防科技大学出版社, 1997.
|
| [78] |
MARKLEY F L, CRASSIDIS J L. Fundamentals of spacecraft attitude determination and control[M]. New York: Springer, 2014.
|
| [79] |
章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1998.
|
| [80] |
WIE B, ROITHMAYR C M. Attitude and orbit control of a very large geostationary solar power satellite[J]. Journal of guidance, control, and dynamics, 2005, 28(3): 439. DOI:10.2514/1.6813 |
| [81] |
WIE B, ROITHMAYR C. Integrated orbit, attitude, and structural control system design for space solar power satellites[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Montreal, Canada: AIAA, 2001. DOI: 10.2514/6.2001-4273
|
| [82] |
LIU Yuliang, WU Shunan, ZHANG Kai, et al. Gravitational orbit-attitude coupling dynamics of a large solar power satellite[J]. Aerospace Science and Technology, 2017, 62: 46. DOI:10.1016/j.ast.2016.11.030 |
| [83] |
吴志刚, 刘玉亮, 张开明, 等. 高阶重力和力矩对空间太阳能电站运动的影响[J]. 空间控制技术与应用, 2016, 42(4): 1. WU Zhigang, LIU Yuliang, ZHANG Kaiming, et al. The influences of higher order gravitational force and torque to the motion of space solar power station[J]. Aerospace Control and Application, 2016, 42(4): 1. DOI:10.3969/j.issn.1674-1579.2016.04.001 |
| [84] |
刘玉亮, 邬树楠, 刘家夫, 等. 空间太阳能电站重力姿态-轨道-结构耦合特性[J]. 航空学报, 2017, 38(12): 221244. LIU Yuliang, WU Shunan, LIU Jiafu, et al. Gravitational attitude-orbit-structure coupling of space solar power station[J]. Acta Aeronautica ET Astronautica Sinica, 2017, 38(12): 221244. DOI:10.7527/S1000-6893.2017.221244 |
| [85] |
魏乙, 邓子辰, 李庆军, 等. 光压摄动对空间太阳能电站轨道的影响研究[J]. 应用数学和力学, 2017, 38(4): 399. WEI Yi, DENG Zichen, LI Qingjun, et al. Effects of solar radiation pressure on orbits of space solar power station[J]. Applied Mathematics and Mechanics, 2017, 38(4): 399. DOI:10.21656/1000-0887.370309 |
| [86] |
MCNALLY I, SCHEERES D, RADICE G. Locating large solar power satellites in the geosynchronous Laplace plane[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(3): 489. DOI:10.2514/1.G000609 |
| [87] |
MCNALLY I, SCHEERES D, RADICE G, et al. Orbital dynamics of large solar power satellites[C]//Proceedings of the 64th International Astronautical Congress. Beijing, CN: IAF, 2013: 6619 http://eprints.gla.ac.uk/89946/
|
| [88] |
刘玉亮, 邬树楠, 吴志刚, 等. 空间太阳能电站地球同步拉普拉斯轨道动力学特性[J]. 中国空间科学技术, 2016, 36(5): 1. LIU Yuliang, WU Shunan, WU Zhigang, et al. Dynamic characteristics of geosynchronous Laplace orbit for space solar power station[J]. Chinese Space Science and Technology, 2016, 36(5): 1. DOI:10.16708/j.cnki.1000-758X.2016.0053 |
| [89] |
MCNALLY I, SCHEERES D, RADICE G. Attitude dynamics of large geosynchronous solar power satellites[C]//AIAA/AAS Astrodynamics Specialist Conference. San Diego, CA: AIAA Space, 2014. DOI: 10.2514/6.2014-4123
|
| [90] |
ELROD B D. A quasi-inertial attitude mode for orbiting spacecraft[J]. Journal of Spacecraft and Rockets, 1972, 9(12): 889. DOI:10.2514/3.30407 |
| [91] |
SINCARSIN G B, HUGHES P C. Gravitational orbit-attitude coupling for very large spacecraft[J]. Celestial Mechanics, 1983, 31(2): 143. DOI:10.1007/BF01686816 |
| [92] |
MALLA R B, NASH W A, LARDNER T J. Thermal effects on very large space structures[J]. Journal of Aerospace Engineering, 1988, 1(3): 171. DOI:10.1061/(ASCE)0893-1321(1988)1:3(171) |
| [93] |
LIN Chijie, MALLA R B. Coupled thermo-structural analysis of an earth orbiting flexible structure[C]//Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference.[S.l.]: AIAA, 2004: 3084. DOI: 10.2514/6.2004-1793
|
| [94] |
SATO D, YAMADA N, TANAKA K. Thermal characterization of hybrid photovoltaic module for the conversion of sunlight into microwave in Solar Power Satellite[C]//Proceedings of the 42nd Photovoltaic Specialist Conference (PVSC). New Orleans, LA: IEEE, 2015: 1. DOI: 10.1109/PVSC.2015.7355860
|
| [95] |
YANG Chen, HOU Xinbin, WANG Li. Thermal design, analysis and comparison on three concepts of space solar power satellite[J]. Acta Astronautica, 2017, 137: 382. DOI:10.1016/j.actaastro.2017.05.004 |
| [96] |
赵利军.地球同步轨道绳系太阳能发电站系统热结构分析[D].大连: 大连理工大学, 2016 ZHAO Lijun.The thermal-structure analysis of tethered solar power satellite on the geo·synchronous orbit[D]. Dalian: Dalian University of Technology, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10141-1016219380.htm |
| [97] |
冯康, 秦孟兆. 哈密尔顿系统的辛几何算法[M]. 杭州: 浙江科技出版社, 2003. FENG Kang, QIN Mengzhao. Symplectic geometric algorithms for Hamiltonian systems[M]. Hangzhou: Zhejiang Science andTechnology Press, 2003. |
| [98] |
钟万勰.应用力学的辛数学方法[D].北京: 高等教育出版社, 2006 ZHONG Wanxie. Symplectic solution methodology in applied mechanics[M]. Beijing: Higher Education Press, 2006 http://202.118.72.26/jspui/handle/123456789/5114 |
| [99] |
钟万勰, 高强, 彭海军. 经典力学辛讲[M]. 大连: 大连理工大学出版社, 2013. ZHONG Wanxie, GAO Qiang, PENG Haijun. Classical mechanics:Its symplectic description[M]. Dalian: Dalian University of Technology Press, 2013. |
| [100] |
钟万勰, 欧阳华江, 邓子辰. 计算结构力学与最优控制[M]. 大连: 大连理工大学出版社, 1993. ZHONG Wanxie, OUYANG Huajiang, DENG Zichen. Computational structural mechanics and optimal control[M]. Dalian: Dalian University of Technology Press, 1993. |
| [101] |
姚伟岸, 钟万勰. 辛弹性力学[M]. 北京: 高等教育出版社, 2002. YAO Weian, ZHONG Wanxie. Symplectic elasticity[M]. Beijing: Higher Education Press, 2002. |
| [102] |
廖新浩, 刘林. 辛算法在限制性三体问题数值研究中的应用[J]. 计算物理, 1995, 12(1): 102. LIAO Xinhao, LIU Lin. Applications of symplectic algorithms to the numerical researches of restricted three-body problem[J]. Chinese Journal of Computational Physics, 1995, 12(1): 102. DOI:10.19596/j.cnki.1001-246x.1995.01.015 |
| [103] |
刘林, 廖新浩, 季江徽. 辛算法在近地小行星轨道演化数值研究中的应用[J]. 计算物理, 1997, 14(S1): 649. LIU Lin, LIAO Xinhao, JI Jianghui. The application of symplectic algorithm on numerical research of the orbital evolution of the neas[J]. Chinese Journal of Computational Physics, 1997, 14(S1): 649. DOI:10.19596/j.cnki.1001-246x.1997.z1.097 |
| [104] |
李庆军, 叶学华, 王博, 等. 辛Runge-Kutta方法在卫星交会对接中的非线性动力学应用研究[J]. 应用数学和力学, 2014, 35(12): 1299. LI Qingjun, YE Xuehua, WANG Bo, et al. Nonlinear dynamic behavior of the satellite rendezvous and docking based on the symplectic runge-kutta method[J]. Applied Mathematics and Mechanics, 2014, 35(12): 1299. DOI:10.3879/j.issn.1000-0887.2014.12.002 |
| [105] |
吴志刚, 杨今朝, 彭海军, 等. 轨道预报的一种乘法保辛摄动方法[J]. 中国科学:技术科学, 2016, 46(12): 1232. WU Zhigang, YANG Jinzhao, PENG Haijun, et al. A multiplicative perturbation method for satellite orbit prediction based on symplectic property[J]. Scientia Sinica Technologica, 2016, 46(12): 1232. DOI:10.1360/N092016-00204 |
| [106] |
徐斌, 欧进萍, 姜节胜, 等. 经典阻尼系统响应求解的分离变换辛解法[J]. 机械强度, 2008, 30(1): 1. XU Bin, OU Jinping, JIANG Jiesheng, et al. Symplectic method for classical damped system response based on separative transform[J]. Journal of Mechanical Strength, 2008, 30. DOI:10.16579/j.issn.1001.9669.2008.01.005 |
| [107] |
YIN Tingting, DENG Zichen, HU Weipeng, et al. Dynamic modeling and simulation of deploying process for space solar power satellite receiver[J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(2): 261. DOI:10.1007/s10483-018-2293-6 |
| [108] |
吴锋, 高强, 钟万勰. 基于祖冲之类方法的多体动力学方程保能量保约束积分[J]. 计算机辅助工程, 2014, 23(1): 64. WU Feng, GAO Qiang, ZHONG Wanxie. Energy and constraint preservation integration for multibody equations based on Zu Chongzhi method[J]. Computer Aided Engineering, 2014, 23(1): 64. DOI:10.13340/j.cae.2014.01.013 |
| [109] |
NEWMARK N M. A method of computation for structural dynamics[J]. Journal of the Engineering Mechanics Division, 1959, 85(3): 67. |
| [110] |
ARNOLD M, BRVLS O. Convergence of the generalized-α scheme for constrained mechanical systems[J]. Multibody System Dynamics, 2007, 18(2): 185. DOI:10.1007/s11044-007-9084-0 |
| [111] |
ASCHER U M, PETZOLD L R. Projected implicit Runge-Kutta methods for differential-algebraic equations[J]. SIAM Journal on Numerical Analysis, 1991, 28(4): 1097. DOI:10.1137/0728059 |
| [112] |
HAIRER E, WANNER G. Solving ordinary differential equations Ⅱ: Stiff: and differential-algebraic problems[M]. Berlin Heidelberg: Springer-Verlag, 1996.
|
| [113] |
钟万勰, 高强. 约束动力系统的分析结构力学积分[J]. 动力学与控制学报, 2006, 4(3): 193. ZHONG Wanxie, GAO Qiang. Integration of constrained dynamical system via analytical structural mechanics[J]. Journal of Dynamics and Control, 2006, 4(3): 193. DOI:10.3969/j.issn.1672-6553.2006.03.001 |
| [114] |
吴锋, 钟万勰. 基于祖冲之类方法具有保辛性[J]. 计算力学学报, 2015, 32(4): 447. WU Feng, ZHONG Wanxie. The Zu-type method is symplectic[J]. Chinese Journal of Computational Mechanics, 2015, 32(4): 447. DOI:10.7511/jslx201504001 |
| [115] |
WEI Yi, DENG Zichen, WANG Yan, et al. An improved energy and constraint conserving algorithm for constrained hamiltonian systems[J]. Journal of Computational and Theoretical Nanoscience, 2016, 13(1): 1055. DOI:10.1166/jctn.2016.4558 |
| [116] |
WEI Yi, DENG Zichen, LI Qingjun, et al. Projected Runge-Kutta methods for constrained Hamiltonian systems[J]. Applied Mathematics and Mechanics, 2016, 37(8): 1077. DOI:10.1007/s10483-016-2119-8 |
| [117] |
徐方暖, 王博, 邓子辰, 等. 基于四元数方法的绳系机器人姿态控制[J]. 应用数学和力学, 2017, 38(12): 1309. XU Fangnuan, WANG Bo, DENG Zichen, et al. Attitude control of targets captured by tethered space robots based on the quaternion theory[J]. Applied Mathematics and Mechanics, 2017, 38(12): 1309. DOI:10.21656/1000-0887.380168 |
| [118] |
王新栋, 胡伟鹏, 邓子辰. 空间太阳能电站太阳能接收器二维展开过程的保结构分析[J]. 动力学与控制学报, 2015, 13(6): 406. WANG Xindong, HU Weipeng, Deng Zichen. Structure-preserving analysis of 2D deploying process for solar power receiver of solar power satellite[J]. Journal of Dynamics and Control, 2015, 13(6): 406. DOI:10.6052/1672-6553-2014-032 |
| [119] |
文奋强, 邓子辰, 魏乙, 等. 太阳帆塔轨道和姿态耦合动力学建模及辛求解[J]. 应用数学和力学, 2017, 38(7): 762. WEN Fenqiang, DENG Zichen, WEI Yi, et al. Dynamic modelling and symplectic solution of coupled orbit & attitude for solar sail towers[J]. Applied Mathematics and Mechanics, 2017, 38(7): 762. DOI:10.21656/1000-0887.370321 |
| [120] |
HU Weipeng, LI Qingjun, JIANG Xianhong, et al. Coupling dynamic behaviors of spatial flexible beam with weak damping[J]. International Journal for Numerical Methods in Engineering, 2017, 111: 660. DOI:10.1002/nme.5477 |
| [121] |
HU Weipeng, SONG Mingzhe, DENG Zichen. Energy dissipation/transfer and stable attitude of spatial on-orbit tethered system[J]. Journal of Sound Vibration, 2018, 412: 58. DOI:10.1016/j.jsv.2017.09.032 |
| [122] |
DONATIELLO D, DIPAOLA A. Preliminary study on a vibration suppression system for a large flexible space structure[C]//Facolta di Ingegneria, Politecnico Di Milano.[S.l.]: [s.n.], 2012
|
| [123] |
GLAESE J R, MCDONALD E J. Space solar power multi-body dynamics and controls, concepts for the integrated symmetrical concentrator configuration: TCD20000222A[R]. Huntsville, AL: NASA Marshall Space Flight Center, 2000
|
| [124] |
WU Shunan, ZHANG Kaiming, PENG Haijun, et al. Robust optimal sun-pointing control of a large solar power satellite[J]. Acta Astronautica, 2016, 127: 226. DOI:10.1016/j.actaastro.2016.05.019 |
| [125] |
刘明洋.基于连续小推力空间太阳能电站静止轨道保持方法研究[D].哈尔滨: 哈尔滨工业大学, 2014 LIU Mingyang. Study of low thrust station keeping maneuver planning for Solar Power Satellite on geostationary orbit[D]. Harbin: Harbin Institute of Technology, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10213-1014084343.htm |
| [126] |
ARIMOTO S, KAWAMURA S, MIYAZAKI F. Bettering operation of robots by learning[J]. Journal of Robotic Systems, 1984, 1(2): 123. DOI:10.1002/rob.4620010203 |
| [127] |
ARIMOTO S, KAWAMURA S, MIYAZAKI F. Bettering operation of dynamic systems by learning: A new control theory for servomechanism or mechatronics systems[C]//Proceedings of the 23rd IEEE Conference on Decision and Control. Las Vegas, Nevada: IEEE, 1984: 1064. DOI: 10.1109/CDC.1984.272176
|
| [128] |
MOORE K L, DAHLEH M, BHATTACHARYYA S P. Iterative learning control: A survey and new results[J]. Journal of Robotic Systems, 1992, 9(5): 563. DOI:10.1002/rob.v9:5 |
| [129] |
AHN H S, CHEN Y Q, MOORE K L. Iterative learning control: Brief survey and categorization[J]. IEEE Transactions on Systems, Man and Cybernetics Part C: Applications and Reviews, 2007, 37(6): 1099. DOI:10.1109/TSMCC.2007.905759 |
| [130] |
WU B, WANG D, POH E K. High precision satellite attitude tracking control via iterative learning control[J]. Journal of Guidance, Control, and Dynamics, 2014, 38(3): 528. |
| [131] |
SENDA K, GOTO T. Dynamics simulation of flexible solar power satellite using geomagnetic control[C]//Proceedings of the 24th Workshop on JAXA Astrodynamics and Flight Mechanics.[S.l.]: [s.n.], 2014: 215
|
| [132] |
刘宇飞, 侯欣宾, 王立, 等. 太空发电站大型柔性结构控制系统设计[J]. 载人航天, 2017, 23(4): 440. LIU Yufei, HOU Xinbin, WANG Li, et al. Design of control system for huge flexible structures in space solar power station[J]. Manned Spaceflight, 2017, 23(4): 440. DOI:10.16329/j.cnki.zrht.2017.04.002 |
| [133] |
FUJⅡ H A, WATANABE T, KOJIMA H, et al. Control of attitude and vibration of a tethered space solar power satellite[C]//AIAA Guidance, Navigation and Control Conference and Exhibit.[S.l]: AIAA, 2003. DOI: 10.13140/RG.2.2.28696.49921
|
| [134] |
ZHOU Di, FAN Jixiang. Slewing maneuver and vibration control of tethered space solar power satellite[C]//Second International Conference on Mechanic Automation and Control Engineering. Hohhot, China: IEEE, 2011: 5239. DOI: 10.1109/MACE.2011.5988172
|
| [135] |
Fujii H A, Sugimoto Y, Watanabe T, et al. Tethered actuator for vibration control of space structures[J]. Acta Astronautica, 2015, 117: 55. DOI:10.1016/j.actaastro.2015.07.029 |
 2018, Vol. 50
2018, Vol. 50