空气污染物种类日趋繁多,空气体积分数越来越高,空气质量越来越差,对人们的健康造成了巨大的影响.评价空气质量的主要手段是通过检测空气中的污染物成分及其体积分数来判别污染程度.空气污染物的扩散过程呈现逐渐衰减的趋势,一般的整数阶扩散方程由于其阶数变动过大,因此在描述扩散过程时会存在较大的误差;相对而言,分数阶扩散方程[1-2]对问题的描述则更加细致,能较好地模拟空气污染物的运动和变化过程,能够更准确地模拟空气中污染物的反常扩散现象[3].
近年来,由于工程技术领域对问题描述的要求越来越高,整数阶微分方程逐渐不能满足其需求,从而使得分数阶微分方程快速发展.Murio[4]建立了一类分数阶扩散方程反问题求解的稳定数值方法;孙春龙等[5]采用同伦正则化算法研究了由观测数据确定微分阶数的反问题,并讨论了时空步长和数据扰动等因素对反演算法产生的影响;Li等[6]基于边界测量数据,由光滑的初始函数同时反演一维时间分数阶扩散方程的扩散系数和分数阶数;谷文娟等[7]构造了时间分数阶扩散方程的隐式差分格式,并应用最佳摄动量正则化算法对一维时间分数阶扩散方程中的参数进行反演;Wei等[8]在最佳摄动法的基础上,提出了一种求解空间分数阶反常扩散方程源项反演问题的耦合方法.上述方法多是针对一维分数阶扩散方程,都取得了较好的研究结果,但所采用的反演方法均要求函数本身光滑,对于初值的要求较高,且需要进行相应的梯度计算,在一定程度上限制了方法的应用范围.而近些年来发展起来的现代智能优化方法(例如:遗传算法、蚁群算法和粒子群算法等)对初值依赖性小,不需要计算复杂的偏导数矩阵,因此被广泛的应用于各个研究领域,在微分方程参数反演领域中也取得了一定的研究成果.江思珉等[9-10]尝试将单纯形模拟退火混合算法与和声搜索算法应用于地下水污染源反演问题和含水层参数反演问题中,通过数值算例验证了算法的高效及稳定性.韩一龙等[11]将改进的模拟退火遗传算法运用于地下水参数反演,该混合算法有效结合了遗传算法并行性和模拟退火算的全局搜索优势,克服了传统算法在收敛速度及迭代次数上的缺陷.
花朵授粉算法(flower pollination algorithm, FPA)是英国学者Yang[12]在2012年提出了一种新型智能优化算法.算法中的转换概率P可以实现在局部寻优与全局寻优之间的相互变换,Lévy飞行则模拟了花朵授粉过程中花粉随机游走的行为,从而可以快速并高效的求解最优化问题.随后,该算法被广泛使用在各个领域. Bekda等[13]利用花授粉算法最大限度地减少桁架结构的质量和尺寸设计变量的数量,对3种经典的二维和三维桁架结构尺寸优化问题进行了测试,取得了较为显著的效果. Yang等[14]将花朵授粉算法应用到多目标函数寻优中,提出了多目标花朵授粉算法(MFPA).通过7个单目标函数和4个多目标函数的测试,验证了MFPA具有良好的收敛效果. Henawy等[15]将花朵授粉算法和粒子群算法相结合来解决算法易陷入局部最优的问题;肖辉辉等[16]提出了基于差分进化策略的改进花朵授粉算法(SFPA);井福荣等[17]提出一种基于反向学习策略的改进花朵授粉算法.这些算法融合了其他算法和花朵授粉算法各自的特性,在一定程度上减少了花朵授粉算法易陷入局部最优的影响.但据本文调研所知,将花朵授粉算法及其改进算法应用于参数反演问题研究,尤其是空间分数阶反常扩散方程的参数反演,还未见相关报道.本文将基于适应值共享策略的小生境技术与花朵授粉算法相结合,提出了小生境花朵授粉算法,并将之应用于空间分数阶反常扩散方程的参数反演,有效克服了局部极值的影响,提高了反演精度.
1 花朵授粉算法及其改进 1.1 花朵授粉算法自然界中,约有90%花朵植物是交叉授粉,即从另一朵花上得到配子进行授粉,剩下的10%是不需要授粉者而进行自花传粉.基于自然界中花朵授粉的过程,英国学者Yang[12]于2012年提出了花朵授粉算法,并通过与遗传算法及粒子群算法在20个测试函数寻优能力上的对比,验证了算法的优越性,其实现步骤如下.
Step1 初始阶段.初始化各个参数,如花朵种群数n,转换概率p,优化问题维数d,最大迭代次数N;随机生成一个花朵种群Xi=(x1, x2, …, xd),d=1, 2, …,随机产生初始解,分别计算目标函数值,依据所得到的目标函数值,从中选出当前最优值,即当前全局最优解,并将其代入下次寻优过程中进行计算.
Step2 当随机数rand < p,则按照Lévy飞行进行全局寻优搜索求解,若求得的解没有超出界限,则更新当前解,否则保留当前解到下代进行计算.
Step3 当随机数rand > p,则进行局部寻优搜索求解,若求得的解没有超出界限,则更新当前解,否则保留当前解到下代进行计算.
Step4 对Step2或者Step3产生的解与全局最优解进行比较,如果新解比全局最优解还优,则更新当前最优解,否则保留当前最优解;
Step5 判断是否符合最大迭代次数要求,若满足要求,则输出最优值,否则转Step2继续进行运算.
1.2 共享机制的小生境花朵授粉算法小生境是指生物生活在一个特定的比较小的生存场所.1975年,Holland[18]根据此进化规律提出小生境策略,该策略借助了生物学中小生境的概念和核心,现已发展到较为成熟的阶段.该策略可以与其他算法相融合,能够避免陷于局部最优,以达到寻找全局最优的效果.通常情况下,可以采用预选择、排挤、分享机制等方式来生成新的种群[19].
1987年Goldberg等[20]基于共享机制共同提出了小生境技术,其实质是利用共享函数来调整种群个体间的适应度值来更新种群,之后按照新的适应度值进行计算,从而保护了种群的多样性.小生境技术不仅可以提高对多峰函数值的寻优能力,同时能提高寻找多解的能力.将花朵授粉算法与该机制的小生境相融合,可以用于解决花朵授粉算法遇到多峰函数时易陷入局部寻优的难题.
在花朵授粉算法的基础上添加小生境策略的方法如下.
1) 种群划分.计算种群中个体之间的欧式距离dij,即代表个体的相似值.
2) 计算种群共享值.通过共享函数求出每个个体的共享函数值,来判定个体之间的相似程度.共享函数的表达式如下
| $ {\rm{Sh}}\left( {{d_{ij}}} \right) = \left\{ \begin{array}{l} 1 - {\left( {\frac{{{d_{ij}}}}{\sigma }} \right)^\alpha }, {d_{ij}} < \sigma ;\\ 0, \;其他. \end{array} \right. $ |
式中:dij为i与j个体间的距离; α为调节参数(通常情况下,α=1);σ为小生境的半径.
3) 计算小生境的半径为
| $ \sigma = \left( {1/\left( {2\sqrt[n]{q}} \right)} \right)\sqrt {\sum\limits_{j = 1}^n {{{\left( {x_j^u - x_j^l} \right)}^2}} .} $ |
式中:n为优化问题的维数; q为小生境的数量; xju、xjl分别为j维的上下限.
4) 计算个体i在种群中的共享值为
| $ {m_i} = \sum\limits_{j = 1}^N {} {\rm{Sh}}\left( {{d_{ij}}} \right), $ |
式中N为花朵种群的数量.
5) 调整种群个体之间的适应度为
| $ {f'_i} = {\rm{ }}\frac{{{f_i}}}{{{m_i}}}. $ |
式中:fi为种群当前适应度, f′i为经过调整后的适应度.
基于共享机制的小生境策略可以很好地解决多峰值函数优化问题,提高全局寻优能力,并且通过调节适应度来限制某些特殊个体的数量增大,从而保证了种群的多样性.将小生境策略与花朵授粉算法相结合,就是在花朵种群初始化后,进行个体之间及种群中个体共享值的计算,调整种群个体之间的适应度,避免算法陷入局部寻优中.
以下给出小生境花朵授粉算法的实现步骤.
Step1 初始阶段.初始化各个参数, 如花朵种群数n,转换概率p,优化问题维数d,最大迭代次数N;随机生成一个花朵种群Xi=(x1, x2, …, xd),d=1, 2, …,随机产生初始解,分别计算目标函数值,依据所得到的目标函数值,从中选出当前最优值,即当前全局最优解,并将其代入下次寻优过程中进行计算.
Step2 计算种群求出共享函数值和个体在种群中的共享值,调整种群个体之间的适应度,形成新的种群.
Step3 当随机数rand < p,则按照Lévy飞行进行全局寻优搜索求解,若求得的解没有超出界限,则更新当前解,否则保留当前解到下代进行计算;
Step4 当随机数rand > p,则进行局部寻优搜索求解,若求得的解没有超出界限,则更新当前解,否则保留当前解到下代进行计算;
Step5 对Step3或者Step4产生的解与当前全局最优解进行比较,如果新解优于当前全局最优解,则更新当前最优解,否则保留当前最优解.
Step6 判断是否符合最大迭代次数要求,若满足要求,则输出最优值,否则转Step2继续进行运算.
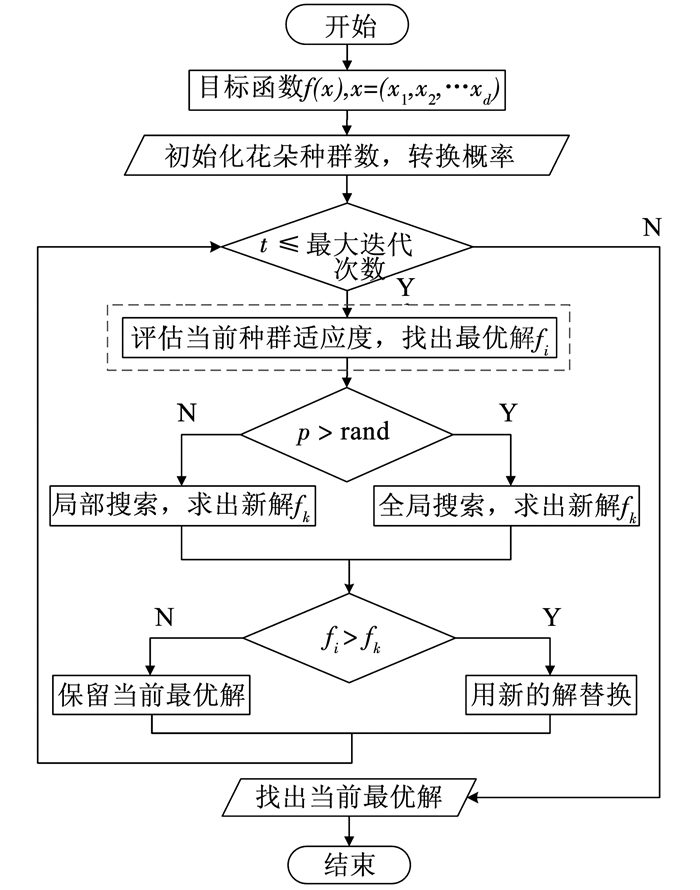
综上所述,本文可以发现花朵授粉算法及其改进算法思路明确,涉及参数少,简单易行.为了更好地展示算法实施流程,本文给出改进的花朵授粉算法流程图,如图 1所示.需要说明的是,如果在流程图中去掉虚线包含的部分,即为花朵授粉算法.
|
图 1 小生境花朵授粉算法的基本流程 Figure 1 Flowchart of niche flower pollination algorithm |
为验证花朵授粉算法的性能,本文将该算法和二进制编码遗传算法(standard binary-coded genetic algorithm,SGA)与改进的遗传算法[21](improved genetic algorithm,IGA)对20个测试函数(具体函数形式详见文献[22])的结果进行对比,其结果见表 1.花朵授粉算法(FPA)的统一参数设定:种群数为20,全局与局部的转换概率为0.8,低维函数迭代次数为400次,高维函数迭代次数为5 000次.为减少随机性的影响,本文将计算30次后的平均值作为得到的最终结果.
| 表 1 SGA、FPA和IGA寻优结果 Table 1 Results with SGA, FPA and IGA |
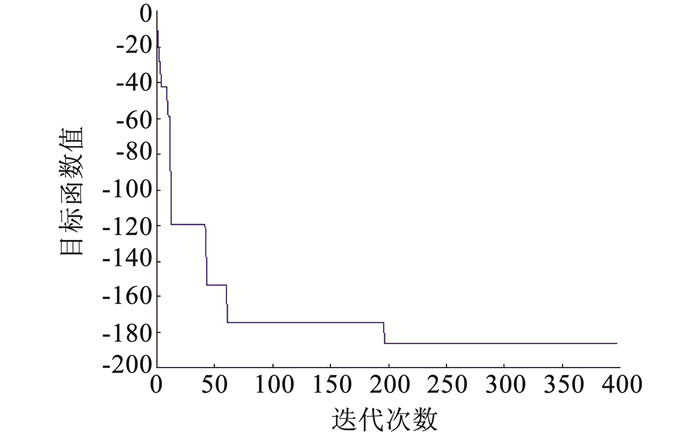
通过表 1,不难看出3个算法对于大部分函数而言都能够取得较为理想的结果.在部分情况下FPA和SGA的寻优效果相同,甚至对于函数Hosc45而言,SGA的效果还略优于FPA.但是多数情况下,FPA比SGA的寻优效果更加明显,精度上也有所提高.同样的,花朵授粉算法的寻优能力也明显强于IGA,相对于IGA有较高的精度,这表明了花朵授粉算法在多模态函数优化问题上的优越性.下面给出部分多模态函数的收敛曲线图来直观地反映花朵授粉算法的收敛速度,如图 2~5所示.从收敛曲线图可以看出,算法收敛的迭代次数与函数的维数密切相关,对于,维数较低的函数,400次迭代就可以获得全局最优值;但对于维数较高的函数,则需要较大的迭代次数(1 000次以上),才能获得最优的结果.
|
图 2 Pshubert2的收敛曲线 Figure 2 Convergence of Pshubert2 |
|
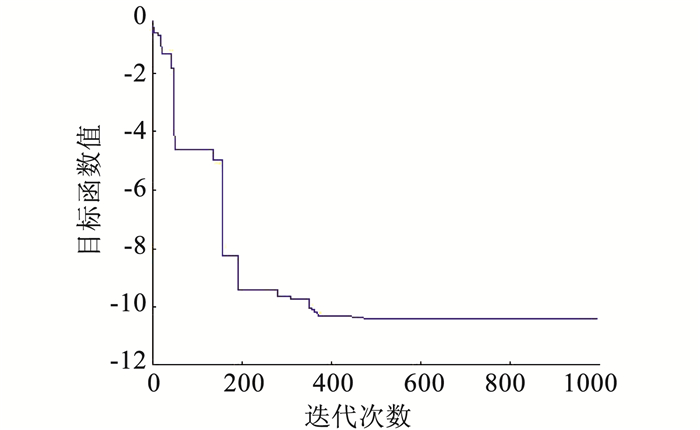
图 3 Shekel2的收敛曲线 Figure 3 Convergence of Shekel2 |

|
图 4 Hartman2的收敛曲线 Figure 4 Convergence of Hartman2 |

|
图 5 F15n的收敛曲线 Figure 5 Convergence of F15n |
针对花朵授粉算法在某些多峰值函数(如:F5n、F10n、F15n等)的寻优过程中,易陷入局部最优无法得到最优值的问题,将共享机制的小生境策略与花朵授粉算法相结合,提出小生境花朵授粉算法,以提高全局寻优能力.为了验证改进算法的优越性,同样用20个测试函数来进行测试.设定种群数为20,小生境的个数为2,转换概率为0.8.同样的,所有计算结果均为30次计算后的平均值,寻优结果见表 2.
| 表 2 NFPA与FPA寻优结果 Table 2 Results withNFPA and FPA |
通过表 2可知,对于维数较低的函数(如:F1、F3、Branin、Camelback、Goldprice等),花朵授粉算法和基于共享机制的小生境花朵授粉算法的寻优结果较为一致;但对于高维函数(如:F5n、F10n、F15n等)的求解,基于共享机制的小生境花朵授粉算法的精度明显优于花朵授粉算法的精度.为了更加清晰的阐述改进算法相对于原始算法的优越性,表 3给出了两个算法对于变量个数超过2的多模态函数寻优结果的统计分析.从表 3所列出的多模态函数寻优结果的统计分析来看,NFPA的最优值、平均值、最差值、标准差(std)都优于FPA,这说明NFPA相对于FPA取得了较大的提升.并且在高维函数寻优问题上,NFPA算法在搜索过程能更有效地避免陷入局部最优的情况.
| 表 3 NFPA与FPA寻优结果统计分析 Table 3 Statistical analysis of results with NFPA and FPA |
考虑有限域上的一维变系数空间分数阶扩散方程[23]为
| $ \begin{array}{l} \frac{{\partial u}}{{\partial t}} = d\left( x \right){\rm{ }}\frac{{{\partial ^\alpha }u}}{{{\partial ^\alpha }t}} + q\left( {x, t} \right), {\rm{ }}\\ \;\;\;\;\;\;\;\;\;\;1 < \alpha < 2, t > 0, 0 < x < l. \end{array} $ | (1) |
式中:u=u(x, t)为t时刻x点处的值; d(x)为扩散系数; q(x, t)为源项.该方程的初边值条件选择为
| $ \left\{ \begin{array}{l} u\left( {x, 0} \right) = {f_0}\left( x \right), \\ u\left( {0, t} \right) = {b_1}\left( t \right), \\ u\left( {l, t} \right) = {b_2}\left( t \right). \end{array} \right. $ | (2) |
如果分数阶扩散方程中的扩散系数d(x)和源项q(x, t)已经给出,那么由扩散方程(1)和初边值条件(2)就可以构成一个正问题,即求u(x, t).如果扩散系数d(x)和源项q(x, t)是未知的(在本文中指的是两者的系数未知), 那么就需要添加其他的附加条件来反演.附加条件可以选用某一时刻t=T时u=u(x, t)的值为
| $ u\left( {x, t} \right) = u\left( {x, T} \right) = {u_{\rm{T}}}\left( x \right), 0 \le x \le l. $ | (3) |
此时,扩散方程(1)、初边值条件(2)、附加条件(3)就构成了一个空间分数阶扩散方程的参数反演问题.
对上述正问题的求解,本文采用隐式差分格式求解,差分方程如下
| $ \frac{{u_i^{j + 1} - u_i^j}}{{\Delta t}} = \frac{{{d_i}}}{{\Gamma \left( { - \alpha } \right){{\left( {\Delta x} \right)}^\alpha }}}\sum\limits_{k = 0}^{i + 1} {\frac{{\Gamma \left( {k - \alpha } \right)}}{{\Gamma \left( {k + 1} \right)}}} u_{i - k + 1}^{j + 1} + q_i^j, $ | (4) |
整理式(4),得到相应矩阵形式为
| $ \left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{C}}} \right){\mathit{\boldsymbol{U}}^{j + 1}} = \mathit{\boldsymbol{I}}{\mathit{\boldsymbol{U}}^j} + {\mathit{\boldsymbol{Q}}^j}. $ | (5) |
式中:I是M×M的单位矩阵; Uj=[u0j, u1j, …, uM-1j]T; Dj=[1, d1, …, dM-1]T; Qj=[0, q1jΔt, …, qM-1jΔt+ηM-1jb2j+1]T; b2j=b2(tj)(即右边界的值),矩阵C为
| $ \begin{array}{l} {c_{ij}} = \left\{ {\begin{array}{*{20}{l}} {0, }&{i = 0;}\\ {\eta _i^j{g_{\alpha , i + 1 - j}}, }&{j \le i, i \ne 0;}\\ {\eta _i^j{g_{\alpha , 0}}, }&{j = i + 1, i \ne 0;}\\ {0, }&{j > i + 1, i \ne 0.} \end{array}} \right.\\ (\eta _i^j = \frac{{{d_i}\Delta t}}{{{{\left( {\Delta x} \right)}^\alpha }}}, j = 0, 1, \ldots , M - 1) \end{array} $ |
对于式(5),本文就可以采用经典的数值方法求解.
取空间分数阶导数项α=1.8,d(x)=1.101 8x2.8/8,源项q(x, t)=-(1+x)e-tx3,f0(x)=x3, b1(t)=0, b2(t)=e-t,则上述方程的精确解为u(x, t)=e-tx3.将区间[0, 1]划分为40等份,即M=N=41(时间步长与空间步长取值相等),然后利用隐式差分格式求解T=1时的数值解,数值解与真解的对比如图 6所示.从图 6可以明显看出数值解和准确解具有相同的变化趋势,数值解与准确解吻合良好,在误差允许范围之内,数值逼近效果性能良好.

|
图 6 T=1时初边值问题的准确解与数值解 Figure 6 Comparison of results for T=1 |
选取一维变系数空间分数阶扩散方程:
| $ \frac{{\partial u}}{{\partial t}} = d\left( x \right)\frac{{{\partial ^\alpha }u}}{{{\partial ^\alpha }t}} + q\left( {x, t} \right), t > 0, 0 < x < l. $ | (6) |
初边值条件为
| $ \left\{ {\begin{array}{*{20}{l}} {u\left( {x, 0} \right) = {x^3}, }&{0 < x < 1;}\\ {u\left( {0, t} \right) = 0, }&{t > 0;}\\ {u\left( {l, t} \right) = {{\rm{e}}^{ - t}}, }&{t > 0.} \end{array}} \right. $ | (7) |
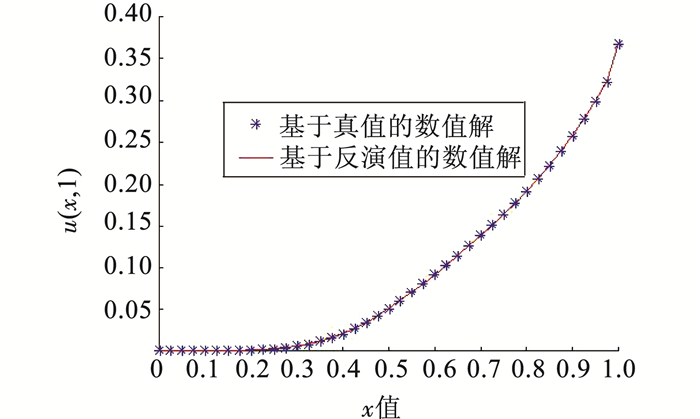
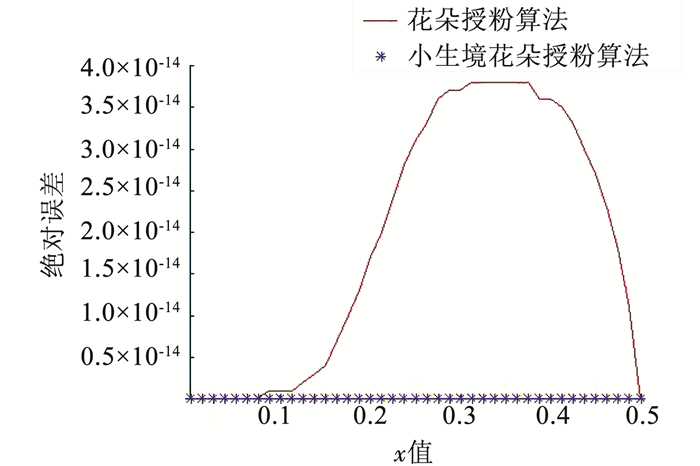
设分数阶扩散方程的扩散系数d(x)=a0x2.8/8,a0=1.101 8/8=0.137 725,源项为q(x, t)=-(1+x)e-tx3=-e-tx3-e-tx4.附加条件选取为时刻T=1时的函数值u(x, 1),空间节点数和时间节点数都取40,保持其他参量不变,反演系数a0.花朵授粉算法反演的结果为a0=0.137 724 999 999 898;小生境花朵授粉算法反演的结果为a0=0.137 725 000 000 000,与其真值相等.图 7、8分别给出了扩散系数取真值和反演值时所得到的T=1时刻的数值解.由图中可见,花朵授粉算法及其改进算法在反演一维扩散系数时,都具有较高的数值精度,从图中几乎分辨不出不同.图 9给出了基于两种方法(FPA和NFPA)反演结果的T=1时刻的数值解与基于真值的T=1时刻的数值解之间的绝对误差对比.由图中可以看出,相比花朵授粉算法,小生境花朵授粉算法的反演精度更高,结果更为理想.
|
图 7 T=1时刻数值解(FPA) Figure 7 Comparison of results for T=1 based on FPA |

|
图 8 T=1时刻数值解(NFPA) Figure 8 Comparison of results for T=1 based on NFPA |
|
图 9 T=1时刻数值解绝对误差对比 Figure 9 Comparison of absolute error for T=1 |
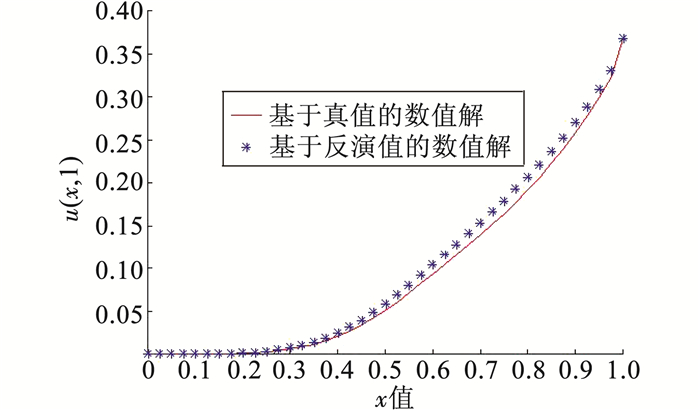
同样采用一维变系数空间分数阶反常扩散方程式(6)及其初边值条件式(7).选取源项函数q(x, t)= -(1+x)e-tx3=-e-tx3-e-tx4,扩散系数为d(x)=1.101 8x2.8/8,其他参数保持不变.设q(x, t)=a1e-tx3+b1e-tx4,本文反演其系数a1和b1.花朵授粉算法的反演结果为(a1, b1)= (-0.927 791 867 484 196, -0.964 627 736 395 022),小生境授粉算法反演结果为(a1, b1)=(-1, -1).图 10、11分别给出了源项系数取真值和反演值时所得到的T=1时刻的数值解.可以看到,在图 10中,源项系数取真值时所求的数值解明显位于反演源项系数求得的数值解之下,结果存在着明显的差异;而从图 11中可以看出,两者的吻合程度很好.这说明相对于花朵授粉算法而言,小生境花朵授粉算法对二维的源项反演效果更为显著.
|
图 10 T=1时数值解(FPA) Figure 10 Comparison of results for T=1 based on FPA |

|
图 11 T=1时数值解(NFPA) Figure 11 Comparison of results for T=1 based on NFPA |
为了验证改进算法的稳定性,本文对参数进行灵敏度分析(以扩散系数为例).一般来说,算法的模拟结果容易受到参数影响,如种群个数、转换概率、初始区间等.本文综合分析其取值对花朵授粉算法和小生境花朵授粉算法反演扩散系数的影响,来检验新算法的稳定性和可靠性.
3.3.1 扩散系数反演的灵敏度分析1) 种群数
对花朵授粉算法(FPA)和小生境花朵授粉算法(NFPA)统一设定转换概率p= 0.8,迭代次数600次,小生境个数q= 2,搜索区间为[0, 0.3],扩散系数真值选为0.137 725.种群个数分别取n=10、n= 15、n=20、n= 25、n= 30、n= 50、n= 100对空间分数阶反常扩散方程的扩散系数进行反演,结果见表 4.
| 表 4 种群数对扩散系数反演结果的影响 Table 4 The effect of population on inversion results |
从表 4可以看出,当种群数取30时,花朵授粉算法反演扩散系数的效果是比较理想的,最接近扩散系数真值.而小生境花朵授粉算法在种群数取20的时候,效果最好,得到了扩散系数真值.总的来说,种群数对反演结果的影响不大,最差结果的绝对误差也在10-10这一数量级,但是随着种群数的变化,扩散系数的反演结果还是有所区别.
2) 转换概率
对花朵授粉算法设定种群数n=30,迭代次数600次,搜索区间为[0, 0.3];小生境花朵授粉算法设定种群数为n=20,迭代次数600次,小生境个数q=2,搜索区间为[0, 0.3].转换概率在[0, 1]取10个数分别对空间分数阶扩散方程的扩散系数进行反演,来观察转换概率对反演结果的影响,结果见表 5.
| 表 5 转换概率对扩散系数反演结果的影响(FPA) Table 5 The effect of transition probability on inversion results (FPA) |
从上述表格可以看出,当转换概率取0.8时,花朵授粉算法和小生境花朵授粉算法反演扩散系数的结果都是最理想的,其中小生境花朵授粉算法反演扩散系数的结果与扩散系数真值相等,而当转换概率取0.1时,在小生境花朵授粉算法中,其绝对误差是最大的.
3) 初始搜索区间
对花朵授粉算法设定种群数n=30,迭代次数600次,转换概率p=0.8;小生境花朵授粉算法设定种群数为n=20,迭代次数600次,转换概率p=0.8,小生境个数q=2.搜索区间分别为[0, 0.3]、[0, 0.5]、[0, 1.0]对空间分数阶反常扩散方程的扩散系数进行反演,来观察搜索区间对反演结果的影响,结果见表 6.
| 表 6 初始搜索区间对扩散系数反演结果的影响(FPA) Table 6 The effect of initial interval on inversion results (FPA) |
根据表 6可知,当搜索区间为[0, 0.3]、[0, 0.5]和[0, 1.0]时,花朵授粉算法及其改进算法对反演结果影响效果不大,说明两种算法均具有大范围的全局收敛性.主要差别在于算法运行时间,搜索区间大,则搜索所需时间长;反之,则搜索所需时间短.
3.3.2 算法抗噪性分析算法的抗噪性也是判断算法稳定性的重要准则,为研究花朵授粉算法和小生境花朵授粉算法的抗噪性.对方程(4)的数值解u(x, t)分别添加5%、10%、15%的白噪声,服从N(0, 1)分布,利用花朵授粉算法(FPA)和小生境花朵授粉算法(NFPA)对方程(7)的扩散系数和源项进行反演,各个参数选择上述最佳参数.扩散系数和源项的搜索区间分别为[0, 0.3]、[-2, 2],反演结果见表 7、8.白噪声公式如下
| $ u'\left( {x, t} \right) = u\left( {x, t} \right) \cdot \left[ {1 + k \times {\rm{rand}}} \right]. $ |
| 表 7 不同噪声下扩散系数反演结果(FPA) Table 7 Inversion results of diffusion coefficients under different levels of noise (FPA) |
| 表 8 噪声对源项反演结果的影响(FPA) Table 8 Inversion results of source term under different levels of noise (FPA) |
式中:k为噪声比例;rand为随机产生的数;u′(x, t)为加噪声后的数值解;u(x, t)为加噪声前的数值解.
从表 7、8可以看出,随着噪声的增加,花朵授粉算法及小生境花朵授粉算法参数反演结果的精度都有所下降.但相对而言,小生境花朵授粉算法的结果比花朵授粉算法要精确一些.由此可以看出,小生境策略的加入在一定程度上改善了原有算法的抗噪性,但效果还不是太理想,有待进一步研究.
4 结论1) 针对花朵授粉算法在多峰函数优化方面的不足,将基于适应值共享原则的小生境技术与花朵授粉算法相结合,提出了一种新的改进算法-小生境花朵授粉算法,并通过20个多模态测试函数验证了新算法的优越性.
2) 将花朵授粉算法及其改进算法应用于空间分数阶扩散方程的扩散系数及源项反演研究,通过数值算例验证了算法的有效性.
3) 从种群个数、转换概率、初始区间和抗噪性等因素对所提算法用于参数反演的稳定性进行了分析,验证了算法的鲁棒性.
| [1] |
OLDHAM K B, SPANIER J. The fractional calculus[J]. Mathematical Gazette, 1974, 56(247): 396. DOI:10.1007/978-3-642-18101-6_2 |
| [2] |
SAMKO S G, KILBAS A A, MARICHEV O I. Fractional integrals and derivatives:theory and applications[M]. Yverdon: Gordon and Breach Scien Publishers, 1993.
|
| [3] |
阮周生, 张文, 王泽文. 一类空间分数阶扩散方程系数反问题的数值解[J]. 黑龙江大学自然科学学报, 2012(6): 759. RUAN Zhousheng, ZHANG Wen, WANG Zewen. The numerical solution of coefficient inverse problem for a kind of space fractional diffusion equation[J]. Journal of Natural Science of Heilongjiang University, 2012(6): 759. DOI:10.13482/j.issn1001-7011.2012.06.020 |
| [4] |
MURIO D A. Stable numerical solution of a fractional-diffusion inverse heat conduction problem[J]. Computers & Mathematics with Applications, 2007, 53(10): 1492. DOI:10.1016/j.camwa.2006.05.027 |
| [5] |
孙春龙, 李功胜, 贾现正, 等. 含三个时间分数阶导数的反常扩散方程求解与微分阶数反演[J]. 山东理工大学学报(自然科学版), 2015, 29(3): 1. SUN Chunlong, LI Gongsheng, JIA Xianzheng, et al. The solution to three time-fractional anomalous diffusion equation and numerical inversion of the fractional orders[J]. Journal of Shangdong University of Technology (Natural Science Edition), 2015, 29(3): 1. DOI:10.3969/j.issn.1672-6197.2015.03.001 |
| [6] |
LI Gongsheng, ZHANG Dali, JIA Xianzheng, et al. Simultaneous inversion for the space-dependent diffusion coefficient and the fractional order in the time-fractional diffusion equation[J]. Inverse Problems, 2013, 29(6): 519. DOI:10.1088/0266-5611/29/6/065014 |
| [7] |
谷文娟, 李功胜, 殷凤兰, 等. 一个时间分数阶扩散方程的参数反演问题[J]. 山东理工大学学报(自然科学版), 2010, 24(6): 22. GU Wenjuan, LI Gongsheng, YIN Fenglan, et al. Parameter inversion for a time fractional diffusion equation[J]. Journal of Shangdong University of Technology (Natural Science Edition), 2010, 24(6): 22. DOI:10.3969/j.issn.1672-6197.2010.06.006 |
| [8] |
WEI Hui, CHEN Wen, SUN Hongguang, et al. A coupled method for inverse source problem of spatial fractional anomalous diffusion equations[J]. Inverse Problems in Science and Engineering, 2010, 18(7): 945. DOI:10.1080/17415977.2010.492515 |
| [9] |
江思珉, 蔡奕, 王敏, 等. 基于和声搜索算法的地下水污染源与未知含水层参数的同步反演研究[J]. 水利学报, 2012, 43(12): 1470. JIANG Simin, CAI Yi, WANG Min, et al. Simultaneous identification of ground contaminant source and aquifer parameters by harmony search algorithm[J]. Shuili Xuebao, 2012, 43(12): 1470. |
| [10] |
江思珉, 张亚力, 蔡奕, 等. 单纯形模拟退火算法反演地下水污染源强度[J]. 同济大学学报(自然科学版), 2013, 41(2): 253. JIANG Simin, ZHANG Yali, CAI Yi, et al. Groundwater contaminant identification by hybrid simplex method of simulated annealing[J]. Journal of Tongji University (Natural Science), 2013, 41(2): 253. DOI:10.3969/j.issn.0253-374x.2013.02.017 |
| [11] |
韩一龙, 单永明. 运用模拟退火遗传算法估计地下水反演参数[J]. 计算机工程与应用, 2012, 48(12): 224. HAN Yilong, SHAN Yongming. Using improved simulated annealing genetic algorithm to estimate parameters in groundwater inverse problem[J]. Computer Engineering and Application, 2012, 48(12): 224. DOI:10.3778/j.issn.1002-8331.2012.12.047 |
| [12] |
YANG Xinshe. Flower pollination algorithm for global optimization[C]//Proceedings of the 11th International Conference on Unconventional Computation and Natural Computation. Orléan: Springer-Verlag, 2012, 7445: 240. DOI: 10.1007/978-3-642-32894-7_27
|
| [13] |
BEKDA G, NIGDELI S M, YANG Xinshe. Sizing optimzation of truss structures using flower pollination algorithm[J]. Applied Soft Computing, 2015, 37: 322. DOI:10.1016/j.asoc.2015.08.037 |
| [14] |
YANG Xinshe, KARAMANOGLU M, HE Xingshi. Flower Pollination algorithm: a novel approach for multiobjective optimization[J]. Engineering Optimization, 2014, 46(9): 1222. DOI:10.1080/0305215X.2013.832237 |
| [15] |
HENAWY I M, ABDEL-RAOUF O, ABDEL-BASET M. A new hybrid flower pollination algorithm for solving constrained global optimization problems[J]. International Journal of Applied Operational Research, 2014, 4(2): 1. DOI:10.12785/aeta/030202 |
| [16] |
肖辉辉, 万常选, 段艳明. 一种改进的新型元启发式花朵授粉算法[J]. 计算机应用研究, 2016, 33(1): 126. XIAO Huihui, WAN Changxuan, DUAN Yanming, et al. Improved novel metaheuristic flower pollination algorithm[J]. Journal of computer applications, 2016, 33(1): 126. DOI:10.3969/j.issn.1001-3695.2016.01.030 |
| [17] |
井福荣, 郭肇禄, 罗会兰. 一种使用反向学习策略的改进花粉授粉算法[J]. 江西理工大学学报, 2015, 36(3): 101. JING Furong, GUO Zhaolu, LUO Huilan. A flower pollination algorithm based on reverse learning strategy[J]. Journal of Jiangxi University of Science and Technology, 2015, 36(3): 101. DOI:10.13265/j.cnki.jxlgdxxb.2015.03.018 |
| [18] |
HOLLAND J H. Adaptation in natural and artificial systems[M]. Michigan: The University of Michigan Press, 1975.
|
| [19] |
LI Xiaodong. Niching without Niching parameters: particle swarm optimization using a ring topology[J]. IEEE Transactions on Evolutionary Computation, 2010, 14(1): 150. DOI:10.1109/TEVC.2009.2026270 |
| [20] |
GOLDBERG D E, RICHARDSON J. Genetic algorithms with sharing for multimodal function optimization[C]//Proceedings of the 2th International Conference on Genetic Algorithms and Their Application. Hillsdale, NJ: L. Erlbaum Associates Inc., 1987: 41. DOI: 10.1109/ICEC.1996.542701
|
| [21] |
YANG Xiaohua, YANG Zhifeng, YIN Xinan, et al. Chaos gray-coded genetic algorithm and its application for pollution source identifications in convection-diffusion equation[J]. Communications in Nonlinear Science & Numerical Simulation, 2008, 13(8): 1676. DOI:10.1016/j.cnsns.2007.03.003 |
| [22] |
ANDRE J, SIARRY P, DOGNON T. An improvement of the standard genetic algorithm fighting premature convergence in continuous optimization[J]. Advances in Engineering Software, 2001, 32(1): 49. DOI:10.1016/S0965-9978(00)00070-3 |
| [23] |
韦慧, 陈文, 孙洪广.空间分数阶反常扩散方程的源项反问题[C]//中国力学学会2009学术大会.郑州: 中国力学学会2009学术大会论文集, 2009 WEI Hui, CHEN Wen, SONG Hongguang. The inverse source problem of space fractional abnormal diffusion equation[C]//The Chinese Society of Mechanical 2009 Academic Conference. Zhengzhou: CCTAM, 2009 |
 2018, Vol. 50
2018, Vol. 50


