2. 船舶振动噪声重点实验室(中国舰船研究设计中心),武汉 430064
2. National Key Laboratory on Ship Vibration and Noise (China Ship Development and Design Center), Wuhan 430064, China
水管路系统是船舶设备的重要组成部分,用于液体(如动力系统冷却液)的输送,在其运转过程中,泵与阀门等引起流体运动不稳定(湍流及空化等)会产生水动力噪声,水管路系统成为噪声的重要传播途径之一,直接由出水口向水下环境辐射,辐射效率极高,影响船舶的隐身性能[1-2],而且也会影响海洋生物的生存环境.为了有效地控制管路系统水噪声问题,水消声器被应用于水管路系统,消声器的消声效果是衡量其性能的重要指标.但目前,水消声器声学性能的计算结果与试验结果往往不一致,难以指导水消声器的优化设计.
目前,国内外针对水消声器的公开研究文献很少,且多是借鉴气体消声器的研究方法,如传递矩阵法[3]、解析法[4]、有限元法[5-6]、边界元法[7]、有限体积法[8-10].虽然水消声器和气体消声器消声原理基本一致,内部均为流体,但液体、气体与消声器结构的相互作用存在很大区别.消声器结构弹性通常远远小于气体的压缩性,结构与气体的耦合是极小的,可以基本忽略,所以气体消声器声学性能的预测方法基本不考虑结构与气体介质的耦合.然而水介质声阻抗要比气体介质的大的多,其压缩性与结构弹性更接近,所以结构与水介质的耦合强度要远大于结构与气体介质的耦合强度[11-12].因此,水消声器声学性能的预测有必要考虑结构声耦合造成的影响.现有文献较少考虑结构弹性对水消声器声学性能的影响.周城光等[13]基于集中参数法研究了结构弹性对充水亥姆霍兹共振器声学特性的影响.何涛等[2]基于理论方法研究了结构弹性对充水背腔板式水消声器声学特性的影响.这两种方法的缺点在于难于应用于工程中复杂结构的消声器.Xuan等[9]基于时域有限体积法研究了充水亥姆霍兹共振腔的声学性能,该方法可用于工程中的复杂结构,但时域法计算耗时较大.
本文采用基于频域法的结构声耦合模型计算充水膨胀腔消声器的声学性能,可以快速、有效的考虑结构声耦合效应对水消声器声学性能的影响,同时采用二维轴对称模型简化计算,大大提高了计算效率.通过与刚性条件下的数值结果及理论结果比较,验证方法的正确性,进一步研究消声器腔壁厚度、不同位置结构对水消声器声学性能的影响.
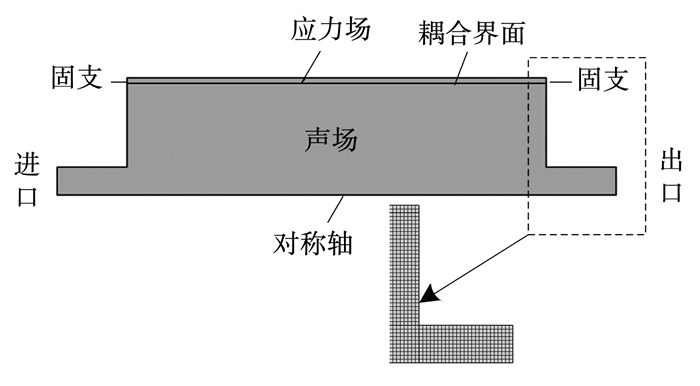
1 数值模拟 1.1 研究对象研究结构声耦合对充水膨胀腔消声器声学性能的影响,消声器结构尺寸如图 1所示.其中,模型A忽略结构声耦合影响,仅计算流体区域;模型B、模型C、模型D均考虑结构声耦合的影响,其区别在于考虑结构声耦合的部位不同,各模型的内部尺寸均相同,图 1中ϕ1、ϕ2分别为消声器的膨胀腔、主管路直径,l、L分别为消声器的膨胀腔、整体长度,t为消声器结构的厚度,在消声器结构的两端施加固支约束.

|
图 1 计算模型示意 Figure 1 Sketch map of the muffler |
采用计算多物理场软件Comsol进行数值模拟.消声器外形尺寸及边界条件具有轴对称性,为节约计算量、提高计算速度,拟采用二维轴对称模型计算消声器传递损失.
消声器结构材料为钢,密度ρs=7 800 kg/m3,杨氏模量E=1010 Pa,泊松比v=0.30;消声器内部水介质的密度ρf=1 000 kg/m3,声速cf=1 500 m/s.边界条件为:
1) 声场进口.设定为平面波条件,进口压力幅值设定为1 Pa;
2) 声场出口.设定为平面波辐射边界条件;
3) 结构与水介质接触界面.不考虑结构弹性时,选择压力声学模型,消声器壁面设定为绝对硬反射边界.考虑结构弹性时,选择声结构耦合模型,结构与流体接触界面设定为声结构耦合界面.
以模型B为例,相关边界条件如图 2所示.采用边长ΔL=0.005 m的四边形网格划分计算域.在一个波长内包含10个空间步长的前提下,计算模型能够考虑的最大有效频率为
| $ {f_{{\rm{max}}}} = {c_f}/(10\Delta L) = 30\;000\;{\rm{Hz}}. $ |
|
图 2 边界及网格说明 Figure 2 Information of the boundary and meshes |
基于平面波理论,消声器进出口管的截止频率[14]为
| $ {f_{{\rm{cut - off}}}} = \frac{{3.832}}{{{\rm{ \mathsf{ π} }}{\phi _2}}}{c_f} = \frac{{3.832}}{{{\rm{ \mathsf{ π} }} \times 0.1}} \times 1\;500\;{\rm{Hz}} = 18\;296\;{\rm{Hz}}. $ |
在评价消声器性能时,常采用传递损失衡量其声学性能.消声器的传递损失可由下式计算:
| $ {\rm{TL}} = 10{\rm{log}}\left( {\frac{{{P_{{\rm{in}}}}}}{{{P_{{\rm{out}}}}}}} \right), $ |
式中:Pin、Pout分别为进口处的入射声功率、出口处的透射声功率,二者可分别由下式计算:
| $ \begin{array}{l} {P_{{\rm{in}}}} = {\smallint _{\rm{A}}}\frac{{p_i^2}}{{2{\rho _f}{c_f}}}{\rm{d}}s, \\ {P_{{\rm{out}}}} = {\smallint _{\rm{A}}}\frac{{{{\left| {{p_o}} \right|}^2}}}{{2{\rho _f}{c_f}}}{\rm{d}}s. \end{array} $ |
式中:pi为进口处的入射声压; po为出口处的透射声压; A为进口或出口面积.
2 结果与分析 2.1 二维轴对称模型计算结果当采用二维轴对称模型时,弹性结构的对称边界可能会造成结构固有频率丢失,因此有必要验证采用二维轴对称模型是否会对计算结果造成影响.基于结构声耦合模型,分别利用二维轴对称模型、三维整体模型计算模型B中消声器的传递损失,计算结果如图 3所示,二者吻合良好.后续分析中均采用二维轴对称模型.

|
图 3 对称模型与整体模型计算结果对比 Figure 3 Comparison of the predicted TL based on the full model and the axisymmetric model |
采用模型A验证刚性条件下水消声器声学性能计算的正确性.简单膨胀腔消声器的消声量ΔLmax及通过频率fn分别为[15]:
| $ \Delta {L_{{\rm{max}}}} = 10{\rm{lg}}\left[ {1 + \frac{1}{4}\left( {m - \frac{1}{m}} \right){^2}} \right], $ | (1) |
| $ {f_n} = \frac{{n{c_f}}}{{2l}}, \;\;\left( {n = 1, 2, 3, \ldots } \right) $ | (2) |
式中:m=(ϕ1/ϕ2)2=16为消声器的膨胀比.依据式(1)、(2)可得,文中膨胀腔消声器的最大消声量ΔLmax≈18.1 dB,通过频率f1=1 000 Hz,这与本文模型A的数值结果(见图 4)吻合良好,验证了本文计算刚性条件下水消声器声学性能的正确性.
|
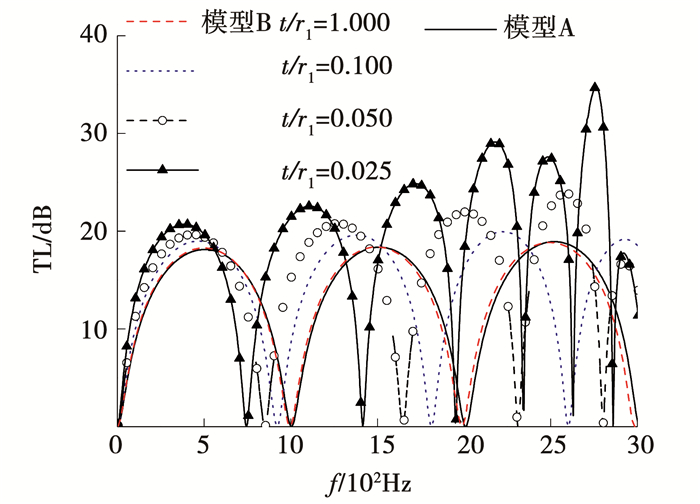
图 4 模型B周向腔壁厚度对消声器传递损失的影响 Figure 4 Effects of the thickness of the circumferential chamber wall on the TL of the muffler |
采用模型B研究膨胀腔周向壁厚变化对水消声器传递损失的影响,腔壁的两端固支.研究4种周向腔壁厚度(厚径比t/r1=1.000,0.100,0.050,0.025)对水消声器声学性能的影响,其中r1=ϕ1/2表示消声器膨胀腔腔体半径,计算得到的传递损失如图 4所示.模型A、模型B的前3阶通过频率对比见表 1,其中相对偏差的定义为
| $ 相对偏差 = \frac{{{f_i} - f_i^0}}{{f_i^0}} \times 100\% . $ |
| 表 1 模型B与模型A前3阶通过频率对比 Table 1 Comparison of the first three order passing frequencies based on Model A and Model B |
式中:fi0为模型A的第i阶通过频率; fi为模型B的第i阶通过频率.
由图 4和表 1可知,当t/r1=1.000时,模型B与刚性情况下模型A的计算结果仅略有差别,此时弹性结构与流体的耦合程度很弱,通过频率平均相对偏差在1%左右,进一步证明本文方法的正确性;随着t/r1的减小,弹性结构与流体的耦合作用愈加明显.与t/r1=1.000时模型B的传递损失相比,随着壁厚的减小,水消声器的通过频率降低,而最大消声量有增大的趋势.
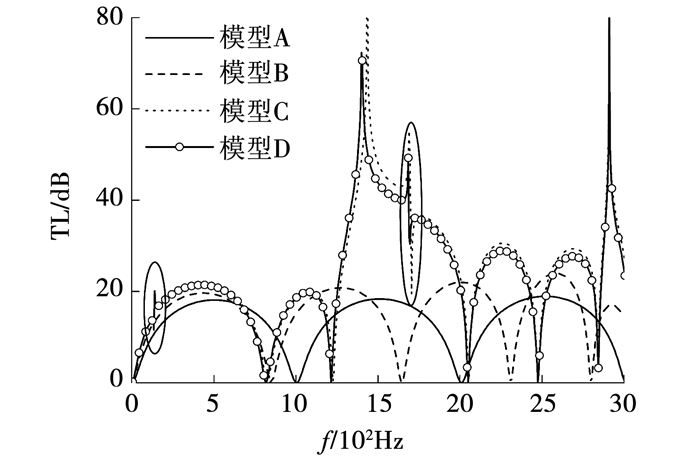
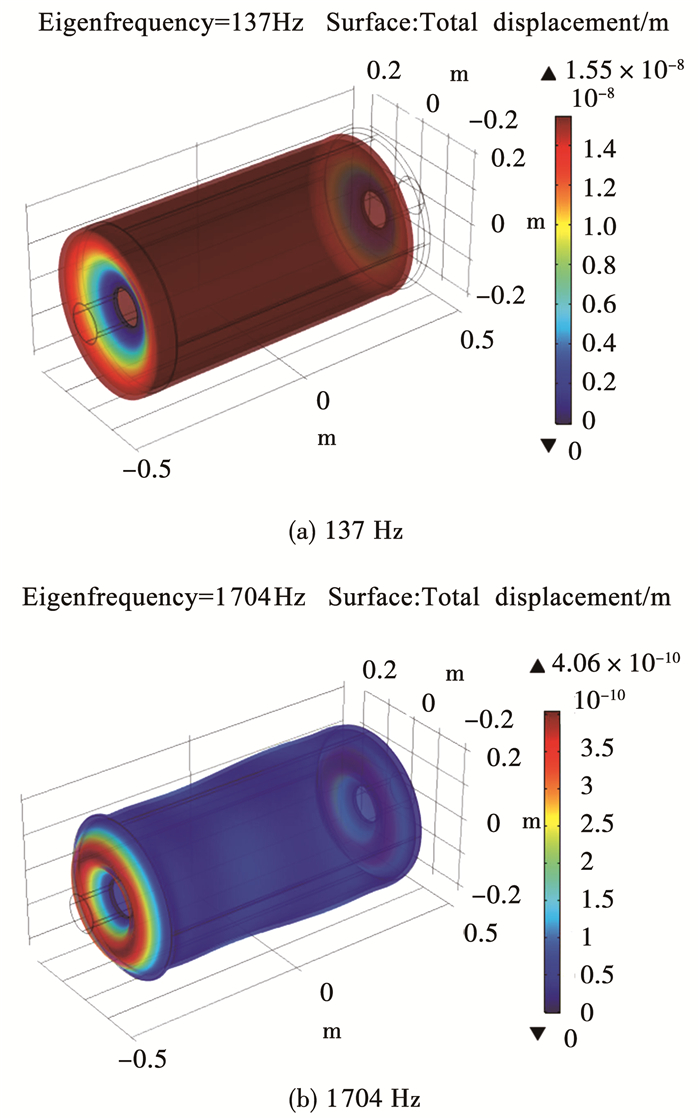
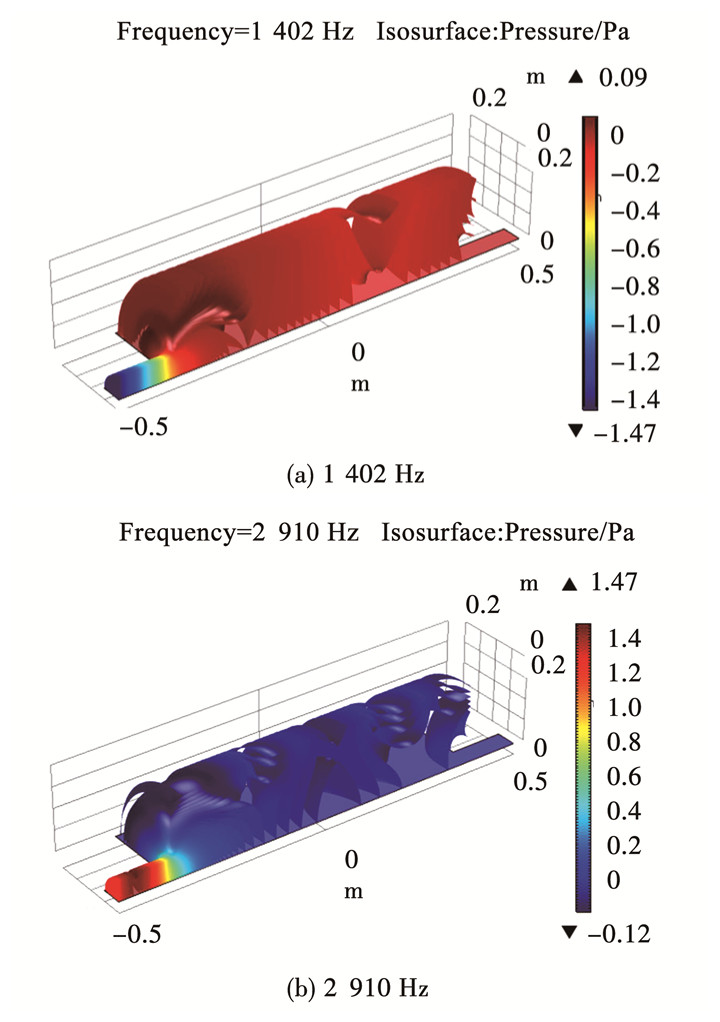
2.3 不同部位结构声耦合效应的影响分别计算模型A、模型B、模型C、模型D的声学性能,研究不同部位结构声耦合效应对膨胀腔消声器性能的影响,结构厚度均为t=10 mm,图 5为不同工况下消声器的传递损失.对比模型A、模型B计算结果,周向腔壁的结构声耦合效应会造成膨胀腔消声器的传递损失曲线向低频方向移动;模型C、模型D计算结果区别不大,说明本文算例中管路结构声耦合效应对水消声器声学性能的影响不大;对比模型B、模型C计算结果,传递损失曲线发生了较大变化,特别是模型C在137、1 704 Hz处出现了反共振峰,且在其附近出现了共振峰,通过固有模态分析得到充水结构在137、1 704 Hz处的模态振型(见图 6),这两阶固有模态振型以两侧端板相同的(0,1)、(0,2)阶振型为主,可见膨胀腔消声器传递损失曲线的反共振峰、共振峰现象与端板的(0,n)阶固有模态相关,当处于这两个频率处的声压在腔体内传播时,声压激起端部结构在固有频率处的共振而产生较大的二次声,从而降低充水消声器在端部结构固有频率处的消声量;同时模型C、模型D均在1 402、2 910 Hz处出现明显峰值,图 7为模型D在1 402、2 910 Hz处腔内声压分布,可以看出由于结构声耦合效应的影响,腔内声压出现了三维高次波,这是出现峰值的主要原因.
|
图 5 不同模型对消声器传递损失的影响 Figure 5 TL of mufflers based on different models |
|
图 6 充水结构(模型C)模态振型 Figure 6 Modal shapes of the water muffler based on model C |
|
图 7 充水结构(模型D)腔内声压分布 Figure 7 Acoustic pressure distribution in the water muffler based on model D |
1) 通过与刚性情况、三维整体模型的计算结果对比表明,采用结构声耦合数值模型、二维轴对称模型可以有效的计算消声器传递损失.
2) 随着水消声器腔壁厚度的减少,弹性结构与流体的耦合程度越强烈,结构声耦合效应对水消声器声学性能的影响程度越大,膨胀腔的通过频率向低频方向移动越多,且最大消声量有增大的趋势.
3) 周向腔壁的结构声耦合效应会造成膨胀腔消声器的传递损失曲线向低频方向移动,端部腔壁与水介质的耦合效应会使消声器传递损失曲线出现反共振峰、共振峰,这与充水消声器端板结构的(0,n)阶固有模态相关;膨胀腔壁的结构声耦合作用使传递损失曲线出现明显峰值,这是由于腔内声压出现了三维高次波;管路结构声耦合效应对水消声器声学性能的影响不大.
| [1] |
程广福, 张文平, 柳贡民, 等. 船舶水管路噪声及其控制研究[J]. 噪声与振动控制, 2004, 24(2): 31. CHENG Guangfu, ZHANG Wenping, LIU Gongmin, et al. The liquid-born noise and its control in water pipelines of ship[J]. Noise and Vibration Control, 2004, 24(2): 31. DOI:10.3969/j.issn.1006-1355.2004.02.009 |
| [2] |
何涛, 孙刚, 孙玉东, 等. 充液背腔板式水动力噪声消声器参数分析[J]. 船舶力学, 2014, 18(4): 459. HE Tao, SUN Gang, SUN Yudong, et al. Parameter analysis on hydrodynamic noise plate-silencer with fluid cavity[J]. Journal of Ship Mechanics, 2014, 18(4): 459. DOI:10.3969/j.issn.1007-7294.2014.04.014 |
| [3] |
MUNJAL M L, RAO K N, Sahasrabudhe A D. Aeroacoustic analysis of perforated muffler components[J]. Journal of Sound and Vibration, 1987, 114(2): 173. DOI:10.1016/S0022-460X(87)80146-3 |
| [4] |
SELAMET A, JI Z L. Acoustic attenuation performance of circular expansion chambers with extended inlet/outlet:Ⅱ. comparison with experimental and computational studies[J]. Journal of Sound and Vibration, 1998, 213(4): 619. DOI:10.1006/jsvi.1998.1515 |
| [5] |
MEHDIZADEH O Z, PARASCHIVOIU M. A three-dimensional finite element approach for predicting the transmission loss in mufflers and silencers with no mean flow[J]. Applied Acoustics, 2005, 66(8): 902. DOI:10.1016/j.apacoust.2004.11.008 |
| [6] |
徐贝贝, 季振林. 穿孔管消声器声学特性的有限元分析[J]. 振动与冲击, 2009, 28(9): 112. XU Beibei, JI Zhenlin. Finite element analysis of acoustic attenuation performance of perforated tube silencers[J]. Journal of Vibration and Shock, 2009, 28(9): 112. DOI:10.3969/j.issn.1000-3835.2009.09.024 |
| [7] |
WU T, ZHANG P, CHENG C R Y. Boundary element analysis of mufflers with an improved method for deriving the four-pole parameters[J]. Journal of Sound and Vibration, 1998, 217(4): 767. DOI:10.1006/jsvi.1998.1800 |
| [8] |
宣领宽, 张文平, 明平剑, 等. 预测消声器声学性能的时域非结构有限体积法[J]. 哈尔滨工程大学学报, 2012, 33(2): 185. XUAN Lingkuan, ZHANG Wenping, MING Pingjian, et al. Unstructured finite volume time domain method for prediction of a muffler's acoustic attenuation performance[J]. Journal of Harbin Engineering University, 2012, 33(2): 185. DOI:10.3969/j.issn.1006-7043.201104067 |
| [9] |
XUAN Lingkuan, LIU Yan, GONG Jingfeng, et al. A time-domain finite volume method for the prediction of water muffler transmission loss considering elastic walls[J]. Advances in Mechanical Engineering, 2017, 9(2): 1. DOI:10.1177/1687814017690068 |
| [10] |
XUAN Lingkuan, GONG Jingfeng, MING Pingjian, et al. A time-domain finite volume approach for prediction of muffler transmission loss including thermal effects[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2014, 228(1): 108. DOI:10.1177/0954406213481714 |
| [11] |
DEU J F, LARBI W, OHAYON R. Vibration and transient response of structural-acoustic interior coupled systems with dissipative interface[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(51/52): 4894. DOI:10.1016/j.cma.2008.07.013 |
| [12] |
BER ÚDEZ A, RODRÍGUEZ R. Modelling and numerical solution of elastoacoustic vibrations with interface damping[J]. International Journal for Numerical Methods in Engineering, 1999, 46(10): 1763. DOI:10.1002/(SICI)1097-0207(19991210)46:10<1763::AID-NME723>3.0.CO;2-6 |
| [13] |
周城光, 刘碧龙, 李晓东, 等. 腔壁弹性对充水亥姆霍兹共振器声学特性的影响:圆柱形腔等效集中参数模型[J]. 声学学报, 2007, 32(5): 426. ZHOU Chengguang, LIU Bilong, LI Xiaodong, et al. Effect of elastic cavity walls on acoustic characteristics of a water-filled Helmholtz resonator: equivalent lumped parameter model for cylindrical cavity[J]. Acta Acustica, 2007, 32(5): 426. DOI:10.3321/j.issn:0371-0025.2007.05.006 |
| [14] |
何祚镛, 赵玉芳. 声学理论基础[M]. 北京: 国防工业出版社, 1981. HE Zuoyong, ZHAO Yufang. Theoretical foundation of acoustics[M]. Beijing: National Defense Industry Press, 1981. |
| [15] |
马大猷. 噪声与振动控制工程手册[M]. 北京: 机械工业出版社, 2002. MA Dayou. Handbook of noise and vibration control engineering[M]. Beijing: China Machine Press, 2002. |
 2018, Vol. 50
2018, Vol. 50


