宇宙的起源与演化一直是20世纪以来天文界与物理学界最为关注的问题.通过对宇宙微波背景辐射的观测,人们对早期宇宙的演化有了更深的认识[1-2].进入21世纪,探索宇宙黑暗时代[3-5](dark age)等重大科学问题进入人们的视野.宇宙黑暗时代是指宇宙从大爆炸结束后质子与电子复合之时起,直至第1代恒星形成的演化阶段,即大爆炸后380万年至1.5亿年的阶段[6].对黑暗时代的观测将帮助人们更好的认识现代宇宙形成过程.
目前对黑暗时代唯一的探测方法是对其氢原子产生的21 cm波长的谱线进行探测[7],而黑暗时代的21 cm谱线经红移后正处在超长波的范围.这里的超长波是指电磁频谱中0.3~30 MHz的频段.就低于30 MHz的超长波频段观测而言,地球上各种无线电设备所造成的大量射电干扰以及地球大气电离层湍流对30 MHz以下的电磁波产生很强的随机折射[8],这些都严重制约了地基的低频射电天文观测.因此,美国于1968年发射了radio astronomy explorer-A(RAE-A)地球轨道卫星对空间超长波频段进行观测,但由于地球本身产生的强烈电磁辐射未能开展有效的天文观测.1973年美国发射了绕月的RAE-B卫星[9],其飞行结果表明,月球背面能有效屏蔽来自地球的射电信号,是目前开展超长波观测的最佳选择.
环月超长波干涉仪(以下简称为“干涉仪”)正是利用了月球屏蔽来自地球与太阳的射电干扰的轨道弧段,对产生自黑暗时代的超长波进行观测.由于干涉仪有效载荷工作时,其平台位于月球的背面,无法接收地面测控信号,这就要求干涉仪具有自主预报何时进出其最佳探测区域的能力.
为保证预报精度,日地月星的相对位置的导出采用数值方法,即采用喷气推挤实验室(JPL)高精度星历DE421实时导出日地月相对位置,采用STK软件HPOP模型导出干涉仪相对月球的位置.实际任务中星上虽可以存储日地月相对位置的数值解并进行一定精度的轨道预报,但无法解析地计算干涉仪何时进出最佳探测区域,需要采用适当的方法在时间维度上搜索进出最佳探测区域的时刻,因此该问题的实质为一维边界搜索.常用的试探性一维搜索[10-13]方法如二分法[14-15]、黄金分割法[16]与斐波那契法[17]都被用于寻找单变量函数在某一区间的极值,并且函数值往往是连续的.上述方法难以直接套用于一维边界搜索问题,因此本文设计了改进的二分法搜索、黄金分割法搜索与斐波那契法搜索.其中改进的斐波那契法的区间收敛方式与改进黄金分割法相似,仅是生成试探点时采用了斐波那契数列,比较了上述3种方法对该问题的搜索效率.
1 最佳探测区域几何描述干涉仪环月轨道中月球同时遮挡太阳与地球射电辐射的弧段定义为最佳探测区域,如图 1所示.所以干涉仪位于最佳探测区域的时间段为其处于太阳辐射阴影时间与地球辐射阴影时间的重合部分.这里的辐射阴影指的是本影.

|
图 1 最佳探测区域示意 Figure 1 Diagram of the best observation region |
以太阳或者地球作为光源(辐射源)计算由月球遮挡产生的阴影时,为保证精度对太阳辐射阴影使用平行光源模型[18-19], 而对地球辐射阴影则应使用球形光源模型[20-22].若判断干涉仪同时位于太阳辐射阴影与地球辐射阴影内,则可认为干涉仪位于最佳探测区域.
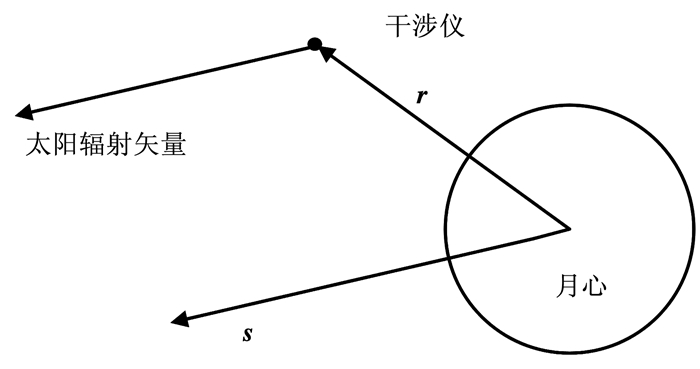
首先介绍判断干涉仪是否位于太阳辐射阴影的方法.由于假设来自太阳的辐射为平行光,则如图 2所示,在月心系下,干涉仪处太阳辐射的方向与相对月心的太阳矢量方向s平行.因此在月心系下干涉仪处的太阳辐射直线方程可表示为
| $ \frac{{x - {r_1}}}{{{s_1}}} = \frac{{y - {r_2}}}{{{s_2}}} = \frac{{z - {r_3}}}{{{s_3}}}, $ | (1) |
|
图 2 平行光模型示意 Figure 2 Diagram of parallel light source model |
式中:rj、sj(j=1, 2, 3)分别为干涉仪相对月心位置矢量r与太阳相对月心位置矢量s在月心系下的分量.
将式(1)代入以下月球球面方程:
| ${x^2} + {y^2} + {z^2} = R_{\rm{m}}^2, $ |
式中Rm为月球平均半径.
由此可得:
| $ {x^2} + {\left[{{s_2}/{s_1}\left( {x-{r_1}} \right) + {r_2}} \right]^2} + {\left[{{s_3}/{s_1}\left( {x-{r_1}} \right) + {r_3}} \right]^2} = R_{\rm{m}}^2. $ |
该方程表示过干涉仪位置的太阳光线与月球相交的部分,若该相交部分存在并且月球位于太阳与干涉仪之间,即r·s<0,则可认为干涉仪位于太阳辐射阴影.同时为了判断相交部分是否存在,上式可以整理为一般一元二次方程的形式为
| $ {\mathit{A}_{\rm{s}}}{x^2} + {\mathit{B}_{\rm{s}}}x + {\mathit{C}_{\rm{s}}} = 0, $ |
式中As、Bs、Cs仅为了方程表述简洁,并无特殊物理意义,具体如下式
| $ \left\{ \begin{array}{l} {A_{\rm{s}}} = R_{\rm{m}}^2\left( {1 + {{\left( {\frac{{{s_2}}}{{{s_1}}}} \right)}^2} + {{\left( {\frac{{{s_3}}}{{{s_1}}}} \right)}^2}} \right),\\ {B_{\rm{s}}} = 2R_{\rm{m}}^2\left( {\left( {{r_2} - \frac{{{s_2}}}{{{s_1}}}{r_1}} \right)\frac{{{s_2}}}{{{s_1}}} + \left( {{r_3} - \frac{{{s_3}}}{{{s_1}}}{r_1}} \right)\frac{{{s_3}}}{{{s_1}}}} \right),\\ {C_{\rm{s}}} = R_{\rm{m}}^2\left( {{{\left( {{r_2} - \frac{{{s_2}}}{{{s_1}}}{r_1}} \right)}^2} + {{\left( {{r_3} - \frac{{{s_3}}}{{{s_1}}}{r_1}} \right)}^2}} \right) - R_{\rm{m}}^4. \end{array} \right. $ | (2) |
若Bs2-4AsCs>0,即相交部分存在,并且r·s<0,则可认为干涉仪进入了太阳辐射阴影.
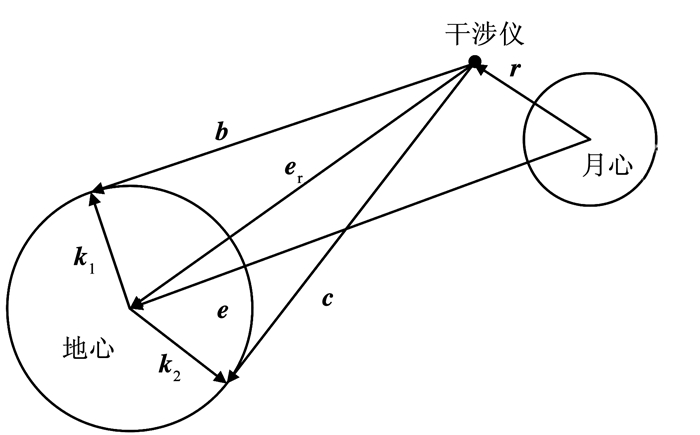
对于地球辐射阴影,如图 3所示,在干涉仪月心与地心确定的平面内,干涉仪处到地球圆形边界的两条切线为地球辐射到达干涉仪处的极限“光线”,设这两条“光线”的方向矢量分别为b与c,而这两条极限“光线”在月心系下的直线方程为:
| $ \frac{{x - {r_1}}}{{{b_1}}} = \frac{{y - {r_2}}}{{{b_2}}} = \frac{{z - {r_3}}}{{{b_3}}}, $ | (3) |
| $ \frac{{x - {r_1}}}{{{c_1}}} = \frac{{y - {r_2}}}{{{c_2}}} = \frac{{z - {r_3}}}{{{c_3}}}, $ | (4) |
|
图 3 球光源模型示意 Figure 3 Diagram ofspherical light source model |
式中:bj、cj(j=1, 2, 3)分别为矢量b与c在月心下的坐标.
同时可由已知的地心相对月心的矢量e与干涉仪矢量r,求出地心相对干涉仪的矢量er:
| $ {\mathit{\boldsymbol{e}}_{\rm{r}}} = \mathit{\boldsymbol{e}} - \mathit{\boldsymbol{r}}. $ |
此外,设地心到两条极限“光线”与地球边界的切点的矢量分别为k1与k2(由于地月距离遥远k1与k2近似为共线):
| $ \begin{array}{l} {\mathit{\boldsymbol{k}}_1} = -\frac{{ \mathit{\boldsymbol{r}} \times \mathit{\boldsymbol{e}} \times {\mathit{\boldsymbol{e}}_{\rm{r}}}}}{{\left| {\mathit{\boldsymbol{r}} \times \mathit{\boldsymbol{e}} \times {\mathit{\boldsymbol{e}}_{\rm{r}}}} \right|}}{\mathit{R}_{\rm{e}}}, \\ {\mathit{\boldsymbol{k}}_2} = \frac{{\mathit{\boldsymbol{r}} \times \mathit{\boldsymbol{e}} \times {\mathit{\boldsymbol{e}}_{\rm{r}}}}}{{\left| {\mathit{\boldsymbol{r}} \times \mathit{\boldsymbol{e}} \times {\mathit{\boldsymbol{e}}_{\rm{r}}}} \right|}}{\mathit{R}_{\rm{e}}}, \end{array} $ |
式中:Re为地球平均半径.
由此便通过以下表达式求得b与c矢量在月心下的坐标分量:
| $ \begin{array}{l} \mathit{\boldsymbol{b}} = {\mathit{\boldsymbol{e}}_{\rm{r}}} + {\mathit{\boldsymbol{k}}_1}, \\ \mathit{\boldsymbol{c}} = {\mathit{\boldsymbol{e}}_{\rm{r}}} + {\mathit{\boldsymbol{k}}_2}. \end{array} $ |
最后将式(3)、(4)代入月球球面方程(1)可得:
| $ \begin{array}{l} {x^2} + {\left[{{b_2}/{b_1}\left( {x-{r_1}} \right) + {r_2}} \right]^2} + {\left[{{b_3}/{b_1}\left( {x-{r_1}} \right) + {r_3}} \right]^2} = R_{\rm{m}}^2, \\ {x^2} + {\left[{{c_2}/{c_1}\left( {x-{r_1}} \right) + {r_2}} \right]^2} + {\left[{{c_3}/{c_1}\left( {x-{r_1}} \right) + {r_3}} \right]^2} = R_{\rm{m}}^2. \end{array} $ |
上述方程同样可以整理为一般一元二次方程的形式,其系数表达形式与式(2)相同不再赘述:
| $ \begin{array}{l} {A_{\rm{b}}}{x^2} + {B_{\rm{b}}}x + {C_{\rm{b}}} = 0, \\ {A_{\rm{c}}}{x^2} + {B_{\rm{c}}}x + {C_{\rm{c}}} = 0. \end{array} $ |
若以上一元二次方程的根判别式均大于等于零,且r·e<0,则可认为干涉仪完全进入地球辐射阴影.
综上所述,若干涉仪同时位于太阳辐射阴影与地球辐射阴影,即满足以下不等式,则可认为干涉仪位于最佳探测区域为:
| $ \left\{ \begin{array}{l} B_{\rm{s}}^2 - 4{A_{\rm{s}}}{C_{\rm{s}}} \ge 0, \\ B_{\rm{b}}^2 - 4{A_{\rm{b}}}{C_{\rm{b}}} \ge 0, \\ B_{\rm{c}}^2 - 4{A_{\rm{c}}}{C_{\rm{c}}} \ge 0;\\ \mathit{\boldsymbol{r}}\cdot\mathit{\boldsymbol{s}} < 0, \\ \mathit{\boldsymbol{r}}\cdot\mathit{\boldsymbol{e}} < 0. \end{array} \right. $ |
为了校核本文提出快速预报方法的正确性,以STK软件所得结果作为对照,但STK中未将地球视为球光源,仅可将太阳与地球设为星座,即将太阳与地球都视为空间点光源故此以下简略介绍判断干涉仪进入点光源阴影的方法.
如图 4所示,在月心系下由干涉仪位置矢量r,地球矢量e与太阳矢量s,可得干涉仪处表示地球辐射方向与太阳辐射方向的矢量er与sr为:
| $ \begin{array}{l} {\mathit{\boldsymbol{e}}_{\rm{r}}} = \mathit{\boldsymbol{e}} - \mathit{\boldsymbol{r}}, \\ {\mathit{\boldsymbol{s}}_{\rm{r}}} = \mathit{\boldsymbol{s}} - \mathit{\boldsymbol{r}}, \end{array} $ |

|
图 4 点光源模型示意 Figure 4 Diagram of point light source model |
由此可得干涉仪处表示地球辐射与太阳辐射的直线方程:
| $\frac{{x - {r_1}}}{{{e_{{\rm{r}}1}}}} = \frac{{y - {r_2}}}{{{e_{{\rm{r}}2}}}} = \frac{{z - {r_3}}}{{{e_{{\rm{r}}3}}}}, $ | (5) |
| $ \frac{{x - {r_1}}}{{{s_{{\rm{r}}1}}}} = \frac{{y - {r_2}}}{{{s_{{\rm{r}}2}}}} = \frac{{z - {r_3}}}{{{s_{{\rm{r}}3}}}}, $ | (6) |
式中:erj、srj(j=1, 2, 3)分别为矢量er与sr在月心系下的分量.
将式(5)、(6)代入月球球面方程(1)可得:
| $ \begin{array}{l} {x^2} + {[{e_{{\rm{r2}}}}/{e_{{\rm{r1}}}}\left( {x-{r_1}} \right) + {r_2}\left] {^2 + } \right[{e_{{\rm{r3}}}}/{e_{{\rm{r1}}}}\left( {x-{r_1}} \right) + {r_3}]^2} = R_{\rm{m}}^2, \\ {x^2} + {[{s_{{\rm{r2}}}}/{s_{{\rm{r1}}}}\left( {x-{r_1}} \right) + {r_2}\left] {^2 + } \right[{s_{{\rm{r3}}}}/{s_{{\rm{r1}}}}\left( {x-{r_1}} \right) + {r_3}]^2} = R_{\rm{m}}^2, \end{array} $ |
以上方程同样可整理为一元二次方程的形式:
| $ \begin{array}{l} {A_{\rm{e}}}{x^2} + {B_{\rm{e}}}x + {C_{\rm{e}}} = 0, \\ {A_{\rm{s}}}{x^2} + {B_{\rm{s}}}x + {C_{\rm{s}}} = 0, \end{array} $ |
则点光源模型下判断干涉仪进入最佳探测区域的判别式如下:
| $ \left\{ \begin{array}{l} B_{\rm{e}}^2 - 4{A_{\rm{e}}}{C_{\rm{e}}} \ge 0, \\ B_{\rm{s}}^2 - 4{A_{\rm{s}}}{C_{\rm{s}}} \ge 0, \\ \mathit{\boldsymbol{r}}\cdot\mathit{\boldsymbol{e}} < 0, \\ \mathit{\boldsymbol{r}}\cdot\mathit{\boldsymbol{s}} < 0. \end{array} \right. $ |
本文针对关于进出最佳探测区域时刻预报的一维边界搜索问题改进了常用的二分法、黄金分割法与斐波那契法,其中改进黄金分割法与斐波那契法的流程类似.
由于日地相对月球运动的角速度于干涉仪相对月球运动的角速度相差2~3个量级,可以认为较短时间内(如,一个轨道周期)内干涉仪的最佳探测区域固定不变,即在轨道周期内干涉仪至多只存在一次进入最佳探测区域的机会.由此无论采用何种搜索算法,最多仅有一次进出最佳探测区域的情况.
改进二分法搜索首先在轨道周期内快速确定存在进入或离开最佳探测区域时刻的区间,再采用传统二分法的收敛方式精确定位进出最佳探测区域的时刻,具体流程如下如图 5所示.

|
图 5 改进二分法搜索流程 Figure 5 Improved binary search workflow |
Step 1 给定轨道周期起始时刻ts与终止时刻te(一般情况在ts与te干涉仪不位于最佳探测区域),计算轨道周期中点时刻tmid.
Step 2 判断干涉仪在时刻tmid是否位于最佳探测区域,是则令tr=tmid,tr1=ts,tr2=te并转入Step5,否则转入Step3.
Step 3 由小到大排序已经判断干涉仪不位于最佳探测区域的时刻(如第1次转入Step3时有3个时刻, 即ts、tmid、te,并排序为t1, t2, t3,第k次转入Step3则有2k+1个时刻,2k个区间), 转入Step4.
Step 4 依次判断Step3中2k个区间的中点时刻上干涉仪是否位于最佳探测区域,记录第1个干涉仪位于最佳探测区的中点时刻tr与其所在区间的边界时刻tr1与tr2,转入Step5;若所有新产生的中点时刻上干涉仪都不位于最佳探测区域,且区间长度大于要求精度,则转回Step3,否则认为在该轨道周期内不存在最佳探测区域,结束搜索流程.
Step 5 对区间[tr1, tr]与[tr, tr2]分别使用二分法精确搜索函数(其流程见图 5)可分别得到该轨道周期内干涉仪进出最佳探测区域的时刻tin与tout.
在上述流程中使用了二分法精确搜索函数,其流程框图如图 6所示.在二分法精确搜索函数中使用了G(t)函数,本函数的作用为干涉仪是否位于最佳探测区域,其中日地月的相对位置由JPL高精度星历DE421给出,干涉仪相对月球位置由STK轨道外推模型HPOP给出,G(t)的表达式如下
| $ G\left( t \right) = \left\{ \begin{array}{l} 1, {\text{干涉仪在}}t{\text{时刻位于最佳探测区域}};\\ 0, {\text{干涉仪在}}t{\text{时刻不位于最佳探测区域}}. \end{array} \right. $ |
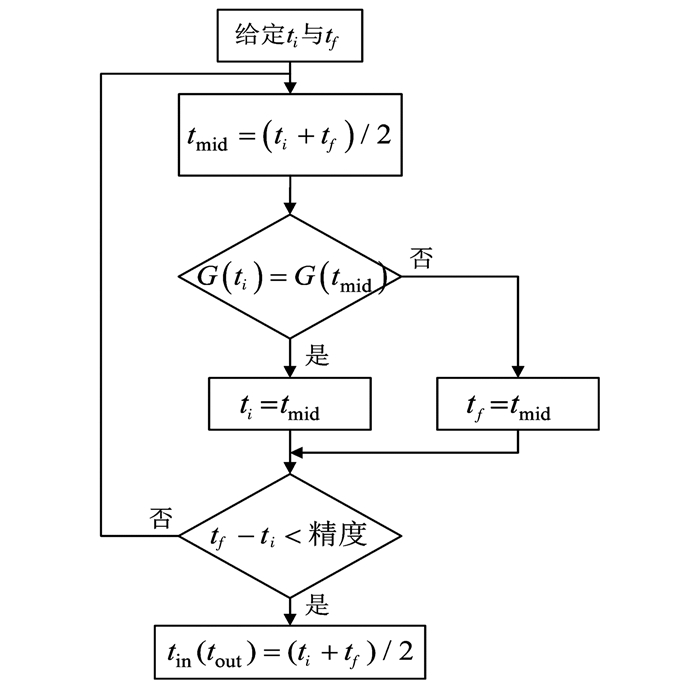
|
图 6 二分法精确搜索函数流程 Figure 6 Workflow of accurate binary search function |
由于改进黄金分割法与斐波那契法的搜索流程类似,这里着重介绍黄金分割法的搜索流程.
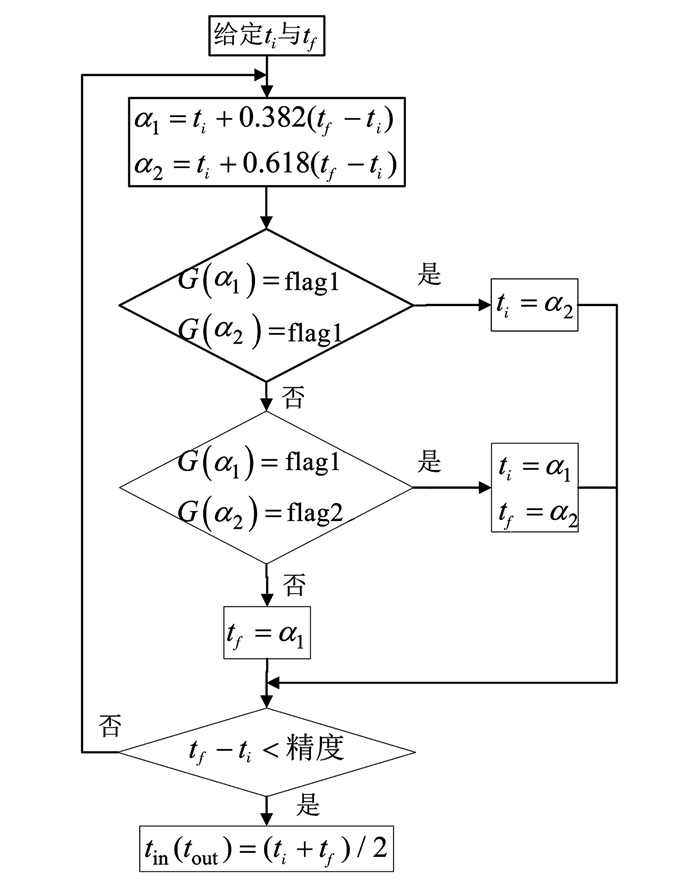
改进黄金分割法首先以黄金分割比例划分搜索区间,快速存在进入或离开最佳探测区域时刻的小区间后,在以传统黄金分割法的收敛方式精确搜索干涉仪进出最佳探测区域的时刻,其流程框图如图 7、8所示.
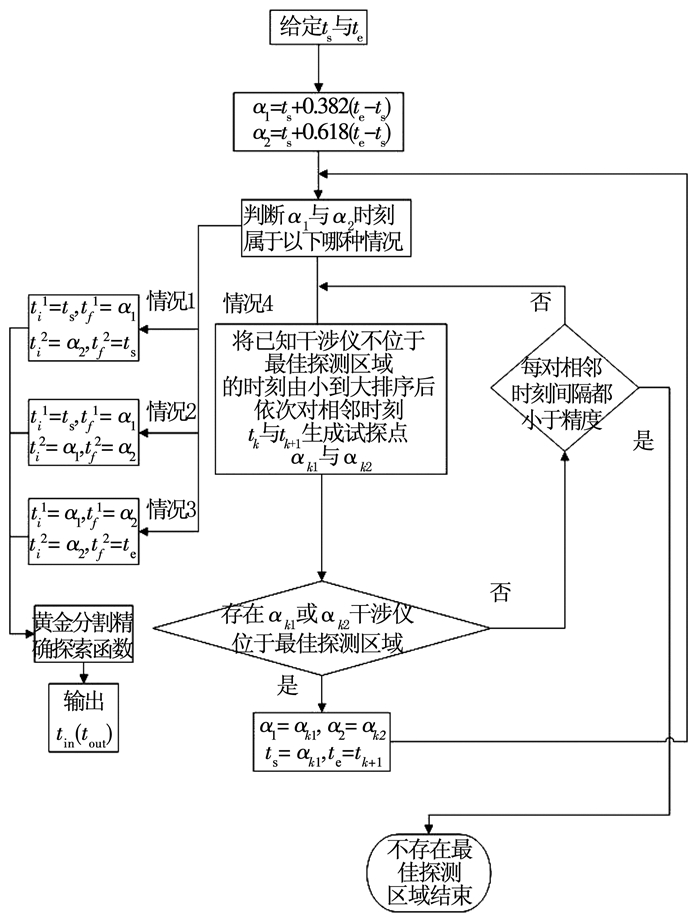
|
图 7 改进黄金分割法搜索流程 Figure 7 Improved golden section search workflow |
|
图 8 黄金分割精确搜索函数流程 Figure 8 Workflow of golden section search function |
图 7中情况1表示在α1与α2时刻干涉仪均位于最佳探测区域,情况2表示仅α1时刻干涉仪均位于最佳探测区域,情况3表示仅α2时刻干涉仪均位于最佳探测区域,情况4表示在α1与α2时刻干涉仪均不位于最佳探测区域.
此外改进斐波那契搜索的流程与以上流程基本相同,只是α1与α2生成采用了斐波那契数列,具体公式如下
| $ \left\{ \begin{array}{l} {F_1} = 1, \\ {F_2} = 2, \\ {F_n} = {F_{n - 1}} + {F_{n - 2}}, \\ {\alpha _1} = {t_{\rm{s}}} + {F_{n - 2}}/{F_n}({t_{\rm{e}}} - {t_{\rm{s}}}), \\ {\alpha _2} = {t_{\rm{s}}} + {F_{n - 1}}/{F_n}({t_{\rm{e}}} - {t_{\rm{s}}}), \end{array} \right. $ |
式中:n为搜索循环的次数.
3 结果与分析为了比较改进二分法、改进黄金分割法与斐波那契法3种一维搜索方法的效率,本文对任务轨道连续10个轨道周期进行了仿真.仿真中发现每种搜索方法搜索时间近似与该方法调用G函数的次数成正比,即认为调用G函数次数少的方法效率更高.
仿真轨道历元时间为25 Jul 2018 00:00:00.000.仿真在STK中月球Inertial坐标系下初始轨道根数见表 1.
| 表 1 历元轨道根数 Table 1 Epoch orbit elements |
由于3种搜索方法相比STK仿真结果的误差均在4 s以内,并且误差量级相同.因此仅给出改进二分法的预报结果,见表 2,表中的结果为干涉仪进出最佳探测区域相对轨道历元的时刻.3种搜索方法仿真的结果相比STK软件仿真结果的误差的绝对值如图 9、10所示.
| 表 2 二分法搜索的结果 Table 2 Result of the binary search |

|
图 9 仿真进入时刻相比STK的误差绝对值 Figure 9 Absolute error of entry times |

|
图 10 仿真离开时刻相比STK的误差绝对值 Figure 10 Absolute error of departure times |
图 11给出在这10个轨道周期的仿真中分别使用改进的二分法、斐波那契法与黄金分割法进行搜索时调用G函数的次数与程序运行时间.

|
图 11 3种搜索方法调用G函数次数 Figure 11 Number of times that the G function is called |
二分法的调用G函数的次数为348次,比黄金分割法与斐波那契法分别少了224次与228次.此外二分法的搜索时间为0.876 s,而其余两种方法分别使用了1.447、1.484 s.如果以程序运行时间倒数作为效率的指标,则改进二分法的效率为其余两种方法的1.65倍左右.
此外为了辨明改进二分法在粗略搜索部分还是在精细搜索部分由于其他两种方法,以下分别给出了3种方法在粗略搜索与精细搜索时调用G函数的次数与运行时间.
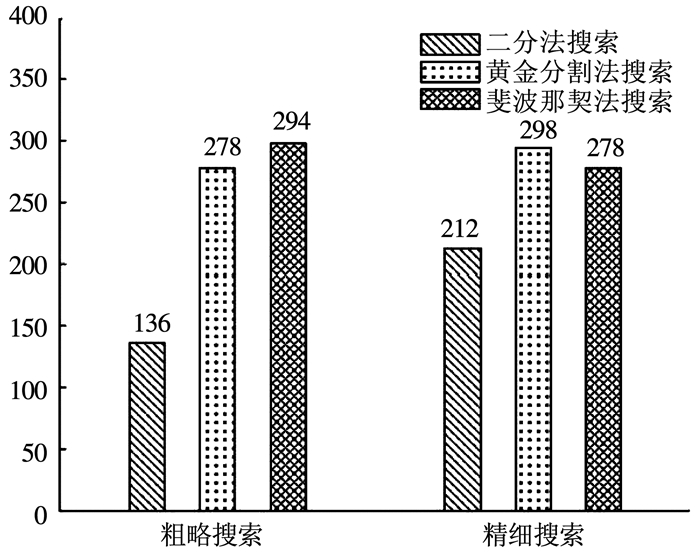
由图 12可知,在粗略搜索中改进二分法调用G函数的次数为136次,而其余两种方法则为278次与298次;在精确搜索中二分法、黄金分割法与斐波那契法调用G函数的次数为212次、294次与278次.
|
图 12 在精细搜索与粗略搜索中不同方法调用G函数次数 Figure 12 Number of times that the G function is called in accuratesearch and rough search |
1) 3种搜索方法相比STK仿真结果的误差均在±4 s以内,并且误差量级相同.
2) 在粗略搜索还是精确搜索中改进二分法都要优于其余两种方法,在粗搜索中改进二分法的计算量小于其余两种方法的0.5倍,而在精细搜索中改进二分法的计算量为其余两种方法的0.7倍左右.
3) 改进二分法的搜索时间与计算量均为斐波那契法与黄金分割法的0.6倍.因此可认为改进二分法的效率是其余两种方法的两倍左右,适合用于环月超长波自主快速预报最佳探测区域.
| [1] |
冯珑珑, 向守平. 宇宙微波背景辐射的观测和理论[J]. 天文学进展, 1999, 17(4): 357. FENG Longlong, XIANG Shouping. The observation and theory of the cosmic microwave background radiation[J]. Progress in Astronomy, 1999, 17(4): 357. |
| [2] |
邓雪梅. 夸克和宇宙[J]. 世界科学, 2007(6): 2. DENG Xuemei. The quark and the universe[J]. Worldwide Science, 2007(6): 2. DOI:10.3969/j.issn.1000-0968.2007.06.001 |
| [3] |
VANGIONI E, OLIVE K A, PRESTEGARD T, et al. The impact of star formation and gamma-ray burst rates at high redshift on cosmic chemical evolution and reionization[J]. Monthly Notices of the Royal Astronomical Society, 2015, 447(3): 2575. DOI:10.1093/mnras/stu2600 |
| [4] |
SAZONOV S, SUNYAEV R. Preheating of the universe by cosmic rays from primordial supernovae at the beginning of cosmic reionization[J]. Monthly Notices of the Royal Astronomical Society, 2015, 454(4): 3464. DOI:10.1093/mnras/stv2255 |
| [5] |
CHEN Xuelei, KAMIONKOWSKI M. Particle decays during the cosmic dark ages[J]. Physical Review D, 2004, 70(4): 0453502-1. DOI:10.1103/PhysRevD.70.043502 |
| [6] |
PRITCHARD J R, LEOB A. 21 cm cosmology in the 21st century[J]. Report on Progress in Physics, 2012, 75(8): 1. DOI:10.1088/0034-4885/75/8/086901 |
| [7] |
LIU A, PARSONS A R. Constraining cosmology and ionization history with combined 21 cm power spectrum and global signal measurements[J]. Monthly Notices of the Royal Astronomical Society, 2016, 457(2): 1864. DOI:10.1093/mnras/stw071 |
| [8] |
林荣刚.复杂天候环境下集群式车载通信系统天线间干扰分析[D].西安: 西安电子科技大学, 2007 LIN Ronggang. Analysis for the antenna interference of multi-vehicular communication system in spatial weather[D]. Xi'an: Xidian University, 2007 http://cdmd.cnki.com.cn/article/cdmd-10701-2007048886.htm |
| [9] |
NOVACO J C, BROWN L W. Nonthermal galactic emission below 10 megahertz[J]. Astrophysical Journal, 1978, 221(1): 114. DOI:10.1086/156009 |
| [10] |
龚建华. 深度优先搜索算法及其改进[J]. 现代电子技术, 2007(22): 90. GONG Jianhau. Depth first search algorithm and its improvement[J]. Modern Electronic Technique, 2007(22): 90. DOI:10.3969/j.issn.1004-373X.2007.22.032 |
| [11] |
陈宝林. 最优化理论与算法[M]. 北京: 清华大学出版社, 2006: 95. CHEN Baolin. Theory and algorithms of optimization[M]. Beijing: Tsinghua University Press, 2006: 95. |
| [12] |
朱训芝.关于一维搜索某些问题的研究[D].大连: 大连理工大学, 2005 ZHU Xunzhi. Research on some problems of one dimension search[D]. Dalian: Dalian University of Technology, 2005 http://cdmd.cnki.com.cn/Article/CDMD-10141-2005070916.htm |
| [13] |
DAI Y H. On the nonmonotone line search[J]. Journal of Optimization Theory and Applications, 2002, 112(2): 315. DOI:10.1023/A:1013653923062 |
| [14] |
王海涛, 朱洪. 改进的二分法查找[J]. 计算机工程, 2006, 32(10): 60. WANG Haitao, ZHU Hong. Modified binary search[J]. Computer Engineering, 2006, 32(10): 60. DOI:10.3969/j.issn.1000-3428.2006.10.022 |
| [15] |
KIEFER J. Sequential minimax search for a maximum[J]. Proceedings of the American Mathematical Society, 1953, 4(3): 502. DOI:10.2307/2032161 |
| [16] |
PARDALOS P M, RESENDE G C. Handbook of applied optimization[M]. Oxford: Oxford University Press, 2002: 35.
|
| [17] |
MORDECAI A, WILDE D J. Optimality proof for the symmetric fibonacci search technique[J]. Fibonacci Quarterly, 1966, 4(1): 265. |
| [18] |
李运泽, 宁献文, 王晓明, 等. 纳卫星轨道热环境仿真分析[J]. 系统仿真学报, 2007, 19(14): 3166. LI Yunze, NING Xianwen, WANG Xiaoming, et al. Simulating analysis of nano-satellite's orbital thermal environment[J]. Journal of System Simulation, 2007, 19(14): 3166. DOI:10.16182/j.cnki.joss.2007.14.010 |
| [19] |
侯增祺, 胡金刚. 航天器热控制技术—原理及其应用[M]. 北京: 中国科学技术出版社, 2008: 329. HOU Zengqi, HU Jingang. The principle and application of spacecraft thermal control technology[M]. Beijing: China Science & Technology Press, 2008: 329. |
| [20] |
KULSHRESTHA S, BHASKAR M K. Moon shadow eclipse prediction of a lunar orbiting spacecraft[J]. International Research Journal of Engineering and Technology, 2015, 2(4): 1545. |
| [21] |
SRIVASTAVA V K, ASHUTOSH, PITCHAIMANI M, et al. Eclipse prediction methods for LEO satellites with cylindrical and cone geometries[J]. Astronomy and Computing, 2013(2): 11. DOI:10.1016/j.ascom.2013.06.001 |
| [22] |
SRIVASTAVA V K, KUMAR J, KULSHRESTHA S, et al. Lunar shadow eclipse prediction models for the earth orbiting spacecraft: comparison and application to LEO and GEO spacecrafts[J]. Acta Astronautica, 2015, 11: 206. DOI:10.1016/j.actaastro.2015.01.020 |
 2018, Vol. 50
2018, Vol. 50


