2. 水下机器人技术重点实验室(哈尔滨工程大学),哈尔滨 150001
2. Science and Technology on Underwater Vehicle Laboratory(Harbin Engineering University), Harbin 150001, China
随着航天器结构设计需求趋于轻型化,大挠性空间桁架结构的应用日趋广泛,如国际空间站[1]、日本月亮女神号探月卫星[2]、日本工程试验卫星ETS-Ⅷ[3]等都充分采用了桁架结构.随着压电智能材料的出现,人们开始考虑实现挠性结构的减振控制,压电堆式传感器/作动器一体化智能桁架结构具有重要的应用前景[4].鉴于桁架结构普遍具有的低阻尼、大柔性等特性,在轨运行时容易受到内部或外界的干扰而产生大幅度的振荡,从而影响航天器的正常工作.因此对挠性空间桁架结构开展减振研究具有一定的工程实际意义.
早期主要采用的振动抑制方法是不需要外界提供能量的被动方法[5].但被动减振方法的适用性较差,在控制精度方面也低于主动减振方法.针对挠性结构的主动减振控制需求,可以与多种控制方法结合[6].例如文献[7]采用输入成型方法对航天器残余振动进行抑制,并结合自适应滑模控制技术处理模态参数不确定性问题,有效提高了控制器在挠性航天器姿态机动过程中的挠性振动抑制能力,但所采用的线性滑模面对复杂非线性系统的可操作性较低.文献[8]针对挠性结构设计了改进型H∞正位置反馈控制器和正速度反馈控制器,并在铝制悬臂梁上验证了控制器的振动抑制能力.但由于H∞控制考虑的是系统不确定性最严重的情况,因此具有一定的保守性.文献[9]将自抗扰控制方法与自适应技术结合,对参数选取过程进行合理简化,使系统各通道实现了解耦控制,针对三棱柱智能桁架结构展开主动振动抑制并获得了良好的控制效果,但自抗扰控制本质是一种改进的PID控制,因此控制性能可以进一步提高.文献[10]将动力吸振器安装在三棱柱桁架的顶端,利用ARX模型辨识桁架结构的动力学模型,采用自适应最小均方算法获得其逆模型,进而设计主动振动控制律,并使用DSPACE装置验证了该方法的有效性,但最小均方算法的固定步长特性导致收敛速度较慢,且收敛速度的提高将导致稳态误差增大.
值得说明的是,上述已有结果在处理桁架振动时会导致控制溢出问题,独立模态空间控制(independent modal space control, IMSC)对该问题具有较好的抑制效果,其中模态滤波器可有效降低观测溢出,且使控制系统的复杂程度降低,因此可将多种控制方法与IMSC结合设计振动抑制方法.文献[11]基于LQR和IMSC方法设计智能桁架结构的主动振动抑制控制律.但LQR方法需要获得控制对象的精确数学模型,而实际建立的数学模型一般都具有建模误差.作为一种不依赖对象精确数学模型的控制方法,模糊控制也广泛应用于桁架的振动抑制控制中,文献[12]针对压电旋转桁架结构提出了一种独立于位置跟踪控制的振动抑制模糊控制器,并结合遗传算法优化控制增益,保证系统的稳定性.然而现有的大多数成果都需要较长时间令桁架结构的振动收敛,而有限时间控制具有更好的控制性能和鲁棒性.因此本文主要研究一种在有限时间内实现桁架结构减振的控制方法.
动态补偿线性化技术在处理复杂非线性系统方面具有普遍应用,该技术把系统的总干扰有效补偿,从而简化控制对象形式,降低控制器设计难度.文献[13]将Stewart平台的动力学模型基于这一技术进行简化,并采用PD控制有效抑制了挠性振动.文献[14]针对无速度反馈的挠性航天器采用这一技术降低了高精度姿态跟踪控制器的设计难度.终端滑模控制可以保证系统状态的有限时间收敛,并具有较好的鲁棒性和抗干扰特性,近年来在挠性结构振动抑制控制方面得到了广泛的应用.文献[15]设计了一种连续非奇异终端滑模控制器,并实现了双连杆柔性机械臂系统的有限时间关节角轨迹跟踪控制.文献[16]采用双闭环结构设计了一种快速终端滑模控制器实现了挠性航天器的高精度指向控制.
针对空间智能桁架结构的振动抑制问题,本文基于IMSC方法,结合动态补偿线性化思想设计了基于终端滑模的有限时间控制器.首先,建立桁架结构的动力学模型.然后,设计模态滤波器和状态观测器,利用观测器对系统总干扰进行实时估计的特点,采用动态补偿线性化的思想将桁架动力学模型进行简化,并提出了一种结合双幂次趋近律与终端滑模面的有限时间控制器.仿真结果表明,本文提出的算法能够在有限时间内对空间智能桁架结构实现较好的振动抑制效果.
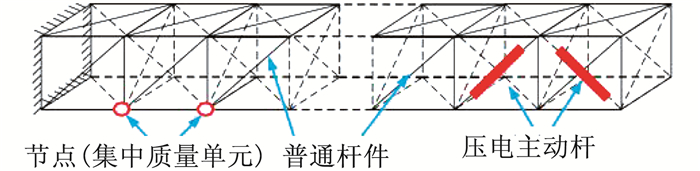
1 空间智能桁架结构的动力学建模本文以如图 1所示的一字型空间智能桁架模型(截面构型为正方形)为研究对象,作动器/传感器配置采用文献[17]的方案,基于有限元方法建立桁架的动力学模型:
| $ \mathit{\boldsymbol{M\ddot \delta }} + \mathit{\boldsymbol{C\dot \delta }} + \mathit{\boldsymbol{K\delta }} = {\mathit{\boldsymbol{B}}_d}{\mathit{\boldsymbol{F}}_d} + {\mathit{\boldsymbol{B}}_c}{\mathit{\boldsymbol{F}}_c}. $ | (1) |
|
图 1 空间智能桁架简化模型 Figure 1 Simplified model of space intelligent truss |
式中:δ∈
考虑在工程实际中高频模态难以被激起,因此对其进行模态截断处理,根据振型的叠加原理可以得到:
| $ \mathit{\boldsymbol{\delta }} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_\mathit{\boldsymbol{c}}}\mathit{\boldsymbol{q}}. $ | (2) |
式中:q为模态坐标向量;Φc为由系统的前nc阶质量归一化的振型构成的受控模态集(模态矩阵).
令式(1)等号两侧同时左乘ΦcT,由于M=ΦcTMΦc=diag[1],可以得到如下形式
| $ \mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{\bar C\dot q}} + \mathit{\boldsymbol{\bar Kq}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c^{\rm{T}}{\mathit{\boldsymbol{B}}_d}{\mathit{\boldsymbol{F}}_d} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c^{\rm{T}}{\mathit{\boldsymbol{B}}_c}{\mathit{\boldsymbol{F}}_c}, $ | (3) |
其中:
| $ \mathit{\boldsymbol{\bar C}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c^{\rm{T}}\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c} = {\rm{diag}}\left[ {2{\xi _i}{\omega _i}} \right], $ |
| $ \mathit{\boldsymbol{\bar K}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c^{\rm{T}}\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c} = {\rm{diag}}\left[ {\omega _i^2} \right],i = 1,2, \cdots ,{n_c}. $ |
式中:ξi、ωi分别为第i阶系统振动的阻尼比和固有频率;ΦcTBdFd、ΦcTBcFc分别为系统受到的nc×1维的模态干扰力和模态控制力.
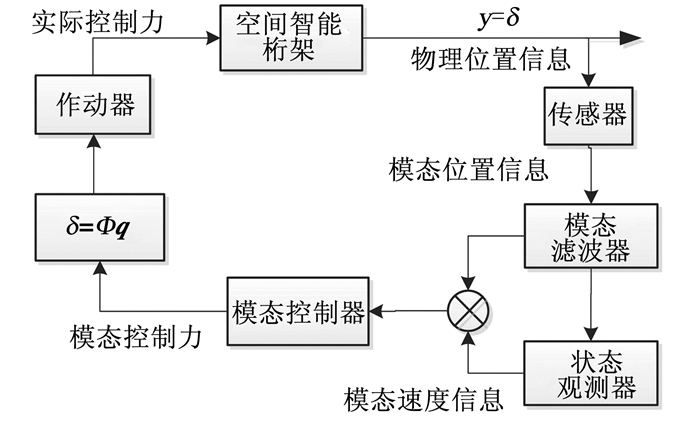
2 基于IMSC方法的终端滑模控制IMSC方法实现了抑制结构振动和控制各阶模态响应之间的转化,可以在不对其他模态产生影响的前提下仅对特定模态设计控制律.IMSC的具体流程如图 2所示,其中模态滤波器建立模态坐标与物理坐标的转换关系,状态观测器结合位置信息求取速度信息,最后对各阶模态分别设计控制器.
|
图 2 IMSC方法流程 Figure 2 Flow chart of IMSC method |
由式(2)可知,桁架结构的实际物理信息可以表示为模态信息的线性叠加,根据模态正交性和模态矩阵归一化等运算,得到如下转换方程:
| $ \mathit{\boldsymbol{q}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c^{\rm{T}}\mathit{\boldsymbol{M\delta }} = {\mathit{\boldsymbol{\psi }}^{\rm{{\rm T}}}}\mathit{\boldsymbol{\delta }} = \sum\limits_{i = 1}^n {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_i^{\rm{T}}{\mathit{\boldsymbol{\delta }}_i}} . $ |
式中:Ψi为第i阶模态滤波器向量,Φ为模态振型矩阵.
则模态滤波器表示为
| $ {\mathit{\boldsymbol{\psi }}^{\rm{{\rm T}}}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{M}}. $ | (4) |
模态滤波器可将空间桁架的实际物理信息转化为模态信息,但是在桁架结构上只安装有位置传感器,因此要采用扩张状态观测器(extended state observer, ESO)求取模态速度信息,从而实现振动抑制控制律的设计.
设x1=q, x2=
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot x}}}_1} = {\mathit{\boldsymbol{x}}_2},\\ {{\mathit{\boldsymbol{\dot x}}}_2} = - \mathit{\boldsymbol{\bar K}}{\mathit{\boldsymbol{x}}_1} - \mathit{\boldsymbol{\bar C}}{\mathit{\boldsymbol{x}}_2} + \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c^{\rm{T}}{\mathit{\boldsymbol{B}}_c}{\mathit{\boldsymbol{F}}_c} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_c^{\rm{T}}{\mathit{\boldsymbol{B}}_d}{\mathit{\boldsymbol{F}}_d},\\ \mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{x}}_1}. \end{array} \right. $ | (5) |
令x3=-Kx1-Cx2+ΦcTBdFd表示环境干扰和模型摄动组成的系统总干扰,b1=ΦcTBc, 式(5)可表示为
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot x}}}_1} = {\mathit{\boldsymbol{x}}_2},\\ {{\mathit{\boldsymbol{\dot x}}}_2} = {\mathit{\boldsymbol{b}}_1}{\mathit{\boldsymbol{F}}_\mathit{\boldsymbol{c}}} + {\mathit{\boldsymbol{x}}_3},\\ \mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{x}}_1}. \end{array} \right. $ | (6) |
针对式(6),构造如下形式的三阶ESO:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot {\hat x}}}}_1} = {\mathit{\boldsymbol{\hat x}}_2} - {l_1}g\left( {{{\mathit{\boldsymbol{\hat x}}}_1} - \mathit{\boldsymbol{y}}} \right),\\ {{\mathit{\boldsymbol{\dot {\hat x}}}}_2} = {b_1}{\mathit{\boldsymbol{F}}_c} + {{\mathit{\boldsymbol{\hat x}}}_3} - {l_2}g\left( {{{\mathit{\boldsymbol{\hat x}}}_1} - \mathit{\boldsymbol{y}}} \right),\\ {{\mathit{\boldsymbol{\dot {\hat x}}}}_3} = - {l_3}g\left( {{{\mathit{\boldsymbol{\hat x}}}_1} - \mathit{\boldsymbol{y}}} \right). \end{array} \right. $ | (7) |
式中:
注1 传统的ESO中,为获得较好的估计效果,函数g(z)取为
| $ \begin{array}{l} g\left( z \right) = {\rm{fal}}\left( {z,a,\sigma } \right) = \\ \;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} z{\sigma ^{a - 1}},\;\;\;\;\;\;\;\;\;\;\;\left| z \right| \le \sigma ;\\ {\left| z \right|^a}{\mathop{\rm sgn}} \left( z \right),\;\;\;\;\;\left| z \right| > \sigma . \end{array} \right. \end{array} $ |
式中:σ为线性区间的长度,a∈(0, 1).虽然fal(z, a, σ)是连续的,但并不可导.当σ的取值较小时,fal(z, a, σ)的导数将突变并导致系统的高频振荡加剧.因此将fal(z, a, σ)中的线性段部分替换成如下的连续光滑非线性函数:
| $ \begin{array}{l} g\left( z \right) = {\rm{qin}}\left( {z,a,\sigma } \right) = \\ \;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} \left( {a - 1} \right){\sigma ^{a - 3}}{z^3} - \\ \left( {a - 1} \right){\sigma ^{a - 2}}{z^2}{\mathop{\rm sgn}} \left( z \right) + \\ {\sigma ^{a - 1}}z,\;\;\;\;\;\;\;\;\left| z \right| \le \sigma ;\\ {\left| z \right|^a}{\mathop{\rm sgn}} \left( z \right),\;\left| z \right| > \sigma . \end{array} \right. \end{array} $ |
由于ESO实现了对空间智能桁架结构系统总干扰的实时估计,因此采用“动态补偿线性化”方法对模态控制力Fc作如下处理:
| $ {\mathit{\boldsymbol{F}}_c} = \mathit{\boldsymbol{b}}_1^{ - 1}\left( {u - {{\mathit{\boldsymbol{\hat x}}}_3}} \right). $ | (8) |
将式(8)带入桁架结构的动力学方程,则可将二阶非线性系统(6)转化为线性“积分器串联型”系统:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot x}}}_1} = {\mathit{\boldsymbol{x}}_2},\\ {{\mathit{\boldsymbol{\dot x}}}_2} = \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}},\\ \mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{x}}_1}. \end{array} \right. $ | (9) |
式中,d=x3-
针对系统(9),定义终端滑模面为
| $ \mathit{\boldsymbol{s}} = {\mathit{\boldsymbol{x}}_2} + {\alpha _1}{\rm{si}}{{\rm{g}}^\eta }\left( {{\mathit{\boldsymbol{x}}_1}} \right). $ |
式中:sigη(x)=|x|ηsgn(x),其中sgn(x)为x的符号函数,α1>0,η∈(0, 1).
本文为同时削弱系统抖振和提高远离滑模面时的收敛速度,采用如下形式的双幂次趋近律:
| $ \mathit{\boldsymbol{\dot s}} = - {k_1}{\rm{si}}{{\rm{g}}^\alpha }\left( \mathit{\boldsymbol{s}} \right) - {k_2}{\rm{si}}{{\rm{g}}^\beta }\left( \mathit{\boldsymbol{s}} \right). $ | (10) |
式中:α>1, 0<β<1, k1>0, k2>0.
注2 采用趋近律(10)时,在滑模面附近,k1 sigα(s)项可以忽略,则由0<β<1可知,趋近滑动模态的速度逐渐减小,抖振现象有所削减.在远离滑模面时,k2sigβ(s)项可以忽略,则由于α>1,趋近滑模面的速度将加快,因此会使收敛时间减小.
为了让系统状态同时满足有限时间到达滑模面以及在滑模面上有限时间趋近平衡点的需求,设计如下形式的控制律:
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{u}}_{{\rm{eq}}}} + {\mathit{\boldsymbol{u}}_{{\rm{reach}}}}, $ | (11) |
式中ueq为等效控制律.令
| $ {\mathit{\boldsymbol{u}}_{{\rm{eq}}}} = - \left( {\mathit{\boldsymbol{d}} + \eta {\alpha _1}{{\left| {{\mathit{\boldsymbol{x}}_1}} \right|}^{\left( {\eta - 1} \right)}}{\mathit{\boldsymbol{x}}_2}} \right). $ | (12) |
由于η∈(0, 1),因此式(12)中第2项ηα1|x1|(η-1)x2在x1=0且x2≠0时会引起奇异.并且在系统状态到达滑模面后,由于计算误差或各种不确定因素的影响,不能保证系统状态始终在s=0上运动,尤其在(x1, x2)=(0, 0)附近,系统状态易偏离,x1=0且x2≠0的情况将会存在,奇异现象将会产生.为了避免奇异现象,采用“饱和函数”对ueq进行如下处理:
| $ {\mathit{\boldsymbol{u}}_{{\rm{eq}}}} = - \left[ {\mathit{\boldsymbol{d}} + {\rm{satur}}\left( {{\mathit{\boldsymbol{u}}_f},{\mathit{\boldsymbol{u}}_s}} \right)} \right]. $ | (13) |
式中:satur(uf, us)=
式(13)中包含ESO对桁架结构总干扰的观测误差d,在实际工程应用中,这一项是不可知的,因此假设观测误差的上界为dmax≥|d|,并采用自适应律对dmax进行估计:
| $ {{\dot {\hat d}}_{\max }} = \rho \left| \mathit{\boldsymbol{s}} \right|,{{\hat d}_{\max }}\left( 0 \right) > 0. $ | (14) |
式中ρ为自适应律的增益,满足ρ≥1.
因此,可将式(13)改写为
| $ {\mathit{\boldsymbol{u}}_{{\rm{eq}}}} = - \left[ {\rho {{\hat d}_{\max }}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) + {\rm{satur}}\left( {{\mathit{\boldsymbol{u}}_f},{\mathit{\boldsymbol{u}}_s}} \right)} \right]. $ |
式(11)中第2项主要是保证系统状态在到达阶段的有限时间特性,形式如下
| $ {\mathit{\boldsymbol{u}}_{{\rm{reach}}}} = - \left[ {{k_1}{\rm{si}}{{\rm{g}}^\alpha }\left( \mathit{\boldsymbol{s}} \right) + {k_2}{\rm{si}}{{\rm{g}}^\beta }\left( \mathit{\boldsymbol{s}} \right)} \right]. $ |
因此,本文设计的空间智能桁架结构控制律形式如下
| $ \begin{array}{l} \mathit{\boldsymbol{u}} = - \rho {{\hat d}_{\max }}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) - {\rm{satur}}\left( {{\mathit{\boldsymbol{u}}_f},{\mathit{\boldsymbol{u}}_s}} \right) - \\ \;\;\;\;\;{k_1}{\rm{si}}{{\rm{g}}^\alpha }\left( \mathit{\boldsymbol{s}} \right) - {k_2}{\rm{si}}{{\rm{g}}^\beta }\left( \mathit{\boldsymbol{s}} \right). \end{array} $ | (15) |
引理1[18] 考虑系统
| $ \mathit{\boldsymbol{\dot x}} = f\left( \mathit{\boldsymbol{x}} \right),f\left( 0 \right) = 0. $ | (16) |
式中:x∈
1) V为正定函数;
2) 存在k1>0, 0<k2<1, k3>0,如果V满足下列任一微分不等式:
| $ \dot V\left( x \right) + {k_1}{V^{{k_2}}}\left( x \right) \le 0, $ |
| $ \dot V\left( x \right) + {k_3}V\left( x \right) + {k_1}{V^{{k_2}}}\left( x \right) \le 0, $ |
则系统(16)满足有限时间稳定.
定理1 对于空间智能桁架系统(5),当采用观测器(7)、控制律(15)和自适应律(14)时,系统模态振动满足有限时间稳定.
证明 将状态空间[x1T, x2T]T∈
| $ A = \left\{ {\left( {{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2}} \right):\eta {\alpha _1}{{\left| {{\mathit{\boldsymbol{x}}_1}} \right|}^{\left( {\eta - 1} \right)}}{\mathit{\boldsymbol{x}}_2} \le {\mathit{\boldsymbol{u}}_s}} \right\}, $ |
| $ B = \left\{ {\left( {{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2}} \right):\eta {\alpha _1}{{\left| {{\mathit{\boldsymbol{x}}_1}} \right|}^{\left( {\eta - 1} \right)}}{\mathit{\boldsymbol{x}}_2} > {\mathit{\boldsymbol{u}}_s}} \right\}. $ |
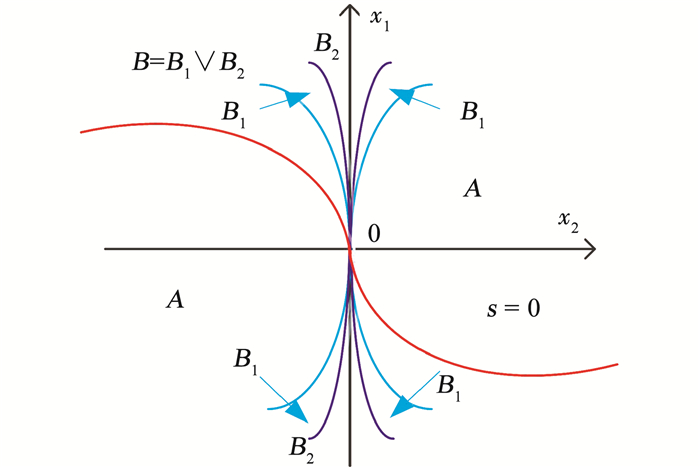
图 3给出了区域A、B划分的示意图[19].可以看出,s始终保持在区域A,只有当x1=0且x2=0时,s才会穿越至区域B.此时在滑模面s=0上,由x1→0且x2→0可知lim|x1|(η-1)x2=0.因此,在整个滑模面上没有奇异现象发生.
|
图 3 状态空间的区域划分示意 Figure 3 Different areas of state space |
情况1 当系统状态(x1, x2)位于A区域时,等效控制律(13)中的“饱和函数”取
| $ {\rm{satur}}\left( {{\mathit{\boldsymbol{u}}_f},{\mathit{\boldsymbol{u}}_s}} \right) = {\mathit{\boldsymbol{u}}_f} = \eta {\alpha _1}{\left| {{\mathit{\boldsymbol{x}}_1}} \right|^{\left( {\eta - 1} \right)}}{\mathit{\boldsymbol{x}}_2}, $ |
则可以将控制律(15)改写为
| $ \begin{array}{l} \mathit{\boldsymbol{u}} = - \rho {{\hat d}_{\max }}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) - \eta {\alpha _1}{\left| {{\mathit{\boldsymbol{x}}_1}} \right|^{\left( {\eta - 1} \right)}}{\mathit{\boldsymbol{x}}_2} - \\ \;\;\;\;\;{k_1}{\rm{si}}{{\rm{g}}^\alpha }\left( \mathit{\boldsymbol{s}} \right) - {k_2}{\rm{si}}{{\rm{g}}^\beta }\left( \mathit{\boldsymbol{s}} \right). \end{array} $ |
定义Lyapunov函数:
| $ {V_1} = \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{s + }}\frac{1}{2}\bar d_{\max }^2, $ |
式中,
对V1求导可得
| $ \begin{array}{l} {{\dot V}_1} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} + {{\bar d}_{\max }}{{\dot {\bar d}}_{\max }} = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( { - {k_1}{\rm{si}}{{\rm{g}}^\alpha }\left( \mathit{\boldsymbol{s}} \right) - {k_2}{\rm{si}}{{\rm{g}}^\beta }\left( \mathit{\boldsymbol{s}} \right) + \mathit{\boldsymbol{d}}} \right) - \\ \;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\rho {{\hat d}_{\max }}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) - {{\bar d}_{\max }}{{\dot {\hat d}}_{\max }} = - {k_1}\sum\limits_{i = 1}^{{n_c}} {{{\left| {{s_i}} \right|}^{\alpha + 1}}} - \\ \;\;\;\;\;\;{k_2}\sum\limits_{i = 1}^{{n_c}} {{{\left| {{s_i}} \right|}^{\beta + 1}}} + {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{s}}^{\rm{T}}}\rho {{\hat d}_{\max }}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) - \\ \;\;\;\;\;\;\left( {{d_{\max }} - {{\hat d}_{\max }}} \right)\rho \left| \mathit{\boldsymbol{s}} \right| \le - {k_1}\sum\limits_{i = 1}^{{n_c}} {{{\left| {{s_i}} \right|}^{\alpha + 1}}} - \\ \;\;\;\;\;\;{k_2}\sum\limits_{i = 1}^{{n_c}} {{{\left| {{s_i}} \right|}^{\beta + 1}}} + \left| \mathit{\boldsymbol{s}} \right|{d_{\max }}\left( {1 - \rho } \right). \end{array} $ |
由于ρ≥1,所以可以得到
再定义Lyapunov函数:
| $ {V_2} = \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{s}}, $ |
对V2求导可得
| $ \begin{array}{l} {{\dot V}_2} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} = \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( { - {k_1}{\rm{si}}{{\rm{g}}^\alpha }\left( \mathit{\boldsymbol{s}} \right) - {k_2}{\rm{si}}{{\rm{g}}^\beta }\left( \mathit{\boldsymbol{s}} \right)} \right) + \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {d - \rho {{\hat d}_{\max }}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right)} \right) = - {k_1}\sum\limits_{i = 1}^{{n_c}} {{{\left| {{s_i}} \right|}^{\alpha + 1}}} - \\ \;\;\;\;\;\;\;{k_2}\sum\limits_{i = 1}^{{n_c}} {{{\left| {{s_i}} \right|}^{\beta + 1}}} + {\mathit{\boldsymbol{s}}^{\rm{T}}}d - {\mathit{\boldsymbol{s}}^{\rm{T}}}\rho {{\hat d}_{\max }}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) \le \\ \;\;\;\;\;\;\; - {k_1}\sum\limits_{i = 1}^{{n_c}} {{{\left| {{s_i}} \right|}^{\alpha + 1}}} - {k_2}\sum\limits_{i = 1}^{{n_c}} {{{\left| {{s_i}} \right|}^{\beta + 1}}} + \\ \;\;\;\;\;\;\;\left( {{{\left| \mathit{\boldsymbol{s}} \right|}^{\rm{T}}}{d_{\max }} - {{\left| \mathit{\boldsymbol{s}} \right|}^{\rm{T}}}\rho {{\hat d}_{\max }}} \right). \end{array} $ | (17) |
根据自适应律(14),可知
| $ \rho \ge 1 + \frac{{\sqrt {\hat d_{\max }^2\left( 0 \right) + {\varepsilon ^2}} }}{{{{\hat d}_{\max }}\left( 0 \right)}}, $ |
其中ε为任意常值.则有
| $ \begin{array}{l} {d_{\max }} - \rho {{\hat d}_{\max }} \le - {{\hat d}_{\max }}\left( {1 + \frac{{\sqrt {\hat d_{\max }^2\left( 0 \right) + {\varepsilon ^2}} }}{{{{\hat d}_{\max }}\left( 0 \right)}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{d_{\max }} \le {{\bar d}_{\max }}\left( 0 \right) - \sqrt {\hat d_{\max }^2\left( 0 \right) + {\varepsilon ^2}} \le \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{{\bar d}_{\max }}\left( 0 \right)} \right| - \sqrt {\hat d_{\max }^2\left( 0 \right) + {\varepsilon ^2}} \le 0. \end{array} $ | (18) |
将式(18)带入式(17)可得
| $ \begin{array}{*{20}{c}} {{{\dot V}_2} \le - {k_1}\sum\limits_{i = 1}^{{n_c}} {{{\left| {{s_i}} \right|}^{\alpha + 1}}} - {k_2}\sum\limits_{i = 1}^{{n_c}} {{{\left| {{s_i}} \right|}^{\beta + 1}}} = }\\ { - 2{k_1}V_2^{\left( {\alpha + 1} \right)/2} - 2{k_2}V_2^{\left( {\beta + 1} \right)/2}.} \end{array} $ |
根据引理1可知,系统状态可以在有限时间内到达s=0.
情况2 当系统状态(x1, x2)位于B区域时,等效控制律(13)中的“饱和函数”取
| $ {\rm{satur}}\left( {{\mathit{\boldsymbol{u}}_f},{\mathit{\boldsymbol{u}}_s}} \right) = {\mathit{\boldsymbol{u}}_s}, $ |
则可以将控制律(15)改写为
| $ \mathit{\boldsymbol{u}} = - \rho {{\hat d}_{\max }}{\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right) - {\mathit{\boldsymbol{u}}_s} - {{\rm{k}}_1}si{g^\alpha }\left( \mathit{\boldsymbol{s}} \right) - {k_2}{\rm{si}}{{\rm{g}}^\beta }\left( \mathit{\boldsymbol{s}} \right), $ |
则有
| $ \begin{array}{l} \mathit{\boldsymbol{\dot s}} = - {k_1}{\rm{si}}{{\rm{g}}^\alpha }\left( \mathit{\boldsymbol{s}} \right) - {k_2}{\rm{si}}{{\rm{g}}^\beta }\left( \mathit{\boldsymbol{s}} \right) - \\ \;\;\;\;{\mathit{\boldsymbol{u}}_s} + \eta {\alpha _1}{\left| {{\mathit{\boldsymbol{x}}_1}} \right|^{\left( {\eta - 1} \right)}}{\mathit{\boldsymbol{x}}_2} + \mathit{\boldsymbol{d}} - \\ \;\;\;\;\rho {{\hat d}_{\max }}{\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right). \end{array} $ | (19) |
此时将区域B划分为B1、B2两部分,如图 3所示.可知,当系统状态从区域A进入区域B1时,由于k1、k2是正数,因此在B1内仍满足
| $ \mathit{\boldsymbol{\dot s}} = {\rm{O}}\left( {\eta {\alpha _1}{{\left| {{x_1}} \right|}^{\left( {\eta - 1} \right)}}{x_2}} \right) \to \infty , $ |
| $ {\mathit{\boldsymbol{x}}_1} \to 0,{\mathit{\boldsymbol{x}}_2} \ne 0, $ |
式中O为无穷大渐近的朗道符号[19].
那么此时
因此在区域B,以下情况一直成立:
| $ B = {B_1} \vee {B_2}, $ |
| $ {B_1} = \left\{ {\left( {{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2}} \right):{{\dot V}_1} < 0,{{\dot V}_2} < 0} \right\}, $ |
| $ {B_2} = \left\{ {\left( {{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2}} \right):{{\dot V}_1} > 0,{{\dot V}_2} > 0} \right\}. $ |
根据式(9)可知,状态x1(t)的解可以表示为
| $ {\mathit{\boldsymbol{x}}_1}\left( \mathit{\boldsymbol{t}} \right) = {\mathit{\boldsymbol{x}}_1}\left( 0 \right) + \int_0^t {{\mathit{\boldsymbol{x}}_2}\left( t \right){\rm{d}}t} . $ |
则根据图 3可知,在区域B内,当x2(t)>0时,x1(t)单调递增直到穿越区域B和区域A的边界;当x2(t)<0时,x1(t)单调递减直到穿越区域B和区域A的边界.因此可知,状态(x1, x2)不会一直保持在区域B内,会在有限时间内穿越到区域A.当(x1, x2)到达区域A时,系统将再次满足上述情况1分析得到的结论.
最后当系统在滑模面s=0上运动时,定义Lyapunov函数为
| $ {V_3} = \frac{1}{2}\mathit{\boldsymbol{x}}_1^{\rm{T}}{\mathit{\boldsymbol{x}}_1}, $ |
对V3求导可得
| $ \begin{array}{l} {{\dot V}_3} = \mathit{\boldsymbol{x}}_1^{\rm{T}}{{\mathit{\boldsymbol{\dot x}}}_1} = \mathit{\boldsymbol{x}}_1^{\rm{T}}{\mathit{\boldsymbol{x}}_2} = - {\alpha _1}\mathit{\boldsymbol{x}}_1^{\rm{T}}{\rm{si}}{{\rm{g}}^\eta }\left( {{\mathit{\boldsymbol{x}}_1}} \right) = \\ \;\;\;\;\; - {\alpha _1}\sum\limits_{i = 1}^{{n_c}} {{{\left| {{x_{1i}}} \right|}^{\eta + 1}}} . \end{array} $ |
根据引理1可知,系统(9)的状态可以在有限时间内收敛到原点,即桁架结构系统(5)的模态振动可以有限时间稳定.
注3 为了改善控制效果,可以在双幂次趋近律中采用下式的函数替换函数sgn(s)来削弱常值切换导致的抖振:
| $ {\rm{sat}}\left( \mathit{\boldsymbol{s}} \right) = \left\{ \begin{array}{l} \frac{\mathit{\boldsymbol{s}}}{{\left\| \mathit{\boldsymbol{s}} \right\|}},\left\| \mathit{\boldsymbol{s}} \right\| \ge {\sigma _2};\\ \frac{\mathit{\boldsymbol{s}}}{{{\sigma _2}}},\ \ \left\| \mathit{\boldsymbol{s}} \right\| < {\sigma _2}. \end{array} \right. $ |
对本文提出算法的有效性进行仿真验证.鉴于终端滑模控制方法的有限时间特性,在对桁架结构施加不同形式干扰的情况下,将本文提出的控制器与常见的基于齐次方法的有限时间控制器进行比较.
对比过程中用到的齐次方法控制器形式为[20]
| $ \mathit{\boldsymbol{u}} = - {g_1}{\rm{si}}{{\rm{g}}^{{\gamma _1}}}\left( {{\mathit{\boldsymbol{x}}_1}} \right) - {g_2}{\rm{si}}{{\rm{g}}^{{\gamma _2}}}\left( {{\mathit{\boldsymbol{x}}_2}} \right). $ | (20) |
式中:0<γ1<1,γ2=2γ1/(1+γ1),g1>0,g2>0.
空间智能桁架的结构参数见表 1.
| 表 1 空间智能桁架结构参数 Table 1 Structure parameters of space intelligent truss |
仿真过程中考虑如下两种工况:
1) t=1 s时产生持续时间为0.1 s的模态坐标下的瞬态干扰力为
| $ {\mathit{\boldsymbol{F}}_d} = 5 \times {\left[ {\begin{array}{*{20}{c}} 1&1&1&1&1&1 \end{array}} \right]^{\rm{T}}}{\rm{N}}. $ |
2) 考虑一种比较苛刻的情况,即比较剧烈的干扰力形式,桁架从初始时刻开始就持续受到模态坐标下的周期干扰力为
| $ {\mathit{\boldsymbol{F}}_d} = 5 \times \sin \left( {15 \times 2{\rm{ \mathsf{ π} }}} \right) \times {\left[ {\begin{array}{*{20}{c}} 1&1&1&1&1&1 \end{array}} \right]^{\rm{T}}}{\rm{N}}. $ |
仿真过程中选取仿真参数如下:
1) 扩张状态观测器(7)为:
| $ {a_1} = 0.01,{a_2} = 0.005,{a_3} = 0.002\ 5, $ |
| $ \sigma = 0.001,{l_1} = 5,{l_2} = 2\ 000,{l_3} = 4\ 000. $ |
2) 基于齐次方法的有限时间控制器(20)为:
| $ {g_1} = 5,{g_2} = 5,{\gamma _1} = 0.3. $ |
3) 本文提出的有限时间控制器(15)为:
| $ \eta = 0.6,{\alpha _1} = 1,{k_1} = 15,{k_2} = 15, $ |
| $ \alpha = 1.1,\beta = 0.1,\rho = 1. $ |
仿真中考虑桁架的作动器可以产生6 N以内的控制力.本文仅给出第1阶模态在两种工况下的仿真结果,第2~6阶模态的仿真结果与对比分析与第1阶模态情况的类似,因此不再赘述.
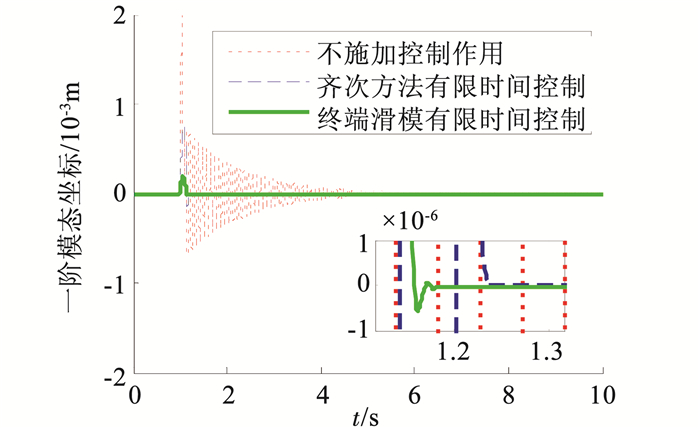
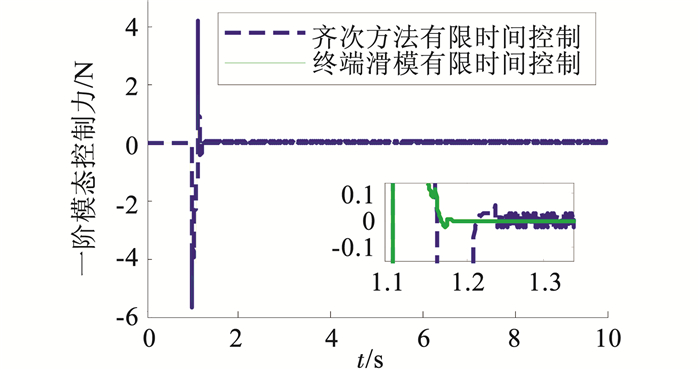
3.1 工况1的仿真结果与分析当对空间智能桁架结构施加瞬态干扰力时,模态位移坐标变化情况如图 4所示,可以看出,在自然状态下结构振动衰减缓慢,当施加控制作用后,振动幅值明显减小,稳定时间从5 s减少至0.3 s以内,两种控制器都具有较好的阻尼作用,且本文控制律(15)的稳定时间明显小于对比控制律(20)的情况.根据图 5可以看出,虽然两种控制律在施加控制作用的瞬间都产生较大的控制力,但本文控制律(15)提供的模态控制力能在较短时间内收敛到零附近,而齐次方法控制律(20)提供的模态控制力则会在零附近产生小幅度振荡.
|
图 4 一阶模态位移仿真 Figure 4 First-order modal displacement |
|
图 5 一阶模态控制力仿真 Figure 5 First-order modal control force |
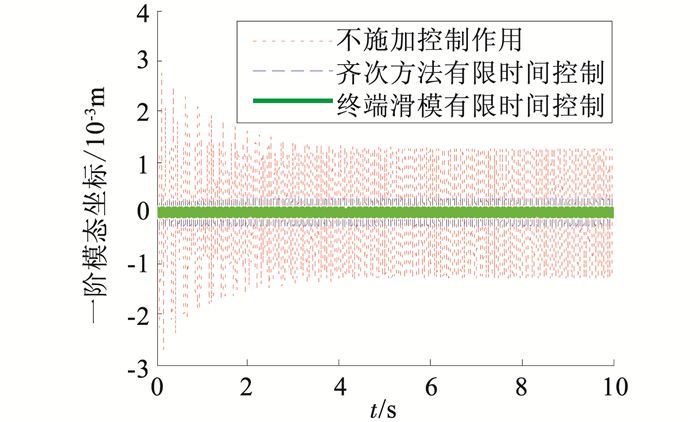
当桁架结构(1)存在较为苛刻的周期干扰力作用时,模态位移坐标变化情况如图 6所示,可以看出,在自然状态下桁架结构产生周期振荡,振幅较大且衰减缓慢,当施加控制作用后,振荡幅值明显减小,两种控制器都提供了良好的阻尼作用,且在本文提出的控制律(15)作用下,振荡幅值要明显小于施加齐次方法控制律(20)的情况.根据图 7可以看出,由于所施加的周期干扰力振荡比较剧烈,因此两种控制律提供的模态控制力同样振荡比较剧烈,且最终都稳定在5 N左右.
|
图 6 一阶模态位移仿真 Figure 6 First-order modal displacement |

|
图 7 一阶模态控制力仿真 Figure 7 First-order modal control force |
通过对工况1和工况2的仿真分析可知,虽然两种控制律都能够有效抑制空间智能桁架结构的振动,但与常见的齐次方法控制律(20)相比,本文提出的基于终端滑模的有限时间控制律(15)能够使振动在更短时间内收敛到更小的幅值范围,因此振动抑制效果更好.
4 结论1) 本文针对航天任务中常见的智能桁架结构的振动抑制问题,基于有限元方法建立动力学模型.
2) 在IMSC能够实现各阶模态响应解耦的基础上,将ESO能够实时估计模型摄动和外界干扰的特点与“动态补偿线性化”思想相结合,设计了一种终端滑模控制器.
3) 将本文控制器与基于齐次方法的有限时间控制器进行了对比仿真分析,验证了本文算法具有更好的振动抑制控制效果.
| [1] |
MEHRINFAR M. A cost saving berthing verification of ISS truss Segment to Segment Attach System (SSAS)[C]//Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Norfolk: AIAA, 2013: 1788. DOI: 10.2514/6.2003-1954
|
| [2] |
MATSUMOTO S, TAYAMA S, ISHIJIMA Y, et al. Selene "KAGUYA" attitude and orbit control system and its flight results[J]. Journal of Space Technology and Science, 2009, 25(1): 1_17-1_26. DOI:10.11230/jsts.25.1_17 |
| [3] |
MEGURO A, SHINTATE K, USUI M, et al. In-orbit deployment characteristics of large deployable antenna reflector onboard Engineering Test Satellite VⅢ[J]. Acta Astronautica, 2009, 65(9/10): 1306. DOI:10.1016/j.actaastro.2009.03.052 |
| [4] |
LUO Yajun, XU Minglong, YAN Bo, et al. PD control for vibration attenuation in Hoop truss structure based on a novel piezoelectric bending actuator[J]. Journal of Sound and Vibration, 2015, 339: 11. DOI:10.1016/j.jsv.2014.11.003 |
| [5] |
杨凯, 张业伟, 陈立群, 等. 基于非线性消振器的空间结构被动振动抑制[J]. 动力学与控制学报, 2014, 12(3): 205. YANG Kai, ZHANG Yewei, CHEN Liqun, et al. Space structure vibration control based on space nonlinear energy sink[J]. Journal of Dynamics and Control, 2014, 12(3): 205. DOI:10.6052/1672-6553-2014-059 |
| [6] |
常雅杰.智能桁架卫星的振动抑制与姿态控制方法研究[D].哈尔滨: 哈尔滨工业大学, 2016 CHANG Yajie. Vibration suppression and attitude control methods for intelligent truss satellite[D]. Harbin: Harbin Institute of Technology, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10213-1016914295.htm |
| [7] |
苗双全, 丛炳龙, 刘向东. 基于输入成形的挠性航天器自适应滑模控制[J]. 航空学报, 2013, 34(8): 1906. MIAO Shuangquan, CONG Binglong, LIU Xiangdong. Adaptive sliding mode control of flexible spacecraft on input shaping[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1906. DOI:10.7527/S1000-6893.2013.0322 |
| [8] |
OMIDI E, MAHMOODI S N. Vibration control of collocated smart structures using H∞ modified positive position and velocity feedback[J]. Journal of Vibration and Control, 2016, 22(10): 2434. DOI:10.1177/1077546314548471 |
| [9] |
陈文英, 褚福磊, 阎绍泽. 基于自适应遗传算法分步优化设计智能桁架结构自抗扰振动控制器[J]. 机械工程学报, 2010, 46(7): 74. CHEN Wenying, CHU Fulei, YAN Shaoze. Stepwise optimal design of active disturbance rejection vibration controller for intelligent truss structure based on adaptive genetic algorithm[J]. Journal of Mechanical Engineering, 2010, 46(7): 74. DOI:10.3901/JME.2010.07.074 |
| [10] |
崔龙, 杨恺, 黄海. 基于自适应动力吸振器的空间桁架结构振动抑制研究[J]. 宇航学报, 2011, 32(9): 2074. CUI Long, YANG Kai, HUANG Hai. Vibration suppression of space truss structure based on adaptive dynamic vibration absorber[J]. Journal of Astronautics, 2011, 32(9): 2074. DOI:10.3873/j.issn.1000-1328.2011.09.029 |
| [11] |
曹玉岩, 王志臣, 付世欣, 等. 智能桁架结构最优振动控制与作动器优化配置[J]. 振动与冲击, 2015, 34(5): 26. CAO Yuyan, WANG Zhichen, FU Shixin, et al. Optimal vibration control and actuator placement for intelligent truss structures[J]. Journal of Vibration and Shock, 2015, 34(5): 26. DOI:10.13465/j.cnki.jvs.2015.05.005 |
| [12] |
LIN J, ZHENG Y B. Vibration suppression control of smart piezoelectric rotating truss structure by parallel neuro-fuzzy control with genetic algorithm tuning[J]. Journal of Sound and Vibration, 2012, 331(16): 3677. DOI:10.1016/j.jsv.2012.04.001 |
| [13] |
徐高楠, 黄海, 李伟鹏, 等. 空间挠性结构的Stewart平台主动基座振动控制[J]. 宇航学报, 2015, 36(4): 438. XU Gaonan, HUANG Hai, LI Weipeng, et al. Active vibration control of space flexible structure using stewart platform as active base[J]. Journal of Astronautics, 2015, 36(4): 438. DOI:10.3873/j.issn.1000-1328.2015.04.010 |
| [14] |
ZHONG Chenxing, LAI Aifang, GUO Yu, et al. On attitude maneuver control of flexible spacecraft without angular velocity sensors[C]//Proceedings of the 2013 IEEE/SICE International Symposium on System Integration. Kobe: IEEE press, 2013: 318. DOI: 10.1109/SⅡ.2013.6776646 http://ieeexplore.ieee.org/xpl/abstractCitations.jsp?tp=&arnumber=6776646&searchWithin%3Dp_Authors%3A.QT.Ai+Fang.QT.
|
| [15] |
WANG Yanmin, HAN Fengling, FENG Yong, et al. Hybrid continuous nonsingular terminal sliding mode control of uncertain flexible manipulators[C]//Proceedings of the 34th Chinese Control Conference. Hangzhou: IEEE press, 2014: 190. DOI: 10.1109/IECON.2014.7048498
|
| [16] |
SONG Zhankui, LI Hongxing, SUN Kaibiao. Finite-time control for nonlinear spacecraft attitude based on terminal sliding mode technique[J]. ISA Transactions, 2014, 53(1): 117. DOI:10.1016/j.isatra.2013.08.008 |
| [17] |
LI W, HUANG H. Integrated optimization of actuator placement and vibration control for piezoelectric adaptive trusses[J]. Journal of Sound and Vibration, 2013, 332(1): 17. DOI:10.1016/j.jsv.2012.08.005 |
| [18] |
HU Qinglei, JIANG Boyan, FRISWELL M I. Robust saturated finite time output feedback attitude stabilization for rigid spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(6): 1914. DOI:10.2514/1.G000153 |
| [19] |
FENG Yong, YU Xinghuo, HAN Fenglong. On nonsingular terminal sliding-mode control of nonlinear systems[J]. Automatica, 2013, 49(6): 1715. DOI:10.1016/j.automatica.2013.01.051 |
| [20] |
DU Haibo, LI Shihua. Finite-time attitude stabilization for a spacecraft using homogeneous method[J]. Journal of Guidance, Control, and Dynamics, IFAC Proceedings Volumes, 2011, 44(1): 2620. DOI:10.3182/20110828-6-IT-1002.01261 |
 2018, Vol. 50
2018, Vol. 50


