卫星编队协同控制是卫星编队系统完成空间任务的重要保证.实际的卫星编队系统资源和通信带宽是有限的，而传统的周期性时间驱动控制需要卫星根据邻居周期采样信息调节自身状态，以实现卫星编队协同^[1-3].通信压力较大，控制输入更新较为频繁，造成资源浪费；并容易受到空间环境干扰，影响卫星编队协同控制的效果.

为克服时间驱动控制的局限性，事件驱动控制方法受到众多学者的关注.事件驱动控制在保证系统控制性能的同时，根据设计的事件驱动函数来调节控制更新周期，从而有效减少信息传输量和控制输入更新次数，节约星上资源.近年来，基于事件驱动的控制策略已在多智能体系统一致性问题中得到应用^[4-7].Dimarogonas等^[8]首次研究了基于事件驱动控制的多智能体系统协同控制一致性问题，分别针对集中式和分布式控制策略设计了状态依赖的事件驱动函数，并排除了Zeno现象的发生.Seyboth等^[9]采用时间依赖的阈值函数限定智能体状态误差，使得事件驱动函数不再依赖邻居智能体状态信息，并研究了一阶和二阶多智能体系统的平均一致性问题.文献[4-5]分别针对一阶、二阶领导跟随多智能体系统提出了基于事件驱动控制的一致性算法，文献[6-7]分别针对线性和非线性多智能体系统的一致性进行了研究.

但到目前为止，事件驱动控制主要用于积分器型多智能体系统中，对于具有非线性特性的多刚体系统模型研究较少.Weng等^[10]研究了多刚体系统的姿态协同控制问题，针对系统中的每个刚体设计了分布式事件触发姿态协同控制器.Huang等^[11]研究了固定无向通信拓扑下基于事件驱动的多智能体Euler-Lagrange系统分布式一致性问题，Liu等^[12]针对具有参数不确定性的多智能体Euler-Lagrange系统设计了自适应事件驱动控制器，实现了固定通信拓扑下机械臂系统的领航者—跟随者一致.

本文针对卫星编队系统资源和通信带宽受限情况下的姿态协同控制问题，设计了基于事件驱动的分布式自适应控制器.首先在Euler-Lagrange框架下，针对卫星转动惯量不确定的情况，设计了可保证闭环系统渐近稳定的事件驱动函数和自适应控制器，并证明此系统不会出现Zeno现象.最后进行数值仿真验证所设计控制器的有效性，并将其与传统自适应控制器比较，表明所设计控制器在保证系统控制性能的同时能有效降低控制输入更新频次，节约星上资源.

1 问题描述

本文考虑由1个领航者(记为0)与N个跟随者(1, 2, …, N)组成的卫星编队领航者—跟随者姿态协同控制问题，采用修正罗德里格斯参数(MRPs)描述卫星姿态.其姿态向量σ∈ ${{\mathbb{R}}^{3}}$用欧拉轴e和欧拉角Φ表示为σ=etan $\frac{\mathit{\Phi }}{4}$，-2π＜Φ＜2π.则跟随者i的姿态运动学和动力学方程分别为:

$ {{\mathit{\boldsymbol{\dot \sigma }}}_i} = \mathit{\boldsymbol{G}}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){\mathit{\boldsymbol{\omega }}_i}, $

(1)

$ {\mathit{\boldsymbol{J}}_i}{{\mathit{\boldsymbol{\dot \omega }}}_i} = - \mathit{\boldsymbol{\omega }}_i^ \times {\mathit{\boldsymbol{J}}_i}{\mathit{\boldsymbol{\omega }}_i} + {\mathit{\boldsymbol{\tau }}_i}, $

(2)

其中

$ \mathit{\boldsymbol{G}}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right) = \frac{1}{4}\left\{ {\left( {1 - \mathit{\boldsymbol{\sigma }}_i^{\rm{T}}{\mathit{\boldsymbol{\sigma }}_i}} \right){I_3} + 2\mathit{\boldsymbol{\sigma }}_i^ \times + 2{\mathit{\boldsymbol{\sigma }}_i}\mathit{\boldsymbol{\sigma }}_i^{\rm{T}}} \right\}. $

式中：σ_i∈ ${{\mathbb{R}}^{3}}$、ω_i∈${{\mathbb{R}}^{3}}$分别为第i颗卫星的本体坐标系相对于参考坐标系的姿态和姿态角速度；J_i∈ ${{\mathbb{R}}^{3\times 3}}$为正定对称的转动惯量矩阵；τ_i∈${{\mathbb{R}}^{3}}$为作用于第i颗卫星的控制力矩；(·)^×为3×3斜对称矩阵；I₃为3×3单位阵.

将式(1)改写为ω_i=G(σ_i)^-1${{\mathit{\boldsymbol{\dot \sigma }}}_i}$并代入式(2)中，可得到Euler-Lagrange形式的卫星编队姿态动力学方程为

$ {\mathit{\boldsymbol{M}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){{\mathit{\boldsymbol{\ddot \sigma }}}_i} + {\mathit{\boldsymbol{C}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i},{{\mathit{\boldsymbol{\dot \sigma }}}_i}} \right){{\mathit{\boldsymbol{\dot \sigma }}}_i} = {\mathit{\boldsymbol{u}}_i}. $

(3)

式中：M_i(σ_i)=G^-T(σ_i)J_iG^-1(σ_i)为第i颗卫星的转动惯量矩阵；C_i(σ_i, ${{\mathit{\boldsymbol{\dot \sigma }}}_i}$)=-G^-T(σ_i){J_iG^-1(σ_i)$ {\mathit{\boldsymbol{\dot G }}}$(σ_i)+[J_iG^-1(σ_i)${{\mathit{\boldsymbol{\dot \sigma }}}_i}$]^×}G^-1(σ_i)为第i颗卫星的哥氏及离心力矩矩阵；u_i=G^-T(σ_i)τ_i为控制力矩.

本文利用有向图$\mathscr{G}$=(v, ε)描述编队卫星的信息交互.节点集v($\mathscr{G}$)={v₁, …, v_N}表示编队卫星，由有序节点对(v_i, v_j)组成的边集ε($\mathscr{G}$)表示星间信息传递关系.图$\mathscr{G}$的邻接矩阵为$\mathscr{A}$=[a_ij]∈${{\mathbb{R}}^{n\times n}}$.当(v_j, v_i)∈ε($\mathscr{G}$)时，a_ij＞0；否则a_ij=0，其中a_ii=0.

本文目标是在有向固定通信拓扑结构下针对每个跟随者设计协同控制算法，使得编队卫星在模型不确定的情况下，实现领航者固定的领航者—跟随者姿态一致.即对于

$ {{\mathit{\boldsymbol{\dot \sigma }}}_0} = {\bf{0}},t \to \infty \;时\;{\mathit{\boldsymbol{\sigma }}_i}\left( t \right) \to {\mathit{\boldsymbol{\sigma }}_0}\left( t \right),\;{{\mathit{\boldsymbol{\dot \sigma }}}_i}\left( t \right) \to {\bf{0}}. $

其中σ₀、${{\mathit{\boldsymbol{\dot \sigma }}}_0}$分别为领航者的姿态及其导数.

2 分布式自适应控制器设计

本文针对存在转动惯量不确定性的卫星编队系统设计事件驱动自适应控制器，使得编队系统实现领航者—跟随者姿态一致，并减少控制输入更新频次和信息交互.

令第i颗卫星的事件触发时间序列为t₀ⁱ, t₁ⁱ, …, t_kⁱ, …，其中k=0, 1, …, n，t₀ⁱ=0.则作用于跟随者i的事件驱动控制器为

$ {\mathit{\boldsymbol{u}}_i}\left( t \right) = {\mathit{\boldsymbol{Y}}_i}\left( {t_k^i} \right){{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}\left( {t_k^i} \right) - {\mathit{\boldsymbol{K}}_i}{\mathit{\boldsymbol{\eta }}_i}\left( {t_k^i} \right),t \in \left[ {t_k^i,t_{k + 1}^i} \right). $

(4)

自适应更新律为

$ {{\mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }}}_i} = - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_i}\mathit{\boldsymbol{Y}}_i^{\rm{T}}\left( t \right){\mathit{\boldsymbol{\eta }}_i}\left( t \right). $

(5)

式中：K_i、Γ_i分别为对称正定矩阵；Y _i为已知的回归矩阵函数，由式(4)可知控制力矩在[t_kⁱ, t_k+1ⁱ)内保持为常数，即u_i(t)是分段常数；Θ_i(t)为Θ_i在时间t的估计，在卫星编队姿态协同控制中，Θ_i=[J₁₁, J₂₂, J₃₃, J₁₂, J₁₃, J₂₃]^T为具有不确定性的转动惯量矩阵.η_i为

$ \begin{array}{l} {\mathit{\boldsymbol{\eta }}_i} = {{\mathit{\boldsymbol{\dot \sigma }}}_i}\left( t \right) - {\mathit{\boldsymbol{\sigma }}_r}\left( t \right) = {{\mathit{\boldsymbol{\dot \sigma }}}_i}\left( t \right) + \\ \;\;\;\;\;\;\alpha \sum\limits_{j = 0}^n {{a_{ij}}\left( {{\mathit{\boldsymbol{\sigma }}_i}\left( t \right) - {\mathit{\boldsymbol{\sigma }}_j}\left( t \right)} \right)} . \end{array} $

(6)

式中：α为正常数；a_ij为有向图$\mathscr{G}$邻接矩阵$\mathscr{A}$的权值；σ_r(t)为辅助函数.根据Euler-Lagrange方程参数线性化性质^[13]，有

$ {\mathit{\boldsymbol{M}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){{\mathit{\boldsymbol{\dot \sigma }}}_r} + {\mathit{\boldsymbol{C}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i},{{\mathit{\boldsymbol{\dot \sigma }}}_i}} \right){\mathit{\boldsymbol{\sigma }}_r} = {\mathit{\boldsymbol{Y}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i},{{\mathit{\boldsymbol{\dot \sigma }}}_i},{\mathit{\boldsymbol{\sigma }}_r},{{\mathit{\boldsymbol{\dot \sigma }}}_r}} \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i}, $

(7)

其中

$ \begin{array}{l} {\mathit{\boldsymbol{Y}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i},{{\mathit{\boldsymbol{\dot \sigma }}}_i},{\mathit{\boldsymbol{\sigma }}_r},{{\mathit{\boldsymbol{\dot \sigma }}}_r}} \right) = {\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right)L\left( {{\mathit{\boldsymbol{G}}^{ - 1}}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){{\mathit{\boldsymbol{\dot \sigma }}}_r}} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right)\mathit{\boldsymbol{L}}\left( {{\mathit{\boldsymbol{G}}^{ - 1}}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right)\mathit{\boldsymbol{\dot G}}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){\mathit{\boldsymbol{G}}^{ - 1}}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){\mathit{\boldsymbol{\sigma }}_r}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{G}}^{ - {\rm{T}}}}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){\left( {{\mathit{\boldsymbol{G}}^{ - 1}}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){\mathit{\boldsymbol{\sigma }}_r}} \right)^ \times }\mathit{\boldsymbol{L}}\left( {{\mathit{\boldsymbol{G}}^{ - 1}}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){{\mathit{\boldsymbol{\dot \sigma }}}_i}} \right), \end{array} $

L(x)为线性算子，对于∀x∈${{\mathbb{R}}^3}$，有J_ix=L(x)Θ_i.

将式(4)、(6)和(7)代入到式(3)中，可得

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){{\mathit{\boldsymbol{\dot \eta }}}_i}\left( t \right) + {\mathit{\boldsymbol{C}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i},{{\mathit{\boldsymbol{\dot \sigma }}}_i}} \right){\mathit{\boldsymbol{\eta }}_i}\left( t \right) = }\\ { - {\mathit{\boldsymbol{K}}_i}{\mathit{\boldsymbol{\eta }}_i}\left( {t_k^i} \right) + {\mathit{\boldsymbol{Y}}_i}\left( {t_k^i} \right){{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}\left( {t_k^i} \right) - {\mathit{\boldsymbol{Y}}_i}\left( t \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i},t \in \left[ {t_k^i,t_{k + 1}^i} \right).} \end{array} $

(8)

定义两类状态误差：

$ \begin{array}{l} {\mathit{\boldsymbol{e}}_{{\eta _i}}}\left( t \right) = {\mathit{\boldsymbol{\eta }}_i}\left( {t_k^i} \right) - {\mathit{\boldsymbol{\eta }}_i}\left( t \right),\\ {\mathit{\boldsymbol{e}}_i}\left( t \right) = {\mathit{\boldsymbol{Y}}_i}\left( {t_k^i} \right){{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}\left( {t_k^i} \right) - {\mathit{\boldsymbol{Y}}_i}\left( t \right){{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}\left( t \right),t \in \left[ {t_k^i,t_{k + 1}^i} \right). \end{array} $

(9)

事件驱动函数为

$ \begin{array}{l} {f_i}\left( {{\mathit{\boldsymbol{e}}_i}\left( t \right),{\mathit{\boldsymbol{e}}_{{\eta _i}}}\left( t \right)} \right) = \left\| {{\mathit{\boldsymbol{e}}_i}\left( t \right)} \right\| + {\lambda _{\max }}\left( {{\mathit{\boldsymbol{K}}_i}} \right)\left\| {{\mathit{\boldsymbol{e}}_{{\eta _i}}}\left( t \right)} \right\| - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\gamma _i}}}{2}{\lambda _{\min }}\left( {{\mathit{\boldsymbol{K}}_i}} \right)\left\| {{\eta _i}\left( t \right)} \right\| - {\mathit{\boldsymbol{\mu }}_i}\left( t \right). \end{array} $

(10)

式中：μ_i(t)=ρ_i$\sqrt {{\lambda _{\min }}\left( {{\mathit{\boldsymbol{K}}_i}} \right)} $exp(-v_it)，ρ_i＞0，0＜v_i＜1，0＜γ_i＜1；λ_max(K_i)、λ_min(K_i)分别为K_i的最大、最小特征值.μ_i(t)函数的引入可完全避免Zeno现象.卫星i连续检测辅助状态η_i(t)和不确定参数${{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}$(t)，当f_i(e_i(t), e_ηi(t))≥0时，立即触发事件，此时t_kⁱ=t.事件触发后，状态误差e_ηi(t)和e_i(t)被重置为0，卫星i控制输入更新.对于t∈[t_kⁱ, t_k+1ⁱ)，控制输入为u_i(t)=u_i(t_kⁱ).

定理1  假设卫星编队通信拓扑$\mathscr{G}$固定不变，其邻接矩阵为常值，且$\mathscr{G}$包含领航者作为根节点的有向生成树.则卫星编队系统(3)在事件驱动自适应控制器(4)、自适应更新律(5)、事件驱动函数(10)作用下可实现领航者—跟随者姿态一致.即t→∞时σ_i→σ₀，${{\mathit{\boldsymbol{\dot \sigma }}}_i}$→0，i=1, 2, …, N.

证明  对非自治系统(8)进行稳定性分析.考虑如下所示类Lyapunov函数

$ V = \frac{1}{2}\sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}{\mathit{\boldsymbol{M}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){\mathit{\boldsymbol{\eta }}_i}} + \frac{1}{2}\sum\limits_{i = 1}^N {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_i^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_i^{ - 1}{{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_i}} , $

(11)

其中真值与估计值之间的误差为

$ {{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_i} = {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i} - {{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}. $

(12)

对V求导并代入式(8)，可得

$ \begin{array}{l} \dot V = \frac{1}{2}\sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot M}}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){\mathit{\boldsymbol{\eta }}_i}} + \sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}{\mathit{\boldsymbol{M}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right){{\mathit{\boldsymbol{\dot \eta }}}_i}} + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^N {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_i^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_i^{ - 1}{{\mathit{\boldsymbol{ \boldsymbol{\dot {\tilde \varTheta}} }}}_i}} = \sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}\left( {\frac{1}{2}{{\mathit{\boldsymbol{\dot M}}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i}} \right) - } \right.} \\ \;\;\;\;\;\;\left. {{\mathit{\boldsymbol{C}}_i}\left( {{\mathit{\boldsymbol{\sigma }}_i},{{\mathit{\boldsymbol{\dot \sigma }}}_i}} \right)} \right){\mathit{\boldsymbol{\eta }}_i} - \sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_i}{\mathit{\boldsymbol{\eta }}_i}\left( {t_k^i} \right)} + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}{\mathit{\boldsymbol{Y}}_i}\left( {t_k^i} \right){{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}\left( {t_k^i} \right)} - \sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}{\mathit{\boldsymbol{Y}}_i}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_i}} + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^N {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_i^{\rm{T}}\mathit{\boldsymbol{Y}}_i^t{\mathit{\boldsymbol{\eta }}_i}} . \end{array} $

由于$\frac{1}{2}{{\mathit{\boldsymbol{\dot M}}}_i}\left( {{{\mathit{\boldsymbol{ \sigma }}}_i}} \right)$-C_i(σ_i)是反对称矩阵^[13]，再代入式(12)和式(9)，可得

$ \begin{array}{l} \dot V = - \sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_i}{\mathit{\boldsymbol{\eta }}_i}\left( {t_k^i} \right)} + \sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}{\mathit{\boldsymbol{Y}}_i}\left( {t_k^i} \right){{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}\left( {t_k^i} \right)} - \\ \;\;\;\;\;\;\sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}{\mathit{\boldsymbol{Y}}_i}\left( {{{{\rm{\tilde \Theta }}}_i}\mathit{\boldsymbol{ + }}{{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}} \right)} + \sum\limits_{i = 1}^N {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_i^{\rm{T}}\mathit{\boldsymbol{Y}}_i^{\rm{T}}{\mathit{\boldsymbol{\eta }}_i}} = \\ \;\;\;\;\;\; - \sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_i}{\mathit{\boldsymbol{\eta }}_i}} - \sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}{\mathit{\boldsymbol{K}}_i}{\mathit{\boldsymbol{e}}_{{\mathit{\boldsymbol{\eta }}_i}}}} + \sum\limits_{i = 1}^N {\mathit{\boldsymbol{\eta }}_i^{\rm{T}}{\mathit{\boldsymbol{e}}_i}} . \end{array} $

因为K_i是对称正定矩阵，${\dot V}$的上界为

$ \begin{array}{l} \dot V \le - \sum\limits_{i = 1}^N {{\lambda _{\min }}\left( {{\mathit{\boldsymbol{K}}_i}} \right){{\left\| {{\mathit{\boldsymbol{\eta }}_i}} \right\|}^2}} + \\ \;\;\;\;\;\sum\limits_{i = 1}^N {{\lambda _{\max }}\left( {{\mathit{\boldsymbol{K}}_i}} \right)\left\| {{\mathit{\boldsymbol{\eta }}_i}} \right\|\left\| {{\mathit{\boldsymbol{e}}_{{\mathit{\boldsymbol{\eta }}_i}}}} \right\|} + \\ \;\;\;\;\;\sum\limits_{i = 1}^N {\left\| {{\mathit{\boldsymbol{\eta }}_i}} \right\|\left\| {{\mathit{\boldsymbol{e}}_i}} \right\|} . \end{array} $

根据式(11)，f_i(e_i(t), e_ηi(t))≤0在系统(8)变化过程中始终成立.有

$ \begin{array}{l} \dot V \le - \sum\limits_{i = 1}^N {{\lambda _{\min }}\left( {{\mathit{\boldsymbol{K}}_i}} \right){{\left\| {{\mathit{\boldsymbol{\eta }}_i}} \right\|}^2}} + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^N {\frac{{{\gamma _i}}}{2}{\lambda _{\min }}\left( {{\mathit{\boldsymbol{K}}_i}} \right){{\left\| {{\mathit{\boldsymbol{\eta }}_i}} \right\|}^2}} + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^N {\sqrt {{\lambda _{\min }}\left( {{\mathit{\boldsymbol{K}}_i}} \right)} \left\| {{\mathit{\boldsymbol{\eta }}_i}} \right\|{\rho _i}\exp \left( { - {v_i}t} \right)} , \end{array} $

∀x, y∈${{\mathbb{R}}}$，有|xy|≤ $\frac{{{\gamma _i}}}{2}{x^2} + \frac{1}{{2{\gamma _i}}}{y^2}$，可得

$ \begin{array}{l} \dot V \le \sum\limits_{i = 1}^N {\left( {{\gamma _i} - 1} \right){\lambda _{\min }}\left( {{\mathit{\boldsymbol{K}}_i}} \right){{\left\| {{\mathit{\boldsymbol{\eta }}_i}} \right\|}^2}} + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^N {\frac{{\rho _i^2}}{{2{\gamma _i}}}\exp \left( { - 2{v_i}t} \right)} , \end{array} $

对上式进行积分，有

$ \begin{array}{*{20}{c}} {V\left( t \right) + \sum\limits_{i = 1}^N {\left( {1 - {\gamma _i}} \right){\lambda _{\min }}\left( {{\mathit{\boldsymbol{K}}_i}} \right)\int_0^t {{{\left\| {{\mathit{\boldsymbol{\eta }}_i}\left( \mathit{\boldsymbol{\tau }} \right)} \right\|}^2}{\rm{d}}\mathit{\boldsymbol{\tau }}} } \le }\\ {V\left( 0 \right) + \sum\limits_{i = 1}^N {\frac{{\rho _i^2}}{{4{\gamma _i}{v_i}}}} .} \end{array} $

(13)

根据0＜γ_i＜1，可得V有界.Euler-Lagrange方程中M_i，C_i有界，再根据式(11)，可知η_i和${{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_i}$均有界.由η_i有界，根据文献[15]可知σ_i, ${{\mathit{\boldsymbol{\dot \sigma }}}_i}$有界.再由σ_i, ${{\mathit{\boldsymbol{\dot \sigma }}}_i}$有界，根据式(7)中σ_r的描述可得σ_r, ${{\mathit{\boldsymbol{\dot \sigma }}}_r}$有界.由式(7)得到‖Y_iΘ_i‖≤‖M_i‖‖${{\mathit{\boldsymbol{\dot \sigma }}}_r}$‖+‖C_i‖‖σ_r‖，因此‖Y_i‖有上界.M_i, C_i, η_i, Y_i有界，由式(8)可得${{\mathit{\boldsymbol{\dot \eta }}}_i}$有界.据此，η_i, ${{\mathit{\boldsymbol{\dot \eta }}}_i}$∈L_∞，再根据式(13)可得

$ \begin{array}{*{20}{c}} {\sum\limits_{i = 1}^N {\left( {1 - {\gamma _i}} \right){\lambda _{\min }}\left( {{\mathit{\boldsymbol{K}}_i}} \right)\int_0^t {{{\left\| {{\mathit{\boldsymbol{\eta }}_i}\left( \mathit{\boldsymbol{\tau }} \right)} \right\|}^2}{\rm{d}}\mathit{\boldsymbol{\tau }}} } \le }\\ {V\left( 0 \right) + \sum\limits_{i = 1}^N {\frac{{\rho _i^2}}{{4{\gamma _i}{v_i}}}} .} \end{array} $

说明$\int_0^t {} $‖η_i(τ)‖²dτ有界，且η_i∈L₂.根据文献[14]，可知当t→∞时，η_i→0.再根据文献[15]，可知当t→∞时，σ_i→σ₀且${{{\mathit{\boldsymbol{\dot \sigma }}}_i}} $→0.由ω_i=G(σ_i)^-1${{\mathit{\boldsymbol{\dot \sigma }}}_i}$，可知当t→∞时，ω_i→0.跟随者姿态可渐近收敛到领航者姿态，姿态角速度收敛到0.

3 Zeno现象的排除

Zeno现象定义为：如果在一个有限的时间区间内，一个事件发生了无限次，则该系统中存在Zeno现象^[16].Zeno现象是事件驱动控制中最糟糕的情况，出现了Zeno现象说明该控制由离散控制变为连续控制，通信也是连续的，这样无法体现事件驱动控制在节约资源和减少通信负荷方面的优势，说明此次事件驱动控制失败.因此，在事件驱动控制中，除了事件驱动函数及事件驱动控制器的设计，还需要排除Zeno现象，即确定事件触发间隔时间有一个正下界.

定义事件驱动函数(10)的触发间隔时间为t_k+1ⁱ-t_kⁱ≥T，其中t_kⁱ、t_k+1ⁱ分别为卫星i的第k次和第k+1次事件触发时刻.T表示事件触发间隔时间的下界，需证明T严格正定，不会出现Zeno现象.

定理2  如果定理1的条件成立，则事件驱动函数(10)的事件触发间隔时间具有正下界，即整个闭环系统不会产生Zeno现象.

对‖e_ηi(t)‖求导并带入式(11)，其中t∈[t_kⁱ, t_k+1ⁱ)

$ \frac{{\rm{d}}}{{{\rm{d}}t}}\left\| {{\mathit{\boldsymbol{e}}_{{\eta _i}}}\left( t \right)} \right\| \le \left\| {{{\mathit{\boldsymbol{\dot \eta }}}_i}\left( t \right)} \right\|. $

(14)

已在分布式自适应控制器设计中证明${{\mathit{\boldsymbol{\dot \eta }}}_i}$(t)有界.令正常数U_η表示‖${{\mathit{\boldsymbol{\dot \eta }}}_i}$(t)‖的上界，得到$\frac{{\rm{d}}}{{{\rm{d}}\mathit{t}}}\left\| {{\mathit{\boldsymbol{e}}_{{\mathit{\boldsymbol{\eta }}_i}}}\left( t \right)} \right\| \le {U_\eta } $.

类似于式(14)，对‖e_i(t)‖求导可得

$ \begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}t}}\left\| {{\mathit{\boldsymbol{e}}_i}\left( t \right)} \right\| \le \left\| {\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\mathit{\boldsymbol{Y}}_i}\left( t \right){{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}\left( t \right)} \right)} \right\| = }\\ {\left\| {{{\mathit{\boldsymbol{\dot Y}}}_i}\left( t \right){{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}\left( t \right) + {\mathit{\boldsymbol{Y}}_i}\left( t \right){{\mathit{\boldsymbol{ \boldsymbol{\dot {\hat \varTheta}} }}}_i}\left( t \right)} \right\|.} \end{array} $

在分布式自适应控制器设计中证明了Y_i(t)和${{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}$(t)有界，根据文献[12]中的假设1可知，${\mathit{\boldsymbol{\dot Y}}}$有界.又由Y_i(t)、η_i(t)有界，根据式(5)可知${{\mathit{\boldsymbol{ \boldsymbol{\dot {\hat \varTheta}} }}}_i}$(t)有界.令正常数U_e表示‖ $\left\| {\frac{{\rm{d}}}{{{\rm{d}}\mathit{t}}}\left( {{\mathit{\boldsymbol{Y}}_\mathit{i}}\left( t \right){{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}_i}\left( t \right)} \right)} \right\|$的上界，可得$\frac{{\rm{d}}}{{{\rm{d}}\mathit{t}}}\left\| {{\mathit{\boldsymbol{e}}_i}\left( t \right)} \right\| \le {U_e}$.

令U=max{U_e, λ_max(K_i)U_η}，可得

$ \begin{array}{*{20}{c}} {\left\| {{\mathit{\boldsymbol{e}}_i}\left( t \right)} \right\| + {\lambda _{\max }}\left( {{\mathit{\boldsymbol{K}}_i}} \right)\left\| {{\mathit{\boldsymbol{e}}_{{\eta _i}}}\left( t \right)} \right\| \le }\\ {2\int_{t_k^i}^t {U{\rm{d}}t} = 2U\left( {t - t_k^i} \right),t \in \left[ {t_k^i,t_{k + 1}^i} \right).} \end{array} $

(15)

根据事件驱动函数(10)，‖e_i(t)‖+λ_max(K_i)‖e_ηi(t)‖≥ $\frac{{{\gamma _i}}}{2}$λ_min(K_i)‖η_i(t)‖+μ_i(t)在下一触发时刻t_k+1ⁱ成立.分布式自适应控制器设计中证明了当t→∞时η_i→0.但在t_k+1ⁱ时刻可能存在η_i(t)=0，${{\dot \eta }_i}$(t)≠0的情况，此时系统并未达到领航者—跟随者姿态一致.因此，在下列两种情况下t_k+1ⁱ时刻事件触发.

情况1  当‖η_i(t_k+1ⁱ)‖≠0时，事件触发条件为‖e_i(t_k+1ⁱ)‖+λ_max(K_i)‖e_ηi(t_k+1ⁱ)‖≥ $\frac{{{\gamma _i}}}{2}$λ_min(K_i)‖η_i(t_k+1ⁱ)‖+μ_i(t_k+1ⁱ).

情况2  当‖η_i(t_k+1ⁱ)‖=0时，事件触发条件为‖e_i(t_k+1ⁱ)‖+λ_max(K_i)‖e_ηi(t_k+1ⁱ)‖≥μ_i(t_k+1ⁱ).

由于‖η_i(t_k+1ⁱ)‖≥0，分析可知情况1成立需要的时间更长，说明T₂＜T₁.因此只需证明事件触发间隔时间T₂为严格正常数，使得卫星编队系统不会出现Zeno现象.根据式(15)，可推导事件触发间隔时间T₂的下界为

$ 2U{T_2} \ge {\mathit{\boldsymbol{\rho }}_i}\sqrt {{\lambda _{\min }}\left( {{\mathit{\boldsymbol{K}}_i}} \right)} \exp \left( { - {v_i}{T_2}} \right), $

式中:U为正常数，所以解严格正定，卫星编队系统不会出现Zeno现象.

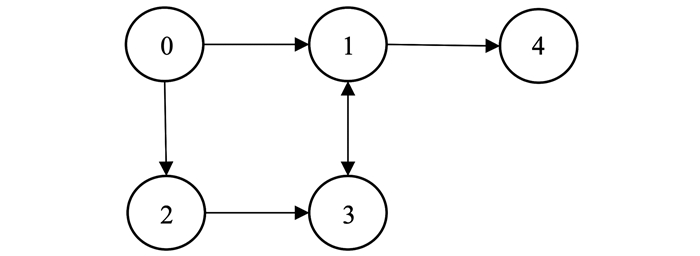
4 数值仿真

本文将进行数值仿真验证所提控制器(5)的有效性.以5颗卫星编队飞行为例，领航者和跟随者间通信拓扑如图 1所示.其中：0表示领航卫星，1-4表示跟随卫星.编队卫星的初始姿态和姿态角速度见表 1.仿真过程中领航者姿态不变.

跟随者的转动惯量矩阵如下:

$ {\mathit{\boldsymbol{J}}_1} = \left( {\begin{array}{*{20}{c}} {20.0}&0&{0.2}\\ 0&{25.0}&0\\ {0.2}&{0.0}&{29.0} \end{array}} \right){\rm{kg}} \cdot {{\rm{m}}^2}, $

$ {\mathit{\boldsymbol{J}}_2} = \left( {\begin{array}{*{20}{c}} {22.0}&{0.1}&{0.5}\\ {0.1}&{24.0}&0\\ {0.5}&{0.0}&{22.0} \end{array}} \right){\rm{kg}} \cdot {{\rm{m}}^2}, $

$ {\mathit{\boldsymbol{J}}_3} = \left( {\begin{array}{*{20}{c}} {25.0}&{0.4}&{0.2}\\ {0.4}&{29.0}&{0.1}\\ {0.2}&{0.1}&{21.0} \end{array}} \right){\rm{kg}} \cdot {{\rm{m}}^2}, $

$ {\mathit{\boldsymbol{J}}_4} = \left( {\begin{array}{*{20}{c}} {23.0}&{0.4}&0\\ {0.4}&{26.0}&{0.8}\\ 0&{0.8}&{28.0} \end{array}} \right){\rm{kg}} \cdot {{\rm{m}}^2}. $

初始估计参数为${\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}$(0)=[23.0, 25.0, 25.0, 0, 0, 0]^T

控制器和事件驱动函数参数分别为

$ {\mathit{\boldsymbol{K}}_i} = {\left[ {\begin{array}{*{20}{c}} 5&5&5 \end{array}} \right]^{\rm{T}}},{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_i} = {\rm{diag}}\left( {\left[ {\begin{array}{*{20}{c}} 2&2&2 \end{array}} \right]} \right), $

$ \alpha = 0.08,{\gamma _i} = 0.6,{\rho _i} = 5,{v_i} = 0.4. $

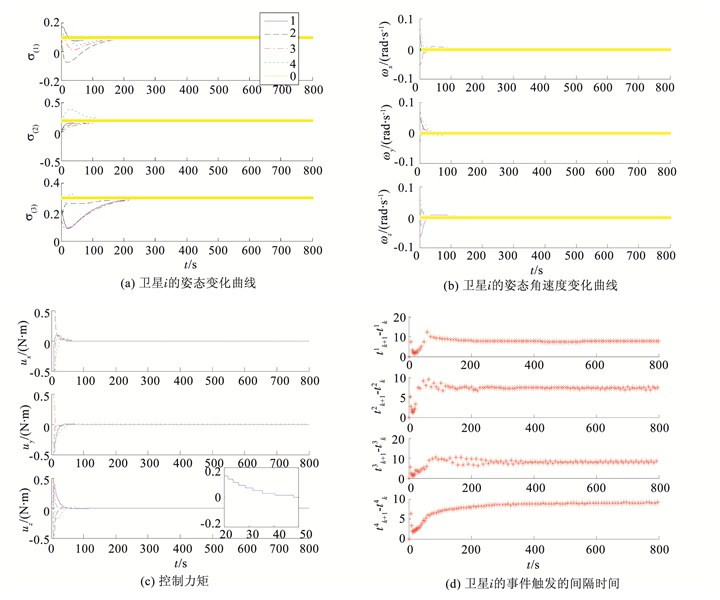
仿真结果如图 2所示.在事件驱动自适应控制器作用下，跟随卫星在300 s内收敛至领航卫星姿态，姿态角速度在180 s左右收敛到0.控制力矩如图 2(c)所示，在100 s左右收敛到0，其中u_1z在20~50 s的仿真结果如局部放大图所示，为分段函数，说明设计的事件驱动自适应控制输入在非触发时刻使用上一触发时刻的数据，只有在下一个触发时刻控制输入才更新.各卫星的事件触发间隔时间如图 2(d)所示，在初始阶段，卫星编队系统状态与期望控制状态相差很远，事件触发次数多一些，控制输入的更新较为频繁，但当系统渐近收敛到期望状态时，事件触发次数减少，相邻事件触发间隔时间增大，最后趋于稳定.

在相同控制参数及初始条件下，采用传统的姿态自适应控制器^[17]，仿真结果如图 3所示.系统的姿态在300 s左右收敛到领航者状态，姿态角速度在150 s左右收敛到0.控制器连续更新，在100 s内收敛到0.可以看出，通过合理设计事件触发函数及控制器，事件驱动控制可以在保证系统控制性能的同时，减少计算量和通信量，降低控制输入更新频次，节省星上资源.

表 2为控制参数的选择对系统稳定性和事件触发频次的影响.随着K_i增大，卫星编队系统的收敛速度增大，系统的稳定时间变短.但事件触发频次随之增大，控制输入更新次数增多，计算量变大，需要更多的计算及通信资源.在K_i确定的情况下，分析α变化对系统和事件触发频次的影响：初始阶段，随着α增大，系统稳定时间减小，事件触发频次也随之减小；当α增大到一定范围后，随着α的增大，系统稳定时间减小，但事件触发频次也随之增大.需要根据具体任务需求和系统性能合理选择控制参数.Γ_i对系统稳定性和事件触发频次影响较小.

5 结论

1) 针对卫星编队系统资源和通信带宽受限的问题，在Euler-Lagrange框架内设计了基于事件驱动的卫星编队相对姿态分布式自适应控制算法.利用Lyapunov理论证明了设计的事件驱动自适应控制器和事件驱动函数可以使得闭环系统渐近稳定，并证明了卫星编队系统不会产生Zeno现象.

2) 在仿真条件和初始条件相同的情况下，将其与传统的自适应控制算法比较.证明了所设计的事件驱动控制器在保证系统性能的前提下，可有效降低控制输入更新频次，减少信息交互量，有效节约星上资源.

3) 分析了控制参数对系统稳定性和控制输入更新频次的影响.随着控制参数K_i的增加，系统收敛速度增大，稳定时间减小，但事件触发频次随之增大，不利于星上资源的利用.在一定范围内，α增大事件触发频次减小，当α超过一定范围，随着α增大事件触发频次增大.需要在满足系统控制性能的前提下，合理选择控制参数.