2. 上海机电工程研究所,上海 201109
2. Shanghai Institute of Electro-Mechanical Engineering, Shanghai 201109 China
旋转导弹是指弹体在飞行过程中绕自身纵轴连续滚转的一类导弹[1].滚转产生的陀螺定轴效应有利于增强姿态的稳定性[2],减少不对称等干扰因素的影响,简化控制系统结构.因此,旋转体制广泛用于各类导弹[3-4].
但是,旋转导弹除绕纵轴旋转外,还存在弹体纵轴绕速度矢量的锥形运动[5].对此,文献[6]阐述了角运动失稳的机理和形式;文献[7]使用拟线性法得到了旋转导弹锥形运动近似解;文献[8]给出了弹道顶点附近锥形运动的稳定判据;文献[9-10]研究了弹性对旋转导弹锥形运动的影响;文献[11]则对控制系统作用下旋转导弹的锥形运动进行了分析.绝大多数相关文献在研究时都认为旋转导弹的质量不变,但这与事实不符[12-13].文献[14]针对均匀燃烧的变质量圆柱体推导了动力学模型并给出了旋转角速度表达式.文献[15]利用变质量力学原理给出了较为详细的喷气阻尼和变质量特性模型.上述文献都未考虑影响较大的气动力矩,且忽略了药柱燃烧导致的质心变化.
针对该问题,本文建立了综合考虑变质量特性、气动力矩和气动阻尼效应的旋转导弹动力学模型,并利用常微分方程理论得出旋转导弹锥形运动的解析解,并分析了喷气阻尼效应对锥形运动的影响,最后通过仿真对分析结果进行了验证.
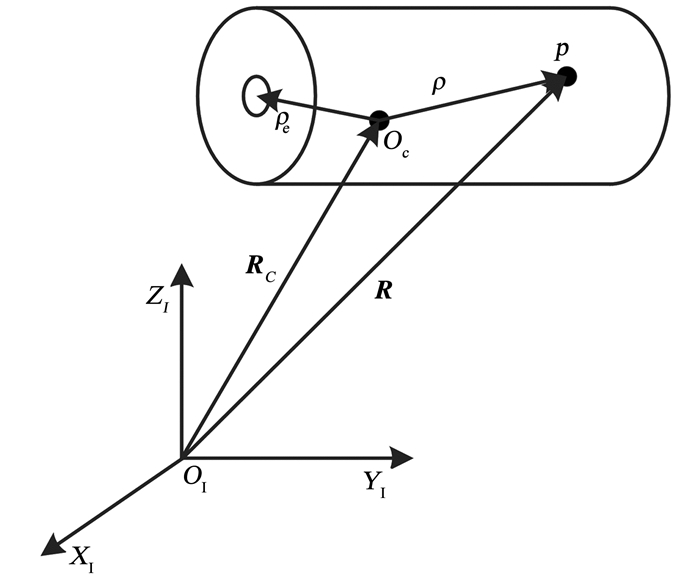
1 数学模型 1.1 喷气阻尼效应旋转导弹实际上是由无数个质点组成的连续质点系,如图 1所示.其中:OI-XIYIZI为惯性参考系,Oc为系统的质心,p为系统中任一质点元,Rc为惯性坐标系中系统质心Oc的矢径,ρ为质心Oc到质点元p的矢量,R为惯性坐标系中质点元p的矢径,ρe为质心Oc到喷口截面中心的矢量.
|
图 1 连续质点系 Figure 1 Continuous particle system |
根据变质量力学的基本原理,连续质点系的转动方程为[16]
| $ {{\mathit{\boldsymbol{\bar I}}}_{\rm{c}}} \cdot \frac{{{\rm{d}}{\mathit{\boldsymbol{\omega }}_{\rm{T}}}}}{{{\rm{d}}t}} + {\mathit{\boldsymbol{\omega }}_{\rm{T}}} \times \left( {{{\bar I}_{\rm{c}}} \cdot {\mathit{\boldsymbol{\omega }}_{\rm{T}}}} \right) = {\mathit{\boldsymbol{M}}_{\rm{c}}} + {{\mathit{\boldsymbol{M'}}}_{\rm{k}}} + {{\mathit{\boldsymbol{M'}}}_{{\rm{rel}}}}. $ |
式中:Ic为惯量张量;ωT为质点系的旋转角速度;Mc为质点系所受外力矩;M′k为附加哥氏力矩;M′rel为附加相对力矩.结合旋转导弹的特性,惯量张量、附加哥氏力矩和附加相对力矩的具体计算公式分别为
| $ {{\mathit{\boldsymbol{\bar I}}}_{\rm{c}}} = \left[ {\begin{array}{*{20}{c}} {{J_x}}&0&0\\ 0&{{J_e}}&0\\ 0&0&{{J_e}} \end{array}} \right]. $ |
式中:Jx为旋转导弹相对纵轴的转动惯量,Je为旋转导弹相对横轴的转动惯量.
| $ {{\mathit{\boldsymbol{M'}}}_{\rm{k}}} = - \frac{{{\rm{ \mathsf{ δ} }}{{\mathit{\boldsymbol{\bar I}}}_{\rm{c}}}}}{{\delta t}} \cdot {\mathit{\boldsymbol{\omega }}_{\rm{T}}} - \dot m{{\mathit{\boldsymbol{\bar J}}}_e} \cdot {\mathit{\boldsymbol{\omega }}_{\rm{T}}}. $ |
其中:
| $ {{\mathit{\boldsymbol{\bar J}}}_e} = \left[ {\begin{array}{*{20}{c}} {\frac{{R_e^2}}{2}}&0&0\\ 0&{\rho _{ex1}^2 + \frac{{R_e^2}}{4}}&0\\ 0&0&{\rho _{ex1}^2 + \frac{{R_e^2}}{4}} \end{array}} \right]. $ |
式中:Re为喷口截面半径,ρex1为旋转导弹质心到喷口截面中心的距离.
| $ {{\mathit{\boldsymbol{M'}}}_{{\rm{rel}}}} = - \dot m{\mathit{\boldsymbol{\rho }}_e} \times {\mathit{\boldsymbol{V}}_{rb}}. $ |
式中:ρ
旋转导弹在准弹体坐标系下的转动方程为
| $ \left\{ \begin{array}{l} {J_x}\frac{{{\rm{d}}{\omega _{x4}}}}{{{\rm{d}}t}} = {M_{sx}} + {{\mathit{\boldsymbol{M'}}}_{kx}},\\ {J_e}\frac{{{\rm{d}}{\omega _{y4}}}}{{{\rm{d}}t}} + \left( {{J_x} - {J_e}} \right){\omega _{x4}}{\omega _{z4}} + {J_e}{\omega _{z4}}\dot \gamma = {M_{sy}} + {{M'}_{ky}},\\ {J_e}\frac{{{\rm{d}}{\omega _{z4}}}}{{{\rm{d}}t}} + \left( {{J_e} - {J_x}} \right){\omega _{y4}}{\omega _{x4}} - {J_e}{\omega _{y4}}\dot \gamma = {M_{sz}} + {{M'}_{kz}}. \end{array} \right. $ | (1) |
式中:ωx4、ωy4、ωz4分别为导弹旋转角速度在准弹体坐标系下的3个分量;
对于旋转导弹的纵向转动,由于有
| $ \left\{ \begin{array}{l} {M_{sx}} = {M_{x0}} + M_x^{\omega x}{\omega _x},\\ {{M'}_{kx}} = - \left( {\frac{{{\rm{ \mathsf{ δ} }}{J_x}}}{{{\rm{ \mathsf{ δ} }}t}} + \frac{{R_e^2}}{2}\dot m} \right){\omega _{x4}}. \end{array} \right. $ |
式中:Mx0为导弹转速为0时的滚转力矩,Mxωx为滚转阻尼力矩系数.
因此旋转导弹纵向运动方程如下
| $ {J_x}\frac{{{\rm{d}}{\omega _{x4}}}}{{{\rm{d}}t}} + \left( {\frac{{{\rm{ \mathsf{ δ} }}{J_x}}}{{{\rm{ \mathsf{ δ} }}t}} + \frac{{R_e^2}}{2}\dot m} \right){\omega _{x4}} = {M_{x0}} + M_x^{\omega x}{\omega _x}. $ | (2) |
对于旋转导弹的横向转动,则有
| $ \left\{ \begin{array}{l} {{M'}_{ky}} = - \left( {\frac{{\delta {J_e}}}{{\delta t}} + \rho _{ex1}^2\dot m + \frac{{R_e^2}}{4}\dot m} \right){\omega _{y4}},\\ {{M'}_{kz}} = - \left( {\frac{{\delta {J_e}}}{{\delta t}} + \rho _{ex1}^2\dot m + \frac{{R_e^2}}{4}\dot m} \right){\omega _{z4}}. \end{array} \right. $ | (3) |
将式(3)代入式(1)可得旋转导弹横向转动的动力学方程:
| $ \left\{ \begin{array}{l} {J_e}\frac{{{\rm{d}}{\omega _{y4}}}}{{{\rm{d}}t}} + {J_x}{\omega _{x4}}{\omega _{z4}} + \left( {\frac{{\delta {J_e}}}{{\delta t}} + \rho _{ex1}^2\dot m + \frac{{R_e^2}}{4}\dot m} \right){\omega _{y4}} = {M_{sy}},\\ {J_e}\frac{{{\rm{d}}{\omega _{z4}}}}{{{\rm{d}}t}} - {J_x}{\omega _{x4}}{\omega _{y4}} + \left( {\frac{{\delta {J_e}}}{{\delta t}} + \rho _{ex1}^2\dot m + \frac{{R_e^2}}{4}\dot m} \right){\omega _{z4}} = {M_{sz}}. \end{array} \right. $ | (4) |
此外,气动力矩的表达式为
| $ \left\{ \begin{array}{l} {M_{sy}} = m_z^\alpha qSL{\beta ^ * } + m_z^{\omega x\alpha }qSL{\omega _{x4}}{\alpha ^ * } + m_z^{\omega z}qSL{\omega _{y4}},\\ {M_{sz}} = m_z^\alpha qSL{\alpha ^ * } - m_z^{\omega x\alpha }qSL{\omega _{x4}}{\beta ^ * } + m_z^{\omega z}qSL{\omega _{z4}}. \end{array} \right. $ | (5) |
式中:mzα为气动稳定力矩系数; mzωxα为马格努斯力矩系数; mzωz为气动阻尼力矩系数; q为动压; S为参考面积; L为参考长度; α*、β*分别为准攻角和准侧滑角.
在研究旋转导弹短时姿态运动时可假设速度参数不变和角度较小[1].
| $ \left\{ \begin{array}{l} {\omega _x} = \dot \gamma ,\\ {\omega _y} = \dot \psi = {{\dot \beta }^ * },\\ {\omega _z} = \dot \vartheta = {{\dot \alpha }^ * }. \end{array} \right. $ | (6) |
式中:γ为滚转角; ψ为偏航角; ϑ为俯仰角; β*为准侧滑角; α*为准攻角.
将式(5)、(6)代入式(4)可得
| $ \left\{ \begin{array}{l} {J_e}{{\ddot \beta }^ * } + {J_x}\dot \gamma {{\dot \alpha }^ * } + \left( {\frac{{\delta {J_e}}}{{\delta t}} + \rho _{ex1}^2\dot m + \frac{{R_e^2}}{4}\dot m} \right){{\dot \beta }^ * } = \\ m_z^\alpha qSL{\beta ^ * } + m_z^{\omega x\alpha }qSL\dot \gamma {\alpha ^ * } + m_z^{\omega z}qSL{{\dot \beta }^ * },\\ {J_e}{{\ddot \alpha }^ * } - {J_x}\dot \gamma {{\dot \beta }^ * } + \left( {\frac{{\delta {J_e}}}{{\delta t}} + \rho _{ex1}^2\dot m + \frac{{R_e^2}}{4}\dot m} \right){{\dot \alpha }^ * } = \\ m_z^\alpha qSL{\alpha ^ * } - m_z^{\omega x\alpha }qSL\dot \gamma {\beta ^ * } + m_z^{\omega z}qSL{{\dot \alpha }^ * }. \end{array} \right. $ | (7) |
令
| $ \left\{ \begin{array}{l} {D_{\rm{J}}} = \frac{{\delta {J_e}}}{{\delta t}} + \rho _{ex1}^2\dot m + \frac{{R_e^2}}{4}\dot m,\\ M_s^\delta = m_z^\alpha qSL,\\ {{M''}_m} = m_z^{\omega x\alpha }qSL,\\ M_d^{\omega b} = m_z^{\omega z}qSL. \end{array} \right. $ | (8) |
式中:DJ为附加哥氏力矩,包含了变质量特性和喷气阻尼力矩;Msδ为气动稳定力矩;Mm″为马格努斯力矩;Mdωb为气动阻尼力矩.
则式(7)可转化为
| $ \left\{ \begin{array}{l} {{\ddot \beta }^ * } + \frac{{{D_{\rm{J}}} - M_d^{\omega b}}}{{{J_e}}}{{\dot \beta }^ * } + \frac{{{J_x}}}{{{J_e}}}\dot \gamma {{\dot \alpha }^ * } - \frac{{M_s^\delta }}{{{J_e}}}{\beta ^ * } - \frac{{{{M''}_m}}}{{{J_e}}}\dot \gamma {\alpha ^ * } = 0,\\ {{\ddot \alpha }^ * } + \frac{{{D_{\rm{J}}} - M_d^{\omega b}}}{{{J_e}}}{{\dot \alpha }^ * } - \frac{{{J_x}}}{{{J_e}}}\dot \gamma {{\dot \beta }^ * } - \frac{{M_s^\delta }}{{{J_e}}}{\alpha ^ * } + \frac{{{{M''}_m}}}{{{J_e}}}\dot \gamma {\beta ^ * } = 0. \end{array} \right. $ | (9) |
在质量特性的计算中需引入定心体坐标系,该坐标系由弹体坐标系的原点平移至药柱前端面而成,坐标轴指向保持不变.设导弹在弹体坐标系中的转动惯量张量矩阵为Jc,在定心体坐标系中的惯量张量矩阵为Jo,导弹质心相对固定中心的矢径在体坐标系中的分量rc=[xc yc zc]T,导弹的质量为M.则有
| $ {{\mathit{\boldsymbol{\bar J}}}_c} = {{\mathit{\boldsymbol{\bar J}}}_o} - M\left( {\mathit{\boldsymbol{\bar r}}_c^{\rm{T}}{{\mathit{\boldsymbol{\bar r}}}_c}\mathit{\boldsymbol{\bar E}} - {{\mathit{\boldsymbol{\bar r}}}_c}\mathit{\boldsymbol{\bar r}}_c^{\rm{T}}} \right), $ | (10) |
式中,E为单位矩阵.
对式(10)等号两边求导可得
| $ \begin{array}{l} \frac{{{\rm{ \mathsf{ δ} }} {{\mathit{\boldsymbol{\bar J}}}_c}}}{{{\rm{ \mathsf{ δ} }}t}} = \frac{{{\rm{ \mathsf{ δ} }} {{\mathit{\boldsymbol{\bar J}}}_o}}}{{{\rm{ \mathsf{ δ} }}t}} - M\left( {\frac{{{\rm{ \mathsf{ δ} }} \mathit{\boldsymbol{\bar r}}_c^{\rm{T}}}}{{{\rm{ \mathsf{ δ} }}t}}{{\mathit{\boldsymbol{\bar r}}}_c}\mathit{\boldsymbol{\bar E}} - \frac{{{\rm{ \mathsf{ δ} }} {{\mathit{\boldsymbol{\bar r}}}_c}}}{{{\rm{ \mathsf{ δ} }}t}}\mathit{\boldsymbol{\bar r}}_c^{\rm{T}}} \right) + \\ \;\;\;\;\;\;\;\;\dot m\left( {\mathit{\boldsymbol{\bar r}}_c^{\rm{T}}{{\mathit{\boldsymbol{\bar r}}}_c}\mathit{\boldsymbol{\bar E}} - {{\mathit{\boldsymbol{\bar r}}}_c}\mathit{\boldsymbol{\bar r}}_c^{\rm{T}}} \right) - \mathit{\boldsymbol{M}}\left( {\mathit{\boldsymbol{\bar r}}_c^{\rm{T}}\frac{{{\rm{ \mathsf{ δ} }} {{\mathit{\boldsymbol{\bar r}}}_c}}}{{{\rm{ \mathsf{ δ} }}t}}\mathit{\boldsymbol{\bar E}} - {{\mathit{\boldsymbol{\bar r}}}_c}\frac{{{\rm{ \mathsf{ δ} }} \mathit{\boldsymbol{\bar r}}_c^{\rm{T}}}}{{{\rm{ \mathsf{ δ} }}t}}} \right). \end{array} $ | (11) |
导弹的质量M分为发动机药柱的质量M1和除发动机药柱的导弹质量M2,这两部分质量相对定心体坐标系的转动惯量张量矩阵分别为Jo1和Jo2,有
| $ \left\{ \begin{array}{l} M = {M_1} + {M_2},\\ {{\bar J}_o} = {{\bar J}_{o1}} + {{\bar J}_{o2}}. \end{array} \right. $ | (12) |
设药柱初始后端面(初始燃烧面)距前端面的距离为L20,药柱燃烧时间为tw.因此在发动机点火后t时刻,药柱燃烧面距oByBzB平面的距离L2为
| $ {L_2} = {L_{20}} - \frac{{{L_{20}}}}{{{t_w}}}t. $ | (13) |
设药柱初始质量为M10,则t时刻药柱的质量为
| $ {M_1} = {M_{10}} - \dot mt, $ | (14) |
而t时刻药柱转动惯量张量矩阵各分量为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{J}}_{ox1}} = \frac{1}{2}{M_1}R_c^2,\\ {\mathit{\boldsymbol{J}}_{oe1}} = {M_1}\left( {\frac{{R_c^2}}{4} + \frac{{L_2^2}}{3}} \right), \end{array} \right. $ | (15) |
式中Rc为药柱的半径.
设导弹除发动机药柱之外的质量M2的质心在定心体坐标系中的位置矢量为
| $ {{\mathit{\boldsymbol{\bar r}}}_{c2}} = {\left[ {\begin{array}{*{20}{c}} {{x_{c2}}}&0&0 \end{array}} \right]^{\rm{T}}}, $ | (16) |
而导弹质心在定心体坐标系中的位置矢量为
| $ {{\mathit{\boldsymbol{\bar r}}}_{c2}} = {\left[ {\begin{array}{*{20}{c}} {{x_c}}&0&0 \end{array}} \right]^{\rm{T}}}, $ | (17) |
则有
| $ \mathit{xc} = \frac{{ - \frac{{{M_1}{L_2}}}{2} + {M_2}{x_{c2}}}}{{{M_1} + {M_2}}}. $ | (18) |
将式(12)~(18)代入式(11)即可计算得到导弹在弹体坐标系下的转动惯量变化率.
2 喷气阻尼对自旋转速的影响分析对于自旋转速,由式(2)整理可得
| $ {J_x}\frac{{{\rm{d}}{\omega _{x4}}}}{{{\rm{d}}t}} + \left( {\frac{{{\rm{ \mathsf{ δ} }}{J_x}}}{{{\rm{ \mathsf{ δ} }}t}} + \frac{{R_e^2}}{2}\dot m - M_x^{\omega x}} \right){\omega _{x4}} - {M_{x0}} = 0. $ | (19) |
假设发动机药柱均匀燃烧,此时Jx线性变化为
| $ {J_x} = {J_{x0}} + {{\dot J}_x}t. $ | (20) |
式中:Jx0为初始时刻的转动惯量,
将式(20)代入式(19)可得
| $ \frac{{{\rm{d}}{\omega _{x4}}}}{{{\rm{d}}t}} + \frac{{{{\dot J}_x} + \frac{{R_e^2}}{2}\dot m - M_x^{\omega x}}}{{{J_{x0}} + {{\dot J}_x}t}}{\omega _{x4}} = \frac{{{M_{x0}}}}{{{J_{x0}} + {{\dot J}_x}t}}. $ | (21) |
式(21)的解为
| $ \begin{array}{l} {\omega _{x4}} = \frac{{{M_{x0}}}}{{{{\dot J}_x} + \frac{{R_e^2}}{2}\dot m - M_x^{\omega x}}} + \\ \;\;\;\;\;\;\;\;C{\left( {{J_{x0}} + {{\dot J}_x}t} \right)^{ - \left( {1 + \frac{{{R^2}\dot m}}{{2{{\dot J}_x}}} - \frac{{M_x^{\omega x}}}{{{{\dot J}_x}}}} \right)}}, \end{array} $ | (22) |
式中,C为常数,表达式如下
| $ C = J_{x0}^{1 + \frac{{{R^2}\dot m}}{{2{{\dot J}_x}}} - \frac{{M_x^{\omega x}}}{{{{\dot J}_x}}}}\left( {{\omega _{x0}} - \frac{{{M_{x0}}}}{{{{\dot J}_x} + \frac{{R_e^2}}{2}\dot m - M_x^{\omega x}}}} \right). $ |
式(22)右端第1项为常值,代表角速度的稳态值; 右端第2项的变化规律取决于指数的符号.
1) 当|δJx/δt|>
2) 当|δJx/δt|<
3) 当|δJx/δt|=
由上述分析可知,转速的变化取决于气动阻尼力矩,以及药柱半径和喷口半径的相对大小.
若需保持转速不变,则应有
| $ {R_c} = {R_e}\sqrt {1 - \frac{{2M_x^{\omega x}}}{{\dot mR_e^2}}} . $ |
因此在考虑气动力矩的情况下,若要保持转速不变应使药柱半径略小于喷口截面半径.
3 喷气阻尼对锥形运动的影响分析对于锥形运动,引入复攻角Δ=β*+iα*,式(9)可化为
| $ \ddot \Delta + \left( {\frac{{{D_{\rm{J}}} - M_d^{\omega b}}}{{{J_e}}} - {\rm{i}}\frac{{{J_x}}}{{{J_e}}}\dot \gamma } \right)\dot \Delta - \left( {\frac{{M_s^\delta }}{{{J_e}}} - {\rm{i}}\frac{{{{M''}_m}}}{{{J_e}}}\dot \gamma } \right)\Delta = 0. $ | (23) |
式(23)的特征方程为
| $ {\lambda ^2} + \left( {\frac{{{D_{\rm{J}}} - M_d^{\omega b}}}{{{J_e}}} - {\rm{i}}\frac{{{J_x}}}{{{J_e}}}\dot \gamma } \right)\lambda - \left( {\frac{{M_s^\delta }}{{{J_e}}} - {\rm{i}}\frac{{{{M''}_m}}}{{{J_e}}}\dot \gamma } \right) = 0, $ |
其根为
| $ \begin{array}{l} {\lambda _{1,2}} = \frac{1}{2}\left( {\frac{{M_d^{\omega b} - {D_{\rm{J}}}}}{{{J_e}}} + {\rm{i}}\frac{{{J_x}}}{{{J_e}}}\dot \gamma } \right) \pm \\ \;\;\;\;\;\;\;\;\frac{1}{2}\sqrt {{{\left( {\frac{{{D_{\rm{J}}} - M_d^{\omega b}}}{{{J_e}}} - {\rm{i}}\frac{{{J_x}}}{{{J_e}}}\dot \gamma } \right)}^2} + 4\left( {\frac{{M_s^\delta }}{{{J_e}}} - {\rm{i}}\frac{{{{M''}_m}}}{{{J_e}}}\dot \gamma } \right)} = \\ \;\;\;\;\;\;\;\;\frac{1}{2}\left( {\frac{{M_d^{\omega b} - {D_{\rm{J}}}}}{{{J_e}}} + {\rm{i}}\frac{{{J_x}}}{{{J_e}}}\dot \gamma } \right) \pm \frac{1}{2}\sqrt {{R_{{\rm{Re}}}} + {\rm{i}}{R_{{\mathop{\rm Im}\nolimits} }}} , \end{array} $ | (24) |
其中
| $ \left\{ \begin{array}{l} {R_{{\rm{Re}}}} = {\left( {\frac{{{D_{\rm{J}}} - M_d^{\omega b}}}{{{J_e}}}} \right)^2} + 4\frac{{M_s^\delta }}{{{J_e}}} - {\left( {\frac{{{J_x}}}{{{J_e}}}\dot \gamma } \right)^2},\\ {R_{{\mathop{\rm Im}\nolimits} }} = - 4\frac{{{{M''}_m}}}{{{J_e}}}\dot \gamma + 2\frac{{{J_x}\dot \gamma \left( {M_d^{\omega b} - {D_{\rm{J}}}} \right)}}{{J_e^2}}. \end{array} \right. $ | (25) |
设
| $ \begin{array}{l} {\lambda _{1,2}} = \frac{1}{2}\left( {\frac{{M_d^{\omega b} - {D_{\rm{J}}}}}{{{J_e}}} + {\rm{i}}\frac{{{J_x}}}{{{J_e}}}\dot \gamma } \right) + \\ \;\;\;\;\;\;\;\;\frac{1}{2}\left( { \pm \sqrt {\frac{{R + {R_{{\rm{Re}}}}}}{2}} \pm {\rm{i}}\sqrt {\frac{{R - {R_{{\rm{Re}}}}}}{2}} } \right), \end{array} $ | (26) |
式(26)中的正负号搭配由虚部RIm的符号决定.
引入动稳定因子[1]为
| $ {S_d} = 2\frac{{{J_e}{{M''}_m}}}{{{J_x}\left( {M_d^{\omega b} - {D_{\rm{J}}}} \right)}} - 1. $ |
虚部RIm可改写为
| $ {R_{{\mathop{\rm Im}\nolimits} }} = - 2\frac{{{J_x}\dot \gamma \left( {M_d^{\omega b} - {D_{\rm{J}}}} \right)}}{{J_e^2}}{S_d}. $ |
在发动机定常燃烧的状态下,有
| $ \frac{{\delta {J_e}}}{{\delta t}} = - \left( {{z^2}\dot m + \frac{{R_c^2}}{4}\dot m} \right), $ | (27) |
式中z为燃烧端面距瞬时质心的距离.对此应有
| $ {\rho _{ex1}} > z. $ | (28) |
由喷气阻尼对自旋转速的影响的分析可知,若要保持自旋转速不变,应有
| $ {R_c} \le {R_e}. $ | (29) |
根据式(8)、(27)~(29),此时有
| $ {D_{\rm{J}}} > 0, $ |
又Mdωb<0,因此有
| $ - 2\frac{{{J_x}\dot \gamma \left( {M_d^{\omega b} - {D_{\rm{J}}}} \right)}}{{J_e^2}} > 0. $ |
结合式(28)可知RIm的符号与Sd一致.因此:
1) 当Sd>0时,特征根为
| $ \begin{array}{l} {\lambda _{1,2}} = \frac{1}{2}\left( {\frac{{M_d^{\omega b} - {D_{\rm{J}}}}}{{{J_e}}} \pm \sqrt {\frac{{R + {R_{{\rm{Re}}}}}}{2}} } \right) + \\ \;\;\;\;\;\;\;\;\;\frac{1}{2}{\rm{i}}\left( {\frac{{{J_x}}}{{{J_e}}}\dot \gamma \pm \sqrt {\frac{{R - {R_{{\rm{Re}}}}}}{2}} } \right). \end{array} $ |
2) 当Sd<0时,特征根为
| $ \begin{array}{l} {\lambda _{1,2}} = \frac{1}{2}\left( {\frac{{M_d^{\omega b} - {D_{\rm{J}}}}}{{{J_e}}} \pm \sqrt {\frac{{R + {R_{{\rm{Re}}}}}}{2}} } \right) + \\ \;\;\;\;\;\;\;\;\;\frac{1}{2}{\rm{i}}\left( {\frac{{{J_x}}}{{{J_e}}}\dot \gamma \mp \sqrt {\frac{{R - {R_{{\rm{Re}}}}}}{2}} } \right). \end{array} $ |
若要保证锥形运动稳定,需有
| $ \frac{{M_d^{\omega b} - {D_{\rm{J}}}}}{{{J_e}}} + \sqrt {\frac{{R + {R_{{\rm{Re}}}}}}{2}} < 0. $ | (30) |
引入陀螺稳定因子[1]
| $ {S_g} = \frac{{\left( {{J_x}{{\dot \gamma }^2}} \right)}}{{4{J_e}M_s^\delta }}. $ |
式(30)可变形为
| $ R < {\left( {\frac{{M_d^{\omega b} - {D_{\rm{J}}}}}{{{J_e}}}} \right)^2} + {\left( {\frac{{{J_x}}}{{{J_e}}}\dot \gamma } \right)^2}\left( {1 - \frac{1}{{{S_g}}}} \right), $ | (31) |
将式(25)代入(31)并整理可得
| $ S_d^2 < 1 - \frac{1}{{{S_g}}}, $ | (32) |
式(32)即为锥形运动稳定的充要条件
4 仿真分析 4.1 质量特性导弹质量为60 kg,其中药柱质量为30 kg,长度为2.7 m,质心位于距导弹头部1.35 m处,除药柱以外部分的质心位于距导弹头部1.05 m处.在整个燃烧过程中导弹的质量特性变化如图 2所示.由图 2可知,质心位置和横向转动惯量的变化都不是线性的,这在以往的研究中往往被忽略.

|
图 2 质量特性 Figure 2 Mass characteristics |
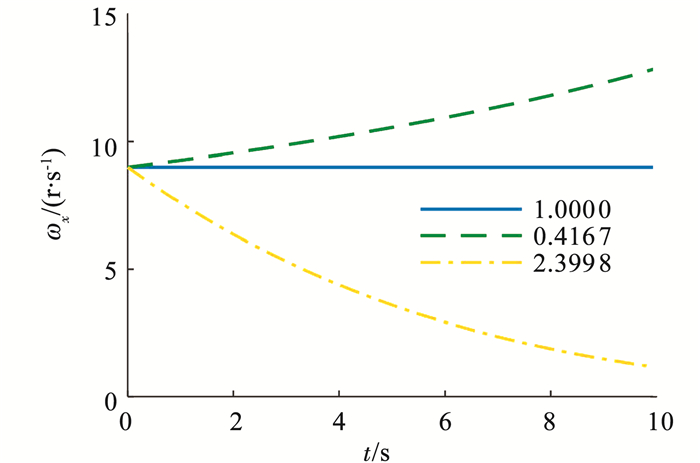
不同发动机喷口与燃烧室内径比情况下,自旋转速变化如图 3所示.由图 3可知, 仿真结果与喷气阻尼对自旋转速的影响的理论分析一致.
|
图 3 自旋转速 Figure 3 Spin speed |
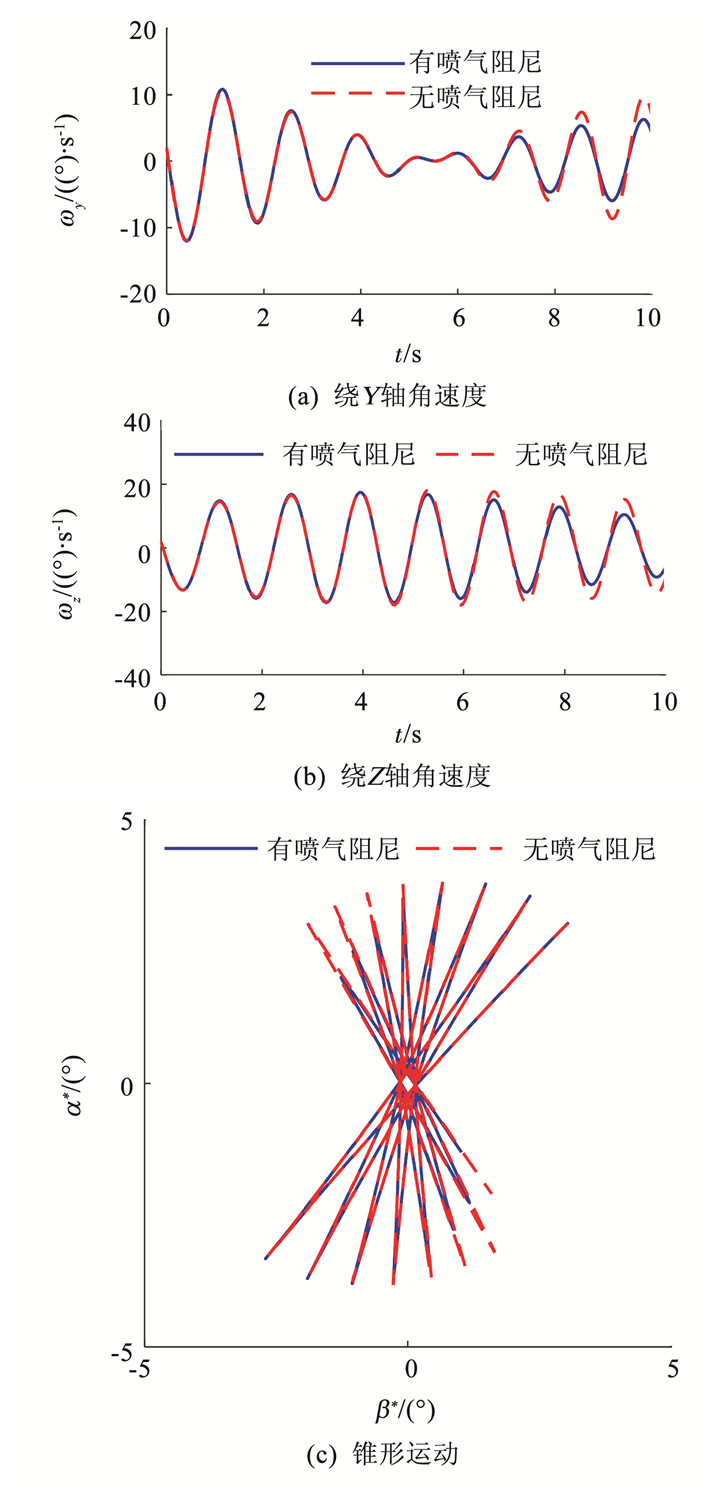
设速度大小v=170 m/s,弹道倾角θ=0°,弹道偏角ψv=0°,导弹转速
|
图 4 喷气阻尼效应对锥形运动的影响 Figure 4 The influence of jet damping effect on coning motion |
由图 4可知,喷气阻尼效应对锥形运动起阻尼作用,有利于锥形运动的稳定,且对其相位无影响, 在主动段对锥形运动的影响不可忽略,在旋转导弹设计中应加以考虑.
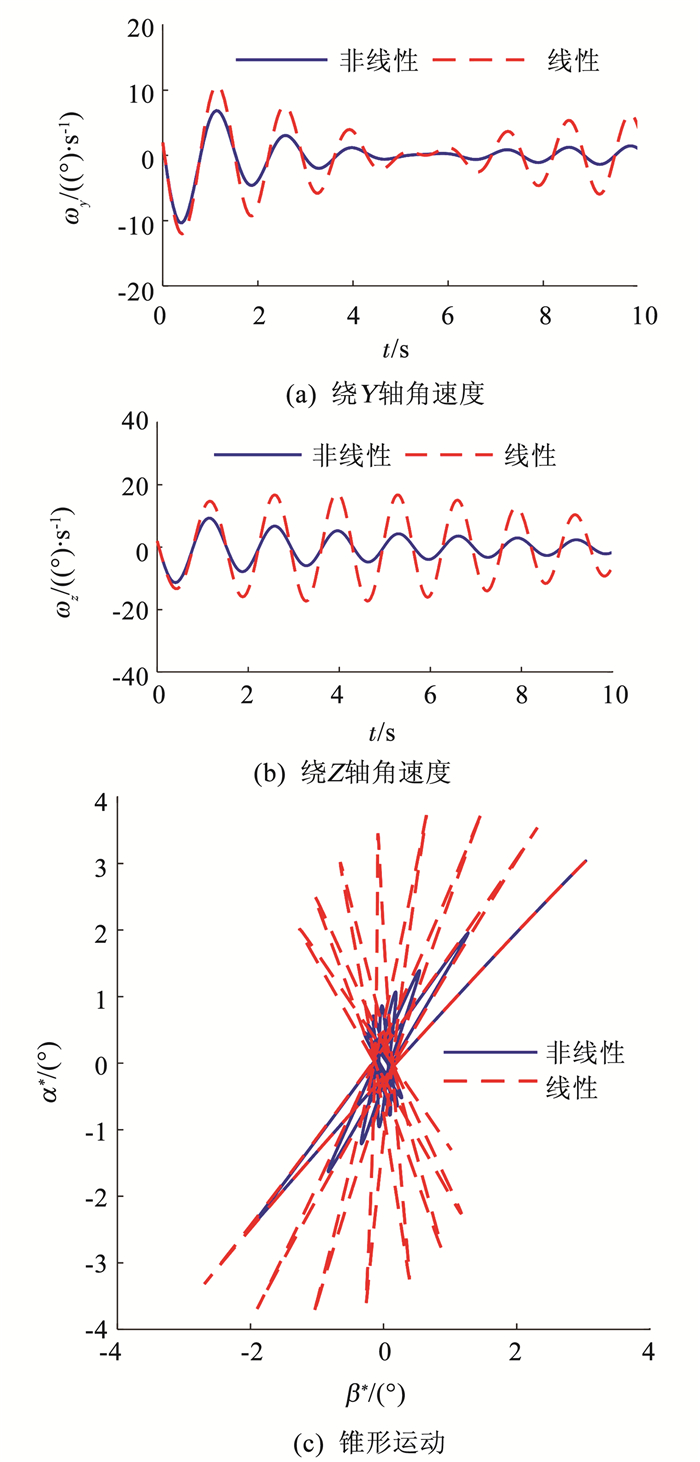
质量特性非线性变化影响如图 5所示.
|
图 5 质量特性非线性变化对锥形运动的影响 Figure 5 The influence of mass characteristics' nonlinear variation on coning motion |
由图 5可知,在质心变化导致的非线性变化的质量特性作用下导弹的锥形运动收敛更快,质量特性非线性变化对锥形运动的影响不可忽略.
5 结论1) 将旋转导弹看作连续质点系,建立了较为精确地同时考虑变质量特性、喷气阻尼效应和气动力矩的动力学模型,并基于此模型推导了旋转角速度的解析表达式,分析了锥形运动的稳定性.
2) 喷气阻尼效应会使导弹转速变化,若要保持导弹转速不变,应使药柱半径略小于发动机喷口截面半径.
3) 主动段旋转导弹的非线性质量特性变化对锥形运动有一定影响;而喷气阻尼效应增大了锥形运动的阻尼,但对相位无影响.
| [1] |
杨树兴, 赵良玉, 闫晓勇. 旋转弹动态稳定性理论[M]. 北京: 国防工业出版社, 2014. YANG Shuxing, ZHAO Liangyu, YAN Xiaoyong. Dynamic stability of spinning missiles[M]. Beijing: National Defense Industry Press, 2014. |
| [2] |
李于衡, 杨小芹, 关鹏, 等. 基于遥测数据的定点自旋卫星姿态选优方法[J]. 哈尔滨工业大学学报, 2009, 41(5): 175. LI Yuheng, YANG Xiaoqin, GUAN Peng, et al. A telemetry-based method to optimize the attitude of an on-orbit spin stabilized geostationary satellite[J]. Journal of Harbin Institute of Technology, 2009, 41(5): 175. DOI:10.3321/j.issn:0367-6234.2009.05.042 |
| [3] |
马克茂, 贺风华. 弹体自旋条件下姿控发动机控制律设计[J]. 航空学报, 2009, 30(10): 1816. MA Kemao, HE Fenghua. Control law design of lateral attitude jets for spinning missile[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(10): 1291. DOI:10.3321/j.issn:1000-6893.2009.10.004 |
| [4] |
高庆丰. 旋转导弹飞行动力学与控制[M]. 北京: 中国宇航出版社, 2016. GAO Qingfeng. Flight dynamics and control of spinning missiles[M]. Beijing: China Astronautic Publishing House, 2016. |
| [5] |
PLATUS D H. Ballistic re-entry vehicle flight dynamics[J]. Journal of Guidance, Control, and Dynamics, 1982, 5(1): 4. DOI:10.2514/3.56131 |
| [6] |
PLATUS D H. Missile and spacecraft coning instability[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(5): 1011. DOI:10.2514/3.21303 |
| [7] |
MURPHY C H. Symmetric missile dynamic instabilities[J]. Journal of Guidance, Control, and Dynamics, 1981, 4(5): 464. DOI:10.2514/3.56099 |
| [8] |
李克勇, 赵良玉, 周伟. 一类旋转弹在高空中的锥形运动稳定性[J]. 动力学与控制学报, 2012, 10(3): 239. LI Keyong, ZHAO Liangyu, ZHOU Wei. Stability of coning motion of spinning rocket projectiles at high altitude[J]. Journal of Dynamics and Control, 2012, 10(3): 239. DOI:10.3969/j.issn.1672-6553.2012.03.009 |
| [9] |
李敏娇, ABBASL K, 芮筱亭, 等. 柔性火箭弹气动力计算精度预测[J]. 哈尔滨工业大学学报, 2016, 48(10): 91. LI Minjiao, ABBAS L K, RUI Xiaoting, et al. The prediction of flexible rocket's aerodynamic force computational accuracy[J]. Journal of Harbin Institute of Technology, 2016, 48(10): 91. DOI:10.11918/j.issn.0367-6234.2016.10.013 |
| [10] |
LI Minjiao, RUI Xiaoting, ABBAS L K. Elastic dynamic effects on the trajectory of a flexible launch vehicle[J]. Journal of Spacecraft and Rockets, 2015, 52(6): 1586. DOI:10.2514/1.A33181 |
| [11] |
LI Keyong, YANG Shuxing, ZHAO Liangyu. Stability of spinning missiles with an acceleration autopilot[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(3): 774. DOI:10.2514/1.56122 |
| [12] |
POTTSEPP L, ROTT N. Simplified calculation of the jet-damping effects[J]. AIAA Journal, 1964, 2(4): 764. DOI:10.2514/3.2423 |
| [13] |
MURPHY C H. Spin jet damping of rocket-assisted projectiles[J]. Journal of Guidance, Control, and Dynamics, 1981, 4(3): 350. DOI:10.2514/3.19741 |
| [14] |
NANJANGUD A, EKE F. Approximate solution to the angular speeds of a nearly-symmetric mass-varying cylindrical body[J]. Journal of the Astronautical Sciences, 2017, 64(2): 99. DOI:10.1007/s40295-016-0099-8 |
| [15] |
VAN DER HA J C, JANSSENS F L. Jet damping and misalignment effects during solid-rocket-motor burn[J]. Journal of Guidance, Control, and Dynamics, 2005, 28(3): 412. DOI:10.2514/1.3852 |
| [16] |
贾沛然, 陈克俊, 何力. 远程火箭弹道学[M]. 长沙: 国防科技大学出版社, 1993. JIA Peiran, CHEN Kejun, HE Li. Long-range rocket ballisitics[M]. Changsha: National University of Defense Technology Press, 1993. |
 2018, Vol. 50
2018, Vol. 50


