2. 水下机器人技术重点实验室(哈尔滨工程大学),哈尔滨 150001
2. Science and Technology on Underwater Vehicle Laboratory (Harbin Engineering University), Harbin 150001, China
多智能体系统是由多个可独立进行控制的智能体组成的集合.在多智能体系统中,各个智能体以一定的方式进行信息通讯,协同完成特定的任务.相比于单运动体系统,多智能体系统具有灵活性强、生存能力高和成本低的优势,在卫星编队系统[1-2]、多机器人系统[3-4]、多机械臂系统[5]等工程领域中有着广泛的应用.对多智能体系统进行控制的首要问题是对多智能体系统进行建模.文献[6-7]分别在一阶和二阶积分器模型下对多智能体的控制问题进行了研究.考虑到实际的多智能体系统都存在一定的非线性,文献[6-7]存在对系统模型过于简化的问题.实际上,Euler-Lagrange(EL)方程可以用来刻画大多非线性系统的动力学特性[2, 4],利用EL方程进行建模的多智能体系统可称为多EL系统.文献[5]在EL模型下,对多机械臂系统的控制问题进行了研究.文献[5-7]对多EL系统的控制方法都是分布式控制.相比于集中式控制系统,分布式控制系统具有更强的灵活性和更好的环境适应性.通讯拓扑描述了分布式控制系统中各智能体之间的信息传递关系,可以分为无向和有向通讯拓扑.文献[5]的研究是在无向通讯拓扑下进行的,各智能体之间的信息传递是双向的.实际应用中,信息的双向传递对通讯系统的要求较高,而在有向通讯拓扑下,只需满足系统的通讯拓扑具有有向生成树[2],因此有向通讯拓扑的研究更具有实际应用价值.
考虑到EL系统中有无领航者以及领航者的数目,可以分为无领航者情形下的分布式一致性控制问题、存在单个领航者情形下的分布式跟踪控制问题以及存在多个领航者情形下的分布式包含控制问题.文献[8-9]分别研究了多EL系统的分布式一致性和跟踪控制问题.文献[10]针对多EL系统提出了分布式包含控制算法,使所有跟随者能够收敛到多个领航者形成的凸包内.存在多领航者的分布式包含控制在实际工程中有着广泛的应用.例如,在一些特定的情况下,多智能体系统需要集结在某一个特定的区域,来避免外界的一些危险因素,通过分布式包含控制算法,可以实现在仅有部分智能体(领航者)检测到危险时,整个多智能体系统对危险的规避.文献[10]没有考虑实际系统中的模型不确定性和外界干扰.文献[11]利用神经网络估计系统中存在的模型不确定性与外界干扰,实现了多EL系统的分布式包含控制.
对于多EL系统的包含控制而言,收敛时间是一个重要的性能指标.例如,在危险规避情形下,需要跟随者尽快地进入领航者围成的凸包内.然而,传统的线性滑模变量只能保证系统的渐近收敛.有限时间控制方法的提出和应用,可以保证系统在有限时间内收敛到原点.文献[4]在针对多机器人系统,在有向拓扑结构下,通过选取合适的终端滑模变量,分别实现了分布式有限时间跟踪控制和包含控制.然而,在文献[4]的控制律中,由于存在非连续特性的切换项,控制器的输出存在明显的抖振现象.抖振现象的存在,会对系统产生燃料消耗增加等不利影响.让符号函数出现在控制律的导数中,积分后仍然可以保证控制律的连续性,从而能够抑制抖振现象.针对操作机器人系统,文献[12]在控制律的导数项中包含符号函数项,实现了抑制抖振的渐近跟踪控制.文献[13]采用高阶非奇异滑模面,设计了有限时间跟踪控制律,实现了无抖振的控制输出.
在上述研究的基础上,本文对多EL系统的分布式有限时间包含控制进行研究.考虑控制输出存在抖振现象,在存在模型不确定性和外界干扰的情形下,提出一种实现多EL系统具有抑制抖振特性的分布式有限时间包含控制律.首先,选取高阶有限时间滑模变量,使系统能在有限时间内收敛到原点.然后,为实现控制器输出的抑制抖振特性,将符号项包含在控制律的导数中.考虑到系统存在模型不确定性和外界干扰,采用自适应估计律对其上界信息进行实时估计和补偿.通过Lyapunov方法证明了控制律的有限时间特性.最后对所提出的算法进行了仿真验证.
1 数学基础和问题描述本文用到的一些基本符号定义如下:1n为n维全1列向量;0n为n维全0列向量;0n×n为n×n全0矩阵;En为n×n单位阵;
假设多EL系统包含m个领航者和N个跟随者,领航者集合表示为vL={N+1, …, N+m},跟随者集合表示为vF={1, …, N}.各智能体之间的通讯拓扑为有向图[14].
用G=(v, ε)表示有向图,v为节点集合,ε⊆v×v为边集合.对于智能体i与j,如果智能体j可以接收智能体i的信息,则(vi, vj)∈ε.定义满足关系(vj, vi)∈ε的所有智能体j的集合为节点vi的邻居,用Ni={vj:(vj, vi)∈ε}来表示.有向图的加权邻接矩阵A=[aij]的各元素满足关系:如果(vj, vi)∈ε,则aij=1,否则aij=0.一般假设aii=0,即节点自身不具有连通性.有向图的路径是一个有限的节点序列vi1, …, vis,满足(vik, vik+1)∈ε.在有向图中,若对除根节点之外的每个节点,均有且仅有一个父节点,且存在根节点到达其余节点的有向路径,则该有向图称为有向树.若一个有向树包含有向图的所有节点,则称该有向树为有向图的有向生成树.若一个有向图包含一个为有向生成树的子图,则称该有向图具有有向生成树.Laplacian矩阵L=[lij]定义为lii=
当存在多个领航者时,Laplacian矩阵可以写成如下分块矩阵的形式
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_1}}&{{\mathit{\boldsymbol{L}}_2}}\\ {{{\bf{0}}_{m \times N}}}&{{{\bf{0}}_{m \times m}}} \end{array}} \right]. $ |
式中:L1∈
令:
| $ {b_{Li}} = \sum\limits_{j \in {\mathit{\boldsymbol{\nu }}_L}} {{a_{ij}}} ,i \in {\mathit{\boldsymbol{\nu }}_F},{{\mathit{\boldsymbol{\bar B}}}_L} = {\rm{diag}}\left( {{b_{L1}}, \cdots ,{b_{LN}}} \right), $ |
| $ {d_i} = \sum\limits_{j \in {\mathit{\boldsymbol{\nu }}_F},\mathit{\boldsymbol{j}} \ne i} {{a_{ij}}} ,i \in {\mathit{\boldsymbol{\nu }}_F},\mathit{\boldsymbol{\bar D}} = {\rm{diag}}\left( {{d_1}, \cdots ,{d_N}} \right), $ |
| $ \mathit{\boldsymbol{\bar A}} = \left[ {\begin{array}{*{20}{c}} 0&{{a_{12}}}&{}& \cdots &{{a_{1N}}}\\ {{a_{21}}}&0&{}& \ddots &{}\\ \vdots&\ddots &{}&{}& \vdots \\ {{a_{\left( {N - 1} \right)1}}}&{}& \ddots &0&{{a_{\left( {N - 1} \right)N}}}\\ {{a_{N1}}}&{}& \cdots &{{a_{N\left( {N - 1} \right)}}}&0 \end{array}} \right], $ |
则L1=D+BL-A.
自由度为n的多EL系统的动力学方程可以表示为
| $ {\mathit{\boldsymbol{M}}_i}\left( {{\mathit{\boldsymbol{q}}_i}} \right){{\mathit{\boldsymbol{\ddot q}}}_i} + {\mathit{\boldsymbol{C}}_i}\left( {{\mathit{\boldsymbol{q}}_i},{{\mathit{\boldsymbol{\dot q}}}_i}} \right){{\mathit{\boldsymbol{\dot q}}}_i} + {\mathit{\boldsymbol{G}}_i}\left( {{\mathit{\boldsymbol{q}}_i}} \right) = {\mathit{\boldsymbol{u}}_i} + {\mathit{\boldsymbol{\rho }}_i}. $ | (1) |
式中:i∈vL∪vF;qi∈
假设1 对于领航者,不存在广义干扰.即对于i∈vL,有
| $ {\mathit{\boldsymbol{M}}_i}\left( {{\mathit{\boldsymbol{q}}_i}} \right){{\mathit{\boldsymbol{\ddot q}}}_i} + {\mathit{\boldsymbol{C}}_i}\left( {{\mathit{\boldsymbol{q}}_i},{{\mathit{\boldsymbol{\dot q}}}_i}} \right){{\mathit{\boldsymbol{\dot q}}}_i} + {\mathit{\boldsymbol{G}}_i}\left( {{\mathit{\boldsymbol{q}}_i}} \right) = {\mathit{\boldsymbol{u}}_{Li}}. $ |
定义1 [15]令C为实向量空间S⊆
假设2 对于任意一个跟随者,至少存在一个领航者,该领航者有到该跟随者的有向路径.
引理1[16] 若假设2成立,则矩阵-L1-1L2的每个元素均是非负的,且其所有的行和均为1,即-L1-1L21m= 1N.
假设3 存在正常数MLmin,使得
| $ 0 < {M_{L\min }} \le \min \left[ {\left\| {{\mathit{\boldsymbol{M}}_1}} \right\|, \cdots ,\left\| {{\mathit{\boldsymbol{M}}_{N + m}}} \right\|} \right]. $ |
引理2[17] 系统
引理3 [18]考虑如下三阶系统
首先定义如下的误差函数:
| $ \mathit{\boldsymbol{e}}_i^x = \sum\limits_{j \in {v_F}} {{a_{ij}}\left( {{\mathit{\boldsymbol{q}}_i} - {\mathit{\boldsymbol{q}}_j}} \right)} + \sum\limits_{j \in {v_L}} {{a_{ij}}\left( {{\mathit{\boldsymbol{q}}_i} - {\mathit{\boldsymbol{q}}_j}} \right)} , $ | (2) |
| $ \mathit{\boldsymbol{e}}_i^v = \sum\limits_{j \in {v_F}} {{a_{ij}}\left( {{{\mathit{\boldsymbol{\dot q}}}_i} - {{\mathit{\boldsymbol{\dot q}}}_j}} \right)} + \sum\limits_{j \in {v_L}} {{a_{ij}}\left( {{{\mathit{\boldsymbol{\dot q}}}_i} - {{\mathit{\boldsymbol{\dot q}}}_j}} \right)} , $ | (3) |
可得
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}\mathit{\boldsymbol{\dot e}}_i^v = \frac{{\rm{d}}}{{{\rm{d}}t}}\left\{ {\sum\limits_{j \in {v_F}} {{l_{ij}}\left[ {\mathit{\boldsymbol{M}}_j^{ - 1}\left( {{\mathit{\boldsymbol{u}}_j} + {\mathit{\boldsymbol{\rho }}_j} - {\mathit{\boldsymbol{C}}_j}{{\mathit{\boldsymbol{\dot q}}}_j} - {\mathit{\boldsymbol{G}}_j}} \right)} \right]} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\sum\limits_{j \in {v_L}} {{l_{ij}}{{\mathit{\boldsymbol{\ddot q}}}_j}} } \right\} = \sum\limits_{j \in {v_F}} {{l_{ij}}\left\{ {\mathit{\boldsymbol{M}}_j^{ - 1}\left[ {{{\mathit{\boldsymbol{\dot u}}}_j} - \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\mathit{\boldsymbol{C}}_j}{{\mathit{\boldsymbol{\dot q}}}_j} + } \right.} \right.} \right.} \\ \;\;\;\;\;\;\;\;\;\;\left. {\left. {{\mathit{\boldsymbol{G}}_j}} \right)} \right] + \left[ {\left( {\frac{{\rm{d}}}{{{\rm{d}}t}}\mathit{\boldsymbol{M}}_j^{ - 1}} \right)\left( {{\mathit{\boldsymbol{u}}_j} - {\mathit{\boldsymbol{C}}_j}{\mathit{\boldsymbol{q}}_j} - {\mathit{\boldsymbol{G}}_j}} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{D}}_j}} \right\} - \sum\limits_{j \in {v_L}} {{a_{ij}}\frac{{\rm{d}}}{{{\rm{d}}t}}{{\mathit{\boldsymbol{\ddot q}}}_j}} . \end{array} $ | (4) |
式中:Dj=Mj-1
假设4 式(4)中的Dj=Mj-1
误差函数定义如式(2)~(4)所示,并根据引理3,定义如下有限时间滑模变量[18]:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{s}}_i} = \mathit{\boldsymbol{\dot e}}_i^v + \int_0^t {{\mathit{\boldsymbol{\nu }}_i}{\rm{d}}\tau } ,}\\ {{\mathit{\boldsymbol{\nu }}_i} = {\lambda _2}{{\left\{ {{{\left[ {{\lambda _1}{{\left( {\mathit{\boldsymbol{e}}_i^x} \right)}^{\left( {1 + {k_0}} \right){\delta _1}}} + {{\left( {\mathit{\boldsymbol{e}}_i^v} \right)}^{{\delta _1}}}} \right]}^{\frac{{{r_2} + {k_0}}}{{{r_2}{\delta _1}}}}} + \mathit{\boldsymbol{\dot e}}_i^v} \right\}}^{\frac{{{r_3} + {k_0}}}{{{r_3}{\delta _2}}}}}.} \end{array} $ | (5) |
式中:k0为闭环系统x1i=eix,
抑制抖振的分布式有限时间包含控制律设计为
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot u}}}_i} = \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\mathit{\boldsymbol{C}}_i}{{\mathit{\boldsymbol{\dot q}}}_i} + {\mathit{\boldsymbol{G}}_i}} \right) - {\mathit{\boldsymbol{M}}_i}\left( {\frac{{\rm{d}}}{{{\rm{d}}t}}\mathit{\boldsymbol{M}}_i^{ - 1}} \right)\left( {{\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{C}}_i}{{\mathit{\boldsymbol{\dot q}}}_i} - {\mathit{\boldsymbol{G}}_i}} \right) - \\ \;\;\;\;\;\;{\mathit{\boldsymbol{M}}_i}\left( {{{\hat F}_{0i}} + {{\hat F}_{1i}}\left\| {{\mathit{\boldsymbol{q}}_i}} \right\| + {{\hat F}_{2i}}{{\left\| {{{\mathit{\boldsymbol{\dot q}}}_i}} \right\|}^2}} \right){\rm{sign}}\left( {{\mathit{\boldsymbol{s}}_i}} \right) + \\ \;\;\;\;\;\;\sum\limits_{j \in {v_F},j \ne i} {{{\left( {{a_{ij}} + {b_i}} \right)}^{ - 1}}{\mathit{\boldsymbol{M}}_i}\left\{ { - {\mathit{\boldsymbol{\nu }}_i} + \sum\limits_{j \in {v_L}} {{a_{ij}}\frac{{\rm{d}}}{{{\rm{d}}t}}{{\mathit{\boldsymbol{\ddot q}}}_j}} - } \right.} \\ \;\;\;\;\;\;k{\rm{sign}}\left( {{\mathit{\boldsymbol{s}}_i}} \right) + \sum\limits_{j \in {v_F},j \ne i} {{a_{ij}}\mathit{\boldsymbol{M}}_j^{ - 1}\left\{ {\left[ {{{\mathit{\boldsymbol{\dot u}}}_j} - \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\mathit{\boldsymbol{C}}_j}{{\mathit{\boldsymbol{\dot q}}}_j} + {\mathit{\boldsymbol{G}}_j}} \right)} \right] + } \right.} \\ \;\;\;\;\;\;{\mathit{\boldsymbol{M}}_j}\left( {\frac{{\rm{d}}}{{{\rm{d}}t}}\mathit{\boldsymbol{M}}_j^{ - 1}} \right)\left( {{\mathit{\boldsymbol{u}}_j} - {\mathit{\boldsymbol{C}}_j}{{\mathit{\boldsymbol{\dot q}}}_j} - {\mathit{\boldsymbol{G}}_j}} \right) + {\mathit{\boldsymbol{M}}_j}\left( {{{\hat F}_{0j}} + {{\hat F}_{1j}}\left\| {{\mathit{\boldsymbol{q}}_j}} \right\| + } \right.\\ \;\;\;\;\;\;\left. {\left. {\left. {{{\hat F}_{2j}}{{\left\| {{{\mathit{\boldsymbol{\dot q}}}_j}} \right\|}^2}} \right){\rm{sign}}\left( {{\mathit{\boldsymbol{s}}_j}} \right)} \right\}} \right\}. \end{array} $ | (6) |
式中:
控制力为
设计自适应估计律为:
| $ \begin{array}{l} {{\dot {\hat F}}_{0i}} = \frac{1}{{{\mu _0}}}\left( {\sum\limits_{j \in {\mathit{\boldsymbol{v}}_F}} {{a_{ij}}\left( {{{\left| {{\mathit{\boldsymbol{s}}_{2i}}} \right|}^{\rm{T}}} - {{\left| {{\mathit{\boldsymbol{s}}_{2j}}} \right|}^{\rm{T}}}} \right)} + {b_{Li}}{{\left| {{\mathit{\boldsymbol{s}}_{2i}}} \right|}^{\rm{T}}}} \right){{\bf{1}}_n},\\ {{\dot {\hat F}}_{1i}} = \frac{1}{{{\mu _1}}}\left( {\sum\limits_{j \in {v_F}} {{a_{ij}}\left( {{{\left| {{\mathit{\boldsymbol{s}}_{2i}}} \right|}^{\rm{T}}} - {{\left| {{\mathit{\boldsymbol{s}}_{2j}}} \right|}^{\rm{T}}}} \right)} + {b_{Li}}{{\left| {{\mathit{\boldsymbol{s}}_{2i}}} \right|}^{\rm{T}}}} \right) \times \\ \;\;\;\;\;\;\;\;\left( {{{\bf{1}}_n} \otimes \left\| {{\mathit{\boldsymbol{q}}_i}} \right\|} \right),\\ {{\dot {\hat F}}_{2i}} = \frac{1}{{{\mu _2}}}\left( {\sum\limits_{j \in {v_F}} {{a_{ij}}\left( {{{\left| {{\mathit{\boldsymbol{s}}_{2i}}} \right|}^{\rm{T}}} - {{\left| {{\mathit{\boldsymbol{s}}_{2j}}} \right|}^{\rm{T}}}} \right)} + {b_{Li}}{{\left| {{\mathit{\boldsymbol{s}}_{2i}}} \right|}^{\rm{T}}}} \right) \times \\ \;\;\;\;\;\;\;\;\left( {{{\bf{1}}_n} \otimes {{\left\| {{{\mathit{\boldsymbol{\dot q}}}_i}} \right\|}^2}} \right). \end{array} $ | (7) |
式中:μ0、μ1、μ2均为正常数.
令:
| $ {\mathit{\boldsymbol{\varepsilon }}_x} = {\left[ {{{\left( {\mathit{\boldsymbol{e}}_1^x} \right)}^{\rm{T}}}, \cdots ,{{\left( {\mathit{\boldsymbol{e}}_N^x} \right)}^{\rm{T}}}} \right]^{\rm{T}}},{\mathit{\boldsymbol{\varepsilon }}_v} = {\left[ {{{\left( {\mathit{\boldsymbol{e}}_1^v} \right)}^{\rm{T}}}, \cdots ,{{\left( {\mathit{\boldsymbol{e}}_N^v} \right)}^{\rm{T}}}} \right]^{\rm{T}}}, $ |
| $ {{\mathit{\boldsymbol{\dot \varepsilon }}}_v} = {\left[ {{{\left( {\mathit{\boldsymbol{\dot e}}_1^v} \right)}^{\rm{T}}}, \cdots ,{{\left( {\mathit{\boldsymbol{\dot e}}_N^v} \right)}^{\rm{T}}}} \right]^{\rm{T}}},\mathit{\boldsymbol{\rho }} = {\left[ {\mathit{\boldsymbol{\rho }}_1^{\rm{T}}, \cdots ,\mathit{\boldsymbol{\rho }}_N^{\rm{T}}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{U}}_F} = {\left[ {\mathit{\boldsymbol{u}}_1^{\rm{T}}, \cdots ,\mathit{\boldsymbol{u}}_N^{\rm{T}}} \right]^{\rm{T}}},{\mathit{\boldsymbol{U}}_L} = {\left[ {\mathit{\boldsymbol{u}}_{N + 1}^{\rm{T}}, \cdots ,\mathit{\boldsymbol{u}}_{N + m}^{\rm{T}}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{Q}}_F} = {\left[ {\mathit{\boldsymbol{q}}_1^{\rm{T}}, \cdots ,\mathit{\boldsymbol{q}}_N^{\rm{T}}} \right]^{\rm{T}}},{{\mathit{\boldsymbol{\dot Q}}}_F} = {\left[ {\mathit{\boldsymbol{\dot q}}_1^{\rm{T}}, \cdots ,\mathit{\boldsymbol{\dot q}}_N^{\rm{T}}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{Q}}_L} = {\left[ {\mathit{\boldsymbol{q}}_{N + 1}^{\rm{T}}, \cdots ,\mathit{\boldsymbol{q}}_{N + m}^{\rm{T}}} \right]^{\rm{T}}},{{\mathit{\boldsymbol{\dot Q}}}_L} = {\left[ {\mathit{\boldsymbol{\dot q}}_{N + 1}^{\rm{T}}, \cdots ,\mathit{\boldsymbol{\dot q}}_{N + m}^{\rm{T}}} \right]^{\rm{T}}}, $ |
| $ {{\mathit{\boldsymbol{\dot Q}}}_L} = {\left[ {\mathit{\boldsymbol{\ddot q}}_{N + 1}^{\rm{T}}, \cdots ,\mathit{\boldsymbol{\ddot q}}_{N + m}^{\rm{T}}} \right]^{\rm{T}}},{\mathit{\boldsymbol{M}}_F} = {\rm{diag}}\left( {{\mathit{\boldsymbol{M}}_1}, \cdots ,{\mathit{\boldsymbol{M}}_N}} \right), $ |
| $ {\mathit{\boldsymbol{M}}_L} = {\rm{diag}}\left( {{\mathit{\boldsymbol{M}}_{N + 1}}, \cdots ,{\mathit{\boldsymbol{M}}_{N + m}}} \right),{\mathit{\boldsymbol{C}}_F} = {\rm{diag}}\left( {{\mathit{\boldsymbol{C}}_1}, \cdots ,{\mathit{\boldsymbol{C}}_N}} \right), $ |
| $ {\mathit{\boldsymbol{C}}_L} = {\rm{diag}}\left( {{\mathit{\boldsymbol{C}}_{N + 1}}, \cdots ,{\mathit{\boldsymbol{C}}_{N + m}}} \right),{\mathit{\boldsymbol{G}}_F} = {\left( {\mathit{\boldsymbol{G}}_1^{\rm{T}}, \cdots ,\mathit{\boldsymbol{G}}_N^{\rm{T}}} \right)^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{G}}_L} = {\left( {\mathit{\boldsymbol{G}}_{N + 1}^{\rm{T}}, \cdots ,\mathit{\boldsymbol{G}}_{N + m}^{\rm{T}}} \right)^{\rm{T}}},\mathit{\boldsymbol{s}} = {\left[ {\mathit{\boldsymbol{s}}_1^{\rm{T}}, \cdots ,\mathit{\boldsymbol{s}}_N^{\rm{T}}} \right]^{\rm{T}}}, $ |
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\mathit{\boldsymbol{M}}_F^{ - 1}} \right) = {\rm{diag}}\left( {\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\mathit{\boldsymbol{M}}_1^{ - 1}} \right), \cdots ,\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\mathit{\boldsymbol{M}}_N^{ - 1}} \right)} \right), $ |
| $ \mathit{\boldsymbol{\nu }} = {\left[ {\mathit{\boldsymbol{\nu }}_1^{\rm{T}}, \cdots ,\mathit{\boldsymbol{\nu }}_N^{\rm{T}}} \right]^{\rm{T}}},{\mathit{\boldsymbol{F}}_0} = {\left[ {{F_{01}}, \cdots ,{F_{0N}}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{F}}_1} = {\left[ {{F_{11}}, \cdots ,{F_{1N}}} \right]^{\rm{T}}},{\mathit{\boldsymbol{F}}_2} = {\left[ {{F_{21}}, \cdots ,{F_{2N}}} \right]^{\rm{T}}}, $ |
| $ {{\mathit{\boldsymbol{\hat F}}}_0} = {\left[ {{{\hat F}_{01}}, \cdots ,{{\hat F}_{0N}}} \right]^{\rm{T}}},{{\mathit{\boldsymbol{\hat F}}}_1} = {\left[ {{{\hat F}_{11}}, \cdots ,{{\hat F}_{1N}}} \right]^{\rm{T}}}, $ |
| $ {{\mathit{\boldsymbol{\hat F}}}_2} = {\left[ {{{\hat F}_{21}}, \cdots ,{{\hat F}_{2N}}} \right]^{\rm{T}}},{{\mathit{\boldsymbol{\dot {\hat F}}}}_0} = {\left[ {{{\dot {\hat F}}_{01}}, \cdots ,{{\dot {\hat F}}_{0N}}} \right]^{\rm{T}}}, $ |
| $ {{\mathit{\boldsymbol{\dot {\hat F}}}}_1} = {\left[ {{{\dot {\hat F}}_{11}}, \cdots ,{{\dot {\hat F}}_{1N}}} \right]^{\rm{T}}},{{\mathit{\boldsymbol{\dot {\hat F}}}}_2} = {\left[ {{{\dot {\hat F}}_{21}}, \cdots ,{{\dot {\hat F}}_{2N}}} \right]^{\rm{T}}}, $ |
| $ {{\mathit{\boldsymbol{ {\hat F}}}}_{0M}} = {\rm{diag}}\left( {{{\hat F}_{01}}, \cdots ,{{\hat F}_{0N}}} \right),{{\mathit{\boldsymbol{ {\hat F}}}}_{1M}} = {\rm{diag}}\left( {{{\hat F}_{11}}, \cdots ,{{\hat F}_{1N}}} \right), $ |
| $ {{\mathit{\boldsymbol{{\hat F}}}}_{2M}} = {\rm{diag}}\left( {{{\hat F}_{21}}, \cdots ,{{\hat F}_{2N}}} \right),{\mathit{\boldsymbol{q}}_f} = {\rm{diag}}\left( {\left\| {{\mathit{\boldsymbol{q}}_1}} \right\|, \cdots ,\left\| {{\mathit{\boldsymbol{q}}_N}} \right\|} \right), $ |
| $ \mathit{\boldsymbol{\dot q}}_f^2 = {\rm{diag}}\left( {{{\left\| {{{\mathit{\boldsymbol{\dot q}}}_1}} \right\|}^2}, \cdots ,{{\left\| {{{\mathit{\boldsymbol{\dot q}}}_N}} \right\|}^2}} \right),\mathit{\boldsymbol{D}} = {\left[ {\mathit{\boldsymbol{D}}_1^{\rm{T}}, \cdots ,\mathit{\boldsymbol{D}}_N^{\rm{T}}} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{\bar D}} = {\rm{diag}}\left( {{{\bar D}_1}, \cdots ,{{\bar D}_N}} \right),\mathit{\boldsymbol{\hat {\bar D}}} = {\rm{diag}}\left( {{{\hat {\bar D}}_1}, \cdots ,{{\hat {\bar D}}_N}} \right). $ |
定理1 考虑多EL系统(1),在跟随者具有模型广义干扰的情形下,当假设1~4成立时,如果领航者的信息只能被部分跟随者获得,那么在控制律(6)和自适应估计律(7)的作用下,可使系统有限时间到达滑模面,所有的跟随者会在有限时间内收敛到领航者围成的凸包内,实现分布式有限时间包含控制,且控制律(6)具有抑制抖振的特性.
证明
Step 1 选取如下Lyapunov函数
| $ V = \frac{1}{2}\left( {{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{s}} + {\mu _0}\mathit{\boldsymbol{\tilde F}}_0^{\rm{T}}{{\mathit{\boldsymbol{\tilde F}}}_0} + {\mu _1}\mathit{\boldsymbol{\tilde F}}_1^{\rm{T}}{{\mathit{\boldsymbol{\tilde F}}}_1} + {\mu _2}\mathit{\boldsymbol{\tilde F}}_2^{\rm{T}}{{\mathit{\boldsymbol{\tilde F}}}_2}} \right). $ | (8) |
式中:
对式(8)求导,得到:
| $ \dot V = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} + {\mu _0}\mathit{\boldsymbol{\tilde F}}_0^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat F}}}}_0} + {\mu _1}\mathit{\boldsymbol{\tilde F}}_1^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat F}}}}_1} + {\mu _2}\mathit{\boldsymbol{\tilde F}}_2^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat F}}}}_2}. $ | (9) |
根据式(2)~(4),误差函数
| $ \begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}t}}{{\mathit{\boldsymbol{\dot \varepsilon }}}_v} = \left( {{\mathit{\boldsymbol{L}}_1} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\left\{ {\mathit{\boldsymbol{M}}_F^{ - 1}\left[ {{{\mathit{\boldsymbol{\dot U}}}_F} - \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\mathit{\boldsymbol{C}}_F}{{\mathit{\boldsymbol{\dot Q}}}_F} + {\mathit{\boldsymbol{G}}_F}} \right)} \right] + } \right.}\\ {\left. {{\mathit{\boldsymbol{M}}_F}\left( {\frac{{\rm{d}}}{{{\rm{d}}t}}\mathit{\boldsymbol{M}}_F^{ - 1}} \right)\left( {{\mathit{\boldsymbol{U}}_F} - {\mathit{\boldsymbol{C}}_F}{{\mathit{\boldsymbol{\dot Q}}}_F} - {\mathit{\boldsymbol{G}}_F}} \right)} \right\} + }\\ {\left( {{\mathit{\boldsymbol{L}}_1} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\mathit{\boldsymbol{D}} + \left( {{\mathit{\boldsymbol{L}}_2} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\frac{{\rm{d}}}{{{\rm{d}}t}}{{\mathit{\boldsymbol{\ddot Q}}}_L},} \end{array} $ | (10) |
| $ \mathit{\boldsymbol{\dot s}} = \frac{{\rm{d}}}{{{\rm{d}}t}}{{\mathit{\boldsymbol{\dot \varepsilon }}}_v} + \mathit{\boldsymbol{\nu }}, $ | (11) |
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot U}}}_F} = \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\mathit{\boldsymbol{C}}_F}{{\mathit{\boldsymbol{\dot Q}}}_F} + {\mathit{\boldsymbol{G}}_F}} \right) - {\mathit{\boldsymbol{M}}_F}\left( {\mathit{\boldsymbol{\hat {\bar D}}} \otimes {\mathit{\boldsymbol{E}}_n}} \right){\rm{sign}}\left( \mathit{\boldsymbol{s}} \right) - \\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{M}}_F}\left( {\frac{{\rm{d}}}{{{\rm{d}}t}}\mathit{\boldsymbol{M}}_F^{ - 1}} \right)\left( {{\mathit{\boldsymbol{U}}_F} - {\mathit{\boldsymbol{C}}_F}{{\mathit{\boldsymbol{\dot Q}}}_F} - {\mathit{\boldsymbol{G}}_F}} \right) + \left[ {\left( {\mathit{\boldsymbol{\bar D}} + } \right.} \right.\\ \;\;\;\;\;\;\;\;\left. {{{\left. {{{\mathit{\boldsymbol{\bar B}}}_L}} \right)}^{ - 1}} \otimes {\mathit{\boldsymbol{E}}_n}} \right]{\mathit{\boldsymbol{M}}_F}\left\{ { - \mathit{\boldsymbol{\nu }} - k{\rm{sign}}\left( s \right) + \left( {\mathit{\boldsymbol{\bar A}} \otimes } \right.} \right.\\ \;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{E}}_n}} \right)\mathit{\boldsymbol{M}}_F^{ - 1}\left[ {{{\mathit{\boldsymbol{\dot U}}}_F} - \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\mathit{\boldsymbol{C}}_F}{{\mathit{\boldsymbol{\dot Q}}}_F} - {\mathit{\boldsymbol{G}}_F}} \right) + {\mathit{\boldsymbol{M}}_F} \times } \right.\\ \;\;\;\;\;\;\;\;\left. {\left( {\mathit{\boldsymbol{\hat {\bar D}}} \otimes {\mathit{\boldsymbol{E}}_n}} \right){\rm{sign}}\left( \mathit{\boldsymbol{s}} \right)} \right] + {\mathit{\boldsymbol{M}}_F}\left( {\frac{{\rm{d}}}{{{\rm{d}}t}}\mathit{\boldsymbol{M}}_F^{ - 1}} \right) \times \\ \;\;\;\;\;\;\;\;\left. {\left( {{\mathit{\boldsymbol{U}}_F} - {\mathit{\boldsymbol{C}}_F}{{\mathit{\boldsymbol{\dot Q}}}_F} - {\mathit{\boldsymbol{G}}_F}} \right) - \left( {{\mathit{\boldsymbol{L}}_2} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\left( {\frac{{\rm{d}}}{{{\rm{d}}t}}{{\mathit{\boldsymbol{\ddot Q}}}_L}} \right)} \right\}. \end{array} $ | (12) |
受文献[19]的启发,有如下关系式成立:
| $ \begin{array}{l} \mathit{\boldsymbol{I}} - \left[ {{{\left( {\mathit{\boldsymbol{\bar D}} + {{\mathit{\boldsymbol{\bar B}}}_L}} \right)}^{ - 1}} \otimes {\mathit{\boldsymbol{E}}_n}} \right]{\mathit{\boldsymbol{M}}_F}\left( {\mathit{\boldsymbol{\bar A}} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\mathit{\boldsymbol{M}}_F^{ - 1} = \\ \;\;\;\;{\mathit{\boldsymbol{M}}_F}\left[ {{{\left( {\mathit{\boldsymbol{\bar D}} + {{\mathit{\boldsymbol{\bar B}}}_L}} \right)}^{ - 1}} \otimes {\mathit{\boldsymbol{E}}_n}} \right]\left( {{\mathit{\boldsymbol{L}}_1} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\mathit{\boldsymbol{M}}_F^{ - 1}, \end{array} $ | (13) |
由式(13),可将式(12)简化得到如下关系式
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot U}}}_F} = \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{\mathit{\boldsymbol{C}}_F}{{\mathit{\boldsymbol{\dot Q}}}_F} + {\mathit{\boldsymbol{G}}_F}} \right) - {\mathit{\boldsymbol{M}}_F}\left( {\mathit{\boldsymbol{\hat {\bar D}}} \otimes {\mathit{\boldsymbol{E}}_n}} \right){\rm{sign}}\left( \mathit{\boldsymbol{s}} \right) - \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{M}}_F}\left( {\frac{{\rm{d}}}{{{\rm{d}}t}}\mathit{\boldsymbol{M}}_F^{ - 1}} \right)\left( {{\mathit{\boldsymbol{U}}_F} - {\mathit{\boldsymbol{C}}_F}{{\mathit{\boldsymbol{\dot Q}}}_F} - {\mathit{\boldsymbol{G}}_F}} \right) + {\mathit{\boldsymbol{M}}_F}\left( {\mathit{\boldsymbol{L}}_1^{ - 1} \otimes } \right.\\ \;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{E}}_n}} \right)\left[ { - \mathit{\boldsymbol{\nu }} - \left( {{\mathit{\boldsymbol{L}}_2} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\frac{{\rm{d}}}{{{\rm{d}}t}}{{\mathit{\boldsymbol{\ddot Q}}}_L} - k{\rm{sign}}\left( \mathit{\boldsymbol{s}} \right)} \right]. \end{array} $ | (14) |
将式(10)、(11)、(14)代入式(9)可得
| $ \begin{array}{l} \dot V = - {\mathit{\boldsymbol{s}}^{\rm{T}}}\left\{ {\left( {{\mathit{\boldsymbol{L}}_1} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\left[ {\left( {\mathit{\boldsymbol{\bar D}} \otimes {\mathit{\boldsymbol{E}}_n} + \left( {{{\mathit{\boldsymbol{\hat F}}}_{0M}} - {\mathit{\boldsymbol{F}}_{0M}}} \right) \otimes {\mathit{\boldsymbol{E}}_n} + } \right.} \right.} \right.\\ \;\;\;\;\;\;\left( {\left( {{{\mathit{\boldsymbol{\hat F}}}_{1M}} - {\mathit{\boldsymbol{F}}_{1M}}} \right){\mathit{\boldsymbol{q}}_f}} \right) \otimes {\mathit{\boldsymbol{E}}_n} + \left( {\left( {{{\mathit{\boldsymbol{\hat F}}}_{2M}} - {\mathit{\boldsymbol{F}}_{2M}}} \right)\mathit{\boldsymbol{\dot q}}_f^2} \right) \otimes \\ \;\;\;\;\;\;\left. {\left. {\left. {{\mathit{\boldsymbol{E}}_n}} \right){\rm{sign}}\left( \mathit{\boldsymbol{s}} \right) - \mathit{\boldsymbol{D}}} \right] + k{\mathop{\rm sign}\nolimits} \left( \mathit{\boldsymbol{s}} \right)} \right\} + {\mu _0}\left( {\mathit{\boldsymbol{\hat F}}_0^{\rm{T}} - } \right.\\ \;\;\;\;\;\;\left. {\mathit{\boldsymbol{F}}_0^{\rm{T}}} \right){{\mathit{\boldsymbol{\dot {\hat F}}}}_0} + {\mu _1}\left( {\hat F_1^{\rm{T}} - \mathit{\boldsymbol{F}}_1^{\rm{T}}} \right){{\mathit{\boldsymbol{\dot {\hat F}}}}_1} + {\mu _2}\left( {\mathit{\boldsymbol{\hat F}}_2^{\rm{T}} - \mathit{\boldsymbol{F}}_2^{\rm{T}}} \right){{\mathit{\boldsymbol{\dot {\hat F}}}}_2}. \end{array} $ |
令S=diag(|s211|, |s212|, …, |s2ij|, …, |s2Nn|),其中i=1, …, N,j=1, …, n,有
| $ \begin{array}{l} \dot V = - {\mathit{\boldsymbol{s}}^{\rm{T}}}\left\{ {\left( {{\mathit{\boldsymbol{L}}_1} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\left[ {\left( {\mathit{\boldsymbol{\bar D}} \otimes {\mathit{\boldsymbol{E}}_n} + \left( {{{\mathit{\boldsymbol{\hat F}}}_{0M}} - {\mathit{\boldsymbol{F}}_{0M}}} \right) \otimes {\mathit{\boldsymbol{E}}_n} + } \right.} \right.} \right.\\ \;\;\;\;\;\;\left. {\left( {\left( {{{\mathit{\boldsymbol{\hat F}}}_{1M}} - {\mathit{\boldsymbol{F}}_{1M}}} \right){\mathit{\boldsymbol{q}}_f}} \right) \otimes {\mathit{\boldsymbol{E}}_n} + \left( {\left( {{{\mathit{\boldsymbol{\hat F}}}_{2M}} - {\mathit{\boldsymbol{F}}_{2M}}} \right)\mathit{\boldsymbol{\dot q}}_f^2} \right) \otimes {\mathit{\boldsymbol{E}}_n}} \right) \times \\ \;\;\;\;\;\;\left. {\left. {{\rm{sign}}\left( \mathit{\boldsymbol{s}} \right) - \mathit{\boldsymbol{D}}} \right] + k{\rm{sign}}\left( \mathit{\boldsymbol{s}} \right)} \right\} + \left( {\mathit{\boldsymbol{\hat F}}_0^{\rm{T}} - \mathit{\boldsymbol{F}}_0^{\rm{T}}} \right)\left( {{\bf{1}}_N^{\rm{T}} \otimes } \right.\\ \;\;\;\;\;\;\left. {{\mathit{\boldsymbol{E}}_n}} \right)\left( {{\mathit{\boldsymbol{L}}_1} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\mathit{\boldsymbol{S}}{{\bf{1}}_{Nn}} + \left( {\mathit{\boldsymbol{\hat F}}_1^{\rm{T}} - \mathit{\boldsymbol{F}}_1^{\rm{T}}} \right)\left( {{\bf{1}}_N^{\rm{T}} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\left( {{\mathit{\boldsymbol{L}}_1} \otimes } \right.\\ \;\;\;\;\;\;\left. {{\mathit{\boldsymbol{E}}_n}} \right)\mathit{\boldsymbol{S}}\left( {{\mathit{\boldsymbol{q}}_f} \otimes {\mathit{\boldsymbol{E}}_n}} \right){{\bf{1}}_{Nn}} + \left( {\mathit{\boldsymbol{\hat F}}_2^{\rm{T}} - \mathit{\boldsymbol{F}}_2^{\rm{T}}} \right)\left( {{\bf{1}}_N^{\rm{T}} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\left( {{\mathit{\boldsymbol{L}}_1} \otimes } \right.\\ \;\;\;\;\;\;\left. {{\mathit{\boldsymbol{E}}_n}} \right)\mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{\dot q}}_f^2 \otimes {\mathit{\boldsymbol{E}}_n}} \right){{\bf{1}}_{Nn}} = - {\mathit{\boldsymbol{s}}^{\rm{T}}}\left\{ {\left( {{\mathit{\boldsymbol{L}}_1} \otimes {\mathit{\boldsymbol{E}}_n}} \right) \cdot \left[ {\left( {\mathit{\boldsymbol{\bar D}} \otimes } \right.} \right.} \right.\\ \;\;\;\;\;\;\left. {\left. {\left. {{\mathit{\boldsymbol{E}}_n}} \right){\rm{sign}}\left( \mathit{\boldsymbol{s}} \right) - \mathit{\boldsymbol{D}}} \right] + k{\rm{sign}}\left( \mathit{\boldsymbol{s}} \right)} \right\} \le - k{\mathit{\boldsymbol{s}}^{\rm{T}}}{\rm{sign}}\left( \mathit{\boldsymbol{s}} \right) \le 0. \end{array} $ |
因此有V(t)≤V(0).由式(8)可知,s、
Step2 考虑如下Lyapunov函数
| $ {V^ * } = \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{s}}, $ | (15) |
对式(15)求导可得
| $ {{\dot V}^ * } = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}}. $ | (16) |
将式(10)、(11)、(14)代入式(16),可得
| $ \begin{array}{l} {{\dot V}^ * } = - {\mathit{\boldsymbol{s}}^{\rm{T}}}\left\{ {\left( {{\mathit{\boldsymbol{L}}_1} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\left[ {\left( {\mathit{\boldsymbol{\bar D}} \otimes {\mathit{\boldsymbol{E}}_n} + {{\mathit{\boldsymbol{\tilde F}}}_{0M}} \otimes {\mathit{\boldsymbol{E}}_n} + \left( {{{\mathit{\boldsymbol{\tilde F}}}_{1M}}{\mathit{\boldsymbol{q}}_f}} \right) \otimes } \right.} \right.} \right.\\ \;\;\;\;\;\;\;\;\left. {\left. {\left. {{\mathit{\boldsymbol{E}}_n} + \left( {{{\mathit{\boldsymbol{\tilde F}}}_{2M}}\mathit{\boldsymbol{\dot q}}_f^2} \right) \otimes {\mathit{\boldsymbol{E}}_n}} \right){\rm{sign}}\left( \mathit{\boldsymbol{s}} \right) - \mathit{\boldsymbol{D}}} \right] + k{\rm{sign}}\left( \mathit{\boldsymbol{s}} \right)} \right\} \le \\ \;\;\;\;\;\;\;\; - {\mathit{\boldsymbol{s}}^{\rm{T}}}\left\{ {\left( {{\mathit{\boldsymbol{L}}_1} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\left[ {{{\mathit{\boldsymbol{\tilde F}}}_{0M}} \otimes {\mathit{\boldsymbol{E}}_n} + \left( {{{\mathit{\boldsymbol{\tilde F}}}_{1M}}{\mathit{\boldsymbol{q}}_f}} \right) \otimes {\mathit{\boldsymbol{E}}_n} + } \right.} \right.\\ \;\;\;\;\;\;\;\;\left. {\left. {\left. {\left( {{{\mathit{\boldsymbol{\tilde F}}}_{2M}}\mathit{\boldsymbol{\dot q}}_f^2} \right) \otimes {\mathit{\boldsymbol{E}}_n}} \right){\rm{sign}}\left( \mathit{\boldsymbol{s}} \right)} \right] + k{\rm{sign}}\left( \mathit{\boldsymbol{s}} \right)} \right\}. \end{array} $ |
式中:
由假设4可知,qf、
| $ \begin{array}{l} - {\bf{1}}_{Nn}^{\rm{T}}\left( {{\mathit{\boldsymbol{L}}_1} \otimes {\mathit{\boldsymbol{E}}_n}} \right)\left[ {{{\mathit{\boldsymbol{\tilde F}}}_{0M}} \otimes {\mathit{\boldsymbol{E}}_n} + \left( {{{\mathit{\boldsymbol{\tilde F}}}_{1M}}{\mathit{\boldsymbol{q}}_f}} \right) \otimes {\mathit{\boldsymbol{E}}_n} + } \right.\\ \left. {\left( {{{\mathit{\boldsymbol{\tilde F}}}_{2M}}\mathit{\boldsymbol{\dot q}}_f^2} \right) \otimes {\mathit{\boldsymbol{E}}_n}} \right]{{\bf{1}}_{Nn}} \le \bar F, \end{array} $ | (17) |
由式(16)、(17),有
| $ \begin{array}{l} {{\dot V}^ * } \le - \left( {k - \bar F} \right){\mathit{\boldsymbol{s}}^{\rm{T}}}{\rm{sign}}\left( \mathit{\boldsymbol{s}} \right) \le - \left( {k - \bar F} \right)\left\| \mathit{\boldsymbol{s}} \right\| = \\ \;\;\;\;\;\;\; - \sqrt 2 \left( {k - \bar F} \right){\left( {{V^ * }} \right)^{1/2}}. \end{array} $ |
通过选取k>F,由引理2可知,系统有限时间内到达滑模面si,即si=0n.
当si=0n时,由有限时间滑模变量定义式(5),有
| $ \mathit{\boldsymbol{\dot e}}_i^v = - \int_0^t {{\mathit{\boldsymbol{\nu }}_i}{\rm{d}}\mathit{\boldsymbol{\tau }}} , $ | (18) |
式(18)两边对时间t求导,可得
| $ \mathit{\boldsymbol{\ddot e}}_i^v = - {\mathit{\boldsymbol{\nu }}_i}. $ |
由引理3可知,eix将在有限时间内收敛到原点,即eix=0n.当eix=0n时,εx=0Nn,由误差定义式(2),有
| $ \left( {{\mathit{\boldsymbol{L}}_1} \otimes {\mathit{\boldsymbol{E}}_n}} \right){\mathit{\boldsymbol{Q}}_F} + \left( {{\mathit{\boldsymbol{L}}_2} \otimes {\mathit{\boldsymbol{E}}_n}} \right){\mathit{\boldsymbol{Q}}_L} = {{\bf{0}}_{Nn}}, $ |
可得
| $ {\mathit{\boldsymbol{Q}}_F} = - \left( {\mathit{\boldsymbol{L}}_1^{ - 1}{\mathit{\boldsymbol{L}}_2} \otimes {\mathit{\boldsymbol{E}}_n}} \right){\mathit{\boldsymbol{Q}}_L}. $ |
由引理1和定义1,跟随者系统将在有限时间内收敛到领航者围成的凸包内,即实现了有限时间包含控制.
3 仿真验证多机械臂系统是一类典型的多EL系统,选取由8个跟随机械臂(编号1, …, 8)和5个领航机械臂(编号9, …, 13)组成的多机械臂系统,进行仿真验证.
跟随机械臂的动力学模型可以描述为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_i}\left( {{\mathit{\boldsymbol{q}}_i}} \right){{\mathit{\boldsymbol{\ddot q}}}_i} + \mathit{\boldsymbol{C}}\left( {{\mathit{\boldsymbol{q}}_i},{{\mathit{\boldsymbol{\dot q}}}_i}} \right){{\mathit{\boldsymbol{\dot q}}}_i} + {\mathit{\boldsymbol{G}}_i}\left( {{\mathit{\boldsymbol{q}}_i}} \right) = {\mathit{\boldsymbol{u}}_i} + {\mathit{\boldsymbol{\rho }}_i},}\\ {i = 1, \cdots ,8.} \end{array} $ |
领航机械臂的动力学模型可以描述为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_i}\left( {{\mathit{\boldsymbol{q}}_i}} \right){{\mathit{\boldsymbol{\ddot q}}}_i} + \mathit{\boldsymbol{C}}\left( {{\mathit{\boldsymbol{q}}_i},{{\mathit{\boldsymbol{\dot q}}}_i}} \right){{\mathit{\boldsymbol{\dot q}}}_i} + {\mathit{\boldsymbol{G}}_i}\left( {{\mathit{\boldsymbol{q}}_i}} \right) = {\mathit{\boldsymbol{u}}_{Li}},}\\ {i = 9, \cdots ,13.} \end{array} $ |
以二连杆转动机械臂为例,假设所有机械臂的动力学为相同的EL方程[20].各机械臂的动力学项分别为:
| $ {\mathit{\boldsymbol{q}}_i} = \left[ {\begin{array}{*{20}{c}} {{q_{i1}}}\\ {{q_{i2}}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{M}}_i}\left( {{\mathit{\boldsymbol{q}}_i}} \right) = \left[ {\begin{array}{*{20}{c}} {{\theta _{i1}} + {\theta _{i2}} + 2{\theta _{i3}}\cos {q_{i2}}}&{{\theta _{i2}} + {\theta _{i3}}\cos {q_{i2}}}\\ {{\theta _{i2}} + {\theta _{i3}}\cos {q_{i2}}}&{{\theta _{i2}}} \end{array}} \right], $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{C}}_i}\left( {{\mathit{\boldsymbol{q}}_i},{{\mathit{\boldsymbol{\dot q}}}_i}} \right) = \\ \left[ {\begin{array}{*{20}{c}} { - {\theta _{i3}}\left( {\sin {q_{i2}}} \right){q_{i2}}}&{ - {\theta _{i3}}\left( {\sin {q_{i2}}} \right)\left( {{{\dot q}_{i1}} + {{\dot q}_{i2}}} \right)}\\ {{\theta _{i3}}\left( {\sin {q_{i2}}} \right){{\dot q}_{i1}}}&0 \end{array}} \right], \end{array} $ |
| $ {\mathit{\boldsymbol{G}}_i}\left( {{\mathit{\boldsymbol{q}}_i}} \right) = \left[ {\begin{array}{*{20}{c}} {{\theta _{i4}}\cos {q_{i1}} + {\theta _{i5}}g\cos \left( {{q_{i1}} + {q_{i2}}} \right)}\\ {{\theta _{i5}}g\cos \left( {{q_{i1}} + {q_{i2}}} \right)} \end{array}} \right]. $ |
式中:g=9.8 m/s2为重力加速度;参数θi1=Ji1+mi2li12, θi2=Ji2+0.25mi2li22, θi3=0.5mi2li1li2, θi4=(0.5mi1+mi2)li1, θi5=0.5mi2li2,其中mi1、mi2分别为连杆质量,li1、li2分别为连杆长度,Ji1、Ji2分别为连杆的转动惯量.
图 1为领航机械臂与跟随机械臂之间的通讯拓扑图.
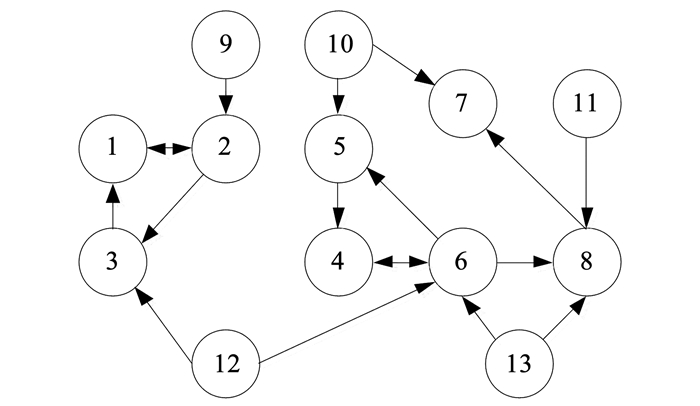
|
图 1 跟随机械臂与领航机械臂的通讯拓扑图 Figure 1 Communication topology for leader manipulators and follower manipulators |
控制参数选取为λ1=diag(10, 10),λ2=diag(100, 100),k=150,k0=
| 表 1 跟随机械臂的初始角位置 Table 1 Initial angular positions of follower manipulators |
| 表 2 跟随机械臂的初始角速度 Table 2 Initial angular velocities of follower manipulators |
选取li1=li2=L, i=1, …, 13, L=1 m.其他的仿真参数分别见表 3~6.
| 表 3 跟随机械臂的连杆质量 Table 3 Masses of the follower manipulators |
| 表 4 跟随机械臂的连杆转动惯量 Table 4 Moments of inertia of the follower manipulators |
| 表 5 领航机械臂的连杆质量 Table 5 Masses of the leader manipulators |
| 表 6 领航机械臂的连杆转动惯量 Table 6 Moments of inertia of the leader manipulators |
假设跟随机械臂的广义干扰为
| $ {\rho _{i1}} = {\rho _{i2}} = 0.05\sin \left( {\frac{{\rm{ \mathsf{ π} }}}{2}t} \right){\rm{N}} \cdot {\rm{m}},i = 1, \cdots ,8. $ |
领航机械臂的角位置轨迹见表 7.
| 表 7 领航机械臂的角位置轨迹 Table 7 The angular trajectories of leader manipulators |
不失一般性,在说明跟随机械臂的力矩输出情况时,以跟随机械臂5为例.仿真结果如图 2~4所示.
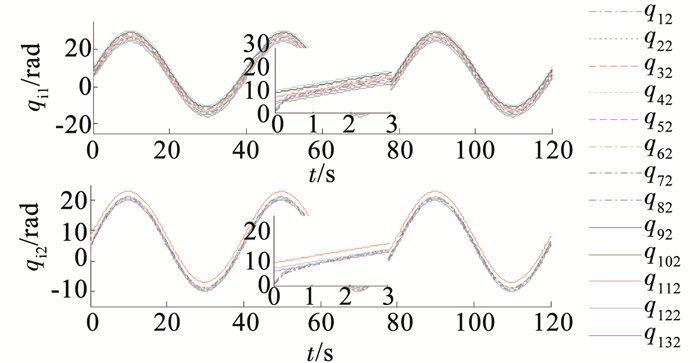
|
图 2 连杆1、2的角位置轨迹 Figure 2 The angular trajectories for links 1 and 2 |
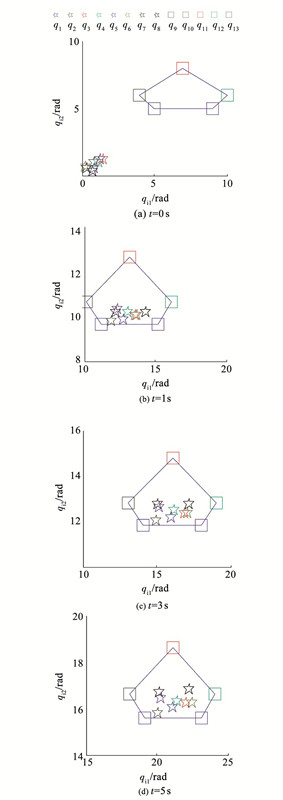
|
图 3 t=0、2、3、5 s时领航机械臂与跟随机械臂的相对角位置 Figure 3 The relative angular positions of leader manipulators and follower manipulators at t=0, 2, 3, 5 s |
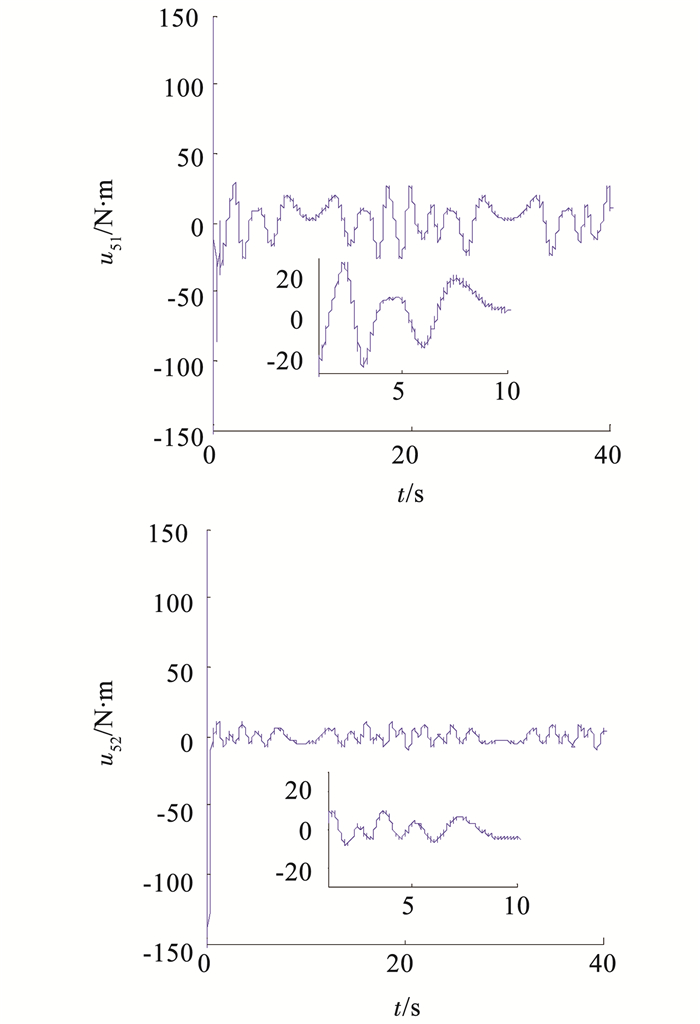
|
图 4 跟随机械臂5的控制力矩 Figure 4 The control torques of manipulator 5 |
由图 2可以看出,在控制律(6)作用下,领航机械臂系统可以实现对跟随机械臂系统的有限时间包含控制.由图 3可知,t=0 s时,所有的跟随机械臂的角位置均位于领航机械臂系统围成的凸包之外.t=1 s时,所有的跟随机械臂均已经进入领航机械臂系统围成的凸包内.t=2 s、t=5 s时,所有跟随机械臂仍位于领航机械臂系统围成的凸包内.图 4表明,跟随机械臂在初始时间段需要比较大的力矩输出,t=2 s后,控制力矩幅值减小到25 N·m范围内,并且整个控制过程中控制力矩没有抖振现象.因此,在控制律(6)的作用下,多EL系统实现了抑制抖振的分布式有限时间包含控制.
4 结论1) 基于有向通讯拓扑,通过定义包含控制误差变量,选取高阶有限时间滑模变量,提出一种分布式有限时间包含控制律.
2) 不连续的符号函数项包含在控制律的导数中,实现了抑制抖振的特性.
3) 利用自适应估计律对系统模型不确定性与外界干扰的上界进行了有效估计和补偿.最后仿真算例验证了本文算法的有效性.
| [1] |
CAO Lu, CHEN Xiaoqian. Input-output linearization minimum sliding-mode error feedback control for spacecraft formation with large perturbations[J]. Proceedings of Institution of Mechanical Engineering, Part G: Journal of Aerospace Engineering, 2015, 229(2): 352. DOI:10.1177/0954410014533674 |
| [2] |
SUN Yanchao, MA Guangfu, LIU Mengmeng, et al. Distributed finite-time configuration containment control for satellite formation[J]. Proceedings of the Institution of Mechanical Engineers Part G: Journal of Aerospace Engineering, 2017, 231(9): 1609. DOI:10.1177/0954410016656877 |
| [3] |
BULLO F, FRAZZOLI E, PAVONE M, et al. Dynamics vehicle routing for robotic systems[J]. Proceedings of the IEEE, 2011, 99(9): 1482. DOI:10.1109/JPROC.2011.2158181 |
| [4] |
SUN Yanchao, MA Guangfu, LIU Mengmeng, et al. Distributed finite-time coordinated control for multi-robot systems[J]. Transactions of the Institute of Measurement and Control, 2018, 40(9): 2912. DOI:10.1177/0142331217711493 |
| [5] |
DONG Weijie. On consensus algorithms of multiple uncertain mechanical systems with a reference trajectory[J]. Automatica, 2011, 47(9): 2023. DOI:10.1016/j.automatica.2011.05.025 |
| [6] |
HONG Yiguang, HU Jiangping, GAO Linxin. Tracking control for multi-agent consensus with an active leader and variable topology[J]. Automatica, 2006, 42(7): 1177. DOI:10.1016/j.automatica.2006.02.013 |
| [7] |
QIN Jiahu, ZHENG Weixin, GAO Huijun. Consensus of multiple second-order vehicles with a time-varying reference signal under directed topology[J]. Automatica, 2011, 47(9): 1983. DOI:10.1016/j.automatica.2011.05.014 |
| [8] |
REN Wei. Distributed leaderless consensus algorithms for networked Euler-Lagrange systems[J]. International Journal of Control, 2009, 82(11): 2137. DOI:10.1080/00207170902948027 |
| [9] |
梅杰, 张海博, 马广富. 有向图中网络Euler-Lagrange系统的自适应协调跟踪[J]. 自动化学报, 2011, 37(5): 596. MEI Jie, ZHANG Haibo, MA Guangfu. Adaptive coordinated tracking for networked Euler-Lagrange systems under a directed graph[J]. Acta Automatica Sinica, 2011, 37(5): 596. DOI:10.3724/SP.J.1004.2011.00596 |
| [10] |
JI M, FERRARI-TRECATE G, EGERSTEDT M, et al. Containment control in mobile networks[J]. IEEE Transactions on Automatic Control, 2008, 53(5): 1972. DOI:10.1109/TAC.2008.930098 |
| [11] |
孙延超, 李传江, 姚俊羽, 等. 无需相对速度信息的多Euler-Lagrange系统自适应神经网络包含控制[J]. 控制与决策, 2016, 31(4): 693. SUN Yanchao, LI Chuanjiang, YAO Junyu, et al. Adaptive neural-network containment control of multiple Euler-Lagrange systems without using relative velocity information[J]. Control and Decision, 2016, 31(4): 693. DOI:10.13195/j.kzyjc.2015.0198 |
| [12] |
MONDAL S, MAHANTA C. Adaptive second order terminal sliding mode controller for robotic manipulators[J]. Journal of the Franklin Institute, 2014, 351(4): 2356. DOI:10.1016/j.jfranklin.2013.08.027 |
| [13] |
GALICKI M. Finite-time control of robotic manipulators[J]. Automatica, 2015, 51: 49. DOI:10.1016/j.automatica.2014.10.089 |
| [14] |
MEI Jie, REN Wei, MA Guangfu. Distributed coordinated tracking with a dynamic leader for multiple Euler-Lagrange systems[J]. IEEE Transactions on Automatic Control, 2011, 56(6): 1415. DOI:10.1109/TAC.2011.2109437 |
| [15] |
ROCKAFELLAR R T. Convex analysis[M]. New Jersey: Princeton University Press, 1972.
|
| [16] |
MEI Jie, REN Wei, MA Guangfu. Distributed containment control for Lagrangian networks with parametric uncertainties under a directed graph[J]. Automatica, 2012, 48(4): 653. DOI:10.1016/j.automatica.2012.01.020 |
| [17] |
BHAT S P, BERNSTEIN D S. Finite-time stability of continuous autonomous systems[J]. SIAM Journal on Control and Optimization, 2000, 38(3): 751. DOI:10.1137/S0363012997321358 |
| [18] |
HONG Yiguang. Finite-time stabilization and stabilizability of a class of controllable systems[J]. System & Control Letters, 2002, 46(4): 231. DOI:10.1016/S0167-6911(02)00119-6 |
| [19] |
KHOO Suiyang, XIE Lihua, MAN Zhihong. Robust finite-time consensus tracking algorithm for multirobot systems[J]. IEEE/ASME Transactions on Mechatronics, 2009, 14(2): 219. DOI:10.1109/TMECH.2009.2014057 |
| [20] |
SPONG M W, HUTCHINSON S, VIDYASAGAR M. Robot modeling and control[M]. [S.l.]: John Wiley & Sons, Inc., 2006
|
 2018, Vol. 50
2018, Vol. 50


