近几年来, 随着科学技术的发展, 群智能算法逐渐成为学者们研究的焦点.由于群智能算法具有简单性, 灵活性, 无衍生机制和避免局部最优特性, 不仅应用在计算机领域, 而且也能应用在农业、冶金工程, 光学工程等等.迄今为止, 研究人员对此已经提出很多种智能算法, 例如遗传算法[1]、粒子群算法[2-3]、差分算法[4]等.这些算法的共同目标是找到最佳解及更好的收敛性能.但是, 没有文献模拟以狩猎闻名的灰狼领导阶级.因此, 2014年Mirjalili等[5]提出灰狼优化算法(grey wolf optimization algorithm, GWO), 其主要是模拟灰狼社会阶级以及灰狼狩猎过程.狼的领导层次分为4类:α, β, δ, ω狼, 其中α, β狼负责领导整个狼群.狩猎过程主要由三个步骤组成:搜索, 包围, 攻击.同时, Mirjalili通过一系列标准测试函数验证GWO算法比PSO算法、GA算法、DE算法等收敛速度快, 稳定性更强.但是, GWO算法在进行猎物攻击时易陷入停滞.Saremi等[6-7]提出利用动态进化种群与灰狼算法相结合, 从而提高算法的局部搜索能力.但忽略算法的全局搜索能力.Zhu等[8-10]通过引入差分进化算法的全局搜索来改善灰狼算法的搜索能力.为增加种群的多样性, 龙文等[11]提出一种改进的灰狼优化算法(the improved grey wolf optimization algorithm, IGWO), 其利用佳点集法初始化种群, 使初始种群分布均匀.同时, 郭振洲等[12]引入动态权重策略来优化灰狼算法的性能.
但是上述算法在研究灰狼捕食过程时未考虑灰狼个体经验对整个种群的影响.因此, 本文提出一种改进的灰狼优化算法, 其主要是利用Tent映射初始化种群, 增加种群的多样性; 采用非线性控制参数策略, 加强权衡局部及全局搜索的能力; 同时, 引入PSO算法的思想改进灰狼位置更新公式, 避免种群提前寻优停滞.
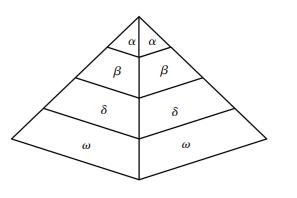
1 灰狼优化算法 1.1 灰狼社会等级和捕猎行为灰狼是处于食物链最顶端的捕食动物[13-14], 其中大部分灰狼是群居生存, 每个种群平均5~12只灰狼, 并且种群中每个灰狼都有自己的角色, 因此它们具有非常严格的社会等级制度见图 1.
|
图 1 灰狼社会阶级制度 Figure 1 Grey wolf social class system |
第1层是灰狼中最高领导者, 称为α, 其主要负责狩猎、栖息地等等各项决策; 第2层是灰狼中次位领导者, 称为β, 其主要负责协助领导者管理群体; 第3层为δ, 主要负责侦察、照顾年老体弱者、狩猎等等; 第4层是种群中最低等级的灰狼, 称为ω, 其需要服从于所有其他阶级的灰狼, 看似ω狼不是一个重要的角色, 但对于平衡种群内部关系来说却是不可缺少的.
灰狼的种群等级在实现群体高效捕杀猎物的过程中发挥着至关重要的作用.首先, 灰狼群体进行搜寻、跟踪、逐渐靠近猎物; 其次, 由α狼带领其余灰狼对猎物进行全方位包围; 然后, α灰狼指挥最靠近猎物的β, δ狼进行攻击, 若猎物逃跑, 其它剩余灰狼从后方进行补给、围攻; 最终捕获猎物.
1.2 灰狼算法描述灰狼算法是模拟灰狼的社会阶级制度以及其捕食行为, 然后利用灰狼在捕食过程中的搜索、包围以及捕猎等行为实现优化的目的.假设灰狼数量为N, 搜索区域为d维, 其中第i只灰狼的位置可表示为:Xi=(Xi1, Xi2, Xi3, …, Xid), 在种群中适应度值最大的个体记为α, 将适应度值排名第2及第3的对应个体记为β和δ, 其它剩余的个体记为ω, 猎物的位置对应于算法中的α狼的位置.
在搜索猎物过程中, 灰狼接近并包抄猎物行为的数学模型[5]为
| $ D = \left| {C \times {X_p}\left( t \right) - X\left( t \right)} \right|, $ | (1) |
| $ X\left( {t + 1} \right) = {X_p}\left( t \right) - A \times D. $ | (2) |
式中:Xp(t)为第t代猎物的位置; X(t)为第t代灰狼个体的位置; C为摆动因子, 由下式决定[5]:
| $ C = 2{r_1}. $ | (3) |
式中:r1为[0, 1]之间的随机数; A为收敛因子, 由下式决定[5]:
| $ A = 2a{r_2} - a, $ | (4) |
| $ a = 2\left( {1 - \frac{t}{{{T_{\max }}}}} \right). $ | (5) |
式中:Tmax为最大迭代数目; r2为[0, 1]之间的随机数; a为控制参数, 其值随着迭代次数的增加而线性减小, amax=2, amin=0.
当灰狼搜索到猎物所在位置时, 首先, 头狼α带领狼群对猎物进行包围; 然后, 头狼α带领β狼和δ狼对猎物进行攻击捕捉.在灰狼群体中, α, β, δ狼距离猎物位置最近, 因此可以通过这三者的位置来计算灰狼个体向猎物移动的位置, 其具体的数学模型如下:
| $ {D_\alpha } = \left| {{C_1} \times {X_\alpha }\left( t \right) - X\left( t \right)} \right|, $ | (6) |
| $ {D_\beta } = \left| {{C_2} \times {X_\beta }\left( t \right) - X\left( t \right)} \right|, $ | (7) |
| $ {D_\delta } = \left| {{C_3} \times {X_\delta }\left( t \right) - X\left( t \right)} \right|. $ | (8) |
由式(6)~(8)计算出其余灰狼个体与灰狼α, β, δ的距离.
| $ {X_1}\left( t \right) = {X_\alpha }\left( t \right) - {A_1} \times {D_\alpha }, $ | (9) |
| $ {X_2}\left( t \right) = {X_\beta }\left( t \right) - {A_2} \times {D_\beta }, $ | (10) |
| $ {X_3}\left( t \right) = {X_\delta }\left( t \right) - {A_3} \times {D_\delta }. $ | (11) |
由式(9)~(11)计算出其余灰狼个体移动的方向.
| $ X\left( {t + 1} \right) = \frac{{{X_1}\left( t \right) + {X_2}\left( t \right) + {X_3}\left( t \right)}}{3}. $ | (12) |
然后由式(12)更新灰狼个体的位置.
从图 2能够直观地看出灰狼个体根据α, β, δ的位置信息移动自身的位置.

|
图 2 灰狼位置更新原理 Figure 2 Grey wolf location update schematic |
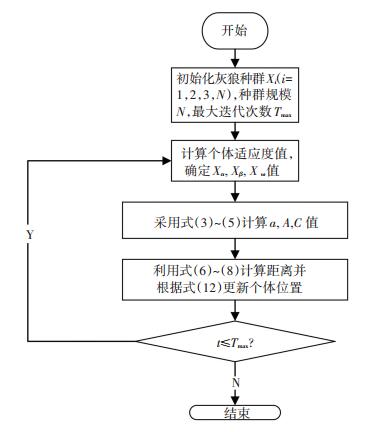
基本GWO算法流程见图 3.算法的主要步骤:
|
图 3 GWO算法优化流程图 Figure 3 GWO algorithm optimization flow chart |
Step1:初始化算法参数, 即设置种群的规模为N, 维数d, 最大迭代次数Tmax, 参数A, C, a值;
Step2:初始化种群个体:随机产生种群个体{Xi, i=1, 2, 3...N};
Step3:根据适应度函数, 计算种群中每一个灰狼的适应度值{fi, i=1, 2, 3..., N}, 然后将按照适应度值大小进行顺序排列, 同时将适应度值排在前三位的灰狼个体设置为α, β, δ, 其对应的位置信息分别为:Xα, Xβ, Xδ;
Step4:利用式(6)~(8)计算其他剩余灰狼与灰狼α, β, δ的距离, 然后根据式(9)~(11)计算其余灰狼移动的方向, 最后利用式(12)对其余灰狼位置进行更新.
Step5:根据适应度函数重新计算种群中灰狼个体的适应度值, 并对适应度值进行排序, 更新灰狼α, β, δ及其对应的位置信息.
Step6:判断t是否达到Tmax值, 如果达到则输出最佳解即α值的适应度值, 否则返回Step4继续执行.
2 改进的灰狼算法 2.1 Tent混沌映射GWO算法在解决函数优化问题中, 通常利用随机产生的数据作为初始种群信息, 这将难以保留种群的多样性, 会造成算法的寻优结果较差.然而, 混沌运动具有随机性、规律性、以及遍历性的特征, 在求解函数优化问题时这些特性能够使算法容易逃离局部最优解, 从而可以维持种群的多样性, 同时提高全局搜索能力.现有的混沌映射有Tent映射、Logistic映射等.但是, 不同的混沌映射对于提高函数优化能力不同.目前文献中大多数采用Logistic映射, 但是该映射在[0, 0.1]和[0.9, 1]两个区域内有较高的取值率.因而, Logistic映射遍历不均匀性会导致算法的收敛速度较慢, 从而导致算法的效率降低.单梁[15]等证明Tent映射比Logistic映射的遍历均匀性更好以及能够提高算法的寻优速度, 与此同时能够在[0, 1]之间产生分布较均匀的初始值.因此, 本文将利用Tent映射初始化种群.
Tent映射表达式:
| $ {x_{t + 1}} = \left\{ \begin{array}{l} \frac{{{x_t}}}{u},\;\;0 \le {x_t} < u;\\ \frac{{1 - {x_t}}}{{1 - u}},u \le {x_t} \le 1. \end{array} \right. $ | (13) |
当u= 1/2时, Tent映射具有最典型的形式, 此时所得的序列具有均匀的分布, 对不同的参数有近似一致的分布密度.
因而, 本文引用的Tent混沌映射的公式为
| $ {x_{t + 1}} = \left\{ \begin{array}{l} 2{x_t},\;\;\;\;0 \le {x_t} \le \frac{1}{2};\\ 2\left( {1 - {x_t}} \right),\;\;\;\frac{1}{2} \le {x_t} \le 1. \end{array} \right. $ | (14) |
即xt+1=(2xt)mod1
Tent混沌映射产生序列值的具体步骤如下所示:
Step1:随机产生初始值x0(在[0, 1]之间且避免x0落在(0.2, 0.4, 0.6, 0.8)), 记入标记组, 即y(1)=x0, i=1, j=1;
Step2:按式(14)迭代产生一个x序列, i=i+1;
Step3:If 达到最大迭代次数, 则转向Step4;Else if xi={0, 0.25, 0.5, 0.75}或者xi=xi-k, k={0, 1, 2, 3, 4}, 则按式x(i)=y(j+1)=y(j)+c改变迭代初值, c是随机数, j=j+1;Else返回Step2;
Step4:运行停止, 保留x序列.
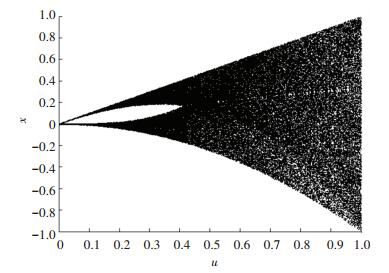
|
图 4 Tent混沌映射分岔 Figure 4 Tent chaotic map bifurcation |
GWO算法主要通过对猎物定位以及灰狼个体移动行为两个步骤构成.根据式(2), 参数A对协调GWO算法的全局和局部开发能力具有非常关键的作用.当|A|>1时, 群体将扩大搜索范围, 以找到更好的候选解, 即为GWO算法的全局探索能力; 当|A| < 1时, 群体将缩小搜索范围, 在局部区域进行精细搜索, 即为GWO算法的局部开发能力.同时, 由式(2)可知, 在进化过程中, A值随控制参数a的变化而不断变化.即GWO算法的全局和局部开发能力取决于控制参数a的变化.通过上述式(4)可知, 控制参数a随迭代次数的增加而线性减小.然而, GWO算法的寻优过程非常复杂, 参数a的线性变化不能体现算法的实际优化搜索过程.在文献[16]和文献[17]中学者们提出控制参数a随迭代次数非线性变化, 并通过标准测试函数优化结果表明, 采用非线性变化策略比线性策略寻优更好.文献[11]和文献[13]在此基础之上也提出非线性控制参数a, 虽然其效果有所改进, 但是仍不能满足算法的需求.
因此, 本文提出一种新的非线性控制参数为
| $ {a_1}\left( t \right) = {a_{{\rm{ini}}}} - \left( {{a_{{\rm{ini}}}} - {a_{{\rm{fin}}}}} \right) \times {\left( {\frac{t}{{{T_{\max }}}}} \right)^2}. $ | (15) |
式中:aini和afin分别为控制参数的初始值及终值; t为当前的迭代次数; Tmax为最大迭代数目.
为验证本文提出控制参数a的有效性, 将与线性控制参数以及文献[11], [13]提出非线性控制参数进行对比.线性控制参数、文献[11]和[13]的非线性控制参数的公式为
| $ {a_2}\left( t \right) = {a_{{\rm{ini}}}} - {a_{{\rm{ini}}}} \times \left( {\frac{t}{{{T_{\max }}}}} \right), $ | (16) |
| $ {a_3}\left( t \right) = {a_{{\rm{ini}}}} - \left( {{a_{{\rm{ini}}}} - {a_{{\rm{fin}}}}} \right) \times \tan \left( {\frac{1}{\varepsilon } \times \frac{t}{{{T_{\max }}}} \times {\rm{ \mathsf{ π} }}} \right), $ | (17) |
| $ {a_4}\left( t \right) = {a_{{\rm{ini}}}} - {a_{{\rm{ini}}}} \times \left( {\frac{1}{{e - 1}} \times \left( {{e^{\frac{t}{{{T_{\max }}}}}} - 1} \right)} \right.. $ | (18) |
式(17)中ε为非线性调节系数.
本文对4种控制参数进行仿真见图 5, 从图 5可看出, 本文提出的控制参数的非线性能更有效地平衡局部搜索和全局搜索能力.
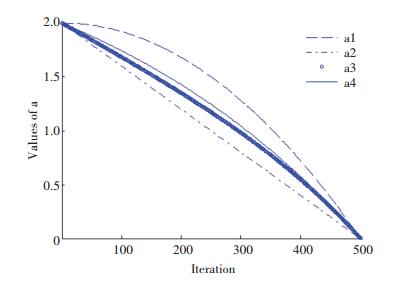
|
图 5 控制参数a的变化曲线 Figure 5 The change curve of the control parameter a |
收敛因子的公式为
| $ {A_i} = 2{a_i}{r_2} - {a_i}. $ | (19) |
式中i=1, 2, 3, 4, 分别代表不同的收敛因子.
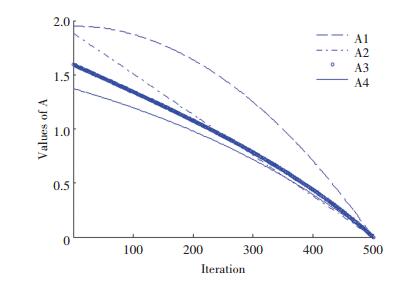
4种收敛因子A的动态变化见图 6.
|
图 6 收敛因子分析动态变化曲线 Figure 6 Convergence factor dynamic curve |
从图 6可看出本文提出的收敛因子A前期递减速度慢, 能够增加全局搜索能力, 避免算法陷入局部最优; 后期收敛因子递减速度快, 从而能够改善局部搜索, 加快算法寻优速度.
2.3 PSO思想GWO算法在位置更新过程中只考虑灰狼个体位置信息与种群的最优解、优解、次优解位置信息, 并实现灰狼个体与种群之间的信息交流.但是忽略灰狼个体与自身经验之间的信息交流.因此, 引入粒子群算法(particle swarm optimization, PSO)的思想来改进位置更新过程.
在PSO算法中, 利用粒子自身经历过的最佳位置信息以及群体最佳位置信息来更新当前粒子的位置.因此, 本文结合PSO算法思想将灰狼个体经历过的最优位置信息引入位置更新公式, 使其能够保留自身最优位置信息.新的位置更新为
| $ \begin{array}{*{20}{c}} {{X_i}\left( {t + 1} \right) = {c_1}{r_3}\left( {{w_1}{X_1}\left( t \right) + {w_2}{X_2}\left( t \right) + {w_3}{X_3}\left( t \right)} \right)}\\ { + {c_2}{r_4}\left( {{X_{ibest}} - {X_i}\left( t \right)} \right).} \end{array} $ | (20) |
式中:c1为社会学习因子, c2为认知学习因子, 其分别表示个体所经历的最优值和群体最优值对算法搜索能力的影响.如果c1值太大, 则会造成过多的粒子在局部附近停留; 如果c2值太大, 则会造成粒子提前达到局部最佳值并收敛于此值.根据文献[18], 本文选择c1=c2=2.r3, r4为[0, 1]之间的随机数; Xibest表示灰狼个体本身经历过最优的位置; w1, w2, w3为惯性权重系数, 通过调节α, β, δ狼对更新个体影响的权重比例, 能够动态权衡算法的全局及局部搜索能力, 其具体公式如下:
| $ {w_1} = \frac{{\left| {{X_1}} \right|}}{{\left| {{X_1} + {X_2} + {X_3}} \right|}}, $ | (21) |
| $ {w_2} = \frac{{\left| {{X_2}} \right|}}{{\left| {{X_1} + {X_2} + {X_3}} \right|}}, $ | (22) |
| $ {w_3} = \frac{{\left| {{X_3}} \right|}}{{\left| {{X_1} + {X_2} + {X_3}} \right|}}. $ | (23) |
本文提出改进之后的灰狼算法(grey wolf optimization algorithm based on particle swarm optimization, 简称PSO_GWO)的具体实现步骤:
Step1:设置种群的规模为N, 维数d, 初始化A, C, a值;
Step2:利用Tent映射产生种群个体{Xi, i=1, 2, 3...N}, 同时计算各个个体的适应度值{fi, i=1, 2, 3..., N};
Step3:按照适应度值从大到小排列顺序, 取前三个适应度值所对应的个体为α, β, δ, 其对应的位置信息分别为:Xα, Xβ, Xδ;
Step4:利用式(15)计算非线性变化参数a, 然后根据式(2)、(19)更新A以及C值;
Step5:利用式(20)更新种群个体的位置, 重新计算适应度值, 更新α, β, δ值;
Step6:判断t是否达到Tmax值, 如果达到则输出最佳解即α值的适应度值, 否则返回Step3继续执行.
3 实验数据及仿真分析 3.1 基本测试函数为验证改进之后的灰狼算法的有效性, 本文从已有文献中选择9个基准测试函数[18-21]做仿真实验, 并与基本粒子群算法(PSO)、基本灰狼算法(GWO)[5]、改进的灰狼算法(the improved grey wolf optimization algorithm, IGWO)[11]的优化结果进行比较并分析本文算法的性能, 其具体的基准测试函数见表 2.
| 表 1 PSO_GWO算法的伪代码 Table 1 PSO_GWO algorithm pseudo-code |
| 表 2 基准测试函数 Table 2 Benchmarking function |

|
图 7 单峰基准函数 Figure 7 Unimodal benchmark functions |

|
图 8 多峰基准函数 Figure 8 Multimodal benchmark functions |
通过MATLAB对上述的9个基准测试函数进行仿真实验对比, 具体的实验数据设置如下所示:种群规模均为N=30;种群维数均为d=30、50、100;最大迭代数目均为Tmax=500;控制参数aini和afin分别2, 0;IGWO算法中ε=5, b1=0.5, b2=0.5.
3.3 仿真分析 3.3.1 与基本PSO算法的比较为验证本文提出的PS0_GWO与PSO算法寻优性能优劣, 对两种算法分别单独进行30次仿真实验, 记录其平均值以及标准差, 其结果见表 3.
| 表 3 PSO、PSO_GWO算法的寻优结果 Table 3 Optimization results of PSO and PSO_GWO algorithms |
由于基本灰狼算法在寻找猎物过程中只考虑灰狼个体位置信息与种群的最优解、优解、次优解位置信息, 但是忽略灰狼个体与自身经验之间的信息交流.所以本文根据粒子群算法的思想将灰狼个体自身经验引入位置更新公式.通过表 3数据可以得到, 本文提出的PSO_GWO算法迭代次数高于PSO算法, 同时所得到的计算结果优于PSO算法的计算结果, 说明算法能有效地平衡局部搜索和全局搜索能力, 从而促使PSO_GWO算法避免在搜索过程中提前收敛而停滞现象, 更好地寻找全局最优解.
3.3.2 与基本GWO以及改进的GWO算法的比较对GWO算法、IGWO算法、PSO_GWO算法分别单独进行30次仿真实验, 记录其平均值及标准差.具体结果见表 4.
| 表 4 GWO、IGWO、PSO_GWO算法的寻优结果 Table 4 Optimization results of GWO, IGWO, and PSO_GWO algorithms |
由表 4可知, 当维数d=30时, PSO_GWO比GWO算法、IGWO算法在F1~F9测试函数上所得到的平均值更加理想.因此, PSO_GWO算法比其他三种算法寻优性能更好.PSO_GWO算法在9个测试函数中的标准差较小, 说明该算法的鲁棒性较好.同时, 不管维数30、50还是100, PSO_GWO算法均比其他三种算法得到更好的最优解.但是, 随着维数的增加, PSO_GWO算法的寻优能力略有下降.
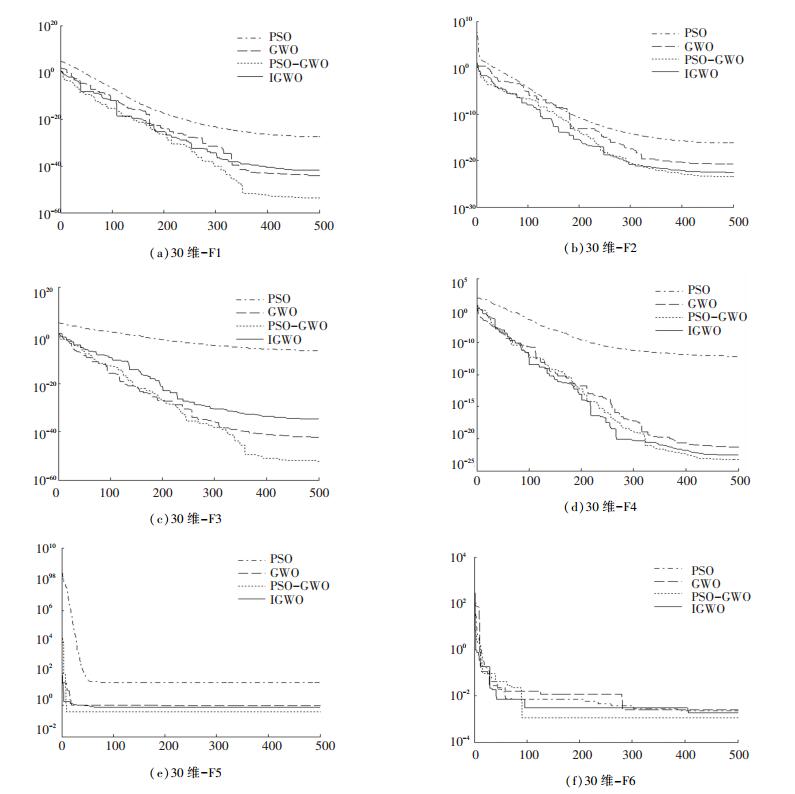
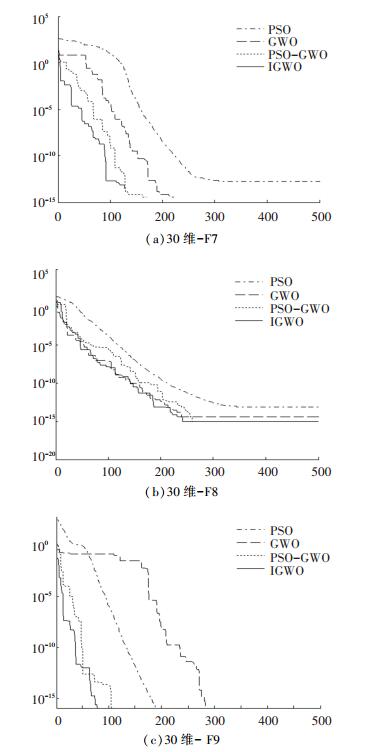
为比较4种算法的收敛性能, 本文对4种算法进行仿真图对比, 如图 9和图 10所示.
|
图 9 PSO, GWO, IGWO和PSO_GWO在单峰函数上的收敛曲线 Figure 9 Convergence curves of PSO, GWO, IGWO, and PSO_GWO on unimodal functions |
|
图 10 PSO, GWO, IGWO和PSO_GWO在多峰函数上的收敛曲线 Figure 10 Convergence curves of PSO, GWO, IGWO, and PSO_GWO in multimodal functions |
从图 9可看出, 4种算法在搜索初期时搜索速度大致相同, 但是随着迭代次数的增加, 本文提出的PSO_GWO算法一直搜索最优解, 而其他三种算法提前达到寻优停滞状态, 造成寻优效果差.因此PSO_GWO算法在单峰函数上寻优效果优于其他三种算法.从图 10可看出, 本文提出的算法在多峰函数上搜索到的最优解更加理想, 不易陷入局部最优.
从CPU和TIC/TOC两方面对算法进行计算时间统计.CPU反映CPU全速工作时完成该进程所花费的时间, 而TIC/TOC是用来计算程序运行的时间.计算结果见表 5.从表 5可看出, PSO_GWO算法比IGWO算法在计算时间复杂度方面效果较好.但是相比PSO算法与GWO算法, PSO_GWO算法具有较大的计算复杂度, 从而运行时间较长.这是由于PSO_GWO算法是在基本GWO算法的基础之上引入PSO算法的思想, 从而加大算法的计算复杂度.因此, PSO_GWO算法牺牲计算复杂度来提高寻优效果.
| 表 5 GWO、PSO、IGWO、PSO_GWO算法的运行时间 Table 5 Run time of GWO, PSO, IGWO, and PSO_GWO algorithm |
为验证种群规模对本文算法的影响, 将种群规模即N设置为30、35、40、45、50, 并分别单独进行30次仿真实验, 其结果如表 6所示.
| 表 6 不同种群规模的PSO_GWO的寻优结果 Table 6 Results of optimization of PSO_GWO for different population sizes |
从表 6可得到, 当N=50时, PSO_GWO算法的寻优结果最好; 随着N逐渐增大, PSO_GWO算法收敛值逐渐增大.这是由于种群数量增加将会使算法在初始化时多样性更好, 从而能够提高算法的全局能力及局部搜索能力, 增强算法的寻优性能.因此, 本文提出的算法随着种群规模增大收敛值逐渐接近理想值.
4 结论为进一步提高算法的寻优能力及收敛精度, 本文提出一种改进的灰狼算法.其思路是利用Tent混沌映射初始化灰狼种群增加种群的多样性; 采用非线性控制参数来权衡算法的局部及全局搜索能力, 从而能够提高种群的收敛速度; 与此同时, 引进PSO算法的思想将灰狼个体经验引入位置更新公式中, 使其能够保留自身最优位置信息, 从而提高算法的收敛精度.为验证本文提出的算法的有效性, 对9个标准测试函数进行仿真实验.实验结果显示, PSO_GWO算法比GWO、PSO、IGWO算法更快搜索到全局最优解, 且其鲁棒性更好.下一阶段将围绕利用PSO_GWO算法来提高无线传感器网络覆盖效果开展研究.
| [1] |
ZAMZAMIAN S M, HOSSEINI S A, SAMADFAM M. Optimization of the marinelli beaker dimensions using genetic algorithm[J]. Journal of Environmental Radioactivity, 2017, 172: 81. DOI:10.1016/j.jenvrad.2017.03.020 |
| [2] |
GARG H. A hybrid PSO-GA algorithm for constrained optimization problems[J]. Applied Mathematics and Computation, 2016, 274(11): 292. DOI:10.1016/j.amc.2015.11.001 |
| [3] |
MADOLIAT R, KHANMIRZA E, POURFARD A. Application of PSO and cultural algorithms for transient analysis of natural gas pipeline[J]. Journal of Petroleum Science & Engineering, 2016, 149: 504. DOI:10.1016/j.petrol.2016.09.042 |
| [4] |
SAKR W S, El-SEHIEMY R A, Azmy A M. Adaptive differential evolution algorithm for efficient reactive power management[J]. Applied Soft Computing, 2017, 53: 336. DOI:10.1016/j.asoc.2017.01.004 |
| [5] |
Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69(3): 46. DOI:10.1016/j.advengsoft.2013.12.007 |
| [6] |
SAREMI S, MIRJALILI S Z, MIRJALILI S M. Evolutionary population dynamics and grey wolf optimizer[J]. Neural Computing and Applications, 2015, 26(5): 1257. DOI:10.1007/s00521-014-1806-7 |
| [7] |
MIRJALILI S, SAREMI S, MIRJALILI S M, et al. Multi-objective grey wolf optimizer:A novel algorithm for multicriterion optimization[J]. Expert Systems with Applications, 2016, 47: 106. DOI:10.1016/j.eswa.2015.10.039 |
| [8] |
ZHU Aijun, XU Chuanpei, LI Zhi, et al. Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC[J]. Journal of Systems Engineering and Electronics, 2015, 26(2): 317. DOI:10.1109/JSEE.2015.00037 |
| [9] |
龙文, 蔡绍洪, 焦建军, 等. 求解高维优化问题的混合灰狼优化算法[J]. 控制与决策, 2016, 31(11): 1991. LONG Wen, CAI Shaohong, JIAO Jianjun, et al. Hybrid grey wolf optimization algorithm for high-dimensional optimization[J]. Control and Decision, 2016, 31(11): 1991. DOI:10.13195/j.kzyjc.2015.1183 |
| [10] |
姚鹏, 王宏伦. 基于改进流体扰动算法与灰狼优化的无人机三维航路规划[J]. 控制与决策, 2016, 31(04): 701. YAO Peng, WANG Honglun. Three dimensional path planning for UAV based on improved interfered fluid dynamical system and grey wolf optimizer[J]. Control and Decision, 2016, 31(04): 701. DOI:10.13195/j.kzyjc.2015.0191 |
| [11] |
龙文, 伍铁斌. 协调探索和开发能力的改进灰狼优化算法[J]. 控制与决策, 2017, 32(10): 1. LONG Wen, WU Tiebin. Improved grey wolf optimization algorithm coordinating the ability of exploration and exploitation[J]. Control and Decision, 2017, 32(10): 1. DOI:10.13195/j.kzyjc.2016.1545 |
| [12] |
郭振洲, 刘然, 拱长青, 等. 基于灰狼算法的改进研究[J]. 计算机应用研究, 2017, 34(12): 3603. GUO Zhenzhou, LIU Ran, GONG Changqing, et al. Study on improvement of grey wolf algorithm[J]. Application Research of Computers, 2017, 34(12): 3603. DOI:10.3969/j.issn.1001-3695.2017.12.019 |
| [13] |
左剑, 张程稳, 肖逸, 等. 基于灰狼优化算法的多机电力系统稳定器参数最优设计[J]. 电网技术, 2017, 41(09): 2987. ZUO Jian, ZHANG Chengwen, XIAO Yi, et al. Multi-machine PSS parameter optimal tuning based on Grey Wolf Optimizer algorithm[J]. Power System Technology, 2017, 41(09): 2987. DOI:10.13335/j.1000-3673.pst.2017.0011 |
| [14] |
SAHOO A, CHANDRA S. Multi-objective Grey Wolf Optimizer for improved cervix lesion classification[J]. Applied Soft Computing, 2016, 52: 64. DOI:10.1016/j.asoc.2016.12.022 |
| [15] |
单梁, 强浩, 李军, 等. 基于Tent映射的混沌优化算法[J]. 控制与决策, 2005, 20(2): 179. SHAN Liang, QIANG Hao, LI Jun, et al. Chaotic optimization algorithm based on Tent map[J]. Control and Decision, 2005, 20(2): 179. DOI:10.3321/j.issn:1001-0920.2005.02.013 |
| [16] |
魏政磊, 赵辉, 李牧东, 等. 控制参数值非线性调整策略的灰狼优化算法[J]. 空军工程大学学报:自然科学版, 2016, 17(3): 68. WEI Zhenglei, ZHAO Hui, LI Mudong, et al. A grey wolf optimization algorithm based on non-linear adjustment strategy of control parameter[J]. Journal of Air Force Engineering University (Natural Science Edition), 2016, 17(3): 68. DOI:10.3969/j.issn.1009-3516.2016.03.013 |
| [17] |
MITTAL N, SINGH U, SOHI B S. Modified grey wolf optimizer for global engineering optimization[J]. Applied Computational Intelligence and Soft Computing, 2016, 2016(4598): 1. DOI:10.1155/2016/7950348 |
| [18] |
CLERC M.The swarm and the queen: Towards adeterministic and adaptive particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation.Washington, IEEE, 2002: 1951.DOI: 10.1109/CEC.1999.785513
|
| [19] |
KAO Y T, ZAHARA E. A hybrid genetic algorithm and particle swarm optimization for multimodal functions[J]. Applied Soft Computing, 2008, 8(2): 849. DOI:10.1016/j.asoc.2007.07.002 |
| [20] |
LIU Tianhua, YIN Shoulin. An improved particle swarm optimization algorithm used for BP neural network and multimedia course-ware evaluation[J]. Multimedia Tools and Applications, 2016, 76(9): 11961. DOI:10.1007/s11042-016-3776-5 |
| [21] |
LU Chao, GAO Liang, LI Xinyu, et al. A hybrid multi-objective grey wolf optimizer for dynamic scheduling in a real-world welding industry[J]. Engineering Applications of Artificial Intelligence, 2017, 57(C): 61. DOI:10.1016/j.engappai.2016.10.01 |
 2018, Vol. 50
2018, Vol. 50


