2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Science, Beijing 100049
图像融合是计算机视觉中的一个重要领域,其目标在于提取2幅及以上源图像的有效信息,合成为1幅包含所有有效信息的图像.图像融合技术应用广泛,如遥感图像融合[1],医学图像融合[2],多聚焦图像融合[3-4]等.本文主要针对的是金属表面纹理的多聚焦图像融合.由于镜头景深受到限制,使CCD图像传感器获得的图像呈现部分位置聚焦、其他位置虚焦的状态.因此需要使用图像融合算法提取出所有聚焦的部分合成一幅完全聚焦的图像,使其能够更加方便人眼观察或者计算机处理.
常用的图像融合算法主要分为2大类:基于空间域和基于变换域.基于空间域的算法主要通过提取图像的空间特征得到对应的权重,然后加权源图像得到最终的融合图像.其代表算法有形态学滤波图像融合[3]、引导滤波图像融合[4]、脉冲耦合神经网络图像融合[5]等.其优点在于能够保持较好的空间连续性,但是细节还原能力较差.基于变换域的算法,其基本思想在于通过对源图像进行多尺度变换,然后对细节部分和近似部分采用不同的融合规则得到融合系数,再进行逆变换得到融合图像.其代表算法有基于Laplacian金字塔分解[6]、基于离散小波变换[7]、基于非下采样轮廓波变换[8]的图像融合等.近年来,基于稀疏表示[9-11]图像融合的出现,使得图像融合效果有了进一步的提升,但是稀疏表示不具有全局性,容易产生块效应.具有全局性的低秩表示算法[12],能够有效解决块效应的问题,但是局部细节保持能力欠缺.
结合已有算法的优缺点,提出一种基于SIFT字典学习的引导滤波图像融合算法.图像的低秩表示具有全局表示能力,但是局部细节描述不足,本文通过学习不同类别的子字典,增强了融合图像中的细节部分,并且能够适用于未配准的源图像.基于SIFT字典学习的引导滤波图像融合算法首先使用滑动窗口技术对图像进行分块,再提取每个块的SIFT特征,接着使用k-means对SIFT特征进行聚类,然后对每个类别学习子字典,最后合成一个整体字典.得到字典之后,首先将每幅源图像进行低秩表示,按列向量取1范数最大者为融合图的低秩表示系数,最后乘以字典得到融合图像.为增加融合图的空间连续性,在融合阶段引入引导滤波[13],并使用熵对内容(特征内容和非特征内容)进行区分,根据不同内容类别选取不同大小的引导滤波窗口.实验结果表明,基于SIFT字典学习的引导滤波图像融合在局部细节保留能力、空间连续性和未配准问题方面都取得了非常好的结果.
1 相关技术 1.1 低秩表示低秩表示[12](Low-Rank Representation, LRR)是将数据集S表示为字典D和一个系数矩阵W的乘积,即S = DW.其中W是低秩的,则称W是数据集S在字典D下的低秩表示,可转换为求解如下的优化问题
| $ \mathop {\min }\limits_{W,E} \left( {{{\left\| \mathit{\boldsymbol{W}} \right\|}_ * } + \lambda {{\left\| \mathit{\boldsymbol{E}} \right\|}_{2,1}}} \right),{\rm{s}}.{\rm{t}}.\;\mathit{\boldsymbol{S}} = \mathit{\boldsymbol{DW}} + \mathit{\boldsymbol{E}}. $ | (1) |
式中:λ>0为平衡因子,E为误差矩阵,‖ X ‖*为X的核范数,即求X奇异值之和,‖ X ‖2, 1为21范数,其计算公式如下
| $ {\left\| \mathit{\boldsymbol{X}} \right\|_{2,1}} = \sum\nolimits_{j = 1}^n {\sqrt {\sum\nolimits_{i = 1}^m {{{\left[ \mathit{\boldsymbol{X}} \right]}_{ij}}^2} } } . $ | (2) |
式中X ∈ Rm×n.式(1)由拉格朗日乘子相关算法[14]计算即可.
1.2 引导滤波引导滤波[13](Guided Filtering, GF)是一种线性移可变的滤波操作,并希望输出图像能与原始图像尽量接近.假设引导图像G和输出图像q间是一种局部线性关系,即
| $ {\mathit{\boldsymbol{q}}_i} = {a_k}{\mathit{\boldsymbol{G}}_i} + {b_k},{\forall _i} \in {\mathit{\boldsymbol{\omega }}_k}. $ | (3) |
式中:ak、bk为线性系数,ωk是以像素k为中心的局部窗口,可见在局部窗口内,线性系数为常量.为求解线性系数,需要最小化如下的误差函数Er.
| $ {E_r}\left( {{a_k},{b_k}} \right) = \sum\limits_{i \in {\omega _k}} {\left( {{{\left( {{a_k}{\mathit{\boldsymbol{G}}_i} + {b_k} - {\mathit{\boldsymbol{p}}_i}} \right)}^2} + \varepsilon {a_k}^2} \right)} . $ | (4) |
式中:p为输入图像,ε为衰减系数,εak2为衰减项,防止参数过大.由求解结果可知,当引导图像G为输入图像本身时,引导滤波则起到边缘保持滤波的作用,即图像平滑的同时,边缘能够保持不变.
2 本文算法 2.1 基于SIFT的字典学习基于SIFT的字典学习方法主要包括以下几个部分:基于滑动窗口技术分块、SIFT特征提取、k-means聚类、子字典学习和字典合成.
1) 分块.将源图像Ii(i=1, 2, ..., N)使用滑动窗口技术进行分块,N为源图像总数.设W, H分别为源图像宽高,s为滑动窗口大小,步长为t,则每幅源图像有
2) SIFT特征提取.计算第j块的SIFT特征,记为Bj(j=1, 2, ..., NQ).为能够满足k-means聚类输入要求,每个块的SIFT特征维度应该保持一致.提取SIFT特征前需先提取每个块的关键点,即为DoG尺度空间共26个邻域(见图 1)的极大、极小值点,并去除部分不合格的点所剩下的特征点. DoG有效层数S=3,初始尺度δ0=1.6,参数和去除条件均参考文献[15].由于每个块的关键点个数不一致,SIFT特征提取将分为以下3种情况:
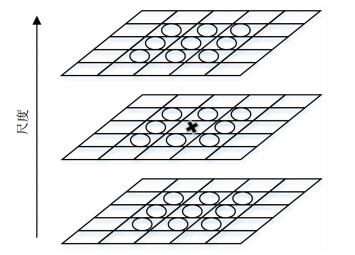
|
图 1 DoG尺度空间及26个邻域 Figure 1 DoG scale space and 26 neighborhoods |
情况1:无关键点.
若第j块无关键点,则直接将其分为第0类,记Uj=0,Uj为第j块的类别.
情况2:关键点个数为1.
若第j块只有1个关键点,则直接使用该关键点的特征作为第j块的特征,即
| $ {\mathit{\boldsymbol{B}}_j} = {\mathit{\boldsymbol{P}}_1}. $ | (5) |
式中: Pj′为第j′个关键点的SIFT特征,Pj′∈ RT,T为SIFT特征的维度,本文采用8个方向和统计16个小块的梯度方向直方图,因此T=128.
情况3:关键点个数大于1.
若第j块大于1个关键点,则取特征最明显的关键点,本文使用了1范数,SIFT特征的1范数越大表示方向越多或越明显,即
| $ {\mathit{\boldsymbol{B}}_j} = \mathop {\max }\limits_{{\mathit{\boldsymbol{P}}_{j'}}} {\left\| {{\mathit{\boldsymbol{P}}_{j'}}} \right\|_1}. $ | (6) |
情况2、3的块将用于第3)步的聚类算法.
3) k-means聚类.假设聚类总数为K,若按照SIFT特征方向进行聚类,则有K=8,具体流程如下:
S1:首先初始化K个聚类中心,分别为
S2:使用欧氏距离作为特征向量间距离的度量标准,并对所有特征向量进行初始划分
| $ \mathit{\boldsymbol{U}}_j^{it} = \mathop {\min }\limits_k {\left\| {{\mathit{\boldsymbol{B}}_j} - \mathit{\boldsymbol{\mu }}_k^{it}} \right\|_2}, $ | (7) |
| $ \mathit{\boldsymbol{C}}_k^{it} = \mathit{\boldsymbol{C}}_k^{it} \cup \left\{ {{\mathit{\boldsymbol{B}}_j}} \right\}. $ | (8) |
式中:k={1, 2, ..., K}为类别标签,μkit为第k类的聚类中心在第it次迭代的结果,Ujit为第j块在第it次迭代的类别,Ckit为第k类的特征向量在第it次迭代的集合.
S3:it+1→it,更新每个类别样本的聚类中心为
| $ \mathit{\boldsymbol{\mu }}_k^{it} = \frac{1}{{\left| {\mathit{\boldsymbol{C}}_k^{it - 1}} \right|}}\sum\limits_{{\mathit{\boldsymbol{B}}_j} \in \mathit{\boldsymbol{C}}_k^{it - 1}} {{\mathit{\boldsymbol{B}}_j}} . $ | (9) |
如果*为标量,则| *|为求绝对值; 若*为向量,则|* |为求向量元素个数.
S4:如果满足式(10)或者it≥Tmax,则聚类结束,否则转到S2继续执行.
| $ {\left\| {\mathit{\boldsymbol{\mu }}_k^{it} - \mathit{\boldsymbol{\mu }}_k^{it - 1}} \right\|_2} < \zeta , $ | (10) |
式中ζ为误差允许范围,取ζ=10-6.
4) 子字典学习和字典合成
采用一种标准无监督字典学习方法K奇异值分解算法[16](K-Singular Value Decomposition, K-SVD)对K+1(包括无关键点的块)个类别的块分别进行字典学习.学习之前,先将每个块按照行优先顺序展开成列向量的形式.通过K-SVD算法学习之后分别得到子字典D0, D1, ..., DK,最终合成一个完整的字典D = {D0, D1, ..., DK},字典大小设置为256,字典学习过程见图 2.
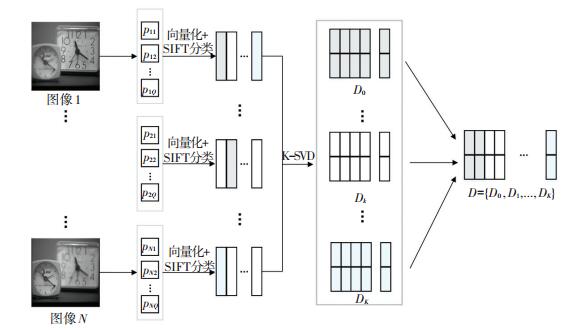
|
图 2 基于SIFT的字典学习过程 Figure 2 SIFT-based dictionary learning process |
字典学习完毕之后,对单张源图像Ii进行低秩表示.即将求取的Ii的分块向量化,得到对应的Vi,然后结合式(1)得到如下优化公式
| $ \mathop {\min }\limits_{{\mathit{\boldsymbol{W}}_i},{{\mathit{\boldsymbol{\tilde E}}}_i}} \left( {{{\left\| {{\mathit{\boldsymbol{W}}_i}} \right\|}_ * } + \lambda {{\left\| {{{\mathit{\boldsymbol{\tilde E}}}_i}} \right\|}_{2,1}}} \right),{\rm{s}}.{\rm{t}}.\;{\mathit{\boldsymbol{V}}_i} = \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{W}}_i} + {{\mathit{\boldsymbol{\tilde E}}}_i}. $ | (11) |
式中:i={1, 2, ..., N},Wi为第i幅图像的低秩表示系数,
S1:构建输入图像.若Wi的第q列的1范数沿着z轴方向取得最大值,则该列置1,否则置0,公式为
| $ {\mathit{\boldsymbol{G}}_i}\left( {:,q} \right) = \left\{ \begin{array}{l} 1,\;\;\;\;{\rm{s}}.{\rm{t}}.\;i = \mathop {\max }\limits_{i'} \left\{ {{{\left\| {{\mathit{\boldsymbol{W}}_{i'}}\left( {:,q} \right)} \right\|}_1}} \right\};\\ 0,\;\;\;\;其他. \end{array} \right. $ | (12) |
式中Gi为输入图像,Gi(:, q)为Gi的第q列.
S2:进行引导滤波.以Gi作为输入图像,对应的Wi作为引导图像进行引导滤波,得到引导滤波后的结果ri
| $ {\mathit{\boldsymbol{r}}_i} = {f_{{s_\mathit{\boldsymbol{\omega }}},\varepsilon }}\left( {{\mathit{\boldsymbol{G}}_i},{\mathit{\boldsymbol{W}}_i}} \right). $ | (13) |
式中:f为引导滤波操作,sω, ε是f的输入参数,sω是引导滤波的窗口大小,即式(3)中的ωk的大小,ε=0.01对应式(4)中的衰减系数.
S3:计算窗口自适应条件. sω会根据内容(特征内容和非特征内容)进行自适应变化,规则如下:沿着z轴方向求各列的熵(本文使用列的2范数),然后设置阈值,大于阈值者为非特征内容,引导滤波时使用较大窗口; 否则为特征内容,引导滤波时使用较小窗口.熵计算公式为
| $ {\mathit{\boldsymbol{\varphi }}_i}\left( {:,q} \right) = {\left\| {{\mathit{\boldsymbol{W}}_i}\left( {:,q} \right)} \right\|_2}/\sum\limits_{j = 1}^{j = N} {{{\left\| {{\mathit{\boldsymbol{W}}_j}\left( {:,q} \right)} \right\|}_2}} , $ | (14) |
| $ {\mathit{\boldsymbol{E}}_{\rm{n}}}\left( {p,q} \right) = \sum\limits_{i = 1}^{i - N} { - {\varphi _i}\left( {p,q} \right)\log {\varphi _i}\left( {p,q} \right)} . $ | (15) |
式中:φ为概率,是直接将第q列的低秩表示系数的2范数沿z轴方向归一化得到,‖*‖2为2范数,p, q为低秩系数的坐标,En为熵.将En除以最大值进行归一化:
| $ {E_{\max }} = \max \left( {{\mathit{\boldsymbol{E}}_{\rm{n}}}} \right), $ | (16) |
| $ {\mathit{\boldsymbol{E}}_{\rm{n}}}\left( {p,q} \right) = {\mathit{\boldsymbol{E}}_{\rm{n}}}\left( {p,q} \right)/{E_{\max }}, $ | (17) |
式中Emax为En的最大值. sω将满足如下等式
| $ {s_\mathit{\boldsymbol{\omega }}}\left( {p,q} \right) = \left\{ \begin{array}{l} {s_{\rm{b}}},\;\;\;{\rm{s}}.{\rm{t}}.\;\;{\mathit{\boldsymbol{E}}_{\rm{n}}}\left( {p,q} \right) > \tau ;\\ {s_{\rm{s}}},\;\;\;{\rm{s}}.{\rm{t}}.\;\;{\mathit{\boldsymbol{E}}_{\rm{n}}}\left( {p,q} \right) \le \tau . \end{array} \right. $ | (18) |
式中:τ为阈值,取τ=0.95,ss, sb为两个正整数,分别为特征内容和非特征内容区域引导滤波的窗口大小,并满足ss < sb,取ss=3, sb=7.
S4:求取融合系数.使用ri作为权重对Wi进行加权,得到最终的融合低秩表示系数Wf
| $ {\mathit{\boldsymbol{W}}_{\rm{f}}}\left( {p,q} \right) = \sum\nolimits_{i = 1}^{i = N} {{\mathit{\boldsymbol{r}}_i}\left( {p,q} \right){\mathit{\boldsymbol{W}}_i}\left( {p,q} \right)} . $ | (19) |
S5:获取融合图.结合式(1),可求出融合图的块向量展开形式Vf:
| $ {\mathit{\boldsymbol{V}}_{\rm{f}}} = \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{W}}_{\rm{f}}}. $ | (20) |
将Vf还原成图像的形式,重叠部分取平均值即可,得到融合图F.图像融合的整体流程图见图 3.
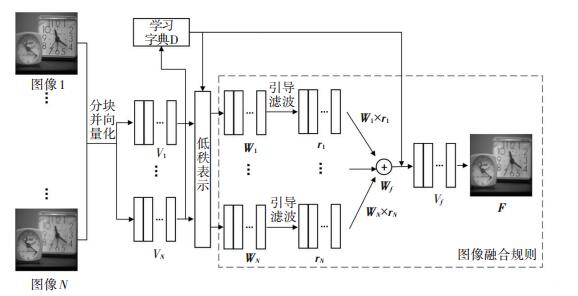
|
图 3 整体图像融合框架 Figure 3 The framework of proposed algorithm |
实验使用Genie Nano系列的200万像素的黑白相机,分辨率5.5 μm,同轴光照明. Mitutoyo的物镜和目镜,物镜放大倍率为20X,景深1.8 μm.日本Oriental Motor公司的PMM33BH2步进电机,每次步进1 μm.连续拍摄100帧图像,图像大小为1 472×1 472像素,实验装置见图 4.实验运行环境为MATLAB R2016a,2.4 GHz,16 GB内存.

|
图 4 实验装置 Figure 4 Experimental device |
为验证提出算法的有效性,使用6组实验数据,包括3组广泛用于研究的多聚焦图像(2帧/组,见图 5)和3组使用图 4装置实际拍摄的图像(100帧/组,见图 6).为说明本文算法的有效性,将其与以下算法进行对比分析:基于引导滤波的图像融合[4](Image Fusion based on Guided Filtering, IF-GF)、基于离散小波变换的图像融合[7](Image Fusion based on Discrete Wavelet Transform, IF-DWT)、基于轮廓波变换的图像融合[8](Image Fusion based on Non-Subsampled Contourlet Transform, IF-NSCT)、基于稀疏表示的图像融合[10](Image Fusion based on Sparse Representation, IF-SR).

|
图 5 广泛应用于研究的多聚焦图像数据 Figure 5 Examples of widely used multi-focus images |
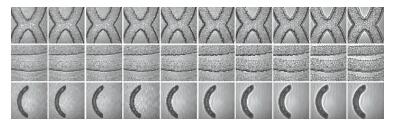
|
图 6 实际拍摄的多聚焦图像数据 Figure 6 Examples of real-world multi-focus images |
为给块大小s和步长t设置一个合理的值,本节随机选取1组图像进行仿真实验分析,为方便计算,参数都取2的幂次方.表 1显示了子字典的块数分布,0~8分别代表 9个子字典.块越小越能学习更多的细节,但是块太小不能有效提取SIFT特征,从表 1中可看出,取s=4, 8基本不能提取块的SIFT特征,当s=16, t=1, 2块数分布已经基本合理(如黑体字),而s=16, t=4块数太少,不符合学习条件.若块数过于冗余,会导致字典求解过程中冗余信息反复迭代,使图像有用信息不能完整表达,表 2显示了s=16, t=1, 2重构子字典的误差分布,t=2误差更小(如黑体字).综上,s=16, t=2为较为合理的选择.
| 表 1 分块大小对子字典学习的块数分布比较 Table 1 The comparison of block size on the distribution of sub-dictionary learning blocks |
| 表 2 步长对子字典学习的残差分布比较 Table 2 The comparison of step size on the distribution of sub-dictionary learning residual |
为更加直观的说明实验的效果,使用5类质量评价函数[17](以2幅源图像为例,可推广到多幅),每类评价函数都是值越大,表示融合质量越好.
1) 归一化的互信息(Normalized Mutual Information, QNMI)来源于信息论,是测量源图像的信息在融合图像中的保留程度,式(21)使用其改进形式
| $ {Q_{{\rm{NMI}}}} = 2\left[ {\frac{{MI\left( {{\mathit{\boldsymbol{S}}_1},\mathit{\boldsymbol{F}}} \right)}}{{H\left( {{\mathit{\boldsymbol{S}}_1}} \right) + H\left( \mathit{\boldsymbol{F}} \right)}} + \frac{{MI\left( {{\mathit{\boldsymbol{S}}_2},\mathit{\boldsymbol{F}}} \right)}}{{H\left( {{\mathit{\boldsymbol{S}}_2}} \right) + H\left( \mathit{\boldsymbol{F}} \right)}}} \right]. $ | (21) |
式中:
| $ MI\left( {{\mathit{\boldsymbol{S}}_i},\mathit{\boldsymbol{F}}} \right) = H\left( {{\mathit{\boldsymbol{S}}_i}} \right) + H\left( \mathit{\boldsymbol{F}} \right) - H\left( {{\mathit{\boldsymbol{S}}_i},\mathit{\boldsymbol{F}}} \right), $ | (22) |
式中i={1, 2},H(Si, F)为Si和F的联合熵.
2) 梯度相关性(Gradient-based Fusion Metric, QG)是度量图像间边缘信息的相关性为
| $ {Q_{\rm{G}}} = \frac{{\sum\limits_{x = 1}^H {\sum\limits_{y = 1}^W {\left[ {Q_{xy}^{{\mathit{\boldsymbol{S}}_1}\mathit{\boldsymbol{F}}}\omega _{xy}^{{\mathit{\boldsymbol{S}}_1}} + Q_{xy}^{{\mathit{\boldsymbol{S}}_2}\mathit{\boldsymbol{F}}}\omega _{xy}^{{\mathit{\boldsymbol{S}}_2}}} \right]} } }}{{\sum\limits_{x = 1}^H {\sum\limits_{y = 1}^W {\left[ {\omega _{xy}^{{\mathit{\boldsymbol{S}}_1}} + \omega _{xy}^{{\mathit{\boldsymbol{S}}_2}}} \right]} } }}, $ | (23) |
式中:x, y为图像中的坐标,
3) 相位一致性(Phase Congruency, QP)定义了和矩相关的度量,因为矩包含角点和边缘的信息,定义如下:
| $ {Q_{\rm{P}}} = {\left( {{P_{\rm{p}}}} \right)^\alpha }{\left( {{P_{\rm{M}}}} \right)^\beta }{\left( {{P_{\rm{m}}}} \right)^\gamma }. $ | (24) |
式中:
4) 结构相似度(Structural Similarity, QS)的测量能够近似的反映出图像的形变情况,公式如下:
| $ \begin{array}{l} {Q_{\rm{S}}} = \frac{1}{{\left| {\mathit{\boldsymbol{\dot W}}} \right|}}\sum\limits_{w \in \dot W} {\left[ {{\lambda _\mathit{\boldsymbol{w}}}Q\left( {{\mathit{\boldsymbol{S}}_1},\mathit{\boldsymbol{F}}\left| \mathit{\boldsymbol{w}} \right.} \right) + \left( {1 - } \right.} \right.} \\ \;\;\;\;\;\;\;\left. {\left. {{\lambda _\mathit{\boldsymbol{w}}}} \right)Q\left( {{\mathit{\boldsymbol{S}}_2},\mathit{\boldsymbol{F}}\left| \mathit{\boldsymbol{w}} \right.} \right)} \right]. \end{array} $ | (25) |
式中:
5) Chen-Blum度量法(Chen-Blum Metrics, QCB)计算对比度特征在融合图像中的保留程度,公式如下:
| $ {Q_{{\rm{CB}}}} = \frac{1}{{HW}}\sum\limits_{x = 1}^H {\sum\limits_{y = 1}^W {\left[ {\lambda _{xy}^{{\mathit{\boldsymbol{S}}_1}}Q_{xy}^{{\mathit{\boldsymbol{S}}_1}\mathit{\boldsymbol{F}}} + \lambda _{xy}^{{\mathit{\boldsymbol{S}}_2}}Q_{xy}^{{\mathit{\boldsymbol{S}}_2}\mathit{\boldsymbol{F}}}} \right]} } , $ | (26) |
式中:x, y为图像中的下标,
将实验结果分成2部分进行分析:广泛用于研究的多聚焦图像和实际拍摄的多聚焦图像.前者验证提出算法的有效性,后者说明提出算法的泛化能力及有效性.
3.4.1 广泛用于研究的多聚焦图像分析图 5中每组图都是左幅图左部分清晰,右幅图右部分清晰,其中第3组为2幅未完全配准的图像.
图 7分别显示了IF-GF、IF-DWT、IF-NSCT、IF-SR和本文算法对3组图像的融合结果.为便于分析,图 8显示了对应的部分细节放大图(图 8的列对应图 7的行).从放大的细节图中可看出IF-GF的空间连续性较好,没有明显的块效应,但是细节部分较其他变化域算法更为模糊,由A1的“倒影字母”可明显看出. IF-DWT整体较差,融合图基本不能反映出源图像的有效信息. IF-NSCT和本文算法对未配准图像鲁棒性较高,从A13、A15的头发边缘可明显看出,而IF-GF、IF-DWT、IF-SR都有明显的伪影产生,对应矩形框所示. IF-SR因为不具备全局性,所以边缘部分产生了块效应,A9较明显.综上,IF-NSCT和本文算法在细节保留和克服未配准问题都取得了较好的结果,但是IF-NSCT在空间连续性上比较欠缺,如A13矩形框所示.

|
(a)IF-GF (b) IF-DWT (c) IF-NSCT (d) IF-SR (e)本文算法 图 7 广泛应用于研究的多聚焦图像融合结果 Figure 7 Widely used multi-focus image fusion results |

|
图 8 部分细节放大图A Figure 8 Magnified partial details A |
表 3用具体的数据进行客观质量评价,利用5个融合质量评价函数,其中加粗的数字为所有算法中的最大值.表中的数据可看出,本文算法除了第2组的QS不是最大值,其他都保持领先,说明该算法在原始信息保留、细节保留、结构保持、对比度保持等方面都比其他主流融合算法更好.此外,IF-GF在QNMI和QS指标下取得较好结果,说明基于空域的算法在空间连续性和结构保持方面更占优势.而IF-NSCT在QG、QCB指标下的值更高,说明细节保持能力更强.因此,实验结果与理论分析基本达成一致.
| 表 3 不同融合算法的融合质量比较A Table 3 Comparison of fusion quality of 5 fusion algorithms A |
实际拍摄图像的每1组都是由凹坑部分(前景)和平面部分(背景)组成,由于拍摄是从上至下进行的,因此都呈现平面部分先聚焦,凹坑后聚焦的状态.
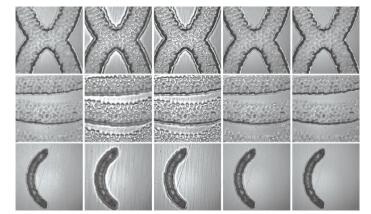
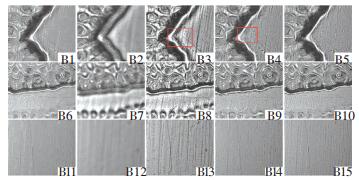
图 9显示了3组图像使用不同融合算法的融合结果图,图 10则显示了对应的部分细节放大图(分别选择边缘、凹坑和平面).从整体融合图中可发现IF-DWT算法存在明显模糊,同广泛应用于研究的图像结果达成一致.图 10的B1~B5选择边缘进行分析,其中B1整体比较平滑,但是细节存在丢失的现象,从边缘附近平面的纹理较明显看出. B3整体对比度非常强烈,但是由边缘旁边的“光晕”可看出(矩形框所示)IF-NSCT算法的结果并不符合人眼的主观视觉感受. B4~B5则表现较好,但是B4仍存在局部块效应(矩形框所示). B6~B10、B11~B15分别选择凹坑细节部分和平面部分进行分析,结果与B1~B5保持一致,需要补充的是B10、B15较B6、B11分别在凹坑和平面上细节更加丰富,且都保持着较高的空间连续性.
|
(a)IF-GF (b) IF-DWT (c) IF-NSCT (d) IF-SR (e)本文算法 图 9 实际拍摄多聚焦图像融合结果 Figure 9 Real-world multi-focus image fusion results |
|
(a) IF-GF (b) IF-DWT (c) IF-NSCT (d) IF-SR (e)本文算法 图 10 部分细节放大图B Figure 10 Magnified partial details B |
表 4对5种不同的融合算法在5个质量评价指标下的结果进行比较分析,其中加粗的数字为所有算法中的最大值.本文算法在大多数情况下都取得了最优的结果,其他算法的趋势也与广泛应用于研究的图像结果高度一致,验证了本文提出算法在细节保留能力和空间连续性方面的有效性以及对多幅实际拍摄图像具有较好的泛化能力.
| 表 4 不同融合算法的融合质量比较B Table 4 Comparison of fusion quality of 5 fusion algorithms B |
本文提出了一种基于SIFT字典学习的引导滤波图像融合算法.该算法使用低秩表示,使融合图像具有全局性,并且通过SIFT进行分类学习子字典,克服了低秩表示局部细节保持能力弱和对未配准源图像鲁棒性差的缺点.另外,通过加入自适应窗口的引导滤波,增强了融合图像的空间连续性.通过选取3组广泛应用于研究的多聚焦图像和3组实际拍摄的多聚焦图像,使用5类质量评价指标验证了提出算法在细节保留、空间连续性和克服未配准问题方面的有效性.
| [1] |
GHASSEMIAN H. A review of remote sensing image fusion methods[J]. Information Fusion, 2016, 32(PA): 75. DOI:10.1016/j.inffus.2016.03.003 |
| [2] |
EL-GAMAL E Z A, ELMOGY M, ATWAN A. Current trends in medical image registration and fusion[J]. Egyptian Informatics Journal, 2016, 17(1): 99. DOI:10.1016/j.eij.2015.09.002 |
| [3] |
LI S, KANG X, HU J, et al. Image matting for fusion of multi-focus images in dynamic scenes[J]. Information Fusion, 2013, 14(2): 147. DOI:10.1016/j.inffus.2011.07.001 |
| [4] |
LI S, KANG X, HU J. Image fusion with guided filtering[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2013, 22(7): 2864. DOI:10.1109/TIP.2013.2244222 |
| [5] |
XU X, SHAN D, WANG G, et al. Multimodal medical image fusion using PCNN optimized by the QPSO algorithm[J]. Applied Soft Computing, 2016, 46: 588. DOI:10.1016/j.asoc.2016.03.028 |
| [6] |
WANG W, CHANG F. A multi-focus image fusion method based on laplacian pyramid[J]. Journal of Computers, 2011, 6(12): 2559. DOI:10.4304/jcp.6.12.2559-2566 |
| [7] |
PAJARES G, CRUZ J M D L. A wavelet-based image fusion tutorial[J]. Pattern Recognition, 2004, 37(9): 1855. DOI:10.1016/S0031-3203(04)00103-7 |
| [8] |
ZHANG Q, GUO B L. Multifocus image fusion using the nonsubsampled contourlet transform[J]. Signal Processing, 2009, 89(7): 1334. DOI:10.1016/j.sigpro.2009.01.012 |
| [9] |
YIN H, LI S, FANG L. Simultaneous image fusion and super-resolution using sparse representation[J]. Information Fusion, 2013, 14(3): 229. DOI:10.1016/j.inffus.2012.01.008 |
| [10] |
NEJATI M, SAMAVI S, SHIRANI S. Multi-focus image fusion using dictionary-based sparse representation[J]. Information Fusion, 2015, 25: 72. DOI:10.1016/j.inffus.2014.10.004 |
| [11] |
LIU Y, CHEN X, WARD R K, et al. Image fusion with convolutional sparse representation[J]. IEEE Signal Processing Letters, 2016, 23(12): 1882. DOI:10.1109/LSP.2016.2618776 |
| [12] |
LIU G, LIN Z, YAN S, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2010, 35(1): 171. DOI:10.1109/TPAMI.2012.88 |
| [13] |
HE K, SUN J, TANG X. Guided image filtering[C]// European Conference on Computer Vision. Springer-Verlag, 2010: 1. DOI: 10.1109/TPAMI.2012.213
|
| [14] |
LIN Z, CHEN M, MA Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[J]. Eprint Arxiv, 2010, 9. DOI:10.1016/j.jsb.2012.10.010 |
| [15] |
LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [16] |
AHARON M, ELAD M, BRUCKSTEIN A. -SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311. DOI:10.1109/TSP.2006.881199 |
| [17] |
LIU Z, BLASCH E, XUE Z, et al. Objective assessment of multiresolution image fusion algorithms for context enhancement in night vision: a comparative study[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2011, 34(1): 94. DOI:10.1109/TPAMI.2011.109 |
 2018, Vol. 50
2018, Vol. 50


