2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Science, Beijing 100049, China
超声心动图像是评估心脏功能获取心脏生理参数的重要手段[1],而二尖瓣的生理参数又是判断心脏健康与否的重要指标.二尖瓣环内径的大小是判断二尖瓣是否正常的重要生理参数,通常医生获取二尖瓣环内径的大小是凭借自身经验标记两个瓣跟的关键点进行手动测量,其中二尖瓣根是位于二尖瓣膜和心室壁连接处有较为明显的转角特征,这样医生在术中操作非常不便.由于心脏超声图像的形状、姿态和尺寸等变化多样,目前为止,并没有针对二尖瓣环内径关键点进行自动标注的有效算法,因此提出有效可行的二尖瓣环内径自动测量方法能够帮助医生高效的进行疾病诊断.
关键点检测算法在医学图像中一直有广泛应用,通过定位生理结构的一些关键位置能够对自动分析医学图像有很大的帮助.在心脏图像中,很多情况下进行关键点定位是进行图像分析的必要条件,如医学重要切面识别过程中运用关键点能够更为精确的定位生理学结构[2],心室分割过程中可以运用关键点检测算法辅助获取确切的边缘计算心室容积[3].关键点检测方法大体可以分为两类,一类是基于形状先验的轮廓模型方法,该类方法通常检测的关键点处于某个形状轮廓上; 第二类为直接通过分类回归等思想定位目标关键点的方法,该类方法对关键的位置要求较低,但准确度不是很高.第一类方法中,最为著名的为活动形状模型[4]和活动外观模型[5]方法,不少医学图像研究者采用这类方法进行图像分析,Yang等[6]采用基于活动形状模型方法对超声图像进行分割,判断颈动脉粥样硬化性疾病,Vargas等[7]使用了活动外观模型对超声心动图的左心室进行分割.这类基于形状模型的方法通常根据训练数据得到平均形状模型,能够对关键点有全局的形状约束,在提取局部特征的情况下加入了全局形状外观约束.但是这种方法通常需要有良好的初始轮廓位置,并且提取的特征一般是人工设计有局限性的特征.在不通过形状约束的定位关键点方法里,有从事医学图像分析的研究者采用随机森林结合HOG特征检测右心室的关键点[8],为让检测结果能够更好的适应解剖学结构姿态、形状的变化,学者Ozan等[9]在决策森林回归方法的基础上引入了分层思想让检测结果更为精确.近年来,随着深度学习的大力发展,将神经网络运用于解剖学结构关键点检测的研究人员也越来越多,Dong等[10]在3D的医学图像上使用卷积神经网络(CNN)对股骨关键点进行定位,并结合图割方法分割股骨表面,Florin等[11]使用CNN对超声和CT图像进行解剖学关键点的检测.这类方法通常能够得到更好的检测精度,但是依赖于大量的训练数据.虽然上述关键点检测在医学图像上取得了一定的成绩,但实验中发现这些方法直接应用于二维超声图像二尖瓣环内径的测量仍然存在一些问题:
1) 测量二尖瓣环内径仅仅需要标记两个关键点,形状模型方法需要标注多个关键点才能利用其形状轮廓进行约束,并且优化目标是整个轮廓,关心的是所有关键点的平衡,并不是实际需要测量的两个关键点的距离.
2) 超声心动图的边界模糊,采用回归思想的方法虽然能够大致获取关键点的位置,但是现有算法对每个关键点检测都有一定误差,这样对测量距离的稳定性有很大影响.
为解决上述问题,本文提出了一种基于CNN的回归模型来对二尖瓣环的两个关键点进行定位,CNN最初由LeCun等[12]在1998年提出的,再由2012年Hiton等[13]对其改进将算法性能进行大幅度提高,该结构使用网络自己学习特征,避免了人工提取特征的局限性.现有很多关键点检测算法都是基于CNN的,Deng等[14]提出了新的数据增广策略采用了单一的网络结构对人脸关键点进行定位.为了让定位更为精准,许多学者采用级联CNN的方式对关键点由粗糙到精细的定位. Sun等[15]在2013年采用级联的CNN对人脸关键点进行定位,后又引入难样例鉴别机制结合级联的CNN进行服装关键点检测[16],之后Zhang等[17]采用了三个网络对人脸关键点有粗到细的定位.由于此类算法采用的是直接回归关键点的位置,损失函数使用的都是欧式距离损失,在预测关键点的时候通常是孤立的预测每一个关键点,将其直接运用于测量二尖瓣环内径得到的效果并不理想.
本文提出的基于CNN的二尖瓣环内径测量方法,通过使用CNN回归关键点的位置,在欧式距离损失函数基础上加入了距离损失函数,在关键点定位的同时也考虑了距离准确度的问题,实验证明,该方法能够在大部分图像上得到令医生满意的结果.
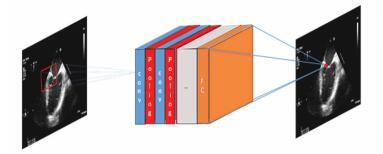
1 基于级联CNN的关键点检测算法基于CNN的关键点检测方法是由Sun在人脸上率先使用的[15],之后大量算法在都是在此基础上改进并对每个关键点由粗到细的进行回归预测[16-17].该算法采用三层级联的卷积网络进行:第一级的卷积网络分为三个单独的卷积网络,分别回归出不同部位的关键点粗略的位置,第二级和第三级的卷积网络以前一级的预测点为中心的小块(patch)作为输入,对前一级的网络输出做微调.每个网络框架见图 1.其中每个卷积层有多个特征矩阵组成,运用于整个特征图像,减少了参数数目,目的是提取图像特征,然后通过池化层降采样,之后通过全连接层输出所需特征点坐标.其中卷积层的输入输出可用式(1)来表达
| $ {{Y}_{1}}=\text{tanh }\!\!~\!\!\text{ }\left( W\otimes Y+B \right)\text{ }. $ | (1) |
|
图 1 卷积神经网络回归关键点框架 Figure 1 Pipeline of landmark detection with convolution neural network |
式中:Y代表输入特征图,Y1代表输出特征图,W为权重参数,B是偏置项,文中采用的是双曲正切函数(tanh)作为激活函数,损失函数采用的是式(2)表达的欧式距离损失(Euclidean loss, EL),即方根均差(root mean squared error, RMSE).
| $ {{R}_{\text{RMSE}}}=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}{\left( {{y}_{i}}-{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}}}_{i}} \right){{~}^{2}}}}. $ | (2) |
式中:yi为n个关键点构成的向量
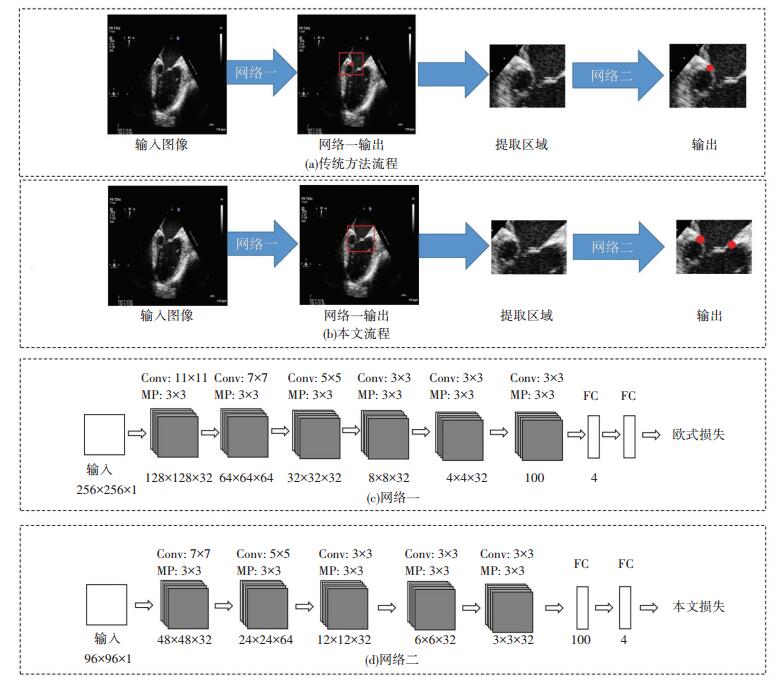
本文提出的超声图像关键点检测算法由两个CNN级联构成,目的是检测二尖瓣根部的两个关键点并计算其长度.传统检测关键点的CNN级联方式见图 2(a),先通过第一个网络定位目标关键点的粗略位置,第二级网络利用第一级预测点为中心的小区域作为输入进行微调.采用传统方法得到的关键点之间关联性较差,预测距离差距较大.为解决这个问题,本文的级联方式见图 2(b),和传统级联方法相同,第一阶段是对关键点位置做粗略定位,采用的是欧式距离损失函数作为优化目标,第二阶段网络在第一阶段预测结果的基础上,选取包含两个预测点的小区域作为输入,并采用带有距离修正的欧式损失函数作为优化目标,得到最终的预测结果.第一个网络结构见图 2(c),输入图像尺寸较大,本文采用含有6个卷积层和2个全连接层的网络进行回归,获得关键点的大概位置,第二个网络见图 2(d),本文选用的是5个卷积层和2个全连接层的结构,回归得到最终的结果.
|
图 2 级联流程及网络结构 Figure 2 Pipeline of method and architectures of two networks |
目前大部分基于回归的关键点检测算法所采用的损失函数都是欧式距离损失,这种损失函数在关键点回归过程中表现良好,针对每一个关键点检测结果都有较高的精度.但在距离测量中,该损失函数并不能体现距离这一重要因素,仅考虑孤立的每个关键点作为损失标准在距离自动测量中具有很大的局限性.
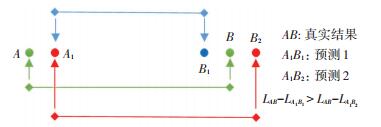
如图 3所示,绿色的点A和B代表真实的关键点位置,A1代表A点的预测位置,B1和B2代表两种不同的B点的预测位置,对于欧式距离损失来说,B1和B2带来的损失值是一样的,显然,预测结果1和2相对真实距离AB是有很大的不同的,预测结果2更为准确,所以实际上更希望出现的是A1B2这种情况,因为这样预测结果更为精确.所以针对只用检测两个关键点测距的目标,本文在原有欧式损失的基础上引入距离损失的度量,提出一种新的带距离修正的损失函数(loss function with distance correction term, DL).如式(3)所表示的.其中
| $ \begin{align} &{{D}_{\text{disloss}}}=\sqrt{\frac{1}{2}\left( {{L}_{1}}^{2}+{{L}_{2}}^{2} \right)+\lambda |\text{ }{{L}_{\text{T}}}^{2}-{{L}_{\text{P}}}^{2}|}~, \\ &{{L}_{1}}=\sqrt{{{\left( x_{1}^{\text{T}}-x_{1}^{\text{P}} \right)}^{2}}+\text{ }{{\left( y_{1}^{\text{T}}-y_{1}^{\text{P}} \right)}^{2}}}, \\ &{{L}_{2}}=\sqrt{{{\left( x_{2}^{\text{T}}-x_{2}^{\text{P}} \right)}^{2}}+\text{ }{{\left( y_{2}^{\text{T}}-y_{2}^{\text{P}} \right)}^{2}}}, \\ &{{L}_{\text{T}}}=\text{ }\sqrt{{{\left( x_{1}^{\text{T}}-x_{2}^{\text{T}} \right)}^{2}}+\text{ }{{\left( y_{1}^{\text{T}}-y_{2}^{\text{T}} \right)}^{2}}}, \\ &{{L}_{\text{P}}}=\text{ }\sqrt{{{\left( x_{1}^{\text{P}}-x_{2}^{\text{P}} \right)}^{2}}+\text{ }{{\left( y_{1}^{\text{P}}-y_{2}^{\text{P}} \right)}^{2}}}. \\ \end{align} $ | (3) |
|
图 3 距离测量示意 Figure 3 Diagram of measuring distance |
实验数据来源四川华西医院麻醉科,获取左室二腔心切面视频135个,其中100个视频用于训练图片抽取,其余35个视频用于测试图片抽取.每个视频根据视频长度选取3~5帧标注,共获得训练数据图片387张,测试数据图片122张.每幅图像标注两个关键点,图像大小为800*600 pixel,全部处理为灰度图像.对于第一个网络,对训练集图像执行如下数据集扩充方法:
1) 对原始图像矩阵X做顺时针旋转操作,即X=X·R,其中R见式(4),旋转后没有填充的部分使用图像的平均值填充,旋转角度随机选取5°~15°,得到774张图片.
| $ R=\left[ \begin{matrix} \text{cos}~\left( \theta \right)&-\text{sin}~\left( \theta \right) \\ \text{sin}~\left( \theta \right)~&\text{cos}~\left( \theta \right) \\ \end{matrix} \right]~.~ $ | (4) |
2) 对1的结果做对比度变换,即
对于第二个级联网络,文章从每个图像中选取包含两个关键点的小区域作为输入,获取区域公式如下表达.
| $ \begin{align} &{{x}_{\text{left-top}}}={{X}_{\text{min}}}-{{R}_{\text{x1}}}, {{X}_{\text{min}}}=\text{min}~\left( {{x}_{1}}, {{x}_{2}} \right); \\ &{{y}_{\text{left-top}}}={{Y}_{\text{min}}}-{{R}_{\text{y1}}}, {{Y}_{\text{min}}}=\text{min }\!\!~\!\!\text{ }\left( {{y}_{1}}, \text{ }{{y}_{2}} \right); \\ &{{x}_{\text{right-bottom}}}={{X}_{\text{max}}}+{{R}_{\text{x2}}}, {{X}_{\text{max}}}=\text{max}\left( {{x}_{1}}, {{x}_{2}} \right)~; \\ &{{y}_{\text{right-bottom}}}={{Y}_{\text{max}}}+{{R}_{\text{y2}}}, {{Y}_{\text{max}}}=\text{max}~\left( {{y}_{1}}, \text{ }{{y}_{2}} \right)~. \\ \end{align} $ | (5) |
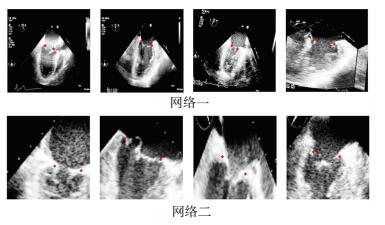
最后从387幅训练图像中每幅选取15个小区域作为训练数据.两个网络的部分数据见图 4.
|
图 4 训练样本展示 Figure 4 Examples of train dataset |
本文采用式(2)展示的方均根差对所有关键点检测测试样本进行评估.并且定义误差不超过图像宽度e < 5%的检测点为正确检测点.距离误差公式见式(6)
| $ e=\text{ }\sqrt{\frac{{{\left( {{x}_{\text{p}}}-{{x}_{\text{t}}}~ \right)}^{2}}+\left( {{y}_{\text{p}}}-{{y}_{\text{t}}} \right){{~}^{2}}}{w}}.~ $ | (6) |
式中:
| $ {{e}_{\text{dis}}}=\frac{\text{ }\!\!|\!\!\text{ }{{l}_{\text{p}}}-{{l}_{\text{t}}}|~}{{{l}_{\text{t}}}}~. $ | (7) |
将edis < 15%并且e < 5%的检测结果视为正确结果,定义检测成功率Ta见式(8),其中fT为检测成功的样本数目,N为测试总样本数目.
| $ {{T}_{a}}=\frac{{{f}_{T}}~}{N}\times 100\%. $ | (8) |
实验环境:操作系统为ubantu14.04,显卡为GTX titan x,代码是采用基于caffe的python实现的.
实验结果见表 1,展示在采用不同损失函数对最终二尖瓣距离测量精度的影响,并同文献[15]的级联方式以及文献[18]采用回归树的方法进行比较.即在第一级级联状况相同的情况下,将第二级改成普通的针对单个关键点进行精细化调整.从表中结果前两行可以看出仅采用第一层网络结构对点的定位效果很差,对左侧关键点和右侧关键点检测成功率均很低,最终的距离测量结果不理想,并且两种损失函数对最终距离测量准确度影响并不大.在采用两层网络的情况下,两个关键点定位效果明显好转,关键点检测成功率均达到了90%以上,对最终距离的准确度也大大提高.但从表中网络二选用不同的损失函数可以看出,在第一个网络采用欧式损失的情况下,第二个网络采用本文提出的损失函数在关键点定位精度上和采用普通欧式损失的网络区别并不大,但是在最终的距离准确度上效果要好很多,获得的平均距离误差也更小.而两个网络都采用本文提出的损失并不能提升定位效果和测量精度.并且对比文献[15]的级联方法,相对普通针对每个关键点进行精细回归的级联方法,在关键点检测和距离测量的结果上,本文提出方法精度上提升很大.在和传统学习算法的对比上,将在第一个网络输出的基础上,采用文献[18]的回归算法对检测结果进行调整,结果也显示本文的算法远远优于传统回归算法.
| 表 1 不同级联方式和损失函数实验对比 Table 1 Result of different structures and loss function |
不同算法下的预测效果见图 5.图 5(a)展示的是医生标注的结果,图 5(b)展示的在只使用一个网络并且损失函数采用欧式距离损失下得到的结果,很明显的可以看到仅仅采用一个网络得到的结果并不太理想,图 5(c)是两个级联网络都使用欧式损失得到的结果,图 5(d)是将第二个网络采用本文提出的损失函数得到的结果,在采用本文提出的损失函数后再检测二尖瓣环内径的距离上能够得到更为准确的结果,图 5(e)为采用文献[15]的级联方式得到的实验结果,图 5(f)为采用文献[18]的回归树算法得到的实验结果.无论是从视觉上还是数值上,本文提出的算法都能够达到较为准确的结果.并且算法在定位关键点和预测距离上做一个较好的平衡.
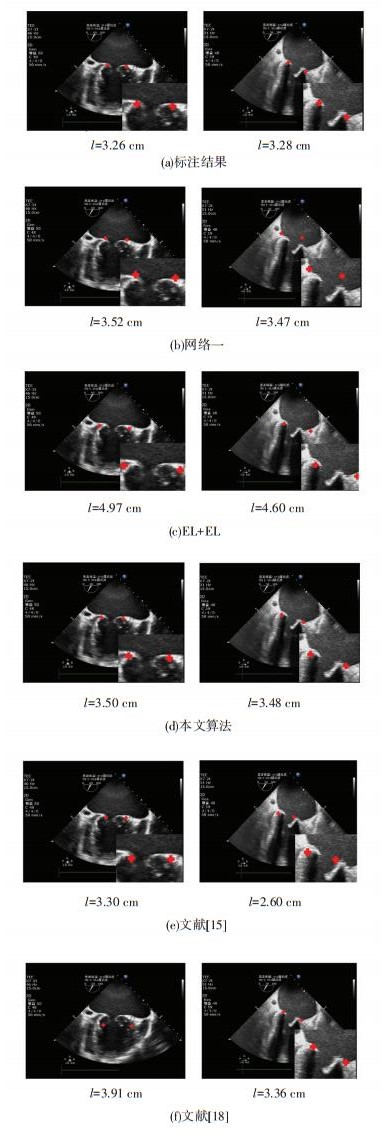
|
图 5 不同级联方式和损失函数检测样例 Figure 5 Examples of different structures and loss function |
训练损失和迭代轮次的关系见图 6.训练过程中采用固定学习率为0.001方式,采用带动量的优化方法.在本文数据量不大的情况下,算法能快速收敛.
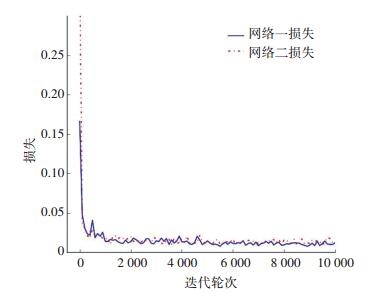
|
图 6 两个阶段网络训练损失和轮次的关系 Figure 6 Losses across epoch of two stages |
在第一级网络选取相同的情况下,第二个网络损失函数采用不同的λ对最终模型表现影响见图 7所示.从图中可看出,在参数λ增大的情况下,对关键点的定位精度和最终的距离精度有一定的影响,但是加入距离修正项的损失函数能够让距离检测更好,实验中可以看出在λ=1的情况下能够对点的检测精度和距离测量的准确度有较好的表现.在λ选取过小的情况下,距离约束不够明显,导致最终测量结果不理想,而λ过大的情况下对关键点检测精度会有较大影响,也会导致距离测量结果出现较大误差.
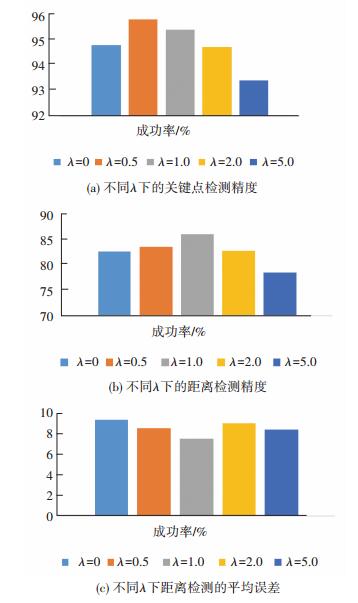
|
图 7 参数λ对测量结果的影响对比 Figure 7 Results of different λ |
本文提出一种基于关键点检测的超声图像的二尖瓣环内径测量方法,该方法通过两个CNN级联对二尖瓣环内径的两个关键点进行了有粗糙到精细的定位.另外,通过加入带距离修正的损失函数作为优化目标,相对仅仅关心关键点精度的欧式距离损失,该损失让最终检测的距离更为精准.并且本文探讨了距离损失权重参数λ对最终结果的影响.本文是首先将关键点检测算法运用于超声图像二尖瓣环内径的自动测量的,通过实验证明,在误差范围内算法的测量结果更接近实际距离.
| [1] |
HEIDENREICH P A, MADDOX T M, NATH J. Measuring the quality of echocardiography using the predictive value of the left ventricular ejection fraction[J]. Journal of the American Society of Echocardiography, 2013, 26(3): 237. DOI:10.1016/j.echo.2012.12.011 |
| [2] |
LU X, JOLLY M P, GEORGESCU B, et al. Automatic view planning for cardiac MRI acquisition[J]. Medical Image Computing and Computer-Assisted Intervention-MICCAI 2011, 2011, 479. DOI:10.1007/978-3-642-23626-6_59 |
| [3] |
纪祥虎, 高思聪, 黄志标, 等.基于Centripetal Catmull-Rom曲线的经食道超声心动图左心室分割方法[J].四川大学学报: 工程科学版, 2016, 48(5): 84. DOI: 10.15961/j.jsuese.2016.05.013 JI X, GAO S, HUANG Z, et al. Left ventricle segmentation in transesophageal echocardiography based on centripetal catmull-rom curve[J]. Sichuan Daxue Xuebao (Gongcheng Kexue Ban)/Journal of Sichuan University (Engineering Science Edition), 2016. DOI: 10.15961/j.jsuese.2016.05.013 http://kns.cnki.net/KCMS/detail/detail.aspx?filename=SCLH201605013&dbname=CJFD&dbcode=CJFQ |
| [4] |
COOTES T F, TAYLOR C J, COOPER D H, et al. Active shape models-their training and application[J]. Computer Vision and Image Understanding, 1995, 61(1): 38. DOI:10.1006/cviu.1995.1004 |
| [5] |
COOTES T F, EDWARDS G J, TAYLOR C J. Active appearance models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(6): 681. DOI:10.1109/34.927467 |
| [6] |
YANG X, JIN J, XU M, et al. Ultrasound common carotid artery segmentation based on active shape model.[J]. Computational and Mathematical Methods in Medicine, 2013, (2013-3-6), 2013, 2013(2): 345968.DOI: 10.1155/2013/345968 http://europepmc.org/abstract/med/23533535
|
| [7] |
VARGAS-QUINTERO L, ESCALANTE-RAMÍREZ B, MARÍN L C, et al. Left ventricle segmentation in fetal echocardiography using a multi-texture active appearance model based on the steered Hermite transform[J]. Computer Methods and Programs in Biomedicine, 2016, 137: 231. DOI:10.1016/j.cmpb.2016.09.021 |
| [8] |
SEDAI S, ROY P K, GARNAVI R. Right ventricle landmark detection using multiscale HOG and random forest classifier[C]//Biomedical Imaging (ISBI), 2015 IEEE 12th International Symposium on. New York: IEEE, 2015: 814. DOI: 10.1109/isbi.2015.7163996
|
| [9] |
OKTAY O, BAI W, GUERRERO R, et al. Stratified decision forests for accurate anatomical landmark localization in cardiac images[J]. IEEE Transactions on Medical Imaging, 2017, 36(1): 332. DOI:10.1109/tmi.2016.2597270 |
| [10] |
YANG D, ZHANG S, YAN Z, et al. Automated anatomical landmark detection ondistal femur surface using convolutional neural network[C]//Biomedical Imaging (ISBI), 2015 IEEE 12th International Symposium on. New York: IEEE, 2015: 17. DOI: isbi.2015.7163806
|
| [11] |
GHESU F C, GEORGESCU B, MANSI T, et al. An artificial agent for anatomical landmark detection in medical images[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention. Athens: Springer International Publishing, 2016: 229. DOI: 10.1007/978-3-319-46726-9_27
|
| [12] |
LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278. DOI:10.1109/5.726791 |
| [13] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[C] //Advances in Neural Information Processing Systems. New York MIT Press Curran Associates Inc.2012: 1097. DOI: 10.1145/3065386
|
| [14] |
DENG Z, LI K, ZHAO Q, et al. Effective face landmark localization via single deep network[J]. ArXiv Preprint ArXiv: 1702.02719, 2017
|
| [15] |
SUN Y, WANG X, TANG X. Deep convolutional network cascade for facial point detection[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Portland: IEEE Computer Society. 2013: 3476. DOI: 10.1109/cvpr.2013.446
|
| [16] |
LIU Z, YAN S, LUO P, et al. Fashion landmark detection in the wild[C]//European Conference on Computer Vision. Amsterdam: Springer International Publishing, 2016: 229. DOI: 10.1007/978-3-319-46475-6_15
|
| [17] |
ZHANG K, ZHANG Z, LI Z, et al. Joint face detection and alignment using multitask cascaded convolutional networks[J]. IEEE Signal Processing Letters, 2016, 23(10): 1499. DOI:10.1109/lsp.2016.2603342 |
| [18] |
KAZEMI V, SULLIVAN J. One millisecond face alignment with an ensemble of regression trees[C]// Computer Vision and Pattern Recognition. Columbus: IEEE, 2014: 1867. DOI: 10.1109/cvpr.2014.241
|
 2018, Vol. 50
2018, Vol. 50


