量子密钥分配[1](quantum key distribution, QKD)允许合法用户Alice和Bob之间共享绝对安全的密钥,已成为近年来的研究热点[2-6].基于量子力学基本原理,QKD具有传统密码学所无法企及的完美安全性,并早已得到理论上的严格证明[7-9].然而,实际QKD系统中使用的各类仪器设备存在非完美性,导致系统出现很多安全漏洞[10-13].例如,实际系统常采用衰减的激光脉冲来替代理想的单光子光源,这必然会使发送脉冲中含有多个光子,从而引起光子数分离攻击[13](photon number splitting, PNS),使窃听者得到合法用户的共享信息而不被发现.为了有效克服PNS,Hwang [14]提出了诱骗态方案,该方案通过发送端Alice随机调制光脉冲到不同强度来制备诱骗态,并随信号态一同发送给接收端Bob,双方利用检测到的诱骗态来估计系统的单光子计数率下界和误码率上界,以此来判定此次通信是否安全.此方案不仅现实可行,而且能显著提高实际QKD系统的安全性能[15-16].
目前,研究者们[16-23]提出许多不同的方案来实现诱骗态QKD.其中大多数使用的是3强度诱骗态[16-19],也有一些采用2强度[20-21]或被动诱骗态[22](单一强度),虽然它们实现起来较为简单,但其性能却远不如无穷诱骗态.为获得更好的性能,Zhou等[23]提出了一种4强度诱骗态方案,该方案虽然原则上能显著提高系统密钥率和安全传输距离,但在实际实现中却面临着许多技术困难,并且会造成强度调制过程中的不确定性,带来更多的光源误码.
为避免上述问题,在降低系统实现难度的同时优化系统性能,本文提出一种新的基于双模态光源的被动诱骗态(BB84)量子密钥分配方案,给出改进后双模态光源对应的光子数分布通用公式.并结合预报单光子源(heralded single-photon source, HSPS)和标记配对相干态光源(heralded pair coherent state, HPCS)对此方案进行了详细地性能分析,讨论了发端不同探测效率的影响.同时考虑到实际码长有限,对本方案进行了统计波动分析.
1 理论与模型 1.1 基于双模态光源的QKD改进方案提出新的QKD方案是在传统BB84协议的基础上对发送端(Alice)进行了相应的改造.由于双模态光源制备纠缠光子对来得到双模光场,两者具有相同的特性,在光子数上是完全关联的.所以将其中之一作为信号态来进行密钥分配,另一模式作为标记态,由发送端(Alice)的探测器探测吸收,以此来预报信号态中光子数分布.该方案利用这一优点,在发送端采用双模态光源,由信号态(S模态)来完成编码传输,标记态(T模态)则对信号态进行预报探测,标记态被Alice端的分束器分离成两态,再分别经过各自路径上的衰减器后被Alice端的探测器检测,由此获得4类探测结果.据此可将信号态分成4个非空集合,从而利用这4类非零脉冲来实现系统的参数估计和密钥提取.由此可知,本方案无需改变光强,只需采用单一强度的信号态就能以4强度诱骗态的形式实现有效且更精确的参数估计.
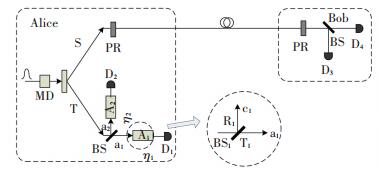
QKD改进方案模型见图 1. Alice端发射光脉冲产生双模态,其中T模态由Alice进行分束和探测,S模态则发送给Bob. Alice端改造的具体过程:
|
图 1 基于单一强度双模态光源的QKD改进方案模型 Figure 1 The model of modified QKD scheme with single-intensity two-mode state source |
1) 生成双模态后,T模态经由分束器(beam splitter, BS)分离,直接通过透射和反射得到频率相同的两束出射光,将其记为a1和a2态.
2) a1和a2分别通过衰减器A1和A2后被发送到单光子探测器Dj(j=1, 2);此处的衰减器实际上分别表示a1和a2态所在路径上的总的传输、探测和耦合效率η1、η2,且其也可用分束器模型来表示,将其称为虚拟分束器,具体如图 1中的放大图所示.所以,衰减器A1和A2分别等效为透射率为η1和η2的虚拟分束器,此后,a1和a2的反射光被丢弃,透射光则被发送到Alice端的单光子探测器D1和D2中进行检测.
3) 记录T模态的探测器D1和D2所有响应结果(4种),并可将其分成4类探测事件,分别记为Xi(i=1, 2, 3, 4),即X1:两个探测器D1、D2都不响应,X2:D1响应但D2不响应,X3:D2响应但D1不响应,X4:D1和D2都响应.由此,标记态可依据这4类探测事件分成4个脉冲集合.同时由双模态光源的特性可知,两个模式在光子数上完全关联,则S模态同样被分成了4个不同的光脉冲集合,再经过极化旋转器(polarization rotator, PR)完成极化编码后,发送至Bob处进行测量.最后双方根据Bob公布的测量基执行基对比等操作以提取安全密钥.
由于探测器D1(D2)的探测效率被考虑到衰减器A1(A2)中,故此处的D1(D2)可看成是一个探测效率为100%的探测器.所以,在Alice置信区域内如果探测器的入射脉冲为非真空态即含有光子,那么探测器Dj必定响应; 反之,若其投影到真空态,Dj的响应概率为dj(即该探测器的暗计数率),不响应概率则为(1-dj).参考文献[24]给出的被动HSPS光源概率公式,可得到本方案的光子数分布通用式(1)~(6).
假设探测器的入射脉冲为|r1r2〉,则此时事件Xi发生的概率PXi|r1r2为
| $ \begin{array}{l} {P_{{X_1}\left| {{r_1}{r_2}} \right.}} = \left\{ \begin{array}{l} \left( {1 - {d_1}} \right)\left( {1 - {d_2}} \right);\exists {r_1} = 0,{r_2} = 0,\\ 0;\exists {r_1} \ne 0\;{\rm{or}}\;{r_2} \ne 0, \end{array} \right.\\ {P_{{X_2}\left| {{r_1}{r_2}} \right.}} = \left\{ \begin{array}{l} {d_1}\left( {1 - {d_2}} \right);\exists {r_1} = 0,{r_2} = 0,\\ \left( {1 - {d_2}} \right);\exists {r_1} \ne 0{\rm{,}}\;{r_2} = 0,\\ 0;\exists {r_1}{r_2} \ne 0{\rm{,}} \end{array} \right.\\ {P_{{X_3}\left| {{r_1}{r_2}} \right.}} = \left\{ \begin{array}{l} {d_2}\left( {1 - {d_1}} \right);\exists {r_1} = 0,{r_2} = 0,\\ \left( {1 - {d_1}} \right);\exists {r_1} = 0,{r_2} \ne 0,\\ 0;\exists {r_1}{r_2} \ne 0{\rm{,}} \end{array} \right.\\ {P_{{X_4}\left| {{r_1}{r_2}} \right.}} = \left\{ \begin{array}{l} {d_1}{d_2};\exists {r_1} = 0,{r_2} = 0,\\ {d_1};\exists {r_1} = 0,{r_2} \ne 0,\\ {d_2};\exists {r_1} \ne 0,{r_2} = 0,\\ 0;\exists {r_1}{r_2} \ne 0. \end{array} \right. \end{array} $ | (1) |
假设T模态下的任意n光子态(即Alice的发射脉冲)均以PXi|n概率获得事件Xi,且当Xi发生时,S模态将被投影到
| $ {P_{{X_i}\left| {\rm{n}} \right.}} = \sum\limits_{{r_1},{r_2}} {{P_{{X_i}\left| {{r_1}{r_2}} \right.}}{P_{{r_1}{r_2}\left| n \right.}}} . $ | (2) |
事件Xi对应的信号态为
| $ \rho = \sum\limits_{n,{r_1},{r_2}} {{P_n}{P_{{X_i}\left| {{r_1}{r_2}} \right.}}{P_{{r_1}{r_2}\left| n \right.}}\left| n \right\rangle \left\langle n \right|} , $ | (3) |
式中PXi|r1r2已由式(1)给出,下面对Pr1r2|n进行计算.
T模态下的n光子态在经过Alice端的BS后将转变为
| $ \frac{1}{{\sqrt {n!} }}{\left( {Ta_1^\mathit{\dagger } + Ra_2^\mathit{\dagger }} \right)^n}\left| 0 \right\rangle = \frac{1}{{\sqrt {n!} }}\sum\limits_{k = 0}^n {C_n^k{R^{n - k}}{T^k}a{{_1^\mathit{\dagger }}^k}a{{_2^\mathit{\dagger }}^{n - k}}\left| 0 \right\rangle } . $ | (4) |
式中:T2=t为BS的传输率,R2=1-t为BS的反射率,t∈[0, 1/2].
为便于计算,用ηi(i=1, 2)表示衰减器A1、A2内部虚构的BS的总传输效率(如图 1所示),且经过该BS后,只有部分透射光a1(a2)被发送至探测器D1(D2).因此,通过A1和A2后上述光子态转变为
| $ \begin{array}{l} \left| \Phi \right\rangle = \frac{1}{{\sqrt {n!} }}\sum\limits_{k = 0}^n {\sum\limits_{{r_2} = 0}^{n - k} {\sum\limits_{{r_1} = 0}^k {C_n^k{T^k}{R^{n - k}}C_k^{{r_1}}T_1^{{r_1}}R_1^{k - {r_1}}} } } \times \\ \;\;\;\;\;\;\;\;\;C_{n - k}^{{r_2}}T_2^{{r_2}}R_2^{n - k - {r_2}}a{_1^\mathit{\dagger {{r_1}}}}a{_2^\mathit{\dagger {{r_2}}}}c_1^{\mathit{\dagger }k - {{r_1}}}{}c{_2^{\mathit{\dagger n} - k - {{r_2}}}}\left| 0 \right\rangle . \end{array} $ | (5) |
式中
可得出Pr1r2|n的表达式为
| $ \begin{array}{l} {P_{{r_1}{r_2}\left| n \right.}} = \frac{1}{{n!}}\sum\limits_{k = 0}^n {\sum\limits_{{r_2} = 0}^{n - k} {\sum\limits_{{r_1} = 0}^k {\left| {C_n^kC_k^{{r_1}}C_{n - k}^{{r_2}}{T^k}{R^{n - k}}T_1^{{r_1}}R_1^{k - {r_1}} \times } \right.} } } \\ \;\;\;\;{\left. {T_2^{{r_2}}R_2^{n - k - {r_2}}} \right|^2}{r_1}!{r_2}!\left( {k - {r_1}} \right)!\left( {n - k - {r_2}} \right)! = \\ \;\;\;\;\sum\limits_{k = 0}^n {\sum\limits_{{r_2} = 0}^{n - k} {\sum\limits_{{r_1} = 0}^k {\frac{{n!}}{{{r_1}!{r_2}!\left( {k - {r_1}} \right)!\left( {n - k - {r_2}} \right)!}}{t^k}} } } \times \\ \;\;\;\;{\left( {1 - t} \right)^{n - k}}\eta _1^{{r_1}}\eta _2^{{r_2}}{\left( {1 - {\eta _1}} \right)^{k - {r_1}}}{\left( {1 - {\eta _2}} \right)^{n - k - {r_2}}}!. \end{array} $ | (6) |
根据式(1)~(6),若已知原始双模态光源的光子数分布Pn,则可得到探测事件Xi对应的信号态(S模态)光子数分布的具体表达式.
1.2 基于HSPS和HPCS的QKD改进方案实际上,本方案只要求光源能产生光子数分布概率相关的两路信号,并未规定其具体形式,因此后续将结合常见的HSPS和HPCS光源,对方案性能进行详细分析.
HSPS是指光脉冲经过非退化的参量下转换过程[25](parametric down-conversion, PDC),同时生成一个特性相同的双模态[26],用其中一个模式进行编码,作为信号态来传输,另一模式则由发送端的探测器探测来预报信号态的到达,即
| $ {\left| \mathit{\Psi } \right\rangle _{TS}} = \sum\limits_{n = 0}^\infty {\sqrt {{P_n}} {{\left| n \right\rangle }_T}{{\left| n \right\rangle }_S}} , $ | (7) |
其中,
| $ {P_n}\left( \mu \right) = \frac{{{\mu ^n}}}{{n!}}{e^{ - \mu }}\left( {\Delta {t_c} \ll \Delta t} \right), $ | (8) |
| $ {P_n}\left( \mu \right) = \frac{{{\mu ^n}}}{{{{\left( {1 + \mu } \right)}^{n + 1}}}}\left( {\Delta {t_c} \gg \Delta t} \right). $ | (9) |
式中:|n〉为n光子态,Pn为其对应的光子数分布概率,μ为平均光强,Δtc为发射的相干时间,Δt则为泵浦脉冲的持续时间.通过改变文献[27-28]中所述的实验条件(如改变Δt)可得到两种分布类型,即式(8)的泊松分布和式(9)的热分布.
HPCS则是指由激光源产生配对相干态[29](pair coherent state,PCS),生成两个相互对称的模式,与HSPS光源类似,模式之一作为信号态,另一则为标记态,且两者的光子数分布都服从亚泊松分布
| $ {P_n}\left( \mu \right) = \frac{1}{{{I_0}\left( {2\mu } \right)}}\frac{{{\mu ^{2n}}}}{{{{\left( {n!} \right)}^2}}}. $ | (10) |
式中I0(x)为修正的第一类贝塞尔函数.
在利用上述两类光源分析本方案的性能之前,必须要先估算出其单光子计数率Y1下界和单光子误码率e1上界.传统QKD方案通常是随机改变光强制备诱骗态来估计参数,而本方案仅需Alice发射一个平均光强为μ的光脉冲,再利用Alice端得到的4类探测事件Xi(i=1, 2, 3, 4)就可完成相对精确的参数估计.由于文献[23]中推导的Y1和e1的界限是目前常用且较精确的,其中使用了3个非零强度的光源进行估算,因此本文选取3个事件Xi(如X1、X2、X3,概率分布为
式(8)~(10)给出原始HSPS和HPCS光源光子数分布Pn(μ)的3种形式,结合2.1节的式(1)~(6),可求出改进后本方案采用HSPS或HPCS光源所对应的光子数分布表达式
1) 采用泊松分布的HSPS光源时,光子数分布
| $ \begin{array}{l} a_n^x = {\left( {1 - {d_A}} \right)^2}{\left( {1 - {\eta _A}} \right)^n}\frac{{{\mu ^n}}}{{n!}}{e^{ - \mu }},\\ a_n^y = \left( {1 - {d_A}} \right){\left( {1 - {\eta _A}} \right)^n}\left[ {{{\left( {1 - \frac{{t{\eta _A}}}{{1 - {\eta _A}}}} \right)}^n} + {d_A} - 1} \right]\frac{{{\mu ^n}}}{{n!}}{e^{ - \mu }},\\ a_n^z = \left( {1 - {d_A}} \right){\left( {1 - {\eta _A}} \right)^n}\left[ {{{\left( {\frac{{1 - t{\eta _A}}}{{1 - {\eta _A}}}} \right)}^n} + {d_A} - 1} \right]\frac{{{\mu ^n}}}{{n!}}{e^{ - \mu }}. \end{array} $ | (11) |
式中:t∈[0, 1/2],Alice端探测器的探测效率ηA∈[0, 1],暗计数率dA
2) 采用热分布的HSPS光源时,光子数分布
| $ \begin{array}{l} b_n^x = {\left( {1 - {d_A}} \right)^2}{\left( {1 - {\eta _A}} \right)^n}\frac{{{\mu ^n}}}{{{{\left( {1 + \mu } \right)}^{n + 1}}}},\\ b_n^y = \left( {1 - {d_A}} \right){\left( {1 - {\eta _A}} \right)^n}\left[ {{{\left( {1 - \frac{{t{\eta _A}}}{{1 - {\eta _A}}}} \right)}^n} + } \right.\\ \;\;\;\;\;\;\;\left. {{d_A} - 1} \right]\frac{{{\mu ^n}}}{{{{\left( {1 + \mu } \right)}^{n + 1}}}},\\ b_n^z = \left( {1 - {d_A}} \right){\left( {1 - {\eta _A}} \right)^n}\left[ {{{\left( {\frac{{1 - t{\eta _A}}}{{1 - {\eta _A}}}} \right)}^n} + } \right.\\ \;\;\;\;\;\;\;\left. {{d_A} - 1} \right]\frac{{{\mu ^n}}}{{{{\left( {1 + \mu } \right)}^{n + 1}}}}. \end{array} $ | (12) |
3) 采用亚泊松分布的HPCS光源时,光子数分布
| $ \begin{array}{l} c_n^x = {\left( {1 - {d_A}} \right)^2}{\left( {1 - {\eta _A}} \right)^n}\frac{1}{{{I_0}\left( {2\mu } \right)}}\frac{{{\mu ^{2n}}}}{{{{\left( {n!} \right)}^2}}},\\ c_n^y = \left( {1 - {d_A}} \right){\left( {1 - {\eta _A}} \right)^n}\left[ {{{\left( {1 - \frac{{t{\eta _A}}}{{1 - {\eta _A}}}} \right)}^n} + } \right.\\ \;\;\;\;\;\;\;\left. {{d_A} - 1} \right]\frac{1}{{{I_0}\left( {2\mu } \right)}}\frac{{{\mu ^{2n}}}}{{{{\left( {n!} \right)}^2}}},\\ c_n^z = \left( {1 - {d_A}} \right){\left( {1 - {\eta _A}} \right)^n}\left[ {{{\left( {\frac{{1 - t{\eta _A}}}{{1 - {\eta _A}}}} \right)}^n} + } \right.\\ \;\;\;\;\;\;\;\left. {{d_A} - 1} \right]\frac{1}{{{I_0}\left( {2\mu } \right)}}\frac{{{\mu ^{2n}}}}{{{{\left( {n!} \right)}^2}}}. \end{array} $ | (13) |
当Alice发送ρl量子态脉冲时,系统的总计数率和误码可表示为
| $ {S_l} = \sum\limits_{k \ge 0} {f_k^l{Y_k}} ,\left( {l = x,y,z} \right), $ | (14) |
| $ {T_l} = \sum\limits_{k \ge 0} {f_k^l{t_k}} ,\left( {l = x,y,z} \right). $ | (15) |
式中:
易证明上述所用的HSPS和HPCS改进光源满足如下条件
| $ \frac{{f_n^z}}{{f_n^y}} \ge \frac{{f_2^z}}{{f_2^y}} \ge \frac{{f_1^z}}{{f_1^y}},\frac{{f_n^y}}{{f_n^x}} \ge \frac{{f_2^y}}{{f_2^x}} \ge \frac{{f_1^y}}{{f_1^x}},\left( {n \ge 2,f = a,b,c} \right). $ | (16) |
故参考文献[23]可得出单光子计数率Y1下界的通用公式为
| $ {\underline Y _1}\left( {x,y} \right) = \frac{{f_2^y{S_x} - f_2^x{S_y} + \left( {f_2^xf_0^y - f_2^yf_0^x} \right){Y_0}}}{{f_1^xf_2^y - f_1^yf_2^x}}. $ | (17) |
估算出单光子误码率e1上界.为简化计算,先定义如下表达式
| $ \begin{array}{l} G\left( {i,j,k} \right) = \left( {g_i^x - g_j^x} \right)\left( {g_j^y - g_k^y} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {g_i^y - g_j^y} \right)\left( {g_j^x - g_k^x} \right), \end{array} $ | (18) |
其中,
| $ g_m^l = \frac{{f_m^l}}{{f_m^z}},\left( {m \ge 1,l = x,y,z,f = a,b,c} \right). $ | (19) |
由于本方案的HSPS和HPCS改进光源已满足条件(16),故易证明只要k-j≥j-i≥0,则有
| $ G\left( {i,j,k} \right) \ge 0. $ | (20) |
对于单光子误码率e1来说,以往的估计中,基本是将所有误码都简单看成由单光子脉冲造成,从而得到一个比较粗略的e1上界.而本方案使用的原始双模态光源虽只产生一个强度的光脉冲,但经改造后得到了4个非零量子态,所以根据文献[23],利用其中3个态(x、y、z态)就能推导出更精确的e1上界.
首先,利用式(15)消除变量可得
| $ {t_1} = {{\bar t}_1} + \sum\limits_{k \ge 4} {{h_{{t_1}}}\left( k \right){t_k}} , $ | (21) |
其中,
| $ \begin{array}{l} {{\bar t}_1} = \frac{{\left( {f_2^yf_3^z - f_2^zf_3^y} \right){T_x} - \left( {f_2^xf_3^z - f_2^zf_3^x} \right){T_y}}}{{f_1^zf_2^zf_3^zG\left( {1,2,3} \right)}} + \\ \;\;\;\;\;\;\frac{{\left( {f_2^xf_3^y - f_2^yf_3^x} \right){T_z} + \left( {f_2^xf_3^z - f_2^zf_3^x} \right)f_0^y{Y_0}{e_0}}}{{f_1^zf_2^zf_3^zG\left( {1,2,3} \right)}} + \\ \;\;\;\;\;\;\frac{{\left( {f_2^zf_3^y - f_2^yf_3^z} \right)f_0^x + \left( {f_2^xf_3^y - f_2^yf_3^x} \right)}}{{f_1^zf_2^zf_3^zG\left( {1,2,3} \right)}}{Y_0}{e_0}, \end{array} $ | (22) |
| $ {h_{{t_1}}}\left( k \right) = - \frac{{G\left( {2,3,k} \right)}}{{G\left( {1,2,3} \right)}},\left( {k \ge 4} \right). $ | (23) |
结合式(20)可知,对于所有k≥4,均满足ht1(k)≤0,由此可得式(22)即为t1的上界,故e1上界可表示为
| $ {{\bar e}_1} = \frac{{{{\bar t}_1}}}{{{{\underline Y }_1}}}. $ | (24) |
最后,由文献[22]的密钥生成率公式计算出该系统的最终密钥生成率为
| $ R \ge a_1^z\underline Y _1^Z\left[ {1 - H\left( {\bar e_1^X} \right)} \right] - {S^z}fH\left( {{E^z}} \right). $ | (25) |
式中:上标
对最终密钥生成率进行数值计算,并通过数值仿真比较分析本文方案与已有的传统诱骗态QKD方案性能,同时讨论本方案密钥率与发送端探测器效率之间的关系.
参考文献[20, 24]中的线性模型,可估算出观测到的系统计数率和误码率:
| $ {Y_n} = 1 - \left( {1 - {Y_0}} \right){\left( {1 - \eta } \right)^n}, $ | (26) |
| $ {e_n} = \frac{{{e_0}{Y_0}{{\left( {1 - \eta } \right)}^n} + {e_d}\left[ {1 - {{\left( {1 - \eta } \right)}^n}} \right]}}{{1 - \left( {1 - {Y_0}} \right){{\left( {1 - \eta } \right)}^n}}}. $ | (27) |
式中:η=ηB×10-αL/10为全局传输效率,ηB为Bob端的探测效率,α为信道的损耗系数,设为0.2 dB/km,L为传输距离.据此可得出不同量子态的总计数率Sl和总误码率El(l=x, y, z).主要仿真参数[23-24]见表 1,信号态则根据传输距离选用最优信号态强度.
| 表 1 主要仿真参数设置 Table 1 Main parameters set in numerical simulations |
为便于比较,传统QKD方案的诱骗态依次设为0、μ1=0.1.仿真结果如图 2~4所示,图中各曲线分别表示的是:1)本文方案——基于泊松分布的HSPS光源、基于热分布的HSPS光源以及基于HPCS光源的单强度QKD改进方案; 2)基于WCS光源的3强度QKD方案[23];3)基于HSPS光源的3强度QKD方案[23].
|
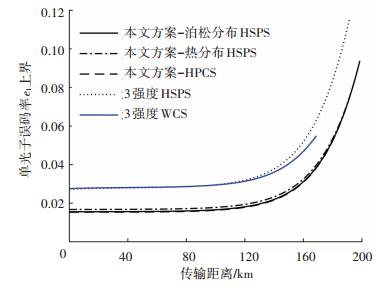
图 2 不同QKD方案下的单光子误码率上界 Figure 2 The upper bound of single photon error rate under different QKD schemes |

|
图 3 不同QKD方案下的最优信号态强度 Figure 3 The optimal intensity of signal state under different QKD schemes |

|
图 4 不同QKD方案下的最终密钥生成率 Figure 4 The key generation rate under different QKD schemes |
从图 2可看出:1)不论采用哪种双模态光源,本文方案的e1上界都明显小于WCS或HSPS 3强度传统QKD方案.这是因为本方案虽只产生单一强度的光脉冲,但经改造发送端后,获得了4个可参与系统参数估计的脉冲集合,从而能得到更加精确的e1上界. 2)对于本文方案来说,采用HPCS的e1上界要略优于HSPS,而采用泊松分布的HSPS则要优于热分布的HSPS,但三者都比较相近.
从图 3可看出:1)基于泊松分布HSPS和HPCS的本文方案的最优信号态强度要优于WCS和HSPS 3强度方案,而基于热分布HSPS的本文方案总体要略低于上述两种传统方案. 2)对于采用不同光源的本文方案,最优信号态强度从大到小依次为:HPCS、泊松分布的HSPS以及热分布的HSPS,且HPCS的最优信号态强度接近于1.而信号态强度越大,可使密钥率在一定范围内得到提高.
图 4表明:1)基于不同光源的本文方案的最大安全距离都为198.6 km,这均要高于WCS 3强度方案(168 km)和HSPS 3强度方案(191 km). 2)基于HPCS的本文方案的密钥率最大,均要优于其他4种方案.这主要是因为HPCS对应的最优信号态强度最大.且基于泊松分布HSPS的本文方案的密钥率要高于热分布HSPS. 3)WCS 3强度方案和其他3种HSPS方案(包括本文方案)的性能曲线都存在一个交点.在交点之前,WCS方案的密钥率要略高于HSPS方案,在交点之后则相反.这一差距主要是由HSPS中多光子脉冲比例大于WCS所导致,但是HSPS可利用标记光子数法来降低暗计数的影响,延长有效传输距离.
综上所述,本文方案虽只采用单一强度的脉冲,却能使系统性能得到提升.且若采用HPCS光源,此方案可在最大程度上优化系统性能,获得最佳的密钥生成率和最大的安全传输距离.
2.2 QKD改进方案密钥率与发端探测效率的关系假定Alice端的两个探测器完全相同,其探测效率ηA依次取为0.1、0.3、0.6、0.9,其他仿真参数与表 1一致.通过对密钥生成率的数值仿真,可得到基于不同光源的本文方案在发送端不同探测效率条件下的性能曲线,见图 5(a)~(c).

|
图 5 发端不同探测效率下密钥生成率的变化 Figure 5 The change of key generation rate under different detection efficiency at the sender |
从图 5可看出,当Alice端探测器的探测效率ηA从0.1变化到0.9时,无论采用哪种双模态光源,本文方案的最大安全距离并未发生变化,但不同光源对应的密钥生成率却得到了逐步提升.由于探测效率越高,就有越多的非空脉冲被成功探测,这使得在Alice端划分信号态的4类探测事件对应的概率增大,从而提高了该系统的性能.
3 统计波动分析在实际QKD系统中,生成的量子密钥往往都是有限长的,而密钥有限长效应会引入统计波动问题,从而降低密钥生成率和安全传输距离.因此,在实际系统的参数估计过程中需要考虑数据有限长效应.本节将采用文献[30]中的有限密钥分析法对本文方案进行统计波动分析.
根据标准波动理论,可得
| $ X = E\left[ X \right] + \delta , $ | (28) |
| $ \Pr \left( {\left| {X - E\left[ X \right]} \right| \ge \Delta } \right) \le \varepsilon . $ | (29) |
式中:
若总脉冲数(即数据长度)记为N,可知
| $ N{{\hat S}_l} = N{S_l} + {\delta _l},N{{\hat T}_l} = N{T_l} + {{\delta '}_l}. $ | (30) |
其中:
为简化计算,式(30)可写为
| $ {{\hat S}_l} - \frac{{{{\hat \Delta }_l}}}{N} \le {S_l} \le {{\hat S}_l} + \frac{{{\Delta _l}}}{N},{{\hat T}_l} - \frac{{{{\hat \Delta '}_l}}}{N} \le {T_l} \le {{\hat T}_l} + \frac{{{{\hat \Delta '}_l}}}{N}. $ | (31) |
由此,可得到如下不等式:
| $ \begin{array}{l} {{\hat S}_l}\left( {1 - \Delta _1^l} \right) \le {S_l} \le {{\hat S}_l}\left( {1 - \Delta _2^l} \right),\\ {{\hat T}_l}\left( {1 - \Delta _3^l} \right) \le {T_l} \le {{\hat T}_l}\left( {1 + \Delta _4^l} \right). \end{array} $ | (32) |
其中:
| $ \Delta _1^l = \sqrt {2\ln \left( {{\varepsilon ^{ - 3/2}}} \right)/N{{\hat S}_l}} ,\Delta _2^l = \sqrt {2\ln \left( {16{\varepsilon ^{ - 4}}} \right)/N{{\hat S}_l}} , $ |
且
| $ \Delta _3^l = \sqrt {2\ln \left( {{\varepsilon ^{ - 3/2}}} \right)/N{{\hat T}_l}} ,\Delta _4^l = \sqrt {2\ln \left( {16{\varepsilon ^{ - 4}}} \right)/N{{\hat T}_l}} . $ |
再结合式(17)、(22)和(24),可得统计波动下的Y1下界和e1上界:
| $ {\underline{\underline Y} _1} = \frac{{f_2^y{S_x}\left( {1 - \Delta _1^x} \right) - f_2^x{S_y}\left( {1 - \Delta _2^y} \right) + \left( {f_2^xf_0^y - f_2^yf_0^x} \right){{\underline Y }_0}}}{{f_1^xf_2^y - f_1^yf_2^x}}, $ | (33) |
| $ {\overline{\overline e} _1} = \frac{{{{\overline{\overline t} }_1}}}{{{{\underline{\underline Y} }_1}}}, $ | (34) |
其中:
| $ \begin{array}{l} {\overline{\overline t} _1} = \frac{{\left( {f_2^yf_3^z - f_2^zf_3^y} \right){{\hat T}_x}\left( {1 + \Delta _4^x} \right)}}{{f_1^zf_2^zf_3^zG\left( {1,2,3} \right)}} - \\ \;\;\;\;\;\;\frac{{\left( {f_2^xf_3^z - f_2^zf_3^x} \right){{\hat T}_y}\left( {1 - \Delta _3^y} \right)}}{{f_1^zf_2^zf_3^zG\left( {1,2,3} \right)}} + \\ \;\;\;\;\;\;\frac{{\left( {f_2^xf_3^y - f_2^yf_3^x} \right){{\hat T}_z}\left( {1 + \Delta _4^z} \right)}}{{f_1^zf_2^zf_3^zG\left( {1,2,3} \right)}} + \\ \;\;\;\;\;\;\frac{{\left( {f_2^xf_3^z - f_2^zf_3^x} \right)f_0^y{{\bar Y}_0}{e_0}}}{{f_1^zf_2^zf_3^zG\left( {1,2,3} \right)}} + \\ \;\;\;\;\;\;\frac{{\left( {f_2^zf_3^y - f_2^yf_3^z} \right)f_0^x + \left( {f_2^xf_3^y - f_2^yf_3^x} \right)}}{{f_1^zf_2^zf_3^zG\left( {1,2,3} \right)}}{{\bar Y}_0}{e_0}. \end{array} $ | (35) |
| $ \begin{array}{l} 且~{\underline Y _0} = {Y_0}\left( {1 - \sqrt {2\ln \left( {{\varepsilon ^{ - 3/2}}} \right)/N{Y_0}} } \right),\\ {{\bar Y}_0} = {Y_0}\left( {1 + \sqrt {2\ln \left( {16{\varepsilon ^{ - 4}}} \right)/N{Y_0}} } \right). \end{array} $ |
最后将式(33)~(35)代入式(25)中,可得统计波动条件下的最终密钥生成率
| $ R\ge a_{1}^{z}\underline{\underline{Y}}_{1}^{z}\left[ 1-H\left( \overline{\bar{e}_{1}^{X}} \right) \right]-{{S}^{z}}fH\left( {{E}^{z}} \right). $ | (36) |
设定系统的不安全系数ε=10-7,Alice发送总脉冲数N =109~1011.仿真结果如图 6(a)~(c)所示,分别为本文方案采用不同双模态光源时,不同数据长度对应的密钥生成率的变化曲线,其中实线表示理想情况下即数据无限长时的密钥生成率,虚线则表示数据有限长时对应的密钥生成率.

|
图 6 不同统计波动下密钥生成率的变化 Figure 6 The change of key generation rate under statistical fluctuation |
从图 6可看出,1)对本文方案来说,不论采用哪种双模态光源,在当前的实验条件下,数据有限长效应并未导致密钥生成率的急剧下滑,且在较远距离处仍能获得较高的密钥生成率. 2)就不同光源而言,对比图 6(a)~(c)可知,统计波动对基于HPCS的本文方案的影响要小于HSPS的.对于HPCS光源,总脉冲数N=109时,本方案的最大安全距离就可达164 km; 总脉冲数N=1011时,最大安全距离达190 km,且在182 km光纤链路上仍具有较大的密钥生成率,其性能比较接近理想情况.
4 结论1) 基于BB84协议,提出一种双模态光源被动诱骗态量子密钥分配改进方案.该方案无需调制脉冲强度,只需发送单一强度的双模态光源,其中标记态在发端被分束和检测后得到4类探测结果,据此将信号态分成4个脉冲集合来估计参数,所以本方案能获得更精确的单光子计数率下界和误码率上界.
2) 基于HSPS光源和HPCS光源,在密钥生成率、误码率和最优信号态强度方面对此方案进行了比较分析,讨论了发端不同探测效率对该方案的影响,同时分析了实际系统有限码长效应的影响.
3) 仿真结果表明:本方案性能在误码率和安全传输距离方面均优于现有基于HSPS和WCS的3强度QKD方案; 基于HPCS的本文方案可使密钥生成率得到显著提升,其性能不仅优于其他传统方案,总体来说也优于基于HSPS的本文方案,但两者的安全传输距离相同,均可达198.6 km; 随着发端探测效率的增大,本方案性能也随之明显提高; 在统计波动条件下,本方案在远距离处仍具有较大的密钥生成率,且数据长度达到109以上即可保证较大的安全传输距离(如164 km以上).
4) 与其他多强度QKD方案相比,本方案仅需采用单一强度脉冲,从而避免了光强调制误差,降低了系统实现难度,易于工程实现.
| [1] |
BENNETT C H, BRASSARD G. Quantum cryptography: public key distribution and coin tossing[C]//Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, Bangalore, India, IEEE, New York, 1984, 175
|
| [2] |
ZHOU Yuanyuan, ZHOU Xuejun, SU Binbin. A measurement-device-independent quantum key distribution protocol with a heralded single photon source[J]. Optoelectron. Lett., 2016, 12(2): 148. DOI:10.1007/s11801-016-5275-3 |
| [3] |
BARTKIEWCZ K, CERNOCH A, LEMR K, et al. Temporal steering and security of quantum key distribution with mutually-unbiased bases against individual attacks[J]. Phys. Rev. A, 2016, 93(6): 062345. DOI:10.1103/PhysRevA.93.062345 |
| [4] |
胡康, 毛钱萍, 赵生妹. 基于预报单光子源和探测器诱骗态的循环差分相移量子密钥分发协议[J]. 光学学报, 2017, 37(5): 331. HU Kang, MAO Qianping, ZHAO Shengmei. Round robin differential phase shift quantum key distribution protocol based on heralded single photon source and detector decoy state[J]. Acta Optica Sinica, 2017, 37(5): 331. DOI:10.3788/aos201737.0527002 |
| [5] |
WANG Le, ZHAO Shengmei. Round-robin differential-phase-shift quantum key distribution with heralded pair-coherent sources[J]. Quantum Inf. Process., 2017, 16(4): 100. DOI:10.1007/s11128-017-1550-x |
| [6] |
何业锋. 基于四粒子纠缠态的两方量子密钥协商协议[J]. 电子科技大学学报, 2017, 46(2): 340. HE Yefeng. Two-party quantum key agreement protocols based on four-particle entangled states[J]. Journal of University of Electronic Science and Technology of China, 2017, 46(2): 340. DOI:10.3969/j.issn.1001-0548.2017.02.004 |
| [7] |
LO H K, CHAU H F. Unconditional security of quantum key distribution over arbitrarily long distances[J]. Science, 1999, 283(5410): 2050. DOI:10.1126/science.283.5410.2050 |
| [8] |
LO H K, CHAU H F, ARDEHALI M. Efficient quantum key distribution scheme and a proof of its unconditional security[J]. Journal of Cryptology, 2005, 18(2): 133. DOI:10.1007/s00145-004-0142-y |
| [9] |
MAYERS D. Unconditional security in quantum cryptography[J]. Journal of the ACM, 2001, 48(3): 351. DOI:10.1145/382780.382781 |
| [10] |
HUANG Jingzheng, YIN Zhenqiang, WANG Shuang, et al. Effect of intensity modulator extinction on practical quantum key distribution[J]. Eur. Phys. J. D, 2012, 66(6): 159. DOI:10.1140/epjd/e2012-20757-5 |
| [11] |
SUN Shihai, GAO Ming, JIANG Musheng, et al. Partially random phase attack to the practical two-way quantum-key-distribution system[J]. Phys. Rev. A, 2012, 85(3): 032304. DOI:10.1103/PhysRevA.85.032304 |
| [12] |
PFISTER C, COLES P J, WEHNER S, et al. Sifting attacks in finite-size quantum key distribution[J]. New J. Phys., 2016, 18(5): 053001. DOI:10.1088/1367-2630/18/5/053001 |
| [13] |
BRASSARD G, LTTTKENHAUS N, MOR T, et al. Limitations on practical quantum cryptography[J]. Phys. Rev. Lett., 2000, 85(6): 1330. DOI:10.1103/PhysRevLett.85.1330 |
| [14] |
HWANG W Y. Quantum key distribution with high loss: toward global secure communication[J]. Phys. Rev. Lett., 2003, 91(5): 057901. DOI:10.1103/PhysRevLett.91.057901 |
| [15] |
LO H K, MA X, CHEN K. Decoy state quantum key distribution[J]. Phys. Rev. Lett., 2005, 94(23): 230504. DOI:10.1103/PhysRevLett.94.230504 |
| [16] |
PENG Chengzhi, ZHANG Jun, YANG Dong, et al. Experimental long-distance decoy-state quantum key distribution based on polarization encoding[J]. Phys. Rev. Lett., 2007, 98(1): 010505. DOI:10.1103/PhysRevLett.98.010505 |
| [17] |
WANG Qin, CHEN W, XAVIER G, et al. Experimental decoy-state quantum key distribution with a sub-poissonian heralded single-photon source[J]. Phys. Rev. Lett., 2008, 100(9): 090501. DOI:10.1103/PhysRevLett.100.090501 |
| [18] |
WANG Qin, WANG Xiangbin, GUO Guangcan. Practical decoy-state method in quantum key distribution with a heralded single-photon source[J]. Phys. Rev. A, 2007, 75(1): 012312. DOI:10.1103/PhysRevA.75.012312 |
| [19] |
WANG Xiangbin. Three-intensity decoy-state method for device-independent quantum key distribution with basis-dependent errors[J]. Phys. Rev. A, 2013, 87(1): 012320. DOI:10.1103/PhysRevA.87.012320 |
| [20] |
ZHAO Yi, QI Bing, MA Xiongfeng, et al. Experimental quantum key distribution with decoy states[J]. Phys. Rev. Lett., 2006, 96(7): 070502. DOI:10.1103/PhysRevLett.96.070502 |
| [21] |
MA Xiongfeng, QI Bing, ZHAO Yi, et al. Practical decoy state for quantum key distribution[J]. Phys. Rev. A, 2005, 72(1): 012326. DOI:10.1103/PhysRevA.72.012326 |
| [22] |
CURTY M, MA Xiongfeng, QI Bing, et al. Passive decoy-state quantum key distribution with practical light sources[J]. Phys. Rev. A, 2010, 81(2): 022310. DOI:10.1103/PhysRevA.81.022310 |
| [23] |
ZHOU Yiheng, YU Zongwei, WANG Xiangbin. Tightened estimation can improve the key rate of measurement-device-independent quantum key distribution by more than 100%[J]. Phys. Rev. A, 2014, 89(5): 052325. DOI:10.1103/PhysRevA.89.052325 |
| [24] |
WANG Qin, ZHANG Chunhui, WANG Xiangbin. Scheme for realizing passive quantum key distribution with heralded single-photon sources[J]. Phys. Rev. A, 2016, 93(3): 032312. DOI:10.1103/PhysRevA.93.032312 |
| [25] |
周淳.有限长诱骗态量子密钥分配安全性研究[D].郑州: 解放军信息工程大学, 2014 ZHOU Chun. Research on security of decoy-state quantum key distribution with finite resources[D]. Zhengzhou: PLA Information Engineering University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-90005-1016058182.htm |
| [26] |
LUTKENHAUS N. Security against individual attacks for realistic quantum key distribution[J]. Phys. Rev. A, 2000, 61(5): 052304. DOI:10.1103/PhysRevA.61.052304 |
| [27] |
MORI S, SODERHOLM J, NAMEKATA N, et al. On the distribution of 1550-nm photon pairs efficiently generated using a periodically poled lithium niobate waveguide[J]. Opt. Commun, 2006, 264(1): 156. DOI:10.1016/j.optcom.2006.02.010 |
| [28] |
RIBORDY G, BRENDEL J, GAUTHIER J D, et al. Long-distance entanglement-based quantum key distribution[J]. Phys. Rev. A, 2000, 63(1): 012309. DOI:10.1103/PhysRevA.63.012309 |
| [29] |
ZHANG Shengli, ZOU Xubo, LI Chuanfeng, et al. A univeral coherent source for quantum key distribution[J]. Chin. Sci. Bull., 2009, 54(11): 1863. DOI:10.1007/s11434-009-0330-0 |
| [30] |
ZHANG Chunhui, LUO Sunlong, GUO Guangcan, et al. Approaching the ideal quantum key distribution with two- intensity decoy states[J]. Phys. Rev. A, 2015, 92(2): 022332. DOI:10.1103/PhysRevA.92.022332 |
 2018, Vol. 50
2018, Vol. 50


