2. 上海大学 微电子研究与开发中心,上海 200072
2. Microelectronic Research and Development Center, Shanghai University, Shanghai 200072, China
随着人工智能和自动驾驶的出现,移动机器人逐步进入自主化和智能化阶段,而同步定位与地图创建(Simultaneous Localization and Mapping,SLAM)的应用是移动机器人实现自主化和智能化的关键.目前,制约SLAM发展的主要障碍是累积误差导致的地图变形,尤其在创建较大规模的地图时,累积误差剧增直接导致创建地图失败.因此,有效地处理SLAM累积误差显得尤为迫切.
处理误差涉及误差检测和误差修正.在视觉SLAM中,闭环检测是误差检测中较为流行和可靠的方法之一.目前闭环检测主要采用词袋(Bag of Word,BOW)模型和神经网络[1]. Xiang Gao构建的深度神经网络闭环检测准确率可达50%~70%,但是不能满足商业应用的要求[2]. Heba Abdelnasser等在室内环境中引入地标修正地图误差,与不引入地标相比,在精度上有62%的提升,但是由于地标的局限性,难以广泛应用[3-4]. Shuichi Kurogi等提出竞争关系网络结合弃一交叉验证法对拐角处的地图进行修正,实验显示可在拐角处减少40 mm的误差,但是此算法具有局限性,只能针对局部地图进行修正[5]. Hang Y J等借助惯性传感器对整个地图进行修正,在地图边界匹配中把累积误差从30 cm缩减到5 cm,但是惯性传感器带来的误差是其无法处理的[6-7]. ICP利用两帧点云所有数据求取匹配关系[8];ICP-SLAM脱胎于ICP,可清除偶然误差,但是多次迭代产生的累积误差是无法消除的[9].
本文以激光雷达ICP-SLAM为基础,针对累积误差导致创建地图变形的缺陷,引入视觉SLAM的闭环检测方法,提出融合双重闭环检测算法的ICP-SLAM修正策略.该策略首先对激光雷达采集的点云数据进行特征提取匹配,然后分析ICP对准产生的变换矩阵以确定闭环检测,最后采用均值分配方法修正地图变形.实验验证表明:该策略中的闭环检测准确率略高于常规闭环检测方法,和深度神经网络的闭环检测相比有13.33%提升; 同时该策略可以计算出导致地图变形的累积误差; 并且在旋转方向上修正变形效果显著,可以提升54.61%.
1 ICP-SLAM的双重闭环检测融合双重闭环检测算法的ICP-SLAM修正策略,完整的修正流程见图 1.

|
图 1 地图变形修正策略流程图 Figure 1 Map deformation correction strategy process |
该策略涉及ICP-SLAM、双重闭环检测以及地图修正,主要研究双重闭环检测与地图修正,本节主要探讨双重闭环检测.
1.1 特征提取匹配完成初步闭环检测闭环检测是指当机器人到达一个先前已经构建过地图的位置时,能够判断出这个位置已经构建过地图.通常在进行闭环检测的同时需要计算累积误差,这样才能对原来构建的地图进行更新修正[10-11].现有的激光雷达,其采集的点云数据都以点集的形式表现环境中障碍物和边界的位置信息,无法直接用于闭环检测.于是本文提出对点云数据提取直线段特征,把闭环检测优劣程度转换成直线段特征的匹配度大小,匹配度越高,闭环检测越成功.点云数据提取直线段特征使用最小二乘法,经最小二乘法提取点云数据提取后的直线段特征为
| $ {F_l} = \left( {{P_s},{P_e},{P_m},l,{\phi _l}} \right). $ | (1) |
式中:Ps和Pe分别为拟合直线的起点和终点; Pm为拟合直线的中心,其值等于起点和终点的平均值; l为直线段的长度; ϕl为直线段在当前坐标系下与横轴的夹角[12].
直线段的匹配要在统一坐标系下进行,故本文所有的直线段匹配都会转换到ICP-SLAM创建地图使用的全局坐标系下.对于两个要进行匹配的直线段L1和L2,其匹配度为
| $ {M_l} = {K_{{l_1}}} \cdot {K_{{l_2}}} \cdot {K_m} \cdot K, $ | (2) |
其中
| $ {K_{{l_1}}} = \left\{ {\begin{array}{*{20}{c}} {0,{l_1} < {l_{\min }};}\\ {1 - \frac{{{l_{\min }}}}{{{l_1}}},{l_1} > {l_{\min }};} \end{array}} \right. $ | (3) |
| $ {K_{{l_2}}} = \left\{ {\begin{array}{*{20}{c}} {0,{l_2} < {l_{\min }};}\\ {1 - \frac{{{l_{\min }}}}{{{l_2}}},{l_2} > {l_{\min }};} \end{array}} \right. $ | (4) |
| $ \left\{ {\begin{array}{*{20}{c}} {{K_m} = 0.}\\ {\left| {{P_{m1}} - {P_{m2}}} \right| > {D_{\max }},}\\ {{K_m} = 1 - \frac{{\left| {{P_{m1}} - {P_{m2}}} \right|}}{{{D_{\max }}}},}\\ {\left| {{P_{m1}} - {P_{m2}}} \right| < {D_{\max }},} \end{array}} \right. $ | (5) |
| $ \left\{ {\begin{array}{*{20}{c}} {K = 0,}\\ {\left| {{l_1} - {l_2}} \right| > {\Delta _{\max }},}\\ {K = 1 - \frac{{\left| {{l_1} - {l_2}} \right|}}{{{\Delta _{\max }}}},}\\ {\left| {{l_1} - {l_2}} \right| < {\Delta _{\max }}.} \end{array}} \right. $ | (6) |
式中:lmin为用于直线段匹配的最短长度; Dmax为用于两个直线段匹配的最大中心距离差; △max为用于两个直线段匹配的最大夹角差; Kl1和Kl2分别为归一化的L1和L2的长度; Km为L1和L2的中心匹配度; K为L1和L2的夹角匹配度.匹配度Ml满足:
| $ 0 \le {M_l} \le 1. $ | (7) |
其值越靠近1匹配度越高.经本文实验验证确定,当匹配度达到0.78以上时可认为闭环检测成功.
1.2 分析变换矩阵进行二次闭环确认在实施直线段特征提取匹配过程中发现,由于ICP-SLAM累积误差,两帧在同一个地方采集到的点云数据提取的直线段特征在起点、终点、中心和夹角上存在较大差值,依据式(2)~(6)计算,得到的匹配度不能达到闭环检测的要求.针对这个问题,本文提出二次闭环确认,其与初次闭环检测相互协调共同完成双重闭环检测,流程见图 2.

|
图 2 双重闭环检测流程图 Figure 2 Double loop closure detection process |
激光雷达获取新的点云数据A后,与之前获取的要匹配的点云数据B之间进行ICP计算.
| $ \varphi = {\left\| {\mathit{\boldsymbol{RA}} + \mathit{\boldsymbol{T}} - \mathit{\boldsymbol{B}}} \right\|^2}. $ | (8) |
当φ取最小时获取A相对于B的变换矩阵,即平移矩阵T和旋转矩阵R.本文使用的是二维激光雷达,所以计算得到的平移矩阵T表示为
| $ \mathit{\boldsymbol{T}} = \left( {x,y} \right). $ | (9) |
式中x和y为全局坐标系下横坐标和纵坐标的偏移.旋转矩阵R表示为
| $ \mathit{\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta }\\ { - \sin \theta }&{\cos \theta } \end{array}} \right). $ | (10) |
式中θ为点云数据位置变换时的旋转角度.当确定了闭环检测时,T和R也就包含了累积误差信息.
在ICP计算获得变换矩阵后,点云数据A按照T和R进行变换,使其与点云数据B对准,这样再进行特征提取匹配就不会有累积误差的影响.除此之外,实验发现在对称的室内环境中不同的墙角和边存在很大的相似性,导致在平移和旋转后产生较大的匹配度,干扰闭环检测.为了消除对称环境对闭环检测的影响,本文重新利用ICP计算得到的变换矩阵.在对称室内环境中,边角在平移一定距离或者旋转
| $ \alpha = \left\{ {\begin{array}{*{20}{c}} {1,\left| x \right| \le \mu L,\left| y \right| \le \mu W;}\\ {0,{\rm{other}}{\rm{.}}} \end{array}} \right. $ | (11) |
| $ \beta = \left\{ \begin{array}{l} 1,\left| \theta \right| < 5\mu {\rm{ \mathsf{ π} }};\\ 0,\left| \theta \right| \ge 5\mu {\rm{ \mathsf{ π} }}. \end{array} \right. $ | (12) |
式中:L为对称环境的长; W为对称环境的宽; μ为最大变形常数,用于衡量实验中SLAM允许的最大变形程度,其值在0和1之间,其具体数值依据环境调整.当且只有α和β同时为1并且Ml>0.78时才能判定为正确的闭环.
2 累积误差表征与地图修正成功完成闭环检测后,在二次闭环确认中ICP计算获取的平移矩阵T和旋转矩阵R包含累积误差信息.为了把累积误差更加细致和程式化地表现出来,引入变形度ρ,分别在室内长、宽和旋转方向做计算:
| $ \left\{ \begin{array}{l} {\rho _x} = \frac{{\left| x \right|}}{L},\\ {\rho _y} = \frac{{\left| y \right|}}{W},\\ {\rho _\theta } = \frac{{\left| \theta \right|}}{{2{\rm{ \mathsf{ π} }}}}. \end{array} \right. $ | (13) |
式中:ρx,ρy和ρθ为在室内长,宽和旋转方向上的变形度. x,y和θ来源于二次闭环确认的T和R.
为了修正地图变形,采用均值分配处理包含累积误差信息的T和R ,然后把处理的结果融入到ICP-SLAM算法中,重新增量式地构建地图.为此,首先计算从开始创建地图到成功完成闭环检测之间的所有激光点云数据帧数,记为N; 然后对平移矩阵T和旋转矩阵R做均值计算:
| $ \mathit{\boldsymbol{t}} = \frac{\mathit{\boldsymbol{T}}}{{N - 1}}, $ | (14) |
| $ \mathit{\boldsymbol{r}} = \frac{\mathit{\boldsymbol{R}}}{{N - 1}}. $ | (15) |
得到均值平移矩阵t和均值旋转矩阵r; 最后利用ICP-SLAM算法对保存的点云数据重新进行地图构建.传统ICP-SLAM算法公式.
| $ h\left( {{\mathit{\boldsymbol{R}}_n},{\mathit{\boldsymbol{T}}_n}} \right) = \sum\limits_{i = 1}^n {{{\left\| {{\mathit{\boldsymbol{R}}_n}{\mathit{\boldsymbol{A}}_n} + {\mathit{\boldsymbol{T}}_n} - {\mathit{\boldsymbol{B}}_n}} \right\|}^2}} . $ | (16) |
式中:An和Bn为第n次需要匹配的点云数据组,Tn和Rn为计算得到的平移矩阵和旋转矩阵.把平移矩阵t与Tn结合,旋转矩阵r和Rn结合,于是得到修正后的ICP-SLAM算法公式为
| $ h\left( {{\mathit{\boldsymbol{R}}_n},\mathit{\boldsymbol{r}},{\mathit{\boldsymbol{T}}_n},\mathit{\boldsymbol{t}}} \right) = \sum\limits_{i = 1}^n {{{\left\| { - {\mathit{\boldsymbol{R}}_n}\mathit{\boldsymbol{r}}{\mathit{\boldsymbol{A}}_n} + \left( {{\mathit{\boldsymbol{T}}_n} - \mathit{\boldsymbol{t}}} \right) - {\mathit{\boldsymbol{B}}_n}} \right\|}^2}} . $ | (17) |
该算法在原算法基础上增加两个常数, 复杂度仍为O(n2).在重新构建地图时仍然要进行闭环检测和变形度计算,与之前地图形成对比验证.
3 验证与结果分析 3.1 验证体系构建借助MRPT上的ICP-SLAM开源程序,配合搭建的移动小车、路由器和电脑共同完成修正策略的验证.图 3为搭建的移动小车,主要包括采集环境信息的RPlidar和用于控制的Raspberry Pi.

|
图 3 移动小车 Figure 3 Mobile vehicle acquisition platform |
实际操作时通过路由器连接移动小车和电脑.电脑向移动小车发送控制指令; RPlidar采集数据并传回到电脑; 电脑接收数据并做相应的处理.
3.2 实验结果分析为验证本文提出修正策略的有效性,验证实验在非对称环境和对称环境中进行,如图 4、5所示.
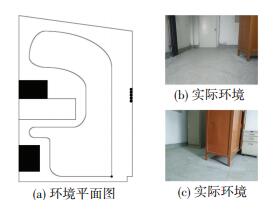
|
图 4 非对称关系实验环境 Figure 4 Asymmetric relation experimental environment |

|
图 5 对称关系实验环境 Figure 5 Symmetric relation experimental environment |
非对称环境的验证在如图 4所示的房间进行,其中图 4(a)是房间平面图,黑色圆点是水管,黑实心方框是落地的箱体,空心方框是离地15 cm的柜子,移动小车沿黑色环线逆时针行进; 图 4(b)和图 4(c)是部分环境照片.图 5是高度对称的电梯间平面图.
首先是闭环检测的验证.图 4、5所示的环境中都进行实验150次.图 4成功闭环检测142次,闭环检测准确率94.67%.图 5闭环检测准确率见图 6,其中μ=0代表未设置双重闭环检测.
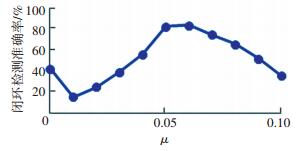
|
图 6 不同μ时正确闭环检测结果 Figure 6 Correct loop closure detection results with different μ |
其次是闭环检测准确率的验证.闭环检测准确率低于50%没有应用价值,高于80%有商业应用价值.非对称环境下闭环检测准确率高达94.67%,有商业应用价值; 对称环境中,只有在设置双重闭环检测并且μ取值在0.05~0.06之间时,才可以达到80%.综合来说,本文提出的修正策略在对称环境和非对称环境下,都可以把闭环检测准确率提升到80%以上,具有很大的商业应用价值.
为不重复验证修正地图的效果,选择在不规则的图 4环境中进行实验.随机抽取闭环检测成功的实验数据20组,分别计算修正前后的变形度,其具体数值分布见图 7~9.

|
图 7 X方向修正前后变形度对比 Figure 7 Comparison of deformation in X direction correction |
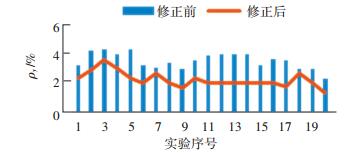
|
图 8 Y方向修正前后变形度对比 Figure 8 Comparison of deformation in Y direction correction |
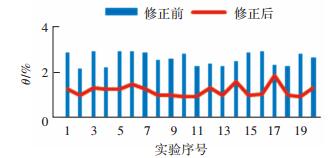
|
图 9 θ方向修正前后变形度对比 Figure 9 Comparison of deformation in θ direction correction |
分析修正前后在X方向上的变形度变化,对X方向的变形度做一个改良率计算,其中修正前平均变形为6.30%,修正后为3.21%,改良
| $ \frac{{6.30\% - 3.21\% }}{{6.30\% }} * 100\% = 49.05\% . $ |
同理求得Y方向改良率为37.18%;θ方向上改良率为54.61%.实验数据表明修正策略在θ方向改善效果显著.
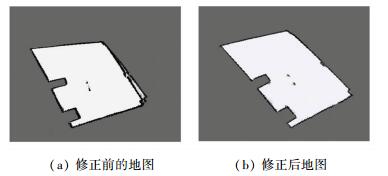
为更加直观地看出修正效果,随机选取图 4环境中一组闭环检测成功的实验数据,绘制见图 10所示的地图.图中10(a)图和图 10(b)图为ICP-SLAM修正前后创建的地图.可以发现,图 10(a)中当移动小车回归到起点时,之后创建的地图与之前创建地图不重合,地图发生了明显的变形.相比于图 10(a),修正后重新绘制的图 10(b)没有明显变形缺陷.
|
图 10 ICP-SLAM修正前后绘制的地图 Figure 10 Map contrast before and after correction of ICP-SLAM |
综上验证,本文提出的修正策略在非对称实验环境中闭环检测准确率为94.67%;对称实验环境中,μ=0.06的情况下,闭环检测准确率为83.33%,完全满足实际应用需求.同时变形度在各个方向修正效果明显,尤其是旋转方向有54.61%的提升.
4 结论针对ICP-SLAM创建地图变形的缺陷,在充分确认ICP-SLAM创建地图变形的原因后,提出融合双重闭环检测算法的ICP-SLAM修正策略.该策略首先对激光雷达采集的点云数据进行特征提取匹配,然后分析ICP对准产生的变换矩阵以确定闭环检测,最后采用均值分配方法修正地图变形.实验验证表明:该策略中的闭环检测准确率高于常规闭环检测方法,即使在对称关系实验环境中,也比深度神经网络的闭环检测高13.33%;同时该策略在闭环检测过程中可以计算出导致地图变形的累积误差; 并且在旋转方向上修正变形效果显著,可以提升54.61%.
| [1] |
KEJRIWAL N, KUMAR S, SHIBATA T. High performance loop closure detection using bag of word pairs[J]. Robotics & Autonomous Systems, 2015, 77(C): 55. DOI:10.1016/j.robot.2015.12.003 |
| [2] |
GAO Xiang, ZHANG Tao. Loop closure detection for visual SLAM systems using deep neural networks[C]// Control Conference. Hangzhou: IEEE Press, 2015: 5851
|
| [3] |
ABDELNASSER H, MOHAMED R, ELGOHARYA, et al. SemanticSLAM: using environment landmarks for unsupervised indoor localization[J]. IEEE Transactions on Mobile Computing, 2016, 15(7): 1770. DOI:10.1109/TMC.2015.2478451 |
| [4] |
XIANG Lingzhu, REN Z, NI M, et al. Robust graph SLAM in dynamic environments with moving landmarks[C]// IEEE/RSJ International Conference on Intelligent Robots and Systems. Hamburg: IEEE Press, 2015: 2543
|
| [5] |
KUROGI S, YAMASHITA Y, YOSHIKAWA H, et al. Accuracy improvement of localization and mapping of ICP-SLAM via competitive associative nets and leave-one-out cross-validation[C]// International Conference on Neural Information Processing. Cham: Springer, 2014: 160
|
| [6] |
HANG Yijun, LIU Jianye, Li Rongbing, et al. Optimization method of MEMS IMU/LADAR integrated navigation system based on compressed-EKF[C]// Position, Location and Navigation Symposium-PLANS 2014, 2014 IEEE/ION. Monterey: IEEE Press, 2014: 115
|
| [7] |
ZHANG Honghui, ZHANG Jinyi, ZHOU Duo, et al. Axis-exchanged compensation and gait parameters analysis for high accuracy indoor pedestrian dead reckoning[J]. Journal of Sensors, 2015, 2015(2): 1. DOI:10.1155/2015/915837 |
| [8] |
OOMORI S, NISHIDA T, KUROGI S. Point cloud matching using singular value decomposition[J]. Artificial Life & Robotics, 2016, 21(2): 149-154. DOI:10.1007/s10015-016-0265-x |
| [9] |
DJEHAICH M, ZIANE H, ACHOUR N, et al. SLAM-ICP with a boolean method applied on a car-like robot[C]// International Symposium on Programming and Systems. Algiers: IEEE Press, 2013: 116-121
|
| [10] |
董海霞, 曾连荪. 视觉SLAM中闭环检测算法的研究[J]. 微型机与应用, 2016, 35(5): 1. DONG Haixia, ZENG Lianmiao. Loop detection algorithm in VLSLAM[J]. Microcomputer & Its Applications, 2016, 35(5): 1. DOI:10.3969/j.issn.1674-7720.2016.05.001 |
| [11] |
李永锋, 张国良, 王蜂, 等. 一种基于历史模型集的改进闭环检测算法[J]. 机器人, 2015, 37(6): 663. LI Yongfeng, ZHANG Guoliang, WANG Feng, et al. An improved loop closure detection algorithm based on historical model set[J]. Robot, 2015, 37(6): 663. DOI:10.13973/j.cnki.robot.2015.0663 |
| [12] |
廖自威, 李荣冰, 雷廷万, 等. 基于几何特征关联的室内扫描匹配SLAM方法[J]. 导航与控制, 2016, 15(3): 26. LIAO Ziwei, LI Rongbing, LEI Tingwan, et al. Indoor scan-matching SLAM method based on geometric features association[J]. Navigation and Control, 2016, 15(3): 26. DOI:10.3969/j.issn.1674-5558.2016.03.005 |
 2018, Vol. 50
2018, Vol. 50


