近年来,随着MFR在军事上的广泛应用,促使对MFR的识别[1]、状态跟踪及预测技术[2]成为电子情报侦察领域研究的热点,波形单元作为MFR信号的基本构成,其识别的优劣决定后续对MFR状态跟踪、预测的准确度,对MFR的威胁和态势感知具有重要意义.
传统思想将波形单元识别定位为脉冲序列分析技术[3],大多从单一特征、匹配等方面进行研究. Kauppi J.等[4]在无先验知识条件下利用脉冲重复间隔(Pulse Repetition Interval, PRI)特征对波形单元进行提取,但其前提是每个波形单元只具备一种PRI特征且相邻波形单元的PRI特征互不相同.刘海军等[5]利用波形库、脉冲到达时间和编码序列三级匹配的思想不断地提高匹配精度,实现波形单元的提取,但其归根结底为匹配技术,存在着鲁棒性不强的问题.
2006年Hinton等[6]通过构建深层网络结构提取出较常规网络更有价值的特征信息,从而引发研究深度学习的热潮.与此同时,栈式自编码器(Stacked Autoencoders, SAE)应运而生,常用于其它深度学习框架的初始化阶段,获得显著的成果[7].随后Pascal等[8]提出“从加噪的输入信号中重构出原始输入信号能够获得更好的特征表述”理论,进而构建SDAE,提取出更为鲁棒的特征信息.
综上所述,一方面为提高MFR波形单元的识别准确率和鲁棒性,另一方面为引入优异的模式识别算法来解决波形单元识别问题,首先通过分析波形单元的结构特点,提出一种波形单元分段识别模型; 然后在该模型的基础上,针对MFR波形单元识别问题,结合SDAE深度特征提取及SVM全局最优、泛化能力强的优点,提出一种基于SDAE与SVM相结合的MFR波形单元识别方法(SDAE-SVM).
1 波形单元分段识别模型构建 1.1 波形单元分析由于MFR的多功能特性,为最大限度地发挥MFR的系统性能,实际中需要针对所面临的各种环境及目标特点设计相应的波形单元,并存储在称为“波形库”的存储器中[9].波形单元是指为提取特定的目标信息,或实现某种能力,而对有限脉冲的一个固定优化排列[10],由内嵌脉冲列和空载时间两部分构成,其结构见图 1.
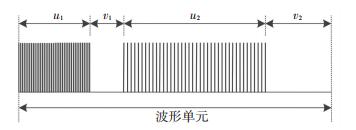
|
图 1 波形单元结构 Figure 1 Waveform unit structure |
图 1展示由两组内嵌脉冲列和两组空载时间构成的波形单元,其中u代表内嵌脉冲列,v代表空载时间.一般地,一个波形单元内可拥有多组内嵌脉冲列和空载时间,各个内嵌脉冲列具备相互独立的参数信息,即独立的参数值和调制样式,同一内嵌脉冲列的参数调制样式保持不变; 空载时间的时长按需求设定,并可分布在波形单元的起始端、中间区域及末端.
1.2 波形单元参数表述为充分利用信号参数信息实现波形单元的识别,首先需要对其进行参数表述.在前期研究中[11],为反映MFR运行机制和全面详尽描述信号特征,构建任务、状态、参数的MFR层级模型,见图 2,其中F代表MFR所执行的任务、P代表内置的状态、ω则代表波形单元.
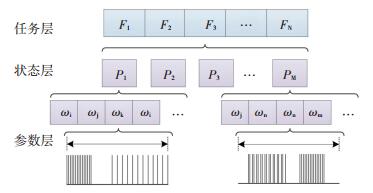
|
图 2 MFR辐射源层级模型 Figure 2 Hierarchical modeling of MFR emitter |
参照文献[12]对MFR层级模型的具体分析.波形单元ωi可利用集合Hωi表示,
M为各个参数的描述信息,通过分析总结信号参数的变化规律,可将其描述为4种:M=x0,参数值固定不变的描述(包含空集);
T为参数调制类型,利用常数0, 1, 2…表述,不同参数的T具备不同意义,0代表无调制.例如常规脉冲描述字PRI、RF、PW,各个参数的调制类型可表示为:PRI:1固定,2参差,3组变,4抖动,5滑变,6正弦调制; RF:1固定,2捷变,3组变,4跳变; PW:1区间,2多脉宽组合,3抖动.
V代表波形单元的空载时间,按其在波形单元中的分布位置进行表述,其中分布在起始端和末端的用D第一个和最后一个数据表述,如果某个位置不存在空载时间,则用常数0表述.
N代表波形单元内嵌脉冲列的脉冲个数,在该段脉冲序列中,所有参数均保持其各自的调制样式不变.
1.3 识别模型构建波形单元分段识别基本原理简述如下:
1) 训练集初始化.已知MFR内置波形单元训练集
2) 识别算法优化.令f指代机器学习、深度学习等识别算法,首先对波形单元库X进行训练f(X),得到优化后的识别模型f′.
3) 内嵌脉冲列识别.利用模型f′对内嵌脉冲列集
任选波形库中某一波形单元
4) 波形单元重构.当kuj=1,即ωj只包含一个u时,对于识别出的脉冲列ζj1,按照ωj中的Vωj即可重构出ωj′; 当
SAE是一种具备编码和译码对称结构的多层前馈网络,通过重构输入数据,最小化重构误差来实现无监督学习和非线性特征提取.可将SAE理解为堆叠多个隐层的AE,网络结构通常关于中间层对称,见图 3.
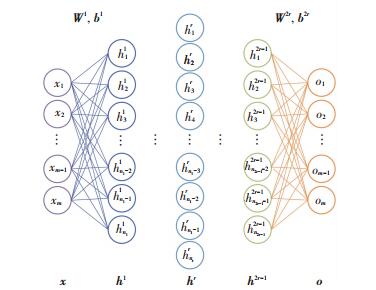
|
图 3 SAE的网络结构 Figure 3 Network structure of SAE |
图 3展示包含2r-1个隐含层的SAE网络结构,其输入、输出层各包含m个神经元,输入、输出向量分别表示为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{W}}{^1} = {(w_{ij}^1)_{{n_1} \times m}};\\ \mathit{\boldsymbol{W}}{^k} = {(w_{ij}^k)_{{n_k} \times {n_{k - 1}}}}, \;\;2 \le k \le 2r - 1;\\ \mathit{\boldsymbol{W}}{^{2r}} = {(w_{ij}^{2r})_{m \times {n_{2r - 1}}}}. \end{array} \right. $ | (1) |
分别代表输入与第1个隐层、第k-1个隐层到第k(2≤k≤2r-1)个隐层、第2r-1隐层到输出的权重矩阵,b1、bk、b2r分别为相应的偏置.则SAE的各层神经元的输出为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{h}}{\mathit{\boldsymbol{}}^1} = {\sigma _1}(\mathit{\boldsymbol{W}}{^1}\mathit{\boldsymbol{x}}{\rm{ }} + {\rm{ }}\mathit{\boldsymbol{b}}{^1});\\ \mathit{\boldsymbol{h}}{^k} = {\sigma _k}(\mathit{\boldsymbol{W}}{^k}\mathit{\boldsymbol{h}}{^{k - 1}} + {\rm{ }}\mathit{\boldsymbol{b}}{^k}), \;\;2 \le k \le 2r - 1;\\ \mathit{\boldsymbol{o}} = {\sigma _{2r}}(\mathit{\boldsymbol{W}}{^{2r}}\mathit{\boldsymbol{h}}{^{2r - 1}} + {\rm{ }}{\mathit{\boldsymbol{b}}^{2r}}). \end{array} \right. $ | (2) |
SAE通常利用反向传播(Backpropagation, BP)算法调整优化参数,寻找网络收敛的极小点.设存在N个训练样本x(l)(1≤l≤N),o(l)为相应的网络输出,则整体的代价函数可表示为
| $ {\mathit{\boldsymbol{J}}_{\mathit{\boldsymbol{x, o}}}}\left( {{\rm{ }}\mathit{\boldsymbol{W}}{\rm{ }}, {\rm{ }}\mathit{\boldsymbol{b}}{\rm{ }}} \right) = \left[ {\frac{1}{N}\sum\limits_{l = 1}^N {} \left( {\frac{1}{2}\parallel \mathit{\boldsymbol{o}}{^{(l)}} - {\rm{ }}\mathit{\boldsymbol{x}}{^{(l)}}{\parallel ^2}} \right)} \right] + \frac{\lambda }{2}\parallel W{\parallel ^2}. $ | (3) |
其中右侧第一项为输入、输出的均方差项,第二项为防止过度拟合,对权重衰减进行的约束,λ为权重衰减系数.通过随机梯度下降、Momentum、Adam(Adaptive Moment Estimation)等优化算法求解式(3)的最小化
SDAE的基本思想是利用栈式自编码器从加噪的输入中重构出原始的、未受污染的输入,从而学习到更稳健鲁棒的深层表达、挖掘出更有意义的分布特征[8].例如单隐层降噪自编码器(Denoising Autoencoders, DAE),其基本原理见图 4.
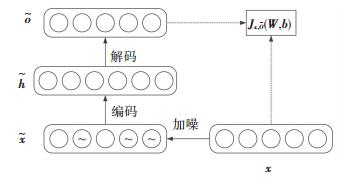
|
图 4 DAE原理框图 Figure 4 Functional block diagram of DAE |
图 4中首先对初始输入x随机加入噪声,得到加噪后的输入
针对MFR波形单元识别的应用场景,将加噪处理分为训练样本加噪和隐含层加噪两部分,分别指对波形库中的训练样本、隐含层神经元节点加入偏离误差(Error Deviation Level, EDL)α、β的过程,其中EDL=| ξi/xi| ×100%,ξi为误差值,xi为参数真实值.
3 SDAE-SVM波形单元识别SVM能够利用核函数非线性映射的方法,将数据空间不明显的特征在高维特征空间中放大、提取并清晰的展现出来,具备全局最优和推广能力强的特点,结合SDAE和SVM的优势,提出一种SDAE-SVM波形单元识别方法,其流程见图 5.

|
图 5 SDAE-SVM波形单元识别流程图 Figure 5 Waveform unit recognition flow of SDAE-SVM |
SDAE-SVM波形单元识别方法主要包括波形库初始化、SDAE网络优化、SVM模型优化和未知波形单元识别4部分.
1) 波形库初始化.这里的初始化是指将MFR内置的训练波形库和分选后的临时未知波形库都参照波形单元参数表述进行描述.
2) SDAE网络优化.训练过程中首先对输入的波形单元参数向量x加噪处理,得到
3) SVM模型优化.首先为实现多分类目的,对经典的C-SVM进行一类对余类的多分类处理; 然后利用提取的深层特征和训练标签进行k折交叉验证,实现SVM模型参数的优化.
4) 未知波形单元识别.经过上述运算,即可得到参数调优后的SDAE-SVM收敛网络模型,进而利用该模型对未知波形单元进行识别.
4 实验结果与分析为验证SDAE-SVM波形单元识别方法的有效性,共进行4组实验.首先模拟生成MFR辐射源波形库,包含A、B、C、D,4部波形单元各异的MFR,同时各个波形单元具备参数特征互不相同的内嵌脉冲列,共计12组波形单元和21组内嵌脉冲列.
选用PRI、RF和PW三种常规参数作为识别特征,波形库的具体信息见表 1.其中MFR-A波形单元ω1A的各组内嵌脉冲列u11A、u12A、u13A中的PRI为组变调制样式,每隔3个脉冲变化一次; MFR-C波形单元ω1C只含有1组内嵌脉冲列u11C,其RF与PW存在联合变化调制,每6个脉冲共同变化一次; MFR-C波形单元ω3C包含的2组内嵌脉冲列u31C、u32C中的RF为组变调制样式,每隔5个脉冲变化一次.
依据波形单元分段识别的要求,将表 1所示的波形库参照波形单元参数表述,并作为已知训练样本,进行下列3组实验.
| 表 1 MFR波形库信息表 Table 1 MFR waveform database information |
为提取稳健优异的特征,针对SDAE网络深度对其性能的影响进行分析.实验按照表 1所示的波形库信息进行样本扩充,每个内嵌脉冲列扩充为100个脉冲描述,共生成2 100个脉冲数据.对这些脉冲样本随机排序,选取前200个作为训练样本,对后1 900个脉冲样本参数加入5%的EDL,作为测试样本.由于训练样本数据量不大,为提高收敛效率,进行分批处理,Batch_Size=100即将训练样本分为8批处理,每批100个.选取sigmoid为激活函数,Adam为SDAE优化方法,令权重衰减系数λ=1×10-4,初始学习速率η=5×10-3,迭代200次,并在迭代过程中逐步减小学习速率ηnext loop=η×0.96.选取径向基RBF作为SVM的核函数,设定SVM惩罚因子C=10,核函数宽度g =2.对训练样本进行加噪处理,对输入数据和隐含层神经元分别加入α=5%、β=1%的EDL.
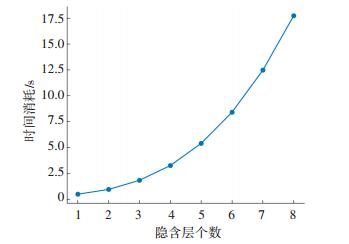
设定隐含层层数依次为{1, 2, 3, 4, 5, 6, 7, 8},相应的隐含层神经元数目为{100, 200, 300, 400, 500, 600, 700, 800},实验中逐步增加SDAE的隐含层层数,利用具备不同隐含层的SDAE-SVM方法进行训练和测试,每个层级重复50次实验,得到的识别结果见图 6,训练过程的平均时耗见图 7.

|
图 6 不同隐含层SDAE-SVM的识别结果 Figure 6 Recognition results of SDAE-SVM with different hidden layers |
|
图 7 SDAE-SVM训练时耗 Figure 7 Time consumption of SDAE-SVM training process |
图 6(a)为小提琴图,其轮廓展示实验结果的密度分布,图中的横线代表中位数; 图 6(b)为盒状图,单个盒形标注自上至下依次代表统计的最大值、上四分位、中位数、下四分位和最小值,其中圆形标记代表离群点.当隐含层数目从1~3逐步增加时,识别准确率的密度分布和中位数也随之提高; 当隐含层数目为3、4时,识别准确率趋于稳定且达到最高,统计中位数分别为94.72%、94.78%.然而从5~8层逐渐增加隐含层层数时,由于训练样本一定,过多的层数和神经元导致网络过拟合,识别效果迅速下降.图 7中随着网络深度的增加,SDAE-SVM的训练时耗呈指数递增,在隐含层为8时,其训练时耗达到17.7 s.
SDAE-SVM方法的时间复杂度主要包括模型训练和对测试样本识别两部分,其中由于模型训练阶段又包含SDAE、SVM两部分的训练优化,因此时间复杂度较高,而测试阶段是在已优化的识别模型基础上进行的,时间复杂度较低.除隐含层层数外,训练样本、迭代次数及神经元节点数都对网络的训练时耗有较大影响.为保证取到优异的深度特征,同时兼顾时效性,选取3个隐含层的SDAE-SVM网络进行后续实验.此外算法的收敛性与迭代次数相关.当迭代次数为50时,损失函数
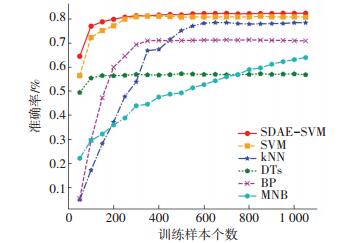
为验证SDAE-SVM算法在不同训练样本数目条件下的识别性能,利用SVM、KNN(K-nearest Neighbors)、DTs(Decision Trees)、MNB(Multinomial Naive Bayes)及BP(Back Propagation)神经网络5种经典的监督识别方法进行对比实验.对表 1的每个内嵌脉冲列分别扩充为50、100个脉冲描述,共生成1 050个训练样本和2 100个测试样本.样本随机排序,对测试样本参数加入15%的EDL. SDAE-SVM、SVM的参数与深度特征提取实验设置相同; KNN的近邻点个数为30;DTs利用信息增益为准则; MNB采用Lidstone smoothing优化,平滑参数为0.9;BP包含1个隐含层,隐含层节点数为10,优化算法为Adam,学习速率为0.5.依次增加训练样本数目,重复进行100次实验,识别结果见图 8.
|
图 8 不同训练数目下识别结果对比 Figure 8 Identification results contrast with different training samples |
实验测得的各算法运算时间都随着训练样本的增加而变大,对于SDAE-SVM而言,其运算时间从0.595 s近似线性增长指9.73 s,由于在实验过程中测试样本数目不变,其测试阶段的运算时间稳定在0.21 s左右,因此该方法的运算量主要在训练阶段且受训练样本数目影响较大.图 8中随着训练样本的增多,各个算法的识别准确率都有明显的提高,并趋于收敛.由于SDAE-SVM挖掘底层鲁棒特征,具备更强的泛化能力,因而在各个训练样本条件下都具备较高的识别准确率.特别地,在训练样本小于300的条件下,SDAE-SVM的优势较为明显,进一步证实该算法的有效性.
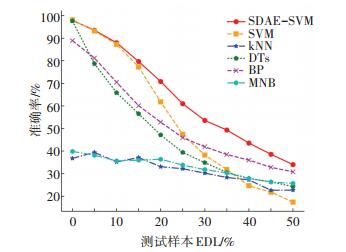
4.3 测试误差对识别性能的影响为验证SDAE-SVM算法在不同测试误差条件下的识别性能,分别利用SVM、KNN、DTs、MNB、BP进行对比实验.按训练样本数目对识制性能影响实验生成2 100个测试样本,并随机选取200个训练样本,对SDAE-SVM和SVM算法进行3折交叉验证,分别得到的最佳参数为CSDAE-SVM=20.565 1、gSDAE-SVM=0.811 1,CSVM=10.023 1、gSVM=100.026 3,其余算法的参数与设置与训练样本数目对识别性能的影响实验相同,依次增加测试样本的EDL,重复进行100次实验,识别结果见图 9.
|
图 9 不同测试误差下识别结果对比 Figure 9 Identification results contrast with different test samples error |
图 9中当测试样本EDL=0时,SDAE-SVM、SVM及DTs都能取得优异的识别结果,但随着测试样本EDL的增加,各个算法的准确率都逐步下降,其中SDAE-SVM下降的最为缓慢,且相同EDL条件下,其识别准确率最高,进一步证实该算法具备较强的鲁棒性和泛化能力.
5 结论1) 通过分析MFR的运行机制和波形单元结构,充分利用各个特征参数信息,构建波形单元分段识别模型,不仅能够借助成熟的数据挖掘、模式识别方法进行运算,还在波形单元识别的过程中完成对辐射源的识别.
2) 结合栈式降噪自编码器的深度特征提取与支持向量机的全局最优,提出一种SDAE-SVM波形单元识别方法,能够取得较好的识别效果,具备优异的鲁棒性和泛化能力.
| [1] |
刘海军, 李悦, 柳征, 等. 基于随机文法的多功能雷达识别方法[J]. 航空学报, 2010, 31(9): 1809. LIU Haijun, LI Yue, LIU Zheng, et al. Approach to multi-function radar identification based on stochastic grammars[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(9): 1809. |
| [2] |
ARASARATNAM I, HAYKIN S, KIRUBARAJAN T, et al. Tracking the mode of operation of multi-function radars[C]// 2006 IEEE Conference on Radar. New York, USA: IEEE Press, 2006: 233-238. DOI: 10.1109/RADAR.2006.1631804
|
| [3] |
刘海军.雷达辐射源识别关键技术研究[D].长沙: 国防科学技术大学, 2010 LIU Haijun. Researches on identification key technology for radar emitter[D]. Changsha: National University of Defense Technology, 2010 http://cdmd.cnki.com.cn/Article/CDMD-90002-2010271175.htm |
| [4] |
KAUPPI J P, MARTIKAINEN K, RUOTSALAINEN U. Hierarchical classification of dynamically varying radar pulse repetition interval modulation patterns[J]. Neural Networks the Official Journal of the International Neural Network Society, 2010, 23(10): 1226. DOI:10.1016/j.neunet.2010.06.008 |
| [5] |
刘海军, 樊昀, 李悦, 等. 多功能雷达建模中的雷达字提取技术研究[J]. 国防科技大学学报, 2010, 32(2): 91. LIU Haijun, FAN Yun, LI Yue, et al. Research on extracting of radar words in modeling of multi-function radar[J]. Journal of National University of Defense Technology, 2010, 32(2): 91. DOI:10.3969/j.issn.1001-2486.2010.02.017 |
| [6] |
马爽, 柳征, 姜文利. 基于幅度变化点检测的多功能雷达脉冲列解析方法[J]. 电子学报, 2013, 41(7): 1436-1441. MA Shuang, LIU Zheng, JIANG Wenli. A method for multifunction radar pulse train analysis based on amplitude change point detection[J]. Acta Electronica Sinica, 2013, 41(7): 1436. DOI:10.3969/j.issn.0372-2112.2013.07.030 |
| [7] |
HINTON G E, SSLAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504. DOI:10.1126/science.1127647 |
| [8] |
ERHAN D, BENGIO Y, COURVILLEe A, et al. Why does unsupervised pre-training help deep learning[J]. Journal of Machine Learning Research, 2010, 11(3): 625. DOI:10.1007/978-3-319-24211-8_18 |
| [9] |
VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked denoising autoencoders: learning useful representations in a deep network with a local denoising criterion[J]. Journal of Machine Learning Research, 2010, 11(12): 3371. DOI:10.15760/etd.1549 |
| [10] |
TANIZA R, JADIA K, Raju G S N, et al. High density FPGA based waveform generation for radars[C]// 2010 IEEE Radar Conference. Washington, DC, USA: IEEE Press, 2010: 310. DOI: 10.1109/RADAR.2010.5494606
|
| [11] |
VISNEVSKI N, KRISHNAMURTHY V, Wang A, et al. Syntactic modeling and signal processing of multifunction radars: a stochastic context-free grammar approach[J]. Proceedings of the IEEE, 2007, 95(5): 1000. DOI:10.1109/jproc.2007.893252 |
| [12] |
陈维高, 贾鑫, 朱卫纲, 等.基于HMM的雷达状态转移估计方法[J/OL]. (2017-02-03)[2017-05-01]. http://www.cnki.net/kcms/detail/11.2625.V.20170203.1533.002html CHEN Weigao, JIA Xin, ZHU Weigang, et al. The radar state transfer estimation algorithm based on HMM model[J/OL]. (2017-02-03)[2017-05-01]. http://www.cnki.net/kcms/detail/11.2625.V.20170203.1533.002html |
 2018, Vol. 50
2018, Vol. 50


