以NDN网络为代表的信息中心网络(ICN,Information-Centric Network)的数据传输是将大文件进行分块,信息对象的片段分散在网络中的节点缓存,由于发布者传输的Data包沿着请求者Interest包探寻到的路径原路逐跳返回,很容易出现回传失败或网络中断的情况,因此当前迫切需要解决大文件高效可靠传输的问题[1]. NDN逐跳逐包的传输方式可以把具有检错能力的物理层和链路层等效为删除信道[3-4],传统的删除信道网络一般采用Turbo码、RS码和LDPC码进行逐条链路纠错[5-6],但是译码复杂度较高;而TCP/IP网络针对丢包问题采用的自动反馈重传(ARQ)和超时确认(ACK)机制由于反馈时延和反馈风暴等问题在NDN中并不适用[7-9]. NDN与喷泉码结合可以实现分布式的存储架构,能够优化无线网络的通信和缓存效率,减少传输的信息量及加快数据内容恢复时间[2].以LT码、Raptor码为代表的喷泉编码[10-14]以其无速率、通用性、接近Shannon限以及低编译码复杂度的优势成为应用层编码首选,应用层协议以数据包为研究对象,因此可以通过喷泉编码将传统的编码单位从bit扩展至数据包,引入删除码恢复数据信息,提升传输可靠性.
目前关于喷泉码可靠传输的研究都是基于确定性的删除概率信道模型的,文献[4]中给出了频率学派中无先验信息的无反馈删除信道可靠数据传输,文献[15-16]都是根据经典统计研究喷泉码的数据传输性能,但是由于网络的异构性和信道噪声会造成信道随机性丢包,而且由于数据包传输不像符号传输具有同步性,本质上假设网络中每条链路上的数据包传输统一分布也具有局限性,因此确定性的信道模型适用性不高.本文主要研究贝叶斯学派的具有相关性伯努利(Bernoulli)随机变量和的分布下删除信道的文件传输协议,根据贝叶斯统计中的Beta-Binomial(BB)分布模型假设信道丢包概率也是一个随机变量,在先验信息的基础上研究了基于喷泉码的可靠文件传输协议,理论推导显示了能够在保证文件接收成功概率不小于1-δ的同时得到文件的最少发送包数,减少冗余发包,提升传输可靠性,增加系统鲁棒性.
1 理论模型 1.1 Beta-Binomial(BB)分布模型在某些问题中可以将模型建立为实验数据是计数型比例数据Y/m的形式,其中m是总试验次数,Y是试验成功的次数,当m是个确定值时,随机变量Y可以看作是m之间线性独立的伯努利(Bernoulli)随机变量的和,即Y=W1+W2+…+Wm是服从二项分布Binomial(m, p)的随机变量.可是在实际中可能会遇到W1, W2, …, Wm之间存在相关性的情形,则试验结果就不再满足独立性,此时如果仍然基于二项分布进行建模会导致估计偏差较大,预测不准确等缺陷[17].为了准确描述过度分布的情况,研究者们提出使用混合分布即Beta-Binomial(BB)分布来进行建模[17-19].
假设每次试验成功的概率为p=P(Wj=1),j=1, 2, …, m,则任意两个试验结果之间的相关性可以表示为式(1),其中j≠k,j, k=1, 2, …, m,
| $ \zeta = \frac{{P\left( {{W_j} = 1,{W_k} = 1} \right) - {p^2}}}{{p\left( {1 - p} \right)}}. $ | (1) |
| $ E\left( Y \right) = mp. $ | (2) |
则整个试验单元内试验成功总数的期望和方差分别为式(2)和式(3),
| $ {\rm{Var}}\left( Y \right) = mp\left( {1 - p} \right)\left[ {1 + \left( {m - 1} \right)\zeta } \right]. $ | (3) |
其中
| $ P\left( {Y = y} \right) = C_m^y\int_0^1 {{p^y}{{\left( {1 - p} \right)}^{n - y}}{p^{a - 1}}{{\left( {1 - p} \right)}^{b - 1}}{\beta ^{ - 1}}\left( {a,b} \right){\rm{d}}p} . $ | (4) |
其中
| $ \begin{array}{l} P\left( {Y = y} \right) = C_m^y\frac{{\prod\nolimits_{j = 0}^{y - 1} {\left( {a + j} \right)} \prod\nolimits_{j = 0}^{m - y - 1} {\left( {b + j} \right)} }}{{\prod\nolimits_{j = 0}^{m - 1} {\left( {a + b + j} \right)} }},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;y = 1,2, \cdots ,m. \end{array} $ | (5) |
Beta-Binomial分布的期望和方差分别为式(6)和式(7):
| $ E\left( Y \right) = ma{\left( {a + b} \right)^{ - 1}}. $ | (6) |
| $ {\rm{Var}}\left( Y \right) = mab{\left( {a + b} \right)^{ - 2}}\left[ {1 + \left( {m - 1} \right){{\left( {a + b + 1} \right)}^{ - 1}}} \right]. $ | (7) |
令
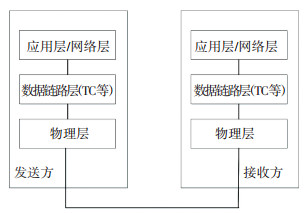
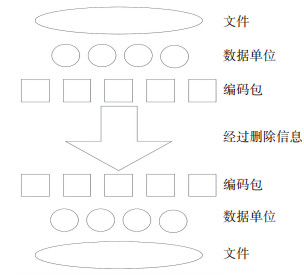
系统模型见图 1,由于研究对象是针对应用层和网络层,为了适用于所有的传输层,不失一般性,此层协议在此模型中暂不予考虑.当文件到达网络层时,需要对文件进行分片,划分成多个包含文件信息的数据块.在信源节点对以块为单位的数据包进行喷泉编码,经过物理层的调制解调后传输至信宿节点.当接收到足够多线性无关的编码包时,网络层将根据相应的译码算法译出原始信息,传输至应用层.文件传输的编译码过程见图 2,其中文件分片和数据块编码在应用层和网络层进行,将链路层和物理层两者等同于删除信道.
|
图 1 系统模型 Figure 1 System model |
|
图 2 文件与数据单元的编译码 Figure 2 File and data encoding and decoding |
图 1中物理层信道特性可以通过误比特率BER来表示,在信宿的链路层,如果接收的编码包无法通过CRC校验,则丢弃该错误包.因此数据包删除概率PER为
| $ {\rm{PER}} = 1 - {\left( {1 - {\rm{BER}}} \right)^{{L_{{\rm{PDU}}}}}}. $ | (8) |
当误码率BER较小时,可近似为式(9),其中LPDU表示数据块PDU的长度.
| $ {\rm{PER}} \approx {\rm{BER}} \cdot {L_{{\rm{PDU}}}}. $ | (9) |
根据图 1和2以及式(8)和式(9),由BER所表示的物理层传输信道模型可以等效为应用层/网络层的删除信道模型,相应的信道特征可以用丢包率PER来表示.
2 基于喷泉码的Beta-Binomial信道模型的文件传输协议假设待传输文件包含k个数据包,信道删除概率Pe即丢包率是一个随机变量,则数据包成功接收的概率为p=1-Pe.此时需要发送n个数据包,使得文件成功接收的概率p≥1-δ.假设信源通过信道发送数据包能成功接收的概率p服从参数为α和β的Beta(α, β)先验概率分布,由于发送n个数据包的过程可以看成进行n次Bernoulli实验,则根据Beta-Binomial共轭分布可知,数据包接收成功率p服从参数为α+K和β+n-K的Beta(α+K, β+n-K)后验概率分布,其中K是n次Bernoulli实验的成功次数,因此接收到的数据包数是一个服从BB分布的随机变量X.根据BB分布的性质可得X的期望和方差分别为式(10)和式(11)所示,其中认为p是一个来自于[0, 1]区间的均匀分布的样本,因此令α=β=1.
| $ E\left( X \right) = \mu = \frac{{n\alpha }}{{\alpha + \beta }} = \frac{n}{2}. $ | (10) |
| $ {\rm{Var}}\left( X \right) = {\sigma ^2} = \frac{{{n^2}\alpha \beta - n\alpha \beta \left( {\alpha + \beta } \right)}}{{{{\left( {\alpha + \beta } \right)}^2}\left( {\alpha + \beta + 1} \right)}} = \frac{{{n^2} - 2n}}{{12}}. $ | (11) |
根据理想喷泉码的性质可知文件传输失败的概率可以表示为式(12),其中K=(1+ε)k.
| $ P\left[ {X \le K} \right] = P\left[ {\frac{{X - \mu }}{\sigma } \le \frac{{K - \mu }}{\sigma }} \right]. $ | (12) |
当n足够大时,BB分布服从中心极限定理,此时近似于正态分布函数N(0, 1),如式(13).
| $ P\left[ {X \le K} \right] \approx P\left[ {N \le \frac{{K - \mu }}{{\sqrt \sigma }}} \right] = \Phi \left( {\frac{{K - \frac{n}{2}}}{{\sqrt {\frac{{{n^2} - 2n}}{{12}}} }}} \right). $ | (13) |
式中Φ是标准正态分布N(0, 1)的分布函数.要保证此编码机制下接收节点能够成功译码,则需确定使得文件成功接收的概率≥1-δ时最小发包数n,所以有式(14).
| $ \Phi \left( {\frac{{K - \frac{n}{2}}}{{\sqrt {\frac{{{n^2} - 2n}}{{12}}} }}} \right) \le \delta . $ | (14) |
对不等式(14)两边同时取标准正态分布的分位数函数,有式(15).
| $ \frac{{K - \frac{n}{2}}}{{\sqrt {\frac{{{n^2} - 2n}}{{12}}} }} \le {\mathit{\Phi }^{ - 1}}\left( \delta \right) = {\rm{probit}}\left( \delta \right). $ | (15) |
将式(15)平方化简成关于n的一元二次不等式可得式(16)
| $ \left[ {3 - {\rm{probi}}{{\rm{t}}^2}\left( \delta \right)} \right]{n^2} - \left[ {12K - 2{\rm{probi}}{{\rm{t}}^2}\left( \delta \right)} \right]n + 12{K^2} \le 0. $ | (16) |
利用求根公式求解得式(17),
| $ \begin{array}{l} {n_{1,2}} = \\ \frac{{6K - {\rm{probi}}{{\rm{t}}^2}\left( \delta \right) \pm {\rm{probit}}\left( \delta \right)\sqrt {12{K^2} - 12 + {\rm{probi}}{{\rm{t}}^2}\left( \delta \right)} }}{{3 - {\rm{probi}}{{\rm{t}}^2}\left( \delta \right)}}. \end{array} $ | (17) |
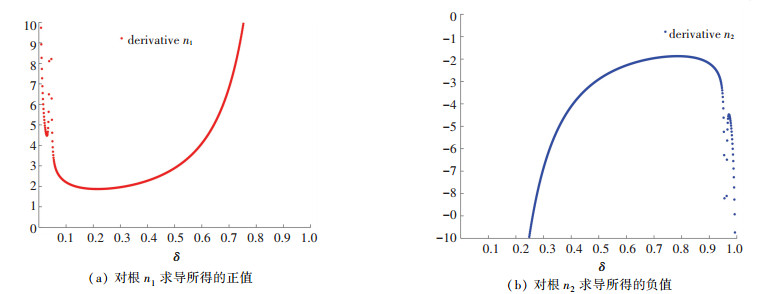
可以根据发送包数与文件传输失败概率的负相关关系即dn/dδ≤0排除增根,利用Matlab对式(17)进行画图求导找出零点,如图 3(a)和(b)所示,可得式(18).
| $ n = {n_2} = \frac{{6K - {\rm{probi}}{{\rm{t}}^2}\left( \delta \right) - {\rm{probit}}\left( \delta \right)\sqrt {12{K^2} - 12 + {\rm{probi}}{{\rm{t}}^2}\left( \delta \right)} }}{{3 - {\rm{probi}}{{\rm{t}}^2}\left( \delta \right)}}. $ | (18) |
|
图 3 对根求导所得的值 Figure 3 The derivative of the root |
利用式(19)和(20)[22]可以给出n的解析式(21),其中a=0.147.
| $ {\rm{probit}}\left( x \right) = \sqrt 2 er{f^{ - 1}}\left( {2x - 1} \right). $ | (19) |
| $ er{f^{ - 1}}\left( x \right) \approx - {\left[ { - \frac{2}{{{\rm{ \mathsf{ π} }}a}} - \frac{{\ln \left( {1 - {x^2}} \right)}}{2} + \sqrt {{{\left( {\frac{2}{{{\rm{ \mathsf{ π} }}a}} + \frac{{\ln \left( {1 - {x^2}} \right)}}{2}} \right)}^2} - \frac{1}{a}\ln \left( {1 - {x^2}} \right)} } \right]^{1/2}}\;\;\;x \le 0. $ | (20) |
要确保失败概率δ≤0.5,根据以上推导可得发包数服从式(21).
| $ \begin{array}{l} n = {n_2} = \frac{{6K - 2\left[ { - \frac{2}{{{\rm{ \mathsf{ π} }}a}} - \frac{{\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)}}{2} + \sqrt {{{\left( {\frac{2}{{{\rm{ \mathsf{ π} }}a}} + \frac{{\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)}}{2}} \right)}^2} - \frac{1}{a}\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)} } \right]}}{{3 - 2\left[ { - \frac{2}{{{\rm{ \mathsf{ π} }}a}} - \frac{{\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)}}{2} + \sqrt {{{\left( {\frac{2}{{{\rm{ \mathsf{ π} }}a}} + \frac{{\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)}}{2}} \right)}^2} - \frac{1}{a}\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)} } \right]}} + \\ \left( {\sqrt 2 {{\left[ { - \frac{2}{{{\rm{ \mathsf{ π} }}a}} - \frac{{\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)}}{2} + \sqrt {{{\left( {\frac{2}{{{\rm{ \mathsf{ π} }}a}} + \frac{{\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)}}{2}} \right)}^2} - \frac{1}{a}\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)} } \right]}^{1/2}}} \right) \times \\ \frac{{\sqrt {12{K^2} - 12 + 2\left[ { - \frac{2}{{{\rm{ \mathsf{ π} }}a}} - \frac{{\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)}}{2} + \sqrt {{{\left( {\frac{2}{{{\rm{ \mathsf{ π} }}a}} + \frac{{\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)}}{2}} \right)}^2} - \frac{1}{a}\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)} } \right]} }}{{3 - 2\left[ { - \frac{2}{{{\rm{ \mathsf{ π} }}a}} - \frac{{\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)}}{2} + \sqrt {{{\left( {\frac{2}{{{\rm{ \mathsf{ π} }}a}} + \frac{{\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)}}{2}} \right)}^2} - \frac{1}{a}\ln \left( {1 - {{\left( {2\delta - 1} \right)}^2}} \right)} } \right]}}. \end{array} $ | (21) |
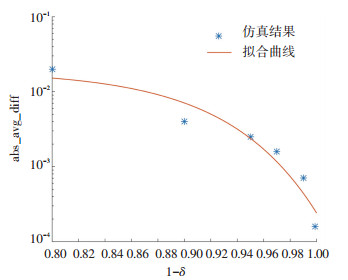
在推导最少发包数n和文件接收成功率1-δ的关系式(21)的过程中使用式(19)进行近似,因此还要研究实际文件接收成功率与设计值1-δ之间的误差.定义绝对平均误差为
| $ {\rm{abs\_avg\_diff}}\left( \delta \right) = \frac{{\sum\limits_{{P_e} \in \Omega } {\left| {\delta '\left( {{P_e}} \right) - \delta } \right|} }}{{\left| \Omega \right|}}. $ | (22) |
式中:Ω={0.05, 0.1, 0.2, 0.3, 0.4, 0.45, 0.5}是丢包率集合,δ'(Pe)是对特定丢包率Pe进行仿真得到的文件传输失败概率. δ={0.001, 0.01, 0.03, 0.05, 0.1, 0.2},K=1 000,仿真次数为100 000,所得目标接收成功率与绝对平均误差的关系见图 4. 图 4的结果显示仿真得到的实验结果与采用式(22)进行数据拟合得到的结果基本吻合,而且当设计目标值1-δ的成功概率取值越大,实际中所得的成功率1-δ'绝对平均误差呈指数级下降,即能够在以至少1-δ的精确度保证文件接收成功概率精确度的前提下,采用式(21)确定文件的最少发包数n.
|
图 4 文件接收成功概率绝对平均误差 Figure 4 Absolute average difference of file successful rate |
根据理论推导式(21)仿真得到图 5,因为发送包数n是一个期望值,所以在对p=1-Pe的概率密度函数积分以后就只是和α、β有关,在有先验概率的前提下根据贝叶斯统计的相关知识可知Pe被平均掉了,在此条件下Pe只有统计意义.采用喷泉码源源不断地进行发包,即不停地重复相同的传输数据包实验的情况下,当文件包含的数据块K很大时,丢包率Pe会趋于稳定,即统计学概率,所以在α=β=1的均匀分布前提下n只和δ有关.仿真结果显示发包数n越少,失败概率δ越大,两者呈负相关.当传输文件包含K=104个数据块时,若要保证文件发送成功概率大于等于0.8,则发送的编码包n≈4×105,这是在所有的丢包率下能够保证成功接收文件时的发包数的最小值.由于丢包率Pe在[0, 1]区间上均匀取值,因此涵盖了各种情况的信道,即在信道状况未知的情况下能够根据此文件传输成功率的理论设计值得到文件最少发包数,提高了文件传输的可靠性与系统设计的鲁棒性.
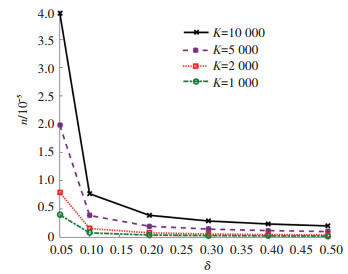
|
图 5 不同失败概率下对应的最小发送包数 Figure 5 The minimum number of packets sent corresponding to different probability of failure |
假设文件包含K个数据包,首次以信道最大速率对所有数据包进行发送,接收端根据丢包情况向发送端发送反馈NAK,发送端收到此信息后对丢失的数据包进行重传,直到文件成功接收.首次发送K个数据包,则经过丢包率为Pe的删除信道后有K·Pe个数据包丢失,需要进行重传.在第二次发送中有(K·Pe)·Pe个数据包需要重传,以此类推可得在第j次发送中有K·Pej个数据包需要重传.由于丢包个数必须小于1时才算文件发送成功,即满足K·Pej < 1.假设ARQ最大反馈重传次数为3次,K=1 000,nF=1 100,图 6的仿真结果显示在相同的丢包率下,基于ARQ重传机制的文件发送成功率比基于无反馈喷泉码机制的性能要低,当文件发送成功时,喷泉码比ARQ能多承受至少0.2的丢包率,喷泉码的重传次数为0,即喷泉码只需一次传输即可正确接收,不需要反馈信道重传数据包,能够以较少的冗余发包数就可达到较高的可靠传输性能,降低延时性能较好. 图 7的结果显示了当文件成功发送时基于选择重传机制的发送次数,结果显示发送次数随丢包率快速上升,ARQ重传机制其实用时间换取了带宽利用率,无法保证实时性;而喷泉码是用带宽利用率换取了时间,在同样的文件发送成功率下喷泉码能够以小量的代价降低文件传输时延.传统的文件传输问题一般针对数据包接收成功率进行研究,而本文则针对整体文件进行研究,并且考虑了先验信息,这对于当前大数据网络中高清视频文件的下载与点播质量改进具有重要意义.

|
图 6 不同传输机制对应的文件发送成功率 Figure 6 The rate of packets sent corresponding to different transmission scheme |
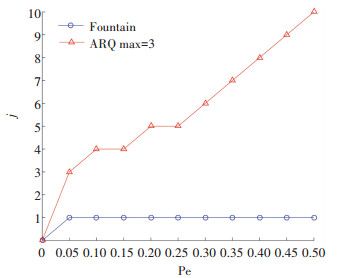
|
图 7 文件发送成功时不同机制丢包率下的发送次数 Figure 7 The number of sending corresponding different scheme when file sent successfully |
本文基于贝叶斯统计中的Beta-Binomial(BB)分布模型,在考虑先验信息的基础上研究了基于喷泉码的可靠文件传输协议,理论推导了最少发包数与文件整体传输成功概率之间的关系式,仿真结果显示了能够在保证文件接收成功概率不小于1-δ的同时,得到文件的最少发送包数,而且设计值贴近实际值,减少冗余发包,提升传输可靠性与系统鲁棒性.在NDN网络大数据传输中包括文件下载和高清流媒体直播等,采用此无反馈喷泉码传输协议进行传输可以提高通信质量与通信系统的鲁棒性,提升文件下载速度,降低视频播放中断概率.由于喷泉码在发送端源源不断地传输数据包,因此只要用户给出一个请求,即可持续地接收文件分块,对改进实时视频的流畅度有较大意义.
| [1] |
雷凯. 信息中心网络与命名数据网络[M]. 北京: 北京大学出版社, 2016. LEI Kai. Information-centric networking (ICN) and named-data networking (NDN)[M]. Beijing: Beijing University Press, 2016. |
| [2] |
ANASTASIADES C, THOMOS N, STRIFFELER A, et al.RC-NDN: Raptor codes enabled named data networking[C]// IEEE International Conference on Communications, London: IEEE, 2015: 3026
|
| [3] |
CCSDS. Overview of space communications protocols, CCSDS 130.0-G-2[M]. Washington, DC, USA: CCSDS, 2007
|
| [4] |
方嘉聪, 张宇, 刘艺, 等. 深空喷泉码文件传输协议设计与误码率性能研究[J]. 北京理工大学学报, 2017, 37(3): 314. FANG Jiacong, ZHANG Yu, LIU Yi, et al. Design and performance analysis versus error rate of fountain code-based file delivery protocol for deep space[J]. Transactions of Beijing Institute of Technology, 2017, 37(3): 314. DOI:10.15918/j.tbit1001-0645.2017.03.017 |
| [5] |
REED I S, SOLOMON G. Polynomial codes over certain finite fields[J]. Journal of the Society for Industrial and Applied Mathematics, 1960, 8(2): 300. DOI:10.1137/0108018 |
| [6] |
GALLAGER R G. Low-density parity-check codes[J]. IRE Transactions on Information Theory, 1962, 8(1): 21. DOI:10.1109/TIT.1962.1057683 |
| [7] |
KUROSE J F, ROSS K W. Computer networking: A top-down approach (7th Edition)[M]. USA: Pearson, 2016.
|
| [8] |
LIU C. Cross-layer protocol interactions inheterogeneous data networks[D]. Massachusetts: Massachusetts Institute of Technology, 2005
|
| [9] |
Assaad M, Zeghlache D. Cross-Layer design in HSDPA system to reduce the TCP effect[J]. IEEE Journal on Selected Areas in Communications, 2006, 24(3): 614. DOI:10.1109/JSAC.2005.862414 |
| [10] |
LUBY M. LT codes[C]// The 43rd Annual IEEE Symposium on Foundation of Computer Science. Vancouver, BC, Canada: IEEE, 2002: 271. DOI: 10.1109/SFCS.2002.1181950
|
| [11] |
SHOKROLLAHI A. Raptor codes[J]. IEEE Transactions on Information Theory, 2006, 52(6): 2551. DOI:10.1109/TIT.2006.874390 |
| [12] |
LUBY M, SHOKROLLAHI A, WATSON M, et al. Raptor forward error correction scheme for object delivery, RFC 5053[M]. Internet Engineering Task Force (IETF), Fremont: IETF RMT Working Group, Work in Progess, 2007. DOI: 10.17487/RFC5053
|
| [13] |
MACKAY D J C. Fountain codes[J]. IEEE Proceedings-Communications, 2005, 152(6): 1062. DOI:10.1049/ip-com:20050237 |
| [14] |
LUBY M, GASIBA T, STOCKHAMMER T, et al. Reliable multimedia download delivery in cellular broadcast networks[J]. IEEE Transactions on Broadcasting, 2007, 53(1): 235. DOI:10.1109/TBC.2007.891703 |
| [15] |
LUBY M, WATSON M, GASIBA T, et al. Raptor codes for reliable download delivery in wireless broadcast systems[C]//CCNC 2006. The 3rd IEEE Consumer Communications and Networking Conference. Las Vegas, NV, USA: IEEE, 2006: 192. DOI: 10.1109/CCNC.2006.1593014
|
| [16] |
LIU X, LIM T J. Fountain codes over fading relay channels[J]. IEEE Transactions on Wireless Communications, 2009, 8(6): 3278. DOI:10.1109/TWC.2009.081102 |
| [17] |
赵为华, 张日权. Beta-Binomial回归模型及其应用[J]. 统计与信息论坛, 2016, 31(3): 9. ZHAO Weihua, ZHANG Riquan. Beta-Binomial regression and its application[J]. Statistics & Information Forum, 2016, 31(3): 9. DOI:10.3969/j.issn.1007-3116.2016.03.002 |
| [18] |
TARANALLI V, UCHIKAWA H, SIEGEL P H. Channel models for multi-level cell flash memories based on empirical error analysis[J]. IEEE Transactions on Communications, 2016, 64(8): 3169. DOI:10.1109/TCOMM.2016.2584602 |
| [19] |
TARANALLI V, UCHIKAWA H, SIEGEL P H. On the capacity of the beta-binomial channel model for multi-level cell flash memories[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(9): 2312. DOI:10.1109/JSAC.2016.2603660 |
| [20] |
CROWDER M. Beta-Binomial ANOVA for proportions[J]. Applied Statistics, 1978, 27(1): 34. DOI:10.2307/2346223 |
| [21] |
MIYAKE S and ASAEDA H. Network coding and its application to content centric networking[C]//Proceedings of the Fourth Workshop on Information Theoretic Methods in Science and Engineering(WITMSE-2013), Tokyo, Japan: WITMSE 2013, 2013: 261
|
| [22] |
WINITZKI S. A handy approximation for the error function and its inverse[OL]. 2008. http://homepages.physik.uni-muenchen.de/Winitzki/erf-approx.pdf
|
 2018, Vol. 50
2018, Vol. 50


