为满足海量资源需求并最小化资源使用费用, 已有的大规模在线服务网站(如Netflix ^[1]和YouTube^[2])通常基于云计算平台搭建系统(如使用Amazon EC2^[3]和Microsoft Azure^[4]).随着大规模应用系统的发展, 为满足来自全球各地用户请求, 需将系统部署在散布在全球各区域的分布式云数据中心里, 就近响应用户请求以满足服务质量要求.云中资源分配方法通常将资源需求均值作为输入, 采用传统的线性规划算法求解^[5-11].但近几年的研究表明^[12-16]:在处理高度动态的随机资源需求时, 随机需求模型由于保留更多的细粒度信息, 比均值资源需求模型更加有效, 相同资源量下可满足更多资源需求.但已有随机需求模型使得调度转化成非线性规划问题, 相比均值模型算法已大大增加计算量, 各区域由于基础设施上的差别, 资源费用函数并不相同, 若在优化目标中考虑各区域异质的非线性计费函数, 会进一步增加调度算法复杂度.现有工作简化或省略费用模型, 调度时仅考虑资源总量限制^[12-16], 不符合云平台调度实际情况, 不能发挥云中资源调度的优势.

本文尝试将通用的异质费用模型融入面向随机需求的调度中, 建立普适性的问题形式, 探索一种适用于跨区域分布式云平台的, 不受各区域价格函数差异和用户访问需求差异影响的, 低开销、高收益的资源调度方法.

1 通用资源分配问题的定义

为准确表示实际系统调度模型, 引入两个时间尺度, 分别是调度间隔S^t和需求测量间隔S^d, 其中调度间隔S^t一般远大于需求测量间隔S^d, 如常见云平台中虚拟机最小计费时间间隔一般为1小时^[3-4], 使得对应的调度间隔也为1个小时, 而随机需求测量间隔一般是10 min.因此设S^t=IS^d, 即一个调度间隔分为I个需求测量间隔, 并记录单个测量间隔内每隔如5 s的需求量, 累计多个值获得测量间隔内需求的分布信息, 基于历史数据预测未来某个测量间隔的需求分布作为调度算法的输入.设有来自J个区域的针对I种资源的用户请求, 用L_j表示将在区域j中部署的资源数量.则在一个调度间隔中, J个区域所有分配构成一个资源配置方案, 记为P={L_j}.对来自区域j的请求, 若可满足, 则它将分配到:位于区域j的资源, 称之为本地满足; 或位于其它区域的资源, 称之为远程满足.若请求未被分配到任何资源, 则将其标记为“未满足”.注意请求是否在本地满足将会影响服务质量, 一般认为本地满足时由于实际地理距离较短, 请求延时较低且受网络状态影响较少, 可保证较高的服务质量.

对于单次调度中第i个需求测量间隔中区域j和所有区域的需求实际采样标量值分别为g_jⁱ和gⁱ.则所有区域的本地满足需求量的和为$\sum\limits_{j = 1}^{\rm{J}} {\min \left({{L_j}, g_j^i} \right)} $, 所有区域本地和远程满足的所有需求量的和为$\min \left({L, {g^i}} \right)$, 其中$L = \sum\limits_{j = 1}^{\rm{J}} {{L_j}} $.则所有区域满足的非本地需求量的和为$\min \left({L, {g^i}} \right)-\sum\limits_{j = 1}^{\rm{J}} {\min \left({{L_j}, g_j^i} \right)} $.因此在需求测量间隔i内资源收益为本地满足需求量和非本地满足需求量的加权和, 即${{\rm{w}}_{\rm{1}}}\min \left({L, {{\rm{g}}^i}} \right) + {{\rm{w}}_{\rm{2}}}\sum\limits_{j = 1}^{\rm{J}} {(\min \left({{L_j}, {g^i}} \right)}-\sum\limits_{j = 1}^{\rm{J}} {\min \left({{L_j}, g_j^i} \right))} $, 通过合并同类项为全部满足需求量和本地满足需求量的加权和:

$ {R^i} = {{\rm{w}}_{{\rm{sat}}}}\min \left( {L, {{\rm{g}}^i}} \right) + {{\rm{w}}_{{\rm{loc}}}}\sum\limits_{j = 1}^{\rm{J}} {\min \left( {{L_j}, {\rm{g}}_j^i} \right)} . $

(1)

则单次调度间隔的收益可表示为各个需求测量间隔中收益的和:

$ R = {{\rm{w}}_{{\rm{sat}}}}\sum\limits_{j = 1}^{\rm{J}} {\min \left( {{L_j}, {{\rm{g}}^i}} \right)} + {{\rm{w}}_{{\rm{loc}}}}\sum\limits_{i = 1}^{\rm{I}} {\sum\limits_{j = 1}^{\rm{J}} {\min \left( {{L_j},{\rm{g}}_j^i} \right)} } . $

(2)

云资源调度限制一般用预算表示, 设为金额总量C, 此时需考虑各个云数据中心内资源的价格, 由于常见云基础设施提供商在不同地区的数据中心采用不同的定价策略, 为使得算法具通用性, 计费函数可为任意的非线性单调递减函数.设区域j的资源计费函数为f_j(·), 设单次调度前预测得知各测量时间段的需求量为g_jⁱ和gⁱ, 在给定预算C下资源调度问题可为如下形式:

$ \max \left( R \right)\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\sum\limits_{j = 1}^{\rm{J}} {{f_j}\left( {{L_j}} \right)} = C. $

(3)

而实际场景中的预测算法无法获取精确的g_jⁱ和gⁱ, 经典方法通过预测两者的均值参与求解, 但丢失较多需求细节信息.现有预测算法可得到g_jⁱ和gⁱ的分布函数, 因此在需求测量间隔i内, 将区域j中所有用户对本地资源的随机需求为随机变量G_jⁱ, 所有区域用户对本地和远程资源的随机需求为随机变量Gⁱ, 累积分布函数为cdf_{i, j}和cdf_i.则求解目标为期望收益最大化:

$ \max \left( {{\rm{E}}\left( R \right)} \right)\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\sum\limits_{j = 1}^{\rm{J}} {{f_j}\left( {{L_j}} \right)} = C. $

(4)

2 算法 2.1 面向随机需求和异质费用的云调度算法

费用总量限制问题在式4中, 求解目标包含min(·)这一类非线性函数, 而约束中同样包含非线性函数, 是一个高度复杂的非线性规划问题.在常见的商用云计算系统中上述问题输入数据量很大, 一般会有资源类型和区域数的乘积I×J≥10⁴.为寻找高效求解算法, 需先简化求解目标.对于任意连续的非负随机变量x与常量M有

$ E\left( {\min \left( {{\rm{M, }}x} \right)} \right) = \int_0^{\rm{M}} {\left( {1-{\rm{cd}}{{\rm{f}}_x}\left( c \right)} \right){\rm{d}}c.} $

(5)

式中cdf_x(·)为x的累积概率分布函数, 则式4中E(R)可转化为如下的闭合形式:

$ \begin{array}{l} E\left( R \right) = {{\rm{w}}_{{\rm{sat}}}}\sum\limits_{i = 1}^{\rm{I}} {\int_0^L {\left( {1-{\rm{cd}}{{\rm{f}}_i}\left( n \right)} \right){\rm{d}}n} } + \\ \;\;\;\;\;\;\;\;\;\;\;\;{{\rm{w}}_{{\rm{loc}}}}\sum\limits_{i = 1}^{\rm{I}} {\sum\limits_{j = 1}^{\rm{J}} {\int_0^{{L_j}} {\left( {1-{\rm{cd}}{{\rm{f}}_{i, j}}\left( n \right)} \right){\rm{d}}n} } } . \end{array} $

(6)

通过考察求解目标的结构, 发现该问题不存在给定费用限制下的全局最优解条件, 获取单个局部最优解的算法复杂度也很高, 因此求解算法采取以下步骤:

算法1  面向随机需求和异质费用的云调度算法

1) 获取算法的预设参数.

2) 迭代调整逼近资源总量限制下资源分配方案.

3) 在不同区域之间交换已分配资源, 并保证整体费用不变并增加收益.

4) 若无法找到可增大收益的交换区域, 输出分配方案作为最终解.

2.2 基于资源总量限制的预分配算法

如何获取符合资源总量限制的解成为影响算法效率的关键, 引入一个针对随机需求的类似问题, 该问题中资源限制由资源总量表示, 问题形式为

$ \max \left( {{\rm{E}}\left( R \right)} \right)\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\sum\limits_{j = 1}^{\rm{J}} {{L_j}} = U. $

(7)

式中U即为资源总量, 例如私有中心中服务器总量.定义式7对应的问题为资源总量限制问题.费用总量限制问题和资源总量限制问题的最优解存在一定关系, 可获取资源总量限制问题的最优解作为费用总量限制问题的初始解.

2.2.1 符合资源总量限制求解算法原理

费用总量限制问题和资源总量限制问题的关系如下所述:

推论1  给定资源限制U, 若对资源总量限制问题的最优解L′_j(1≤j≤J)满足$\sum\limits_{j = 1}^{\rm{J}} {{f_j}\left({L{'_j}} \right)} = C$, 则费用总量限制问题的最优解L_j(1≤j≤J)满足$\sum\limits_{j = 1}^{\rm{J}} {{L_j}} \ge U$.

证明:  首先, 若对费用总量限制问题的最优解L_j(1≤j≤J)有$\sum\limits_{j = 1}^{{J}} {{L_j}} = U'$, 则费用总量限制问题最优解的目标函数值必然不高于资源总量限制问题在限制U=U′时最优解的目标函数值.因为若假设此时费用总量限制问题最优解的目标函数值大于资源限制U′下资源总量限制问题的目标函数值, 而此时费用总量限制问题最优解满足$\sum\limits_{j = 1}^J {{L_j}} \ge U'$, 因此必然也是资源总量限制问题的可行解, 且可行解的目标函数值小于等于资源总量限制问题最优解的目标函数值, 这和假设相矛盾, 因此上述命题成立.

其次, 若U′ < U, 则资源总量限制问题在限制U′下最优解的目标函数值必然小于在限制U下最优解的目标函数值.因为若资源总量限制问题在资源限制U′下获取最优解, 此时将U-U′资源量分配到未满足需求的区域, 可得到资源总量限制问题在资源限制U下的初始解, 且目标函数值大于资源限制U′下的目标函数值, 因此上述命题成立.

在上述证明的基础上, 设给定费用预算C下费用总量限制问题的最优解L_j(1≤j≤J)有$\sum\limits_{j = 1}^{\rm{J}} {{L_j}} = U'$(U′ < U), 因为费用总量限制问题最优解的目标函数值必不会高于资源限制U′下资源总量限制问题最优解的目标函数值, 必小于给定资源限制U下资源总量限制问题最优解的目标函数值, 这和资源总量限制问题获得资源限制U下最优解相矛盾, 因此推论1成立.据推论1, 通过构造合适的资源总量限制问题, 可快速得到满足下限的初始解, 在此基础上持续调整获取逼近最优解.

2.2.2 资源预分配算法

资源总量限制问题是一个非线性规划问题, 为快速求解资源总量限制问题, 引入如下定理:

定理1  有N个函数. F₁(x₁), F₂(x₂), ...F_N(x_N), 满足x_n∈[0, ∞)和F_n(x_n)≥0(1≤n≤N).其导函数是f′₁(x₁), f′₂(x₂), ..., f′_N(x_N), 满足f′_n(x_n)∈[0, Y](Y>0)且均是连续单调递减函数.则对于约束$\sum\nolimits_{i = 1}^N {{x_n}} = U, \sum\nolimits_{i = 1}^N {{f_i}\left({{x_i}} \right)} $达到最大值时, 有f′₁(x₁)=f′₂(x₂)=...=f′_N(x_N).

证明:定义f(X)=$\sum\nolimits_{i = 1}^N {{f_i}\left({{x_i}} \right)} $, 假定f(X)取最大值时并不满足上述导数相等条件, 设f′_a(x_a) < f′_b(x_b) (a, b∈[1, N]), 因f′_a(x_a)和f′_b(x_b)均为单调递减函数, 则必存在x′_a和x′_b, 有x′_a>x_a和x′_b < x_b, 且x′_a+x′_b=x_a+x_b并满足f′_a(x′_a)=f′_b(x′_b).设f′_a(x′_a)=f′_b(x′_b)=Z, 有

$ {f_a}\left( {x{'_a}} \right)-{f_a}\left( {{x_a}} \right) = \int_{{x_a}}^{x{'_a}} {f{'_a}\left( n \right)} > Z\left( {x{'_a}-{x_a}} \right), $

(8)

$ {f_b}\left( {{x_b}} \right){\rm{-}}{f_b}\left( {x{'_b}} \right) = \int_{x{'_b}}^{{x_b}} {f{'_b}\left( n \right) < Z} ({x_b}-x{'_b}). $

(9)

则有f_a(x′_a)-f_a(x_a)>f_b(x_b)-f_b(x′_b)即f_a(x′_a)+f_b(x′_b)>f_a(x_a)+f_b(x_b).对任意不满足f′₁(x₁)=f′₂(x₂)=...=f′_N(x_N)的X, 必存在另外一个X′且f(X′)>f(X), 即均不可能是最大值, 上述定理得证.从而可快速获取资源总量限制问题的最优解.

推论2  资源总量限制问题的最优解L′_j(1≤j≤J)满足$\sum\limits_{i{\rm{ = 1}}}^{\rm{I}} {{\rm{cd}}{{\rm{f}}_{i, 1}}\left({L{'_1}} \right)} = \sum\limits_{i{\rm{ = 1}}}^{\rm{I}} {{\rm{cd}}{{\rm{f}}_{i, 2}}\left({L{'_2}} \right)} = \ldots = \sum\limits_{i{\rm{ = 1}}}^{\rm{I}} {{\rm{cd}}{{\rm{f}}_{i, {\rm{J}}}}\left({L{'_{\rm{J}}}} \right)} $

证明:将资源总量限制问题可转化为F_j(L_j)=${w_{{\rm{sat}}}}\sum\limits_{i = 1}^{\rm{I}} {\int_0^L {\left({1-{\rm{cd}}{{\rm{f}}_i}\left(n \right)} \right){\rm{d}}n/{\rm{J}}} } + {{\rm{w}}_{{\rm{loc}}}}\sum\limits_{i = 1}^{\rm{I}} {\int_0^{{L_j}} {\left({1-{\rm{cd}}{{\rm{f}}_{i, j}}\left(n \right)} \right){\rm{d}}n} } $, 则导函数为$f{'_j}\left({{L_j}} \right) = {{\rm{w}}_{{\rm{loc}}}}\left({{\rm{I-}}\sum\limits_{i{\rm{ = 1}}}^{\rm{I}} {{\rm{cd}}{{\rm{f}}_{i, j}}\left({{L_j}} \right)} } \right)$, 根据定理1, 最优解必然满足推论2中的条件, 推论2得到证明.

根据上述推论, 若寻找给定预算C下费用总量限制问题的初始解, 只需快速遍历满足资源总量限制问题最优条件的解, 找到费用总和为C的解即可.设对资源总量限制问题最优解有$v = \sum\limits_{i{\rm{ = 1}}}^{\rm{I}} {{\rm{cd}}{{\rm{f}}_{i, 1}}\left({L{'_1}} \right)} = \sum\limits_{i{\rm{ = 1}}}^{\rm{I}} {{\rm{cd}}{{\rm{f}}_{i, 2}}\left({L{'_2}} \right)} = \ldots = \sum\limits_{i{\rm{ = 1}}}^{\rm{I}} {{\rm{cd}}{{\rm{f}}_{i, {\rm{J}}}}\left({L{'_{\rm{J}}}} \right)} $, 则对给定的v, 最优解中${L_j} = h_j^{-1}\left(v \right)$, 其中${h_j}\left({{L_j}} \right) = \sum\limits_{i{\rm{ = 1}}}^{\rm{I}} {{\rm{cd}}{{\rm{f}}_{i, j}}\left({{L_j}} \right)} $.构建h_j(·), 再计算不同v值对应最优解的费用, 找到总费用为C的资源总量限制问题的最优解作为费用总量限制问题的初始解; 在不改变总费用C的基础上迭代调整各个L_j增加总的收益直到无法调整.获取初始解的过程如下:

算法2   基于资源总量限制的预分配算法.

输入:需求累积分布函数cdf_i(·), cdf_{i, j}(·)及其反函数; 预算总量C, 各区域资源的价格函数f_j(·), 算法终止条件阈值D.

输出:各区域资源量初始解L′_j.

1) s=I/2，v=I;

2) WHILE (TRUE){

3)   FOR (j=1 to J){

4)    求解$\sum\nolimits_{i = 1}^{\rm{I}} {{\rm{cd}}{{\rm{f}}_{i, 1}}} \left({L{'_j}} \right) = v$以获得L′_j;

5)    }

6) $d = \sum\nolimits_{j = 1}^{\rm{J}} {{{\rm{f}}_j}\left({L{'_j}} \right)-{\rm{C}}} $;

7)  s=s/2;

8)   IF (|d|≤D)输出初始解并返回;

9)   IF (d < 0) v=v-s;

10)   ELSE v=v+s;

11) }

算法2中, 通常情况下的值I=6, 则2~11行的循环在运行50次后, s≈10^-15, 此时9和10行中v值在加上或减去s几乎不发生变化, 则下个循环中3~5行根据v值的求得的L′_j和前次循环中几乎不发生变化, 此时足够逼近最优解.调度前已知3~5行中需要的累计分布函数, 事先表示为快速查询函数值的哈希表, 则3~5行的计算过程可转化为O(1)的查询过程, 则整个函数在大约50次循环后即可获得对应的结果, 该算法的复杂度可优化到O(50)左右.

2.3 费用总量限制下资源分配算法

根据算法2快速获取预分配结果L′_j, 在此基础上快速调整以获取近优解, 主要思路是在不改变整体费用基础上, 在各个区域间交换资源以增大收益, 直到收益无明显增加为止, 如以下算法所示.

算法3  费用总量限制下资源分配算法.

输入:需求累积分布函数cdf_i(·), cdf_{i, j}(·)及其反函数; 预算总量C, 各区域资源的价格函数f_j(·), 迭代控制变量M和N.

输出:费用总量限制下的近优解L′_j.

1) 基于算法1获取初始解L′_j;

2) FOR (m=1 to M){

3)  d=mC/(MJ);

4)  n=0;

5)  FOR (n=1 to N){

6)   获取每区域j增加预算d后整体增加的收益, 保存为长度J列表LA;

7)   获取每区域j降低预算d后整体降低的收益, 保存为长度J列表LD;

8)   IF(max(LA)>max(LD)){

9)    在对应的区域间移动预算d并更新各区域资源量;

10)    }

11)   }

12)}

根据上述过程可知, 计算复杂度取决于循环参数M和N, 循环次数越大则越逼近最优解, 具体取值需要在解的优化性和计算复杂度之间权衡.

3 实验

在各类场景中比较本文算法和均值算法的效果差异.其中, 调度间隔S^t=1 h, 需求测量间隔S^d=10 min, 即I=6.和文献[12]中实验场景类似, 每区域用户请求产生的资源需求表示为随机需求模型且符合zipf分布, 即给定任意一个请求, 来自区域j的概率为${j^{-e}}/\sum\limits_{n = 1}^{\rm{J}} {{n^{-e}}} $, 其中实数e(e＞0)为zipf参数.设所有区域总需求量均值为λ, 则每区域需求符合均值为$\lambda {j^{-e}}/\sum\limits_{n = 1}^{\rm{J}} {{n^{-e}}} $的泊松分布.

实验中各缺省参数如下设定:区域总数缺省值为J=100, 价格模型中, 缺省情况下各区域虚拟机单价相等; zipf参数范围一般为0.4~1.6, 缺省值为折中数值1.0;预算总额C缺省值为一个调度间隔中各区域恰好满足均值需求时资源费用总和.为测试不同迭代次数对效果的影响, 对算法3中迭代控制变量M和N取三组不同的值, 分别为(M=1 000, N=1 000), (M=500, N=500), (M=100, N=100).比较本文算法和基于均值算法的效果, 所对比的均值算法的输入为各区域各需求测量间隔的均值E(G_jⁱ), 目标是各区域供应资源量和需求均值比例相等, 且满足预算总额C.

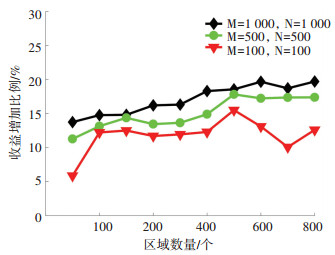
比较区域数量变化时两种方法之间的差别见图 1.横坐标是区域数量J, 纵坐标是本文算法相比均值算法在资源收益上的增加比例.可以看到, 随着区域数量的增加, 本文算法和均值算法的收益差别有增大的趋势, 由于算法通过在两个区域间互换配置寻找更优分配方案, 更多的区域使得有更高的概率找到优化的交换方案, 从而使得收益上升.这也表明算法通过增加收益, 能部分补偿区域数量增加导致的计算量增加, 且迭代次数M和N越大, 算法效果越好.在(M=500, N=500)时, 在算法计算量和效果之间达到一个较好的平衡状态.

由于实际环境中云基础设施提供商资源价格函数存在差别, 甚至单个提供商管理的多个云数据中心之间价格也不相同, 因此需研究各区域价格函数的差别对算法效果的影响.由于各提供商的各区域中价格差别一般不超过2倍^[1-4], 设每个区域均为线性函数, 每个区域的最高和最低单价比率在1.0~2.0之间变化, 结果见图 2, 横坐标是最高和最低单价比率, 纵坐标是本文算法相比均值算法在资源收益上的增加比例.可见价格差别扩大时, 收益有波动并略有升高, 但并没有明显的上升或下降趋势, 意味着本文算法可适应常见各种类型的云平台, 也可满足跨云提供商部署资源调度的需求.

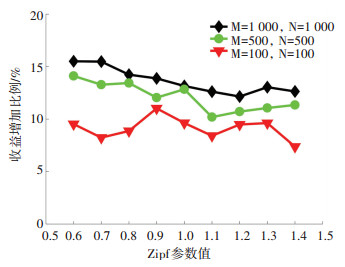
由于常见的跨区域应用往往有一些热门的区域, 即某些区域需求占较大比重, 这种不同区域的热门程度的差别可由zipf参数刻画, zipf参数值一般介于0.6~1.4之间, 参数值越大, 表明各区域需求热门程序差别越大.这里比较不同参数值下收益的变化, 结果见图 3, 横坐标是zipf参数值, 纵坐标是本文算法相比均值算法在资源收益上的增加比例.可见随着zipf参数的增加, 资源收益略有降低, 未发生较大变化.这意味着各区域需求热门程度的差别不会显著影响算法的效果, 可适用于具不同跨区域需求差别的各类应用场景.大的迭代次数会提升算法效果, 但(M=500, N=500)和(M=1 000, N=1 000)之间的差别不明显.

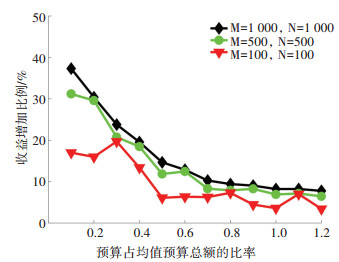
预算总额限制也会影响算法效果, 因此比较不同预算额度下算法收益的变化, 见图 4, 横坐标的预算以和均值预算总额的比例表示, 均值预算总额即每区域采用刚好满足需求均值的资源量对应的费用, 纵坐标是本文算法相比均值算法在资源收益上的增加比例.可见随着预算的减少, 相对均值算法的额外收益迅速增加, 即在预算偏少的情况下, 比均值算法有更大的收益优势.由于常见调度场景中预算相对不足, 因此本文算法可获得明显的优化效果.

4 结束语

本文研究分布式云平台中面向随机需求的通用资源分配问题, 算法考虑各地理区域间异质的费用模型, 采用预算总额的资源限制, 提出可获取近似解的快速求解方法.相比已有的均值计算方法, 可额外满足近40%的资源需求, 因此可作为已有算法的有效补充.