2. 重庆交通大学 土木工程学院,重庆,400074
2. 2 School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, China
沥青路面永久变形问题一直是国内外研究的关键难题之一[1].鉴于目前中国高速公路普遍采用无机结合料稳定材料基层沥青路面结构,导致路面永久变形主要集中于面层[2].现行沥青层永久变形预估方法通常采用固定温度、标准轴载条件下预测[3].然事实上,沥青路面沥青层温度呈周期性变化及梯度变化.同时,目前中国高速公路超载、重载现象十分普遍,若仍仅采用标准轴载,将面临无法如实反映及适应实际路面受力状况[4-5].文献[6-8]从全年路面温度分布频率角度探索沥青路面面层温度分布规律;韦璐等[9]借鉴德国德累斯顿工业大学提出的路面温度场预估模型,采用由多个温度区间组成的路表温度组合代替单一固定路表温度.同时,AASHTO 2002设计指南和中国公路沥青路面设计规范2017版中均考虑了车型和轴型分类以及轴重分布系数等交通荷载参数,以期全面、客观的反映交通荷载特性[10-11].因此,建立准确的沥青路面沥青层温度和轴载分布对沥青层永久变形预估具有重要的理论意义.
本文以江西省泉南高速吉莲段为试验路段,从全温域角度出发,综合考虑环境温度和交通荷载两大主要外界影响因素,以流变学理论和叠加原理为基础,建立了沥青路面全年温度分布频率、沥青层温度场分布、全年轴载分布以及重复荷载作用下沥青混合料永久变形预估修正模型,改进了沥青路面沥青层永久变形叠加方法,提出了一种较为系统的全温域条件下沥青路面沥青层永久变形预估方法,并分析了沥青路面在实际荷载和温度分布下的永久变形特性,同时,基于全温域温度分布进行了沥青路面永久变形预估简化模型研究,为快速预估沥青路面永久变形提供了一种新方式.
1 全温域温度分布温度是影响沥青路面结构承载力和使用性能的重要因素之一[12].然现行路面结构和材料设计往往忽略不同层位间的温度差异以及路面内温度出现的时间频率差异[13].沥青路面全温域温度分布由沥青路面全年温度分布频率和沥青层沿深度的温度分布曲线两项指标控制.沥青路面全年温度分布频率是将沥青路面全年温度分成不同的温度区间,统计不同温度区间通常以距路表 1 cm处温度时数占全年时数的比例,来反映沥青路面不同温度区间的频率差异.沥青层沿深度的温度分布曲线通常采用实测或模型计算确定[14].实测法是在沥青路面沥青层内部安置温度传感器实时观测记录沥青层温度分布;模型计算是运用热传导理论建立沥青路面二维非稳态温度场解析方程,以实测气象资料代入温度预估程序快速求解[15].因此,全温域温度分布综合考虑了全年沥青路面湿度分布和沥青层温度的梯度变化,从而精确评价沥青路面的使用性能.
| 表 1 沥青路面结构组成与设计参数 Table 1 Structure and design parameters of Asphalt Pavement |
| 表 3 沥青混合料动态模量和泊松比分布 Table 3 Distribution of dynamic modulus and Poisson's ratio of asphalt mixture |
以江西省赣中地区为例,以距离路面1 cm处的温度作为路表代表温度,以5 ℃作为间隔划分温度区间.沥青路面全年温度分布频率和沥青层沿深度的温度分布曲线见图 1和图 2.

|
图 1 沥青路面全年温度分布频率 Figure 1 Annual temperature distribution frequency of asphalt pavement |

|
图 2 沥青路面沥青层沿深度的温度分布曲线 Figure 2 Temperature distribution curve along depth of Asphalt layer |
由图 1可知,路面温度20 ℃以下低温区间、20 ℃~40 ℃中温区间、40 ℃以上高温区间分别占全年温度的19.73 %、67.86 %、12.37 %,赣中地区中温区间的分布频率最高,因此,沥青路面永久变形预估时,全面考虑高温区间和中温区间的影响是必要的.
由图 2可知,不同温度区间沥青路面沥青层沿深度的温度分布是不同的.低温时,沥青层上部温度低,下部温度高;高温时,沥青层上部温度高,下部温度低;中温时,沥青层上下部温度分布相近.总体来看,不同温度区间沥青层温度分布沿深度逐渐缩小,符合沥青路面实际温度分布规律.
2 沥青路面沥青层永久变形叠加方法为了更加准确地预估沥青路面的永久变形,在前人研究成果的基础上[16-19],文中提出一种全温域条件下基于叠加原理考虑温度分区和轴载分级的沥青路面永久变形预估方法.该方法将全温域条件下沥青混合料永久变形累积叠加分为温度区间内和温度区间间两种叠加情况.温度区间内叠加按多级荷载作用下沥青混合料永久变形累积叠加过程计算;温度区间间叠加则以分层应变法为基础,以线性累积叠加计算.
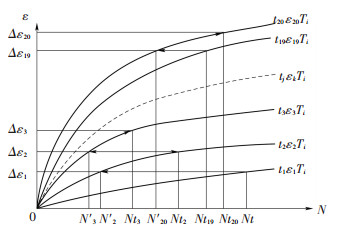
温度区间内叠加见图 3,Ti表示第i个温度区间,温度区间内的永久变形按照轴载等级从小往大逐级反算叠加获得. tj表示第j个轴载等级,本文以1t作为间隔划分20个轴载等级区间,实测高速公路的交通量和轴重,从而确定不同轴载等级区间的轴载分布频率.每个温度区间的永久变形计算均从轴载等级t1开始,将其荷载作用次数N1代入永久应变修正模型中将永久应变Δε1,将Δε1代入轴载等级t2的永久应变修正模型反算其对应的荷载作用次数ΔN2,然后将轴载等级t2的荷载作用次数N2加上ΔN2的值N'2代入轴载等级t2的永久应变修正模型中轴载等级t1、t2作用后的永久应变Δε2,再将Δε2代入轴载等级t3的永久应变修正模型,同轴载等级t2时永久应变的计算过程,依次类推至轴载等级t20时的永久应变ΔN20,ΔN20即为轴载等级t1正向累加至轴载等级t20沥青层所产生的总永久应变,将ΔN20与沥青层厚度相乘即为此温度区间沥青层的永久变形.此种算法命名为反算累积叠加荷载作用次数永久变形计算方法.温度区间间叠加即按重复荷载作用下沥青混合料永久变形黏弹性力学修正模型,以年为单位,计算第1年各温度区间路面轮迹中心位置的永久变形量并线性叠加得路面永久变形量Δh;同理,计算第2、3……n年路面永久变形量,以路面容许永久变形15 mm为临界指标,判断沥青路面容许永久变形使用寿命.该方法考虑了不同轴载在不同温度条件下沥青混合料的永久变形规律及其叠加过程,即进行了温度分区和轴载分级,实现了温度和轴载的全覆盖、全过程评价,分析结果更加贴合实际.
|
图 3 反算累积叠加荷载作用次数永久变形计算方法 Figure 3 Permanent deformation calculation method by counter calculating cumulative number of superimposed load |
以泉南高速吉莲段作为依托工程,实测交通荷载和自然环境条件,根据全温域条件下基于叠加原理的沥青路面永久变形预估方法进行沥青路面永久变形预估分析,同时,结合车辙实测数据修正预估模型.
3.1 吉莲段沥青路面结构及设计参数吉莲段沥青路面结构组成与设计参数见表 1.
根据沥青混合料动态模量试验结果,运用非线性的最小二乘法通过S型函数进行数值拟合,从而建立动态模量与加载频率的关系[20-22].动态模量主曲线方程为
| $ {\rm{log}}\left( {{E^*}} \right) = \delta + \frac{a}{{1 + {e^{\beta + \gamma \left[ {{\rm{log}}\left( \omega \right) + \frac{{\Delta Ea}}{{19.14714}}\left( {\frac{1}{{T + 273.15}} - \frac{1}{{{T_r} + 273.15}}} \right)} \right]}}}}. $ | (1) |
式中:E*为动态模量,MPa;δ为动态模量极小值,MPa;δ+α为动态模量极大值,MPa;β,γ为描述S型函数形状的参数;ω为加载频率,Hz;Tr为参考温度,℃;T为试验温度,℃;ΔEα为拟合系数.
选取20 ℃作为参考温度Tr,则SMA-13、AC-20、AC-25、ATB-25沥青混合料动态模量主曲线方程拟合结果见表 2.
| 表 2 动态模量主曲线方程拟合结果 Table 2 Fitting results of main curve equation of dynamic modulus |
当车速80 km/h,加载频率约为15 Hz时,根据图 1、表 2和式(1)计算可得吉莲段不同温度区间沥青混合料动态模量沿路面深度分布和泊松比设置见表 3.
3.2 温度-轴载分布横向分布是交通荷载的重要特性[23].文中行车道轮迹宽度荷载作用次数计算可方向分配系数取值0.5、车道分配系数取值0.8和轮迹横向分布系数取值0.3[24-25].标准路段80 km/h时,行驶车辆单次荷载作用时间为0.010 2 s,室内三轴重复荷载试验加载作用时间为0.2 s,考虑时间的折减,实际交通荷载作用次数的折减系数为0.051.
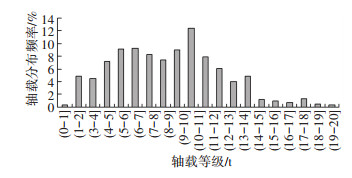
经测算江西温沙高速、樟吉高速等交通分布,得高速公路沥青路面交通轴载分布见图 4.温度-轴载分布即不同温度区间不同轴载等级的交通分布,以不同轴载等级的交通量乘以温度区间的分布频率表示吉莲段温度分布按图 1选取.经统计, 吉莲段收费2013年和2014年的交通量分别为174 008辆、198 974辆(除去小轿车).考虑实测结果,2015年~2019年交通量增长率取10 %,后续年份取6 %,设计年限为15年.吉莲段2013年行车道轮迹宽度温度-轴载分布见图 5.其他设计年份的行车道轮迹宽度温度-轴载分布同理可得,此处不再赘述.
|
图 4 高速公路沥青路面交通轴载分布 Figure 4 Traffic axle load distribution of Expressway asphalt pavement |

|
图 5 2013年行车道轮迹宽度温度-轴载分布 Figure 5 Temperature-axial load distribution of lane width in 2013 |
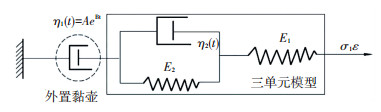
沥青混合料是典型的黏弹性材料,其力学响应依赖加载历史和环境温度[26-27].针对沥青混合料三阶段永久变形特性,以修正Burgers模型为基础,将流变学模型看成由三单元范德普模型与外置黏壶串联组成,见图 6.
|
图 6 流变学模型 Figure 6 Rheological model |
根据流变学模型,同时考虑行车荷载重复作用下存在间歇时间,推导出重复荷载作用下沥青混合料永久变形黏弹性力学修正模型为
| $ \varepsilon = {\sigma _0}\xi {P_1}\left( {1-{e^{-0.2{P_2}N}}} \right) + {\sigma _0}\xi {P_3}\left( {1-{e^{ - {P_4}N}}} \right). $ | (2) |
式中:ε为永久应变;σ0为偏应力,MPa;ξ为平均修正系数,即三轴重复荷载试验实测值与理论值之比;N为荷载作用次数,次;T为温度,℃;P1、P2、P3、P4为拟合参数.
为拓宽沥青混合料黏弹性力学修正模型温度和偏应力的适用范围,建立了温度、偏应力与力学模型参数P1、P2、P3和P4关系方程,即
| $ \begin{array}{l} \;\;\;\;\;{P_i} = {a_i}{e^{{b_i}T}} + {c_i}{e^{{d_i}{\sigma _0}}}, \\ {P_j} = {a_j}{e^{{b_j}T}} + {c_j}{e^{{d_j}{\sigma _0}}} + {f_j}x + {g_j}y + {k_j}. \end{array} $ |
式中:a、b、c、d、f、g、k为回归参数;i=1、3、4;j=2.
为节省篇幅,重复荷载作用下沥青混合料黏弹性力学修正模型建立过程和SMA-13、AC-20、AC-25三种沥青混合料黏弹性力学修正模型回归参数详见文献[28],此处不再赘述.不同温度区间的平均修正系数ξ见表 4.
| 表 4 沥青混合料黏弹性力学模型平均修正系数 Table 4 Average correction coefficient of viscoelastic model of asphalt mixture |
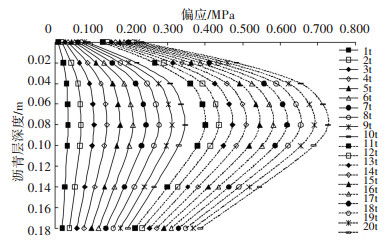
沥青混合料黏弹性力学修正模型以偏应力反映其受力状态,其偏应力σ0等于主应力σ1与侧应力σ3之差.根据弹性力学应力状态分析,最大剪应力与偏应力存在二倍关系[29].本文采用BISAR3.0计算路面结构偏应力,吉莲段沥青路面(10~15] ℃时沥青层偏应力分布见图 7.不同温度区间轴载等级(0~1] t时偏应力沿沥青层深度的分布见表 5.轴载等级2 t~20 t时沥青层偏应力分布按线性成倍增长,此处不再赘述.
|
图 7 (10~15]℃时沥青层偏应力分布 Figure 7 Deviatoric stress distribution of asphalt layer at (10~15]℃ |
| 表 5 轴载等级(0~1]t时沥青层偏应力分布 Table 5 Deviatoric stress distribution of asphalt layer in axial load level(0~1]t |
沥青路面沥青层永久应变计算方法分为两种即原点增长累积永久应变计算方法(简称原点法)和反算累积叠加永久应变计算方法(简称反算法).原点法即每个温度区间和每个轴载等级都从原点开始计算永久应变,再累加得到总永久应变.该方法相当于每个温度区间和每个轴载等级都作用在新路面上,其预估结果偏大.反算法如前所述.
不同温度区间取中间值作为代表温度.将其偏应力、代表温度和轴载作用次数代入永久应变模型,即式(2),采用MATLAB软件编制运算程序计算沥青层永久应变分布.
3.6 沥青层永久变形分布沥青路面沥青层永久变形计算采用改进的分层应变法,引入分区分级分层叠加的思想,即温度分区、轴载分级、路面分层,将路面温度以5 ℃为间隔分为若干个温度区间,记为m;将交通荷载以1 t为间隔分为若干个轴载等级;将沥青层根据实际厚度按每1 cm~4 cm为一亚层,基层、底基层和土基根据需要划分亚层,以此将路面结构划分为若干亚层,记为n;再分别计算不同温度区间和轴载等级下各亚层的变形量.同时考虑沥青混合料的黏弹塑特性和行驶速度对荷载作用时间的影响,则全温域条件下基于叠加原理的沥青路面永久变形预估模型为
| $ \Delta h = \sum\limits_{j = 1}^m {[\sum\limits_{i = 1}^n {{\varepsilon _i}{h_i}}]} . $ | (3) |
式中:Δh为沥青层永久变形,mm;m为路面结构温度分区数;n为路面结构分层数;hi为沥青层第i亚层厚度,mm;εi为沥青层第i亚层永久应变,按式(2)计算.
根据通车第一年即2013年沥青层永久变形的计算方法,同理,通车后第2、3……n年吉莲段沥青路面的永久变形见表 6.
| 表 6 沥青路面永久变形计算结果 Table 6 Calculation results of permanent deformation of asphalt pavement |
鉴于中国高速公路以无机结合料稳定材料基层沥青路面为主,沥青层永久变形是沥青路面结构设计与性能评价的重要指标之一.通常高速公路沥青路面永久变形超过10 mm,(即进入临界状态,容易造成雨天路面积水,导致行驶车辆产生滑漂现象.按原点法计算,路面使用4年后,累积永久变形已超过10 mm).若不及时养护,随着使用年限的增加,当路面累积永久变形超过15 mm时,将严重降低路面服务质量,必须翻修或改建.由此得出,吉莲段的永久变形使用年限为6年;按反算法计算泉南高速吉莲段在设计年限内的累积永久变形为8.87 mm,未超过路面容许永久变形.
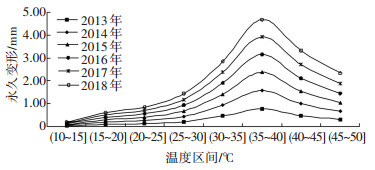
由图 8可知,原点法永久变形分布曲线相似,且逐年呈线性增长.随着温度的增大,永久变形呈现先增大后降低,其中温度区间(35~40] ℃的永久变形最大.由图 9可知,原点法永久变形累积贡献率分布曲线呈现先增大后减小,其中温度区间(35~40] ℃的贡献率最大,这与永久变形分布曲线相同.文献[17]认为,只有当路面温度大于20℃时,路面才会产生永久变形.按原点法计算,小于20 ℃温度区间的永久变形贡献率为4.90 %,考虑其值较小,采用温度修正系数来弥补其差值,其值为1.05.同时,原点法永久变形累积贡献率分布曲线几乎相同,永久变形只随交通量的增加呈线性增长,说明该方法存在一定的缺陷性.
|
图 8 原点法永久变形分布曲线 Figure 8 Distribution curves of permanent deformation by origin method |

|
图 9 原点法永久变形累积贡献率分布曲线 Figure 9 Distribution curves of cumulative contribution rate of permanent deformation by origin method |
由图 10可知,反算法永久变形分布曲线不相似.通车后五年内即2013年~2017年,随着温度的增大,永久变形呈现先增大后减小,其中温度区间(35~40] ℃的永久变形最大.通车五年后即2018年之后,随着温度的增大,永久变形持续增大,其中温度区间(45~50] ℃的永久变形最大.温度区间(25~30] ℃到(35~40] ℃之间永久变形增长最快,是永久变形增长的转折区间.由图 11可知,反算法永久变形累积贡献率分布曲线不相似.设计年限内不同温度区间永久变形累积贡献率持续增大,其中温度区间(45~50] ℃的贡献率最大,这与永久变形分布曲线相同;但在2013年~2017年,通车初期不同温度区间永久变形累积贡献率呈现先增大后减小,其中温度区间(35~40] ℃和(40~45] ℃的贡献率较大;在2018年~2027年,不同温度区间永久变形累积贡献率持续增大,其中温度区间(45~50] ℃的贡献率最大.同时,小于20 ℃温度区间的永久变形贡献率为5.09 %,同理,其温度修正系数取值1.06.

|
图 10 反算法永久变形分布曲线 Figure 10 Distribution curves of permanent deformation by counter calculation method |

|
图 11 反算法永久变形累积贡献率分布曲线 Figure 11 Distribution curves of cumulative contribution rate of permanent deformation by counter calculation method |
由图 12可知,随着轴载等级的逐渐增大,原点法和反算法轴载等级对永久变形的贡献率均呈现先增大后减小,其中轴载等级(9~10] t的贡献率最大;轴载等级(0~1] t的贡献率小于1 %,可忽略不计.

|
图 12 不同轴载等级永久变形累积贡献率分布曲线 Figure 12 Distribution curves of cumulative contribution rate of permanent deformation in different axial load level |
与实测值相比,理论计算的沥青路面永久变形值相对偏小[30].特别是在荷载作用初期,差距是非常明显的.普遍认为在蠕变分析中,未充分考虑压密变形的影响.因此,需要根据实测值对理论值进行修正,以更加接近路面变形的实际情况.
根据吉莲段车辙检测分析,若采用全长路面车辙平均深度评价路面车辙大小,则会抹平不同位置车辙深度分布的差异,影响沥青路面永久变形预估模型修正的准确性.本文采用概率测算法计算路面全长车辙平均深度作为实测值为
| $ R{D_r} = R{D_{qc}} + \lambda S. $ | (4) |
式中,RDr为路面车辙深度,mm;RDqc为路面全长百米车辙平均深度的平均值,mm;S为路面全长百米车辙平均深度的标准差,mm;λ为与保证率有关的系数,本文选取保证率P(λ)=85%,λ=1.05.
通过概率测算法计算得2013年~2017年吉莲段沥青路面全长车辙平均深度为5.60 mm、7.03 mm、7.00 mm、7.35 mm、7.86 mm,线性修正系数取吉莲段沥青路面五年实测值与理论值之比的平均值为1.93.
则全温域条件下基于叠加原理的沥青路面永久变形预估修正模型为
| $ \Delta h = \varphi \cdot \delta \cdot \sum\limits_{{\rm{ }}j = 1}^m {[\sum\limits_{i = 1}^n {{\varepsilon _i}{h_i}}]} . $ | (5) |
式中:φ为理论修正系数,取值为1.93;δ为温度修正系数,若温度分布只取20 ℃以上,则δ取值为1.06.若温度分布为全温域温度分布,则δ取值为1.00.
通过对理论值的修正,吉莲段沥青路面初期的永久变形更加接近实测值,而后期变化仍需长期监控进一步修正.若以沥青路面容许永久变形15 mm作为评定标准,根据修正结果分析,吉莲段15 %的沥青路面在运营12年后需要翻修,以恢复路面正常的使用功能.以此为依据,泉南高速公路吉莲段的使用年限为12年.
5 沥青路面永久变形预估简化模型若高速公路沥青路面的结构类型和材料组成固定,将影响沥青路面沥青层永久变形发展的因素简化为只有温度和轴载.以吉莲段为例,构建基于全温域温度分布的沥青路面永久变形预估简化模型.
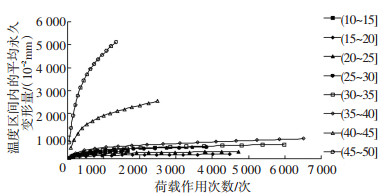
温度区间内的平均永久变形量即设计年份内不同温度区间行车道轮迹宽度永久变形量的理论值与其温度分布频率的比值.结合图 1和图 10得吉莲段不同温度区间内的平均永久变形量与荷载作用次数关系见图 13.
|
图 13 温度区间内的平均永久变形量与荷载作用次数关系 Figure 13 Relationship of load repetition numbers and average permanent deformation in temperature range |
建立温度区间内的平均永久变形量与荷载作用次数关系方程为
| $ f = a{N^b} + c. $ | (6) |
式中:f为温度区间内的平均永久变形量,0.01 mm;N为温度区间行车道轮迹宽度荷载作用次数,次;a、b、c为拟合参数.
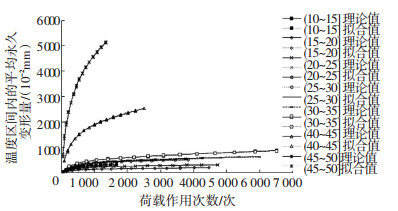
采用1stOpt15软件按式(6)对图 13的数据进行拟合,拟合结果见表 7.理论值与拟合值对比见图 14.
| 表 7 拟合结果 Table 7 Fitting results |
|
图 14 理论值与拟合值对比 Figure 14 Comparison between theoretical and fitting values |
由表 7和图 14可知,沥青路面温度区间内的平均永久变形量与荷载作用次数关系方程的拟合效果较好.在已知设计年份不同温度区间的荷载作用次数和温度分布频率,即可联立式(6)和式(7)求出该年份沥青路面沥青层的永久变形.
| $ \Delta h = \varphi \cdot \delta \cdot \sum\limits_{i = 1}^m {{f_i}{P_i}} . $ | (7) |
式中:fi为第i温度区间内的平均永久变形量,0.01 mm;Pi为第i温度区间的温度分布频率,%;i为1、2、3…n.
需要说明的是,式(7)中第i温度区间内的平均永久变形量fi所采用的荷载作用次数为温度区间内不同轴载等级的荷载作用次数之和,未考虑不同轴载等级的影响,将来可建立温度区间内设计轴载等级的平均永久变形量.
6 结论1) 全温域条件下基于叠加原理的沥青路面永久变形预估方法,即引入分区分级分层的思想,即温度分区、轴载分级、路面分层,综合考虑了全体沥青路面温度分布和沥青温度的梯度变化.
2) 建立了SMA-13、AC-20和AC-25沥青混合料永远变形黏弹性力学修正模型,确定了不同温度区间的平均修正系数,可求解不同温度和偏应力条件下沥青混合料不同荷载作用次数的永久应变.
3) 建立了原点增长累积和反算累积叠加荷载作用次数的沥青路面永久变形计算方法.以容许永久变形15 mm为评价标准,吉莲段使用年限分别为6年和12年.
4) 泉南高速吉莲段按反算累积叠加计算的沥青路面永久变形分布曲线,前五年随温度增大呈现先增大后减小,五年后呈现持续增大的趋势,这与按原点增长累积计算的沥青路面永久变形分布曲线一直是随温度增大呈现先增大后减小,且逐年呈线性增长趋势的情况明显不同.
5) 通过泉南高速吉莲段沥青路面永久变形理论值与实测值的对比分析,提出了全温域条件下基于叠加原理的沥青路面永久变形预估修正模型.
6) 基于全温域温度分布的沥青路面温度区间内的平均永久变形量与荷载作用次数关系方程和永久变形与温度区间内的平均永久变形量、温度分布频率的关系方程,为全温域条件下沥青路面永久变形快速预估提供一种新方式.
| [1] |
HAFEEZ I, KAMAL M A. An experimental-based approach to predict asphalt mixtures permanent deformation behavior[J]. Arabian Journal for Science & Engineering, 2014, 39(12): 8681. |
| [2] |
董泽蛟, 肖桂清, 龚湘兵, 等. 重载沥青路面结构组合的抗车辙性能分析[J]. 哈尔滨工业大学学报, 2014, 46(6): 72. DONG Zejiao, XIAO Guiqing, GONG Xiangbing, et al. Rutting resistance analysis of structure combinations for asphalt pavement subjected to heavy loads[J]. Journal of Harbin Institute of Technology, 2014, 46(6): 72. |
| [3] |
顾兴宇, 袁青泉, 倪富健. 基于实测荷载和温度梯度的沥青路面车辙发展影响因素分析[J]. 中国公路学报, 2012, 25(6): 30. GU Xingyu, YUAN Qingquan, NI Fujian. Analysis of factors on asphalt pavement rut development based on measured load and temperature gradient[J]. China Journal of Highway and Transport, 2012, 25(6): 30. DOI:10.3969/j.issn.1001-7372.2012.06.005 |
| [4] |
康海贵, 郑元勋, 蔡迎春, 等. 实测沥青路面温度场分布规律的回归分析[J]. 中国公路学报, 2007, 20(6): 13. KANG Haigui, ZHENG Yuanxun, CAI Yingchun, et al. Regression analysis of actual measurement of temperature field distribution rules of asphalt pavement[J]. China Journal of Highway and Transport, 2007, 20(6): 13. DOI:10.3321/j.issn:1001-7372.2007.06.003 |
| [5] |
马士杰, 孙同波. 高速公路典型重载交通轴载谱参数与设计轴载分析[J]. 公路, 2014(12): 39. MA Shijie, SUN Tongbo. Analysis of traffic axle load spectrum and design axle load for typical heavy load of expressway[J]. HIGHWAY, 2014(12): 39. DOI:10.3969/j.issn.1002-0268.2014.12.007 |
| [6] |
MAHAN H M. Behavior of Permanent deformation in Asphalt concrete pavementsunder temperature variation[J]. Qadisiya Journal For Engineering Sciences, 2013, 6(1): 62. |
| [7] |
马正军, 谈至明, 钱晨. 沥青路面面层温度分布规律[J]. 中国公路学报, 2014, 27(4): 9. MA Zhengjun, TAN Zhiming, QIAN Chen. Distribution law of asphalt pavement temperature[J]. China Journal of Highway and Transport, 2014, 27(4): 9. DOI:10.3969/j.issn.1001-7372.2014.04.002 |
| [8] |
曹丽萍, 孙立军. 基于AASHTO 2002的沥青路面永久变形叠加方法研究[J]. 武汉理工大学学报:交通科学与工程版, 2010, 24(06): 1095. CAO Liping, SUN Lijun. Superposition method of permanent deformation of asphalt pavement based on AASHTO 2002 design guide[J]. Journal of Wuhan University of Technology:Transportation Science &Engineering, 2010, 24(06): 1095. |
| [9] |
韦璐, SASCHAKAYSER, FROHMUTWELLNER. 路表温度对沥青路面疲劳损伤的影响[J]. 公路交通科技, 2013, 30(1): 1. WEI Lu, SASCHA KAYSER, FROHMUT WELLNER. Impact of surface temperature on fatigue damage in Asphalt Pavement[J]. Journal of Highway and Transportation Research and Development, 2013, 30(1): 1. DOI:10.3969/j.issn.1002-0268.2013.01.001 |
| [10] |
APPLIED RESEARCH ASSOCIATES. Guide for mechanistic-empirical pavement design[R].National Cooperative Highway Research Program (Project No. 1-37A). Washington D C: Transportation Research Board, 2004
|
| [11] |
中交路桥技术有限公司.公路沥青路面设计规范: JTG D50-2017[S].北京: 人民交通出版社有限公司, 2017 CCCC Road & Bridge Technology Co., Ltd.Specifications for design of highway asphalt pavement: JTG D50-2017[S].Beijing: China Communications Press Co., Ltd., 2017 |
| [12] |
陈嘉祺, 罗苏平, 李亮, 等. 沥青路面温度场分布规律与理论经验预估模型[J]. 中南大学学报:自然科学版, 2013, 44(4): 1647. CHEN Jiaqi, LUO Suping, LI Liang, et al. Temperature distribution and method-experience prediction model of asphalt pavement[J]. Journal of Central South University :Science and Technology, 2013, 44(4): 1647. |
| [13] |
曹丽萍, 董泽蛟, 孙立军. 从温度分布频率探讨沥青路面的永久变形[J]. 同济大学学报:自然科学版, 2007, 35(12): 1617. CAO Liping, DONG Zejiao, SUN Lijun. Research on permanent deformation of asphalt pavement considering pavement temperature distribution[J]. Journal of Tong ji University:Natural Science, 2007, 35(12): 1617. |
| [14] |
KAYSER S.Principles for survey of climatic influence within the flexible pavement design process[D].Dresden: Dresden University of Technology, 2007
|
| [15] |
黎晓, 梁乃兴. 基于非稳态温度场解析解的沥青混凝土路面温度分布研究[J]. 公路, 2012(8): 1. LI Xiao, LIANG Naixing. A study on temperature distribution in asphalt concrete pavement based on analytic solution of unstable state temperature field[J]. Highway, 2012(8): 1. |
| [16] |
姚祖康. 沥青路面结构设计[M]. 北京: 人民交通出版社, 2011. YAO Zukang. Asphalt pavement structuredesign[M]. Beijing: China Communications Press, 2011. |
| [17] |
黄晓明, 汪双杰. 现代沥青路面结构分析理论与实践[M]. 北京: 科学出版社, 2013. HUANG Xiaoming, WANG Shuangjie. Analysis theory and practice of modern asphalt pavement structure[M]. Beijing: Science Press, 2013. |
| [18] |
秦旻, 陆兆峰, 梁乃兴. 基于叠加原理的沥青路面永久变形预估方法[J]. 重庆交通大学学报:自然科学版, 2015, 34(2): 54. Qin Min, Lu Zhaofeng, Liang Naixing. Permanent deformation prediction method of asphalt pavement based on superposition principle[J]. Journal of Chongqing Jiaotong University:Natural Science, 2015, 34(2): 54. |
| [19] |
苏凯, 孙立军. 沥青混凝土永久变形预估方法研究[J]. 建筑材料学报, 2007, 10(5): 510. SU Kai, SUN Lijun. A new method for predicting deformation of asphalt concrete[J]. Journal of Building materials, 2007, 10(5): 510. DOI:10.3969/j.issn.1007-9629.2007.05.002 |
| [20] |
马翔, 倪富健, 陈荣生. 沥青混合料动态模量试验及模型预估[J]. 中国公路学报, 2008, 21(3): 35. MA Xiang, NI Fujian, CHEN Rongsheng. Dynamic modulus test of asphalt mixture and prediction model[J]. China Journal of Highway and Transport, 2008, 21(3): 35. DOI:10.3321/j.issn:1001-7372.2008.03.007 |
| [21] |
AASHTO. Standard method of test for determining dynamic modulus of hot-mix asphalt concrete mixture[R].Washing ton DC: American Association of State Highway Transportation Officials, 2005
|
| [22] |
赵毅, 梁乃兴, 秦旻, 等. PR-Module改性沥青混合料力学性能[J]. 长安大学学报:自然科学版, 2015, 35(4): 32. ZHAO Yi, LIANG Naixing, QIN Min, et al. Mechanical properties of PR-Module modified asphalt mixture[J]. Journal of Chang'an University:Science and Technology, 2015, 35(4): 32. |
| [23] |
赵延庆, 王国忠, 谭忆秋. 道路交通荷载横向分布特性分析[J]. 湖南大学学报:自然科学版, 2012, 39(6): 26. ZHAO Yanqing, WANG Guozhong, TAN Yiqiu. Analysis of the transverse distribution of traffic loading on highways[J]. Journal of Hunan University:Science and Technology, 2012, 39(6): 26. |
| [24] |
刘黎萍, 孙立军. 高速公路沥青路面轮迹横向分布研究[J]. 同济大学学报:自然科学版, 2005, 33(11): 1449. LIU Liping, SUN Lijun. Research on wheel path lateral distribution for freeway asphalt pavements[J]. Journal of Tongji University:Natural Science, 2005, 33(11): 1449. |
| [25] |
董忠红, 吕彭民. 考虑轮迹横向分布的沥青路面疲劳寿命修正系数[J]. 长安大学学报:自然科学版, 2011, 31(6): 21. DONG Zhonghong, LU Pengmi. Correcting factor of asphalt pavement fatigue life Considering wheel-path lateral distribution[J]. Journal of Chang'an University:Natural Science Edition, 2011, 31(6): 21. |
| [26] |
张久鹏, 黄晓明, 李辉. 重复荷载作用下沥青混合料的永久变形[J]. 东南大学学报:自然科学版, 2008, 38(3): 511. Zhang Jiupeng, Huang Xiaoming, Li Hui. Permanent deformation of asphalt mixture under repeated load[J]. Journal of Southeast University:Natural Science Edition, 2008, 38(3): 511. |
| [27] |
易军艳, SHENShihui, MUHUNTHANBalasingam, 等. 多孔沥青混合料粘弹塑性损伤模型[J]. 哈尔滨工业大学学报, 2014, 46(2): 66. YI Junyan, SHEN Shihui, MUHUNTHAN Balasingam, et al. Viscoelastic-plastic damage model of porous asphalt mixtures[J]. Journal of Harbin institute of technology, 2014, 46(2): 66. |
| [28] |
赵毅, 郭志敏, 梁乃兴. 沥青混合料永久变形黏弹性力学模型通用性研究[J]. 公路工程, 2018, 43(2): 192. ZHAO Yi, GUO Zhimin, LIANG Naixing. Research on viscoelastic mechanical universal model of permanent deformation of asphalt mixture[J]. Highway Engineering, 2018, 43(2): 192. DOI:10.3969/j.issn.1674-0610.2018.02.036 |
| [29] |
徐芝纶. 弹性力学(第5版)[M]. 北京: 高等教育出版社, 2016. XU Zhilun. Elastic mechanics (Fifth Edition)[M]. Beijing: Higher Education Press, 2016. |
| [30] |
孙立军. 沥青路面结构行为学[M]. 上海: 同济大学出版社, 2013. SUN Lijun. Structural behavior of Asphalt Pavement[M]. Shanghai: Tongji University Press, 2013. |
 2018, Vol. 50
2018, Vol. 50


