人体运动全方位和精确捕捉是新一代以人为中心的人机交互系统中的核心技术[1].目前常用的运动捕捉系统可分为两大类:光学运动捕捉(Optical Motion Capture, OMC)和机械运动捕捉(Mechanical Motion Capture, MMC)[2].上述两类系统均已有成熟的产品在市面出售,但它们均采用单一传感原理,存在着一些固有缺陷.例如带标记点的全方位高精度光学捕捉系统可实现大范围高精度运动捕捉,但系统复杂、价格昂贵且高度依赖标记点;不带标记的廉价光学系统,如Kinect系统和Xtion系列,存在视角遮挡和位置跳变问题;机械运动捕捉系统,如Xsens基于惯性测量单元(Inertial Mesurment Unit, IMU)的三维运动追踪系统存在动态漂移和累计误差明显等问题.多传感信息融合理论和技术可有效克服单一传感器的局限,近年来不少学者尝试利用深度相机(Depth Camera, 深度彩色相机又称RGB-D相机)与IMU融合的方法实现廉价且通用的人体运动全方位和精确捕捉系统[3-4],取得较好效果.
使用多传感信息融合理论和技术要先解决传感器之间的标定问题[5].国内外学者对机器人与传感器之间的标定问题已研究数十年,提出大量可行方法,其中发展最为成熟的是机器人与RGB相机之间的位姿标定.机器人与相机的位姿标定问题可概括为两大模型[6]:AX = XB和AX = YB,其中X和Y是需要求解的机器人手眼位姿转换矩阵,A和B分别使用两组对应的机器人末端位姿矩阵和相机坐标系中的物体位姿矩阵构造,均为刚体转换矩阵.需注意:上述模型只适用于机器人与RGB相机位姿固定的6自由度相对位姿标定. IMU和RGB相机的标定方法[7-10]尚未涉及深度信息,均需借助标定板且只有次优解,如分别通过IMU直接测量和RGB相机拍摄竖直放置的标定板来获取重力加速度方向向量[7],构造标定模型求得两者之间相对姿态的四元素表示.唯一见诸报道的与本文密切相关的研究深度相机与IMU标定的文献[11],其基于卡尔曼滤波器算法且无需借助标定板,传感器都固定于同一辆移动小车上,两者位置关系固定.但应用于人体运动捕捉时,传感系统布置方案为:深度相机静置于场景中,IMU则绑定于人体手臂或腿部等随之运动.换言之,IMU相对于深度相机的位姿是时变的,因而该文中标定方法并不适用.而在深度相机与IMU相对位姿时变的多传感信息融合系统中[12-13],尚未见到传感器相对姿态标定方法的报道,两者相对姿态准确性和可信性无法保证.
针对上述深度相机与IMU的相对姿态标定问题,本文提出一种通过构造同一手部位移向量继而利用最小二乘法来标定深度相机与IMU相对姿态的方法,其具有以下特点:深度相机与IMU位姿可时变;无需借助标定板或其它标定辅助设备;无需直接或者接触式测量.
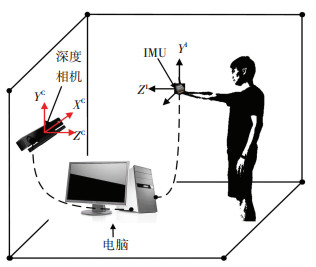
1 标定问题描述 1.1 硬件系统为研究深度相机与IMU相对姿态标定问题所搭建的运动捕捉系统见图 1.其中深度相机指代基于双目视觉、结构光或飞行时间原理,可获取物体三维空间信息的光学传感器,例如Kinect、Xtion和Leap Motion等. IMU则指集成多轴加速度计、多轴陀螺仪和磁力计的可直接测量物体在三维空间中的角速度和加速度的传感器,例如MPU9520和MTI-30等.深度相机静置于场景中,IMU绑定于人手部随手部在空间运动,即IMU相对于深度相机可自由运动.深度相机与IMU均可实时向计算机传输数据;而两者之间无直接连接或者数据共享;计算机中有自主开发的上位机软件,负责采集深度相机和IMU数据,并求解相对姿态.
|
图 1 运动捕捉系统结构示意 Figure 1 Schematic diagram of motion capture system |
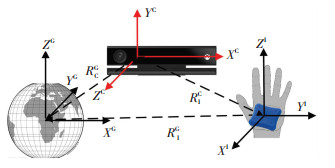
图 2设深度相机和IMU的坐标系分别用{C}与{I}表示,则两者之间相对姿态参数可用欧拉角姿态表示法表示:RIC=(Rz(φ), Ry(θ), Rx(ψ)).标定问题即为求解{C}与{I}之间位置关系不固定,相对位姿不断变化,故而难以直接获知RIC.
|
图 2 传感器和地磁场坐标系 Figure 2 Coordinate systems of sensors and geomagnetic field |
9轴IMU中带有地磁计,在没有外部磁场干扰的情况下,它可以自动校准{I}坐标系与地磁场坐标系(也称Global坐标系,用{G}表示)之间相对姿态信息,每一时刻{I}与{G}之间相对姿态可直接通过IMU读取.固定RGB-D相机位置,可唯一确定{C}与{G}之间相对姿态关系RCG.因此,可以通过旋转矩阵之间的闭环转换求取RIC为
| $ \mathit{\boldsymbol{R}}_{\rm{I}}^{\rm{C}} = {\left( {\mathit{\boldsymbol{R}}_{\rm{C}}^{\rm{G}}} \right)^{ - 1}}\mathit{\boldsymbol{R}}_{\rm{I}}^{\rm{G}}. $ | (1) |
式中右侧待确定的变量只有RCG.因此,深度相机与IMU相对标定问题可转化为求取{C}与{G}之间相对姿态关系RCG.
2 标定方法 2.1 标定方法分析将RCG看作{C}与{G}之间缺省位移信息的外参标定矩阵,可通过构造{C}与{G}之间对应关系(Correspondence)求取RCG.描述为
| $ {\mathit{\boldsymbol{M}}^{\rm{G}}} = \mathit{\boldsymbol{R}}_{\rm{C}}^{\rm{G}}{\mathit{\boldsymbol{M}}^{\rm{C}}} \Rightarrow \mathit{\boldsymbol{R}}_{\rm{C}}^{\rm{G}} = {\mathit{\boldsymbol{M}}^{\rm{G}}}{\left( {{\mathit{\boldsymbol{M}}^{\rm{C}}}} \right)^{ - 1}}. $ |
式中:MG为{C}中3个位移向量组成的向量组,每一列代表一个向量;MG则是由MC经过旋转矩阵RCG转换后在{G}中的位移向量组.当已知了MC和MG后即可通过以上关系求解出RCG.
IMU可提供加速度、角速度等信息,深度相机可提供手心相对于{C}的空间位置信息[14].可以通过向任意方向挥动手部来构造{C}与{G}中的位移向量,从而获得上述的对应向量组MG和MC.
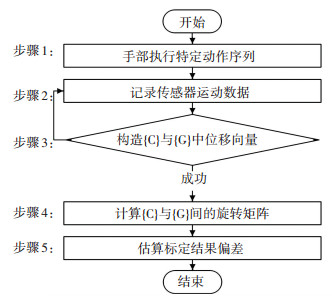
本文提出的标定方法基本操作步骤如图 3所示,分为5个步骤:
|
图 3 标定方法操作步骤流程图 Figure 3 Operation flow chart of the calibration method |
步骤1 手部按照特定序列运动产生运动信息作为系统输入.该特定序列旨在能更准确地判断手部位移方向,如运动系列“静止tb时间→运动→静止te时间”,其中静止段是为了让传感器数据在起止点有足够时间稳定下来.
步骤2 上位机软件每隔一个时间周期记录一次传感器返回数据,包括深度相机中手心位置、IMU中加速度和欧拉角信息、以及相应时间戳等.
步骤3 分别从深度相机与IMU原始数据中提取出位移信息构造位移向量;但当IMU信号长时间不稳定,不能满足判断条件时,将判断为失败.
步骤4 利用最小二乘法构造旋转矩阵求解模型,结合奇异值分解(Singular Value Decomposition, SVD)计算最优旋转矩阵,并得到相对姿态欧拉角.
步骤5 利用n对{C}与{G}中对应位移向量以3对一组的组合方式求解出的Cn3组欧拉角的最小化误差平方和,用于估算结果的偏差程度;该值会随着向量对数量的增加而逐渐趋于稳定,而达到稳态所需的向量对数量与传感器精度有关.
2.2 位移向量构造与提取{C}中位移向量DC可用运动后手心位置与开始时手心位置相减获得.取前后静止时段平均位置值计算DC,以期获得较为准确的位移向量.
构造{G}中位移向量DG的方法分3步:
第1步,使用式(3)将加速度从{I}映射到{G}
| $ {\mathit{\boldsymbol{A}}^{\rm{G}}} = \mathit{\boldsymbol{R}}_{\rm{I}}^{\rm{G}}{\mathit{\boldsymbol{A}}^{\rm{I}}} - \mathit{\boldsymbol{g}}. $ | (3) |
式中:AG是{G}中加速度向量;AI是从IMU中读取的加速度向量;g是{G}坐标系中的重力加速度向量,即 g=[0, 0, g]T.
第2步,准确找出运动段所对应启停时刻.标定算法的估计性能会随着原始数据观测噪声增大而迅速恶化[15].由于IMU固有漂移(Drift)现象,其观测时间越长,积分值可信度越低,所以从原始数据中准确找到运动段启停时间点对提取出准确的位移方向向量至关重要.
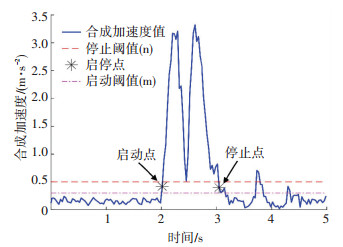
本文使用IMU的合成加速度信息,通过设定阈值的方法识别运动段启停点,如图 4.第i点合成加速度ai满足式(4)即为启动点为
| $ \left\{ \begin{array}{l} b = 0,\\ {t_i} \ge {t_{\rm{b}}},\\ \min \left( {{a_i},{a_{i + 1}},{a_{i + 2}}} \right) > m. \end{array} \right. $ | (4) |
|
图 4 运动启停点示意 Figure 4 Sketch map of start and stop points of the movement |
式中:ti为i时刻时间值;b为表征运动状态的布尔值,0和1分别为运动尚未开始和运动中;m为启动阈值.同理,满足式(5)即为停止点为
| $ \left\{ \begin{array}{l} b = 1,\\ {t_k} - {t_i} < {t_{\rm{e}}},\\ \max \left( {{a_i}, \cdots ,{a_k}} \right) \le n. \end{array} \right. $ | (5) |
式中n为停止阈值,启停点的加速度阈值与IMU精度有关,因而需要根据具体传感器决定.
第3步,使用式(6)和(7)求解每一时刻位移:
| $ \mathit{\boldsymbol{V}}_i^{\rm{G}} = \mathit{\boldsymbol{V}}_{i - 1}^{\rm{G}} + {\mathit{\boldsymbol{A}}^{\rm{G}}}{T_i}, $ | (6) |
| $ \mathit{\boldsymbol{D}}_i^{\rm{G}} = \mathit{\boldsymbol{D}}_{i - 1}^{\rm{G}} + \mathit{\boldsymbol{V}}_{i - 1}^{\rm{G}}{T_i} + \frac{1}{2}{\mathit{\boldsymbol{A}}^{\rm{G}}}T_i^2. $ | (7) |
式中:ViG为i时刻速度向量,Ti为从i-1时刻到i时刻之间时间间隔.通过式(6)得到i时刻速度,用于i+1时刻位移向量求解;式(7)综合i-1时刻位移、速度与加速度求得i时刻位移向量DiG.如此循环可构造出{G}中手部运动段位移向量DG.
2.3 旋转矩阵求解根据式(2),只需3组对应向量可求解一个旋转矩阵,但受测量噪声影响,会偏离很大.借鉴文献[16],基于刚体运动在不同笛卡尔测量坐标系下描述的不变性构造标定求解模型,然后用最小二乘法解算深度相机与IMU相对姿态旋转矩阵,见式(8), R属于特殊正交群(Special Orthoganal, SO).
| $ \mathit{\boldsymbol{R}} = \mathop {\arg \min }\limits_{R \in SO\left( 3 \right)} \sum\limits_{t = 1}^n {{{\left\| {\mathit{\boldsymbol{RD}}_t^{\rm{C}} - \mathit{\boldsymbol{D}}_t^{\rm{G}}} \right\|}^2}} . $ | (8) |
具体的解算过程包括如下4步:
1) 计算权重中心向量
| $ \mathit{\boldsymbol{\bar p}} = \frac{{\sum\nolimits_{i = 1}^n {\mathit{\boldsymbol{D}}_i^{\rm{C}}} }}{n},{\mathit{\boldsymbol{x}}_i} = \mathit{\boldsymbol{D}}_i^{\rm{C}} - \mathit{\boldsymbol{\bar P}}. $ |
2) 计算中心向量
| $ {\mathit{\boldsymbol{x}}_i} = \mathit{\boldsymbol{D}}_i^{\rm{C}} - \mathit{\boldsymbol{\bar P}},{\mathit{\boldsymbol{y}}_i} = \mathit{\boldsymbol{D}}_i^{\rm{G}} - \mathit{\boldsymbol{\bar q}},i = 1,2, \cdots ,n. $ |
3) 计算协方差矩阵
| $ \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{X}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}. $ |
式中X和Y分别为由xi和yi组成的3×n矩阵.
4) 计算奇异值分解矩阵S= U∑VT,V为S原始域的标准正交基,U为S变换后协同域(Co-domain)标准正交基.可得旋转矩阵为
| $ \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{V}}\left( {\begin{array}{*{20}{c}} 1&{}&{}\\ {}&1&{}\\ {}&{}&{\det \left( {\mathit{\boldsymbol{V}}{\mathit{\boldsymbol{U}}^{\rm{T}}}} \right)} \end{array}} \right){\mathit{\boldsymbol{U}}^{\rm{T}}}. $ |
目前,缺乏有效方法精确测量深度相机与地磁场之间相对姿态关系,因而不能为标定结果提供真值(Ground Truth).因本文对IMU的姿态解算使用卡尔曼滤波算法,其误差符合高斯分布,因此可以通过对仿真数据添加高斯白噪声模拟测量误差(以下统称随机误差)的方法设置仿真对比组,验证标定算法准确性.
假定深度相机坐标系{C}与地磁坐标系{G}之间理想RPY角为(90°,0°,0°).首先随机产生{C}中位移向量,然后转换到{G}中,再对{G}中位移向量加上随机误差即可以得到仿真位移向量组.根据式(2),每次采集15组位移向量,每3组成的位移矩阵即可求出一组欧拉角,则每次可求得C153=455组欧拉角;最后用最小二乘法取误差平方和最小的一组,作为优选的欧拉角,即
| $ \begin{array}{l} \left( {\varphi ,\theta ,\psi } \right) = \mathop {\arg \min }\limits_{i \in \left[ {1,n} \right],i \in R} \sum\limits_{j = 1,j \ne i}^n {\left( {{{\left( {{\varphi _i} - {\varphi _j}} \right)}^2} + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left( {{\theta _i} - {\theta _j}} \right)}^2} + {{\left( {{\psi _i} - {\psi _j}} \right)}^2}} \right) \end{array} $ |
式中φ, θ, ψ对应Roll, Pitch, Yaw.同时将最小误差平方和作为描述离散程度的指标.
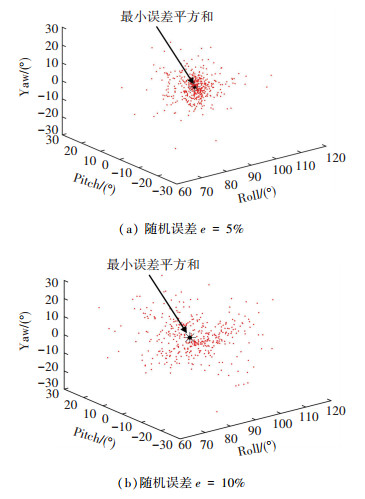
图 5是分别加上5%和10%随机误差的仿真结果,黑星与红点分别表示优选组和其余欧拉角组合.子图(a)和(b)黑星对应误差平方和分别为8.12×104和4.18×105,欧拉角误差平方和随机数据噪声增大而增大.可以利用该值来表征原始数据的测量误差程度,进而获得最终标定结果偏差大小.
|
图 5 不同随机误差对应的欧拉角分布 Figure 5 Euler angle distribution corresponding to different random errors |
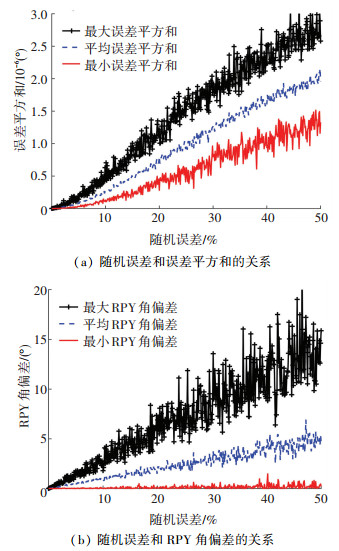
通过设置随机误差大小,0.1%为一个步长,每个步长测量5次,每次采集45组位移向量,构造式(8)最小二乘模型,求得旋转矩阵,进而得到欧拉角;为减少计算量将45组向量平均分为3个部分,每个部分求解一个最小误差平方和.然后分别获得每个步长中的最小误差平方和与最终解算的欧拉角偏差的最小、最大和平均值,见图 6.
|
图 6 随机误差和RPY角与误差平方和的关系 Figure 6 Relation between random errors and RPY angles and error sum squares |
最小误差平方和大小和最终角度偏差均与测量误差正相关.可以用图 6作为参考标准,实际标定时以查表的方式来确定结果偏差大小;其中根据图 6(a)对照最小误差平方和大小可表征原始数据的测量噪声大小,再根据图 6(b)利用测量噪声大小确定最终解算欧拉角偏差大小.
3 实验本文设计了两个实验,侧面验证本标定算法的精确性和可用级IMU搭建实验平台,其中IMU分辨率为Roll和Pitch人体骨架信息刷新频率为30 FPS基于MFC开发的运动信息读取软件,可同时读取和记录Kinettz与IMU数据读取一次数据的时间周期约为31.25 ms.
3.1 实验一每次采集45组位移向量,共进行5次实验.将45组向量平均分成A、B、C3个部分,根据卡尔曼滤波算法分别计算一个最小误差平方和. 5次实验结果如表 1所示.表中α表示最小误差平方和, 其中黑体字为误差平方和的最大值和最小值.
| 表 1 相对姿态角实验解算值 Table 1 Experimental results of relative attitude angles |
15个最小误差平方和的平均值为3.38×105,最小和最大值分别为1.57×105和4.30×105.对比图 7(a),原始数据误差范围在8%到10%之间,再根据图 6(b)最大角度偏差为4°(±4°). 表 1中Roll平均值83.154°,第2次和第4次实验所解算的Roll之间差值最大,与均值最大偏差为(-2.984°, +2.866°),符合上述的最大角度偏差范围.
|
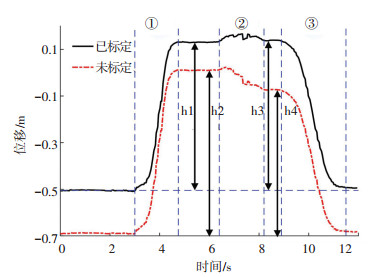
图 7 Global坐标系下Z方向位移 Figure 7 Z-direction displacement in Global coordination system |
综上所述,本标定方法可以得到一个较为精确的深度相机与IMU相对姿态解算值.
3.2 实验二实验者站在Kinect2前面,按照以下动作序列执行:手自然下垂→向前抬手且手心朝下,手臂尽量平行于地面→向右平行于地面旋转手臂→手自然放下. 图 7中所示黑色实线表示地磁场坐标系{G}中Z轴方向空间位置信息,由Kinect2所测得的手心空间位置根据实验一中求得的相对姿态均值转换后所得,该均值用欧拉角姿态表示法描述为(83.154°, 2.726°, 7.628°).红色点划线是使用IMU人工估计的欧拉角(90°, 0°, 0°)转换所得.第①~③阶段分别对应抬手臂、向右旋转手臂和放下手臂3个阶段(见图 7),其他时段均为静止阶段.手抬起的位置以墙面的标记位为参考点,该标记位根据实验者的臂长预先设置.实验者手心到肩膀长度约为63 cm,手臂抬起时尽量与地面平行且手心朝下,设置手部下垂标记位与抬手后标记位垂直高度为63 cm.
图 7中h1= 63.5 cm,h2= 69.9 cm,h3=64.4 cm,h4= 61.6 cm.可见当手臂与地面平行时,标定后结果h1和h3更为接近标记位距离,且在手臂平行地面向右旋转后h4比h2明显减少,这与实验过程不符.因此,标定后结果明显优于未经标定结果,实验二有效验证了该标定算法可信性.
4 结论基于深度相机和IMU的数据融合有望解决单一传感原理的不足,其应用之一即为提升人体双手臂全方位和精确捕捉系统的性能,继而为人机交互和体感游戏等提供新的运动捕捉技术.两者之间相对姿态标定则是开展数据融合工作的基础.
本文针对一类位姿时变但需进行数据融合的深度相机和IMU之间相对姿态标定问题进行了研究,提出一种通过两传感器同时捕捉手部同一运动的方向向量构造标定模型并使用最小二乘法求解最优相对姿态矩阵的方法;同时由于无法对标定结果提供真值,本文还提出一种方法对标定效果进行评价;首先使用n组位移向量组合产生Cn3组欧拉角,然后取所有欧拉角相互之间的最小误差平方和作为参考指标.此外,实验一表明该标定方法可以求得最大角度偏差在4°以内的相对姿态欧拉角;实验二表明使用该标定结果进行手部位置跟踪能获得比无标定结果精度高6.4 cm的结果.
本文所提出的标定方法具有原理简单、易于操作、精度较高、无需额外标定辅助设备、无需接触测量等特点,可应用于机器人远程操纵和体感游戏设备校准等任务.但相对姿态解算结果的精确程度会随位移向量的测量误差线性增长,需要使用精度较高的传感器.
未来的研究工作将会探索通过改进方向向量提取方法从当前传感器数据中提取出精度更高的方向向量,从而提高相对姿态解算精度;同时会将本方法应用于人机交互系统中,实现人类双手臂到双机器人操作任务的远程控制.
| [1] |
徐光佑, 陶霖密, 邸慧军. 人机交互中的体态语言理解[M]. 北京: 电子工业出版社, 2014: 201. XU Guangyao, TAO Linmi, DI Huijun. Body language understanding for human computer interaction[M]. Beijing: Publishing House of Electronics Industry, 2014: 201. |
| [2] |
SICILIANO B, KHATIB O. Springer handbook of robotics[M]. Berlin, Germany: Springer, 2016: 1820.
|
| [3] |
TIAN Yushuang, MENG Xiaoli, TAO Dapeng, et al. Upper limb motion tracking with the integration of IMU and Kinect[J]. NEUROCOMPUTING, 2015, 159(C): 207. DOI:10.1016/j.neucom.2015.01.071 |
| [4] |
CHEN C, JAFARI R, KEHTARNAVAZ N. A survey of depth and inertial sensor fusion for human action recognition[J]. Multimedia Tools & Applications, 2016, 1. DOI:10.1007/s11042-015-3177-1 |
| [5] |
MITCHELL H B. Data fusion: concepts and ideas[M]. Berlin, Germany: Springer, 2012.
|
| [6] |
SHAH M, EASTMAN R D, HONG T. An overview of robot-sensor calibration methods for evaluation of perception systems[C/OL]//NIST, 2012 Performance Metrics for Intelligent Systems Workshop. (2012-3-20)[2017-7-18] https://www.nist.gov/publications/overview-robot-sensor-calibration-methods-evaluation-perception-systems?pub_id=910651
|
| [7] |
LOBO J, DIAS J. Relative pose calibration between visual and inertial sensors[J]. International Journal of Robotics Research, 2007, 26(6): 561. DOI:10.1177/0278364907079276 |
| [8] |
MIZAEI F M, ROUMELIOTIS S I. A kalman filter-based algorithm for imu-camera calibration: observability analysis and performance evaluation[J]. IEEE Transactions on Robotics, 2008, 24(5): 1143. DOI:10.1109/TRO.2008.2004486 |
| [9] |
KELLY J, SUKHATME G S. Visual-inertial sensor fusion: localization, mapping and sensor-to sensor self-calibration[J]. International Journal of Robotics Research, 2011, 30(1): 56. DOI:10.1177/0278364910382802 |
| [10] |
STEPHAN W, MARKUS W A, SIMON L, et al. Real-time onboard visual-inertial state estimation and self-calibration of MAVs in unknown environments[C]//IEEE International Conference on Robotics and Automation, Saint Paul, Minnesota, 2012: 957.
|
| [11] |
GUO C X, ROUMELIOTIS S I. IMU-RGBD camera 3D pose estimation and extrinsic calibration: observability analysis and consistency improvement[C]//IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 2013: 2935
|
| [12] |
FENG S M, RODERICK M S. Fusing kinect sensor and inertial sensors with multi-rate kalman filter[C]// IET Conf. on Data Fusion & Target Tracking: Algorithms & Applications, Liverpool, United Kingdom, 2014: 1
|
| [13] |
卢晓敏.基于混合传感器的机器人人机交互技术研究[D].广州: 华南理工大学, 2014 LU Xiaomin. The research of human-robot interaction technology based on hybrid sensors[D]. Guangzhou, South China University of Technology, 2014 |
| [14] |
SHOTTON J, FITZGIBBON A, COOK M, et al. Real-time human pose recognition in parts from single depth images[C]// IEEE Conference on Computer Vision and Pattern Recognition. Colorado, United States, IEEE Computer Society, 2011: 1297
|
| [15] |
王君臣, 王田苗, 杨艳, 等. 基于无迹卡尔曼滤波的机器人手眼标定[J]. 北京:机器人, 2011, 33(5): 621. WANG Junchen, WANG Tianmiao, YANG Yan, et al. Robot hand-eye calibration using unscented kalman filtering[J]. Beijing: ROBOT, 2011, 33(5): 621. DOI:10.3724/SP.J.1218.2011.00621 |
| [16] |
UMEYAMA S. Least-squares estimation of transforma-tion parameters between two point patterns[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(4): 376. DOI:10.1109/34.88573 |
 2018, Vol. 50
2018, Vol. 50


