2. 兰州交通大学 甘肃省人工智能与图形图像处理工程研究中心, 兰州 730070
2. Gansu Provincial Engineering Research Center for Artificial Intelligence and Graphics & Image Processing Lanzhou Jiaotong University, Lanzhou 730070, China
图像融合是把多个传感器中相关联的互补信息进行有效地提取,获得一幅信息更加丰富全面的综合图像.其中,多聚焦图像融合是图像融合领域中的一个重要分支.由于目前光学传感器的景深有限,很难获取到一幅所有景物同时聚焦的图像.多聚焦图像融合能对多幅聚焦点不同的图像进行融合,得到一幅所有景物均聚焦清晰的图像.目前,多聚焦图像融合已在数码摄影、计算机视觉、目标跟踪监测和显微成像等领域具有广泛的应用前景[1-2].
近年来,由于多分辨率分析变换能更好地提取源图像的细节等信息,基于多分辨率分析变换的多聚焦图像融合方法得到广泛应用.小波变换凭借其良好的时频局部特性,取得较好的融合效果,但小波变换只能提取有限方向上的多聚焦源图像信息,不能有效地提取多聚焦源图像的纹理、边缘等细节信息.针对小波变换存在的缺陷,Do等[3]提出的Contourlet变换弥补了小波变换存在的缺陷.因此,在图像融合领域中基于Contourlet变换的图像融合算法得到广泛的研究.研究学者们发现基于Contourlet变换的图像融合算法容易产生伪吉布斯现象,这是由于Contourlet变换不具备平移不变性所造成的.为解决Contourlet变换存在的缺点,Da等[4]提出非下采样Contourlet变换. Qu等[5]提出在NSCT域内用SF和PCNN相结合的图像融合方法;谢秋莹等[6]提出一种基于SML和PCNN的NSCT域多聚焦图像融合算法.由于NSCT变换分解的方向数有限,造成融合图像丢失部分细节信息.针对这一问题,Easley等[7]提出分解方向数无限的非下采样Shearlet变换(Nonsubsampled Shearlet Transform, NSST). NSST变换具有良好的局部时频特性、多方向性和平移不变性,与NSCT变换相比,NSST变换解决NSCT变换分解方向数受限的问题.因此,基于NSST变换的多聚焦图像融合算法,可以更加有效地提取源图像中的边缘纹理等细节信息,取得更佳的融合效果.邢雅琼等[8]提出一种基于NSST域灰度关联分析的多聚焦图像融合算法,该算法有效地提高融合图像的质量;杨勇等[9]提出一种基于NSST与稀疏表示的多聚焦图像融合算法,该算法有效地减少融合图像的伪吉布斯现象;为避免引入虚假信息,Gao等[10]提出一种基于NSST变换的多聚焦图像融合算法;为较好地保留源图像的细节信息,Huang等[11]提出一种基于不同约束条件与NSST变换相结合的图像融合算法.引导滤波器因为具有保边平滑特性[12],可以较好地保留源图像的轮廓、细节和纹理等信息.
因此,本文将NSST变换与引导滤波的优势相结合,提出一种NSST与引导滤波相结合的多聚焦图像融合算法.首先,利用NSST变换对源图像进行多尺度、多方向分解;其次,针对低频和高频子带系数的特点,利用引导滤波修正初始融合权重,采用不同的引导滤波加权融合规则对低频和高频子带系数进行融合处理;最后,进行NSST逆变换,获得融合图像.仿真结果表明,本文算法使最终的融合图像保留了丰富的轮廓、细节和纹理等信息,同时也提高融合图像的对比度和清晰度.
1 非下采样Shearlet变换由于Shearlet变换不具备平移不变性,Easley等[7]在Shearlet变换的基础上进行改进,提出非下采样Shearlet变换—简称NSST变换. NSST变换是通过非下采样金子塔(Nonsubsampled Pyramid,NSP)和基于改进的剪切波滤波器组(Shearlet Filter, SF)来实现对一幅图像的多尺度分解和方向分解.见图 1所示,首先NSST变换利用NSP对多聚焦源图像进行K级分解,得到低频和高频子带系数;其次,再通过改进的shear滤波器组对高频子带系数进行多方向分解;最终,分解得到一个低频子带系数和K个高频子带系数.

|
图 1 NSST变换的分解示意图 Figure 1 Schematic diagram of NSST transform |
He等[12]在2010年首次提出一个局部线性滤波器—引导滤波器.引导滤波器作为一种保边平滑滤波器,在滤除图像噪声的同时,还具有良好的边缘平滑功能和边缘梯度保持特性.
将引导滤波器的引导图像记为G,滤波输入图像记为I,滤波输出图像记为O.假设,O和G在窗口wm中存在局部线性关系(wm以像素m为中心,r为半径).即O是G在窗口wm中的局部线性变换,则
| $ {\mathit{\boldsymbol{O}}_j} = {a_m}{\mathit{\boldsymbol{G}}_j} + {b_m},\;\;\;\;\forall j \in {\mathit{\boldsymbol{w}}_m}. $ | (1) |
式中:j和m为像素索引,am和bm为式1的线性系数,且在局部窗口wm中为常数.线性系数am和bm的确定需要通过式2对O进行约束,即希望得到I和O之间的最小差值,记为E:
| $ \mathit{\boldsymbol{E}}\left( {{a_m},{b_m}} \right) = \sum\limits_{j \in {w_m}} {\left( {{{\left( {{a_m}{\mathit{\boldsymbol{G}}_j} + {b_m} - {\mathit{\boldsymbol{I}}_j}} \right)}^2} + \varepsilon {a_m}^2} \right)} . $ | (2) |
式中:ε>0,ε的作用是为防止求得过大的am而引入的正则化参数;Ij表示输入图像I的一个像素j,其中j∈ wm.通过最小二乘法,可以求出线性系数am和bm:
| $ {a_m} = \frac{{\frac{1}{{\left| w \right|}}\sum\nolimits_{j \in {w_m}} {{\mathit{\boldsymbol{G}}_j}{\mathit{\boldsymbol{I}}_j} - {\mu _m}\overline {{I_m}} } }}{{{\sigma _m}^2 + \varepsilon }}, $ | (3) |
| $ {b_m} = \overline {{I_m}} - {a_m}{\mu _m}. $ | (4) |
式中:μm和σm2是G在wm中的均值和方差,|w|是wm中像素的个数,
| $ {\mathit{\boldsymbol{O}}_j} = \overline {{a_j}} {\mathit{\boldsymbol{G}}_j} + \overline {{b_j}} . $ | (5) |
式中:
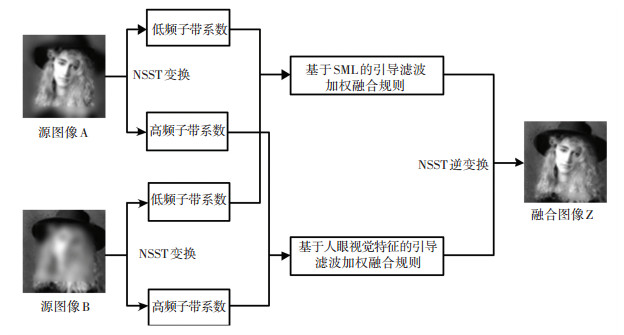
本文算法将NSST变换和引导滤波相结合,来实现不同聚焦源的图像融合.设A和B为输入的两幅聚焦源不同的多聚焦图像,Z为最终的融合图像.思路框图见图 2.
|
图 2 本文算法思路框图 Figure 2 Schematic diagram of the proposed algorithm |
具体的融合步骤如下:
步骤1 利用NSST变换对图像A和B进行分解,获得低频子带系数{Do, kA, Do, kB}和高频子带系数{De, kA, De, kB};
步骤2 针对低频子带系数{Do, kA, Do, kB},设计一种基于局部区域改进拉普拉斯能量和的引导滤波加权融合规则;针对高频子带系数{De, kA, De, kB},根据其显著信息、局部区域平均梯度、边缘信息和局部区域改进拉普拉斯能量和,设计一种基于人眼视觉特征的引导滤波加权融合规则;
步骤3 进行NSST逆变换,获得融合图像Z.
3.2 融合规则 3.2.1 低频子带系数的融合规则低频子带系数主要是源图像的大部分能量和近似信息,而拉普拉斯能量和在一定程度上能恰当的反映源图像的聚焦特性.因此,为使最终的融合图像更加符合人眼的视觉特征,通过计算低频子带系数的局部区域的改进拉普拉斯能量和(Sum Modified Laplacian, SML)能够得到一幅聚焦良好的融合图像.
首先,用基于局部区域的改进拉普拉斯能量和来衡量低频子带系数的聚焦程度,计算公式为
| $ \mathit{\boldsymbol{SML}}_{o,k}^i = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left( {\mathit{\boldsymbol{ML}}_{o,k}^i\left( {x + m,y + n} \right)} \right)}^2}} } . $ | (6) |
式中:SMLo, ki为第i幅图像(1≤i≤L)在局部区域M*N下的改进拉普拉斯能量和,本文取M*N=3*3. MLo, ki(x, y)为在位置(x, y)的改进拉普拉斯能量,计算公式为
| $ \begin{array}{l} \mathit{\boldsymbol{ML}}_{o,k}^i\left( {x,y} \right) = \left| {2\mathit{\boldsymbol{D}}_{o,k}^i\left( {x,y} \right) - \mathit{\boldsymbol{D}}_{o,k}^i\left( {x - 1,y} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{D}}_{o,k}^i\left( {x + 1,y} \right)} \right| + \left| {2\mathit{\boldsymbol{D}}_{o,k}^i\left( {x,y} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{D}}_{o,k}^i\left( {x,y - 1} \right) - \mathit{\boldsymbol{D}}_{o,k}^i\left( {x,y + 1} \right)} \right| + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {1.6\mathit{\boldsymbol{D}}_{o,k}^i\left( {x,y} \right) - 0.8\mathit{\boldsymbol{D}}_{o,k}^i\left( {x - 1,y + } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. 1 \right) - 0.8\mathit{\boldsymbol{D}}_{o,k}^i\left( {x + 1,y - 1} \right)} \right| + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {1.6\mathit{\boldsymbol{D}}_{o,k}^i\left( {x,y} \right) - 0.8\mathit{\boldsymbol{D}}_{o,k}^i\left( {x - 1,y - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. 1 \right) - 0.8\mathit{\boldsymbol{D}}_{o,k}^i\left( {x + 1,y + 1} \right)} \right|. \end{array} $ | (7) |
对获得的低频子带系数的局部区域的改进拉普拉斯能量和进行加权映射,构造初始聚焦度融合权重
| $ \begin{array}{l} \mathit{\boldsymbol{M}}_{o,k}^i\left( b \right) = \\ \left\{ \begin{array}{l} 1,\mathit{\boldsymbol{SML}}_{o,k}^i\left( b \right) = \max \left( {\mathit{\boldsymbol{SML}}_{o,k}^1\left( b \right),\mathit{\boldsymbol{SML}}_{o,k}^2\left( b \right), \cdots ,\mathit{\boldsymbol{SML}}_{o,k}^L\left( b \right)} \right);\\ 0,{\rm{otherwise}}{\rm{.}} \end{array} \right. \end{array} $ | (8) |
式中SMLo, ki(b)为第i幅图像中第b个像素的清晰度信息.
本文采用复杂度较低并且具有边缘保持特性的引导滤波器对初始聚焦度融合权重进行修正,将Do, ki作为引导图像,Mo, ki作为滤波输入图像,则:
| $ \mathit{\boldsymbol{Z}}_{o,k}^i = {\rm{guidefilter}}\left( {\mathit{\boldsymbol{D}}_{o,k}^i,\mathit{\boldsymbol{M}}_{o,k}^i,r1,eps1} \right). $ | (9) |
式中:r1为引导滤波器窗口的大小,eps1为模糊度.其次,为通过取大策略获得最终的融合权重
| $ \begin{array}{l} \mathit{\boldsymbol{W}}_{o,k}^i\left( b \right) = \\ \left\{ \begin{array}{l} 1,\mathit{\boldsymbol{Z}}_{o,k}^i\left( b \right) = \max \left( {\mathit{\boldsymbol{Z}}_{o,k}^1\left( b \right),\mathit{\boldsymbol{Z}}_{o,k}^2\left( b \right), \cdots ,\mathit{\boldsymbol{Z}}_{o,k}^L\left( b \right)} \right);\\ 0,{\rm{otherwise}}{\rm{.}} \end{array} \right. \end{array} $ | (10) |
最后,则融合图像的低频子带系数Do, kZ为
| $ \mathit{\boldsymbol{D}}_{o,k}^Z = \sum\limits_{i = 1}^L {\overline {\mathit{\boldsymbol{W}}_{o,k}^i} \mathit{\boldsymbol{D}}_{o,k}^i} . $ | (11) |
式中
高频子带系数主要是源图像的轮廓、细节及纹理等信息,对高频子带系数的处理直接影响到融合图像的清晰度、对比度和信息丰富度.考虑到人眼视觉系统的特点,通过提取高频子带系数的显著信息、局部区域清晰度、边缘信息和局部区域改进拉普拉斯能量和来构建初始融合权重,并根据引导滤波修正初始融合权重,提出一种基于人眼视觉特征的引导滤波加权融合规则.首先对高频子带系数进行处理,得到高通图像
| $ \mathit{\boldsymbol{H}}_{e,k}^i = \left| {\mathit{\boldsymbol{D}}_{e,k}^i - \mathit{\boldsymbol{D}}_{e,k}^i * \mathit{\boldsymbol{LP}}} \right|. $ | (12) |
式中:De, ki为第i幅源图像(1≤i≤L)在尺度k上第e方向的高频子带系数. LP为3*3的双向拉普拉斯滤波器,计算公式为
| $ \mathit{\boldsymbol{LP}} = \frac{{1 - \alpha }}{{1 + \alpha }}\left[ {\begin{array}{*{20}{c}} 0&1&0\\ 1&{ - 4}&1\\ 0&1&0 \end{array}} \right] + \frac{\alpha }{{1 + \alpha }}\left[ {\begin{array}{*{20}{c}} 1&0&1\\ 0&{ - 4}&0\\ 1&0&1 \end{array}} \right]. $ | (13) |
式中α∈[0, 1],本文中α的取值为0.7.然后对He, ki进行高斯滤波并取其绝对值,构造高频子带系数的显著性映射Se, ki
| $ \mathit{\boldsymbol{S}}_{e,k}^i = \left| {\mathit{\boldsymbol{H}}_{e,k}^i * \mathit{\boldsymbol{g}}} \right|. $ | (14) |
式中g为11*11的标准差为5的高斯低通滤波器.接着利用显著性映射构造加权映射,获得初始显著性融合权重
| $ \begin{array}{l} \mathit{\boldsymbol{U}}_{e,k}^i\left( b \right) = \\ \left\{ \begin{array}{l} 1,\mathit{\boldsymbol{S}}_{e,k}^i\left( b \right) = \max \left( {\mathit{\boldsymbol{S}}_{e,k}^1\left( b \right),\mathit{\boldsymbol{S}}_{e,k}^2\left( b \right), \cdots ,\mathit{\boldsymbol{S}}_{e,k}^L\left( b \right)} \right);\\ 0,{\rm{otherwise}}{\rm{.}} \end{array} \right. \end{array} $ | (15) |
式中Se, ki (b)为第i幅源图像中第b个像素的显著性.
清晰度是人眼视觉特征中的一个重要指标,因此本文对高频子带系数进行清晰度衡量可获得一幅清晰度较好的融合图像.本文用基于局部区域的平均梯度(Average Gradient, AG)来衡量高频子带系数的清晰度,获得局部清晰度图为
| $ \begin{array}{l} \mathit{\boldsymbol{AG}}_{e,k}^i = \frac{1}{{\left( {M - 1} \right)\left( {N - 1} \right)}}\sum\limits_{m = 1}^{M - 1} {\sum\limits_{n = 1}^{N - 1} {} } \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left( {\frac{{\mathit{\boldsymbol{R}}\left( {x + m,y + n} \right) + \mathit{\boldsymbol{C}}\left( {x + m,y + n} \right)}}{2}} \right)^{1/2}}, \end{array} $ | (16) |
| $ \mathit{\boldsymbol{R}}\left( {x,y} \right) = {\left( {\mathit{\boldsymbol{D}}_{e,k}^i\left( {x + 1,y} \right) - \mathit{\boldsymbol{D}}_{e,k}^i\left( {x,y} \right)} \right)^2}, $ | (17) |
| $ \mathit{\boldsymbol{C}}\left( {x,y} \right) = {\left( {\mathit{\boldsymbol{D}}_{e,k}^i\left( {x,y + 1} \right) - \mathit{\boldsymbol{D}}_{e,k}^i\left( {x,y} \right)} \right)^2}. $ | (18) |
式中:M*N为局部区域的大小,本文取M*N=3*3,R (x+m, y+n)代表以(x, y)为中心的局部区域的x方向上的梯度,C (x+m, y+n)代表以(x, y)为中心的局部区域的y方向上的梯度.对获得高频子带系数的局部清晰度图AGe, ki进行加权映射,构建初始清晰度融合权重
| $ \begin{array}{l} \mathit{\boldsymbol{R}}_{e,k}^i\left( b \right) = \\ \left\{ \begin{array}{l} 1,\mathit{\boldsymbol{AG}}_{e,k}^i\left( b \right) = \max \left( {\mathit{\boldsymbol{AG}}_{e,k}^1\left( b \right),\mathit{\boldsymbol{AG}}_{e,k}^2\left( b \right), \cdots ,\mathit{\boldsymbol{AG}}_{e,k}^L\left( b \right)} \right);\\ 0,{\rm{otherwise}}{\rm{.}} \end{array} \right. \end{array} $ | (19) |
式中AGe, ki(b)表示高频子带系数的第b个像素的清晰度.
为丰富最终融合图像的边缘信息,提出一种边缘信息的融合方案.首先,提取高频子带系数的边缘信息,即
| $ \mathit{\boldsymbol{E}}_{e,k}^i = {\left( {{\mathit{\boldsymbol{V}}_1} * \mathit{\boldsymbol{D}}_{e,k}^i} \right)^2} + {\left( {{\mathit{\boldsymbol{V}}_2} * \mathit{\boldsymbol{D}}_{e,k}^i} \right)^2} + {\left( {{\mathit{\boldsymbol{V}}_3} * \mathit{\boldsymbol{D}}_{e,k}^i} \right)^2}. $ | (20) |
式中*为卷积操作,
接着,利用提取的边缘信息Ee, ki构造加权映射,构建初始边缘信息融合权重Ge, ki
| $ \begin{array}{l} \mathit{\boldsymbol{G}}_{e,k}^i\left( b \right) = \\ \left\{ \begin{array}{l} 1,\mathit{\boldsymbol{E}}_{e,k}^i\left( b \right) = \max \left( {\mathit{\boldsymbol{E}}_{e,k}^1\left( b \right),\mathit{\boldsymbol{E}}_{e,k}^2\left( b \right), \cdots ,\mathit{\boldsymbol{E}}_{e,k}^L\left( b \right)} \right);\\ 0,{\rm{otherwise}}{\rm{.}} \end{array} \right. \end{array} $ | (21) |
式中Ee, ki (b)为第i幅源图像的第b个像素的边缘信息.
拉普拉斯能量和在一定程度上能恰当的反映源图像的聚焦特性.因此,通过计算高频子带系数的拉普拉斯能量和能够得到一幅聚焦良好的融合图像.本文用基于局部区域的改进拉普拉斯能量和来衡量源图像的聚焦特性,获得局部区域的改进拉普拉斯能量和
| $ \mathit{\boldsymbol{SML}}_{e,k}^i = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{{\left( {\mathit{\boldsymbol{ML}}_{e,k}^i\left( {x + m,y + n} \right)} \right)}^2}} } . $ | (22) |
式中SMLe, ki为第i幅图像在局部区域M*N下的改进拉普拉斯能量和,本文取M*N=3*3. MLe, ki(x, y)为在位置(x, y)的改进拉普拉斯能量为
| $ \begin{array}{l} \mathit{\boldsymbol{ML}}_{e,k}^i\left( {x,y} \right) = \left| {2\mathit{\boldsymbol{D}}_{e,k}^i\left( {x,y} \right) - \mathit{\boldsymbol{D}}_{e,k}^i\left( {x - 1,y} \right) - } \right.\\ \left. {\mathit{\boldsymbol{D}}_{e,k}^i\left( {x + 1,y} \right)} \right| + \left| {2\mathit{\boldsymbol{D}}_{e,k}^i\left( {x,y} \right) - \mathit{\boldsymbol{D}}_{e,k}^i\left( {x,y - 1} \right) - } \right.\\ \left. {\mathit{\boldsymbol{D}}_{e,k}^i\left( {x,y + 1} \right)} \right| + \left| {1.6\mathit{\boldsymbol{D}}_{e,k}^i\left( {x,y} \right) - 0.8\mathit{\boldsymbol{D}}_{e,k}^i\left( {x - 1,y + } \right.} \right.\\ \left. {\left. 1 \right) - 0.8\mathit{\boldsymbol{D}}_{e,k}^i\left( {x + 1,y - 1} \right)} \right| + \left| {1.6\mathit{\boldsymbol{D}}_{e,k}^i\left( {x,y} \right) - } \right.\\ \left. {0.8\mathit{\boldsymbol{D}}_{e,k}^i\left( {x - 1,y - 1} \right) - 0.8\mathit{\boldsymbol{D}}_{e,k}^i\left( {x + 1,y + 1} \right)} \right|. \end{array} $ | (23) |
对获得的高频子带系数的局部区域的改进拉普拉斯能量和进行加权映射,构造初始聚焦度融合权重
| $ \begin{array}{l} \mathit{\boldsymbol{M}}_{e,k}^i\left( b \right) = \\ \left\{ \begin{array}{l} 1,\mathit{\boldsymbol{SML}}_{e,k}^i\left( b \right) = \max \left( {\mathit{\boldsymbol{SML}}_{e,k}^1\left( b \right),\mathit{\boldsymbol{SML}}_{e,k}^2\left( b \right), \cdots ,\mathit{\boldsymbol{SML}}_{e,k}^L\left( b \right)} \right);\\ 0,{\rm{otherwise}}{\rm{.}} \end{array} \right. \end{array} $ | (24) |
式中SMLe, ki(b)为第i幅图像中第b个像素的清晰度信息.
高频子带系数的初始融合权重由初始显著信息融合权重、初始清晰度融合权重、初始边缘信息融合权重和初始聚焦度融合权重组成,即
| $ \mathit{\boldsymbol{W}}_{e,k}^i = \mathit{\boldsymbol{U}}_{e,k}^i * \mathit{\boldsymbol{R}}_{e,k}^i * \mathit{\boldsymbol{G}}_{e,k}^i * \mathit{\boldsymbol{M}}_{e,k}^i. $ | (25) |
这里采用引导滤波器对高频子带系数的初始融合权重进行修正,将De, ki作为引导图像,而We, ki作为滤波输入图像,则
| $ \mathit{\boldsymbol{P}}_{e,k}^i = {\rm{guidedfilter}}\left( {\mathit{\boldsymbol{D}}_{e,k}^i,\mathit{\boldsymbol{W}}_{e,k}^i,r2,eps2} \right). $ | (26) |
式中:r2表示引导滤波器窗口的大小,eps2表示模糊度.其次,通过取大策略获得最终的融合权重
| $ \begin{array}{l} \mathit{\boldsymbol{X}}_{e,k}^i\left( b \right) = \\ \left\{ \begin{array}{l} 1,\mathit{\boldsymbol{P}}_{e,k}^i\left( b \right) = \max \left( {\mathit{\boldsymbol{P}}_{e,k}^1\left( b \right),\mathit{\boldsymbol{P}}_{e,k}^2\left( b \right), \cdots ,\mathit{\boldsymbol{P}}_{e,k}^L\left( b \right)} \right);\\ 0,{\rm{otherwise}}{\rm{.}} \end{array} \right. \end{array} $ | (27) |
最后,则融合图像的高频子带系数De, kZ为
| $ \mathit{\boldsymbol{D}}_{e,k}^Z = \sum\limits_{i = 1}^L {\overline {\mathit{\boldsymbol{X}}_{e,k}^i} \mathit{\boldsymbol{D}}_{e,k}^i} . $ | (28) |
式中
为验证本文算法的可行性,选取见图 3所示的4组已配准好且大小分别为480 pixel*360 pixel、640 pixel *480 pixel、944 pixel *736 pixel、520 pixel *520 pixel的图像进行融合.将本文算法与文献[13](PCNN方法)、文献[5](NSP方法)、文献[1](ASR方法)和文献[14](MGF方法)分别进行对比实验. PCNN方法、NSP方法、ASR方法和MGF方法的参数取值均与各文献中保持一致;本文融合算法的参数设置为:公式(9)和公式(26)中的引导滤波器参数分别为r1=45、eps1=0.3和r2=7、eps2=10^-6.

|
图 3 四组多聚焦源图像 Figure 3 Four groups of multi-focus source images |
图 4为采用不同融合方法的4组实验的融合结果图.从主观上,图 4(a)中老虎的头部发白,整幅图像的清晰度下降;图 4(b)~4(d)均较好地将源图像的信息保留下来,但丢失部分细节信息;图 4(e)较好地保留源图像的细节等信息,提高融合图像的清晰度,融合效果比较理想. 图 4(f)和图 4(g)中,没有很好地将左聚焦源的信息进行融合,使融合后的图像清晰度下降;图 4(h)和图 4(i)中,丢失部分细节及纹理等信息,对比度下降;图 4(j)则较好地保留图像的细节及纹理等信息,同时还提高图像的清晰度和对比度,融合效果较好. 图 4(k)中产生严重的虚影,清晰度下降,融合效果较差;图 4(l)~4(n)均较好地将源图像的信息保留下来,但损失部分细节信息;图 4(o)则较好地保留源图像的信息,聚焦区域的边缘处融合效果也比较理想,融合效果较好. 图 4(p)中人物的脸部较模糊,清晰度下降;图 4(q)~4(s)融合效果比较理想,但丢失部分边缘轮廓信息;图 4(t)则较好地保留源图像的边缘轮廓和纹理等信息,也无细节信息缺失,融合效果较好.

|
图 4 不同融合方法的实验结果图 Figure 4 Different fusion methods of experimental results |
进一步说明本文算法的有效性,本文选取平均梯度(AG)、标准差(STD)、互信息[15](MI)、边缘信息保留度QAB/Z[16] (其中A和B为待融合的源图像,Z为融合图像)、视觉信息保真度[17](VIFF)和空间频率误差比QSF[18] (其中SF为改进的空间频率)对融合图像进行定量评价.其中,AG越大,说明融合图像越清晰;STD越大,说明融合图像的对比度越高;MI越大,说明融合图像包含的信息越丰富;QAB/Z(其中QAB/Z的值不超过1)越大,说明融合图像包含的边缘信息越丰富;VIFF越高,说明融合图像与人眼视觉观察越一致;QSF的绝对值越小,说明融合图像的融合效果越好.
表 1列出4组多聚焦图像融合的客观评价实验结果.实验1和实验3中,本文算法的AG、STD、MI、QAB/Z、VIFF和QSF值均优于其余4种融合方法.说明本文算法的清晰度、对比度、信息丰富度和边缘信息量等都优于其余4种融合方法;实验2中,本文算法的AG、STD、MI、QAB/Z、VIFF和QSF值均优于PCNN、NSP和ASR方法. MGF方法仅QAB/Z高于本文算法,其余5个指标均不如本文算法.说明本文算法在清晰度、对比度、信息丰富度、人眼视觉上和融合效果都优于其余4种融合方法,只是在边缘信息量上略低于MGF方法;
| 表 1 图像融合的客观评价实验结果 Table 1 Image fusion objective evaluation experiment results |
实验4中,本文算法的AG、STD、MI、QAB/Z、VIFF和QSF值均优于NSP和ASR方法.其中,PCNN方法仅STD值高于本文算法,其余5个指标值均不如本文算法;MGF方法仅QAB/Z高于本文算法,其余5个指标均不如本文算法.说明本文算法在清晰度、信息丰富度、人眼视觉上和融合效果都优于其余4种融合方法,只是在对比度及边缘信息量上不如PCNN方法和MGF方法.
将主观评价与客观评价相结合,发现本文算法的融合效果优于其余4种融合方法.本文算法能够从源图像中提取更多轮廓、细节及纹理等信息,并且还提高融合图像的对比度及清晰度.
5 结论本文根据多聚焦图像的成像特点,为使最终的融合图像含有丰富的纹理边缘等细节信息,将NSST变换的多种优良特性和引导滤波器的保边平滑特性相结合,提出一种NSST与引导滤波相结合的多聚焦图像融合算法.仿真结果表明,本文算法很好地保留源图像的轮廓、细节和纹理等信息,提高融合图像的对比度和清晰度,取得比较理想的融合效果.所以,本文算法是一种行之有效的多聚焦图像融合算法.
| [1] |
LIU Yu, WANG Zengfu. Simultaneous image fusion and denoising with adaptive sparse representation[J]. Institution of Engineering and Technology, 2015, 9(5): 347. DOI:10.1049/iet-ipr.2014.0311 |
| [2] |
程丹松, 刘欢, 张永强, 等. 结合自适应暗通道先验和图像融合策略的单幅图像除雾方法[J]. 哈尔滨工业大学学报, 2016, 48(11): 35. CHENG Dansong, LIU Huan, ZHANG Yongqiang, et al. Single image haze removal using adaptive dark channel prior and image fusion strategy[J]. Journal of Harbin Institute of Technology, 2016, 48(11): 35. DOI:10.11918/j.issn.0367-6234.2016.11.006 |
| [3] |
DO M N, VETTERLI M. The contourlet transform: an efficient directional multiresolution image representation[J]. IEEE Transactions on Image Processing, 2005, 14(12): 2091. DOI:10.1109/TIP.2005.859376 |
| [4] |
DA C A, ZHOU Jianping, DO M N. The nonsubsampled contourlet transform: theory, design, and applications[J]. IEEE Transactions on Image Processing, 2006, 15(10): 3089. DOI:10.1109/TIP.2006.877507 |
| [5] |
QU Xiaobo, YAN Jingwen, XIAO Hongzhi, et al. Image fusion algorithm based on spatial frequency-motivated pulse coupled neural networks in nonsubsampled contourlet transform domain[J]. Acta Automatica Sinica, 2008, 34(12): 1508. DOI:10.3724/SP.J.1004.2008.01508 |
| [6] |
谢秋莹, 易本顺, 柯祖福, 等. 基于SML和PCNN的NSCT域多聚焦图像融合[J]. 计算机科学, 2017, 44(6): 266. XIE Qiuying, YI Benshun, KE Zufu, et al. Multi-focus image fusion based on SML and PCNN in NSCT domain[J]. Computer Science, 2017, 44(6): 266. DOI:10.11896/j.issn.1002-137X.2017.06.046 |
| [7] |
EASLEY G, LABATE D, LIM W Q. Sparse directional image representations using the discrete shearlet transform[J]. Applied and Computational Harmonic Analysis, 2008, 25(1): 25. DOI:10.1016/j.acha.2007.09.003 |
| [8] |
邢雅琼, 王晓丹, 雷蕾, 等. 基于NSST域灰度关联分析的多聚焦图像融合方法[J]. 系统工程理论与实践, 2015, 35(9): 2380. XING Yaqiong, WANG Xiaodan, LEI Lei, et al. Fusion technique for multi-focus image based on analysis of grey relation in NSST domain[J]. Systems Engineering-Theory & Practice, 2015, 35(9): 2380. |
| [9] |
杨勇, 万伟国, 黄淑英, 等. 稀疏表示与非下采样shearlet变换相结合的多聚焦图像融合[J]. 小型微型计算机系统, 2017, 38(2): 386. YANG Yong, WAN Weiguo, HUANG Shuying, et al. Sparse representation and non-subsampled shearlet transform for multi-focus image fusion[J]. Journal of Chinese Computer Systems, 2017, 38(2): 386. |
| [10] |
GAO Guorong, XU Luping, FENG Dongzhu. Multi-focus image fusion based on non-subsampled shearlet transform[J]. IET Image Processing, 2013, 7(6): 633. DOI:10.1049/iet-ipr.2012.0558 |
| [11] |
HUANG Yan, BI Duyuan, WU Dongpeng. Infrared and visible image fusion based on different constraints in the non-subsampled shearlet transform domain[J]. Sensors, 2018, 18(4): 1169. DOI:10.3390/s18041169 |
| [12] |
HE Kaiming, SUN Jian, TANG Xiaoou. Guided image filtering[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2013, 35(6): 1397. DOI:10.1109/TPAMI.2012.213 |
| [13] |
苗启广, 王宝树. 一种自适应PCNN多聚焦图像融合新方法[J]. 电子与信息学报, 2006, 28(3): 466. MIAO Qiguang, WANG Baoshu. A novel algorithm of multi-focus image fusion using adaptive PCNN[J]. Journal of Electronics & Information Technology, 2006, 28(3): 466. |
| [14] |
杨航, 吴笑天, 贺柏根, 等. 基于多尺度导引滤波的图像融合方法[J]. 光电子·激光, 2015, 26(1): 170. YANG Hang, WU Xiaotian, HE Baigen, et al. Image fusion based on multiscale guided filters[J]. Journal of Optoelectronics·Laser, 2015, 26(1): 170. |
| [15] |
QU Guihong, ZHANG Dali, YAN Pingfan. Information measure for performance of image fusion[J]. Electronics Letters, 2002, 38(7): 313. DOI:10.1049/el:20020212 |
| [16] |
XYDEAS C S, PETROVIC V. Objective image fusion performancemeasure[J]. Electronics Letters, 2000, 36(4): 308. DOI:10.1049/el:20000267 |
| [17] |
HAN Yu, CAI Yunze, CAO Yin, et al. A new image fusion performance metric based on visual information fidelity[J]. Information Fusion, 2013, 14(2): 127. DOI:10.1016/j.inffus.2011.08.002 |
| [18] |
ZHENG Yufeng, ESSOCK E A, HANSEN B C, et al. A new metric based on extended spatial frequency and its application to DWT based fusion algorithms[J]. Information Fusion, 2007, 8(2): 177. DOI:10.1016/j.infuss.2005.04.003 |
 2018, Vol. 50
2018, Vol. 50



