2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
在未来无线通信中, 伴随着应用场景需求的多样化, 网络切片技术应用而生.网络切片技术是在通用网络设施资源的基础上, 根据专有需求构建相互隔离的虚拟化端到端网络的技术.通过网络功能及协议的定制, 网络切片可实现不同应用场景的匹配, 提高通信效率[1].网络切片技术已成为5G通信的关键技术之一[2].
目前网络切片技术主要是在已有的无线网络协议层进行切片化调度处理, 实现基于已有网络的性能提升.针对不同服务提供商(service provider, SP)的数据, 采用网络切片进行动态调度分配, 可实现资源利用率的最大化[3];采用虚拟切片业务进行优先排序, 可形成一个先调度实时业务后调度非实时业务的虚拟优先级切片[4].在空口传输协议层, 网络切片技术应用于MAC层(Media Access Control, 媒体接入控制), 采用虚拟媒体接入控制子层的概念, 可实现资源虚拟化管理[5];另外建立MAC层流级别的网络切片调度器, 可以根据不同服务对资源进行设定[6].由于现有网络协议层主要采用基于自动重传请求(Automatic Retransmission Request, ARQ)的纠错机制, 在采用网络切片的传输中, 会导致整个网络切片的端到端重传, 增大传输延时.
喷泉码纠错机制是针对大规模无线数据分发和可靠传输的一种纠删编码方法, 丢包数据不需重传, 具有无需反馈的纠错特性, 可以降低反馈延时.目前喷泉码已被应用于多种无线通信场景.在深空通信中, 采用分布式喷泉码传输方案可降低译码失败率[7].在喷泉编码中加入保密机制, 可用于安全通信[8].在视频传输领域, 喷泉码编解码可支持流媒体以及高清视频的传输[9-10].喷泉码在无线通信的应用中体现出优越的性能, 但其与网络切片技术结合的相关研究较少.本文将网络切片技术与喷泉码纠错技术相结合, 构建新型的无线网络切片传输模型, 降低网络切片端到端传输反馈和重传的延时, 并与ARQ方案进行传输时间的比较和分析.
1 网络切片整体传输模型在无线通信中, 传输协议层通过将应用层的数据流进行组包和分包, 实现符合无线波形结构的规范数据帧, 以便无线波形在物理层进行传送;并对无线波形传送的错漏进行纠正, 保证无线传输的准确性.
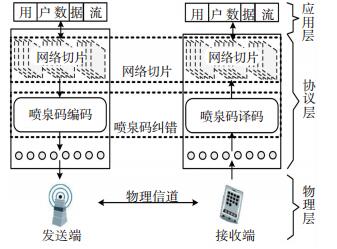
本文针对协议层构建的网络切片传输模型, 主要包括网络切片模块和喷泉码纠错模块两部分, 如图 1所示.其中, 网络切片模块通过对数据流进行切片化组包和分包, 实现包处理的集中和简化;喷泉码纠错模块采用目前最新的编码技术—系统Raptor码[11](Systematic Raptor codes)进行编码和译码, 代替传统的ARQ机制, 实现无重传的纠错处理.
|
图 1 无线网络切片的整体传输模型 Figure 1 Wireless network slicing entirety transmission model |
系统Raptor码编译码的基本原理为:发送端对K个原始切片进行编码, 生成N = K + m个编码切片, 并向接收端发送.其中编码切片包含K个原始切片和m个冗余切片, 每个冗余切片由随机的d个原始切片异或生成. d为编码维度, 平均值为3左右.接收端在收到M (K < M ≤ N)个切片后, 就能以很大概率恢复所有原始切片.由于系统Raptor码优异的译码性能, 接收端仅需少量冗余包即可实现译码[11].
在发送端, 应用层将不同应用场景的源数据流传入协议层, 网络切片模块对数据流进行切片化处理.喷泉码编码模块对切片进行系统Raptor码编码, 并传递给物理层.在接收端, 喷泉码译码模块对物理层传递的切片进行系统Raptor码译码.根据网络的丢包状况, 接收端需接收一定量的冗余切片完成译码.译码成功后, 网络切片模块对译码切片进行解包, 解析出所有源数据流, 提供给上层应用层, 完成数据传输.
采用喷泉码纠错机制的网络切片模型, 避免了端到端的ARQ纠错反馈和重传, 可以降低反馈延时.
2 网络切片的传输结构与时间本节详细论述了将系统Raptor码应用于网络切片的传输结构, 并分析网络切片的传输时间.作为比较, 同时给出应用ARQ机制的网络切片传输方案.
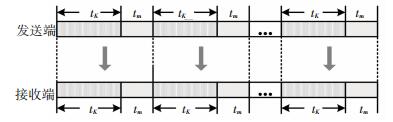
2.1 喷泉码方案系统Raptor码编码将K个源切片编码为N个编码切片.假设所有发送接收设备的处理都是理想的, 没有延迟.发送端连续发送N = K+ m个切片, 需要发送时间为TRap= tK+ tm.当发送结束后, 即转入下一收发状态.则网络切片在喷泉码方案下的传输结构如图 2所示.
|
图 2 喷泉码方案的传输结构 Figure 2 Transmission architecture of fountain code scheme |
在系统Raptor码译码中, 接收端需收到M个切片后才可以恢复数据.故M与K满足:
| $ M = K\left( {1 + \varepsilon } \right). $ | (1) |
式中ε为传输冗余度.
当传输信道的丢包率为p时, 发送的切片数N与接收的切片数M满足:
| $ M = N\left( {1 - p} \right) = K\left( {1 + \varepsilon } \right). $ | (2) |
则采用喷泉码传输一组切片的时间为
| $ {T_{{\rm{Rap}}}} = {t_K} + {t_m} = N{t_{{\rm{slc}}}} = \frac{{K\left( {1 + \varepsilon } \right)}}{{1 - p}}{t_{{\rm{slc}}}}. $ | (3) |
式中tslc为每个网络切片的平均传输时间.
由上式可以看出, 喷泉码方案的传输时间由单个切片的平均传输时间tslc、切片数量K、网络丢包率p以及传输冗余度ε决定.在系统Raptor码中, 切片数量K不同, 译码所需的冗余包数不同, 传输冗余度ε也不相同.
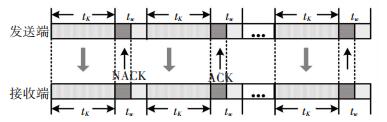
2.2 ARQ方案图 3给出了采用ARQ方案的传输结构, 同样发送切片数量为K的切片.
|
图 3 ARQ方案的传输结构 Figure 3 Transmission architecture of ARQ scheme |
发送端发送完切片后, 进入长度为tw的时隙, 等待反馈校验信息, 并重发没有接收到应答信息(Acknowledge, ACK)的切片.
接收端进行校验反馈和等待重传.假设每一个重传切片的校验反馈所需的时间与重传时间相当, 则每一个丢包的校验反馈、重传、再校验共需3倍的正常发送时间[12].对于丢包率为p的传输系统, 如果丢失的网络切片只需重传一次即可成功, 则发送端向接收端发送的总切片数Narq1和传输时间Tarq1分别为
| $ {N_{{\rm{arq1}}}} = K\left( {1 + p} \right), $ | (4) |
| $ {T_{{\rm{arq1}}}} = K\left( {1 + 3p} \right){t_{{\rm{slc}}}}. $ | (5) |
当丢包概率增大时, 重传数据仍有概率为p的丢包, 需继续重传.累计发送的总切片数Narq2及传输时间Tarq2分别为
| $ {N_{{\rm{arq2}}}} = K\mathop \sum \limits_{i = 0}^n {p^i} = K\frac{{1 - {p^i}}}{{1 - p}} = \frac{K}{{1 - p}}, $ | (6) |
| $ {T_{{\rm{arq2}}}} = \frac{{K{t_{{\rm{slc}}}}}}{{1 - 3p}}. $ | (7) |
可见, ARQ方案的传输时间由单个切片的平均传输时间tslc、切片数量K以及丢包率p决定.当丢包率很小时, 数据重传较小;当丢包率增大时, 重传数据所占比重增大, 传输延时随之增大.
2.3 两种方案的传输时间比较当发送相同数量K的网络切片时, 比较喷泉码方案和ARQ方案的传输时间.
如果重传一次即可正确接收, 则由式(3)和式(5), 得出喷泉码方案与ARQ方案的传输时间比值为
| $ \frac{{{T_{{\rm{Rap}}}}}}{{{T_{{\rm{arq1}}}}}} = \frac{{K\left( {1 + \varepsilon } \right){t_{{\rm{slc}}}}}}{{K\left( {1 + 3p} \right)\left( {1 - p} \right){t_{{\rm{slc}}}}}} = \frac{{1 + \varepsilon }}{{\left( {1 + 3p} \right)\left( {1 - p} \right)}}. $ | (8) |
如果重传仍有丢包, 则由式(3)与式(7), 得出喷泉码方案与ARQ方案的传输时间比值为
| $ \frac{{{T_{{\rm{Rap}}}}}}{{{T_{{\rm{arq2}}}}}} = \frac{{K\left( {1 + \varepsilon } \right)\left( {1 - 3p} \right){t_{{\rm{slc}}}}}}{{K{t_{{\rm{slc}}}}\left( {1 - p} \right)}} = \frac{{\left( {1 + \varepsilon } \right)\left( {1 - 3p} \right)}}{{1 - p}}. $ | (9) |
可见, 传输时间的比值取决于喷泉码的传输冗余度ε和网络丢包率p, 而ε又由系统Raptor码的切片数量K决定.
3 性能仿真与比较本节首先对系统Raptor码的编译码性能在Visual C环境下仿真, 给出不同切片数量K在成功译码时的冗余度.然后在Matlab环境将喷泉码方案与ARQ方案在重传一次和重传多次模式下的传输时间比值进行仿真, 并对结果进行分析.
3.1 系统Raptor码的冗余度当网络切片数量K取不同值时, 进行系统Raptor码编码.当接收冗余包个数分别取10、15、20时, 统计系统Raptor码译码的成功率.经过对上述组合各仿真10 000次以上, 每次仿真的数据均发生随机变化, 仿真结果如表 1所示.可以看出, 在相同切片数量下, 接收冗余包越多, 译码成功率越高;在相同冗余包个数下, 切片数量越多, 冗余包所占比重越低, 译码成功率越低.当冗余包个数为15时, 不同切片数量的译码成功率均大于99.9%.本文取冗余包个数为15进行后续的仿真分析.
| 表 1 系统Raptor码的译码成功率 Table 1 Decoding success rate of systematic Raptor code% |
针对表 1的网络切片分组, 取冗余包个数为15, 计算不同切片数量下的冗余度ε=15/K, 如表 2所示.冗余度ε随着切片数量K的增大而减小.
| 表 2 不同切片方案的冗余度 Table 2 Redundancy rate of different network slicing scheme |
根据表 2中不同网络切片数量的传输冗余度ε, 结合式(8)和式(9), 对网络切片在喷泉码方案和ARQ方案下的传输时间进行仿真比较.
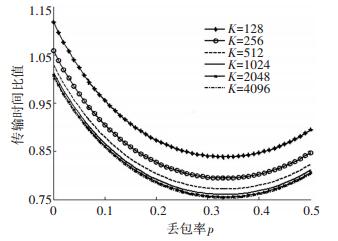
假设在ARQ方案中仅需重传一次即可成功, 当丢包率p变化时, 对式(8)进行仿真, 如图 4所示.图中的曲线为切片数量K取不同值时, 喷泉码方案与ARQ方案的传输时间比值
|
图 4 重传一次成功的传输时间比值 Figure 4 Time ratio of one-time retransmission |
随着丢包率的进一步增大, 喷泉码方案中发送端发送的冗余包更多, 其传输时间超过了ARQ方案的重传处理时间, 此时传输时间比值呈上升趋势.
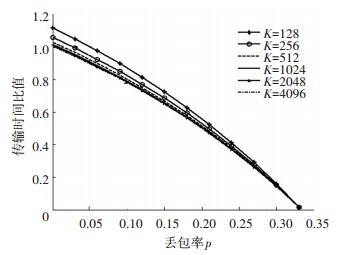
进一步分析, 当网络丢包率较大时, ARQ方案重传一次即成功的可行性下降, 需要重传多次才能成功.接下来对喷泉码方案与ARQ方案中的重传多次模式进行比较, 传输时间比值为式(9), 仿真结果如图 5所示.同样当比值小于1时, 喷泉码方案的传输时间小于ARQ方案.由于ARQ方案中重传多次比重传一次的延时更大, 因此其传输延时性能更差.当网络丢包率大于5×10-2时, 所有K值的喷泉码传输时间均小于ARQ方案.当K取4 096时, 丢包率为10-1, 喷泉码方案的传输时间比ARQ方案降低了约22%.随着丢包率的增大, ARQ方案需重传多次保证可靠性, 导致传输延时持续增大;而喷泉码方案仅需有限的冗余包即可保证译码效率, 其传输优越性越来越明显.
|
图 5 重传多次成功的传输时间比值 Figure 5 Time ratio of multiple retransmissions |
经过上述比较, 喷泉码方案的冗余包数量低于ARQ方案的丢包重传数量时, 单位时间内喷泉码方案可以传输更多的有效数据, 其传输吞吐率更高.在对每个数据包的运算处理中, 喷泉码算法与ARQ算法相比, 需要从相关的d个切片中异或解码, 将增加d次异或运算;由于d的平均值较小, 一般不大于3, 因此其运算开销较小.
4 结论本文将喷泉码纠错方案应用于无线网络切片传输系统, 并给出喷泉码的传输结构, 分析了传输时间.作为对比, 给出了网络切片采用ARQ方案的传输结构, 并分析了重传一次和重传多次的传输时间.
经过理论分析和仿真表明:在喷泉码方案中, 网络切片数量越大, 冗余度越低, 传输延时相对越小;在ARQ方案中, 重传多次比重传一次带来的传输延时更大;将喷泉码方案与重传多次的ARQ方案相比, 当网络丢包率大于5×10-2时, 喷泉码的传输时间小于ARQ方案;当丢包率为10-1时, 喷泉码的切片数K为4 096, 其传输时间可降低约22%;随着网络丢包率的增大, 喷泉码的传输性能更优越.可见, 将喷泉码方案用于网络切片纠错, 其无重传的特征及较好的译码性能, 可以在保证传输可靠性的基础上, 降低传输延时, 提高传输吞吐率.
| [1] |
许阳, 高功应, 王磊. 5G移动网络切片技术浅析[J]. 邮电设计技术, 2016(7): 19. XU Yang, GAO Gongying, WANG Lei. Initial analysis of 5G mobile network slicing technology[J]. Designing Techniques of Posts and Telecommunications, 2016(7): 19. DOI:10.16463/j.cnki.issn1007-3043.2016.07.005 |
| [2] |
CHIHLIN I, ROWELL C, HAN Shuangfeng, et al. Toward green and soft: A 5G perspective[J]. IEEE Communications Magazine, 2014, 52(2): 66. DOI:10.1109/MCOM.2014.6736745 |
| [3] |
KAMEL M I, LE L B, GIRARD A.LTE wireless network virtualization: dynamic slicing via flexible scheduling[C]//IEEE 80th Vehicular Technology Conference (VTC2014-Fall), New Jersey: IEEE Press, 2014: 1.DOI: 10.1109/VTCFall.2014.6966044
|
| [4] |
ABDELHAMID A, KRISHNAMURTHY P, TIPPER D.Resource scheduling for heterogeneous traffic in LTE virtual networks[C]//IEEE International Conference on Mobile Data Management.New Jersey: IEEE Press, 2015: 173.DOI: 10.1109/MDM.2015.34
|
| [5] |
FAN Bo, TIAN Hui, YAN Xiao.A generic framework for heterogeneous wireless network virtualization: virtual MAC design[C]//2016 IEEE wireless Communications and Networking Conference, New Jersey: IEEE Press, 2016: 1.DOI: 10.1109/WCNC.2016.7564845
|
| [6] |
庞晓丹, 李薇薇, 孙茜, 等. LTE无线网络虚拟化中切片调度策略[J]. 电信科学, 2017, 33(2): 66. PANG Xiaodan, LI Weiwei, SUN Qian, et al. LTE wireless network virtualization[J]. Telecommunications Science, 2017, 33(2): 66. DOI:10.11959/j.issn.1000-0801.2017041 |
| [7] |
焦健, 聂胜贤, 杨轶, 等. 面向深空通信的分布式系统Raptor码传输机制[J]. 宇航学报, 2016, 37(10): 1232. JIAO Jian, NIE Shengxian, YANG Yi, et al. Distributed systematic Raptor coding scheme in deep space communications[J]. Journal of Astronautics, 2016, 37(10): 1232. DOI:10.3873/j.issn.1000-1328.2016.10.011 |
| [8] |
赵旦峰, 司佳希, 梁明珅, 等. 基于算术编码的低冗余LT码及其在安全通信中的应用[J]. 系统工程与电子技术, 2016, 38(2): 409. ZHAO Danfeng, SI Jiaxi, LIANG Mingshen, et al. Low redundancy LT code based on arithmetic coding and its application in secure communication[J]. System Engineering and Electronics, 2016, 38(2): 409. DOI:10.3969/j.issn.1001-506X.2016.02.25 |
| [9] |
WU Jiyan, YUEN C, WANG Ming, et al. TCP-oriented Raptor coding for high-frame-rate video transmission over wireless networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(8): 2231. DOI:10.1109/JSAC.2016.2577178 |
| [10] |
VICENTE N, SILVA V, ANDRADE J, et al. Mobile 4K/2K/HD Video streaming supported by real-time FEC RaptorQ codes[J]. IEEE Transactions on Consumer Electronics, 2016, 62(4): 405. DOI:10.1109/TCE.2016.7838093 |
| [11] |
IETF RFC 6330 (2011): RaptorQ forward error correction scheme for object delivery[S].IETF Proposed Standard, 2011.
|
| [12] |
SESIA S, TOUFIK I, BAKER M著; 马霓, 夏斌, 译.LTE—UMTS长期演进理论与实践[M].北京: 人民邮电出版社, 2012: 274
|
| [17] |
SESIA S, TOUFIK I, BAKER M, et al. LTE—The UMTS long term evolution from theory to practice[M]. Beijing: Posts & Telecom Press, 2012: 274.
|
 2018, Vol. 50
2018, Vol. 50


