2. 黑龙江工程学院 土木与建筑工程学院,哈尔滨 150050;
3. 交通运输部公路科学研究院,北京 100029
2. School of Civil and Architectural Engineering, Heilongjiang Institute of Technology, Harbin 150050, China;
3. China Academy of Transportation Sciences, Beijing 100029, China
路面平整度是衡量路面质量优劣的重要技术指标, 它关系到行车的安全、舒适以及路面的使用寿命, 不平整的路面会增大行车阻力, 造成行车的颠簸, 严重影响行车速度和安全.因此, 合理的水泥路面平整度预测[1-8]对于路面养护管理具有十分重要的意义.然而, 路面平整度的预测在国内外开展的时间较短, 各种概率模型需要依靠专家打分, 主观性较强.灰色理论模型[9-10]、神经网络预测模型[11-13]具有很强的非线性拟合能力, 且学习规则简单, 但也存在一些模型本身的缺陷, 需要充足的数据支撑, 且推理过程和推理依据十分严格.国内姚康祖模型[14-15]为指数形式, 该模型对路面的变化实际情况进行了拟合, 然而模型中的参数缺乏明确的物理意义, 且采集数据的误差对参数的影响较大.孙立军等[16]提出的路面平整度预测模型简单实用, 但该模型仅是初始平整度指标、路龄和回归参数的简单函数, 考虑因素较单一, 没有考虑气候因素.因此, 建立适用于季节性冻土地区气候特点的水泥路面平整度预测模型仍需进一步完善.
MEPDG[17-20](mechanistic-empirical pavement design guide)是以力学-经验方法为设计基础, 利用传统的力学方法对路面结构的应力和应变进行计算, 辅以经验方面的方法弥补室内试验和现场试验的差距.此外, 考虑了交通状况、气候条件和道路各层材料的特性.该模型的建立是基于美国40多个州的2 200个试验段的长期路面性能的观测结果得出.基于MEPDG的水泥路面IRI预测模型中, IRI受水泥板裂缝、板角断裂情况、错台情况和环境因素的影响, 且四者构成了线性关系, 这与实际分析更加贴合. MEPDG理论在国外研究较多, 我国却鲜有研究.由于我国地理纬度和精度跨度较大, 各个地区的气候条件存在明显差异, 根据季冻区的水泥路面结构材料性能和实际交通状况, 以黑龙江省典型高速公路为例, 基于MEPDG理论, 充分考虑交通量、降雨、降雪、温度、潮湿天数、冰冻天数等气候因素的影响, 对国际平整度预测模型进行修正, 并对修正后的模型适用性进行研究, 从而提出适用于季冻区的水泥路面国际平整度指数预测修正模型.
1 IRI预测值与实际值对比国际平整度指数IRI(international roughness index)是以四分之一车在速度为80 km/h时的累积竖向位移值, 单位为m/km.基于MEPDG的水泥路面国际平整度指数预测模型为
| $ k = {k_1} + {C_1} \times \alpha + {C_2} \times \beta + {C_3} \times \gamma + {C_4} \times \rho . $ | (1) |
式中:k为国际平整度指数(IRI);k1为国际平整度指数初始值(IRII);α为水泥混凝土板裂缝百分比(CRK);β为板角断裂率(SPALL);γ为道路使用年限内每月平均错台递增量的累计(TFAULT);ρ为环境因素(SF);C1值为0.8203;C2值为0.4417;C3值为0.4929;C4值为25.24.
选择鹤大公路调查路段近10 a的实测IRI数据对MEPDG理论中水泥路面平整度指数预测模型进行验证, IRI统一采用美式计量单位, 横轴为高速公路现场调查的IRI实测值, 纵轴为基于MEPDG的IRI预测值, 将实测值和预测值拟合, 得到的决定性系数R2等于0.827, 预测值与实际调查值偏差较大, 说明IRI的预测并不理想.分析原因是由于IRI预测模型是基于美国本土的试验路段的材料、气候和交通等参数回归而成的, 以上参数和国内道路的实际参数状况差别较大, 因此需建立基于我国季冻区气候状况、交通状况和道路各层材料性能下的水泥路面IRI预测修正模型.
2 预测修正模型参数预测修正模型的构建中, CRK、SPALL、TFAULT、SF 4个指标包括的参数有面层材料的孔隙率, 填缝料密实程度, 面层材料的抗压强度, 冻融循环次数, 面层板厚, 面层材料水灰比, 潮湿天数, 冰冻天数和交通量等.
2.1 材料参数以鹤大高速公路试验路初始年限为例, 调查材料参数包括水泥混凝土路面面层厚度为260 mm, 基层水泥稳定砂砾厚度为180 mm, 底基层水泥石灰综合稳定土厚度为180 mm, 垫层天然砂砾平均厚度为200 mm, 混凝土设计弯拉强度为5 MPa, 混凝土弯拉模量为30 000 MPa, 以及筛孔为0.075 mm时的路基材料通过率等.
2.2 气候参数气候因素对水泥路面平整度影响显著, 其与行车荷载相互作用会加速损坏路面平整度.气候因素中湿度和温度对路面平整度的影响最为突出.水泥路面作为一个体系, 内部的湿度和温度会随环境的湿度和温度改变, 这种改变会造成路面材料的力学性质和结构强度发生变化.温度和湿度两种因素对路基材料和路面材料物理状态的改变, 会使得路面结构在没有受到行车荷载作用, 路面平整度也会逐渐损坏;在车辆荷载的叠加作用下, 平整度损坏持续加剧.故在气候参数中重点分析气候因素中的降水、降雪、温度、潮湿天数、冻融循环次数和冰冻天数等对水泥路面平整度的影响.
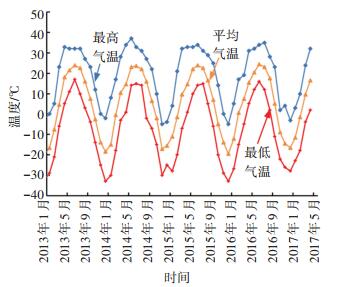
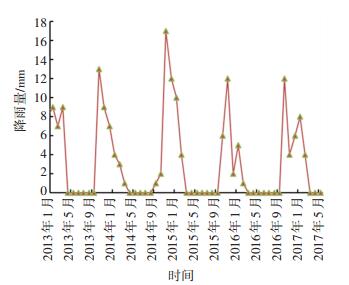
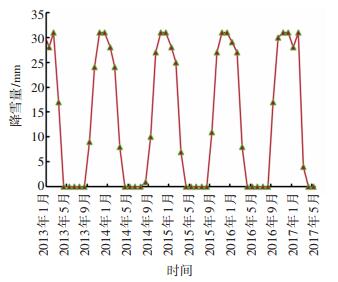
以鹤大高速公路为例, 该地区处于中纬度欧亚大陆东沿, 太平洋西岸, 北面临近寒冷的西伯利亚, 南北跨中温带与寒温带, 气候数据出自黑龙江省内80个气象观测站点中的一部分. 图 1为2013—2017年调查路段所属地区气温走势图.该地区1月份平均气温-18.5~-19.5 ℃, 7月份平均气温为23.5~24.5 ℃. 图 2表明从2003—2017年, 鹤大高速公路所在地区每年的潮湿天数和冰冻天数, 其中降雨量超过2.54 mm即定义为潮湿天数, 温度低于0 ℃即定义为冰冻天数.降水表现出明显的季风性特征如图 3所示, 夏季受东南季风的影响, 降水充沛, 占全年降水量的65%左右;冬季在干冷西北风控制下, 干燥少雪, 仅占全年降水量的5%;春秋两季分别占13%和17%左右.1月份最少, 7月份最多. 图 4为2013—2017年降雪量.
|
图 1 2013—2017年气温走势图 Figure 1 Temperature chart from 2013 to 2017 |

|
图 2 2003—2017年潮湿天数和冰冻天数 Figure 2 Wet days and frozen days from 2003 to 2017 |
|
图 3 2013—2017年降雨量走势图 Figure 3 Rainfall trend chart from 2013 to 2017 |
|
图 4 2013—2017年降雪走势图 Figure 4 Snowfall trend chart from 2013 to 2017 |
交通数据的获得采用交通量常年观测的方法, 即每年观测时间为365 d, 每天观测时间24 h.以2013年鹤岗—大连公路宁安至黑吉界段为例, 中小客车占比61.8%, 小货车占比16.3%, 特大货车占比11.8%, 中货车占比4.3%, 其余车型占比5.8%.鹤大高速公路宁安至黑吉界段自2013年年平均日交通量为3 345辆, 年增长比例约为5.7%, 2017年年平均日交通量为3 925辆.
3 IRI预测模型修正 3.1 IRI中各预测指标验证将上文中的气候、交通和材料参数等代入到基于MEPDG的水泥路面IRI预测模型中, 从道路建成年限开始预测CRK、TFAULT、SPALL和SF 4个指标, 以鹤大高速公路为例, 对4个指标预测的合理性进行验证. CRK表示水泥混凝土板发生裂缝的比例, 该裂缝包括路面横、纵、斜向裂缝、角隅断裂和交叉裂缝. CRK是基于疲劳损坏的复合函数, 疲劳损坏的预测是以Miner的破坏积累法则为基础的, 由交通荷载重复作用次数与允许的荷载重复作用次数之比表示, CRK指标表示为
| $ \alpha = \frac{1}{{1 + {d^{ - 1.98}}}}, $ | (2) |
式中d为车辆施加荷载的累计疲劳损坏.
从图 5(a)中预测曲线可以得到CRK指标随着道路使用年限的增长呈现曲线上升的趋势, 分析原因是道路在交通荷载的作用下, 路面产生疲劳裂缝, 由于交通轴载和气候的耦合作用, 使得裂缝呈现上升的趋势, 实际检测数据与预测曲线趋势相同. CRK的斜率变化较大, 是由于道路个别年份交通量呈现了明显增多或减少的原因造成的.

|
图 5 CRK和SF变化曲线 Figure 5 CRK and SF curves |
气候指标SF是道路年限、冰冻天数和P2003个指标的复合函数, SF通过FI和P200两项指标的复合函数反应温度和湿度在设计使用年限内对路面结构和路基变化的影响, SF指标表示为
| $ \rho = t\left( {1 + 0.5556f} \right)(1 + {P_{200}}) \times {10^{ - 6}}. $ | (3) |
式中:t为道路使用年限, a;f为冰冻指数, ℃·d;P200为筛孔为0.075 mm时的路基材料通过率.
从图 5(b)中曲线分析来看, 随着年份的增加, 环境因素指标SF呈上升趋势, 这与前文分析的环境因素会加重路面平整度损坏一致. 2012年SF值较之其他年份有明显的上升是由于2012年3月份平均温度较其他年份低, 冰冻天数较其他年份长导致的.
SPALL指标中包含道路使用年限, 水泥混凝土的孔隙率, 接缝处的填缝料是否密封, 混凝土板体的抗压强度, 每年的冻融循环次数, 混凝土板厚及混凝土板体的水灰比等多个参数, SPALL指标表示为
| $ \beta = \left( {\frac{t}{{t + 0.01}}} \right)\left( {\frac{{100}}{{1 + {{1.005}^{ - 12t + a}}}}} \right). $ | (4) |
式中:t为道路使用年限, a;a为基于场地设计和气候相关性的等效因素.
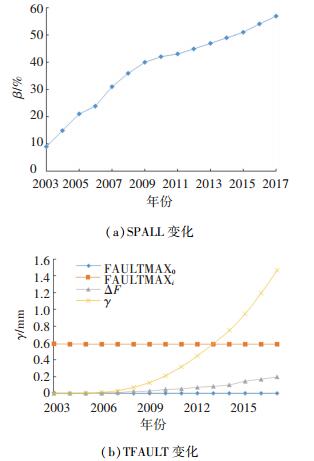
从图 6(a)中可以得出, 随着使用年限的增加, SPALL值呈上升趋势.分析原因是由于在行车荷载和气候的作用下, 材料本身发生损坏, 随着冻融循环次数的增加, 板角断裂加重. 2006—2010年SPALL值增长较快, 这是由于在这4 a间黑龙江省的冻融循环次数较多, 冻融循环次数可达到130次左右.
|
图 6 SPALL和TFAULT变化曲线 Figure 6 SPALL and TFAULT curves |
TFAULT是道路使用年限内每月平均错台递增量的累计, TFAULT指标的表示为
| $ \gamma = \mathop \sum \limits_{i = 1}^m \Delta F. $ | (5) |
式中:ΔF为每月的平均错台递增量, mm;m为月份数.
在图 6(b)中, FAULTMAXi表示每月最大的错台量、FAULTMAX0表示每月最初的错台值, 从图中可以看出, 这两个指标随着道路使用年限的增大呈现下降趋势, 分析原因是由于道路通车后在行车荷载的反复作用下, 板体出现错台, 且错台的最初值较大, 随着道路使用年限的增加, 错台发生趋于稳定, 因此每月的错台量呈下降趋势;由于错台累计值逐年增加, 因此γ和ΔF两个指标随着道路使用年限的增大呈现上升趋势, 错台4个指标的曲线分布均与实际情况吻合.
3.2 IRI与各指标线性相关性验证对CRK、TFAULT、SPALL和SF 4个指标和国际平整度指数的相关性进行验证, 以鹤大高速公路为例, 结合得到的4个指标2003—2017年的预测值, 分别建立国际平整度指数实测值和4个预测指标对应的散点图并进行相关性拟合, 如下图 7所示.由于决定性系数R2是趋势线拟合程度的指标, 趋势线的R2值均接近1, 说明该数值拟合程度越高, 趋势线的可靠性就越高. CRK、TFAULT、SPALL和SF 4个指标的R2分别为0.988、0.873、0.936、0.988, 说明季冻区水泥路面国际平整度指数预测修正模型由上述4项指标的线性拟合是合理的.
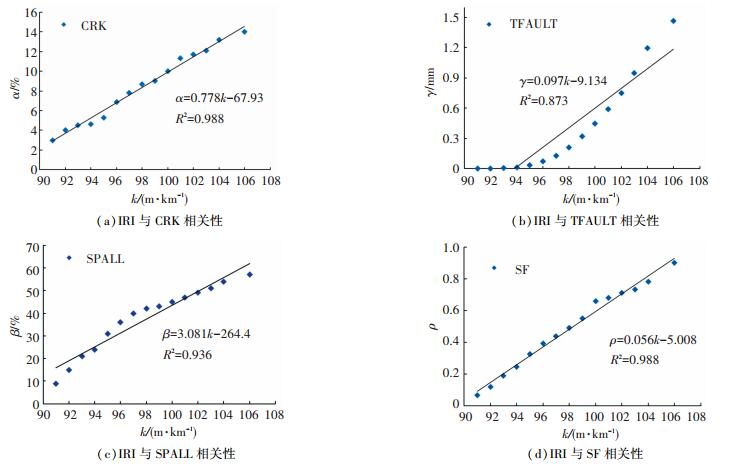
|
图 7 IRI与各指标相关性 Figure 7 IRI and various indicators |
由于数据量的限制, 从路面调查数据中选取24条路段用于线性回归, 8条路段用于验证回归模型的正确性.利用SPSS软件对鹤大高速公路、肇肇公路、哈肇公路等3条试验路近24条路段CRK、SPALL、TFAULT和SF 4项指标的所有预测值和IRI的实测值进行线性回归.选取IRI作为因变量, CRK、SPALL、TFAULT和SF作为自变量, IRI的单位采用美式单位标准.对回归模型进行分析时, 被解释变量(因变量)和解释变量(自变量)的决定性系数为0.999, 调整的决定性系数也为0.999, 回归方程的标准估计误差为0.16.拟合的方程中有4个解释变量, 调整的决定性系数为0.999, 接近于1, 因此认为该拟合度高, 被解释变量可以被模型解释的部分占比为99.9%.
回归模型中被解释变量的总计平方和为294.933, 回归平方和以及回归均方分别为294.637和73.659, 残差平方和以及残差均方分别为0.296和0.03, 统计量F等于平均回归平方和与平均残差平方和之比, 若F值过小说明自变量对因变量的解释力度很差, 拟合的回归直线没有意义, 若F值较大且显著性值Sig.较小, 则说明线性方程回归明显. F值很大, 为355.131, 且Sig.显著性值为0, 小于0.05, 所以该回归直线有意义, F检验的被解释变量与全部的解释变量之间线性关系是显著的, 表明可建立线性模型.
表 1中数值第1列为解释变量的偏回归系数;数值第2列为解释变量偏回归系数的标准误差;数值第3列为解释变量标准化偏回归系数;数值第4列为回归系数显著性检验中统计量的观测值t;数值第5列为解释变量的容忍度和膨胀因子(显著性水平).显著性水平均低于0.05, 4个变量的回归系数显著性检验中统计量的观测值t都大于显著性水平, 所以拒绝零假设.偏回归系数和0差异明显, 4项解释变量与被解释变量的线性关系是显著的, 所以4个自变量均保留在方程中, 不予剔除.偏回归系数表明了各个指标的权值.标准化偏回归系数的绝对值的大小表明了参数对IRI影响的大小, 标准化偏回归系数都是正值, 说明参数与IRI均是正相关.指标IRI1对应的偏回归系数为89.525.由于IRI1是美式计算单位得出的, 将其换算为我国规范下的单位, 换算后的IRI1为1.382 m/km.
| 表 1 回归指标系数 Table 1 Regression index coefficients |
因此, 基于MEPDG的季冻区水泥路面IRI预测修正模型中的IRI1值为1.382, C1为10.208, C2为8.052, C3为2.69, C4为7.313.
4 验证修正后的预测模型 4.1 同一路段不同时期修正模型验证选择鹤大公路的剩余调查路段近10 a实测IRI值对季冻区水泥路面平整度预测修正模型进行验证, 由于边缘车道交通量相对较小且受非机动车的影响大, 因此对路面平整度的现场调查数据的选择为单幅内侧两个车道.利用SPSS软件分别将平整度指数的实测值和基于MEPDG的IRI修正模型预测值, 平整度指数的实测值和基于MEPDG的IRI模型预测值, 平整度指数的实测值和传统模型预测值分别进行拟合, 如图 8所示, 横轴为高速公路现场调查的平整度指数实测值km, 纵轴表示平整度指数的预测值kp.将传统模型IRI的预测值与现场调查的IRI实测值进行拟合, 得到的决定性系数R2=0.802;利用基于MEPDG的季冻区水泥路面平整度指数预测模型的IRI预测值与IRI实测值进行线性拟合, 得到的决定性系数R2=0.827;利用基于MEPDG的季冻区水泥路面平整度指数预测修正模型的IRI预测值与IRI实测值进行拟合, 得到的决定性系数R2=0.997, 证明该模型拟合程度高.
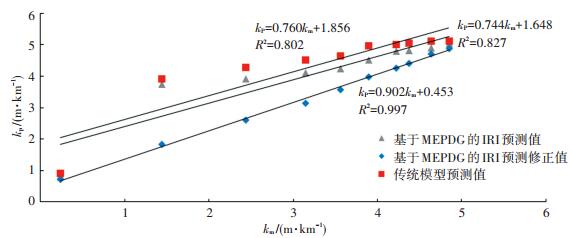
|
图 8 平整度指数IRI预测值与实测值相关性拟合 Figure 8 Flatness index IRI prediction value and the measured value of the correlation fit |
为避免用一条公路路段验证预测修正模型的偶然性, 选择鹤大高速公路、肇肇公路、哈肇公路等3条试验路8条路段(编号1~8)同一年现场调查数据进行模型验证.由于所采集的路面数据在使用性能、交通量方面分布不够均匀, 故将数据较密集段进行了平均处理, 以使数据分布均匀.横坐标为8条现场调查路段, 纵坐标为IRI值, 根据实测和预测结果分别绘制IRI实测值曲线、传统模型预测IRI曲线、基于MEPDG预测IRI曲线和基于MEPDG修正预测IRI曲线如图 9所示, 从图中可以得到基于MEPDG的预测修正模型的IRI预测值与实际值更为接近.
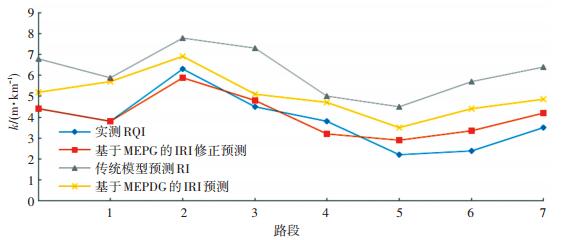
|
图 9 基于MEPDG平整度修正模型预测效果 Figure 9 Effect prediction based on MEPDG flatness correction model |
1) 气候、交通、材料参数均对构成国际平整度指数的4个指标CRK、TFAULT、SPALL和SF有显著影响.
2) CRK、TFAULT、SPALL和SF 4个指标和国际平整度指数线性拟合可靠度高.线性相关决定性系数R2分别为0.988、0.873、0.936、0.988, 证明季冻区IRI由上述4个指标线性构成合理.
3) 利用交通量、降水、降雨、潮湿天数、冻融循环次数、路面材料性能等参数可对季冻区水泥路面国际平整度指数进行预测.预测模型的决定系数R2为0.999, 显著性水平为0, 表明回归模型显著.
4) 运用MEPDG建立的季冻区水泥路面IRI预测修正模型预测精度高.将修正模型与未修正模型和传统模型在同一段路不同时期和不同路段同一时期进行验证表明, 修正后的模型预测水平均好于其他模型.
| [1] |
周岚.高速公路沥青路面使用性能评价及预测研究[D].南京: 东南大学, 2015 ZHOU Lan.Research on performance evaluation and prediction of highway asphalt pavement[D].Nanjing: Southeast University, 2015 |
| [2] |
KER H W, LEE Y H, WU P H. Development of fatigue cracking prediction models using long-term pavement performance database[J]. Journal of Transportation Engineering, 2008, 134(11): 477. DOI:10.1061/(ASCE)0733-947X(2008)134:11(477) |
| [3] |
刘伯莹, 姚祖康. 沥青路面使用性能预测[J]. 中国公路学报, 1991, 4(2): 4. LIU Boying, YAO Zukang. Asphalt pavement performance prediction[J]. Journal of China Highway, 1991, 4(2): 4. |
| [4] |
张占军, 王笑风. 沥青路面使用性能的双参数修正预测模型[J]. 交通运输工程学报, 2007, 7(5): 54. ZHANG Zhanjun, WANG Xiaofeng. Two-parameter modified predictive model of asphalt pavement performance[J]. Journal of Traffic and Transportation Engineering, 2007, 7(5): 54. DOI:10.3321/j.issn:1671-1637.2007.05.012 |
| [5] |
KARAAAHIN M, TERZI S. Performance model for asphalt concrete pavement based on the fuzzy logic approach[J]. Transport, 2014, 29(1): 18. DOI:10.3846/16484142.2014.893926 |
| [6] |
ANASTASOPOULOSP C, SARWAR M T, SHANKAR V N. Safety-oriented pavement performance thresholds: accounting for unobserved heterogeneity in a multi-objective optimization and goal programming approach[J]. Analytic Methods in Accident Research, 2016, 12(12): 35. |
| [7] |
CHU C Y, DURANGO-COHEN P L. Empirical comparison of statistical pavement performance models[J]. Journal of Infrastructure Systems, 2016, 14(2): 138. |
| [8] |
ROBERTS C A, ATTOH-OKINE N O. A comparative analysis of two artificial neural networks using pavement performance prediction[J]. Computer-Aided Civil and Infrastructure Engineering, 2010, 13(5): 339. |
| [9] |
王国晓, 安景峰, 陈荣生. 灰色理论在路面使用性能预测中的应用[J]. 公路交通科技, 2002, 19(3): 16. WANG Guoxiao, AN Jingfeng, CHEN Rongsheng. Application of gray theory in pavement performance prediction[J]. Road Traffic Technology, 2002, 19(3): 16. DOI:10.3969/j.issn.1002-0268.2002.03.005 |
| [10] |
杜二鹏, 马松林, 景海民. 基于灰色系统理论的沥青路面使用性能预测[J]. 同济大学学报(自然科学版), 2010, 38(8): 1161. DU Erpeng, MA Songlin, JING Haimin. Performance prediction of asphalt pavement based on gray system theory[J]. Journal of Tongji University (Natural Science Edition), 2010, 38(8): 1161. DOI:10.3969/j.issn.0253-374x.2010.08.011 |
| [11] |
陈健, 游玮, 田金信. 应用神经网络进行经济预测方法的改进[J]. 哈尔滨工业大学学报, 2006, 38(6): 897-898. CHEN Jian, YOU Wei, TIAN Jinxin. Improvement of economic forecasting method based on neural network[J]. Journal of Harbin Institute of Technology, 2006, 38(6): 897. DOI:10.3321/j.issn:0367-6234.2006.06.019 |
| [12] |
周文献, 李明利, 孙立军. 基于改进神经网络的水泥路面使用性能预测模型[J]. 同济大学学报(自然科版), 2006, 34(9): 1191. ZHOU Wenxian, LI Mingli, SUN Lijun. Prediction model of cement pavement performance based on improved neural network[J]. Journal of Tongji University (Natural Science Edition), 2006, 34(9): 1191. |
| [13] |
张涛.基于人工神经网络的路面使用性能预测[D].哈尔滨: 哈尔滨工业大学, 2009 ZHANG Tao.Performance prediction of pavement based on artificial neural network[D].Harbin: Harbin Institute of Technology, 2009 http://cdmd.cnki.com.cn/Article/CDMD-10213-2010027610.htm |
| [14] |
贺得荣. 基于组合预测模型对公路沥青路面使用性能预测的研究[J]. 公路工程, 2015, 40(6): 264. HE Derong. Study on the prediction of highway asphalt pavement performance based on combination forecasting model[J]. Road Construction, 2015, 40(6): 264. DOI:10.3969/j.issn.1674-0610.2015.06.058 |
| [15] |
武建民, 刘大彬, 李福聪, 等. 基于时间序列分析法的沥青路面使用性能预测[J]. 长安大学学报(自然科学版), 2015, 35(3): 1. WU Jianmin, LIU Dabin, LI Fucong, et al. Study on performance prediction of asphalt pavement based on time series analysis[J]. Journal of Changan University (Natural Science Edition), 2015, 35(3): 1. DOI:10.3969/j.issn.1671-8879.2015.03.001 |
| [16] |
孙立军, 刘喜平. 路面使用性能的标准衰变方程[J]. 同济大学学报(自然科学版), 1995, 23(5): 512. SUN Lijun, LIU Xiping. Standard decay equation of pavement performance[J]. Journal of Tongji University (Natural Science Edition), 1995, 23(5): 512. |
| [17] |
汪海年, 张琛, 尤占平, 等. 基于数理统计方法的MEPDG车辙预估模型校正[J]. 长安大学学报(自然科学版), 2013, 33(6): 1. WANG Hainian, ZHANG Chen, YOU Zhanping, et al. MEPDG rut predictive model calibration based on mathematical statistics[J]. Journal of Chang'an University (Natural Science Edition), 2013, 33(6): 1. DOI:10.3969/j.issn.1671-8879.2013.06.001 |
| [18] |
LI Qiang, XIAO D, KELVIN P, et al. Mechanistic-empirical pavement design guide (MEPDG): a bird′s-eye view[J]. Journal of Modern Transportation, 2011, 19(2): 114. DOI:10.1007/BF03325749 |
| [19] |
安少科.基于MEPDG的四川典型区域沥青路面性能与状况预测[D].成都: 西南交通大学, 2016 AN Shaoke.Measurement and performance prediction of asphalt pavement in typical region of Sichuan Province based on MEPDG[D].Chengdu: Southwest Jiaotong University, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10613-1016177332.htm |
| [20] |
代考.广东省MEPDG气候文件与路面性能预测[D].广州: 华南理工大学, 2014 DAI Kao.Guangdong Province MEPDG climate document and pavement performance prediction[D].Guangzhou: South China University of Technology, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10561-1014063769.htm |
 2018, Vol. 50
2018, Vol. 50


