张力腿平台是一种深海海洋结构物, 筋腱与张力腿平台和海底桩基的连接由张力腿平台筋腱连接器完成[1].张力腿平台在工作过程中会随着海流和海浪产生垂荡、纵荡和横荡等运动, 造成筋腱连接器产生巨大的转矩;同时为了保证平台稳定, 在张力腿平台安装完成后筋腱内部还要保留一分预紧力, 该预紧力会对连接器造成一定的压力, 因此在连接器中设计有球形橡胶轴承.球形橡胶轴承是一种橡胶与金属层叠的结构, 橡胶相对较低的剪切模量为连接器提供一定的摆动柔性, 金属层叠结构使其可以承受巨大压力.因此有必要对橡胶轴承的刚度进行分析研究.
球形橡胶轴承在很多工程领域中都有应用[2-4].然而对于筋腱连接器用球形橡胶轴承, 仍缺乏相关试验研究.由于橡胶材料的高度非线性特性, 因此使用超弹性本构模型结合有限元方法研究橡胶材料的力学特性[5].为了获得材料参数, 需要对橡胶开展一系列材料试验[6-8].已经有很多研究者[9-11]用非线性有限元法对球形弹性轴承进行研究.然而, 对于筋腱连接器用橡胶轴承的研究, 只有Hannus等[12]使用有限元法在线弹性范围内对橡胶轴承做了数值仿真.
本文研究一种球形橡胶轴承专用刚度试验系统, 对5种不同材料或结构的筋腱连接器用球形橡胶轴承进行了压缩与摆动试验.对相应的橡胶材料开展试验, 用有限元法进行仿真.对有限元仿真及试验结果进行了对比验证, 分析了3种本构模型的有效性及准确性, 研究了橡胶材料、金属层数对橡胶轴承压缩刚度和摆动刚度的影响.
1 球形橡胶轴承试验方案 1.1 球形橡胶轴承试件三选择5种球形橡胶轴承进行对比试验, 橡胶材料由铁岭市银港橡胶厂提供, 金属层使用45号钢.该柔性体试件及与其配合的筋腱连接器内部结构如图 1所示, 可以看到柔性体底部与筋腱相连, 承受筋腱上的拉伸载荷与转矩.

|
图 1 筋腱连接器及柔性体试件 Figure 1 Geometry dimension and details of specimens |
表 1为5种球形橡胶轴承的具体尺寸参数, 为了做对比试验, 分别对橡胶材料和钢板层数进行控制:编号D3、D4、D5这3种球形橡胶轴承均使用相同的丁腈橡胶材料(NBR), 橡胶与钢板层数不同, 而橡胶与钢板的总厚度相同;编号D3、Q3、T3这3种球形橡胶轴承的橡胶分别使用了丁腈橡胶(NBR)、氢化丁腈橡胶(HNBR)与天然橡胶, 橡胶与钢板的总厚度相同, 层数也相同.
| 表 1 试件参数 Table 1 Test parameters |
为了测量数据及施加摆动载荷, 设计了刚度试验装置, 如图 2(a)所示.该试验装置底部有4个最大量程为50 t的压力传感器, 顶部有两个铰链可以将压力转化为转矩, 铰链间安装了量程为15 t的压力传感器, 此外试验装置上还设置有角度传感器和位移传感器.如图 2(b)所示, 传感器通过采集器与笔记本电脑连接, 使用Labview软件编写了数据采集程序与界面.该试验由长春科新TAD3000 300T压力试验机提供外部载荷.

|
图 2 试验系统 Figure 2 Experimental system |
采用静力试验方法, 对球形橡胶轴承开展压缩与摆动试验.压缩试验机通过液压系统输出载荷, 通过手动控制液压系统的送油阀和回油阀控制压力.关闭回油阀, 打开送油阀, 压力机施加压缩载荷;同时关闭回油阀和送油阀, 压力机保持压力不变, 打开回油阀, 关闭送油阀, 压力机卸载.
在压缩试验中, 使用压缩试验机直接对试件施加压缩载荷, 使用位移控制压缩载荷, 人工控制压缩速度, 压缩速度约为1 mm/min.通过数据采集程序观察压缩位移, 所有试件最大压缩位移均为3 mm.在试验过程中对试件反复压缩6次, 其中前5次用于弱化橡胶材料的Mullins效应对试验结果的影响, 取最后一次数据与仿真结果做对比.
在摆动试验中, 压缩试验机通过两个铰链将压缩载荷转化为摆动载荷.同样使用位移控制载荷, 压缩速度约为3 mm/min, 所有试件的最大摆动角度均为8°.其他试验过程与压缩试验相同.
2 橡胶材料力学试验为了使球形橡胶轴承仿真结果更为准确, 需要获得精确的橡胶材料数据.进行橡胶的单轴拉伸试验可以得到橡胶材料参数, 但是仅有单轴拉伸试验数据无法描述复杂应力状态下的橡胶变形, 因此还需要对橡胶材料开展简单剪切试验和体积压缩试验.
橡胶试件材料包括天然橡胶、丁腈橡胶和氢化丁腈橡胶.为了防止橡胶性能产生差异, 橡胶材料力学试验所用试件与球形橡胶轴承试件采用相同批次的橡胶材料, 橡胶试件的制备满足ISO 23529:2010国际标准.为了防止个体差异, 每种试验制作了5件试件, 数据处理过程中去掉差异最大的数据, 对其余数据取平均值.该试验在哈尔滨工程大学力学实验室进行.
2.1 单轴拉伸试验橡胶单轴拉伸试验方案参照GBT 528—2009[13], 试验试件采用1A型片状哑铃状试件, 试件厚度2 mm, 见图 3(a).试验在Zwick Z010电子万能试验机上进行, 该试验机可以自动记录拉力与位移数据.试验在室温下进行, 为了获得稳定的橡胶材料数据, 对试件反复拉伸10次, 夹具的拉伸速度为100 mm/min, 拉伸变形范围为0~100 mm, 取最后一次试验数据用于计算材料参数.

|
图 3 单轴拉伸试验 Figure 3 Uniaxial tension test |
单轴拉伸试验的名义拉伸应力σ(MPa)与名义拉伸应变ε可以通过试验机记录的拉力Ft(N)与位移lt(mm)计算得到, 对于本次试验所用试件, 应力应变可以由方程(1)得到. 图 3(b)所示为3种试件单轴拉伸试验的应力应变曲线.
| $ \sigma = {F_{\text{t}}}/12, \varepsilon = {l_{\text{t}}}/33. $ | (1) |
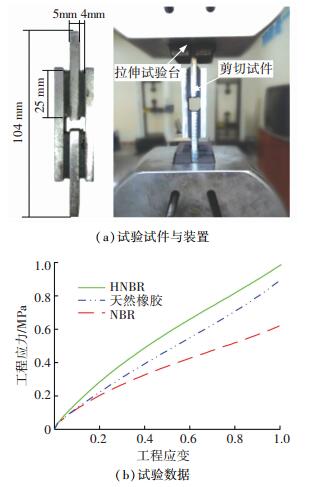
橡胶简单剪切试验方案参照ISO 1827:2011[14], 试验试件采用4面剪力试件, 该试件内有4片橡胶通过粘合剂固定在钢板上, 橡胶片宽度为20 mm, 如图 4(a)所示.试验在拉压试验机上进行, 该试验机可以自动记录拉力与位移数据.试验在室温下进行, 为了获得稳定的橡胶材料数据, 对试件反复拉伸10次, 夹具拉伸速度为10 mm/min, 拉伸变形范围为0~8 mm, 取最后一次试验数据用于计算材料参数.
|
图 4 简单剪切试验 Figure 4 Simple shear test |
简单剪切试验的名义剪切应力τ(MPa)与名义剪切应变γ可以通过试验机记录的拉力Fs(N)与位移ls(mm)计算得到, 对于本次试验所用试件, 应力应变可以由式(2)得到. 图 4(b)所示为3种试件简单剪切试验的应力应变曲线.
| $ \tau = {F_{\text{s}}}/1000, \;\;\;\gamma = {l_{\text{s}}}/8. $ | (2) |
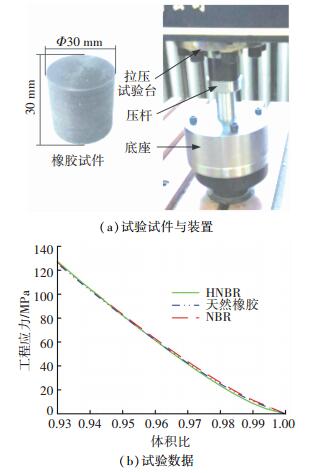
体积压缩试验方案参照BS 903-5—2004[15], 该试验有特殊的工装, 工装包括压杆与底座, 其中底座分为上下两部分, 通过螺栓连接, 如图 5(a)所示.该试验采用圆柱型试件, 试件外径与底座内径大小相同.试验过程中, 将试件塞入底座中, 试件表面涂抹低黏度硅油减小摩擦力对实验结果的影响.底座放在压缩试验台上, 压杆与压力机连接, 对试件缓慢施加压缩载荷.试验在拉压试验机进行, 该试验机可以自动记录拉力与位移数据.试验在室温下进行, 为获得稳定的橡胶材料数据, 对试件反复压缩10次, 压杆的压缩速度为1 mm/min, 压缩变形范围0~1.5 mm, 取最后一次试验数据用于计算材料参数. 图 5(b)为3种试件体积压缩试验的应力应变曲线.
|
图 5 体积压缩试验 Figure 5 Volumetric compression test |
体积压缩试验的静水压力p0(MPa)与体积比Rv可以通过试验机记录的压力Fc(N)与位移lc(mm)计算得到, 对于本次试验所用试件, 体积比与静水压力可以由方程(3)得到:
| $ \begin{array}{l} \;p = {F_{\rm{c}}}/\left( {225{\rm{ \mathsf{ π} }}} \right), \\ {R_{\rm{v}}} = {\left( {30 - l} \right)_{\rm{c}}}/30. \end{array} $ | (3) |
使用Abaqus/Standard对橡胶轴承进行非线性静力学仿真, 当橡胶轴承承受竖直压缩载荷时, 其应力状态是空间轴对称的, 为了减少计算成本, 因此使用二维轴对称模型进行压缩仿真;当橡胶轴承承受摆动载荷时, 使用1/2三维模型进行摆动仿真.
使用线弹性本构模型描述45号钢的力学特性, 其杨氏模量E=2.06×105 MPa, 泊松比v=0.3.与金属材料不同, 橡胶材料具有明显的非线性特性, 单纯的弹性模量不足以描述橡胶材料的特性, 因此使用超弹性本构模型来描述橡胶材料的应力应变特性. Abaqus提供了多种超弹性本构模型, 其中包括:Mooney-Rivlin模型、Neo-Hookean模型、完全多项式模式、缩减多项式模型、Yeoh模型和Ogden模型等[16], 为了获得精确的仿真结果, 本论文选用了Mooney-Rivlin模型、Neo-Hookean模型和Yeoh模型进行对比.
由于Abaqus自带的曲线拟合工具无法拟合简单剪切试验结果, 因此使用ANSYS APDL曲线拟合工具确定本构模型参数, 结合图 3~5所给出的材料试验数据, 得到最终的本构模型参数如表 2所示.
| 表 2 本构模型参数 Table 2 Constitutive model parameters |
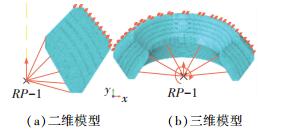
图 6为3层金属橡胶试件两种模型的网格划分图.二维模型中两种材料均采用轴对称单元, 金属材料部分采用CAX4R单元, 橡胶材料部分采用CAX4RH单元.在三维模型中两种材料均采用实体单元, 金属材料部分采用C3D8R单元, 橡胶材料部分采用C3D8RH单元.对于近似不可压缩材料, 在仿真过程中可能发生沙漏和体积锁定的问题.虽然使用二阶单元可以解决这些问题, 但是在橡胶发生大变形时, 这些单元会严重畸变.使得计算难以收敛, 并且结果也不准确.
|
图 6 3层金属橡胶试件的有限元模型 Figure 6 FE model of sample with 3 rubber layers |
在所有模型的仿真中均设置一个载荷步, 增量步固定为0.05, 打开大变形开关.如图 6所示, 橡胶轴承顶板固定, 在球心处设置参考点RP-1, 在相互作用模块中使该参考点与橡胶轴承底板耦合.在2D分析中, 该参考点上施加3 mm的y方向上的位移.在3D分析中在该参考点上施加绕z方向摆动的0.14 rad的角度, 并在对称面上施加对称约束.
4 试验与仿真结果对比与分析 4.1 压缩刚度试验在压缩刚度试验中压力机直接压缩试件, 此时球形橡胶轴承所承受的压力Fc由4个底部力传感器测量得到, 压缩位移dc由位移传感器测量得到, 因此球形橡胶轴承压缩刚度Kc可以表示为
| $ {K_{\rm{c}}} = \frac{{{F_{\rm{c}}}}}{{{d_{\rm{c}}}}}. $ |
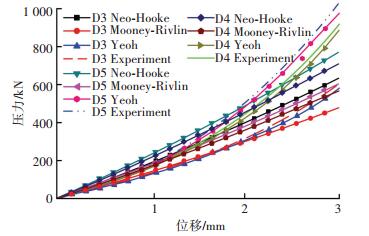
图 7为具有不同金属层数的球形橡胶轴承压缩试验与仿真曲线, 其中虚线为试验结果, 其他曲线为仿真结果.在最大位移处, 使用不同模型的仿真结果(Rs)相对于试验结果(Rt)的误差如表 3所示, 该误差通过公式(Rt–Rs)/Rt计算得到.由试验数据发现, 丁腈橡胶的球形橡胶轴承压缩刚度会随着位移增加而上升;随着金属层数的增加, 每一层橡胶的厚度变薄, 使橡胶层的形状系数增加, 因此轴承压缩刚度也会上升, 并且具有更多金属层数的橡胶轴承刚度上升梯度更大.
|
图 7 不同层数橡胶轴承压缩试验与仿真结果 Figure 7 Compression test and simulation results of flexjoints with different layer quantity |
| 表 3 不同层数橡胶轴承压缩仿真误差 Table 3 Error of compression simulation results of flexjoints with different layer quantity |
图 8为具有不同橡胶材料的球形橡胶轴承压缩试验与仿真曲线.在最大位移处, 使用不同模型的仿真结果误差如表 4所示.由试验数据可以发现, 随着位移增加, 另外两种材料的球形橡胶轴承压缩刚度也会上升.与橡胶材料试验结果类似, 使用氢化丁腈橡胶与天然橡胶的橡胶轴承压缩刚度比较接近;根据材料试验结果可知, 由于氢化丁腈橡胶的杨氏模量最大, 丁腈橡胶的杨氏模量最小, 因此天然橡胶轴承的压缩刚度略小于氢化丁腈橡胶轴承, 而略大于丁腈橡胶轴承.

|
图 8 不同材料橡胶轴承压缩试验与仿真结果 Figure 8 Compression test and simulation results of flexjoints with different rubber material |
| 表 4 不同材料橡胶轴承压缩仿真误差 Table 4 Error of compression simulation results of flexjoints with different rubber material |
对比压缩试验与仿真结果发现, 使用Ye`oh本构模型的仿真结果可以很好地拟合试验结果.当位移较小(本试验≤1.5 mm)时, 使用Mooney- Rivlin本构模型也可以得到比较接近的结果, 该结果略大于试验结果;使用Neo-Hooke本构模型的仿真结果略大于其他两种本构模型的结果.当位移更大时, Mooney-Rivlin本构模型无法表现出刚度迅速上升的阶段, 因此仿真结果会小于试验结果.
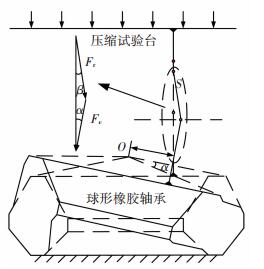
4.2 摆动刚度试验在摆动刚度试验中, 可以通过顶部力传感器测得压力Fr, 并使用图 2所示的角度传感器测量橡胶轴承的转动角度α. 图 9为摆动试验的受力分析图, 当球形橡胶轴承转动时, 铰链两侧的二力杆与竖直方向的虚线可以组成左上角所示的三角形.该三角形中距离S与转动角度α已知, β角是α的函数, 因此通过解该三角形可以得到垂直于橡胶轴承顶端的力Fc与Fr和α的关系, 转动圆形O与Fc作用方向的距离为l, 将Fc与l相乘即可得到转矩Tr.因此球形橡胶轴承摆动刚度Kr可以表示为
|
图 9 摆动试验受力分析 Figure 9 Force analysis of rotation test |
| $ {K_{\rm{r}}} = \frac{{114.5\sin \left( {0.87{\rm{ \mathsf{ π} }} - \alpha } \right){F_{\rm{r}}}}}{{\alpha \cos \alpha /2}}. $ |
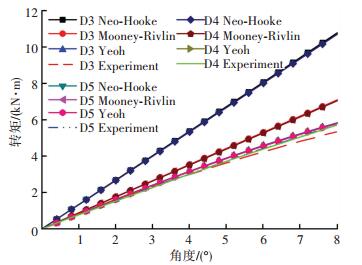
图 10为具有不同金属层数的球形橡胶轴承摆动试验与仿真曲线.在最大转角处, 使用不同模型的仿真结果误差如表 5所示.
|
图 10 不同层数橡胶轴承摆动试验与仿真结果 Figure 10 Rotation test and simulation results of flexjoints with different layer quantity |
| 表 5 不同材料橡胶轴承压缩仿真误差 Table 5 Error of compression simulation results of flexjoints with different rubber material |
由试验数据发现, 丁腈橡胶的球形橡胶轴承摆动刚度会随着转角增加而下降;金属层数对轴承摆动刚度几乎没有影响.
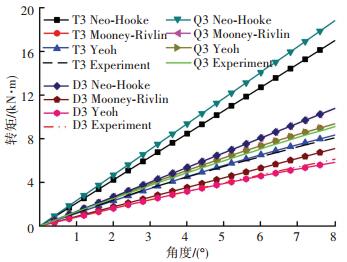
图 11所示为具有不同橡胶材料的球形橡胶轴承压缩试验与仿真曲线.在最大转角处, 使用不同模型的仿真结果误差如表 6所示.由试验数据可以发现, 随着角度增加, 另外两种材料的球形橡胶轴承摆动刚度也会下降.与橡胶材料试验结果类似, 使用氢化丁腈橡胶与天然橡胶的橡胶轴承压缩刚度比较接近, 由于与压缩刚度关系相同的原因, 氢化丁腈橡胶的轴承转动刚度略大于天然橡胶轴承, 丁腈橡胶的轴承转动刚度最小.
|
图 11 不同材料橡胶轴承摆动试验与仿真结果 Figure 11 Rotation test and simulation results of flexjoints with different rubber material |
| 表 6 不同材料橡胶轴承压缩仿真误差 Table 6 Error of compression simulation results of flexjoints with different rubber material |
通过对比摆动试验与仿真结果发现, 使用Yeoh本构模型的仿真结果可以很好地拟合试验结果.当摆动角度较小(本试验≤2°)时, 使用Mooney-Rivlin本构模型与试验结果拟合效果也很好.而使用Neo-Hooke本构模型的仿真结果远大于试验结果, 误差极大.
5 结论本文设计了刚度试验台, 对5种不同材料或结构形式的球形橡胶轴承进行了压缩与摆动试验, 并对橡胶轴承所用橡胶进行了材料性能试验, 将试验结果输入有限元软件进行了仿真.通过对试验数据与仿真结果进行对比分析, 得到如下结论:
1) 丁腈橡胶、氢化丁腈橡胶与天然橡胶制造的球形轴承, 压缩刚度均会随着压缩位移上升而上升, 摆动刚度均会随着摆动角度上升而下降;
2) 球形橡胶轴承中金属层数的增加会提高其压缩刚度, 而对摆动刚度几乎没有影响, 因此当需要较高压缩刚度及较低摆动刚度时, 只需要增加金属层数即可;
3) 使用Yeoh本构模型对球形橡胶轴承进行压缩与摆动载荷下的仿真, 可以得到很好的仿真结果;使用Mooney-Rivlin本构模型进行仿真, 在变形较小条件小也可以得到较为准确的仿真结果;使用Neo-Hooke本构模型进行仿真, 仿真结果误差最大, 其中摆动载荷下的结果完全不可接受.
| [1] |
CHAKRABARTI S. Handbook of Offshore Engineering[M]. Oxford: Elsevier, 2005.
|
| [2] |
CHEN Gaosheng, YANG Yan. Stiffness design, simulation and test of laminated spherical elastomeric bearing[J]. Hangkong Dongli Xuebao/journal of Aerospace Power, 2015, 30(6): 1512. DOI:10.13224/j.cnki.jasp.2015.06.029 |
| [3] |
RAM M V.Design, modelling and experimental validation on a typical flex bearing joint of rocket motor nozzle[D].Hyderrabad: Jawaharlal Nehru Technological University, 2012
|
| [4] |
ZHANG Xiaoguang, LIU Yu, REN Junxue, et al.Nonlinear finite element analysis of the SRM flexible joint[C]//53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference.Hawaii: American Institute of Aeronautics and Astronautics, 2012: 301.DOI: 10.2514/6.2012-1453
|
| [5] |
GENT A N, CAMPION R P. Engineering with rubber:how to design rubber components[M]. Munich: Hanser Gardner Publications, Carl Hanser Publishers, 2001.
|
| [6] |
KOPROWSKI N, JOHLITZ M, DIEBELS S. Compressible rubber materials: experiments and simulations[J]. Archive of Applied Mechanics, 2012, 82(8): 1117. DOI:10.1007/s00419-012-0616-6 |
| [7] |
CROCKER L, DUNCAN B.Measurement methods for obtaining volumetric coefficients for hyperelastic modelling of flexible adhesives[R].Teddington: National Physical Laboratory, 2001
|
| [8] |
MOREIRA D C, NUNES L C S. Comparison of simple and pure shear for an incompressible isotropic hyperelastic material under large deformation[J]. Polymer Testing, 2013, 32(2): 240. DOI:10.1016/j.polymertesting.2012.11.005 |
| [9] |
KUMAR A E, MURTHY V B, MOHAN R C, et al. Study of non-linear static behavior of flex seal of rocket nozzle by varying number of shims[J]. Materials Today: Proceedings, 2015, 2(4): 1613. DOI:10.1016/j.matpr.2015.07.063 |
| [10] |
LAMPANI L, ANGELINI F, BERNABEI M, et al. Finite element analysis of a solid booster flexible bearing joint for thrust vector control[J]. Aerotecnica & Spazio, The Journal of Aerospace Science, Technology and Systems, 2012, 91(1): 53. DOI:10.19249/ams.v91i1-2.79 |
| [11] |
CHEN Gaosheng, ZHANG Lianhong, LI Fuping, et al. finite element analysis for the influence of spherical layered elastomeric bearing structure on the mechanical behavior[J]. Journal of Materials Engineering, 2009, 53(10): 15. DOI:10.3969/j.issn.1001-4381.2009.10.004 |
| [12] |
HANNUS K.A flexelement analysis[C]//23rd Annual Offshore Technology Conference.Dallas: OTC Program Committee, 1991: 187.DOI: 10.4043/6581-MS
|
| [13] |
中橡集团沈阳橡胶研究设计院.硫化橡胶或热塑性橡胶拉伸应力应变性能的测定: GBT 528-200[S].北京: 中华人民共和国国家质量监督检验检疫总局, 2009
|
| [14] |
British Rubber Manufacturers' Association Ltd.Rubber, vulcanized or thermoplastic-determination of shear modulus and adhesion to rigid plates-Quadruple shear methods: BS ISO 1827: 2011[S].London: Standards Policy and Strategy Committee, 2011
|
| [15] |
British Rubber Manufacturers' Association Ltd.Guide to the application of rubber testing to finite element analysis: BS 903-5: 2004[S].London: Standards Policy and Strategy Committee, 2004
|
| [16] |
HIBBITT H, KARLSSON B, SORENSEN P. Abaqus analysis user's manual[M]. Providence: Dassault Systèmes Simulia Corp, 2016.
|
 2018, Vol. 50
2018, Vol. 50


