2. 哈尔滨工程大学 深海工程技术研究中心,哈尔滨 150001
2. Deepwater Engineering Research Center, Harbin Engineering University, Harbin 150001, China
仿生推进技术及其在水下机器人中的应用已经得到了世界上很多有利用海洋条件国家的关注.许多研究将鱼鳍简化为拍动翼, 并开展大量水动力实验工作以开发能被用于水下机器人的仿生拍动翼推进器[1-8]. Jones等[9]、Pan等[10]、李宁宇等[11]、Mantia等[12]应用基于势流理论的面元法对拍动翼的推进性能进行数值计算, 并研究各运动参数对拍动翼推进性能的影响. Lewin等[13]、Lu等[14]、Su等[15]、文敏华等[16]应用基于动网格技术的CFD方法数值模拟拍动翼绕流问题, 分析在黏性流场中拍动翼的水动力性能.上述对于刚性拍动翼的实验和数值研究已经取得了一些有价值的成果, 但实际鱼类在游动过程中, 鱼鳍由于水动力的作用将发生柔性变形.因此, 以刚性拍动翼为模型所开展的工作与真实鱼鳍相比存在较大差距, 研究柔性变形对拍动翼/鳍推进性能的影响是设计具备可与鱼鳍优越性能相比拟的推进器的必由之路. Liu[17]提出了拍动翼的弦向和展向柔性变形模式, 并利用面元法分析变形相位角和变形幅度对水动力性能的影响. Wang等[18]使用FLUENT软件模拟拍动翼的升沉俯仰运动, 以非均匀载荷分布下的悬臂梁作为假定的柔性变形模式, 讨论了柔性翼的推进性能和周围压力分布. Li等[19]采用CFD方法获得了仿胸鳍柔性板尾流场中多个切片上的涡量分布情况, 并分析了在柔性板运动过程中的尾涡耗散和脱落情况. Miao等[20]研究了弦向变形幅度对拍动翼的影响, 应用FLUENT软件计算了在不同雷诺数和无因次频率下柔性翼的推力和效率.上述研究在一定程度上认识了柔性对拍动翼/鳍的水动力和尾流场的影响, 但目前对柔性拍动翼/鳍的推进效率的数值计算方法还没有系统、完备地阐述, 而且缺乏对推进性能随参数变化的内在机制的理解和与真实鱼鳍实验的联系和比较.另一方面, 拍动翼/鳍等仿生流动的数值模拟经常涉及复杂移动边界问题, 而这类问题的高效、精确求解一直是计算流体力学的难点.浸入边界法(IBM)[21-22]为外形复杂结构在黏性流场中运动的数值模拟提供了新的途径, 它利用拉格朗日方法跟踪物体运动边界, 而流场控制方程在固定的笛卡尔网格上求解, 不必按照物体形状生成复杂的贴体网格.
本文自主开发了基于浸入边界法的CFD程序, 改进了前人的拍动翼柔性变形模式, 并从能量的角度提出一种计算柔性拍动翼推进效率的数值方法, 深入分析了弦向变形系数、变形运动控制参数和无因次频率对柔性翼推进性能的影响.
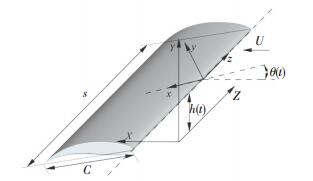
1 计算模型考虑拍动翼的升沉俯仰耦合运动, 设拍动翼的弦长为C, 展长为S, 翼型剖面为NACA0014, 置于均匀来流U中, 如图 1所示, 其中xyz为随体坐标系, 固定在拍动翼上并随之运动;XYZ为固定坐标系, 保持静止不动, X轴沿着流动方向, Z轴沿着翼展方向.
拍动翼在Y方向的升沉运动可以表示为
|
图 1 拍动翼几何及坐标系统 Figure 1 Flapping foil geometry and coordinate system |
| $ h\left( t \right) = {h_0}\sin \left( {\omega t} \right). $ |
式中:h0为升沉幅度, ω为拍动翼的圆频率, t为时间.如果使用f表示拍动翼的运动频率, 则有ω=2πf.拍动翼绕前缘的俯仰运动可描述为
| $ \theta \left( t \right) = {\theta _0}\sin \left( {\omega t - \psi } \right). $ |
式中:θ0为俯仰幅度;ψ为俯仰运动与升沉运动间的相位差, 这里取为π/2, 根据文献[23-25]的研究, 此时拍动翼具有最佳的推进性能.
Liu[17]假设拍动翼的弦向变形只发生在后半部分, 提出如下形式的弦向变形方程:
| $ y = {\delta _c}{\left( {2x - 1} \right)^\varepsilon }\sin \left( {\omega t + \varphi } \right). $ | (1) |
式中:δc为变形运动的幅度, 是弦向变形系数δ与弦长C的乘积即:δc=δ·C. ε为变形运动的控制参数, ε越大, 靠近翼前缘的变形越平缓, 而靠近翼尾缘的变形越剧烈;φ为变形运动与升沉运动之间的相位差(下文简称柔性相位角).实际鱼鳍在水动力的作用下将整体发生变形, 这里对上述弦向变形模式进行改进, 从而使拍动翼的变形不再只局限于后半部分.改进后的变形规律表示为
| $ y = \delta {\left( {_c\frac{\alpha }{{\alpha - 1}}x - \frac{1}{{\alpha - 1}}} \right)^\varepsilon }\sin \left( {\omega t + \varphi } \right). $ | (2) |
式中:α为变形运动的控制参数, 1<α<+ ∞, α越大, 弦向变形的起始位置越靠近拍动翼的前缘, 当α取2时, 所提出的弦向变形方程(2)即退化为Liu[17]的弦向变形方程(1).
在拍动翼推进中, 一个关键的参数是无因次频率[20], 定义如下:
| $ k = \omega C/U. $ |
拍动翼在黏性流中作非定常运动, 定义雷诺数为
| $ Re = UC/\nu . $ |
式中ν为流体的运动黏性系数.
根据图 1中坐标系的定义, 拍动翼的推力系数和升力系数可以表示为
| $ {C_{\rm{T}}} = {F_X}/(0.5\rho {U^2}{A_{{\rm{plan}}}}), {C_{\rm{L}}} = {F_Y}/(0.5\rho {U^2}{A_{{\rm{plan}}}}). $ |
式中:ρ为流体密度, FX为推力, FY为升力, Aplan为翼的投影面积.平均推力系数可由下式计算:
| $ {C_{{\rm{TA}}}} = \frac{1}{T}\smallint _t^{t + T}{C_X}{\rm{d}}t. $ |
式中T为拍动翼的运动周期.
2 数值方法 2.1 控制方程及其离散流动控制方程为三维、非定常、黏性、不可压缩Navier-Stokes方程:
| $ \begin{array}{*{20}{c}} {\mathop \smallint \limits_{{\rm{C}}S} \mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{n}}{\rm{d}}S = 0, }\\ {\frac{\partial }{{\partial t}}\mathop \smallint \limits_{{\rm{C}}V} \mathit{\boldsymbol{u}}{\rm{d}}V + \mathop \smallint \limits_{{\rm{C}}S} \mathit{\boldsymbol{u}}\left( {\mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{n}}} \right){\rm{d}}S = - \frac{1}{\rho }\mathop \smallint \limits_{{\rm{C}}S} p\mathit{\boldsymbol{n}}{\rm{d}}S + \nu \mathop \smallint \limits_{{\rm{C}}S} \nabla \mathit{\boldsymbol{u}} \cdot \mathit{\boldsymbol{n}}{\rm{d}}S.} \end{array} $ |
控制方程在固定的笛卡尔网格上离散, 其中u为单元中心的速度, p为压力, ρ和ν分别为流体的密度与运动黏性系数, CV与CS分别为控制体体积与控制体表面, n为控制体表面的单位法向量.
流动控制方程的求解采用有限体积法, 一个二阶精确的分裂步方法(fractional-step method)[26]被用作压力速度耦合方程组的求解, 将流场的数值解从时间层n推进到时间层n+1.在时间积分方案上选择隐式的Crank-Nicolson格式[27], 空间离散时采用二阶中心差分格式.
2.2 浸入边界的处理通过引入ghost-cell[22; 28](虚拟单元)来施加浸入边界对流动的影响, 其基本思想是利用基于物体内部的一层网格单元的流场局部重构来建立速度和压力边界条件, 这些网格单元相对于绕流问题的流场是虚拟的, 因此被称为ghost-cell.
流场数值计算在固定的六面体结构化网格上完成.由于仿生流动结构的研究经常涉及到复杂的几何和运动, 这里所开发的数值方法以模拟任意复杂移动边界的绕流问题为目标.浸入边界的表面采用强适应性的非结构三角形网格离散(见图 2).三角形网格表示的物体表面如图 2(a)所示, 翼的非结构表面网格被嵌入到流场的固定笛卡尔网格中(见图 2(b)), 从而完成整个网格系统的建立.

|
图 2 浸入边界法的网格系统 Figure 2 Grid system for immersed boundary method |
下面构建对浸入边界问题实施ghost-cell方法所需的数值方案.
首先, 利用射线法[29]进行网格单元相对于物体边界内外状态的判断.然后, 根据网格单元相对于物体边界的位置, 可将其分为以下3类(参考图 3):

|
图 3 流动求解器中的ghost-cell方法示意 Figure 3 Schematic of the ghost-cell method employed in the flow solver |
1) 流体单元(fluid cell), 即单元中心位于物体边界之外的单元;
2) ghost-cell, 即位于物体边界之内且至少有一个相邻单元位于流体内的单元;
3) 固体单元(solid cell), 即单元中心位于物体边界之内除ghost-cell外的其余单元.
利用流场局部重构建立ghost-cell上应满足的方程, 以保证物面边界条件的正确实施.
如图 3所示, 从ghost-cell(G)向物面引垂线, 将垂线与物面的交点O记为边界点, 再将G与O的连线向流体内部延伸, 得到G关于浸入边界在流体域内的镜像点I.在I点周围局部区域的流动变量φ, 可由如下的插值多项式表示:
| $ \varphi = {c_1} + {c_2}x + {c_3}y + {c_4}z. $ |
式中cj(j=1, ..., 4)为多项式的系数, 可用围绕I点的立方体的8个点中的3个流体点, 以及边界点O, 共计4个点作为插值数据点来计算, 即
| $ \left[ \begin{array}{l} {c_1}\\ {c_2}\\ {c_3}\\ {c_4} \end{array} \right] = {\mathit{\boldsymbol{A}}^{ - 1}}\left[ \begin{array}{l} {\varphi _1}\\ {\varphi _2}\\ {\varphi _3}\\ {\varphi _4} \end{array} \right]. $ |
式中A为一个4阶方阵, 其元素值可由上述4个点的坐标给出
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1&{{x_1}}&{{y_1}}&{{z_1}}\\ 1&{{x_2}}&{{y_2}}&{{z_2}}\\ 1&{{x_3}}&{{y_3}}&{{z_3}}\\ 1&{{x_4}}&{{y_4}}&{{z_4}} \end{array}} \right]. $ |
式中(xj, yj, zj)为插值数据点的坐标.对于速度插值, φ在边界点O的值由物面速度的狄利克雷(Dirichlet)边界条件确定(φ=φO), 在速度变量局部重构中多项式系数可表示为
| $ \left[ \begin{array}{l} {c_1}\\ {c_2}\\ {c_3}\\ {c_4} \end{array} \right] = {\mathit{\boldsymbol{A}}^{ - 1}}\left[ \begin{array}{l} {\varphi _O}\\ {\varphi _2}\\ {\varphi _3}\\ {\varphi _4} \end{array} \right] = {\left[ {\begin{array}{*{20}{c}} 1&{{x_O}}&{{y_O}}&{{z_O}}\\ 1&{{x_2}}&{{y_2}}&{{z_2}}\\ 1&{{x_3}}&{{y_3}}&{{z_3}}\\ 1&{{x_4}}&{{y_4}}&{{z_4}} \end{array}} \right]^{ - 1}}\left[ \begin{array}{l} {\varphi _O}\\ {\varphi _2}\\ {\varphi _3}\\ {\varphi _4} \end{array} \right]. $ |
式中φO为边界点O处的物面速度.
而对于压力插值, φ在边界点O由黎曼(Neumann)边界条件
| $ \left[ \begin{array}{l} {c_1}\\ {c_2}\\ {c_3}\\ {c_4} \end{array} \right] = {\mathit{\boldsymbol{A}}^{ - 1}}\left[ {\begin{array}{*{20}{c}} {\partial \varphi /\partial \mathit{\boldsymbol{\hat n}}}\\ {{\varphi _2}}\\ {{\varphi _3}}\\ {{\varphi _4}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} 0&{{{\hat n}_x}}&{{{\hat n}_y}}&{{{\hat n}_z}}\\ 1&{{x_2}}&{{y_2}}&{{z_2}}\\ 1&{{x_3}}&{{y_3}}&{{z_3}}\\ 1&{{x_4}}&{{y_4}}&{{z_4}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {\partial \varphi /\partial \mathit{\boldsymbol{\hat n}}}\\ {{\varphi _2}}\\ {{\varphi _3}}\\ {{\varphi _4}} \end{array}} \right]. $ |
式中:
| $ {\left( {\partial \varphi /\partial \mathit{\boldsymbol{\hat n}}} \right)_O} = - \rho {\left( {{\rm{D}}\mathit{\boldsymbol{u}}/{\rm{D}}t \cdot \mathit{\boldsymbol{\hat n}}} \right)_O}. $ |
其中Du/Dt为速度的物质导数.
多项式的系数一旦确定, 在镜像点I处的φ值即可由下式给出:
| $ {\varphi _I} = \mathop \sum \limits_{j = 1}^4 {\beta _j}{\varphi _j}. $ | (3) |
式中βj(j=1, ..., 4)为由插值多项式确定的权系数.下面建立ghost-cell上应满足的方程.对于速度的狄利克雷边界条件, 根据沿法向线段GI的中点公式有
| $ {\varphi _O} = ({\varphi _I} + {\varphi _G})/2. $ | (4) |
将式(3)代入式(4), 可得
| $ {\varphi _G} + \mathop \sum \limits_{j = 1}^4 {\beta _j}{\varphi _j} = 2{\varphi _O}. $ | (5) |
对于压力的黎曼边界条件, 利用沿法向线段GI的二阶中心差分有
| $ {\left( {\partial \varphi /\partial \mathit{\boldsymbol{\hat n}}} \right)_O} = ({\varphi _I} - {\varphi _G})/\Delta l. $ | (6) |
将式(3)代入式(6), 可得
| $ {\varphi _G} - \mathop \sum \limits_{j = 1}^4 {\beta _j}{\varphi _j} = - \Delta l{\left( {\partial \varphi /\partial \mathit{\boldsymbol{\hat n}}} \right)_O}. $ | (7) |
最后ghost-cell上的流场局部重构方程(5)和(7)与流体单元上的N-S方程联立求解, 从而得到整个物体绕流场的数值解.
2.3 推进效率的计算方法与刚性拍动翼类似, 柔性拍动翼的推进效率仍可以用η=Pout/Pin这样的一般的形式来表示, 其中平均输出功率Pout仍可由平均推力与来流速度的乘积给出.然而, 关于平均输入功率Pin的计算方法需要一些讨论.
对于刚性拍动翼, 在文献[3; 30-31]中平均输入功率已有被普遍认同的计算方法, 即将输入功率表示为拍动翼的刚体平移运动所消耗的功率与刚体旋转运动所消耗的功率之和.但对于本文中的柔性拍动翼, 该计算方法已不再适用, 下面从能量的观点出发, 推导对刚性和柔性拍动翼都适用的平均输入功率计算公式.
根据能量的转化和守恒定律, 因为功是能量转化的量度, 所以拍动翼做耦合旋转运动和柔性变形运动所消耗的功率通过水对拍动翼做负功而被水吸收.一个运动周期内水对拍动翼所做的功可由以下公式计算:
| $ W = \smallint _t^{t + T}{\smallint _{{A_{{\rm{foil}}}}}}\left( {\overrightarrow \sigma \cdot \overrightarrow V } \right){\rm{d}}A{\rm{d}}t. $ |
式中:Afoil为拍动翼表面,
| $ {P_{{\rm{in}}}} = - \frac{1}{T}\smallint _t^{t + T}{\smallint _{{A_{{\rm{foil}}}}}}\left( {\overrightarrow \sigma \cdot \overrightarrow V } \right){\rm{d}}A{\rm{d}}t. $ |
式中翼表面的局部速度可以表示为
| $ \overrightarrow V = {\overrightarrow V _h} + {\overrightarrow V _\theta } + {\overrightarrow V _y}. $ |
式中:
| $ \eta = \frac{{{F_{{\rm{XA}}}}U}}{{ - \frac{1}{T}\smallint _t^{t + T}{\smallint _{{A_{{\rm{foil}}}}}}\left( {\overrightarrow \sigma \cdot \overrightarrow V } \right){\rm{d}}A{\rm{d}}t}}. $ |
式中FXA为平均推力.
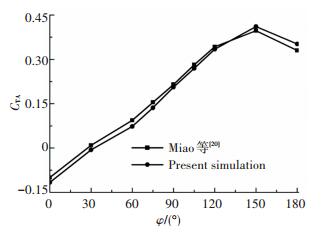
3 结果与讨论 3.1 数值方法的验证为验证浸入边界法CFD程序数值模拟柔性拍动翼问题的精确性, 将用浸入边界法计算得到的CTA与Miao等[20]的计算结果(用Fluent软件计算, 基于贴体动网格技术实现柔性翼的非定常运动模拟)进行了比较.在与Miao等[20]相同的运动规律和流动条件下, 平均推力系数随柔性相位角φ的变化如图 4所示.可以看出, 两个独立的数值模拟得出的CTA有很好地一致性, CTA均是随柔性相位角的增加而先增大后减小, 当φ为150°时, CTA达到最大值.
|
图 4 浸入边界法和Miao等[20]的平均推力系数计算结果比较 Figure 4 Comparison of computed CTA by immersed boundary method with results by Miao et al[20] |
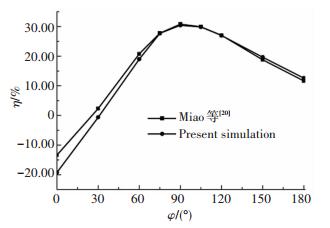
除以上水动力的比较之外, 为验证提出的柔性拍动翼推进效率计算方法, 还将利用本文方法的效率计算结果与Miao等[20]的效率计算值进行对比, 如图 5所示.由图 5发现, 当前的模拟结果与Miao等[20]的计算结果基本吻合, 当柔性相位角为90°时, 柔性翼的推进效率取得最大值.
|
图 5 推进效率计算值与Miao等[20]的结果的比较 Figure 5 Comparison of computed propulsive efficiency with results by Miao et al[20] |
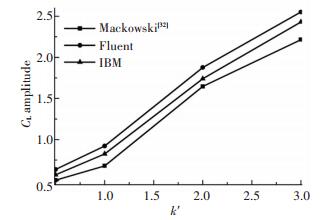
为了给所开发的浸入边界法程序提供物理实验支撑, 将使用IBM程序计算得到的水动力系数与Mackowski等[32]的相应实验结果进行了比较.实验中翼在Re=17 000的来流中做纵倾运动, 用力传感器对水动力进行直接测量.在与实验相同的运动规律和流动条件下, 升力系数幅度(CL amplitude)随诱导频率k′(Mackowski等[32]将k′定义为无因次频率k的1/2)的变化如图 6所示.可以看到, IBM程序的计算结果与实验结果匹配得很好, 相比于Fluent软件, 浸入边界法的模拟结果与实验值更为接近.在相同的网格数量(精确到千)和时间步长下, 对于翼的一个运动周期, IBM程序所花费的时间比Fluent软件大约少了1/4.
|
图 6 升力系数幅度的浸入边界法和Fluent软件的计算结果与Mackowski等[32]实验结果的比较 Figure 6 Comparison of computed CL amplitude by immersed boundary method and Fluent software with experimental results by Mackowski et al[32] |
数值计算基本参数为C=0.064 m, S=0.256 m, Re=3 000, φ=-90°, h0=0.5C, θ0=20°, α=4.0, 不同δ(0≤δ≤0.4)时, 计算达到稳定状态后一个周期内的推力系数随时间变化见图 7(在本节的研究中, 将ε和k分别固定为3和4).
|
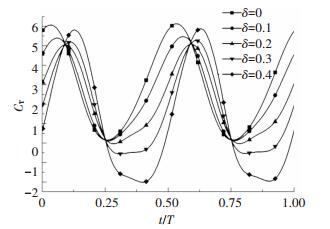
图 7 不同δ时拍动翼的推力系数比较 Figure 7 Comparison of CT of the flapping foil with different δ |
由图 7可知, 对于所有被模拟的情况, 在一个运动周期内推力均产生两次峰值, 同时也注意到当0≤δ≤0.2时, 随着δ的增大, 推力系数的最大值逐渐减小, 最小值并没有明显的数值变化;当拍动翼的柔性较大(δ=0.4)时, 瞬态推力系数曲线将呈现出明显更低的波谷, 可见柔性过大将对推进性能产生不利的影响.不同δ下的柔性翼推进效率和平均推力系数计算结果如图 8所示.
|
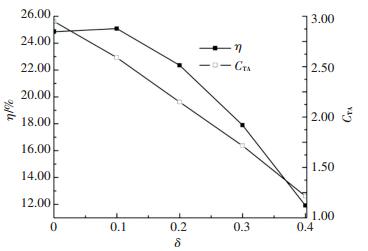
图 8 推进效率及平均推力系数随弦向变形系数δ的变化 Figure 8 Variation of propulsive efficiency and CTA with δ |
由图 8可知, 随着δ的增大, 即拍动翼的变形运动的幅度增加, 平均推力系数呈现出一个减小的趋势; 而推进效率则是随着δ的增大而先增大后减小, 当δ=0.1时, 柔性翼取得最佳效率, 可见适当的柔性会使拍动翼的推进性能相对于刚性的情况有所改善.
3.2.2 变形运动控制参数ε的影响δ取0.1, 而k继续保持为4不变, 变形运动控制参数ε对柔性拍动翼性能的影响见图 9.
|
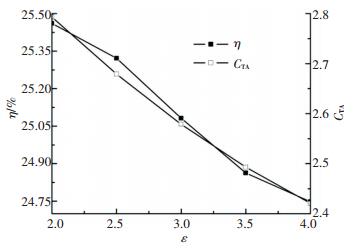
图 9 推进效率及平均推力系数随弦向变形系数ε的变化 Figure 9 Variation of propulsive efficiency and CTA with ε |
由图 9可以看出, 随着ε的增大, 推进效率和平均推力系数均呈现出一个减小的趋势.为分析该现象背后的机理, 绘制了不同ε下的柔性翼展向对称面的Z方向涡量云图, 如图 10所示.
|
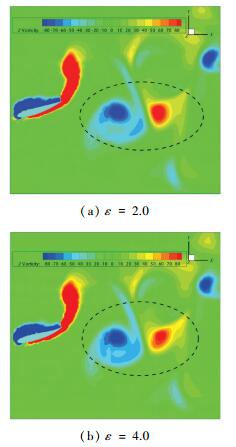
图 10 当t=T/2时不同弦向变形系数ε的涡量云图 Figure 10 Vorticity contours of different ε by the time of t=T/2 |
其中用虚线圈出的为柔性翼尾流场中的一对涡偶极子.可以看出, ε=4.0时的涡偶极子强度明显小于ε=2.0时的.这是因为ε越大, 靠近翼前缘的变形越平缓, 而靠近翼尾缘的变形越剧烈, 相当于增加了拍动翼的纵倾效果, 根据Birch等[33]和Poelma等[34]对拍动板的研究, 由翼的纵倾所诱导的对流输运有利于展向涡量由尾缘向翼梢的释放, 而构成涡偶极子的两个涡事实上是在翼之前的运动过程中从尾缘脱落的展向涡, 因此ε的增大将造成尾流场中涡偶极子强度的降低, 进而由涡偶极子诱导的向后射流减弱, 翼的推力降低.
3.2.3 无因次频率k的影响无因次频率k的物理意义是柔性翼的拍动特征速度(ωC=2πfC)与流动的对流特征速度(U)的比. 3.2.1和3.2.2节的数值研究得到一个柔性拍动翼推进性能的最佳变形参数组合, 即δ=0.1, ε=2.0, 在此基础上, 分析关键运动参数无因次频率对柔性翼水动力性能的影响.如图 11所示, 推进效率随着无因次频率k的增大而先增加后减小, 当k=3时, 推进效率达到最大值;文献[35-36]也已经证实存在一个最优的斯特劳哈尔数(实质上也是一个无因次频率的概念, St=2h0f/U=2(0.5C)f/U=k/2π)使尾鳍的推进效率最佳.同时也观察到, 平均推力系数随k的增大而呈现持续增加的趋势;这与一些种类的鱼通过增加胸鳍的拍动频率来增加推力进而提高游动速度的行为是一致的(见Gibb等[37]以及Drucker等[38]).

|
图 11 推进效率及平均推力系数随无因次频率k的变化 Figure 11 Variation of propulsive efficiency and CTA with k |
1) 水动力和推进效率两方面的比较验证表明, 提出的浸入边界法和推进效率计算方法可很好地完成柔性拍动翼在黏性流场中非定常运动的数值模拟, 并对三维柔性翼的推进性能做出精确预报.
2) 三维拍动翼的平均推力随弦向变形系数δ的增加而减小, 推进效率随δ的增加而表现出先增大后减小的趋势;柔性翼的平均推力和推进效率均随变形运动控制参数ε的增加而减小, 尾流场分析表明ε的增大降低了支配拍动翼尾流场的涡偶极子的强度, 减弱了由非定常拍动所引起的向后射流效果.
3) 变形运动控制参数2.0≤ε≤3.5, 弦向变形系数δ=0.1时, 柔性拍动翼的推进效率超过刚性翼.
4) 与真实鱼鳍研究的比较表明, 浸入边界法模拟所预报的柔性翼推进性能已体现出了真实鱼鳍的一些基本特性:柔性拍动翼的平均推力随无因次频率k的增大而单调增加;存在一个使柔性翼的推进效率最高的最优k.
| [1] |
TRIANTAFYLLOU M, TRIANTAFYLLOU G, GOPALKRISHNAN R. Wake mechanics for thrust generation in oscillating foils[J]. Physics of Fluids A: Fluid Dynamics, 1991, 3(12): 2835. DOI:10.1063/1.858173 |
| [2] |
TRIANTAFYLLOU G S, TRIANTAFYLLOU M S, GROSENBAUGH M A. Optimal thrust development in oscillating foils with applications to fish propulsion[J]. Journal of Fluids and Structures, 1993, 7(2): 205. DOI:10.1006/jfls.1993.1012 |
| [3] |
READ D A, HOVER F S, TRIANTAFYLLOU M S. Forces on oscillating foils for propulsion and maneuvering[J]. Journal of Fluids and Structures, 2003, 17(1): 163. DOI:10.1016/S0889-9746(02)00115-9 |
| [4] |
LICHT S, POLIDORO V, FLORES M, et al. Design and projected performance of a flapping foil AUV[J]. IEEE Journal of Oceanic Engineering, 2004, 29(3): 786. DOI:10.1109/joe.2004.833126 |
| [5] |
TECHET A, LIM K, HOVER F, et al.Hydrodynamic performance of a biologically inspired 3D flapping foil[C]//Proceedings of 14th International Symposium on Unmanned Untethered Submersible Technology.Durham: [s.n.], 2005
|
| [6] |
LIM K K L.Hydrodynamic performance and vortex shedding of a biologically inspired three-dimensional flapping foil[D].Cambridge: Massachusetts Institute of Technology, 2005
|
| [7] |
SIMPSON B J.Experimental studies of flapping foils for energy extraction[D].Cambridge: Massachusetts Institute of Technology, 2009
|
| [8] |
BUCHHOLZ J H.The flowfield and performance of a low aspect ratio unsteady propulsor[D].Princeton: Princeton University, 2006 http://adsabs.harvard.edu/abs/2006PhDT........79B
|
| [9] |
JONES K D, PLATZER M F.Numerical computation of flapping-wing propulsion and power extraction[C]//35th Aerospace Sciences Meeting and Exhibit.Reno: AIAA, 1997
|
| [10] |
PAN Y L, DONG X X, ZHU Q, et al. Boundary-element method for the prediction of performance of flapping foils with leading-edge separation[J]. Journal of Fluid Mechanics, 2012, 698: 446. DOI:10.1017/jfm.2012.119 |
| [11] |
李宁宇, 苏玉民, 王兆立, 等. 三维拍动翼推进效率的计算方法[J]. 上海交通大学学报, 2012, 46(2): 323. LI Ningyu, SU Yumin, WANG Zhaoli, et al. Computation method of propulsive efficiency of a three-dimensional flapping foil[J]. Journal of Shanghai Jiaotong University, 2012, 46(2): 323. |
| [12] |
LA MANTIA M, DABNICHKI P. Unsteady panel method for flapping foil[J]. Engineering Analysis with Boundary Elements, 2009, 33(4): 572. DOI:10.1016/j.enganabound.2008.08.001 |
| [13] |
LEWIN G C, HAJ-HARIRI H. Modelling thrust generation of a two-dimensional heaving airfoil in a viscous flow[J]. Journal of Fluid Mechanics, 2003, 492: 339. DOI:10.1017/s0022112003005743 |
| [14] |
LU X Y, YANG J M, YIN X Z. Propulsive performance and vortex shedding of a foil in flapping flight[J]. Acta Mechanica, 2003, 165(3/4): 189. DOI:10.1007/s00707-003-0013-x |
| [15] |
SU Y M, WANG Z L, ZHANG X, et al. Numerical simulation for hydrodynamic characteristics of a bionic flapping hydrofoil[J]. China Ocean Engineering, 2012, 26(2): 291. DOI:10.1007/s13344-012-0022-4 |
| [16] |
文敏华, 胡文蓉, 刘洪. 翼沉浮运动推力来源的数值研究[J]. 水动力学研究与进展A辑, 2012, 27(2): 154. WEN Minhua, HU Wenrong, LIU Hong. Numerical study of thrust generation mechanism of heaving wings[J]. Chinese Journal of Hydrodynamics, 2012, 27(2): 154. DOI:10.3969/j.issn1000-4874.2012.02.006 |
| [17] |
LIU P F.A time-domain panel method for oscillating propulsors with both spanwise and chordwise flexibility[D].St.John's: Memorial University of Newfoundland, 1996
|
| [18] |
WANG Z D, CHEN P, ZHANG X Q. Wake vortex structure characteristics of a flexible oscillating fin[J]. Journal of Bionic Engineering, 2008, 5(1): 49. DOI:10.1016/s1672-6529(08)60006-2 |
| [19] |
LI N Y, SU Y M, WANG Z L, et al. Hydrodynamic analysis of rigid and flexible pectoral fins[J]. Journal of Environmental Biology, 2016, 37(5): 1105. |
| [20] |
MIAO J M, HO M H. Effect of flexure on aerodynamic propulsive efficiency of flapping flexible airfoil[J]. Journal of Fluids and Structures, 2006, 22(3): 401. DOI:10.1016/j.jfluidstructs.2005.11.004 |
| [21] |
MITTAL R, IACCARINO G. Immersed boundary methods[J]. Annual Review of Fluid Mechanics, 2005, 37: 239. DOI:10.1146/annurev.fluid.37.061903.175743 |
| [22] |
李宁宇, 苏玉民, 刘葳兴, 等. 基于浸入边界法的拍动翼尾涡结构与水动力分析[J]. 应用科技, 2015, 42(6): 26. LI Ningyu, SU Yumin, LIU Weixing, et al. Hydrodynamic analysis and trailing vortex structure of flapping wings based on the immersed boundary method[J]. Applied Science and Technology, 2015, 42(6): 26. |
| [23] |
READ D A.Oscillating foils for propulsion and maneuvering of ships and underwater vehicles[D].Cambridge: Massachusetts Institute of Technology, 2001
|
| [24] |
GUGLIELMINI L, BLONDEAUX P. Propulsive efficiency of oscillating foils[J]. European Journal of Mechanics B-Fluids, 2004, 23(2): 255. DOI:10.1016/j.euromechflu.2003.10.002 |
| [25] |
READ M B.Performance of biologically inspired flapping foils[D].Cambridge: Massachusetts Institute of Technology, 2006
|
| [26] |
LIU W X, LI N Y, ZHAO J X, et al. Wake structure and hydrodynamic performance of flapping foils mimicking fish fin kinematics[J]. Saudi Journal of Biological Sciences, 2017, 24(6): 1344. DOI:10.1016/j.sjbs.2016.09.015 |
| [27] |
FERZIGER J H, PERIC M. Computational methods for fluid dynamics[M]. Berlin/Heidelberg/New York: Springer-Verlag, 2002. DOI:10.1063/1.881751
|
| [28] |
LI N Y, SU Y M. Fluid dynamics of biomimetic pectoral fin propulsion using immersed boundary method[J]. Applied Bionics and Biomechanics, 2016(7): 1. DOI:10.1155/2016/2721968 |
| [29] |
BORAZJANI I.Numerical simulations of fluid-structure interaction problems in biological flows[D].Twin Cities: University of Minnesota, 2008 https://search.proquest.com/docview/304583878
|
| [30] |
PEDRO G, SULEMAN A, DJILALI N. A numerical study of the propulsive efficiency of a flapping hydrofoil[J]. International Journal for Numerical Methods in Fluids, 2003, 42(5): 493. DOI:10.1002/fld.525 |
| [31] |
LI N Y, LIU H X, SU Y M. Numerical study on the hydrodynamics of thunniform bio-inspired swimming under self-propulsion[J]. Plos One, 2017, 12(3): 1. DOI:10.1371/journal.pone.0174740 |
| [32] |
MACKOWSKI A W, WILLIAMSON C H K. Direct measurement of thrust and efficiency of an airfoil undergoing pure pitching[J]. Journal of Fluid Mechanics, 2015, 765: 524. DOI:10.1017/jfm.2014.748 |
| [33] |
BIRCH J M, DICKSON W B, DICKINSON M H. Force production and flow structure of the leading edge vortex on flapping wings at high and low Reynolds numbers[J]. Journal of Experimental Biology, 2004, 207(7): 1063. DOI:10.1242/jeb.00848 |
| [34] |
POELMA C, DICKSON W B, DICKINSON M H. Time-resolved reconstruction of the full velocity field around a dynamically-scaled flapping wing[J]. Experiments in Fluids, 2006, 41(2): 213. DOI:10.1007/s00348-006-0172-3 |
| [35] |
TAYLOR G K, NUDDS R L, THOMAS A L R. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency[J]. Nature, 2003, 425(6959): 707. DOI:10.1038/nature02000 |
| [36] |
ROHR J J, FISH F E. Strouhal numbers and optimization of swimming by odontocete cetaceans[J]. Journal of Experimental Biology, 2004, 207(10): 1633. DOI:10.1242/jeb.00948 |
| [37] |
GIBB A, JAYNE B, LAUDER G. Kinematics of pectoral fin locomotion in the bluegill sunfish Lepomis macrochirus[J]. Journal of Experimental Biology, 1994, 189(1): 133. |
| [38] |
DRUCKER E, JENSEN J. Pectoral fin locomotion in the striped surfperch.I.Kinematic effects of swimming speed and body size[J]. Journal of Experimental Biology, 1996, 199(10): 2235. |
 2018, Vol. 50
2018, Vol. 50


