2. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),哈尔滨 150090;
3. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, Harbin 150090, China;
3. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
由于地震作用的随机性和人类资源的有限性,不可能无限制地使用资源去实现在强震下结构不发生破坏,设防目标也不可能寻求绝对的安全[1].现有各国抗震设计规范尽管设计参数取值和方法存在差异,但在罕遇地震下,基本都以控制倒塌,保障生命安全为设防目标.在这样的抗震设计理念的指导下,一般通过能力设计方法(capacity design)[2]刻意弱化结构的某些部位,使其在地震作用下屈服形成塑性铰耗散能量,并从构造上保证塑性铰的变形能力和延性,使结构达到期望的破坏模式.虽然可以控制结构倒塌,但截面塑性的过度发展常常会导致结构在震后产生损伤和大的残余变形.
从国外近年来的几次大的破坏性地震中可以发现,结构的倒塌和人员伤亡都得到了一定的控制,但经济损失却异常巨大.除了非结构构件和设备的损坏之外,大部分的损失来源于震后结构的修复重建费用,以及漫长的修复和重建期导致建筑使用功能中断带来的经济损失.典型的如2011年新西兰基督城Mw 6.3级地震,死亡185人,但重建费用高达40亿新西兰元,约占新西兰GDP的20%,某街区内1 000余栋建筑就由于残余变形过大(并未倒塌)而不得不拆除.
因此,如何降低震后修复难度,提高结构抗震韧性(resilience),近年来得到广泛关注.而从20世纪90年代开始出现并持续发展的自复位结构体系(self-centering structural system),由于独特的界面摇摆机制和后张预应力技术的应用,可有效控制结构震损和残余变形,降低震后修复费用和修复时间,提高城市的抗震防灾韧性.目前新西兰、美国、日本和中国均在着力开展自复位结构体系的相关研究,提出了摇摆桥墩、自复位框架、自复位剪力墙和自复位耗能支撑等多种自复位结构形式,相关性能分析、设计方法与技术也逐渐发展.
本文聚焦自复位混凝土剪力墙结构(以下简称自复位剪力墙或自复位剪力墙结构),介绍自复位混凝土剪力墙结构的自复位实现与工作原理,总结和分析近年来自复位剪力墙的结构组成与结构体系、设计方法以及非线性模型与模拟方法等,进而,基于自复位剪力墙结构体系、技术与理论发展现状,提出在工作机理、分析模型和设计方法方面需解决的关键科学问题与展望.
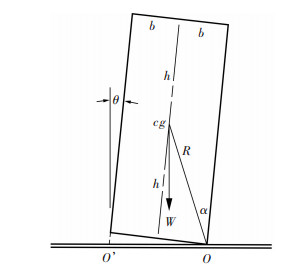
1 自复位原理在1960年的智利大地震中,一些较高的水塔结构由于发生了基础摇摆,结果在地震中免遭破坏.Housner[3]针对这类结构提出了简化的刚性摇摆质量块模型,见图 1,分析了不同工况下摇摆质量块的响应.随后许多学者又针对底部释放约束的摇摆结构展开了研究[4-12],包括摇摆柱、摇摆框架和摇摆核心筒等,发现了约束释放后产生的结构摇摆对结构的保护作用.此类结构的思路为释放约束后结构发生摇摆,刚度降低,结构振动周期延长,减小了地震作用,在自重作用下震后结构将回复原位.但结构的摇摆变形缺乏控制,极有可能在强震下发生倾覆.
在20世纪90年代美日联合进行的预制装配式混凝土结构抗震性能研究的PRESSS项目(precast seismic structural systems)[13]中,Priestley等[14]首次提出将预制装配式结构与后张预应力筋结合,通过施加预应力控制结构的自由摇摆,提出了具备自复位能力的装配式节点连接,见图 2.
自复位涉及结构约束释放后地震输入下的摇摆回复及其倾覆控制,其基本工作原理为节点约束释放后形成的独特的界面摇摆机制.自复位常与装配式混凝土结构相结合,将预制构件通过后张预应力筋预压装配连接,而节点处钢筋和混凝土断开连接,即可形成自复位节点.在变形初始阶段节点近似固结;随变形增大,节点张开,界面发生摇摆,抗侧刚度主要由预应力筋提供,刚度会有大幅下降,变形行为可简化为双线性,卸载后预应力筋提供的回复力将使结构恢复到初始位置,见图 3(a).节点约束释放后结构周期延长,地震作用降低,但承载力和刚度不足,耗能能力偏低[15],可在节点摇摆界面位置附加耗能元件,借助耗能元件的耗能能力,结构的变形将变为旗帜型,见图 3(b).

|
图 3 自复位节点的变形特征 Figure 3 Hysteretic behavior of self-centering connection |
若结构的摇摆不受控制,回复力的来源仅为结构自重,此类摇摆一般称为自由摇摆(free rocking);若在自由摇摆的基础上后张预应力筋对摇摆加以控制,则称为受控摇摆(controlled rocking);若在摇摆界面再安装耗能元件,结构还将具备一定的耗能能力,称为混合摇摆(hybrid rocking).考虑到自由摇摆缺乏控制,容易失去稳定发生倾覆,因此,着重分析具有后两类摇摆机制的自复位剪力墙.
相比于传统节点固结的结构,自复位结构的优势主要体现在:
1) 震损小.节点约束释放,混凝土基本没有拉应力,通过在混凝土局部受压区配置间接钢筋约束,结构的损伤可以得到有效控制.自复位节点类似于塑性铰,但非线性范围更加集中,除节点外结构的其余部分将基本保持弹性;
2) 残余变形小.依靠高强预应力筋较强的弹性变形能力,结构变形能力大幅提高,在地震结束后,回复力(包括结构自重以及后张预应力等)将使结构恢复到初始位置,减小或消除残余变形,促使震后建筑快速恢复使用功能,减少因修复重建和建筑功能中断带来的经济损失和社会影响.
2 自复位剪力墙的分类与试验研究按结构形式,自复位剪力墙可分为单肢墙和联肢墙两类.单肢墙可分为受控摇摆墙和混合摇摆墙,联肢墙可分为通过竖向耗能元件连接的联肢墙和通过自复位连梁连接的联肢墙.自复位剪力墙可由多片预制墙片竖向叠合,再沿墙高布置并后张无黏结预应力筋拼装而成;墙片端部的墙趾受压区域布置间接钢筋形成约束混凝土,以提高墙趾的碰撞能力和变形能力;需要保证拼装节点不发生滑移和剪切破坏,使其仅发生墙底摇摆界面张合.
2.1 单肢墙 2.1.1 受控摇摆墙Kurama等[15]最早提出了受控摇摆墙模型,见图 4.Kurama采用DRAIN-2DX软件进行了大量的拟静力分析和动力响应分析,较为系统地研究了此类结构的抗震性能,发现该类剪力墙可以在低损伤情况下实现较大侧移,而且基本没有残余变形,但耗能能力差,变形偏大,见图 5.
Nazari等[17]对4片5/18受控摇摆墙进行了振动台试验(图 6),研究了摇摆墙在不同地震水平下的动态响应,分析了高速加载条件下墙体与基础间碰撞的辐射阻尼作用.试验发现碰撞过程中的弹性辐射耗能阻尼约为1.5%,总耗能阻尼约为4.2%,辐射阻尼占比可以达到总阻尼的1/3左右.
2.1.2 混合摇摆墙为改善受控摇摆墙的耗能能力,Kurama[18]提出在剪力墙两侧安装黏滞阻尼器,见图 7,分析发现安装黏滞阻尼器后结构的最大层间侧移和楼面加速度大幅降低.Restrepo等[19]在基础摇摆界面设置了软钢滞回耗能元件来补充耗能.采用的耗能元件为在摇摆界面附近一定长度范围内变截面的热轧钢筋,并在此范围内保证无黏结,以防止应变过度集中而导致钢筋过早断裂.配置了耗能钢筋的剪力墙在3%侧移时等效黏滞阻尼系数达到了14%,试验结束后仅墙趾混凝土发生了轻微剥落,剪力墙基本没有残余变形,表现出了非常好的自复位能力,见图 8.
Smith等[20-21]根据ACI 318[22]、ACI-ITG 5.1[23]和ACI-ITG 5.2[24]设计了1片等同现浇剪力墙和5片自复位剪力墙,进行了拟静力试验.考虑到实际的施工情况,剪力墙由上下两部分墙片叠合拼装而成,见图 9.Smith等[25]在ACI-ITG 5.1和ACI-ITG 5.2的基础上完善了设计建议,编写了相应的设计指南,以使自复位剪力墙能够同时满足ACI 318和ACI-ITG 5.1中要求,同时提出了竖向拼接多墙片剪力墙控制水平接缝张开分析方法,使得摇摆只产生在墙-基界面.
Marriott等[26-27]提出将耗能元件外置(图 10),代替在剪力墙内部锚固的普通耗能钢筋,方便在震后进行更换.对4片采用不同外置耗能元件的剪力墙进行了高速拟静力试验和振动台试验,耗能元件包括软钢滞回耗能元件和速度黏滞型耗能元件两种.试验发现破坏主要集中于外置的耗能元件上,通过更换耗能元件,结构的功能可以快速恢复,两种耗能元件结合使用可以比仅使用速度黏滞型耗能元件更好地控制结构的位移响应.
Henry等[29-32]提出了一种新型的带端柱的自复位剪力墙体系(precast wall with end columns, PreWEC)并进行了拟静力试验,如图 11所示.这种自复位剪力墙中部为摇摆墙,两侧为沿柱高通长布置预应力筋锚固的钢柱或混凝土柱,剪力墙与柱间安装O型连接件(图 12),通过O型连接件的弯剪变形耗能. Twigden等[33-34]对这种自复位剪力墙体系进行了振动台试验,研究了这种结构的动力响应与阻尼效应.
陈适才等[35]建立了底部开缝后张预应力预制剪力墙的有限元模型,此类剪力墙在墙底部分设缝,中部与现浇剪力墙结构相同保持正常连接,保留了一定的抗弯和抗剪能力,同时通过后张无黏结预应力筋来保证剪力墙的自复位能力,见图 13.党像梁等[36]设计进行了底部开水平缝预应力自复位剪力墙的拟静力试验,并进行了精细化的有限元模拟[37-39].试验结果表明此类剪力墙兼备现浇式剪力墙和自复位剪力墙的优点,不仅具有一定的耗能能力,还具有较好的自复位能力,变形能力较强,而且损伤和残余变形小.
郭彤等[40]设计了一种新型的自复位剪力墙结构(图 14),形式与PreWEC剪力墙相似,但剪力墙两侧为底部铰接的摇摆柱,并在底部墙片墙趾处外包钢板以防混凝土压溃.所采用的耗能元件为摩擦耗能元件(图 15),由钢板间内夹黄铜片,通过螺栓和弹簧垫圈预紧叠合而成.
2.2 联肢墙 2.2.1 通过竖向耗能元件连接的联肢墙在PRESSS项目[41]中的剪力墙即为采用了带竖向接缝的联肢剪力墙,相邻墙片间竖向接缝通过U型弯曲钢板耗能元件连接,见图 16.水平力作用下墙体产生摇摆,各摇摆墙片间的竖向接缝发生错动,U型钢板在弯剪联合作用下屈服耗能.Sritharan等[42]对这种U型钢板连接件进行了往复加载试验,并针对这种联肢剪力墙提出了简化的分析和设计方法[43].
2.2.2 通过自复位连梁连接的联肢墙Kurama等[45-49]提出将联肢墙间连梁由固结改为摇摆形式,见图 17,连梁与墙间通过后张预应力筋连接,通过连梁端部布置的上下角钢变形耗能.
Barbachyn等[50-51]将联肢墙间连梁弱化,提出了一种新的后张预应力混凝土连梁.这种连梁取消了斜向钢筋,但在截面形心配置了后张预应力筋,见图 18.试验发现这种连梁的自复位能力并不突出,但连梁的变形能力大幅提高,转动能力可达11%,连梁的损伤集中于梁端,损伤表现为两端保护层混凝土剥落,而连梁的其余部分则基本保持弹性,连梁的整体破坏模式改变,而连梁变形延性提高的同时也提高了结构整体的变形能力.
3 分析计算理论与建模方法 3.1 直接基于位移的设计方法 3.1.1 基于力的设计方法的缺陷随着抗震设计理论逐渐发展,人们意识到变形能够更直观地表达结构的损伤情况,从20世纪90年代起,基于性能的抗震设计(performance-based seismic design,PBSD)[52-54]不断发展,成为了结构抗震设计的主流方向之一.基于性能的抗震设计要求根据结构的重要性和用途确定其性能目标,使结构在地震中具备预期的功能,达到期望的变形水平.
目前各国规范中普遍采用的一般为基于力的设计方法(force based design,FBD),分析时需首先估计弹性状态下的基本周期,考虑到地震作用下使结构保持弹性并不现实,一般允许结构进入塑性,采用折减系数R对弹性反应谱进行折减.折减系数R的取值一般根据等位移原理确定,即在中等周期范围(0.6~2.0 s)内,理想弹塑性体系的变形与弹性体系变形相等,可近似认为折减系数R与延性需求μ相同.然而,自复位结构一般表现为旗帜型的变形特征,与理想的弹塑性滞回规则有较大差别,耗能能力差,延性更高(自复位梁柱节点位移延性可达14[14]),并不能满足等位移原理的要求[55],显然,基于力的设计方法并不适合进行自复位结构设计.
Priestley等[56]提出了直接基于位移的设计方法(direct displacement-based design,DDBD).直接基于位移的设计方法属于一种基于性能的抗震设计方法,但与其他方法的区别在于DDBD采用最大位移处的切线刚度而非初始弹性刚度来计算剪力,自复位结构不会因为相对偏高的初始刚度和较高的延性而受到影响.此外,DDBD方法采用位移谱而非加速度谱进行设计,在设计的初始阶段即可确定目标位移,一般不需要进行迭代过程,相比FBD方法,DDBD方法计算获得的基底剪力更低[57-58],从造价角度而言更为经济.
3.1.2 DDBD的分析步骤DDBD的分析过程以Shibata等[59]提出的等代结构为基础,基本步骤如下[56]:
1) 确定目标位移Δd;
2) 根据变形模式,将多自由度体系转化为等效单自由度体系,对于楼层数少于10层的自复位剪力墙,变形模式可近似取为刚体转动变形;
3) 根据延性系数μ确定等效黏滞阻尼(equivalent viscous damping,EVD);
4) 根据位移谱确定等效单自由度体系的周期Te;
5) 计算等效单自由度体系的等效刚度Ke
| $ {K_{\rm{e}}} = \frac{{4{{\rm{ \mathsf{ π} }}^2}{m_{\rm{e}}}}}{{T_{\rm{e}}^2}}; $ |
6) 将此刚度作为割线刚度计算基底剪力
| $ F = {V_{{\rm{base}}}} = {K_{\rm{e}}}{\Delta _{\rm{d}}}; $ |
7) 分配剪力至结构各部分,进行截面设计.
详细的计算公式和参数取值可参考文献[56].
3.2 自复位剪力墙的极限状态与截面设计在获得了截面的内力设计值后,需要对截面进行分析及配筋设计.根据自复位剪力墙的单调推覆曲线,其截面极限状态可分为消压、软化、屈服、耗能元件破坏和倒塌等几个状态,见图 19.在加载初始阶段,界面未发生摇摆,此时结构的变形类似于固结;随着水平力的增大,截面受拉边缘压应力为零,达到消压状态,此时摇摆界面的接触高度(受压区高度)逐渐减小,界面逐渐张开;随着摇摆幅值的提高,耗能元件屈服,结构开始有明显软化,此时刚度主要由预应力筋提供,刚度明显降低;在预应力筋屈服之后承载力基本不再提高,随后耗能元件和预应力筋发生破坏,结构失去稳定发生倾覆.
虽然截面有多个极限状态,但一般取屈服和达到极限承载力时对应的两个极限状态进行截面配筋设计.由于节点约束释放,平截面假定并不满足,而且节点非线性高度集中,曲率近似为无穷大,因而常采用弯矩-转角方法进行分析,并开展具体的截面配筋设计计算[24, 28, 61].
3.3 非线性建模与分析方法非线性模拟分析中的分析模型主要包括纤维单元模型(fiber model)、集中塑性模型(lumped plasticity model)、多弹簧模型(multi-spring model)和连续有限元模型(finite element model)四类.
3.3.1 纤维单元模型Kurama等[15]利用DRAIN-2DX软件建立了自复位剪力墙的纤维单元模型(图 20),进行了单调推覆和动力时程分析,随后又将纤维单元模型应用在混合摇摆墙[62]和自复位联肢墙[45-46, 48]的模拟分析中.Erkmen等[63]将纤维单元模型的分析结果与已有自复位剪力墙试验数据进行了对比验证,发现对力-变形曲线模拟结果较为接近,但对预应力筋应力的模拟结果差距较大.
纤维单元模型分析的基础为平截面假定,混凝土截面被划分为若干纤维,钢筋和预应力筋采用桁架单元,预应力筋仅在两端约束自由度以实现无黏结,通过弯矩-曲率迭代分析,可以模拟从开始加载到最终破坏的全过程.纤维单元模型的优势在于仅采用材料的单轴本构关系即可获得相当精确的模拟结果,但为了模拟摇摆,界面的张合是通过将节点附近单元抗拉强度和刚度设置为零来实现的[64].虽然这样可在宏观上表达界面张开后结构的刚度变化,但却并不能真实反映结构的摇摆抬升和局部行为.
3.3.2 集中塑性模型集中塑性模型是表达自复位结构节点弯矩-转角响应的一种宏观模型,见图 21.通常情况下,摇摆界面由两个零长度的转动弹簧组成,分别代表界面的自复位的双线性变形特征(自复位来源,如后张预应力)和弹塑性耗能特征(如滞回耗能元件),上部结构(如柱、梁、墙或桥墩)可近似简化为弹性梁单元.Pampanin等[65]最早采用这种模型来模拟自复位混凝土框架中的梁柱节点,Parlemo等[66-67]建立了自复位桥墩的分析模型,Nazari等[17]利用这种模型对受控摇摆墙进行了模拟分析,Henry[68]在双弹簧模型的基础上提出了一种七弹簧模型用于模拟PreWEC剪力墙,通过调整各弹簧参数,获得了较精确的模拟结果.
自复位结构的非线性行为高度集中于节点位置,结构的其余部分则基本保持弹性,符合集中塑性模型的假定,但这种模型同样无法表达摇摆界面局部的受力情况.此外,为获得精确模拟结果,需要对摇摆界面进行深入的截面分析[60].有学者提出了悬臂梁等效方法[65, 69],即假定自复位悬臂梁与固结悬臂梁在达到相同侧移时截面应变分布相同,此过程与弯矩-曲率分析方法类似,但需要先假定受压区高度,通过不断迭代确定截面平衡.Sritharan等[42]通过分析发现自复位剪力墙一般在达到0.5%侧移后截面受压区高度基本不再变化,可通过预先定义受压区高度与转角关系,提出简化分析方法[43],从而避免迭代过程,能较准确预测弯矩、受压区高度、预应力筋应力和混凝土墙趾受压应变,而且这种方法的准确性也在后续研究得到了进一步验证[17].
3.3.3 多弹簧模型多弹簧模型同样为一种宏观模型,见图 22.在多弹簧模型中,摇摆界面处布置有多个轴向弹簧,将弹簧设置成仅能受压来实现界面的摇摆,预应力筋和耗能元件同样通过设置成弹簧来进行定义,上部结构则一般简化为弹性梁单元.
Conley等[70]采用多弹簧模型模拟了PRESSS项目中的联肢墙,在墙体底部每侧受压区形心各布置了一个弹簧,近似认为转动中心在两侧弹簧的位置.但实际上截面转动中心应在中和轴,该假设将高估预应力筋的伸长量和截面弯矩[60].Spieth等[71]提出了一种包含10个接触弹簧单元的模型,用于模拟自复位混凝土梁柱节点,同时考虑了不同弹簧数量和弹簧位置分布对于模拟精度的影响.
Palermo等[72]对自复位混凝土梁柱节点和自复位剪力墙进行模拟分析发现,多弹簧模型相比集中塑性模型拟合程度更好,而且在考虑预应力筋的塑性之后能够取得更好的模拟结果.Marriott[60]继续对已有的多弹簧模型进行了改进,提出了确定弹簧轴向刚度的方法,并根据试验的双向加载工况提出了三维多弹簧模型.杨博雅等[73]使用OpenSees在墙体与基础接缝处设置了一系列桁架单元,采用CONCRETE01材料(不考虑受拉)来实现墙体的摇摆抬升.
多弹簧模型的优点在于可对摇摆界面局部行为进行较精确模拟,包括应力、应变、中和轴高度以及构件的伸长效应[74].但为获得较高精度的模拟结果,对自复位混凝土框架节点,至少需要8个弹簧单元[75],而自复位剪力墙截面高度更大,至少需要20个弹簧单元才能更好地模拟刚度的退化[76].弹簧数量提高能够提高模拟精度,但弹簧的参数较难确定,虽然考虑材料塑性而将弹簧设置为双线性更合适,但计算稳定性会降低[60].
3.3.4 连续有限元模型Kurama[18]采用ABAQUS建立了自复位剪力墙的有限元模型,墙体采用平面应力单元,摇摆通过定义接触实现,获得了与纤维单元模型非常接近的结果.马昕等[77]通过实体有限元模拟,研究了软钢滞回耗能元件数量、位置和长度对剪力墙自复位性能及抗震性能的影响.党像梁等[78]分别建立了自复位剪力墙的实体单元、平面应力单元和薄壳单元的有限元模型,与试验结果进行了对比,比较了三种单元的计算效率和精度,并验证了动力显式分析中采用壳单元进行模拟的可行性与合理性.Henry等[31]利用ABAQUS建立了PreWEC剪力墙的实体有限元模型,模拟结果与拟静力试验结果符合良好,并且通过建模分析了剪力墙摇摆抬升对相邻楼板的影响.
相比于其他三类单元,有限元模拟分析多采用通用有限元软件,计算效率最低,但有更多的单元类型和本构参数模型可供选择,通过精细建模,能够在分析过程中反映剪力墙的真实情况,如界面摇摆,受压区高度,耗能元件受力情况等.
4 研究展望新西兰、美国和日本等国家近年来已针对自复位剪力墙进行了较为深入的研究,研究成果已经体现在相关规范和设计指南中[23-24, 79-80],并将研究成果成功应用于一批采用了自复位技术的试点工程[81-83],值得说明的是已有采用混合框架-自复位剪力墙体系的医院建筑在强震后基本无结构损伤,震后使用功能未中断[83],说明了自复位结构体系在抗震设计理念上的先进性.基于前述国内外研究现状的总结和分析,提出了需解决的关键科学问题.
4.1 预应力筋的变形能力后张预应力钢绞线具有较强的弹性变形能力,作为经济可靠的回复力来源,在预应力混凝土结构和自复位结构中都有广泛的应用,但其应变状态没有引起足够的重视.在自复位结构体系中,预应力筋在构件截面中心直线布置,反复的水平侧移导致预应力筋的应力在有效应力的基础上发生反复的变化(图 23),这种变化在进入大变形状态后更加明显,应变也会在有效预应力对应的应变的基础上反复增加.

|
图 23 拟静力滞回加载中预应力筋的应力变化[28] Figure 23 Stress development in post-tensioning tendon subjected to cyclic loading[28] |
虽然钢绞线在普通的单调拉伸试验中延伸率基本可以达到7%左右,但实际上由于锚具中夹片对于钢绞线截面的削弱作用,钢绞线在达到较小应变时即可能发生单丝破断,见图 24.Bruce等[84]通过对12.7 mm直径1 860 MPa级1×7钢绞线的反复加载试验发现,钢绞线在发生单丝断裂后,卸载至张拉应变时预应力就已全部丧失,钢绞线刚度也有较大下降.已有的有关钢绞线的非线性滞回加载试验发现钢绞线发生单丝断裂时的延伸率约在1~4%[84-88].对于自复位结构,在摇摆界面张开后,结构的抗侧刚度则主要由预应力筋提供,预应力筋的破断和屈服是控制结构倒塌和保证其自复位能力的关键,如何提高预应力筋的变形能力有待于进一步研究.
4.2 自复位单元与相邻结构的相互作用自复位剪力墙自身刚度和承载力偏低,很少作为主要抗侧体系独立出现,常与框架结构结合形成框架-摇摆/自复位剪力墙体系[90-95].剪力墙作为整体性关键构件,可以控制框架实现整体屈服破坏机制,避免出现薄弱层,自复位剪力墙提供的回复力也可以降低结构的残余变形.
自复位剪力墙需要与相邻结构形成可靠连接以保证协同工作,但剪力墙摇摆过程中的墙体抬升会对连接构件[96]和相邻的结构构件[68, 97]造成严重损坏.虽然框架对整体结构屈服后刚度的提升有助于控制残余变形[98],但模拟分析中常常忽略的构件,如楼板、填充墙和楼梯等,却会在一定程度上阻碍回复力的作用,削弱结构的自复位性能[99].
4.3 冗余度与鲁棒性的提升为了实现摇摆机制,自复位剪力墙在节点处一般仅通过预应力筋和耗能元件连接,构件内部的纵向受力钢筋和混凝土在节点处断开,约束的释放使得此类结构缺乏足够的冗余度.实际上,在已有的试验研究中预应力筋和耗能元件破坏的情况并不少见.Yamashita等[100]进行的自复位混凝土柱振动台试验中发现锚具夹片破坏,导致预应力失效,此时预应力筋的应变仅为1.05%;Restrepo等[19]进行的混合摇摆墙拟静力试验中,在墙体侧移达到3%时耗能钢筋发生断裂;在UCSD户外振动台完成的三层预制装配式混凝土结构的振动台试验中发现,在设计水平地震下,墙体内部的耗能钢筋发生断裂,且预应力钢绞线存在不均匀张拉,直接导致随后在最大设计地震水平下钢绞线断裂[96].
这充分说明尽管自复位剪力墙在控制震损和残余变形方面有着明显的优势,但却面临着冗余度和鲁棒性不足的问题,结构缺乏足够的安全储备.在极端情况下,剪力墙的摇摆将失去控制,结构的承载力大幅降低,自复位能力丧失,极有可能发生倾覆或倒塌.而通过引入随摇摆幅值提高而分步激活的多组耗能元件,或者结合多种耗能摇摆方式,可以建立抵抗倒塌的多道防线[101],但如何进行分析设计还有待于进一步的试验验证.
4.4 高阶振型的影响与多节点摇摆的利用能力设计的目标是使得结构在预期位置产生塑性铰,对剪力墙而言则希望塑性铰产生在墙底.塑性铰形成后,基底弯矩便不再增加,但结构的其余部分的弯矩和剪力仍可能继续增长[102],高阶振型的分析可以通过分析对应的底部铰接体系来实现[103].随着地震动幅值的提高,塑性铰弯矩的限制导致一阶振型受限,而铰接体系高阶振型占比提高导致剪力合力作用点降低,在塑性铰弯矩不变的情况下,基底剪力相比静力加载情况(线性分布,近似一阶振型)更大,而且这种现象在拥有长自振周期和高延性需求的结构中更加明显[104].
自复位节点的耗能摇摆与塑性铰类似,因此,上述问题在自复位剪力墙中同样存在,研究中也发现了这种剪力的放大效应[16, 76, 105-107].考虑到自复位结构一般为装配式结构,Wiebe等[103]提出通过允许多节点摇摆的形式降低高阶振型的作用,通过设置额外的耗能摇摆界面,新增摇摆界面处的弯矩将被限制,见图 25,而弯矩的微分为剪力,弯矩降低后剪力同样会降低[108].

|
图 25 新增摇摆界面后对弯矩和剪力的控制作用[108] Figure 25 Reduction of moment and shear force with additional rocking joint[108] |
虽然有学者指出设置多个耗能摇摆界面/塑性铰后变形的提高并不大[103, 109],但释放约束会降低结构的刚度,对结构刚度和变形的影响需要进一步验证.在设置多个耗能摇摆界面后,可以尝试在控制内力的同时实现多节点多层次耗能,从整体层面上提升剪力墙的冗余度和鲁棒性.
4.5 残余变形的控制与预测各类耗能元件的使用提高了自复位结构的耗能能力,但也导致了残余变形增大的可能.为保证自复位能力,Stanton等[110]最早提出了一种基于静力平衡的残余变形控制方法,即要求预应力提供的回复力应能够使耗能钢筋屈服来实现自复位,这一思想也体现在许多规范和标准中[24, 79, 80, 111].但是在真实的地震过程中,结构在震后还将进行自由衰减振动,最终的残余变形有减小的趋势[112-113],最终的残余变形可能只产生在很小的范围内,见图 26,说明根据拟静力试验等低速加载条件下获得的结构残余变形可能并不准确.
结构的损伤与变形密切相关,因而基于性态的抗震设计能够比较好地控制结构损伤,但却不一定能够很好地控制残余变形.以往的抗震设计中往往只关注结构在地震过程中的最大响应和结构的耗能能力,但是最终的残余变形也是评估结构震后安全性与修复费用的重要指标.虽然已有学者分析了控制残余变形大小的影响因素[55, 112-117],但如何能够在设计阶段精确预测残余变形仍需要大量的分析研究来实现.
5 结论通过对国内外研究现状的总结和分析,可获得的结论为:
1) 通过对自复位剪力墙结构工作原理、技术优势和理论发展现状的总结和分析,可知作为可恢复功能结构体系的重要组成部分,自复位剪力墙在抗震设计理念上具有明确的先进性.
2) 应在自复位剪力墙结构体系研发,性能、分析与设计方法等方面进行深入系统的研究,为这种具有明确优势的结构体系的应用提供技术和理论支撑.
3) 尚应对预应力筋的受力行为、楼屋盖等水平连接影响、自复位剪力墙的冗余度和鲁棒性、多墙片拼装竖向多节点摇摆的自复位剪力墙高阶振型效应,以及残余变形分析与预测等进一步开展研究.
| [1] |
谢礼立, 马玉宏, 翟长海. 基于性态的抗震设防与设计地震动[M]. 北京: 科学出版社, 2009: 3. XIE Lili, MA Yuhong, ZHAI Changhai. Performance-based seismic design and design ground motion[M]. Beijing: Science Press, 2009: 3. |
| [2] |
鲍雷T, 胡世平. 延性钢筋混凝土建筑的确定性抗震设计步骤[J]. 建筑结构学报, 1983(4): 14. PAULEY T, HU Shiping. Seismic design procedure for ductile reinforced concrete structures[J]. Journal of Building Structures, 1983(4): 14. |
| [3] |
HOUSNER G W. The behavior of inverted pendulum structures during earthquakes[J]. Bulletin of the Seismological Society of America, 1963, 53(2): 403. |
| [4] |
HUKELBRIDGE A A, CLOUGH R W. Preliminary experimental study of seismic uplift of a steel frame[R]. Berkeley: University of California, Berkeley, 1977 https://www.amazon.com/Preliminary-experimental-seismic-uplift-Report/dp/B0006WS694
|
| [5] |
HUKELBRIDGE A A. Earthquake simulation tests of a nine story steel frame with columns allowed to uplift[R]. Berkeley: University of California, Berkeley, 1977 https://www.amazon.com/Earthquake-simulation-columns-allowed-uplift/dp/B0006WT53A
|
| [6] |
PRIESTLEY M J N, EVISON R J, CARR A J. Seismic response of structures free to rock on their foundations[J]. Bulletin of the New Zealand National Society for Earthquake Engineering, 1978, 11(3): 141. |
| [7] |
MEEK J W. Dynamic response of tipping core buildings[J]. Earthquake Engineering and Structural Dynamics, 1978, 6(5): 437. DOI:10.1002/(ISSN)1096-9845 |
| [8] |
YIM C S, CHOPRA A K, PENZIEN J. Rocking response of rigid blocks to earthquake[J]. Earthquake Engineering and Structural Dynamics, 1980, 8(6): 565. DOI:10.1002/(ISSN)1096-9845 |
| [9] |
ASLAM M, GODDEN W G, SCALISE D T. Earthquake rocking response of rigid bodies[J]. Journal of the Engineering Mechanics, ASCE, 1980, 106(2): 377. |
| [10] |
PSYCHARIS I N, JENNINGS P C. Rocking of slender rigid bodies allowed to uplift[J]. Earthquake Engineering and Structural Dynamics, 1983, 11(1): 57. DOI:10.1002/(ISSN)1096-9845 |
| [11] |
ROH H, REINHORN A M. Analytical modeling of rocking elements[J]. Engineering Structures, 2009, 31(5): 1181. |
| [12] |
ROH H, REINHORN A M. Modeling and seismic response of structures with concrete rocking columns and viscous dampers[J]. Engineering Structures, 2010, 32(8): 2099. |
| [13] |
PRIESTLEY M. Overview of PRESSS research program[J]. PCI Journal, 1991, 53. |
| [14] |
PRIESTLEY M, TAO J T. Seismic response of precast prestressed concrete frames with partially debonded tendons[J]. PCI Journal, 1993, 38(1): 60. |
| [15] |
KURAMA Y, SAUSE R, PESSIKI S, et al. Lateral load behavior and seismic design of unbonded post-tensioned precast concrete walls[J]. ACI Structural Journal, 1999, 96(4): 623. |
| [16] |
KURAMA Y, PESSIKI S, SAUSE R, et al. Seismic behavior and design of unbonded post-tensioned precast concrete walls[J]. PCI Journal, 1999, 44(3): 73. |
| [17] |
NAZARI M, SRITHARAN S, AALETI S. Single precast concrete rocking walls as earthquake force-resisting elements[J]. Earthquake Engineering and Structural Dynamics, 2017, 46(5): 757. |
| [18] |
KURAMA Y C. Seismic design of unbonded post-tensioned precast concrete walls with supplemental viscous damping[J]. ACI Structural Journal, 2000, 97(4): 650. |
| [19] |
RESTREPO J I, RAHMAN A. Seismic performance of self-centering structural walls incorporating energy dissipators[J]. Journal of Structural Engineering, 2007, 133(11): 1566. |
| [20] |
SMITH B J, KURAMA Y C, MCGINNIS M J. Design and measured behavior of a hybrid precast concrete wall specimen for seismic regions[J]. Journal of Structural Engineering, 2011, 137(10): 1054. |
| [21] |
SMITH B J, KURAMA Y C, MCGINNIS M J. Behavior of precast concrete shear walls for seismic regions: Comparison of hybrid and emulative specimens[J]. Journal of Structural Engineering, 2013, 139(11): 1918. |
| [22] |
Building code requirements for structural concrete: ACI 318[S]. Farmington Hills, USA: American Concrete Institute, 2014
|
| [23] |
Acceptance criteria for special unbonded post-tensioned precast structural walls based on validation testing and commentary: ACI ITG-5.1[S]. Farmington Hills, USA: American Concrete Institute, 2007
|
| [24] |
Requirements for design of a special unbonded post-tensioned precast shear wall satisfying ACI ITG-5.1 (ACI ITG-5.2-09) and commentary: ACI ITG-5.2[S]. Farmington Hills, USA: American Concrete Institute, 2009
|
| [25] |
SMITH B J, KURAMA Y. Seismic design guidelines for special hybrid precast concrete shear walls[R]. Notre Dame: University of Notre Dame, 2012
|
| [26] |
MARRIOTT D, PAMPANIN S, BULL D, et al. Dynamic testing of precast, post-tensioned rocking wall systems with alternative dissipating solutions[Z]. [S.l.]: NZSEE Conference, 2008
|
| [27] |
MARRIOTT D, PAMPANIN S, PALERMO A, et al. Shake-table testing of hybrid post-tensioned precast wall systems with alternative dissipating solutions[Z]. Beijing: 14WCEE, 2008
|
| [28] |
SMITH B J. Design, analysis, and experimental evaluation of hybrid precast concrete shear walls for seismic regions[D]. Notre Dame: University of Notre Dame, 2012: 67 http://search.proquest.com/docview/1512222433
|
| [29] |
TWIGDEN K M, SRITHARAN S, HENRY R S. Cyclic testing of unbonded post-tensioned concrete wall systems with and without supplemental damping[J]. Engineering Structures, 2017, 140(Supplement C): 408. |
| [30] |
TWIGDEN K M, HENRY R S. Experimental response and design of O-connectors for rocking wall systems[J]. Structures, 2015, 3: 267. |
| [31] |
HENRY R S, SRITHARAN S, INGHAM J M. Finite element analysis of the PreWEC self-centering concrete wall system[J]. Engineering Structures, 2016, 115(Supplement C): 29. |
| [32] |
SRITHARAN S, AALETI S, HENRY R S, et al. Precast concrete wall with end columns (PreWEC) for earthquake resistant design[J]. Earthquake Engineering and Structural Dynamics, 2015, 44(12): 2077. |
| [33] |
TWIGDEN K M, HENRY R S, MA Q T. Dynamic testing of post-tensioned rocking walls[Z]. Lisboa: 15WCEE, 2015
|
| [34] |
TWIGDEN K M. Dynamic response of unbonded post-tensioned concrete walls for seismic resilient structures[D]. Auckland: University of Auckland, 2016: 161 https://researchspace.auckland.ac.nz/handle/2292/28286
|
| [35] |
陈适才, 闫维明, 李振宝, 等. 底部开缝预应力剪力墙结构力学性能的有限元分析[J]. 防灾减灾工程学报, 2010(6): 632. CHEN Shicai, YAN Weiming, LI Zhenbao, et al. Finite element analysis of the mechanical properties of post-tensioned shear wall with bottom slit[J]. Journal of Disaster Prevention and Mitigation Engineering, 2010(6): 632. |
| [36] |
党像梁, 吕西林, 周颖. 底部开水平缝预应力自复位剪力墙试验设计及结果分析[J]. 地震工程与工程振动, 2014(6): 104. DANG Xiangliang, LV Xilin, ZHOU Ying. Experimental design and measured behavior analysis of self-centering shear walls with horizontal bottom slit[J]. Earthquake Engineering and Engineering Dynamics, 2014(6): 104. |
| [37] |
党像梁, 吕西林, 周颖. 底部开水平缝摇摆剪力墙抗震性能分析[J]. 地震工程与工程振动, 2013(5): 187. DANG Xiangliang, LV Xilin, ZHOU Ying. Study on seismic performance of a rocking wall with bottom horizontal slits[J]. Earthquake Engineering and Engineering Dynamics, 2013(5): 187. |
| [38] |
党像梁, 吕西林, 周颖. 底部开水平缝预应力自复位剪力墙试验研究及数值模拟[J]. 地震工程与工程振动, 2014(4): 160. DANG Xiangliang, LV Xilin, ZHOU Ying. Experimental study and numerical simulation of self-centering shear walls with horizontal bottom slit[J]. Earthquake Engineering and Engineering Dynamics, 2014(4): 160. |
| [39] |
党像梁, 吕西林, 钱江, 等. 底部开水平缝预应力自复位剪力墙有限元模拟[J]. 工程力学, 2017(6): 54. DANG Xiangliang, LV Xilin, QIAN Jiang, et al. Finite element simulation of self-centering pre-stressed shear walls with horizontal bottom slits[J]. Engineering Mechanics, 2017(6): 54. |
| [40] |
GUO T, ZHANG G, CHEN C. Experimental study on self-centering concrete wall with distributed friction devices[J]. Journal of Earthquake Engineering, 2014, 18(2): 216. |
| [41] |
NAKAKI S D, STANTON J F, SRITHARAN S. An overview of the PRESSS five-story precast test building[J]. PCI Journal, 1999, 44(2): 37. |
| [42] |
SRITHARAN S, AALETI S, THOMAS D J. Seismic analysis and design of precast concrete jointed wall systems[R]. Ames: Iowa State University, 2007 https://core.ac.uk/display/38898890
|
| [43] |
AALETI S, SRITHARAN S. A simplified analysis method for characterizing unbonded post-tensioned precast wall systems[J]. Engineering Structures, 2009, 31(12): 2969. |
| [44] |
PRIESTLEY M, SRITHARAN S, CONLEY J R, et al. Preliminary results and conclusions from the PRESSS five-story precast concrete test building[J]. PCI Journal, 1999, 44(6): 45. |
| [45] |
SHEN Q, KURAMA Y C. Nonlinear behavior of posttensioned hybrid coupled wall subassemblages[J]. Journal of Structural Engineering, 2002, 128(10): 1291. |
| [46] |
KURAMA Y C, SHEN Q. Posttensioned hybrid coupled walls under lateral loads[J]. Journal of Structural Engineering, 2004, 130(2): 298. |
| [47] |
KURAMA Y C, WELDON B D, QIANG S. Experimental evaluation of posttensioned hybrid coupled wall subassemblages[J]. Journal of Structural Engineering, 2006, 132(7): 1017. DOI:10.1061/(ASCE)0733-9445(2006)132:7(1017) |
| [48] |
QIANG S, KURAMA Y C, WELDON B D. Seismic design and analytical modeling of posttensioned hybrid coupled wall subassemblages[J]. Journal of Structural Engineering, 2006, 132(7): 1031. |
| [49] |
WELDON B D, KURAMA Y C. Nonlinear behavior of precast concrete coupling beams under lateral loads[J]. Journal of Structural Engineering, 2007, 133(11): 1572. |
| [50] |
BARBACHYN B S M, KURAMA Y C, MCGINNIS M J, et al. Testing and behavior of coupled shear wall structure with partially post-tensioned coupling beams[J]. ACI Structural Journal, 2016, 113(1): 112. |
| [51] |
BARBACHYN S M, KURAMA Y C, MCGINNIS M J, et al. Coupled shear wall with fully post-tensioned beams and unbonded reinforcing bar at toes[J]. ACI Structural Journal, 2016, 113(6): 1383. |
| [52] |
NEHRP guidelines and commentary for seismic rehabilitation of buildings: FEMA 273[S]. Washington DC, USA: Federal Emergency Management Agency, 1997
|
| [53] |
Prestandard and commentary for the seismic rehabilitation of buildings: FEMA 356[S]. Washington DC, USA: Federal Emergency Management Agency, 2000
|
| [54] |
Next-generation performance-based seismic design guidelines: FEMA 445[S]. Washington DC, USA: Federal Emergency Management Agency, 2007
|
| [55] |
SEO C Y, SAUSE R. Ductility demands on self-centering systems under earthquake loading[J]. ACI Structural Journal, 2005, 102(2): 281. |
| [56] |
PRIESTLEY M J N, CALVI G M, KOWALSKY M J. Displacement-based seismic design of structures[M]. Pavia, Italy: IUSS Press, 2007: 63.
|
| [57] |
PRIESTLEY M. Direct displacement-based design of precast/prestressed concrete buildings[J]. PCI Journal, 2002, 47(6): 77. |
| [58] |
RAHMAN A, SRITHARAN S. An evaluation of force-based design vs. displacement-based design of jointed precast post-tensioned wall systems[J]. Earthquake Engineering and Engineering Vibration, 2006, 5(2): 285. DOI:10.1007/s11803-006-0620-3 |
| [59] |
SHIBATA A, SOZEN M. Substitute structure method for seismic design in R/C[J]. Journal of the Structural Division-ASCE, 1976, 102(1): 1. |
| [60] |
MARRIOTT D. The development of high-performance post-tensioned rocking systems for the seismic design of structures[D]. Christchurch: University of Canterbury, 2009: 7.67 https://ir.canterbury.ac.nz/handle/10092/2678
|
| [61] |
YANG B, LU X. Displacement-based seismic design approach for prestressed precast concrete shear walls and its application[J]. Journal of Earthquake Engineering, 2017, 5. |
| [62] |
KURAMA Y C. Hybrid post-tensioned precast concrete walls for use in seismic regions[J]. PCI Journal, 2002, 47(5): 40. |
| [63] |
ERKMEN B, SCHULTZ A E. Self-centering behavior of unbonded, post-tensioned precast concrete shear walls[J]. Journal of Earthquake Engineering, 2009, 13(7): 1052. |
| [64] |
LU X, WU H, ZHOU Y. Seismic collapse assessment of self-centering hybrid precast walls and conventional reinforced concrete walls[J]. Structural Concrete, 2017, 18(6): 942. |
| [65] |
PAMPANIN S, PRIESTLEY M, SRITHARAN S. Analytical modelling of the seismic behaviour of precast concrete frames designed with ductile connections[J]. Journal of Earthquake Engineering, 2001, 5(3): 351. |
| [66] |
PALERMO A, PAMPANIN S, CALVI G M. Concept and development of hybrid solutions for seismic resistant bridge systems[J]. Journal of Earthquake Engineering, 2005, 9(6): 906. |
| [67] |
PALERMO A, PAMPANIN S, MARRIOTT D. Design, modeling, and experimental response of seismic resistant bridge piers with posttensioned dissipating connections[J]. Journal of Structural Engineering, 2007, 133(11): 1652. |
| [68] |
HENRY R S. Self-centering precast concrete walls for buildings in regions with low to high seismicity[D]. Auckland: University of Auckland, 2011: 230 https://researchspace.auckland.ac.nz/handle/2292/6875?show=full
|
| [69] |
PALERMO A. The use of controlled rocking in the seismic design of bridges[D]. Milan: Technical University of Milan, 2004 https://www.researchgate.net/publication/267221360_Use_of_Controlled_Rocking_in_the_Seismic_Design_of_Bridges
|
| [70] |
CONLEY J, SRITHARAN S, PRIESTLEY M J N. Precast seismic structural systems PRESSS-3: The five story precast test building Vol. 3-1: Wall direction response[R]. San Diego: University of California, San Diego, 1999: 49
|
| [71] |
SPIETH H A, CARR A J, MURAHIDY A G, et al. Modelling of post-tensioned precast reinforced concrete frame structures with rocking beam-column connections[Z]. [S.l.]: 2004 NZSEE Conference, 2004: 2
|
| [72] |
PALERMO A, PAMPANIN S, CARR A J, et al. Efficiency of simplified alternative modelling approaches to predict the seismic response of precast concrete hybrid systems[Z]. Budapest: FIB Symposium, 2005: 6
|
| [73] |
杨博雅, 吕西林. 预应力预制混凝土剪力墙截面设计方法[J]. 建筑结构学报, 2018, 39(2): 85. YANG Boya, LV Xilin. Design method of prestressed precast concrete shear walls[J]. Journal of Building Structures, 2018, 39(2): 85. |
| [74] |
SPIETH H A, ARNOLD D, DAVIES M, et al. Seismic performance of post-tensioned precast concrete beam to column connections with supplementary energy dissipation[Z]. [S.l.]: 2004 NZSEE Conference, 2004: 4
|
| [75] |
SPIETH H A, CARR A J, PAMPANIN S, et al. Modelling of precast prestressed concrete frame structures with rocking beam-column connections[R]. Christchurch, New Zealand: University of Canterbury, 2004
|
| [76] |
PENNUCCI D, CALVI G M, SULLIVAN T J. Displacement-based design of precast walls with additional dampers[J]. Journal of Earthquake Engineering, 2009, 131(PⅡ 910355070): 55. |
| [77] |
马昕, 吕西林. 软钢阻尼器对自复位剪力墙性能影响研究[J]. 结构工程师, 2013(4): 65. MA Xin, LV Xilin. Effects of the mild steel damper on the self-centering wall performance[J]. Structural Engineers, 2013(4): 65. |
| [78] |
党像梁, 吕西林, 钱江, 等. 自复位预应力剪力墙抗震性能实体和平面单元有限元分析[J]. 建筑结构学报, 2014(5): 24. DANG Xiangliang, LV Xilin, QIAN Jiang, et al. Finite element analysis with solid and plane element of seismic performance of self-centering pre-stressed shear walls[J]. Journal of Building Structures, 2014(5): 24. |
| [79] |
Concrete structures standard part 1-the design of concrete structures: NZS3101[S]. New Zealand: Standard Council, 2006
|
| [80] |
PAMPANIN S, MARRIOTT D, PALERMO A. PRESSS Design Handbook[M]. Auckland, New Zealand: [s.n.], 2010
|
| [81] |
ENGLEKIRK R E. Design-construction of the Paramount-A 39 story precast prestressed concrete apartment building[J]. PCI Journal, 2002, 47(4): 56. DOI:10.15554/pcij |
| [82] |
CATTANACH A, PAMPANIN S. 21st century precast: The detailing and manufacture of NZ's first multi-storey PRESSS-building[Z]. Rotorua, New Zealand: NZ Concrete Industry Conference, 2008
|
| [83] |
PAMPANIN S, KAM W Y, HAVERLAND G, et al. Expectation meets reality: Seismic performance of post-tensioned precast concrete southern cross endoscopy building during the 22nd Feb 2011 Christchurch earthquake[Z]. Auckland, New Zealand: NZ Concrete Industry Conference, 2011
|
| [84] |
BRUCE T L, EATHERTON M R. Behavior of post-tensioning strand systems subjected to inelastic cyclic loading[J]. Journal of Structural Engineering, 2016, 142(10): 04016067-6. DOI:10.1061/(ASCE)ST.1943-541X.0001503 |
| [85] |
WALSH K Q, KURAMA Y C. Behavior of unbonded post-tensioning monostrand anchorage systems under monotonic tensile loading[J]. PCI Journal, 2010, 55(1): 106. |
| [86] |
MUSSELMAN E, FOURNIER M, MCALPINE P, et al. Behavior of unbonded post-tensioning monostrand anchorage systems under short duration, high amplitude cyclical loading[J]. Engineering Structures, 2015, 104: 123. |
| [87] |
SIDERIS P, AREF A J, FILIATRAULT A. Effects of anchorage hardware on the cyclic tensile response of unbonded monostrands[J]. PCI Journal, 2014, 66. |
| [88] |
WALSH K Q, KURAMA Y C. Effects of loading conditions on the behavior of unbonded post-tensioning strand-anchorage systems[J]. PCI Journal, 2012, 83. |
| [89] |
WALSH K Q, KURAMA Y. Effects of anchor wedge dimensional parameters on posttensioning strand performance[J]. PCI Journal, 2015, 65. |
| [90] |
AJRAB J J, PEKCAN G, MANDER J B. Rocking wall-frame structures with supplemental tendon systems[J]. Journal of Structural Engineering, 2004, 130(6): 896. |
| [91] |
曲哲.摇摆墙—框架结构抗震损伤机制控制及设计方法研究[D].北京: 清华大学, 2010: 72 QU Zhe. Study on seismic damage mechanism control and design of rocking wall-frame structures[D]. Beijing: Tsinghua University, 2010: 72 http://cdmd.cnki.com.cn/Article/CDMD-10003-1011280763.htm |
| [92] |
裴星洙, 王佩. 混凝土框架-摇摆墙体系抗震性能研究[J]. 工程抗震与加固改造, 2013(2): 20. PEI Xingzhu, WANG Pei. Study on seismic property of RC frame rocking wall[J]. Earthquake Resistant Engineering and Retrofitting, 2013(2): 20. |
| [93] |
ZIBAEI H, MOKARI J. Evaluation of seismic behavior improvement in RC MRFs retrofitted by controlled rocking wall systems[J]. The Structural Design of Tall and Special Buildings, 2014, 23(13): 996. |
| [94] |
PAN P, WU S, NIE X. A distributed parameter model of a frame pin-supported wall structure[J]. Earthquake Engineering and Structural Dynamics, 2015, 44(10): 1645. |
| [95] |
SUN T, KURAMA Y C, ZHANG P, et al. Linear-elastic lateral load analysis and seismic design of pin-supported wall-frame structures with yielding dampers[J]. Earthquake Engineering and Structural Dynamics, 2018, 47(4): 989. |
| [96] |
SCHOETTLER M J, BELLERI A, ZHANG D, et al. Preliminary results of the shake-table testing for the development of a diaphragm seismic design methodology[J]. PCI Journal, 2009, 54(1): 115. |
| [97] |
LIU Q. Study on interaction between rocking-wall system and surrounding structure[D]. Twin Cities: University of Minnesota, 2016: 315 http://conservancy.umn.edu/handle/11299/185155
|
| [98] |
PETTINGA D, CHRISTOPOULOS C, PAMPANIN S, et al. Effectiveness of simple approaches in mitigating residual deformations in buildings[J]. Earthquake Engineering and Structural Dynamics, 2007, 36(12): 1763. DOI:10.1002/(ISSN)1096-9845 |
| [99] |
CHANCELLOR N, EATHERTON M, ROKE D, et al. Self-centering seismic lateral force resisting systems: High performance structures for the city of tomorrow[J]. Buildings, 2014, 4(3): 529. |
| [100] |
YAMASHITA R, SANDERS D H. Seismic performance of precast unbonded prestressed concrete columns[J]. ACI Structural Journal, 2009, 106(6): 830. |
| [101] |
LIU R, PALERMO A. Low damage design and seismic isolation: What's the difference[Z]. [S.l.]: 2015 NZSEE Conference, 2015: 260
|
| [102] |
PRIESTLEY M J N, AMARIS A D. Dynamic amplification of seismic moments and shear forces in cantilever walls[R]. Pavia, Italy: IUSS Press, 2002 https://www.researchgate.net/publication/239520165_Dynamic_Amplification_of_Seismic_Moments_and_Shear_Forces_in_Cantilever_Walls
|
| [103] |
WIEBE L, CHRISTOPOULOS C. Mitigation of higher mode effects in base-rocking systems by using multiple rocking sections[J]. Journal of Earthquake Engineering, 2009, 13(PⅡ 910354396): 87. |
| [104] |
RUTENBERG A. Seismic shear demand on RC structural walls: Review and bibliography[Z]. Corfu, Greece: Ⅲ ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, 2011: 3
|
| [105] |
SAUSE R, RICLES J M, ROKE D, et al. Design of self-centering steel concentrically-braced frames[Z]. Taipei, Taiwan: 4th International Conference on Earthquake Engineering, 2006
|
| [106] |
SULLIVAN T J, PRIESTLEY M J N, CALVI G M. Estimating the higher-mode response of ductile structures[J]. Journal of Earthquake Engineering, 2008, 12(3): 457. |
| [107] |
SHOUJUN W, PENG P, DONGBIN Z. Higher mode effects in frame pin-supported wall structure by using a distributed parameter model[J]. Earthquake Engineering and Structural Dynamics, 2016, 45(14): 2379. |
| [108] |
WIEBE L, CHRISTOPOULOS C, TREMBLAY R, et al. Mechanisms to limit higher mode effects in a controlled rocking steel frame. 1: concept, modelling, and low-amplitude shake table testing[J]. Earthquake Engineering and Structural Dynamics, 2013, 42(7): 1056. |
| [109] |
PANAGIOTOU M, RESTREPO J I. Dual-plastic hinge design concept for reducing higher-mode effects on high-rise cantilever wall buildings[J]. Earthquake Engineering and Structural Dynamics, 2009, 38(12): 1362. |
| [110] |
STANTON J, STONE W C, CHEOK G S. A hybrid reinforced precast frame for seismic regions[J]. PCI Journal, 1997, 42(2): 22. |
| [111] |
Acceptance criteria for moment frames based on structural testing (T1.1-01) and commentary (T1.1R-01): ACI T1.1[S]. Farmington Hills, Michigan: American Concrete Institute, 2001
|
| [112] |
MACRAE G A, KAWASHIMA K. Post-earthquake residual displacements of bilinear oscillators[J]. Earthquake Engineering and Structural Dynamics, 1997, 26(7): 701. DOI:10.1002/(ISSN)1096-9845 |
| [113] |
EATHERTON M R, HAJJAR J F. Residual drifts of self-centering systems including effects of ambient building resistance[J]. Earthquake Spectra, 2011, 27(3): 719. DOI:10.1193/1.3605318 |
| [114] |
KAWASHIMA K, MACRAE G A, HOSHIKUMA J, et al. Residual displacement response spectrum[J]. Journal of Structural Engineering, 1998, 124(5): 524. |
| [115] |
CHRISTOPOULOS C, FILIATRAULT A, FOLZ B. Seismic response of self-centring hysteretic SDOF systems[J]. Earthquake Engineering and Structural Dynamics, 2002, 31(5): 1131. DOI:10.1002/(ISSN)1096-9845 |
| [116] |
CHRISTOPOULOS C, PAMPANIN S, PRIESTLEY M. Performance-based seismic response of frame structures including residual deformations. Part Ⅰ: Single-degree of freedom systems[J]. Journal of Earthquake Engineering, 2003, 7(1): 99. |
| [117] |
PAMPANIN S, CHRISTOPOULOS C, PRIESTLEY M. Performance-based seismic response of frame structures including residual deformations. Part Ⅱ: Multi-degree of freedom systems[J]. Journal of Earthquake Engineering, 2003, 7(1): 130. |
 2018, Vol. 50
2018, Vol. 50