2. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),哈尔滨 150090;
3. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Structures Dynamic Behavior and Control(Harbin Institute of Technology), Ministry of Education, Harbin 150090, China;
3. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
装配式停车楼结构由于内部停/行车的空间以及有效停/行车坡道需求,需合理布置大跨度预制混凝土结构构件.预制预应力混凝土双T板(以下简称双T板)的板梁结合受力性能良好,具有刚度大、承载力高以及便于铺设形成大跨度楼/屋盖等优势[1],且工业化生产条件下易于保证质量,自1952年设计定型起至今仍持续发展[2-4],在国外发达国家如美、加、澳等广泛应用于停车楼[5-7].国外有关学者针对双T板的受弯、受剪、局部受压、预应力效应等开展了一系列研究工作,相关成果也已体现在有关技术标准及设计手册中.
由于中国尚缺乏以双T板作为装配式停车楼结构楼屋盖/坡道主要结构构件的试验和理论基础,因此结合中国首座装配式停车楼结构的设计建造,总结国内外预制预应力混凝土构件性能和设计方法,尤其是借鉴美国预制/预应力混凝土学会(PCI)设计手册[8],构建了未铺装和预铺装两类双T板,分别针对18 m和24 m两种标志跨度双T板,以现场足尺试验的方式,开展正截面弯曲性能和斜截面受剪性能分析[9],获得了满足试验条件下两类双T板构件的刚度与裂缝及正截面与斜截面承载力等,在装配式停车楼的楼/屋盖与停/行车坡道所需的静力竖向荷载作用下,两类双T板构件的承载能力和变形能力均较大,相对于竖向荷载基本组合作用所需的内力,其抗力富裕程度较大,且两种跨度两类双T板使用阶段的拉区边缘拉应力和跨中挠度也较好地符合裂缝控制和变形控制要求.通过足尺试验获得双T板的弯曲性能和剪切性能,尤其是使用性能和承载能力,为工程应用提供试验支撑.
然而,足尺试件受力性能试验还是受到了诸多条件限制,试验参数和试件数量有限,难以较全面考察各类荷载工况影响.应通过对相同条件下双T板试件的非线性分析获得试验条件下变形发展以及正截面和斜截面承载力等,并与实测结果进行对比分析,通过模拟分析结果与试验结果的吻合程度验证所采用的非线性模型的可靠性,在此基础上模拟分析均布荷载、变剪跨比的单点集中加载以及双T板翼缘在坡道停车的车轮集中荷载等3种工况条件下两类双T板试件整体弯曲性能、支座斜截面性能以及翼缘板的局部受力性能.
为此,在双T板构件足尺试验结果基础上,结合非线性全过程分析方法,进行试验中未能涉及的构件性能和能力的精细考察,可进一步验证双T板在装配式停车楼结构中的适用性,为提出设计计算方法和优化配筋构造提供支持.
1 双T板试验所构建的全跨等截面未铺装双T板均呈现双T的基本构型:板面标志宽度2.4 m,标志跨度18 m,实际跨度17.98 m,标志跨度24 m,实际跨度23.98 m;截面高度则分别为700 mm和900 mm,两肋梁底宽均为120 mm,翼缘板厚度均为50 mm.预铺装双T板除需布置80 mm厚细石混凝土后浇层外,构件其余的几何尺寸与未铺装情况相同.两类双T板均采用强度等级为C50的混凝土浇筑,板面双向布置了由
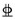
|
注:DT-18T的配筋与DT-18相同;括号内数值运用于DT-24及DT-24T. 图 1 新型双T板的截面与配筋(DT-18) Figure 1 Specimen size and reinforcement of double-tees(DT-18) |
需要说明的是,两类18 m跨双T板自两侧板端1.5 m范围内每根肋梁内各有1根预应力筋通过套管实现无黏结,两类24 m跨双T板以同样方式实现每根肋梁内各2根预应力筋无黏结,避免预应力筋在放张时因较大的局部集中预加力对板端面形成劈裂裂缝[10],虽然采取了一定措施,预应力筋放张后仍在端部发现长度不超过2 m的沿最下排筋的纵向裂缝.
针对两种类型两种跨度的4块足尺双T板开展了现场试验,研究目的分别是获得其弯曲性能尤其是正截面承载力,同时获得其斜截面受力性能和斜截面承载力,弯曲性能采取三分点加载,斜截面受力性能采用了剪跨比均为3的单点集中加载,即未铺装、预铺装的两类18 m跨双T板集中力作用点距支座边缘分别为1 800 mm和2 040 mm,两类24 m跨双T板集中力作用点距支座边缘分别为2 280 mm和2 520 mm,斜截面受力性能试验先后针对同一试件的两端各进行一次.试验获得的各试件弯曲开裂荷载、正截面承载力见表 1.
| 表 1 正截面受力性能 Table 1 Mechanical behavior of flexure experiment |
弯曲性能试验横向裂缝得到了充分发展,但主裂缝的延伸高度直至试件破坏一直在翼缘板以下,试件破坏时未铺装、预铺装18 m跨和24 m跨双T板跨中最大挠度值与计算跨度比值分别达到了1/58、1/51、1/69及1/64,弯曲裂缝宽度最大值分别为2.0(A肋)/1.8(B肋,下同)、2.0/1.9、3/2.5及3.5 mm/2.5 mm.直至试件破坏均未发现两种跨度的两类试件受压翼缘存在压碎迹象.典型试件弯曲破坏现象见图 2.

|
图 2 DT-18T弯曲性能试验 Figure 2 DT-18T flexure experiment |
斜截面受力性能试验中发现,针对同一试件两侧先后进行的两次试验所获得的弯剪区段斜裂缝宽度发展趋势相近,虽然弯曲试验后发现横向裂缝主要集中在纯弯段,而且按剪跨比等于3确定的弯剪区段均距先期进行的弯曲性能试验的近似纯弯区段的长度不小于所采用预应力筋传递长度,但每一试件两侧的单点集中破坏荷载值差异均较大.可以认为,这种差异主要是由于弯曲性能试验后因跨中区段横向裂缝充分开展致使预应力筋与其周围混凝土的黏结性能发生退化,导致预应力筋有效应力降低,使预加力对斜截面受力性能的影响,尤其是斜截面承载力的提高幅度受到了限制.同一试件的前一次一侧斜截面受力性能试验完成后所造成的筋-混凝土黏结性能退化及有效预应力损失,更是加剧了对其另一侧弯剪区段有效预应力的损失,进一步降低了预加力对斜截面承载力的贡献.
需要强调指出,尽管存在着同一试件两端先后进行的弯剪区段斜截面承载力值差异较大的试验现象,但同一试件斜截面承载力试验值的较小值,仍大于依据混凝土实测值、横向钢筋屈服强度实测值、以及实际截面确定的斜截面承载力计算值,斜截面受力性能试验的结果见表 2,典型试件斜截面破坏见图 3.
| 表 2 斜截面受力性能试验结果 Table 2 Results of shear experiment |

|
图 3 DT-24斜截面性能试验 Figure 3 DT-24 shear experiment |
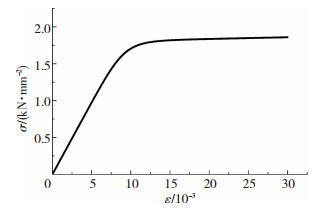
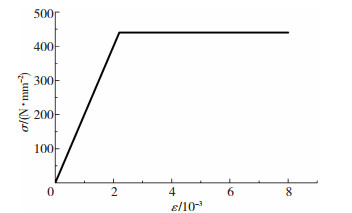
非线性分析模型首先是按所构建两类双T板形状和截面尺寸建立几何模型,依据钢筋和混凝土分离建模方法,基于ANSYS对混凝土采用实体单元,对板面、肋梁的非预应力筋和肋梁内的预应力筋采用杆单元,并将实体单元和杆单元相关结点自由度耦合的思路获得的[11].混凝土的破坏准则采用了SOLID65实体单元中常用的Willam-Warnker五参数模型,材料物理力学性能取为试验实测值,混凝土弹性模量按现行规范取用;非预应力筋的应力应变关系为理想弹塑性模型,预应力筋采用Menegotto and Pinto[12-13]的本构关系,两种钢筋弹性段屈服强度均按其实测值取用,见图 4、5.双T板中预应力采取等效降温法施加给模型中的预应力筋[14],预加力的大小取为前述足尺试件有效预应力平均值.除加载条带加密区域和肋板交接区域外,双T板其余部分按常规方法均匀划分网格单元,预应力筋和双T板钢筋网片的单元划分与混凝土体单元相对应, 混凝土及钢筋网格划分见图 6.
|
图 4 预应力筋应力-应变曲线 Figure 4 Stress-strain for tendons |
|
图 5 非预应力筋应力-应变曲线 Figure 5 Stress-strain for rebars |

|
图 6 网格划分 Figure 6 Meshing |
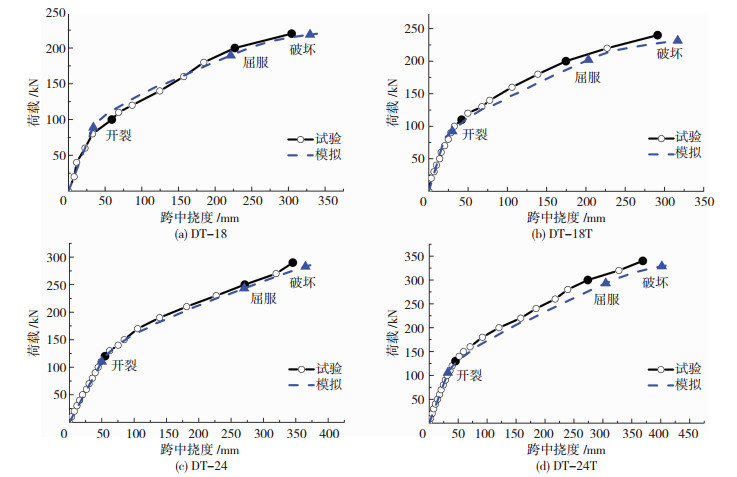
结合图 1的截面配筋及图 6的网格划分建立非线性分析模型,按两端简支边界条件,对已包含构件自重的模型,按逐步施加三分点集中线荷载方式,获得模拟试验加载工况下两类标志跨度双T板的荷载与跨中挠度非线性分析曲线,见图 7.
|
图 7 弯曲跨中荷载-挠度曲线 Figure 7 Load-deflection at mid-span |
由图 7可知,两类双T板跨中荷载-挠度关系均表现为开裂前的弹性、开裂至屈服的非线性、屈服至破坏的变形急速发展的3个主要阶段,其发展趋势与试验所获得的荷载-变形关系实测结果总体上是吻合的.其中,开裂、屈服和破坏3个关键点,试件DT-18、DT-18T、DT-24及DT-24T计算值与实测值比值分别为0.876、0.909、0.973、0.912,0.948、1.01、0.973、0.977,1.0、0.965、0.986、0.977.显然,模拟分析获得的计算结果与实测结果相比差异不大,尤其是峰值荷载的计算值与实测值基本吻合.模拟分析结果发现预铺装双T板较相同条件下未铺装双T板的弹性刚度和开裂后刚度均有一定提高,正截面承载力的计算值也因翼缘厚度的增大而分别提高了5.3%和16.2%,这也与足尺试件试验结果十分吻合.
当然,足尺试件的模拟分析是假设由试件端部至弯剪区段可能发生的最近的斜裂缝范围内预应力筋与其周围混凝土黏结良好,即预应力筋具有足够的锚固长度基础上进行的.由于所完成的足尺试件具有足够长弯剪区段,该假定是合理的.同时,分析时也忽略了纯弯区段或邻近加载点的弯剪区段预应力筋与受拉混凝土以黏结作用体现的混凝土受拉强化效应,即认为达到开裂荷载后相应的拉区混凝土即全部退出工作.
由分析结果还可获得难以由试验结果获得的预应力筋的应力变化、压区混凝土的压应力(受现场条件限制,试件上表面较为粗糙不能粘贴混凝土应变片)等.由图 8荷载-预应力筋应力关系可知(其中1、2分别为跨中位置最上排筋和最下排筋,3、4为三分点位置最上排筋和最下排筋),18 m和24 m未铺装及预铺装两类双T板的肋内布置的最上排预应力筋跨中应力计算值分别为1 725.6、1 757.6、1 552.2、1 818.8 N·mm-2,最下排预应力筋相应的应力计算值分别为1 758.1、1 851.4、1 853.7、1 834 N·mm-2,均不小于所采用的1860级低松弛钢绞线名义屈服强度实测值,即认为试件破坏时预应力筋可达到屈服强度确定的正截面承载力是相对保守的,这也验证了表 1中按现行规范方法的正截面承载力理论值均不大于试验值的结果.

|
图 8 荷载-预应力筋应力曲线 Figure 8 Load-stress of prestressed tendons |
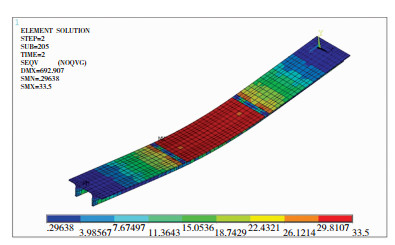
模型DT-18破坏时弯曲应力分布见图 9~10.达到峰值荷载时,各试件跨中控制截面压区边缘混凝土的极限压应变分别为0.003 427、0.003 713、0.003 471、0.003 681,均较中国现行国家标准中确定正截面承载力时采用的不高于C50混凝土极限压应变0.003 3稍大.
|
图 9 DT-18弯曲应力云图 Figure 9 Flexural stress cloud |

|
图 10 DT-18预应力筋和钢筋应力云图 Figure 10 Stress cloud for tendons and rebars |
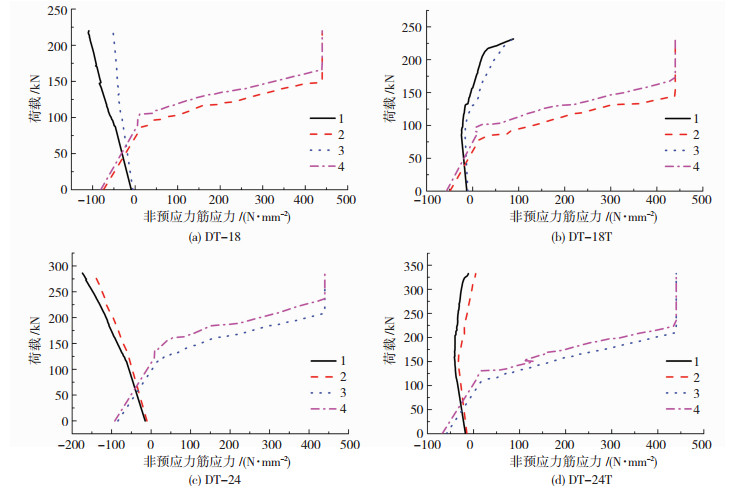
足尺双T板肋梁内非预应力纵筋应力发展情况见图 11(非预应力筋对应位置与预应力筋相同).峰值荷载下,18 m和24 m未铺装及预铺装双T板肋梁内最下排非预应力筋的应力均为440 N·mm-2,均不小于其屈服强度实测值.由于所构建的双T板肋梁钢筋网片纵筋主要对斜截面受力起销栓作用,也能弥散因混凝土收缩和温度应力及支座不均匀沉降等非受力作用可能出现的裂缝,其配筋量有限,其对构件正截面承载力的影响也有限.因此,按双线性本构模型获得的非预应力纵筋应力计算值对非线性分析结果的影响是可以接受的.
|
图 11 荷载-肋梁内非预应力筋应力曲线 Figure 11 Load-stress of rebars in webs |
通过与试验结果的对比分析,说明采用所建立的非线性分析模型适用于所构建的两类双T板弯曲性能全过程分析,可应用于设计荷载工况下构件弯曲性能非线性分析.
2.3 试验工况下斜截面受力性能考虑到同一试件两端分别按相同剪跨比进行斜截面受力性能试验发现的典型状态如开裂荷载及极限荷载差异明显,主要是由于预应力筋有效预应力因前期的弯曲性能试验而降低所导致的.因此,采用一定程度降低双T板的放张应力以模拟受剪性能中这种差异,可使非线性分析的过程与试验情况一致,确定试验条件下的试件端部斜截面承载力.
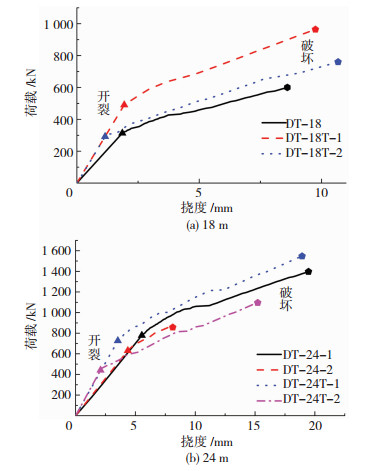
获得的18 m和24 m未铺装和预铺装两类试件荷载-加载点挠度关系见图 12,可以发现曲线总体上在前期表现为线性关系,后期具有明显的非线性,对应于试验结果可知两个阶段的分界点对应的构件出现斜裂缝.4个足尺双T板试件左、右两端斜截面开裂荷载分别为295(左端值,右端无实测值,下同),490与291、750与622、695与440 kN;构件破坏时左、右两端对应的极限荷载分别为600、920与760、1 400与840、1 560与1 080 kN.因此,试件左、右两端开裂荷载计算值与实测值比值分别为0.7、0.72与0.485、0.65与0.86、0.965与0.5.
|
图 12 集中荷载-加载点位移曲线 Figure 12 Load-deflection under concentrate load |
为获得合理计算结果,两类足尺试件放张后施加预应力折减比例分别为0.578、0.903与0.415、0.833与0.639、0.895与0.433.由此,再经模拟分析后,获得两类双T板破坏时非预应力筋应力均为440 N·mm-2;各试件肋梁最下排预应力筋的应力分别为947、1 360与907、1 641与1 117、1 507与975 N·mm-2,均小于预应力筋屈服强度实测值.预应力不同程度地限制斜裂缝开展和延伸,从而对构件斜截面承载力有一定贡献.事实上,非预应力筋、截面几何及混凝土强度主要控制着斜截面破坏状态.按折减端部一定长度范围内有效预应力(预应力筋传递长度、锚固长度范围内预应力)的思路,获得的模拟分析结果表明,连续进行的弯曲试验和斜截面受力试验,试件外在损伤不明显,但是依次进行的加载试验降低了弯剪区段范围内的混凝土与预应力筋的黏结性能,也降低预应力筋有效应力,削弱了预应力筋的销栓作用,从而导致斜截面承载力降低.
2.4 均布加载工况均布荷载是装配式停车楼结构楼盖的设计荷载工况,除结构自重外,停车楼停/行车所需的可变荷载标准值为4.0 kN/m2.结合图 1的模型施加均布荷载得到跨中荷载-挠度关系见图 13~14.

|
图 13 均布荷载下荷载-跨中挠度曲线 Figure 13 Load-deflection at mid-span under uniform load |
|
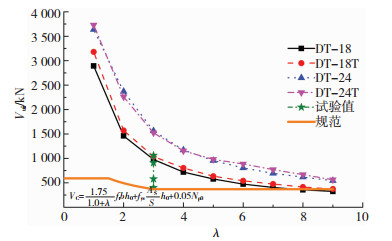
图 14 斜截面承载力 Figure 14 Shear capacity |
考虑长期效应影响后,张拉引起的预加力作用下两类试件4个足尺双T板的反拱计算值分别为13.95、15.13、22.18、23.19 mm,荷载标准组合下跨中挠度计算值分别为37.27、30.2、57.05、48.33 mm.即停车楼要求的正常使用极限状态下各双T板跨中挠度分别为23.32、15.07、34.87及25.14 mm,满足现行国家标准对变形控制的1/400(18 m和24 m两类标志跨度下分别为44.45、59.95 mm)要求.
破坏时,均布外荷载下两类双T板中肋梁跨中控制截面预应力筋应力最大值分别为1 045.45、1 056.66、1 044.32、1 053.02 N·mm-2,非预应力纵筋应力最大值分别为109.04、124.71、194.78、167.03 N·mm-2,预应力筋应力增量及非预应力筋拉应力水平均较低.4个足尺双T板的极限荷载及跨中挠度分别为15.08和506.08、17.46和489.7、15.46和511.23、17.15 kN/m2和524.65 mm.
相对于同条件下未铺装双T板,虽然因预铺装80 mm叠合层使构件自重提高了2 kN/m2,但预铺装双T板的极限外荷载较接近,即预铺装叠合层对双T板正截面承载力影响较小,其主要作为构造措施有效提高装配式楼盖整体性和抗震性能.
2.5 斜截面性能的扩参数分析按前述试验工况下斜截面受力性能分析的思路,对4块足双T板按剪跨比λ=1~9扩参数分析,获得了9种剪跨比条件下双T板的斜截面承载力的模拟分析结果,斜截面承载力与剪跨比的关系见图 14.足尺双T板斜截面承载力随剪跨比增大呈减小,随剪跨比斜截面承载力变化速率负相关的趋势,与双T板跨度及类型无关,且剪跨比越小,现行规范中斜截面承载力计算公式越趋于保守[15].
虽然依次加载造成的筋-混凝土黏结破坏导致足尺双T板试件的斜截面承载力损失较大,但试验值仍略高于按规范方法确定的斜截面承载力计算值.与前述分析结果相一致,铺装层对双T板的斜截面承载力的提高幅度有限,偏于安全地,为简化设计可不考虑预铺装叠合层对斜截面承载力贡献.
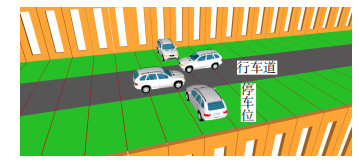
3 停车和行车分析中国首座装配式停车楼采用了标志跨度18 m的双T板,双T板坡道停/行车[16],行车道布置于中部,车位按垂直式布设,即单块双T板可停放乘用车的上限为2.为模拟停/行车最不利工况:停放2辆乘用车,同时行车道双向车辆前轮均行至双T板翼缘处,如图 15所示,加载示意见图 16.
|
图 15 停车和行车示意 Figure 15 Pattern for parking and driving |

|
图 16 加载示意 Figure 16 Pattern for loading |
计算结果显示,放张后、预铺装叠合层后及满布乘用车后双T板反拱分别为27.12、20.62与12.43 mm,跨中位移8.19 mm,跨中挠度满足变形控制要求.该工况下,混凝土、预应力筋及非预应力筋应力云图分别见图 17~18.可知,板面混凝土压应力较低,压应力最大值为0.07 N·mm-2,压应力远小于混凝土抗压强度;跨中控制截面预应力筋应力最大值为1 285.99 N·mm-2,非预应力纵筋应力最大值为106.04 N·mm-2.满足车辆停放和行驶的坡道结构变形和承载能力要求.轮胎边缘处出现明显的拉应力分布,但其最大值仅为0.91 N·mm-2,不大于混凝土抗拉强度,即此工况下车辆行驶对双T板翼缘影响较小.

|
图 17 混凝土应力云图 Figure 17 Stress cloud of concrete |

|
图 18 预应力筋和钢筋应力云图 Figure 18 Stress cloud of tendons and rebars |
1) 采用合适的单元和分离式模型,可较好模拟试验工况下两类双T板弯曲性能,分析结果显示两类状态下正截面承载力和全过程变形发展符合程度较高.
2) 在有效预应力折减工况下进行两类双T板斜截面剪切性能非线性分析,有效地验证了依次进行的弯曲和剪切试验可导致有效预应力因筋-混凝土黏结性能降低而损失进而降低了斜截面承载力的假设.
3) 均布荷载和停车楼楼盖停、行车两种工况下非线性分析验证了双T板的整体弯曲性能和翼缘局部性能满足装配式停车楼楼盖的设计和使用要求.
4) 模拟和试验结果显示设计值富裕程度较高,放张后端部纵向裂缝主要是由于预拉应力较大导致,应在满足设计要求的条件下适当降低预拉应力设计值,并分阶段放张预应力筋.
| [1] |
NASSERG D, TADROS M. The legacy and future of an American icon: The precast, prestressed concrete double tee[J]. PCI Journal, 2015, 60(4): 49. DOI:10.15554/pcij |
| [2] |
庞瑞, 梁书亭. 国外预制混凝土双T板楼盖体系的研究[J]. 工业建筑, 2011, 41(3): 121. PANG Rui, LIANG Shuting. State-of-the-art of overseas research of precast double-tee floors[J]. Industrial Construction, 2011, 41(3): 121. |
| [3] |
MAGUIRE M, MORCOUS G. Structural performance of precast prestressed bridge double-tee girders made of high-strength concrete, welded wire reinforcement, and 18-mm-diameter strands[J]. Journal of Bridge Engineering, 2013, 18(10): 1053. DOI:10.1061/(ASCE)BE.1943-5592.0000458 |
| [4] |
BOTROS A W, LUCIER G. Behavior of free and connected double-tee flanges reinforced with carbon-fiber-reinforced polymer[J]. PCI Journal, 2016, 9: 49. |
| [5] |
MONAHAN D R. Precast concrete parking structure lighting study[J]. PCI Journal, 2007, 52(6): 89. DOI:10.15554/pcij |
| [6] |
MITCHELL D, DEVALL R H, SAATCIOGLU M. Damage to concrete structures due to the 1994 Northridge earthquake[J]. Canadian Journal of Civil Engineering, 1995, 22(2): 361. DOI:10.1139/l95-047 |
| [7] |
CHREST A P, SNYDER R. Curved precast ramp adds elegance and function to aventura parking structure[J]. PCI Journal, 1999, 44(4): 32. DOI:10.15554/pcij |
| [8] |
PCI Industry Handbook Committee. PCI design handbook: precast and prestressed concrete[M]. 6th ed.Chicago, IL: PCI, 2004
|
| [9] |
赵培, 张文龙, 周威.足尺预应力混凝土双T板静力性能研究//第26届全国结构工程学术会议论文集: 1集[C]//北京: 工程力学出版社, 2017: 486 ZHAO Pei, ZHANG Wenlong, ZHOU Wei. Full-scale tests on static behavior of double-tee//Proceedings of the 26th National Conference on Structural Engineering: No.1[C]//Beijing: Engineering Mechanics, 2017: 586 |
| [10] |
OKUMUS P, OLIVER M G. Strand debonding for pretensioned bridge girders to control end cracks[J]. ACI Structural Journal, 2014, 111(1): 201. |
| [11] |
张峰, 徐向锋, 李术才. HB-FRP加固RC梁的精细有限元分析[J]. 哈尔滨工业大学学报, 2015, 47(8): 125. ZHANG Feng, XU Xiangfeng, LI Shucai. Meso-scale finite element analysis of HB-FRP strengthened reinforced concrete beams[J]. Journal of Harbin Institute of Technology, 2015, 47(8): 125. |
| [12] |
LOU T, LOPES S M R. Flexural response of continuous concrete beams prestressed with external tendons[J]. Journal of Bridge Engineering, 2013, 18(6): 525. DOI:10.1061/(ASCE)BE.1943-5592.0000392 |
| [13] |
MENEGOTTO M, PINTO P E.Method of analysis for cyclically loaded reinforced concrete plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending[C]//Proceedings of the IABSE Symposium on Resistance and Ultimate Deformability of Structures.Lisbon: Association for Bridge and Structural Engineering, 1973: 15
|
| [14] |
孟少平, 吴畅. 预应力混凝土复杂结构非线性有限元分析相关问题的探讨[J]. 工业建筑, 2009, 39(12): 1. MENG Shaoping, WU Chang. Discussion on the nonlinear finite element analysis of prestressed concrete complex structures[J]. Industrial Construction, 2009, 39(12): 1. |
| [15] |
混凝土结构设计规范: GB 50010—2010[S].北京: 中国建筑工业出版社, 2011 Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [16] |
周光毅, 宫立宝. 装配式混凝土结构停车楼吊装施工技术[J]. 施工技术, 2016, 45(4): 31. ZHOU Guangyi, GONG Libao. Hoisting construction technology of the precast concrete parking building[J]. Construction Technology, 2016, 45(4): 31. |
 2018, Vol. 50
2018, Vol. 50


