2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
钢管约束钢筋混凝土柱是在钢管混凝土柱与钢筋混凝土柱的基础上发展而来的一种新型组合构件,其钢管不直接承担纵向荷载,而主要为混凝土提供侧向约束作用[1-2].钢管的约束作用可大大提高混凝土的强度和延性,且钢管可兼做施工模板,因此,钢管约束钢筋混凝土柱具有承载能力高、延性好、施工方便等优点[3].基于上述优势,近年来其在超高层建筑和大跨度体育场馆中得到较多应用,如大连中国石油大厦(主体结构地上部分高176 m)、哈尔滨创新创业大厦(主体结构高218 m)、大连市体育馆(屋盖跨度140 m)等.与地震、飓风等灾害相比,火灾发生的频率更高、危害较大,因此该类构件的抗火设计尤为重要.
现行防火设计规范要求的构件耐火极限均是在标准火灾作用下,关于构件抗火性能的研究也多采用ISO-834标准升温曲线[4].与标准火灾不同的是,燃料数量、通风条件和受火房间特性均会影响真实火灾的升温速率和持续时间.关于标准火灾作用下及作用后圆钢管约束钢筋混凝土柱的力学性能,刘发起等已开展相关试验研究和理论分析,提出了相应的设计方法[5-8].但目前尚无真实火灾下圆钢管约束钢筋混凝土柱抗火性能的相关研究.为此,本文针对真实火灾下圆钢管约束钢筋混凝土柱的抗火性能展开研究,分析真实火灾下构件的温度分布、变形发展及耐火极限,并与标准火灾下的结果进行对比,以揭示真实火灾下圆钢管约束钢筋混凝土柱的抗火性能,为圆钢管约束钢筋混凝土柱抗火性能化设计提供参考.
1 真实火灾温度-时间曲线影响火灾升温曲线的因素主要有火灾荷载密度、开口通风因子和房间壁面热惰性[9-10].目前室内火灾升温曲线模型有马忠诚模型、ASCE模型、欧洲规范模型、瑞典模型等[11].对于标准火灾状况,欧洲规范Eurocode 1 Part 1-2[12]建议的参数化的火灾升温曲线与ISO-834标准升降温曲线重合,因此,为便于与标准火灾作用下构件抗火性能进行对比,选用欧洲规范建议的参数化的火灾升温模型.
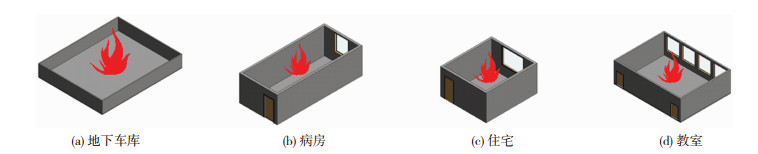
选取地下车库、病房、住宅、教室等四类房间进行分析,见图 1.根据典型的房间尺寸以及门窗洞口尺寸,采用欧洲规范参数化升温曲线求得通风因子O(0.02~0.12),依据O的大小分成A、B、C、D四种火灾场景,见表 1,其中Af为楼板面积,At为房间壁面的面积之和,Hv为开口高度,Av为房间开口面积之和.其中A为地下车库,地下车库防火分区最大允许面积[13]和欧洲规范参数化火灾模型最大适用建筑面积均为500 m2,故取长25 m、宽20 m、层高3.6 m,因地下车库通风条件差,通风因子按规范取最小值0.02;B为医院三床带卫生间的病房,长宽高取为9.0 m×3.9 m×3.6 m,门窗尺寸见表 1,由此计算得到通风因子为0.044;C、D分别为住宅房间和教室,具体尺寸详见表 1,计算得到通风因子分别为0.088和0.120.
|
图 1 房间场景模型 Figure 1 Models for different room scenarios |
| 表 1 不同类型房间参数 Table 1 Parameters for different types of rooms |
火灾房间壁面的热惰性按照混凝土材料取1 500 Jm-2s-1/2K,满足欧洲规范Eurocode 1要求(100≤b≤2 200).规范Eurocode 1给出了不同类型房间的火灾荷载密度统计值,其中病房、住宅、教室分别为230、780、285 MJ/m2.为分析火灾荷载密度的影响,并参考实际统计值,按文献[11]建议的火灾荷载等级Ⅰ、Ⅱ、Ⅲ级(250、500、1 000 MJ/m2)确定火灾荷载密度.不同火灾曲线的参数见表 2,其中当火灾荷载密度为250、500 MJ/m2时场景类型C、D升温时间均小于规范中参数火模型的最小升温时间20 min,因此均取为20 min,即此时两个火灾荷载密度等级对应的火灾曲线重合.因此共建立9组不同火灾温度-时间曲线.
| 表 2 不同火灾曲线参数 Table 2 Parameters for different fire curves |
由上述原则确定的四类9组火灾曲线与ISO-834标准升温曲线的对比见图 2.可见通风因子越大,升温越快,其中B组曲线升温速率与标准火灾相近.另外,火灾荷载密度越大,升温持续时间越长,所能达到的最高温度也越高.

|
图 2 不同火灾模型温度-时间曲线 Figure 2 Temperature-time curves of different natural fires |
利用ABAQUS软件建立标准火灾和真实火灾作用下圆钢管约束钢筋混凝土柱的温度场模型和力学模型,对其抗火性能进行研究.通过分析真实火灾下构件抗火性能,为圆钢管约束钢筋混凝土柱抗火性能化设计提供参考.
2.1 有限元模型建立与验证采用顺序热-力耦合的方式,分析钢管约束钢筋混凝土柱的抗火性能,包含温度场和力学计算两部分.钢材和混凝土的热工性能参数取Lie[14]建议模型,钢材热膨胀系数采用Lie[14]建议模型,混凝土热膨胀系数取为常数6×10-6 m/(m·℃)[15].钢材采用ABAQUS中的等向弹塑性模型,钢管与钢筋应力-应变曲线在常温段和升温段采用Lie[14]建议模型,在降温段和高温后采用陶忠等[16]的模型,降温段考虑钢材材性的恢复.混凝土采用ABAQUS中的塑性损伤模型,混凝土常温和升温段均采用Lie[14]提出的应力-应变关系模型;降温段混凝土材性尚无相关研究,一般认为降温阶段混凝土的材性不能恢复[17],故只与历史最高温度有关.降温段和高温后的混凝土本构均采用韩林海[18]提出的模型.
混凝土的热惰性导致混凝土的升降温明显滞后于环境温度,因此通过编制子程序实现不同温度阶段材料应力-应变关系调用.有限元模型的其他信息参考文献[5-8].
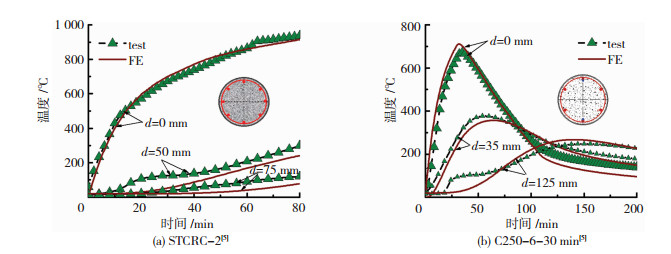
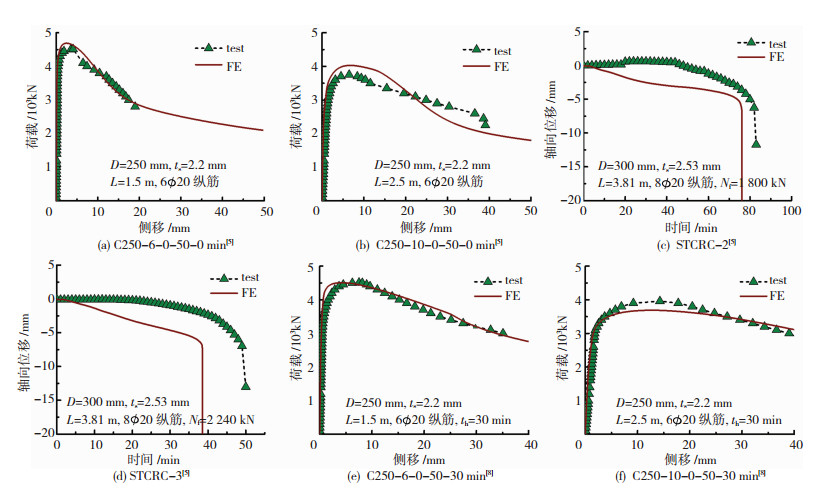
目前暂无真实火灾作用下钢管约束钢筋混凝土柱抗火性能的相关试验,因此利用常温下、ISO-834标准火灾作用下以及火灾作用后圆钢管约束钢筋混凝土柱的试验,对建立的有限元模型分阶段验证.温度场对比结果见图 3,图中d为温度测点距钢管外表面的最短距离.常温下荷载-位移曲线、火灾下位移-时间曲线与火灾后荷载-位移曲线对比结果见图 4,可见计算结果与试验结果吻合较好.表明建立的有限元模型能够较好预测圆钢管约束钢筋混凝土柱常温下力学性能、火灾下的耐火极限和火灾后的剩余力学性能.
|
图 3 温度场验证 Figure 3 Validation of the thermal analysis model |
|
图 4 常温、火灾下、火灾后力学试验验证 Figure 4 Validation of the stress analysis model for columns at room temperature, under fire and after fire |
基于建立的有限元模型分析真实火灾下圆钢管约束钢筋混凝土柱的抗火性能,包括温度分布、轴向变形-时间关系和耐火极限等.典型钢管约束钢筋混凝土柱算例基本信息:直径D=500 mm,长度L=4 m,长细比λ=32,钢管壁厚t=5 mm,配置8根直径26 mm HRB400纵筋,钢筋的保护层厚度为25 mm,混凝土强度等级选为C60,钢材的等级为Q345,荷载比为0.4、0.5、0.6和0.7.
2.2.1 温度场分析图 5为四类火灾场景(A-Ⅰ、B-Ⅰ、C-Ⅱ、D-Ⅱ)以及ISO-834标准火灾下圆钢管约束钢筋混凝土柱截面不同特征点的温度-时间关系曲线.可以看出,随着升温速率的增大、升温时间的增长,钢管、钢筋和混凝土所能达到的最高温度均增大,但A、B、C、D四类场景中构件温度梯度差距较大.升温20 min后,升温最快的D-Ⅱ类曲线对应的钢管、钢筋以及混凝土1/4截面处的温度分别为882.0、64.0和22.0℃;而与之对应的升温最慢的A-Ⅰ类曲线才达到193.4、24.8和20.2℃.

|
图 5 截面不同位置处温度-时间曲线 Figure 5 Temperature-time curves of different locations across the section |
从构件表面至其截面中心最高温度逐渐降低,且越靠近混凝土中心,达到最高温度的时刻越滞后.此温度滞后现象主要是因为混凝土的导热系数低、热容大,且越靠近混凝土中心,外围混凝土的体积越大,吸热能力越大,对环境温度变化的反应越滞后.钢管升温段发展趋势与火灾曲线相似;由于内部热量的存在,钢管降温段比火灾曲线下降更缓;由于钢筋受混凝土保护层的保护,升、降温均比较滞后,如A-Ⅰ曲线升温时间为57 min,但200 min时钢筋温度仍在升高.可见火灾升温速率、升温时间显著影响圆钢管约束钢筋混凝土柱截面温度分布,势必也影响其耐火极限.
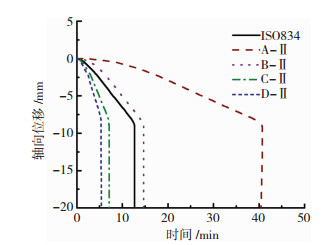
2.2.2 耐火极限分析图 6是真实火灾下和ISO-834标准火灾下圆钢管约束钢筋混凝土柱在荷载比为0.7时的轴向位移-时间曲线.构件轴向变形经历了压缩和骤然下降两个阶段,无明显膨胀变形.构件在不同火灾下前期变形均比较稳定,接近耐火极限时变形迅速增加,最终轴向变形速率达到限值而达到耐火极限.火灾升温速率由类型A至类型D逐渐增大,其中类型B升温速率与ISO-834标准升温曲线接近,类型A的构件耐火极限最大,荷载比为0.7时耐火极限为40.8 min,而同等条件下类型D的构件耐火极限仅为5.4 min.随着升温速率的增加,构件的截面温度增高,高温下材料劣化使得构件的承载力降低更多,进而更早达到耐火极限.可见升温速率不同将引起圆钢管约束钢筋混凝土柱截面温度分布不同,进而影响圆钢管约束钢筋混凝土柱的耐火极限.
|
图 6 荷载比0.7时构件位移-时间曲线 Figure 6 Axial displacement-time curves for different types of natural fire (n=0.7) |
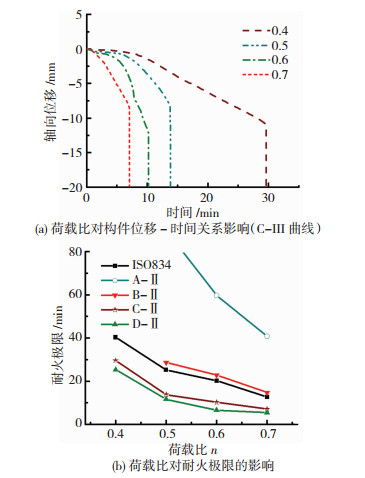
以真实火灾曲线C-Ⅲ为例,不同荷载比下钢管约束钢筋混凝土柱的位移-时间曲线见图 7(a).图 7(b)为不同火灾荷载比、不同火灾场景下圆钢管约束钢筋混凝土柱的耐火极限.荷载比越大构件压缩变形发展越快,构件的耐火极限越低;从A类至D类火灾场景,升温速率增加,构件的耐火极限逐渐降低.
|
图 7 荷载比对构件位移-时间关系和耐火极限的影响 Figure 7 Effects of load ratio on the displacement-time curves and fire resistance of circular STCRC members |
不同火灾场景、不同荷载比情况下构件的耐火极限见表 3.当荷载比为0.4时,A和B类火灾下构件未发生破坏,C类和D类时发生破坏.当荷载比为0.6或0.7时,A类~D类火灾下构件均发生破坏.需要注意的是,构件可能在火灾的降温段发生破坏.如曲线D-Ⅱ的升温时间为20 min,当荷载比为0.4时,构件的耐火极限为26.8 min,构件在降温段发生破坏.这是因混凝土温度滞后,当环境温度开始下降时,核心混凝土仍然处于升温阶段,材性依旧在退化,构件承载力小于外加荷载而达到耐火极限.
| 表 3 真实火灾下构件耐火极限 Table 3 Fire resistance of columns exposed to natural fire |
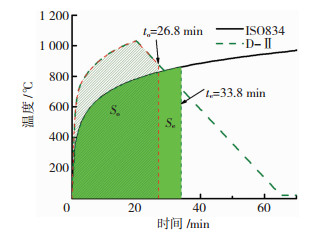
为将真实火灾下与标准火灾下构件的抗火性能联系起来,防火工程中提出了等效曝火时间的概念[11].本文采用等效面积法,当标准升温曲线与时间轴和时刻te围成的曲线多边形的面积Se同真实火灾下的升降温曲线与时间轴和时刻to所围成的曲线多边形的面积So相等时,时间te就是等效曝火时间.如D-Ⅱ火灾下构件的耐火极限为26.8 min,按面积等效的方式,换算成标准火灾下耐火极限为33.8 min,见图 8.
|
图 8 D-Ⅱ荷载比为0.4时等效曝火时间 Figure 8 A typical example for the equivalent fire exposure time method (D-Ⅱ curve, n=0.4) |
采用等效面积法,将真实火灾作用下构件的耐火极限(t0)换算成ISO-834标准火灾下耐火极限(te),再与由ISO-834标准升温曲线计算得到的耐火极限进行对比,见表 4.真实火灾升温速率低于ISO-834标准火灾(类型A、类型B)时,构件的等效耐火极限值大于标准火灾下的耐火极限值,即此时采用标准火灾曲线计算得到的结果偏于保守;而真实火灾升温速率大于ISO-834标准火灾(类型C、类型D)时,构件的等效耐火极限值小于由标准火灾曲线计算得到的结果.例如,当荷载比为0.5时,C-Ⅱ曲线构件的等效耐火极限为16.54 min,D-Ⅱ构件的等效耐火极限为15.95 min,均小于标准火灾曲线计算得到的耐火极限25.20 min,即此时采用标准火灾曲线计算得到的结果偏于不安全.
| 表 4 等效面积法换算耐火极限te Table 4 Fire resistance te calculated by equivalent area method |
1) 真实火灾下,洞口尺寸大、火灾荷载密度小的房间升温速率快、升温时间短,构件截面温度梯度较大;而洞口尺寸小、火灾荷载密度大的房间升温速率较慢、升温时间相对较长,构件截面温度分布较均匀,温度梯度较小.
2) 真实火灾下构件可能在升温段或降温段达到耐火极限,也有可能在整个升降温阶段不发生破坏.随着升温速率的提高,圆钢管约束钢筋混凝土的耐火极限逐渐降低;随着升温时间的延长,构件在升温段发生破坏的可能性增大;随着荷载比的增大,构件的耐火极限逐渐降低.
3) 采用等效面积法将真实火灾下构件的耐火极限等效成ISO-834标准火灾下构件的耐火极限,当真实火灾升温速率比标准火灾小时,等效耐火极限比按照标准升温曲线计算的结果大;而当真实火灾升温速率大于标准火灾时,等效耐火极限比按照标准升温曲线计算的结果小,即按标准火灾进行的设计偏于不安全.如果真实火灾的升温速率大于标准火灾,建议按照真实火灾进行防火设计.
| [1] |
周绪红, 刘界鹏. 钢管约束混凝土柱的性能与设计[M]. 北京: 科学出版社, 2010: 284. ZHOU Xuhong, LIU Jiepeng. Performance and design of steel tube confined concrete columns[M]. Beijing: Science Press, 2010: 284. |
| [2] |
刘界鹏, 张素梅, 郭兰慧. 圆钢管约束高强混凝土短柱的轴压力学性能[J]. 哈尔滨工业大学学报, 2008, 40(4): 528. LIU Jiepeng, ZHANG Sumei, GUO Lanhui. Behavior of circular tube confined high strength concrete (HSC) short columns under axial compression[J]. Journal of Harbin Institute of Technology, 2008, 40(4): 528. DOI:10.3321/j.issn:0367-6234.2008.04.004 |
| [3] |
周绪红, 刘界鹏, 张小冬. 钢管约束混凝土结构的设计方法[J]. 哈尔滨工业大学学报, 2009, 41(增刊2): 8. ZHOU Xuhong, LIU Jiepeng, ZHANG Xiaodong. Design method of tubed RC structures[J]. Journal of Harbin Institute of Technology, 2009, 41(S2): 8. |
| [4] |
International Organization for Standardization. Fire-resistance tests-elements of building construction: ISO-834[S]. Geneva: International Organization for Standardization, 1999: 11
|
| [5] |
刘发起.火灾下与火灾后圆钢管约束钢筋混凝土柱力学性能研究[D].哈尔滨: 哈尔滨工业大学, 2014: 74 LIU Faqi. Fire and post-fire behaviours of circular steel tube confined reinforced concrete columns[D]. Harbin: Harbin Institute of Technology, 2014: 74 http://cdmd.cnki.com.cn/Article/CDMD-10213-1015957439.htm |
| [6] |
LIU Faqi, YANG Hua, GARDNER L. Post-fire behaviour of eccentrically loaded reinforced concrete columns confined by circular tubes[J]. Journal of Constructional Steel Research, 2016, 122: 495. DOI:10.1016/j.jcsr.2016.04.008 |
| [7] |
LIU Faqi, GARDNER L, YANG Hua. Post-fire behaviour of reinforced concrete stub columns confined by circular steel tubes[J]. Journal of Constructional Steel Research, 2014, 102: 82. DOI:10.1016/j.jcsr.2014.06.015 |
| [8] |
YANG Hua, LIU Faqi, GARDNER L. Post-fire behaviour of slender reinforced concrete columns confined by circular steel tubes[J]. Thin-Walled Structures, 2015, 87: 12. DOI:10.1016/j.tws.2014.10.014 |
| [9] |
靳飞, 李国强. 全盛期室内火灾参数化模型的参数随机性[J]. 建筑科学与工程学报, 2006, 23(4): 44. JIN Fei, LI Guoqiang. Parameters randomness of parametric model of fully-developed compartment fire[J]. Journal of Architecture and Civil Engineering, 2006, 23(4): 44. DOI:10.3321/j.issn:1673-2049.2006.04.009 |
| [10] |
FRANSSENJ M. 真实火灾安全思想[J]. 建筑钢结构进展, 2003, 5(2): 38. FRANSSEN J M. Natural fire safety concept[J]. Progress in Steel Building Structures, 2003, 5(2): 38. |
| [11] |
李国强, 韩林海. 钢结构及钢-混凝土组合结构抗火设计[M]. 北京: 中国建筑工业出版社, 2006: 20. LI Guoqiang, HAN Linhai. Steel and steel-concrete composite structure fire resistant design[M]. Beijing: Building Industry Press of China, 2006: 20. |
| [12] |
European Committee for Standardization. Eurocode 1: Actions on structures-Part 1-2. General actions-actions on structures exposed to fire: EN1991-1-2[S]. Brussels: European Committee for Standardization, 2002: 30
|
| [13] |
建筑设计防火规范: GB 50016—2014[S].北京: 中国计划出版社, 2014: 56 Code for fire protection design of buildings: GB 50016—2014[S]. Beijing: China Planning Press, 2014: 56 |
| [14] |
LIE T T. Fire resistance of circular steel columns filled with bar-reinforced concrete[J]. Journal of Structural Engineering, 1994, 120(5): 1489. DOI:10.1061/(ASCE)0733-9445(1994)120:5(1489) |
| [15] |
ESPINOS A, ROMERO M L, HOSPITALER A. Fire design method for bar-reinforced circular and elliptical concrete filled tubular columns[J]. Engineering Structures, 2013, 56: 384. DOI:10.1016/j.engstruct.2013.05.026 |
| [16] |
TAO Zhong, WANG Xingqiang, UY B. Stress-strain curves of structural steel and reinforcing steels after exposure to elevated temperatures[J]. Journal of Materials in Civil Engineering, 2013, 25(9): 1306. DOI:10.1061/(ASCE)MT.1943-5533.0000676 |
| [17] |
YANG Hua, HAN Linhai, WANG Yongchang. Effects of heating and load histories on post-fire cooling behaviour of concrete filled steel tubular columns[J]. Journal of Constructional Steel Research, 2008, 64(5): 556. DOI:10.1016/j.jcsr.2007.09.007 |
| [18] |
韩林海. 钢管混凝土结构-理论与实践[M]. 2版. 北京: 科学出版社, 2007: 106. HAN Linhai. Concrete filled steel tubular structure-theory and practice[M]. 2nd ed. Beijing: Science Press, 2007: 106. |
 2018, Vol. 50
2018, Vol. 50


