2. 西部土木工程防灾减灾教育部工程研究中心(兰州理工大学),兰州 730050
2. Western Center of Disaster Mitigation in Civil Engineering (Lanzhou University of Technology), Ministry of Education, Lanzhou 730050, China
泥石流是易发于山区的严重自然灾害之一,自1950年到2011年,泥石流已在全世界范围内造成巨大的财产损失和人员伤亡[1].尤其近年来,山区泥石流灾害频发,引起越来越多的关注.
为减轻泥石流灾害,学者们展开了大量研究:文献[2]提出了预测泥石流流速的理论模型,并通过实验室和现场试验进行验证;文献[3]以泥石流强度指标代替冲击力来确定建筑物的损坏,提出一种泥石流灾害定量风险评估模型;文献[4]介绍了日本最新的自然灾害早期预警系统;文献[5]基于小尺度建模方法,并结合试验分析泥石流的冲击模型;文献[6]介绍了台湾泥石流非结构性预防策略的过程和影响;文献[7]将柔性防护系统引入泥石流防治工程中,提出其设计方法.目前研究大部分集中于泥石流特性和起动机理方面,对拦挡结构研究较少.
另外,为了治理泥石流灾害,国内修建了重力坝、格栅坝及柔性体系等拦挡结构[8].早期的拦挡结构以浆砌片石筑成的重力坝居多,其抵抗泥石流冲击破坏的能力有限,尤其在大型泥石流作用下容易发生严重的整体破坏(溃坝),这样不仅不能减轻灾害,反而会加重灾害[9].泥石流冲击力主要包括浆体动压力和大块石撞击力,而后者是造成结构破坏的主要因素[10-11],在结构设计中必须重点考虑.鉴于此,针对含巨石的水石流和稀性泥石流,本文提出一种新型拦挡结构—钢管混凝土格栅坝.该结构借鉴空间结构的三维受力思想可提高材料利用率,同时利用钢管混凝土提高整体抗冲击能力,以期有效减轻泥石流灾害.
目前针对钢管混凝土构件的抗冲击性能已有研究[12-14],针对钢管混凝土整体结构抗冲击性能的研究较少.本文对所提出的结构进行抗冲击试验,并对试验过程进行数值模拟,再对结构进行参数分析,探讨其抗冲击性能.
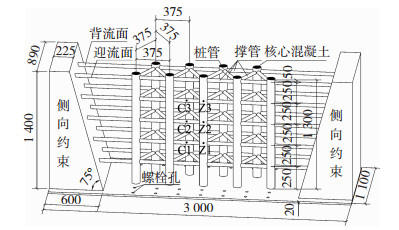
1 试验概况 1.1 试验模型钢管混凝土格栅坝由桩管和撑管构成,构件之间采用相贯焊接,桩管为主受力构件,撑管连接桩管加强结构整体性,共同构成格栅结构.桩管分前后两排,前排5根为迎流面,后排4根为背流面,撑管沿桩管高度方向分布5层,平面呈等边三角形.
试验模型见图 1,考虑两侧山体对结构的约束作用,设置了侧向约束.桩管截面尺寸为89 mm×3.5 mm,内部采用C20细石混凝土浇灌,撑管为空心钢管,截面尺寸为42 mm×3 mm,桩管和撑管都采用Q235B钢.试验模型通过底板与地面采用高强螺栓(10.9级,M24)连接.图中Z1~Z3为桩管受冲击的加载点,冲击高度分别为500、750、1 000 mm;C1~C3为撑管受冲击的加载点,冲击高度分别为500、750、1 000 mm.
|
图 1 试验模型 Figure 1 Test model |
按照GB/T 228.1—2010《金属材料拉伸试验第1部分:室温试验方法》和GB/T 2975—1998《钢及钢产品力学性能试验取样位置及试样制备》中的相关规定进行钢管材性试验,得到其弹性模量E、屈服强度fy、抗拉强度fu及延伸率A,结果见表 1.取混凝土制作标准试块,测得其轴心抗压强度为19.1 MPa.
| 表 1 钢材力学性能 Table 1 Mechanical properties of steel |
本次试验在自主设计的固体冲击加载架(图 2)上完成,该加载架由平台和轨道组成.加载架总高6.5 m,轨道长5.7 m,坡度42°,平台尺寸3 m×3.3 m.加载时,冲击物在轨道顶端与平台交接处无初速度释放,在重力作用下沿轨道自由滚落,对试验模型进行冲击加载.冲击出口高度(轨道底端高度)可根据需要调节,以实现不同冲击高度的加载工况.

|
图 2 试验现场 Figure 2 Test site |
试验中分别采用应变片(电阻值120 Ω,灵敏系数2.12,栅长宽5 mm×3 mm,半桥接法)、CLMD2系列拉线式动态位移传感器(最大量程1 000 mm)和DH151压电式加速度传感器(最大量程30 000 g)对结构在冲击荷载下的动应变、动位移和加速度进行测量,其中动态应变数据采用北京东方所INV3060V测试系统采集,动态位移和加速度数据采用江苏东华DH5922测试系统采集.
1.4 加载工况及测点布置冲击物采用直径100、200和300 mm钢球,重量分别约为4、33和111 kg,冲击速度约为10 m/s,对应冲击能量分别为200、1650和5550 J.冲击物对桩管和撑管分别进行冲击加载,考虑冲击能量和冲击位置对结构动力响应的影响,设计如表 2所示加载工况.表中工况编号Z1-1表示直径100 mm的冲击物撞击桩管500 mm高度的位置(图 1中Z1),C1-1表示直径100 mm的冲击物撞击500 mm高度的撑管中心点位置(图 1中C1),依此类推.
| 表 2 加载工况 Table 2 Loading cases |
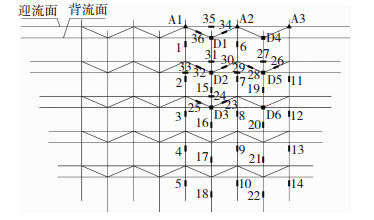
试验之前先完成结构在各工况下的数值模拟,根据数值模拟结果并结合试验条件,选取结构的关键部位进行监测.应变、位移和加速度测点布置如图 3所示,其中1~36为应变测点,D1~D6为位移测点,A1~A3为加速度测点.
|
图 3 测点布置 Figure 3 Layout of measure points |
钢管混凝土格栅坝受冲击的试验现象见图 4.当冲击物直径为100 mm时,只在撞击点处出现轻微损伤(图 4(a)),整体结构发生轻微振荡,处于弹性工作状态.

|
图 4 试验现象 Figure 4 Test phenomenon |
当直径200和300 mm的冲击物撞击桩管时,在撞击点处出现较明显的凹陷变形(图 4(b)),整体结构发生明显振荡.由于核心混凝土的支撑作用,撞击点处凹陷范围较小,桩管基本保持原有承载力.
当直径200 mm的冲击物撞击撑管时,在撞击点区域出现严重的塑性变形,撑管发生局部弯曲破坏,撑管与桩管连接处产生较大裂缝(图 4(c)),整体结构振荡不明显.
当300 mm的冲击物撞击撑管时,在撞击点区域出现非常严重的塑性变形,撑管发生整体弯曲破坏,撑管与桩管的连接焊缝被撕裂,节点发生破坏,撑管被撞飞(图 4(d)).
本试验中结构只出现了局部破坏,整体结构还能继续发挥作用,体现出结构具有良好的抗冲击性能.限于试验条件和安全考虑,本次试验未设计整体结构破坏的试验工况.
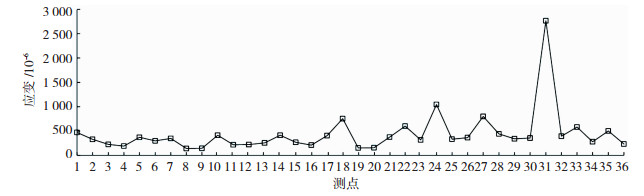
2.2 动态应变以Z3-3为例分析结构的应变响应规律,各测点的峰值应变见表 3.应变由冲击点开始响应,在冲击瞬间,仅在冲击区(冲击点附近区域,即测点1、2、31、32)产生明显应变,之后应力波迅速向非冲击区扩散并耗散冲击能量,从冲击区开始响应至整体结构开始响应耗时很短,约为0.5 ms.各桩管固定端处测点(5、10、14、18、22)的峰值应变均较大,说明撑管有效地传递了冲击能量,使结构产生明显的整体响应.
| 表 3 测点峰值应变 Table 3 Peak strain of measurement points |
撑管受冲击时(以C3-3为例,如图 5所示),冲击区测点(31)的峰值应变远大于非冲击区,这是由于撑管是空心钢管,在较大冲击能量下发生严重变形且节点发生破坏,耗散了大部分冲击能量,导致结构整体响应不明显.
|
图 5 C3-3的峰值应变 Figure 5 Peak strain of C3-3 |
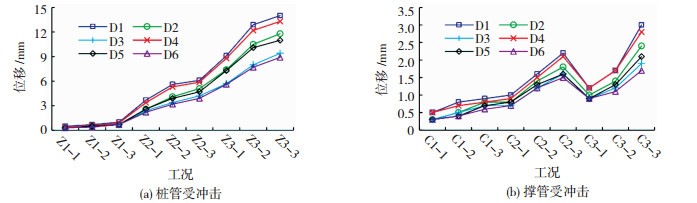
各工况下的峰值位移见图 6,桩管受冲击时各测点的峰值位移显著大于撑管受冲击,说明桩管受冲击时整体结构发生了明显的振荡,冲击能量主要由整体结构振动耗散,而撑管受冲击时整体结构的耗能不明显.随着冲击高度和冲击能量的增加,撑管受冲击时的峰值位移变化不大;桩管受冲击时的峰值位移随冲击高度的增加而有所增大,并随冲击能量的增加而显著增大.
|
图 6 峰值位移 Figure 6 Peak displacement |
各工况下的峰值加速度见图 7,桩管受冲击时各测点的峰值加速度显著大于撑管受冲击.桩管受冲击时,峰值加速度随着冲击高度的增加而增大,而随着冲击能量的增加,峰值加速度变化规律不明显.撑管受冲击时,峰值加速度随着冲击高度的增加而有所增大,但随着冲击能量的增加反而减小.这是由于冲击能量较小时整体结构发生明显的协调振荡,而冲击能量较大时撑管和节点吸收了大部分能量导致整体结构的振荡不明显.

|
图 7 峰值加速度 Figure 7 Peak acceleration |
利用ANSYS/LS-DYNA对本试验进行数值模拟,并与试验结果进行对比分析.有限元模型中冲击物、混凝土和钢管均采用solid164实体单元.其中冲击物忽略变形,采用刚体模型(rigid),混凝土采用双线性随动强化模型(bilinear kinematic).钢管采用塑性随动强化模型(plastic kinematic),该模型采用Cowper-Symonds模型来考虑材料在动力荷载下的应变率效应[15],其屈服应力表示为
| $ {\sigma _{\rm{Y}}} = \left[ {1 + {{\left( {\frac{{\dot \varepsilon }}{C}} \right)}^{\frac{1}{P}}}} \right]({\sigma _0} + \beta {E_{\rm{p}}}\varepsilon _{\rm{p}}^{{\rm{eff}}}), $ |
式中:σ0为初始屈服应力;
有限元模型中不考虑钢管与混凝土之间的滑移,两者采用黏接连接,桩管与撑管也采用黏接连接.对模型底部所有节点施加固定约束,并约束模型两侧所有节点的线位移,以此模拟基础和两侧山体对结构的约束作用.划分网格时对桩管和撑管的连接节点区域进行网格细化,并对冲击点区域进行网格细化.有限元模型见图 8,红色为混凝土,蓝色为钢管,绿色为冲击物.

|
图 8 有限元模型 Figure 8 Finite element model |
结构的冲击力时程曲线见图 9,冲击力为合力.冲击力在碰撞瞬间达到峰值,并迅速衰减,形成基本的脉冲式波形,并在碰撞结束后减小至零.桩管受冲击时冲击物与结构的作用时间明显小于撑管受冲击,而桩管受冲击时的冲击力峰值明显大于撑管受冲击.

|
图 9 冲击力时程曲线 Figure 9 Time history curve of impact force |
另外,桩管受冲击时,冲击物与结构的作用时间随冲击能量的增大而增加,且冲击力峰值显著增大.Z3-3中出现两个波峰是因为冲击物与结构发生了二次碰撞.撑管受冲击时,冲击物与结构的作用时间随冲击能量的增大而增加,而冲击力峰值变化不大.
4.2 响应模式数值模拟中结构的响应模式见图 10,其中(a)~(d)分别对应图 4(a)~(d),数值模拟得到的响应模式与试验结果吻合较好.
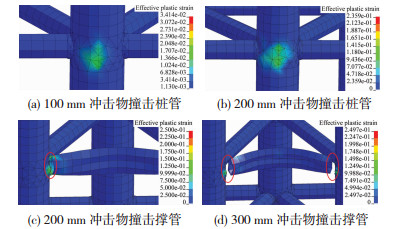
|
图 10 响应模式 Figure 10 Response mode |
取D1的峰值位移进行分析,见图 11.数值模拟得到的位移变化规律与试验结果一致,最大误差28.6%,这是由于位移值偏小(最大值仅14.9 mm),当模拟和试验的位移差值略微增大时便会得到较大的误差值,其中最大位移差值仅0.9 mm.
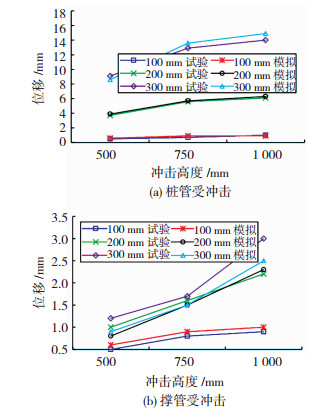
|
图 11 峰值位移对比 Figure 11 Contrast of peak displacement |
取A1的峰值加速度进行分析,见图 12.数值模拟得到的加速度变化规律与试验结果一致,最大误差为13.4%.
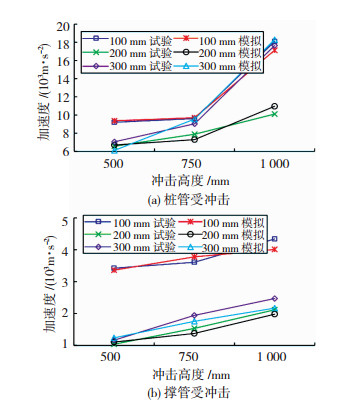
|
图 12 峰值加速度对比 Figure 12 Contrast of peak acceleration |
从数值模拟与试验结果对比可知,对于钢管混凝土格栅坝在冲击荷载下的动力响应问题,本文采用的数值模拟方法比较可靠,加之试验研究成本较高,不利于开展大量研究,故采用数值模拟方法对结构进行参数分析,主要研究桩管套箍系数、撑管径厚比以及桩管与撑管的刚度比对结构动力响应的影响.
5.1 参数方案设计桩管的套箍系数及组合刚度按照GB 50936—2014《钢管混凝土结构技术规范》计算:
套箍系数为
| $ \theta = {\alpha _{{\rm{sc}}}}\frac{f}{{{f_{\rm{c}}}}} = \frac{{{A_{\rm{s}}}f}}{{{A_{\rm{c}}}{f_{\rm{c}}}}}, $ |
式中:θ为套箍系数,αsc为含钢率,f为钢材抗压强度设计值,fc为混凝土抗压强度设计值,As为钢管截面积,Ac为混凝土截面积.
组合刚度为
| $ {\rm{EI}} = {E_{\rm{s}}}{I_{\rm{s}}} + {E_{\rm{c}}}{I_{\rm{c}}}, $ |
式中:EI为组合刚度,Es为钢材弹性模量,Is为钢管截面惯性矩,Ec为混凝土弹性模量,Ic为混凝土截面惯性矩.
以单因素变化为原则,选取不同的外径和壁厚分别确定出桩管和撑管的参数方案,见表 4.为减小计算成本,设定冲击物直径和初速度分别为300 mm和10 m/s并保持不变,分别冲击1 000 mm高度处的桩管和撑管(图 1中Z3和C3).数值模拟相关参数与前文所述相同.
| 表 4 参数分析方案 Table 4 Scheme for parameter analysis |
结构在冲击荷载作用下的动力响应主要包括动态应变、冲击力、动态位移和加速度,经过计算,结构参数发生变化时其动态应变响应规律基本相同(见2.3),而加速度响应较为复杂并无明显规律,故此处仅分析结构参数变化对冲击力和位移响应的影响.
5.2.1 对冲击力的影响9种结构的冲击力时程曲线见图 13,其峰值冲击力变化如下:

|
图 13 9种结构的冲击力时程曲线 Figure 13 Time history curve of impact force of 9 structures |
当桩管壁厚增大时,冲击桩管的峰值冲击力随桩管套箍系数和桩-撑刚度比的增大而增大,而冲击撑管的冲击力时程曲线完全重叠(图 13(a)).
当桩管外径增大时,冲击桩管的峰值冲击力随桩管套箍系数的增大而减小,而随桩-撑刚度比的增大而增大,冲击撑管的峰值冲击力基本相等(图 13(b)).
当撑管壁厚增大时,无论冲击桩管还是撑管,峰值冲击力都随撑管径厚比和桩-撑刚度比的增大而减小(图 13(c)).
当撑管外径增大时,冲击桩管的峰值冲击力随撑管径厚比的增大而增大,而随桩-撑刚度比的增大而减小,冲击撑管的峰值冲击力变化不大(图 13(d)).
综上所述,桩管套箍系数、撑管径厚比和桩-撑刚度比对冲击力的影响不服从单一规律,受到桩管外径、壁厚以及撑管外径、壁厚等单因素变化的制约.
5.2.2 对位移的影响9种结构的位移时程曲线见图 14,其峰值位移变化如下:
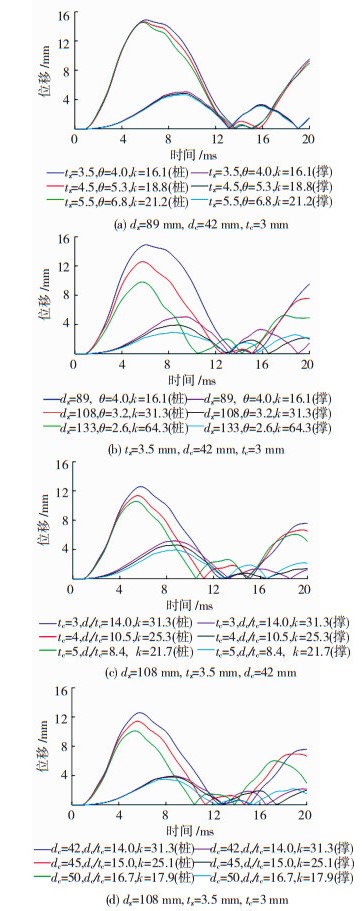
|
图 14 9种结构的位移时程曲线 Figure 14 Time history curve of displacement of 9 structures |
当桩管壁厚增大时,无论冲击桩管还是撑管,峰值位移都随桩管套箍系数和桩-撑刚度比的增大而减小,但变化幅度很小(图 14(a)).
当桩管外径增大时,无论冲击桩管还是撑管,峰值位移都随桩管套箍系数的增大而增大,而随桩-撑刚度比的增大而减小(图 14(b)).
当撑管壁厚增大时,无论冲击桩管还是撑管,峰值位移都随撑管径厚比和桩-撑刚度比的增大而增大(图 14(c)).
当撑管外径增大时,无论冲击桩管还是撑管,峰值位移都随撑管径厚比的增大而减小,而随桩-撑刚度比的增大而增大,其中冲击撑管的变化幅度很小(图 14(d)).
综上,桩管套箍系数、撑管径厚比和桩-撑刚度比对位移的影响不服从单一规律,受到桩管外径、壁厚以及撑管外径、壁厚等单因素变化的制约.
6 结论本文提出了一种钢管混凝土格栅坝,并针对其冲击动力响应进行试验研究和数值模拟,再对结构进行参数分析,得到以下结论:
1) 钢管混凝土格栅坝在冲击荷载作用下呈现出3种典型响应模式:撞击点处轻微损伤;构件发生弯曲破坏;节点连接发生破坏.
2) 本试验中结构只出现了局部的破坏,整体结构还能继续发挥作用,体现出钢管混凝土格栅坝具有良好的抗冲击性能.
3) 桩管受冲击时的冲击力、位移和加速度都显著大于撑管受冲击,桩管受冲击时结构能发挥良好的整体耗能作用,而撑管受冲击时结构整体耗能作用不明显.
4) 桩管套箍系数、撑管径厚比和桩-撑刚度比对结构动力响应的影响受桩管和撑管的外径、壁厚等单因素变化制约.
| [1] |
DOWLING C A, SANTI P M. Debris flows and their toll on human life: a global analysis of debris-flow fatalities from 1950 to 2011[J]. Natural Hazards, 2013, 71(1): 203. DOI:10.1007/s11069-013-0907-4 |
| [2] |
JULIEN P Y, PARIS A. Mean velocity of mudflows and debris flows[J]. Journal of Hydraulic Engineering, 2010, 136(9): 676. DOI:10.1061/(ASCE)HY.1943-7900.0000224 |
| [3] |
JAKOB M, STEIN D, ULMI M. Vulnerability of buildings to debris flow impact[J]. Natural Hazards, 2012, 60(2): 241. DOI:10.1007/s11069-011-0007-2 |
| [4] |
OSANAI N, SHIMIZU T, KURAMOTO K, et al. Japanese early-warning for debris flows and slope failures using rainfall indices with Radial Basis Function Network[J]. Landslides, 2010, 7(3): 325. DOI:10.1007/s10346-010-0229-5 |
| [5] |
SCHEIDL C, CHIARI M, KAITNA R, et al. Analyzing debris-flow impact models, based on a small scale modelling approach[J]. Surveys in Geophysics, 2013, 34(1): 121. DOI:10.1007/s10712-012-9199-6 |
| [6] |
CHEN S C, WU C Y. Debris flow disaster prevention and mitigation of non-structural strategies in Taiwan[J]. Journal of Mountain Science, 2014, 11(2): 308. DOI:10.1007/s11629-014-2987-3 |
| [7] |
BRIGHENTI R, SEGALINI A, FERRERO A M. Debris flow hazard mitigation: A simplified analytical model for the design of flexible barriers[J]. Computers & Geotechnics, 2013, 54(54): 1. |
| [8] |
康志成, 李焯芬, 马蔼乃, 等. 中国泥石流研究[M]. 北京: 科学出版社, 2004. KANG Zhicheng, LI Zhuofen, MA Ainai, et al. Research on debris flow in China[M]. Beijing: Science Press, 2004. |
| [9] |
陈晓清, 游勇, 崔鹏, 等. 汶川地震区特大泥石流工程防治新技术探索[J]. 四川大学学报:工程科学版, 2013, 45(1): 16. CHEN Xiaoqing, YOU Yong, CUI Peng, et al. New control methods for large debris flows in Wenchuan earthquake area[J]. Journal of Sichuan University (Engineering Science Edition), 2013, 45(1): 16. |
| [10] |
何思明, 李新坡, 吴永. 考虑弹塑性变形的泥石流大块石冲击力计算[J]. 岩石力学与工程学报, 2007, 26(8): 1665. HE Siming, LI Xinpo, WU Yong. Calculation of impact force of outrunner blocks in debris flow considering elastoplastic deformation[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(8): 1665. |
| [11] |
陈剑, 王全才, 陈颖骐, 等. 基于Hertz理论的泥石流大块石冲击力修正计算[J]. 哈尔滨工业大学学报, 2017, 49(2): 124. CHEN Jian, WANG Quancai, CHEN Yingqi, et al. Amending calculation on impact force of boulders in debris flow based on Hertz theory[J]. Journal of Harbin Institute of Technology, 2017, 49(2): 124. DOI:10.11918/j.issn.0367-6234.2017.02.020 |
| [12] |
王蕊, 李珠, 任够平, 等. 钢管混凝土梁在侧向冲击荷载作用下动力响应的试验研究和数值模拟[J]. 土木工程学报, 2007, 40(10): 34. WANG Rui, LI Zhu, REN Gouping, et al. Experimental study and numerical simulation of the dynamic response of concrete filled steel tubes under lateral impact load[J]. China Civil Engineering Journal, 2007, 40(10): 34. DOI:10.15951/j.tmgcxb.2007.10.010 |
| [13] |
HAN L H, HOU C C, ZHAO X L, et al. Behaviour of high-strength concrete filled steel tubes under transverse impact loading[J]. Journal of Constructional Steel Research, 2014, 92(1): 25. DOI:10.1016/j.jcsr.2013.09.003 |
| [14] |
BAMBACH M R. Design of hollow and concrete filled steel and stainless steel tubular columns for transverse impact loads[J]. Thin-Walled Structures, 2011, 49(10): 1251. DOI:10.1016/j.tws.2011.05.009 |
| [15] |
HALLQUIST J O. LS-DYNA keyword user's manual version 971[M]. Livermore, CA: Livermore Software Technology Corporation, 2007.
|
 2018, Vol. 50
2018, Vol. 50


