2. 岩土与结构工程安全湖北省重点实验室(武汉大学),武汉 430072
2. The Key Lab of Safety for Geotechnical and Structural Engineering of Hubei Province (Wuhan University), Wuhan 430072, China
钢管混凝土结构由于承载力高、塑性和韧性好、抗震性能突出, 以及特有的高效施工模式, 已被广泛应用于高层和超高层建筑等结构中[1-4].其施工模式一般为:先安装若干层空钢管构件和钢梁以形成结构体系, 再向管内浇灌混凝土, 借助钢管和尚未完全硬化的早龄期混凝土的承载力继续进行上部结构的施工[5].这种施工模式充分利用了钢管和早龄期混凝土的强度和刚度, 较好地解决了混凝土浇筑养护时间长影响施工进度问题.早龄期钢管混凝土的变形性能和承载力随混凝土龄期的变化规律是其施工变形控制以及施工安全的关键.
目前, 对于早龄期钢管混凝土的研究主要集中在徐变变形上, 如:韩冰课题组(何振伟[6]、祁广星[7]和周丽东[8]等)通过早龄期钢管混凝土徐变试验, 系统地研究了早龄期钢管混凝土的徐变值随加载龄期的变化规律.Geng等[9-11]对钢管内填普通混凝土、膨胀混凝土、再生混凝土柱在轴向荷载持续作用下的时效行为进行了研究.刘俊等[12]对钢管混凝土结构进行了数值计算, 得出施工过程和收缩徐变对高层钢管混凝土结构数值计算影响.余敏等[13]进行早龄期钢管混凝土短柱的多级加载试验, 表明多级加载下早龄期钢管混凝土短柱的徐变比较明显.
针对钢管混凝土轴压承载力研究, 主要集中在成熟期钢管混凝土, 如:钟善桐[4]、蔡绍怀[3]、韩林海等[2, 14-15]、Yu等[16-17]、王玉银等[18]和赵均海等[19]等建立不同截面形状的钢管混凝土轴压承载力计算方法.且目前相关规范也给出了成熟期钢管混凝土的轴压承载力计算方法, 如GB 50936—2014[20]、Eurcode 4等.而针对早龄期圆形钢管混凝土的承载力有少量的研究, 如:Wang等[21]对早龄期钢管混凝土的承载力进行了研究, 并提出了圆形构件的早龄期承载力计算公式, 但该公式不能计算混凝土龄期为0时的情况;冯伟[22]分析了圆形钢管混凝土构件在轴压和偏压下承载力随龄期的变化规律.余敏等[13]对早龄期多级加载后的钢管混凝土短柱轴压性能进行了试验研究, 表明多级加载历史对成熟期的极限承载力影响较小.
综上所述, 目前关于早龄期钢管混凝土承载力的研究主要集中在圆形截面而且不能退化为空钢管的情况, 缺少统一的公式.为此, 对同批次浇筑的钢管混凝土短柱进行不同龄期下的轴压破坏试验.并在此基础上, 建立早龄期钢管混凝土的轴压承载力有限元模型, 并进行参数研究, 分析不同龄期下圆形和方形钢管混凝土的套箍作用及轴压承载力变化规律.最终提出考虑不同截面形状的早龄期钢管混凝土的强度承载力计算方法, 为钢管混凝土结构的安全施工提供参考.
1 早龄期钢管混凝土轴压试验 1.1 试件设计总共设计了9根构件, 包括8根同批次浇筑的圆形钢管混凝土短柱和1根空钢管, 其中空钢管可认为是混凝土龄期为0的特例, 此外混凝土龄期分别考虑了6、9、12、15、18、21、24和28 d等8种情况.圆钢管试件主要参数见表 1, 其中钢管的径厚比为40, 满足规范GB 50936—2014[20]限定要求.
| 表 1 试件参数 Table 1 Test parameters |
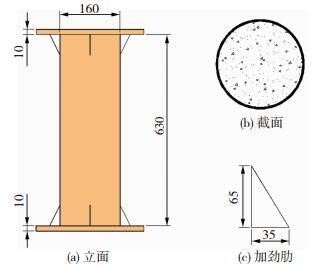
为防止荷载作用下试件端部破坏, 在钢管两端外侧焊接了三角形加劲肋.同时为保证钢管与混凝土共同均匀受力, 在钢管两端焊上厚10 mm端板.试件尺寸和构造见图 1.
|
图 1 试件几何尺寸 Figure 1 Dimension of the specimen |
钢材等级为Q235, 为了测量钢材的实际强度, 从同一批次的钢管中制作了3根哑铃型测试试样.混凝土采用C30的商品混凝土, 配合比见表 2.混凝为了评估管内土强度随龄期的增长规律, 同时还制备了27个混凝土标准立方体试块, 养护条件分别为自然养护、水中养护和锡纸包裹养护, 以分析不同养护条件对强度增长的影响.
| 表 2 混凝土配合比 Table 2 Mixture proportions of concrete |
参照GB/T 228.1—2010《金属材料拉伸试验:第1部分:室温试验方法》相关规定对钢板试样进行拉伸试验, 钢材屈服强度309.6 MPa, 极限强度412.1 MPa, 泊松比0.283.
对不同龄期的锡纸包裹养护、水中养护和自然条件养护的混凝土标准立方体试块进行抗压强度试验, 早龄期混凝土强度试验结果以及其与ACI209(式(1))的比较见图 2.

|
图 2 混凝土抗压强度 Figure 2 Compressive strength of the concrete |
| $ {f_{\rm{c}}}\left( t \right) = \frac{t}{{4 + 0.85t}}{f_{{\rm{c}}, 28}}, $ | (1) |
式中t为龄期, fc, 28为28 d的强度.
由图 2可以看出:3种养护条件下混凝土龄期强度增长规律比较类似, 12 d时强度可达到28 d强度的70%, 12 d后增长相对缓慢.28 d龄期时, 本试验中水中养护的混凝土强度最高, 锡纸包裹养护的强度略低, 总体相差不大.根据ACI209公式的强度计算结果在龄期18 d前比试验结果大, 18 d后和试验结果较为吻合.后续数值模拟验证中考虑到锡纸包裹和钢管内的混凝土养护环境最为接近, 因此最终采用锡纸包裹养护的强度值.
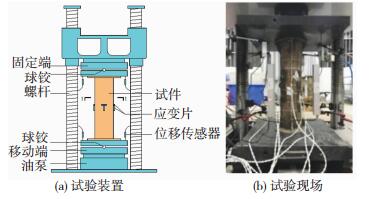
1.3 试验实施方案为便于观察试件破坏时钢管鼓曲情况, 试件钢管表面画有6 cm×6 cm白色网格线.同时在外钢管中部四周分别布置了1个横向和1个竖向的应变片, 用来测量试验中构件4个面的纵向、横向应变.为消除偏心的影响以及压力机自身变形的影响, 在试件顶端和底端的4个角落共布置8个位移计, 用来测量短柱构件的整体轴向压缩变形.具体试验装置和测量方案见图 3.
|
图 3 试验加载装置和测量点布置 Figure 3 Schematic of the test setup and instrumentations |
试验首先对构件进行预加载, 以确保机器、采集仪、应变片及位移计工作正常.同时监测应变片和位移计的数据, 若对称部位的测量数据基本保持一致, 则说明试件位置满足物理对中, 否则对试件位置进行微调.预加载无异常且试件物理对中后进行轴压试验.加载制度采用先力控加载后位移加载, 具体过程为采用5 kN/s力控制的方式加荷至100 kN后采用0.5 mm/min的位移控制方式加载.试验过程中连续记录荷载、位移和应变等数据, 直至构件总变形超过25mm或钢管出现明显腰鼓破坏, 停止加载.
2 试验结果与分析 2.1 破坏形态图 4为空钢管(0 d)和不同龄期钢管混凝土轴压后的破坏形态图.

|
图 4 试件破坏形态 Figure 4 Failure models of specimens |
从图 4可看出8根早龄期钢管混凝土试件的破坏形态比较类似, 破坏集中发生在中部和上端部, 均为腰鼓状破坏.成熟期钢管混凝土的套箍系数定义为ξ=fy As /(fck Ac), 对于早龄期钢管混凝土, 混凝土取龄期强度, 因混凝土龄期强度较低, 故龄期钢管混凝土套箍系数较大(ξ>1), 故不会发生剪切破坏.
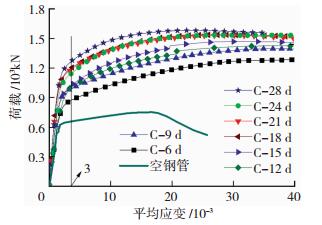
2.2 龄期对构件轴压性能的影响分析图 5为不同龄期钢管混凝土短柱的荷载-平均应变(即试件在轴压下的4个位移计测量出的变形量平均值与构件长度的比值)曲线试验结果.其中, 空钢管的荷载-平均应变曲线有明显的弹性段、强化段和下降段3个阶段.早龄期钢管混凝土短柱的荷载-平均应变与成熟期受力曲线相似, 可分为弹性、弹塑性和强化3个主要阶段.在加载初期, 试件处于弹性阶段, 试件外观上无明显变化, 且随着混凝土龄期的增长, 试件弹性阶段的斜率越来越大, 即钢管混凝土短柱的组合弹性模量也随着龄期不断增大, 极限弹性应变也逐渐变大;随后试件进入弹塑性阶段, 应变增长速度明显加快, 极限承载力也随着龄期增长逐渐变大;最后试件进入一段较长的加强段, 继续加载钢管表明铁锈开始脱落, 最终钢管中部或上部发生明显鼓曲, 试件破坏.
|
图 5 试件荷载-应变曲线 Figure 5 Load versus axial strain curves of specimens |
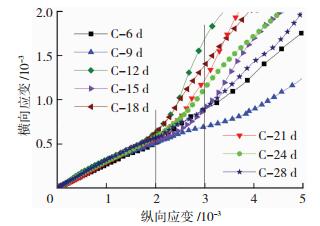
同时, 由图 5可看出构件延性较好, 且进入弹塑性阶段后无明显下降段.为确定早龄期钢管混凝土短柱的承载力, 绘制不同龄期试件的横向应变-纵向应变曲线, 见图 6.
|
图 6 试件横向应变-纵向应变曲线 Figure 6 Transverse and axial strain curves of specimens |
从图 6可以看出纵向应变达0.002前, 曲线基本为直线, 表明钢管处于弹性受力状态, 当纵向应变为0.003时, 钢管已经进入塑性阶段.综上, 早龄期钢管混凝土短柱的极限承载力可以参考成熟期钢管混凝土极限承载力的确定方法[4], 对于无明显下降段的曲线, 极限承载力取0.003变应对应的荷载值.
表 3为不同龄期的极限承载力试验结果, 可看出龄期6 d时构件的承载力达到28 d承载力的69%, 18 d时达到28 d承载力的94%, 强度发展迅速, 18 d后承载力开始趋于稳定.
| 表 3 钢管混凝土龄期承载力 Table 3 Age-bearing capacity of CFSTs |
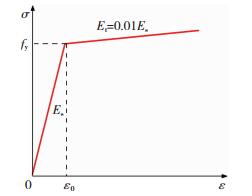
钢材本构关系采用Von Mises屈服准则, 应力-应变曲线采用双折线模型, 见图 7.图中fy和ε0分别是屈服强度及其对应的应变.
|
图 7 钢材应力-应变关系模型 Figure 7 Stress-strain curves of steel |
关于早龄期混凝土的本构模型, 目前国内外混凝土设计规范中并无明确规定.Yi等[23]基于ASTM C469的成熟期混凝土本构公式, 在试验基础上给出了0.5~28 d早龄期的混凝土本构关系:
| $ \frac{{{f_{\rm{c}}}}}{{f{'_{\rm{c}}}}} = \frac{{{\beta _{\rm{m}}}({\varepsilon _{\rm{c}}}/\varepsilon {'_{\rm{c}}})}}{{{\beta _{\rm{m}}} - 1 + {{({\varepsilon _{\rm{c}}}/\varepsilon {'_{\rm{c}}})}^{{\beta _{\rm{m}}}}}}}, $ | (2a) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\beta _{{\rm{m}}, {\rm{a}}}} = {{[1.02 - 1.17({E_0}/{E_{\rm{c}}})]}^{ - 0.74}}, }&{{\varepsilon _{\rm{c}}} \le \varepsilon {'_{\rm{c}}};}\\ {{\beta _{{\rm{m}}, {\rm{d}}}} = {\beta _{{\rm{m}}, {\rm{a}}}} + \left( {a + bt} \right), }&{{\varepsilon _{\rm{c}}} > \varepsilon {'_{\rm{c}}}.} \end{array}} \right. $ | (2b) |
| $ a = {(12.4 - 1.66 \times {10^{ - 2}}{f_{28}})^{ - 0.46}}, $ | (2c) |
| $ b = 0.83\exp ( - 911/{f_{28}}). $ | (2d) |
式中:fc、εc为抗压强度及对应的应变, f'c、ε'c为龄期受压应力-应变曲线峰值应力及对应的峰值应变, f28为龄期28d时的圆柱体抗压强度, E0为龄期受压应力-应变曲线峰值割线模量, E0=f'c/ε'c, Ec为龄期混凝土弹性模量, 根据ACI209的公式.
上述公式需要输入各龄期混凝土的强度及其对应的峰值应变, 较为复杂.为了方便混凝土早龄期应力-应变曲线与中国相关规范对接, 在规范GB 50010[24]成熟期混凝土本构关系基础上, 进行修正来得到早龄期混凝土应力-应变曲线, 其中受压曲线修正方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {y = \frac{{{E_0}{\varepsilon _{\rm{c}}}}}{{{f_{\rm{c}}}}}x, }&{x < {x_0};}\\ {{\alpha _{\rm{a}}}x + (3 - 2{\alpha _{\rm{a}}}){x^2} + ({\alpha _{\rm{a}}} - 2){x^3}, }&{{x_0} \le x < 1;}\\ {\frac{x}{{{a_{\rm{d}}}{{\left( {x - 1} \right)}^2} + x}}, }&{x \ge 1.} \end{array}} \right. $ | (3) |
式中:y为相对应力, x为相对应变, E0取混凝土受拉开裂时的割线模量作为混凝土的初始弹性模量, x0为应力-应变曲线中割线模量为E0点的相对应变值, αa、αd为受压曲线上升段、下降段参数, 具体取值参考GB 50010[24]附录C.使用时只需实测各龄期混凝土轴心抗压强度即可获得相应本构关系.
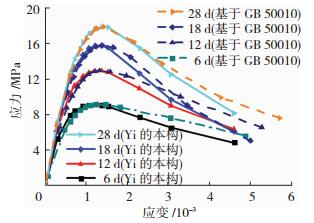
图 8为采用Yi等[23]本构模型和基于GB 50010本构模型的对比.可以看出两者相差较小, 特别是上升段.因此, 基于GB 50010的受压曲线修正模型能够较好预测早龄期混凝土的应力-应变关系.
|
图 8 应力-应变曲线对比 Figure 8 Comparison of stress-strain curves |
对于龄期混凝土的泊松比和膨胀角的取值, 刘宏伟等[25]研究表明, 龄期混凝土的泊松比与龄期没有直接相关性, 基本在0.175~0.20, 故本文统一取值0.2.对于28 d后钢管混凝土短柱在高围压下膨胀角在15°~56.3°[26], 具体取值将通过模拟结果进行反向标定.
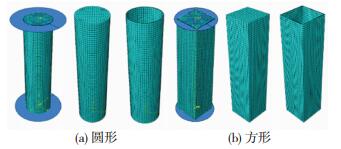
3.1.2 有限元模型建立及相关参数选取钢管和混凝土均采用实体模型, 单元类型为C3D8R.钢管厚度方向考虑三层网格, 网格大小约10 mm, 圆形和方形的网格划分见图 9.
|
图 9 钢管混凝土柱网格划分 Figure 9 Mesh of CFST columns |
钢管和混凝土之间的接触定义, 有通过定义“硬”接触和摩擦来处理[2, 27-28], 也有通过定义双向弹簧来处理[29], 也有不考虑它们之间的相对滑移[27], 直接将接触面完全耦合在一起.对于轴压计算, 它们的差别不是很大, 为了减少计算时间和提高收敛性, 在此采用完全耦合的方式来处理它们的接触面.在钢管混凝土上下端分别设置了刚片以保证钢管和混凝土能协同工作, 并采用位移加载.
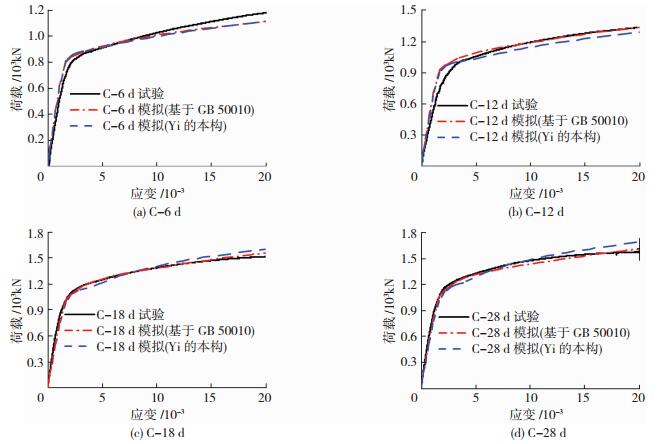
3.2 钢管混凝土短柱龄期模拟验证为验证上述有限元模型, 对早龄期钢管混凝土短柱轴压试验进行模拟.图 10为龄期为6、12、18、28 d的钢管混凝土荷载-应变曲线的试验和模拟结果对比, 可以看出基于GB 50010的本构与Yi等[23]的本构都能较真实模拟早龄期钢管混凝土的轴压性能.
|
图 10 荷载-平均应变试验与模拟结果对比 Figure 10 Comparison of simulation and test results |
同时通过数值反向标定发现, 龄期为6、12、18、28 d时, 对应的混凝土膨胀角取15、32、40和45°时, 试验和有限元结构最为吻合.而混凝土的膨胀角越大, 钢管和混凝土之间的约束作用越大, 从而间接说明钢管和混凝土之间的相互作用随龄期而增大.
3.3 不同截面及龄期对套箍作用的影响分析为分析不同截面形状的早龄期钢管混凝土短柱的轴压性能, 根据等面积原则, 在圆形试验构件的基础上, 设计了方形截面钢管混凝土短柱构件, 试件长630.00 mm, 边长141.8 mm, 钢管厚3.46 mm.
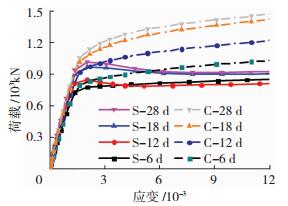
图 11为不同龄期圆形与方形钢管混凝土短柱荷载-应变曲线对比.可得出:在曲线弹性阶段, 方形和圆形截面刚度基本相同;对于圆形构件出现拐点后曲线无明显下降段, 而方形构件达到峰值点后曲线出现下降段;对于极限承载力, 圆形取0.003应变时的承载力大于方形截面峰值点承载力值.即, 同龄期下圆形截面套箍作用明显高于方形截面, 这点和成熟期钢管混凝土短柱的规律一致.
|
图 11 同龄期不同截面承载力模拟曲线 Figure 11 Bearing capacity with different cross sections |
对于成熟期钢管混凝土的轴压承载力, 课题组先前基于厚壁圆筒理论和有效约束方法, 建立了圆形和方形钢管混凝土柱统一的承载力计算方法[16-17], 其中强度承载力公式为
| $ {N_0} = \left( {1 + 0.5{k_{\rm{e}}}\frac{\xi }{{1 + \xi }}} \right)({A_{\rm{c}}}{f_{{\rm{ck}}}} + {A_{\rm{s}}}{f_{\rm{y}}}), $ | (4) |
式中:fck、fy分别为混凝土、钢材的强度标准值, As、Ac分别为钢管、核心混凝土的截面面积, ξ为钢管混凝土套箍系数, ξ=fyAs/(fckAc), ke为等效约束系数, 对于圆形构件ke=1, 对于方形构件ke=1/3.
该公式主要包括两个部分, Acfck+As fy表示叠加承载力, 前面部分为套箍增强部分, 其中系数0.5是用来考虑钢管和混凝土之间的相互作用大小, 该值和混凝土性质有关, 对于成熟期的普通混凝土, 经过和大量试验对比最终简化取0.5[16-17], 并没有考虑早龄期对套箍作用的影响, 因此当混凝土强度为零时, 上述公式并不能退化为空钢管的承载力.
4.2 早龄期钢管混凝土短柱承载力计算公式由于早龄期混凝土和钢管之间的约束效应是随龄期变化的, 因此在此引入一个龄期套箍作用的修正系数kc, 即
| $ {N_0} = \left( {1 + 0.5{k_{\rm{c}}}{k_{\rm{e}}}\frac{{{\xi _{\rm{d}}}}}{{1 + {\xi _{\rm{d}}}}}} \right)({A_c}{f_{{\rm{ck}}, {\rm{d}}}} + {A_{\rm{s}}}{f_{\rm{y}}}). $ | (5) |
当龄期t等于0时, 组合截面退化为空钢管, 则要求:
| $ {k_{\rm{c}}}\left( 0 \right) = 0, $ | (6) |
当龄期t等于28 d时, 即为成熟期钢管混凝土的承载力, 则要求:
| $ {k_{\rm{c}}}\left( {28} \right) \approx 1, $ | (7) |
根据表 3数据, 通过回归分析得
| $ {k_{\rm{c}}}\left( t \right) = t/\left( {16 + 0.4t} \right). $ | (8) |
因此, 最终考虑龄期的钢管混凝土短柱强度承载力计算公式为:
| $ {N_0} = \left( {1 + \eta } \right)({A_{\rm{c}}}{f_{{\rm{ck}}, {\rm{d}}}} + {A_{\rm{s}}}{f_{\rm{y}}}), $ | (9a) |
| $ \eta = 0.5{k_{\rm{c}}}{k_{\rm{e}}}\frac{{{\xi _{\rm{d}}}}}{{1 + {\xi _{\rm{d}}}}}. $ | (9b) |
式中:η为套箍增强系数, fck, d、fy分别为龄期混凝土、钢材的强度标准值, ξd为考虑龄期的套箍系数, ξd=fy As/(fckAc), kc(t)为龄期套箍修正系数, 见式(8).当混凝土龄期为0时, 该公式可退换为空钢管的情况.
4.3 早龄期钢管混凝土承载力计算公式验证为了验证早龄期钢管混凝土承载力计算式(9)的准确性, 采用表 4中“四因素、六水平”共24种组合的均匀设计方法, 分别考虑6种钢管直径、钢管厚度、钢材等级和混凝土等级, 从而避免排列组合导致算例过多, 同时保证所选择的算例具有广泛的代表性.
| 表 4 有限元模拟参数设计 Table 4 Parameter design of the FEA |
龄期选用6、12、18、24、28 d, 因此, 对于圆形、方形钢管混凝土短柱各设计24×5=120个有限元算例.
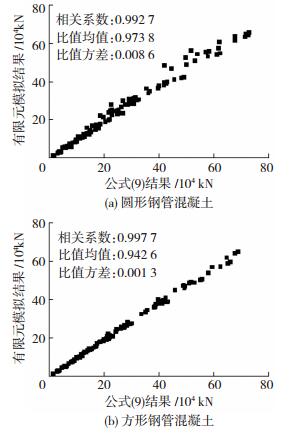
图 12为承载力有限元模拟结果与公式计算结果对比.对于圆形构件, 有限元计算结果与公式计算结果比值的平均值为0.973 8, 方差为0.008 6;对于方形构件比值的均值为0.942 6, 方差为0.001 3.表明理论公式可以较好预测早龄期钢管混凝土短柱的强度承载力, 证明了公式的有效性.
|
图 12 公式值与模拟值对比 Figure 12 Comparisons of the formula and the FEA results |
1) 进行了早龄期钢管混凝土短柱轴压性能试验, 得到了不同混凝土龄期下构件的破坏模式和荷载-变形曲线.结果表明早龄期钢管混凝土短柱的破坏形态、荷载-变形曲线的形状均与成熟期的类似, 曲线可分为弹性、弹塑性和强化3个阶段.早龄期钢管混凝土短柱极限承载力可以近似按取0.003纵向应变对应的荷载值, 龄期18 d时的极限承载力可达成熟期承载力的90 %以上.
2) 将成熟期混凝土强度替换为龄期强度, 并将弹性模型取受拉峰值对应的切线模量后, 规范GB 50010中的成熟期混凝土的本构模型可适用于早龄期的混凝土.结合试验和早龄期钢管混凝土短柱的数值分析, 表明套箍作用随龄期的增长而增大, 早龄期圆形钢管混凝土短柱的套箍作用高于同龄期的方形构件.
3) 在课题组先前提出的成熟期圆形和方形钢管混凝土统一的轴压强度承载力计算公式基础上, 引入龄期套箍作用修正系数, 建立了考虑混凝土龄期影响的钢管混凝土强度承载力计算公式.并结合均匀设计的方法对不同截面的早龄期钢管混凝土短柱轴压承载力进行参数研究, 证明了公式的适用性.
| [1] |
HAN Linhai, LI Wei, BJORHOVDE R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members[J]. Journal of Constructional Steel Research, 2014, 100: 211. DOI:10.1016/j.jcsr.2014.04.016 |
| [2] |
韩林海. 钢管混凝土结构:理论与实践[M]. 3版. 北京: 科学出版社, 2016. HAN Linhai. Concrete-filled steel tubular structures: Theory and application[M]. 3rd ed. Beijing: Science Press, 2016. |
| [3] |
蔡绍怀. 现代钢管混凝土结构[M]. 2版. 北京: 人民交通出版社, 2007. CAI Shaohuai. Modern steel tube confined concrete structures[M]. 2nd ed. Beijing: China Communication Press, 2007. |
| [4] |
钟善桐. 钢管混凝土结构[M]. 3版. 北京: 清华大学出版社, 2003. ZHONG Shantong. Concrete-filled steel tubular structures[M]. 3rd ed. Beijing: Tsinghua University Press, 2003. |
| [5] |
查晓雄. 空心和实心钢管混凝土结构[M]. 北京: 科学出版社, 2011. ZHA Xiaoxiong. Hollow and solid concrete-filled steel tube columns structure[M]. Beijing: Science Press, 2011. |
| [6] |
何振伟.持续应力下密封早龄期混凝土力学性能依时发展规律研究[D].北京: 北京交通大学, 2013 HE Zhenwei. Development of mechanical properties of sealed concrete in early age under sustained stress action[D]. Beijing: Beijing Jiaotong University, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10004-1013278240.htm |
| [7] |
祁广星.密封混凝土早龄期徐变模型[D].北京: 北京交通大学, 2014 QI Guangxing. The creep model in early age of sealed concrete[D]. Beijing: Beijing Jiaotong University, 2014 http://cdmd.cnki.com.cn/article/cdmd-10004-1014369461.htm |
| [8] |
周丽东.钢管混凝土轴心受压构件早龄期徐变研究[D].北京: 北京交通大学, 2015 ZHOU Lidong. Early-age creep of axial compression concrete filled steel tubular members[D]. Beijing: Beijing Jiaotong University, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10004-1015611599.htm |
| [9] |
GENG Yue, RANZI G, WANG Yuyin, et al. Time-dependent behaviour of concrete-filled steel tubular columns: Analytical and comparative study[J]. Magazine of Concrete Research, 2012, 64(1): 55. DOI:10.1680/macr.2012.64.1.55 |
| [10] |
GENG Yue, WANG Yuyin, CHEN Jie. Time-dependent behaviour of steel tubular columns filled with recycled coarse aggregate concrete[J]. Journal of Constructional Steel Research, 2016, 122: 455. DOI:10.1016/j.jcsr.2016.04.009 |
| [11] |
WANG Yuyin, GENG Yue, RANZI G, et al. Time-dependent behaviour of expansive concrete-filled steel tubular columns[J]. Journal of Constructional Steel Research, 2011, 67(3): 471. DOI:10.1016/j.jcsr.2010.09.007 |
| [12] |
刘俊, 吴杰, 罗晓群, 等. 高层钢管混凝土结构施工全过程数值模拟[J]. 土木建筑与环境工程, 2012, 34(5): 50. LIU Jun, WU Jie, LUO Xiaoqun, et al. Numerical simulation on whole construction process of high-rise CFST structures[J]. Journal of Civil, Architectural & Environmental Engineering, 2012, 34(5): 50. |
| [13] |
余敏, 童栋华, 池寅, 等. 截面形状对早龄期钢管混凝土柱多级加载变形及承载力影响的试验研究[J]. 建筑结构学报, 2018, 39(8): 148. YU Min, TONG Donghua, CHI Yin, et al. Experimental investigation on influence of sectional shape on deformation and bearing capacity of early-age concrete-filled steel tubular short columns under multi-level loading[J]. Journal of Building Structures, 2018, 39(8): 148. |
| [14] |
韩林海, 杨有福. 矩形钢管混凝土轴心受压构件强度承载力的试验研究[J]. 土木工程学报, 2001, 34(4): 22. HAN Linhai, Yang Youfu. Experimental study on the axial compression bearing capacity of the concrete-filled rectangular steel tube[J]. Civil Engineering Journal, 2001, 34(4): 22. DOI:10.3321/j.issn:1000-131X.2001.04.004 |
| [15] |
韩林海, 陶忠. 方钢管混凝土轴压力学性能的理论分析与试验研究[J]. 土木工程学报, 2001, 34(2): 17. HAN Linhai, TAO Zhong. Theoretical analysis and experimental study on the stress performance of concrete-filled square steel tube[J]. Civil Engineering Journal, 2001, 34(2): 17. DOI:10.3321/j.issn:1000-131X.2001.02.004 |
| [16] |
YU Min, ZHA Xiaoxiong, YE Jianqiao, et al. A unified formulation for circle and polygon concrete-filled steel tube columns under axial compression[J]. Engineering Structures, 2013, 49: 1. DOI:10.1016/j.engstruct.2012.10.018 |
| [17] |
YU Min, ZHA Xiaoxiong, YE Jianqiao, et al. A unified formulation for hollow and solid concrete-filled steel tube columns under axial compression[J]. Engineering Structures, 2010, 32(4): 1046. DOI:10.1016/j.engstruct.2009.12.031 |
| [18] |
王玉银, 张素梅. 圆钢管高强混凝土轴压短柱性能的试验研究[J]. 哈尔滨工业大学学报, 2004, 36(12): 1646. WANG Yuyin, ZHANG Sumei. Experimental research on axially loaded high-strength concrete-filled steel tubes[J]. Journal of Harbin Institute of Technology, 2004, 36(12): 1646. DOI:10.3321/j.issn:0367-6234.2004.12.016 |
| [19] |
赵均海, 吴鹏, 张常光. 多边形空心钢管混凝土短柱轴压极限承载力统一解[J]. 混凝土, 2013, 10: 38. ZHAO Junhai, WU Peng, ZHANG Changguang. Unified ultimate bearing capacity solution for polygon hollow concrete filled steel tube stub columns[J]. Concrete, 2013, 10: 38. |
| [20] |
钢管混凝土结构技术规范: GB 50936—2014[S].北京: 中国建筑工业出版社, 2014 Technical code for concrete filled steel tubular structures: GB 50936—2014[S]. Beijing: China Architecture & Building Press, 2014 |
| [21] |
WANG Haiyang, ZHA Xiaoxiong. Axial strength of CFST columns considering concrete age[J]. Advance Steel Construction, 2014, 10(2): 139. |
| [22] |
冯伟.施工中混凝土龄期对高层钢管混凝土柱性能的影响[D].哈尔滨: 哈尔滨工业大学, 2009 FENG Wei. Effect of concrete age growth on the behavior of high-rise CFST columns during construction[D]. Harbin: Harbin Institute of Technology, 2009 http://cdmd.cnki.com.cn/Article/CDMD-10213-2010026387.htm |
| [23] |
YI S T, KIM J K, OH T K. Effect of strength and age on the stress-strain curves of concrete specimens[J]. Cement and Concrete Research, 2003, 33(8): 1235. DOI:10.1016/S0008-8846(03)00044-9 |
| [24] |
混凝土结构设计规范: GB 50010—2002[S].北京: 中国建筑工业出版社, 2002 Code for design of concrete structures: GB 50010—2002[S]. Beijing: China Architecture & Building Press, 2002 |
| [25] |
刘宏伟, 谢丽, 吴胜兴. 混凝土早龄期弹性模量无损检测初探[J]. 混凝土, 2008(6): 36. LIU Hongwei, XIE Li, WU Shengxing. Tentative research on non-destructive detection of early-age elastic modulus of concrete[J]. Concrete, 2008(6): 36. |
| [26] |
尧国皇, 黄用军, 宋宝东, 等. 采用塑性损伤模型分析钢-混凝土组合构件的静力性能[J]. 建筑钢结构进展, 2009, 11(3): 12. YAO Guohuang, HUANG Yongjun, SONG Baodong, et al. Analysis for static behavior of steel and concrete composite members with plastic-damage model[J]. Progress in Steel Building Structures, 2009, 11(3): 12. |
| [27] |
丁发兴, 周林超, 余志武, 等. 钢管混凝土轴压短柱非线性有限元分析[J]. 中国科技论文在线, 2009, 4(7): 472. DING Faxing, ZHOU Linchao, YU Zhiwu, et al. Nonlinear finite element analysis of axially loaded concrete-filled steel tubular stub columns[J]. Sciencepaper Online, 2009, 4(7): 472. DOI:10.3969/j.issn.2095-2783.2009.07.002 |
| [28] |
张岩, 张安哥, 陈梦成, 等. 圆钢管混凝土轴压长柱有限元分析[J]. 哈尔滨工业大学学报, 2007, 39(增刊2): 94. ZHANG Yan, ZHANG Ange, CHEN Mengcheng, et al. Finite element analysis of slender CFST columns under axial compression[J]. Journal of Harbin Institute of Technology, 2007, 39(S2): 94. |
| [29] |
SUGIURA K, WATANABE E, OYAWA W O. Assessment on fill material properties for filled steel stub columns[J]. Journal of Structural Engineering, 2001, 47A: 1413. |
 2018, Vol. 50
2018, Vol. 50


