2. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),哈尔滨 150090;
3. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, Harbin 150090, China;
3. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
在土木工程中推广超高强材料和新型结构, 是提高结构性能和发展绿色建筑的有效方法.钢管RPC可为大跨、高层与高耸建筑、重载工程建设提供性能优越的竖向构件.多位学者展开了钢管RPC柱力学性能研究[1-2].文献[3]进行了不同配合比的RPC试块以及钢管RPC短柱轴压承载能力研究, 发现水胶比从0.16增大到0.2时, RPC试块强度降低4.7%, 钢管RPC短柱承载力下降15.7%.文献[4]进行了18根圆钢管RPC短柱的轴心受压试验, 提出了直径不大于152 mm的圆钢管RPC承载力计算式;文献[5]对比分析了40根钢管RPC短柱试验结果, 建立了钢管RPC轴压短柱承载力计算式.
以上研究表明, 现有圆钢管RPC轴压短柱承载力计算公式适用于直径不大于152 mm的钢管RPC柱, 对大直径钢管RPC柱, 计算值偏大.在超高层建筑中, 钢管混凝土柱直径已超过2 m[6].目前, 中国尚缺乏圆钢管RPC轴压短柱相关设计标准.针对上述问题, 本文利用ABAQUS有限元软件, 提出损伤塑性模型中参数的取值建议, 对134种钢管RPC短柱轴压荷载受力全过程进行分析, 揭示截面尺寸、套箍系数、钢材强度、核心RPC强度对RPC轴压短柱荷载-位移曲线的影响规律;结合已有试验结果, 建立圆钢管RPC轴压短柱承载力的计算公式.
1 有限元分析模型的建立与验证 1.1 材料的本构模型采用ABAQUS有限元软件建立钢管RPC轴压短柱分析模型.模型中钢材采用理想弹塑性模型.钢材的屈服强度取实测值, 密度取为7 850 kg/m3, 弹性模量取为200 GPa, 泊松比取为0.3.
核心RPC采用文献[7]提出的塑性损伤模型模拟.RPC塑性损伤模型所需单轴受压应力-应变曲线及单轴受拉应力-应变曲线分别采用文献[8]的单轴受压试验和文献[9]的单轴受拉试验结果.在RPC拉压力学性能试验的基础上, 提出了塑性损伤模型中膨胀角φ、偏心距ε、双轴极限抗压强度与单轴极限抗压强度之比σb0/σc0、拉伸子午面上与压缩子午面上的第二应力不变量之比kc、黏滞系数μ等关键参数的取值建议.
参数φ和ε取值决定了流势面的形状, 以70.7 mm×70.7 mm×220 mm的RPC棱柱体受压应力-应变关系模拟结果与实测结果的对比, 确定膨胀角φ、偏心距ε的取值.图 1为膨胀角不同取值对RPC应力-应变关系影响曲线, 结果表明, 当φ取为25°~40°时, 随φ增大, 应力-应变曲线下降段的斜率变缓, 膨胀角取为38°时, 模拟结果与文献[8]试验结果吻合较好.由于偏心距ε对应力-应变曲线影响较小, 有限元分析中, 建议取1.0.

|
图 1 膨胀角φ与试验结果对比曲线 Figure 1 Influence of φ on stress-strain curves of RPC test |
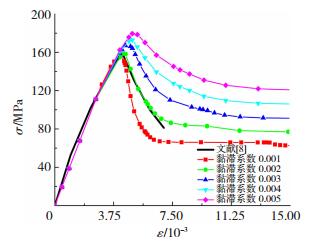
屈服面由σb0/σc0和kc两个参数决定.参考文献[10]完成的RPC200双轴受压试验, 确定参数σb0/σc0的值为1.14.kc为RPC屈服面在扁平面上投影的形状参数, 投影为三角形时取0, 圆形时取0.666 7, 本文建议取值0.666 7.图 2为黏滞系数不同取值与文献[8]试验结果对比曲线, 发现黏滞系数的取值对曲线影响较大.随着黏滞系数的增大, 应力-应变曲线的峰值增大, 下降段斜率变缓.当μ=0.002时, 模拟结果与文献[8]试验结果吻合较好.采用5个关键参数计算的RPC受压应力-应变关系与文献[11]的试验结果也吻合较好(具体对比结果详见文献[12]), 说明这5个关键参数的取值可用于后续计算分析.
|
图 2 黏滞系数μ与试验结果对比曲线 Figure 2 Influence of μ on stress-strain curves of RPC test |
钢管与核心RPC的接触包括切向(沿钢管竖直方向)和法向(垂直于接触面)两个部分.其中法向接触采用硬接触, 切向接触采用库仑摩擦模型, 摩擦系数取为0.25[13].核心区RPC采用三维八节点实体单元C3D8R, 钢管采用四节点壳单元S4R, 划分网格大小为1 cm.完全约束柱底端自由度, 柱顶两个水平方向不施加约束, 仅在柱顶端施加轴向荷载(位移荷载).
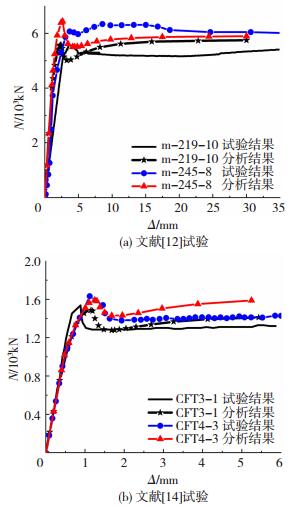
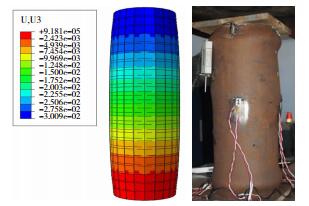
1.3 有限元模型验证采用ABAQUS软件建立了钢管RPC柱有限元分析模型, 与文献[12, 14]完成的圆钢管RPC轴压短柱试验进行对比, 以验证有限元模型的正确性.图 3为试件荷载-位移曲线试验值与有限元计算值的对比.与文献[12]对比表明, 在荷载-位移曲线弹性阶段, 计算值与实测值吻合良好;随后钢材屈服进入塑流阶段, 曲线出现下降段, 也基本吻合, 在之后的承载力回升阶段, 有限元计算的回升速率略快于试验结果.与文献[14]试验结果对比看出, 试件CFT3、CFT4的有限元计算曲线与试验曲线均较为接近.有限元分析钢管RPC柱m-245-8破坏后变形云图和试验后柱实际破坏情况见图 4, 均呈现腰鼓型破坏.结合图 3、4可知, 有限元模拟结果与试验结果吻合较好, 可用于圆钢管RPC轴压短柱受力性能分析.
|
图 3 有限元计算曲线与试验曲线比较 Figure 3 Comparison of load-displacement curves from FEA and the test |
|
图 4 试件m-245-8有限元变形与试验变形对比 Figure 4 Comparison of deformation of specimen m-245-8 from FEA and the test |
基于ABAQUS有限元模型, 完成134种RPC轴压短柱受力过程分析, 为消除柱长和外径之比过大影响柱轴压承载力的问题, 本文分析的钢管RPC短柱, 其柱长和外径之比均为3.由于不同钢管RPC试件荷载位移曲线规律相似, 本节参数分析仅以部分典型试件为例, 研究钢管径厚比、套箍系数、核心RPC强度与钢材强度等对钢管RPC荷载-位移曲线的影响和钢管对核心RPC约束作用的影响规律.
2.1 钢管径厚比通过变换钢管厚度或钢管外径分析钢管径厚比变化对钢管RPC轴压短柱力学性能的影响规律, 分析模型参数见表 1、2.相同外径、不同钢管厚度对钢管RPC短柱荷载-位移曲线的影响见图 5, 其中N为轴压力, Δ为试件的整体纵向位移.当钢管外径相同时, 随着钢管厚度的增大, 钢管径厚比减小, 套箍系数增大, 钢管对核心区RPC的约束作用增强, 试件的峰值承载力提高, 极限承载力得到改善, 表现出良好的延性.不同外径、相同厚度时, 径厚比变化对圆钢管RPC短柱荷载-位移曲线的影响见图 6.
| 表 1 相同外径、不同厚度的试件参数 Table 1 Parameters of specimens with the same diameter |
| 表 2 不同外径、相同厚度的试件参数 Table 2 Parameters of specimens with the same thickness |

|
图 5 不同钢管厚度时荷载-位移曲线对比 Figure 5 Curves of specimens with different tube thicknesses |
|
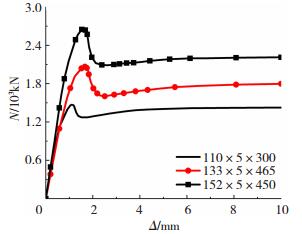
图 6 不同钢管外径时荷载-位移曲线对比 Figure 6 Curves of specimens with different tube diameters |
结果表明, 当钢管厚度相同时, 试件的截面尺寸越大, 轴压承载力越高, 但径厚比变大, 含钢率减小, 套箍系数减小, 钢管对核心区RPC的约束作用减弱, 试件达到峰值承载力后曲线下降较为明显, 且试件承载力的回升程度也明显低于含钢率较大的试件.
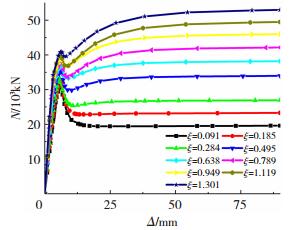
2.2 套箍系数套箍系数ξ(ξ=Asfy/Acfc)对钢管RPC承载力有较大的影响.ξ越大, 钢管所占的比重越大, 核心区RPC所占的比重相对越小, 套箍作用大.对工程常用范围内16种不同截面尺寸(1 mm≤t≤45 mm、110 mm≤D≤560 mm), 共134种不同套箍系数(0.051≤ξ≤1.972)的钢管RPC柱进行模拟分析, 获得其荷载-位移曲线, 得到套箍系数对下降段影响的界限值.其中fy和fc分别取310和100 MPa.图 7给出了不同套箍系数试件的荷载-位移曲线.
|
图 7 钢管RPC轴压短柱(D=560 mm)荷载-位移曲线 Figure 7 Load-displacement curves of RPC-filled circular steel tubes(D=560 mm) |
当套箍系数小于0.5时, 钢管RPC柱荷载-位移曲线不存在强化段;当套箍系数达到0.5~0.6时, 钢管RPC试件在轴压荷载作用下, 在达到极限承载力之后, 极限荷载下降到原来的80%~85%, 之后随着荷载的继续施加, 试件的极限荷载逐渐回升, 并与峰值荷载(荷载-位移曲线第一个峰值点对应的荷载)持平.套箍系数继续增加, 则荷载的回升将超过峰值荷载, 当套箍系数达到1时, 试件在达到峰值荷载之后, 极限荷载的下降幅度很小, 仅为5%左右, 荷载的回升将超过峰值荷载的30%, 荷载继续施加, 钢管RPC荷载-位移曲线呈现回升段, 表现出良好的延性.
2.3 核心RPC轴心抗压强度变化核心区RPC轴心抗压强度, 分析其对钢管RPC短柱受压力学性能的影响规律.其中钢管的屈服强度fy为290 MPa, 试件截面尺寸D×t×L均为133 mm×3 mm×400 mm, 核心RPC轴心抗压强度fc分别为75、100、125、150、175和200 MPa.RPC抗压强度变化对钢管RPC短柱的荷载-位移曲线的影响如图 8所示.分析发现:试件承载能力随着核心RPC轴心抗压强度的提高而增大, 但RPC轴心抗压强度越高, 钢管对核心RPC的约束作用相对减弱, 约束后RPC承载力提升幅度减小;模型中RPC75的抗压强度最低, 套箍系数最大, 承载力的提升幅度达到33%, 即钢管对RPC75试件的约束作用更强.

|
图 8 RPC强度变化时试件的荷载-位移曲线 Figure 8 Load-displacement curves of specimenswith different RPC strengths |
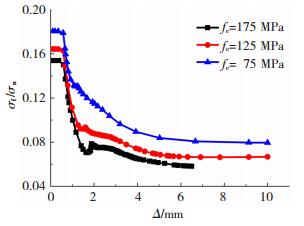
当RPC轴心抗压强度分别为75、125和175 MPa时, 钢管RPC柱中RPC约束应力σf与轴向名义压应力σn(外荷载与钢管RPC柱横截面积之比)之比与钢管轴向位移的关系见图 9.该曲线大致可分为3个阶段:第一阶段, 钢管RPC基本处于弹性阶段, 约束应力与轴向名义压应力之比基本不变;第二阶段, 曲线出现明显下降段, 主要是钢管环向屈服, 约束应力基本不变, 而因RPC未被压碎, 故随柱顶轴向位移增加, 轴向名义压应力增加, 导致曲线出现明显下降段;第三阶段, 曲线基本维持不变, 比值在0.06~0.10, 这主要是RPC被压碎, 约束应力与截面名义压应力均降低至一定水平, 且基本维持不变所致.此外, 对比不同RPC强度的三条曲线, 可看出随RPC抗压强度降低, RPC约束应力与轴向名义压应力之比增大, 说明钢管对低强度的RPC约束作用更强.这与横向约束作用下普通混凝土受约束效果强于高强混凝土受约束效果的规律一致.
|
图 9 RPC强度变化时相对约束应力-位移曲线 Figure 9 Confining stress ratio-displacement curves of specimens with different RPC strengths |
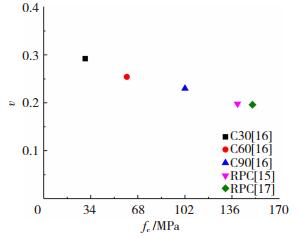
为进一步探索混凝土强度变化对钢管RPC短柱轴压承载力的影响, 参考文献[15-17]中普通混凝土, 高强混凝土及RPC横向变形系数的实测结果, 给出了横向变形系数随混凝土抗压强度变化的关系, 见图 10.随混凝土抗压强度提高, 其横向变形系数降低, RPC横向变形小于高强混凝土和普通混凝土, 钢管对RPC的横向约束效果相对更差.
|
图 10 不同强度混凝土的横向变形系数 Figure 10 Transverse deformation coefficient of concrete with different strengths |
不同钢材屈服强度时钢管RPC试件的荷载-位移对比见图 11, 试件分析参数为:钢管外径133 mm、厚3 mm, 核心RPC抗压强度100 MPa, 变化钢材的屈服强度为300~450 MPa.分析表明:随钢管屈服强度的提高, 套箍系数增大, 钢管RPC的承载力逐渐提高.S4试件的钢材屈服强度是S1试件的1.5倍, S4试件承载力只有S1试件的约1.1倍, 这主要是由于钢材屈服强度越高, 钢管RPC短柱轴压承载力越高, 相同外荷载下, 钢管RPC柱纵向变形越小, 对应的钢管RPC柱横向变形越小, 混凝土的横向变形过小导致钢管与混凝土的接触不明显.故随着钢材屈服强度的提高, 钢管RPC短柱轴压承载力提高幅度不显著.工程应用时, 需注意钢材屈服强度和核心RPC强度的匹配, 提高钢材的屈服强度并不能显著提升其约束效果.

|
图 11 不同钢材屈服强度试件的荷载-位移曲线 Figure 11 Load-displacement curves of specimens with different steel strengths |
基于本课题组[12]和文献[5, 14, 18-20]完成的139根圆钢管RPC轴心受压短柱试验数据及本文分析的134根圆钢管RPC有限元模拟数据, 拟合出钢管RPC柱的极限承载力计算公式.
3.1 极限承载力计算公式钢管RPC柱的极限承载力可表示为
| $ N = {A_{\rm{c}}}{f_{\rm{c}}} + \alpha {A_{\rm{s}}}{f_{\rm{y}}}, $ | (1) |
将ξ=Asfy/Acfc代入式(1)中, 可得
| $ N = {A_{\rm{c}}}{f_{\rm{c}}} \times \left( {\alpha \xi + 1} \right). $ | (2) |
基于最小二乘法, 对上述试验数据和数值模拟结果进行拟合, 得到钢管RPC轴压短柱的极限承载力公式:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;N = {A_{\rm{c}}}{f_{\rm{c}}}\left( {1.23\xi + 1} \right), \\ \xi = {A_{\rm{s}}}{f_{\rm{y}}}/{A_{\rm{c}}}{f_{\rm{c}}}, 0.057 \le \xi \le 1.575. \end{array} $ | (3) |
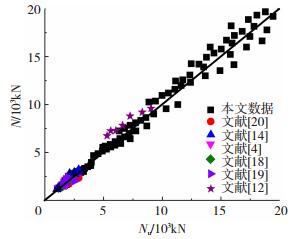
图 12为拟合的极限承载力公式计算结果N与试验及数值模拟结果Nu对比, 计算值N与Nu比值的平均值为0.967, 变异系数0.097, 吻合较好.
|
图 12 拟合公式与试验数据对比 Figure 12 Comparison between fitting formula and test data |
以外径560 mm的圆钢管RPC短柱为例, 将本文拟合式(3)与各学者提出的公式及CECS 28:2012《钢管混凝土结构设计与施工规程》规范公式进行对比, 圆钢管RPC短柱试件的尺寸见表 3(Nu为有限元计算结果), 对比结果见图 13.由对比结果可知:现有圆钢管RPC试件极限承载力公式, 规程(CECS 28:2012)中钢管普通混凝土、钢管高强混凝土极限承载力公式计算值偏大, 而拟合式(3)吻合较好, 适用范围更广.
| 表 3 钢管RPC短柱试件基本参数 Table 3 Parameters of specimens |

|
图 13 计算值与实测值对比 Figure 13 Comparison of calculated and test value |
1) 套箍系数对钢管RPC短柱轴压力学性能影响显著, 随着套箍系数的增大, 钢管对核心RPC的约束作用增强, 柱的延性越好.当套箍系数ξ<0.5, 钢管RPC柱荷载-位移曲线不存在强化段;当0.5≤ξ<1时, 钢管RPC柱荷载-位移曲线出现强化段;当ξ≥1时, 强化段极限荷载相对于承载力的提升将超过30%.
2) 相同截面尺寸的圆钢管RPC柱, 随核心RPC轴心抗压强度降低, 其横向变形系数增大, 钢管对核心RPC的约束作用增强.
3) 提出了直径达560 mm圆钢管RPC轴压短柱极限承载力计算公式, 可用于工程设计.
| [1] |
MEHMET C. The effect of high temperature on reactive powder concrete[J]. Construction & Building Marerials, 2012, 70(6): 508. |
| [2] |
LEE J, XI Yunping, WILLIAM K, et al. A multiscale model for modulus of elasticity of concrete at high temperatures[J]. Cement and Concrete Research, 2009, 39(9): 754. DOI:10.1016/j.cemconres.2009.05.008 |
| [3] |
孟世强. 钢管活性粉末混凝土初步研究[J]. 混凝土与水泥制品, 2003, 1(1): 5. DOI:10.3969/j.issn.1000-4637.2003.01.002 |
| [4] |
林震宇, 吴炎海, 沈祖炎. 圆钢管活性粉末混凝土轴压力学性能研究[J]. 建筑结构学报, 2005, 26(4): 52. DOI:10.3321/j.issn:1000-6869.2005.04.008 |
| [5] |
吴炎海, 林震宇. 钢管活性粉末混凝土轴压短柱受力性能试验研究[J]. 中国公路学报, 2005, 18(1): 57. DOI:10.3321/j.issn:1001-7372.2005.01.011 |
| [6] |
范重, 王倩倩, 李振宝, 等. 大直径钢管混凝土柱抗震性能试验研究及承载力计算[J]. 建筑结构学报, 2017, 38(11): 34. |
| [7] |
LUBLINER J, OLIVER J, OLLER S, et al. A plastic-damagemodel for concrete[J]. International Journal of Solids and Structures, 1989, 5: 299. |
| [8] |
ZHENG Wenzhong, LUO Baifu, WANG Ying. Compressive and tensile properties of reactive powder concrete with steel fibers at elevated temperatures[J]. Construction & Building Materials, 2013, 41: 844. |
| [9] |
安明喆, 杨志慧, 余自若, 等. 活性粉末混凝土抗拉性能研究[J]. 铁道学报, 2010, 32(1): 54. DOI:10.3969/j.issn.1001-8360.2010.01.010 |
| [10] |
余自若, 安明喆, 王志建. 双轴压下活性粉末混凝土的力学性能[J]. 建筑材料学报, 2011, 14(3): 305. DOI:10.3969/j.issn.1007-9629.2011.03.004 |
| [11] |
马亚峰.活性粉末混凝土(RPC200)单轴受压本构关系研究[D].北京: 北京交通大学, 2006 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1081079
|
| [12] |
菅伟.圆钢管活性粉末混凝土短柱轴压性能试验与设计方法[D].哈尔滨: 哈尔滨工业大学, 2016 JIAN Wei. Experimental research and design method on behavior of reactive powder concrete-filled circular steel tube columns under axial compression[D].Harbin: Harbin Institute of Technology, 2016 |
| [13] |
ELLOBODY E, YOUNG B. Nonlinear analysis of concrete-filled steel SHS and RHS columns[J]. Thin-walled Structures, 2006, 44: 919. DOI:10.1016/j.tws.2006.07.005 |
| [14] |
田志敏, 张想柏, 冯建文, 等. 钢管超高性能RPC短柱的轴压特性研究[J]. 地震工程与工程振动, 2008, 28(1): 99. |
| [15] |
吴炎海, 林震宇, 孙士平. 活性粉末混凝土基本力学性能试验研究[J]. 山东建筑工程学院学报, 2004, 19(3): 7. DOI:10.3969/j.issn.1673-7644.2004.03.003 |
| [16] |
张晓东, 仲伟群. 高强混凝土的力学性能[J]. 哈尔滨建筑大学学报, 1996, 29(3): 62. |
| [17] |
李海艳, 王英, 郑文忠. 高温后活性粉末混凝土横向变形性能[J]. 哈尔滨工业大学学报, 2013, 45(4): 1. LI Haiyan, WANG Ying, ZHENG Wenzhong. Transverse deformation properties of reactive powder concrete after exposure to high temperature[J]. Journal of Harbin Institute of Technology, 2013, 45(4): 1. DOI:10.3969/j.issn.1009-1971.2013.04.001 |
| [18] |
罗华, 季文玉, 闫志刚, 等. 加载方式对钢管活性粉末混凝土短柱抗压性能影响的研究[J]. 铁道学报, 2014, 36(9): 105. DOI:10.3969/j.issn.1001-8360.2014.09.20 |
| [19] |
闫志刚, 张武奇, 安明喆. 圆钢管RPC短柱轴心受压极限承载力分析[J]. 北京工业大学学报, 2011, 37(3): 361. |
| [20] |
杨吴生.钢管活性粉末混凝土力学性能及其极限承载力研究[D].长沙: 湖南大学, 2003 http://cdmd.cnki.com.cn/Article/CDMD-10532-2004034047.htm
|
| [21] |
钢管混凝土结构设计与施工规程: CECS 28: 2012[S].中国计划出版社, 2012
|
 2018, Vol. 50
2018, Vol. 50


