2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090;
3. 哈尔滨工业大学 土木工程学院,哈尔滨 150090;
4. 英国利物浦大学 建筑学院,利物浦 L693BX
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China;
3. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China;
4. School of Architecture, University of Liverpool, Liverpool L693BX, the United Kingdom
装配式混凝土结构由预制混凝土构件拼装组合形成,是中国当前正在进行的建筑工业化进程中主要支撑结构形式之一[1-2].装配式混凝土结构正逐步由形式单一的多高层住宅建筑向公共建筑和商业建筑等拓展,这类要求大跨度、大空间的工业化建筑对于预制预应力混凝土双T板等大型先张预制构件提出了性能需求[3-5].为满足裂缝控制和变形控制要求,这种大型预制构件均按全预应力的思路基于一级裂缝控制等级施加了预应力,但其采用的预应力筋仍然沿用了中国曾大量采用的中小预制构件配置预应力钢丝的传统思路,其主导预应力筋主要为ϕ7的螺旋肋钢丝和较小公称直径钢绞线(如12.9mm的1×3钢绞线及9.5、12.7mm的1×7钢绞线等),在相同条件下构件配筋密集、有效高度较低、施工张拉程序较繁琐,降低了预制构件的生产效率,一定程度上阻碍了大型预制构件的推广应用.
采用低松弛1860级15.2、17.8及21.6mm等较大公称直径的钢绞线作为主导预应力筋,有利于保证构件的正截面承载力和降低施工难度,促进中国实现大跨度大空间的工业化建筑结构的发展[6-7].较大直径钢绞线作为先张预应力筋,需在构件端部更长范围内传递预应力效应,且钢绞线与混凝土也需更可靠的锚固.显然,较大直径钢绞线的黏结锚固机理和设计方法是其在大型预制构件中合理应用需解决的瓶颈问题之一.
20世纪90年代,中国相关学者较系统开展了钢绞线混凝土黏结性能试验研究和理论分析,在黏结强度、黏结滑移本构关系、传递长度和锚固长度等方面均取得了较多成果,部分研究成果已纳入了GB 50010—2010《混凝土结构设计规范》.徐有邻等[8]通过对公称直径13.3、15.6mm的钢绞线进行拉拔试验,分析了保护层厚度、配箍率、混凝土强度等对钢绞线黏结性能的影响,发现钢绞线在受力前期接近光圆钢筋,受力后期类似于变形钢筋且锚固延性优于带肋钢筋.国际上,对于钢绞线混凝土黏结性能十分重视,且较早开展了不同直径钢绞线混凝土黏结性能研究.Salmons等[9]通过相关的钢绞线黏结强度锚固试验研究了钢绞线公称直径、混凝土强度、锚固长度等几个因素对黏结强度产生的影响;Gustavson[10]是针对混凝土强度、混凝土密度以及钢绞线外形形状3个方面的因素进行了研究;Dang等[11]基于试验数据提出了黏结应力-滑移模型,研究了钢绞线的应力分布,发现了黏结应力沿埋置长度不均匀分布的特征;Lundgren等[12]进一步分析了钢绞线外形对其黏结性能的影响.虽然,国内外均有针对性地开展了钢绞线混凝土间黏结性能试验与理论分析,并基于相关试验和分析结果确定了钢绞线锚固长度,提出了锚固措施等,但其研究对象主要是较小直径和常规直径的钢绞线,对预应力双T板等大型预制构件中逐步采用的15.2、17.8及21.6mm等较大直径钢绞线黏结性能,特别是黏结破坏机理及其相关影响因素,尚需系统研究.
为此,应聚焦较大直径钢绞线混凝土间黏结性能研究,开展模型试验和理论分析,获得黏结机理与黏结破坏模式;捕捉影响黏结性能的关键参数,进行锚固长度可靠性分析,进而提出基于黏结强度的较大直径钢绞线的极限锚固长度.从而,为以较大直径钢绞线为主导预应力筋的大型先张预应力构件的推广应用提供理论支撑.
1 拔出试验 1.1 试验参数钢绞线黏结锚固性能试验采用拔出试验方法,结合大型预制构件通常采用的设计强度等级为C50混凝土,公称直径为15.2、17.8、21.6mm的三类钢绞线进行.试验考虑了3个主要参数:1)由于保持一定保护层厚度可提高混凝土的抗劈裂能力,保证黏结强度的发挥,且保护层厚度体现了中心拉拔和偏心拉拔受力状态,因此,将保护层厚度作为第一个基本参数;2)由于箍筋能限制可能发生的径向裂缝发展,提高黏结强度,因此,将体积配箍率作为第二个基本参数;3)由于不同埋置长度上黏结应力分布和饱满程度差异影响着黏结强度的充分发挥,因此,将埋置长度作为第三个基本参数.
本试验设计制作了4组拔出试件,各试件截面尺寸均取100 mm×100 mm.其中,试验组A主要分析保护层厚度对钢绞线黏结性能的影响;试验组B主要分析配箍率对钢绞线黏结性能的影响;试验组C主要分析埋置长度对钢绞线黏结性能的影响;试验组D为公称直径21.6 mm的1×7钢绞线,以验证由A、B、C组公称直径15.2、17.8 mm的1×7钢绞线所揭示的黏结机理对公称直径21.6 mm钢绞线的适用性.拔出试件尺寸及配筋和试件设计参数分别见图 1和表 1.
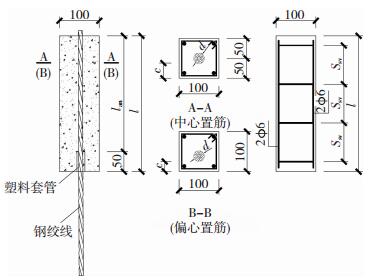
|
图 1 拉拔件尺寸及其配筋图(mm) Figure 1 Geometric dimensions and reinforcement of specimens(mm) |
| 表 1 试件设计参数 Table 1 Design parameters of specimens |
其中,每一试件编号由两个完全相同的试件组成,即试件总数为32个;d为钢绞线公称直径;d0为钢绞线折算直径,表示与钢绞线公称面积相同的等效圆的直径,即d0=2(Ap/π)1/2,其中Ap为钢绞线公称面积;c为保护层厚度,是指试件横截面各侧面外边缘至钢绞线外表面距离的最小值;由于各试件中箍筋直径与肢数均相同,则体积配箍率用箍筋间距表达.钢绞线沿试件长度方向通长布置,为消除试验时加载端垫块对混凝土局部挤压所造成的影响,加载端局部50 mm通过套管使其无黏结,其埋置长度为试件长度l减去50 mm;自由端钢绞线外露出试件端面长度为40 mm.
1.2 材料性能试件采用设计强度等级为C50的商品混凝土,依据与拉拔试件同条件制作和养护的5组15个立方体试块,获得的混凝土抗压强度实测值平均值为fcu=57 N/mm2(标准差为3.636 N/mm2),混凝土抗拉强度实测值为ft=3.65 N/mm2,混凝土的弹性模量Ec=3.34×104 N/mm2.各试件内布置的4根纵向架立钢筋与箍筋均由HPB300级直径为6 mm光圆钢筋制作.采用的1860级与1770级两个级别的三类钢绞线, 物理力学性能见表 2.
| 表 2 钢绞线物理力学性能 Table 2 Physical and mechanical properties of strands |
拔出试验通过四柱式辅助加载框,用1 000 kN万能拉伸试验机进行.试件加载端的外露钢绞线穿过辅助加载框下钢板中心预留孔夹持在试验机下夹头上;辅助加载框的上钢板中心布置加载钢棒,将力传感器固定在加载框上钢板下方,使其上端穿过上钢板预留孔夹持在试验机上夹头.固定在辅助加载框上钢板的位移计用于实测钢绞线自由端的滑移,加载端滑移通过拉伸试验机自动测试,加载与测量装置见图 2.
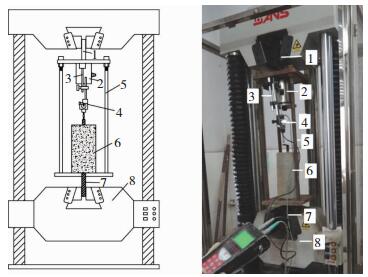
|
1-加载钢棒;2-力传感器;3-位移计托架;4-位移计;5-四柱式辅助加载框;6-拉拔试件;7-加载端钢绞线;8-拉伸试验机 图 2 加载与测量装置 Figure 2 Setup and measuring system |
试验加载制度依据标准[13]的要求,每级按预估极限荷载的10%分级加载.除实测滑移外,试验过程中试件的局部破损、表面裂缝等在加载过程中也予以记录.
1.4 试验现象由图 3所示典型试件的拉拔力-滑移关系可知,钢绞线黏结破坏过程可分为4个阶段:第一阶段从开始加载到化学胶结力基本消失,整个过程自由端无滑移;第二阶段钢绞线与混凝土间产生滑动摩擦,摩擦力的大小基本上与滑移量成正相关,直至钢绞线各外丝对其间隙混凝土的机械咬合力的径向分力超过滑动摩擦力,曲线出现明显转折(图 3中的B点),第二阶段峰值点对应的滑移量通常较大,该阶段的力和滑移关系较第一阶段的刚度有一定程度的减小;第三阶段主要表现为更明显的滑移,主要是由于机械咬合力的径向分力随滑移量的增加而持续增大,贡献着主要的黏结应力,力和滑移关系仍表现为正相关,与上一阶段相比其刚度降低明显,该阶段的末端拉拔力将达到第二个峰值,较第一个峰值增大明显,拔出力达到极限值,这主要是外围捻制成型的6根钢丝空隙间的硬化水泥砂浆的裂缝,将随着径向黏结应力和环向劈裂应力的增大而逐步发展;第四阶段,拉拔力和滑移关系开始下降,此时外围钢丝硬化水泥砂浆破碎,随钢绞线逐步拔出.
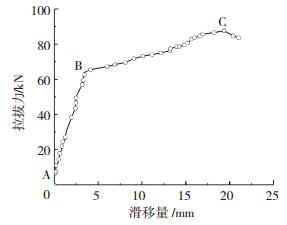
|
图 3 典型试件(B-3-1)拉拔力-滑移关系 Figure 3 Pull-out force-slip curve of typical specimen(B-3-1) |
试验结果表明,依据保护层厚度和配箍率不同,其破坏现象见图 4、5,钢绞线拔出试件的两种主要破坏特征为:一是对于保护层厚度和配箍率较小的试件,随着荷载的持续增加,加载端出现斜裂缝并逐渐向自由端扩展,最终可形成纵向的劈裂裂缝,这种破坏在本次试验所占比例较小(4/32);二是对于保护层厚度或配箍率较大的试件,表面未开裂但钢绞线拔出的破坏,这主要是内部裂缝发展过程中,其径向劈裂趋势受到箍筋约束作用,这是本次试验的主要破坏特征.

|
图 4 保护层厚度影响 Figure 4 Cover effect |

|
图 5 配箍率影响 Figure 5 Effect of volumetric stirrup ratio |
对于不同埋置长度拔出的试件,埋置长度相对较小的试件自由端初次滑移荷载要明显小于埋置长度较大的试件;随着拔出力增大,埋置长度较大的试件加载端易于出现裂缝并逐渐向自由端延伸,而埋置长度较小的试件,在加载全过程中,直到钢绞线拔出,试件表面未开裂,这与黏结应力沿埋置长度呈不均匀分布直接相关,典型试件破坏见图 6.

|
图 6 埋置长度影响 Figure 6 Effect of anchoring length |
结合试验现象和钢绞线黏结破坏机理分析可知,6根外丝形成的钢绞线外表面的类螺旋状肋,随拔出发展的挤压力的径向分力使其周围混凝土环向受拉,依据配箍率和保护层厚度的不同,钢绞线混凝土发生两种黏结破坏:
1) 混凝土劈裂破坏.若保护层厚度较薄或配箍率较小,当环向拉力的大小大于混凝土抗拉强度后,混凝土横向变形持续发展,邻近钢绞线表面的混凝土裂缝由内而外延伸到构件表面,为脆性劈裂破坏.
2) 拔出破坏.具有适中的保护层厚度和配箍率时,钢绞线内部的劈裂裂缝不会延伸到试件表面,钢绞线外围钢丝间的硬化水泥砂浆的咬合齿断裂,在受力后期产生较大滑移,钢绞线拔出,为近似延性破坏.
2.2 平均黏结强度按试件破坏时各试件拉拔试验结果,依据力的平衡方程,可得各级拉拔荷载下沿埋置长度分布的钢绞线混凝土间黏结应力平均值τ,当拉拔荷载达到峰值时,对应的黏结应力最大,认为达到了黏结强度τu,各试件黏结强度见表 3.
| 表 3 黏结强度 Table 3 Bond strength |
不同试验参数对钢绞线混凝土黏结强度影响程度不同,可结合试验结果,获得考虑各关键参数影响的黏结强度表达式.钢绞线混凝土保护层厚度的影响由本次试验的A组试件予以体现,试件黏结应力-滑移曲线见图 7(a).当配箍率、钢绞线公称直径、混凝土强度、埋置长度等条件相同时,黏结强度随保护层厚度增大而增大.显然,钢绞线周围混凝土的“握裹力”对内裂缝的发展具有约束作用,可使钢绞线与混凝土间的黏结更有效地发挥,破坏时可发生更大的滑移.
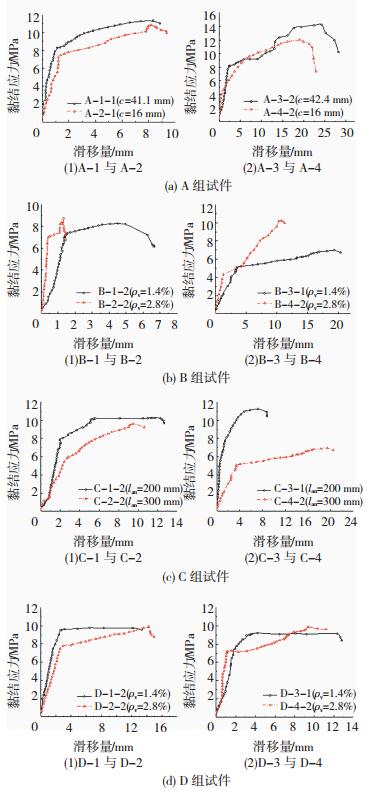
|
图 7 A组~D组试件的典型黏结应力-滑移曲线 Figure 7 Bond stress-slip curves of group A-D |
考虑到保护层厚度与钢绞线折算直径直接相关,且不同混凝土强度条件下黏结强度也差异较大,为此,以相对保护层厚度(保护层厚度与钢绞线折算直径之比)为关键参数,获得了相对黏结强度(黏结强度与混凝土抗拉强度之比)的关系,基于A组试件试验结果,可得
| $ \frac{{{\tau _{\rm{u}}}}}{{{f_{\rm{t}}}}} = 0.289\frac{c}{{{d_0}}} + {e_1}, $ | (1) |
式中:相对保护层厚度c/d0的系数为正体现了其与黏结强度成正相关; 常数项e1代表其他因素对黏结强度的影响,按本组数据,e1为2.966.
配箍率对黏结强度的影响由本次试验的B组试件予以体现,典型黏结应力-滑移曲线见图 7(b),可知配箍率对钢绞线黏结性能影响与保护层厚度有相似性,当保护层厚度、钢绞线公称直径、混凝土强度、埋置长度等条件相同时,黏结强度随配箍率的增大而增大.这是体现出箍筋贡献了环向拉应力,同时其侧向约束改善了钢绞线周围混凝土的“握裹力”,限制了混凝土劈裂裂缝的发展,在提供额外的抵抗径向扩张力的同时,钢绞线横肋横向力的纵向分量即机械咬合力也能增大,故黏结应力增大.由于箍筋能约束劈裂裂缝的发展,锚固失效时滑移量更大.即,随配箍率增大,黏结强度和极限滑移均增大.
相似地,以相对箍筋间距(箍筋间距与钢绞线折算直径之比)为关键参数,获得了相对黏结强度的关系,基于B组试件试验结果,可得
| $ \frac{{{\tau _{\rm{u}}}}}{{{f_{\rm{t}}}}} = 1.675\frac{{{d_0}}}{{{S_{{\rm{sv}}}}}} + {e_2}, $ | (2) |
式中:相对箍筋间距Ssv/d0的系数为正体现了其与黏结强度成负相关;常数项e2代表其他因素对黏结强度的影响,按本组数据,e2为2.251.
埋置长度对黏结强度的影响由本次试验的C组试件予以体现,典型黏结应力-滑移曲线关系见图 7(c).当保护层厚度、配箍率、钢绞线公称直径、混凝土强度等条件相同时,黏结强度随埋置长度的增大而减小.这是因为混凝土骨料分布不均匀导致了黏结应力沿钢绞线埋置长度的不均匀分布,加载端黏结应力较大,自由端黏结应力较小甚至降低为零,尤其是对于本试验采用的有限长度、有限截面的试件,这种不均匀性将更为突出.这将造成,在一定埋置长度范围内,较大埋置长度试件破坏时难以完全发挥相同条件下黏结应力均匀分布时所具有的黏结能力,从而使黏结强度也随着埋置长度的增加而减小.
相似地,以相对埋置长度(埋置长度与钢绞线折算直径之比)为关键参数,获得了相对黏结强度的关系,基于C组试件试验结果,可得
| $ \frac{{{\tau _{\rm{u}}}}}{{{f_{\rm{t}}}}} = 23.462\frac{{{d_0}}}{{{l_{{\rm{an}}}}}} + {e_3}, $ | (3) |
式中:相对埋置长度的倒数d0/lan的系数为正体现了相对埋置长度与黏结强度成负相关;常数项e3代表其他因素对黏结强度的影响,按本组数据,e3为1.477.
由于3个试验参数中相对保护层厚度、相对埋置长度以及相对箍筋间距相互独立,综合考虑式(1)~(3),结合试验的实测结果,可得考虑3个关键参数影响的钢绞线混凝土黏结强度为
| $ \frac{{{\tau _{\rm{u}}}}}{{{f_{\rm{t}}}}} = 0.289\frac{c}{{{d_0}}} + 1.675\frac{{{d_0}}}{{{S_{{\rm{sv}}}}}} + 23.462\frac{{{d_0}}}{{{l_{{\rm{an}}}}}} + 0.774. $ | (4) |
式(4)得黏结强度实测值τut与计算值τuc的比值见表 3.配箍率和保护层厚度对21.6 mm钢绞线黏结强度影响见图 7(d),需要说明的是由公称直径15.2 mm和17.8 mm的三组试验数据获得的计算公式对于公称直径21.6 mm钢绞线混凝土黏结强度预测也有较好的适应性.由式(4)得到的黏结强度实测值与计算值之比,τut/τuc平均值1.005,标准差0.097,变异系数0.096,可见实测值与计算值吻合程度较好.
3 基于近似概率法的钢绞线锚固长度以钢绞线与混凝土间黏结应力达到峰值作为控制锚固作用丧失的极限状态.在极限锚固长度lau下,钢绞线达到名义屈服强度的同时钢绞线混凝土间发生黏结失效,按式(4)考虑3个因素影响的黏结强度,以临界锚固长度lau表示埋置长度lan,依据力的平衡条件,可得黏结失效的极限状态方程为
| $ \begin{array}{*{20}{c}} {4\left( {0.774\frac{{{l_{{\rm{au}}}}}}{{{d_0}}} + 0.289\frac{c}{{{d_0}}}\frac{{{l_{{\rm{au}}}}}}{{{d_0}}} + 1.675\frac{{{l_{{\rm{au}}}}}}{{{S_{{\rm{sv}}}}}} + } \right.}\\ {\left. {23.462} \right){f_{\rm{t}}} - {f_{{\rm{py}}}} = 0.} \end{array} $ | (5) |
锚固强度问题的极限状态方程保证了在钢绞线达到名义屈服强度时,钢绞线与混凝土之间不会发生锚固强度破坏,实际锚固长度大于由式(5)确定的极限锚固长度时即可保证钢绞线达到名义屈服强度时,钢绞线与混凝土间不发生黏结锚固失效.若定义式(5)的左侧第一项为抗力R,第二项为效应S.方程中所有物理量均为随机变量并且这些变量之间互相独立,故R及S不拒绝接受为对数正态分布[14].将R与S视为两个综合的基本变量,采用近似法求解.
由统计资料[8]和本试验数据可知各个变量的平均值μ和变异系数δ见表 4.
| 表 4 各变量的统计参数 Table 4 Statistical parameters of variables |
结合式(5),抗力R表达式为
| $ R = 4{\mathit{\Omega }_{\rm{R}}}{L_1}f_{\rm{t}}^0, $ | (6) |
式中:
| $ {\mu _{\rm{R}}} = 12.140 \times \left( {1.174\frac{{{l_{{\rm{au}}}}}}{{{d_0}}} + 23.462} \right), $ | (7) |
| $ {\delta _{\rm{R}}} = \sqrt {0.021 + \frac{{0.011\frac{{l_{{\rm{au}}}^2}}{{d_{\rm{0}}^2}}}}{{{{\left( {1.174\frac{{{l_{{\rm{au}}}}}}{{{d_0}}} + 23.462} \right)}^2}}}} . $ | (8) |
以钢绞线应力达到名义屈服强度,钢绞线与混凝土黏结应力达到峰值的黏结极限状态作为分析钢绞线黏结锚固强度可靠度的基础.即,结构设计时,钢绞线达到名义屈服强度前不应发生其与混凝土间的黏结失效,根据概率论,出现上述黏结极限状态的总概率为
| $ \begin{array}{l} {P_{{f_{\rm{a}}}}} = P\left( {{\sigma _{\rm{s}}} = {f_{{\rm{py}}}},\tau = {\tau _{\rm{u}}}} \right) = \\ \;\;\;\;\;\;\;\;P\left( {{\sigma _{\rm{s}}} = {f_{{\rm{py}}}}} \right)P\left( {\tau = {\tau _{\rm{u}}}\left| {{\sigma _{\rm{s}}} = {f_{{\rm{py}}}}} \right.} \right) = \\ \;\;\;\;\;\;\;\;{P_f}{P_{{f_0}}}. \end{array} $ | (9) |
取锚固承载力失效概率Pfa=4.0×10-5,相应的可靠指标βa=3.95[14].受力端锚固钢绞线应力是由构件正截面承载力设计确定的,故发生钢绞线受力端应力达到最大值(σs=fpy)事件的允许概率和相应的可靠指标应按标准[15]规定,分别取为Pf =6.9×10-4,β=3.2.式(9)可转换为
| $ {P_{{f_0}}} = \frac{{{P_{{f_{\rm{a}}}}}}}{{{P_f}}}. $ | (10) |
由Pfa=4.0×10-5、βa=3.95、Pf =6.9×10-4和β=3.2,可得“在大型预制构件中的钢绞线受力端应力达到最大值”事件已发生的条件下,进而发生“黏结应力达到最大值”事件的允许概率Pf0=5.80×10-2及相应的可靠指标β0=1.57,可作为后续分析的取值,但需要指出的是,相关文献及标准中钢绞线黏结锚固可靠指标偏低,未来有可能将对此进行有针对性的分析,确定其提高后的合理取值.
由于基本变量效应S与抗力R均可认为服从对数正态分布,根据标准[15]钢绞线锚固可靠指标的表达式:
| $ {\beta _0} = \frac{{\ln {\mu _{\rm{R}}} - \ln {\mu _{\rm{s}}}}}{{\sqrt {\delta _{\rm{R}}^2 + \delta _{\rm{s}}^2} }}, $ | (11) |
从而,可得到相对锚固长度表达式:
| $ \ln {\mu _{\rm{R}}} - \ln {\mu _{\rm{s}}} - {\beta _0}\sqrt {\delta _{\rm{R}}^2 + \delta _{\rm{s}}^2} = 0. $ | (12) |
代入R和S的统计数据并加以整理可得:对于1770级钢绞线:
| $ \begin{array}{*{20}{c}} {\ln \left( {1.174\frac{{{l_{{\rm{au}}}}}}{{{d_0}}} + 23.462} \right) - 4.709 - 1.57 \times }\\ {\sqrt {0.028 + \frac{{0.011\frac{{l_{{\rm{au}}}^2}}{{d_{\rm{0}}^2}}}}{{{{\left( {1.174\frac{{{l_{{\rm{au}}}}}}{{{d_0}}} + 23.462} \right)}^2}}}} = 0,} \end{array} $ | (13) |
对于1860级钢绞线:
| $ \begin{array}{*{20}{c}} {\ln \left( {1.174\frac{{{l_{{\rm{au}}}}}}{{{d_0}}} + 23.462} \right) - 4.793 - 1.57 \times }\\ {\sqrt {0.028 + \frac{{0.011\frac{{l_{{\rm{au}}}^2}}{{d_{\rm{0}}^2}}}}{{{{\left( {1.174\frac{{{l_{{\rm{au}}}}}}{{{d_0}}} + 23.462} \right)}^2}}}} = 0.} \end{array} $ | (14) |
因此,混凝土强度等级为C50时按近似概率法可得1770级与1860级钢绞线锚固长度设计值lau分别为107d0和118d0.
将折算直径d0换算为公称直径d,可得在要求可靠度情况下,1770级和1860级1×7的15.2 mm、17.8 mm及21.6 mm公称直径的钢绞线锚固长度设计值分别为94d和104d,分别小于现行规范的设计值113d和119d.
4 结论聚焦公称直径15.2、17.8、21.6 mm三类较大直径钢绞线,以保护层厚度、配箍率及埋置长度为试验参数,设计并制作了32个拔出试件分析了黏结机理和黏结破坏机制,提出了黏结强度计算方法.
1) 保护层厚度、配箍率和埋置长度对所针对的三类较大直径钢绞线黏结强度影响明显.增大相对保护层厚度、减小相对埋置长度及减小相对箍筋间距可提高钢绞线黏结强度.
2) 综合考虑了保护层厚度、箍筋间距、埋置长度因素,通过对试验数据进行回归分析,得到了合理考虑3个相关参数影响的较大直径钢绞线极限黏结强度计算公式.
3) 通过近似概率法,分析了采用设计强度等级为C50的大型预制构件采用的1770级和1860级较大直径钢绞线的锚固极限状态可靠性,结合统计分析得到了满足相应可靠性水平的锚固长度设计值.
| [1] |
王俊, 赵基达, 胡宗羽. 我国建筑工业化发展现状与思考[J]. 土木工程学报, 2016, 49(5): 1. WANG Jun, ZHAO Jida, HU Zongyu. Review and thinking on development of building industrialization in China[J]. China Civil Engineering Journal, 2016, 49(5): 1. |
| [2] |
刘琼, 李向民, 许清风. 预制装配式混凝土结构研究与应用现状[J]. 施工技术, 2014(22): 9. LIU Qiong, LI Xiangmin, XU Qingfeng. Present research and application of precast concrete structure[J]. Construction Technology, 2014(22): 9. |
| [3] |
徐有邻. 住宅建设与混凝土预制构件[J]. 施工技术, 1998, 27(12): 13. XU Youlin. Housing construction and precast concrete elements[J]. Construction Technology, 1998, 27(12): 13. DOI:10.3969/j.issn.1002-8498.1998.12.005 |
| [4] |
徐有邻, 李晓明. 关于我国住宅楼盖结构形式的讨论[J]. 建筑结构学报, 2001, 31(4): 48. XU Youlin, LI Xiaoming. Discussion on the structure forms of residential buildings slabs in China[J]. Building Structures, 2001, 31(4): 48. |
| [5] |
朱筱俊, 庞瑞, 许清风. 全装配式钢筋混凝土楼盖竖向受力性能试验研究[J]. 建筑结构学报, 2013, 34(1): 123. ZHU Xiaojun, PANG Rui, XU Qingfeng. Experimental study on vertical mechanical behavior of new-type precast RC floor[J]. Journal of Building Structures, 2013, 34(1): 123. |
| [6] |
李伟锋. 多丝大直径低松弛PC钢绞线的应用[J]. 铁道建筑技术, 2014, 35(7): 101. LI Weifeng. Application of multistrand large diameter low relaxation PC steel wire[J]. Railway Construction Technology, 2014, 35(7): 101. DOI:10.3969/j.issn.1009-4539.2014.07.026 |
| [7] |
张小鹏, 王象良, 邢怀念, 等. 预应力钢绞线力学性能试验研究[J]. 金属制品, 2016, 42(3): 1. ZHANG Xiaopeng, WANG Xiangliang, XING Huainian, et al. Experimental research on mechanical properties of prestressing steel strand[J]. Metal Products, 2016, 42(3): 1. DOI:10.3969/j.issn.1003-4226.2016.03.001 |
| [8] |
徐有邻, 宇秉训, 朱龙, 等. 钢绞线基本性能与锚固长度的试验研究[J]. 建筑结构, 1996, 26(3): 34. XU Youlin, YU Bingxun, ZHU Long, et al. Experimental study of essential properties of strand and development lengths[J]. Building Structure, 1996, 26(3): 34. |
| [9] |
SALMONS J R, MCCRATE T E. Bond characteristics of untensioned prestressing strand[J]. PCI, 1977, 22(1): 52. DOI:10.15554/pcij |
| [10] |
GUSTAVSON R. Experimental studies of the bond response of three-wire strands and some influencing parameters[J]. Materials & Structures, 2004, 379(2): 96. |
| [11] |
DANG C N, MURRAY C D, FLOYD R W, et al. Analysis of bond stress distribution for prestressing strand by standard test for strand bond[J]. Engineering Structures, 2014, 72(1): 152. |
| [12] |
LUNDGREN K. Steel-encased pull-through tests of seven-wire strands[J]. Chalmers University of Technology, 2002, 2(13): 10. |
| [13] |
混凝土结构试验方法标准: GB/T 50152—2012[S].北京: 中国建筑工业出版社, 2012 Standard for test method of concrete structures: GB/T 50152—2012[S]. Beijing: China Architecture & Building Press, 2012 |
| [14] |
邵卓民, 沈文都, 徐有邻. 钢筋砼的锚固可靠度及锚固设计[J]. 建筑结构学报, 1987, 8(4): 36. SHAO Zhuomin, SHEN Wendu, XU Youlin. The reliability and design for anchorage of reinforcing bars[J]. Journal of Building Structures, 1987, 8(4): 36. |
| [15] |
建筑结构可靠度设计统一标准: GB 50068—2017[S].北京: 中国建筑工业出版社, 2017 Unified standard for reliability: GB 50068—2017[S]. Beijing: China Architecture & Building Press, 2017 |
 2018, Vol. 50
2018, Vol. 50


