2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨150090;
3. 中国建筑上海设计研究院有限公司, 上海200063
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China;
3. China Shanghai Architectural Design & Research Institute Co., Ltd., Shanghai 200063, China
墙板内置无黏结钢板支撑[1-6](简称墙板内置支撑)即文献[3]中提及的无黏结内藏钢板支撑墙板,实质是一种采用墙板做为约束构件的防屈曲支撑[1](buckling restrained brace),墙板可兼做隔墙.墙板和内置支撑间敷设无黏结材料或留置空隙,使支撑能在墙板孔壁内自由伸缩和尽可能承担全部的轴力,外部墙板基本不分担轴力,仅为内置支撑提供侧向约束.墙板内置支撑可做为中心支撑用于支撑钢框架结构中[3].
目前的应用中,墙板采用钢筋混凝土制成[1-3].文献[2]对钢筋混凝土内置无黏结支撑钢框架结构的试验研究表明,由于钢筋混凝土墙板的受弯开裂和冲切破坏,严重劣化了墙板内置支撑钢框架结构的滞回性能.为防止钢筋混凝土墙板的脆性冲切破坏,文献[4-5, 7]对墙板采用双层闭口型钢板-混凝土组合墙板以及组装墙板的新型墙板内置无黏结支撑的拟静力试验均表明,构造合理的新型墙板内置支撑可避免墙板的局部冲切破坏,获得较好的延性和耗能能力.然而,当用于结构中时,上述新型墙板内置支撑能否仍然发挥其较好的抗震性能则不仅与支撑自身性能有关,而且与支撑与钢框架的连接方式、钢框架的构造等因素有关.
为探讨采用新型墙板内置支撑的中心支撑钢框架结构的合理构造等问题,文献[6]对墙板内置单斜形或人字形钢板支撑、梁柱节点刚接或铰接的3个墙板内置支撑钢框架结构进行了拟静力试验研究.但因试验量测内容和获得的数据有限,不能全面考察墙板内置支撑钢框架结构的滞回性能和主要构造对结构受力性能的影响.
除了试验研究,近年来学者开始尝试采用有限元分析来研究结构的抗震性能.为了提高计算效率,直接采用梁单元模拟钢框架[6, 8],将防屈曲支撑采用杆元模拟[6, 9-10],且有些分析中内置支撑钢材本构采用随动强化模型来简化模拟[6],导致分析结果与试验结果并不完全一致[6].也不能真实再现大侧移下支撑及端部连接的受力情况.特别是,这些分析中均未对支撑外围约束构件进行建模,不能体现约束构件侧向约束作用下内置支撑的真实受力特性[6, 8-10].
因此,结合试验[6],本文主要采用壳单元对试验研究中的3个墙板内置支撑钢框架结构试件进行精细模拟,深入考察墙板内置支撑钢框架结构的受力性能.模拟过程中综合考虑了几何、材料和接触等非线性的影响,给出结构的数值模拟方法,分析了结构的滞回性能,塑性发展规律,破坏模式和变形特点.在此基础上探讨了采用梁、杆单元代替壳单元的简化模拟方法,以及人字形形支撑中一根支撑破坏后被撑梁工作机理.
1 试验概况拟静力试验中,3个试件分别为单斜支撑刚接框架、人字形支撑刚接框架和人字形支撑铰接框架,编号依次为BF1、BF2和BF3,一层和二层的层高均为1.5 m,见图 1.
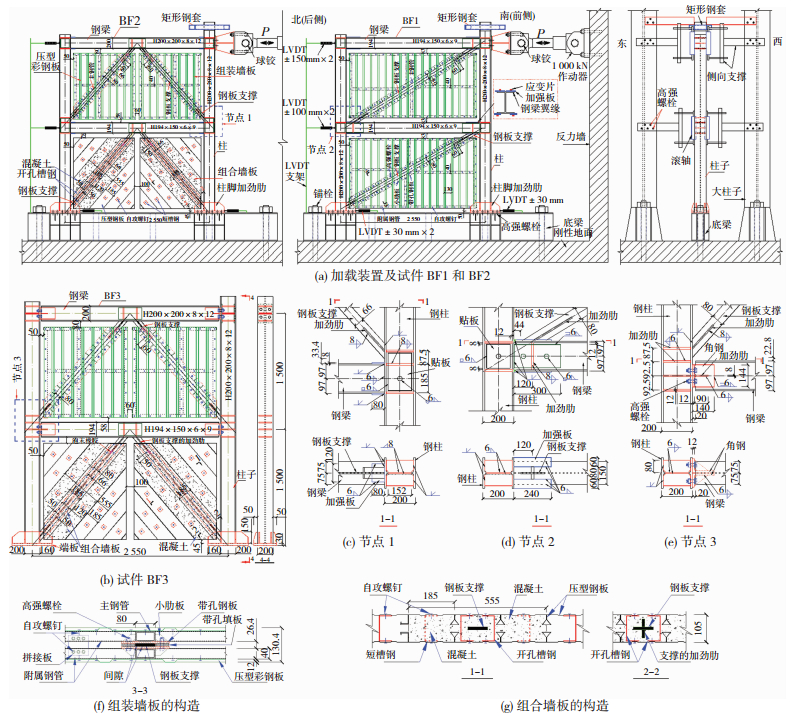
|
图 1 试件的构造及加载装置 Figure 1 Test setup and constructional details of the specimens |
试验加载装置见图 1.水平力由作动器提供.通过控制柱顶水平位移对试件进行往复加载.试验采用两阶段加载[6],第一阶段的弹性阶段每级位移增量为1.5 mm,每级循环一周;墙板内置支撑进入塑性后,每级位移增量为1倍的屈服位移(Δy),每级循环两周,直至最大加载位移为100 mm(对应平均层间侧移角为1/30). Δy对应为支撑屈服时结构的层间水平侧移.根据支撑长度和实测钢材屈服点,加载中,对于BF1,取Δy =5 mm;对于BF2和BF3,取Δy =4 mm.若第一阶段未破坏,则进入第二阶段为加载位移幅值依次为60 mm(10周)、75 mm(10周)和90 mm (若干周)的循环加载,直至破坏.
BF1试件一层和二层均采用组装墙板;BF2和BF3试件一层为组合墙板,二层为组装墙板(图 1).试件的细部构造和测试内容等详见文献[6].本文规定,作动器受拉(拉回试件)和受压(推出试件)时对应的水平承载力分别为正值和负值.
1.2 试验结果在柱顶位移渐增的第一加载阶段中,3个结构中柱顶水平载荷和上层梁端相对柱脚底板的水平位移以及一层和二层层间侧移的滞回曲线见图 2.滞回曲线饱满且较稳定.在最终破坏前,梁柱节点刚接的结构BF1和BF2的主要变形特征和破坏现象类似.详细试验现象见文献[6],概要的变形和破坏现象如下:第一加载阶段,BF1在柱顶加载到±60 mm(平均层间侧移角1/50)时一层和二层非加强区梁端首先出现局部屈曲,约±80 mm时柱脚出现局部屈曲,二层梁靠近加载端的非加强区上翼缘和腹板在往+100 mm(平均层间侧移角1/30)第二圈加载过程中受拉断裂,承载力出现劣化但没有明显下降,第一加载阶段结束.第二加载阶段仅在±60 mm下进行循环往复加载,该阶段钢梁开裂严重,试验在二层支撑受拉断裂后结束.BF2在柱顶加载位移达到±56 mm时一层钢梁非加强区梁端出现局部屈曲,达到±68mm时柱脚出现局部屈曲,达到+100 mm时二层靠近加载端的梁柱节点区域加劲肋和柱翼缘内侧的对接焊缝受拉开裂.第二加载阶段发生局部屈曲位置的钢梁部分截面受拉断裂,前述节点区域钢柱腹板和加劲肋与翼缘连接焊缝受拉断裂,试验终止.试验结束后发现二层南侧支撑屈服段出现局部颈缩现象,趋近受拉断裂.因BF1和BF2在第一加载阶段未破坏,由图 2可知,加载至最大位移时荷载未出现下降.试件BF3第一次往+40 mm加载时加载端梁、柱连接角钢发展塑性变形,导致结构承载力下降;此外一根支撑周围局部混凝土浇筑不密实,支撑提前发生局部破坏,但结构的承载力并没有下降.在-72 mm加载过程中加载端柱子发生严重扭曲(是因第一次加载中柱顶设置的矩形钢套(图 1(a))偏弱,导致钢套不能有效约束柱头的扭转[6]),后续加载中试件只承受拉力且加载位移渐增到+120 mm,为便于和试验对比,本文分析仅给出加载位移72 mm之前的滞回曲线(图 2c).后续加载中,BF3最终因靠近加载处节点中的连接角钢和一层局部破坏处支撑的低周疲劳受拉断裂而破坏[6].
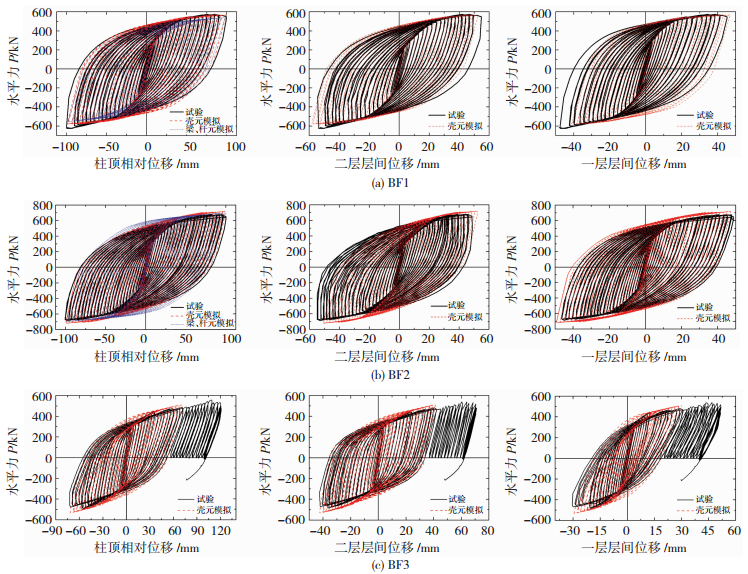
|
图 2 试件第一加载阶段中的柱顶滞回曲线及层间滞回曲线 Figure 2 Hysteresis curves of the specimens at the top of column and in each story in the first load stage |
试验中内置支撑、钢梁和柱子采用Q235B和Q345B钢.钢材的材性实测值见表 1.其他部件的材性实测值详见文献[6].采用ABAQUS建模,因为墙板内置支撑是结构的主要抗侧力构件,能否合理模拟支撑的真实滞回特性是结构数值模拟的关键问题.结合已进行的组合墙板内置无黏结钢板支撑和组装墙板内置钢板支撑的低周往复加载试验[4-5, 7],包括文献[7]的组装墙板内置支撑SPBRB4 (内置支撑与本试验钢板支撑采用同一Q235钢板制作,钢板厚9.68 mm)和文献[5]的组合墙板内置支撑CPBRB3(内置支撑仍采用Q235钢制作,钢板厚11.5 mm).本节对这两种新型墙板内置支撑的滞回性能进行了模拟.试件中,组装墙板中的约束钢板和组合墙板内的混凝土采用实体单元C3D8R模拟,其余部分均用壳单元S4R模拟,外部墙板和内置支撑的初始几何缺陷采用一致缺陷,支撑杆件中部的初弯曲取为支撑长度的1/1 000.钢板支撑的本构关系采用混合强化模型,屈服应力取实测屈服强度,其他主要参数包括强化参数C、γ、Q∞和b;这些参数间的相互关系式:
| $ \begin{array}{l} \alpha = \left( {C/\gamma } \right)\left( {1-{{\rm{e}}^{\gamma \varepsilon pl}}} \right) + {\alpha _1}{{\rm{e}}^{-\gamma \varepsilon pl}}, \\ \;\;\;\;\;\;\;{\sigma ^0} = \sigma \left| {_0 + {Q_\infty }\left( {1-{{\rm{e}}^{ - b\varepsilon pl}}} \right).} \right. \end{array} $ |
| 表 1 构件的材性 Table 1 Material properties of the members |
式中:C和γ控制随动强化部分,α表示背应力(屈服面的中心在应力空间的位置),α1表示初始背应力,C/γ表示背应力最大变化值,γ为背应力随着塑性应变增加的变化率.Q∞和b控制等向强化部分,σ0表示屈服面的大小,σ|0表示等效塑性应变为零时的应力(取为屈服应力),Q∞为屈服面最大变化值,b为屈服面随着塑性应变εpl增加的变化率.
因支撑和墙板间采用接触模拟计算耗时且易导致计算发散[11].为了便于计算收敛且实现内置支撑在加载过程中只屈服不屈曲的特性,支撑与墙板的相互作用通过耦合方式建立.在若干断面上,将二者的横截面在垂直支撑轴向耦合在一起来模拟墙板对支撑的侧向约束作用(即墙板可为支撑提供抗弯刚度);而支撑沿轴向可相对墙板自由变形.
试算表明,当参数C=4 000、γ=37、Q∞=60、b=5时,分析和试验结果大体上吻合(图 3(a)).进一步可见,与随动强化模型相比,混合强化综合考虑了钢材等向强化和随动强化效应,能比较切实地反映内置支撑受力特性(图 3(b)).
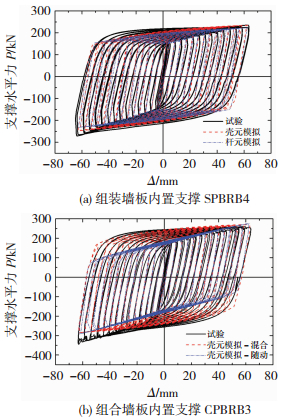
|
图 3 墙板内置支撑的滞回性能 Figure 3 Hysteretic behavior of panel BRBs |
除支撑,其余构件的钢材本构采用双线性随动强化模型,经试算调整,梁、柱切线模量取为0.01E (E为表 1中的弹性模量),其余构件切线模量均取为0.03E,据此得到的分析和试验结果较接近.混凝土本构采用塑性损伤模型,泊松比取0.2.
2.2 结构模型模型严格取试验中实测几何尺寸和材性,详见文献[6].墙板与框架不连接,仅内置支撑端部与框架连接(图 1).以结构BF3为例,梁、柱采用角钢连接,试件的连接和具体建模如图 4所示.因试验中未出现螺栓断裂或滑移等现象,模拟中将角钢与柱在对应螺栓连接的部位直接连接在一起(不额外建立螺栓),考虑螺栓型号等因素,连接区域面积取为24 mm×24 mm;角钢与柱子连接的其余部分建立以柱翼缘为主面、角钢为从属面的接触作用.角钢与框架梁焊接部分也直接连接在一起.
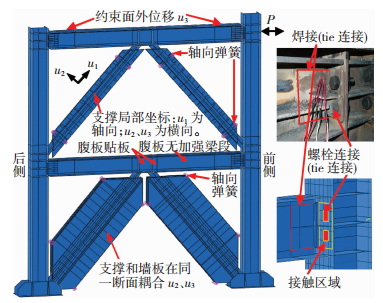
|
图 4 BF3的有限元模型 Figure 4 Finite element model for the BF3 |
考虑靠近支撑的墙板部分对支撑提供主要的侧向约束作用,为简化墙板建模,组装墙板仅建立支撑周围的组装约束构件;组合墙板仅建立支撑周围压型钢板内填有混凝土的部分[6](图 4).因试验中未出现压型钢板相对于混凝土的黏结破坏和滑移,模拟中将压型钢板板肋直接嵌入到混凝土中,钢板支撑的两端直接与梁、柱连接在一起.为限制墙板沿支撑轴向的刚体位移和不影响分析结果,在墙板角点处建立轴向刚度很小的轴向弹簧(图 4).此外,因上述支撑与墙板的耦合做法无法考虑支撑的局部破坏及与墙板的接触作用,对BF3的下层一个支撑采用放大支撑耦合断面间距使支撑可发生局部面外失稳来考虑试验中支撑局部破坏.建立了局部破坏处的接触作用来考虑压型钢板对支撑的约束作用.
2.3 约束条件及荷载按试验采用的约束和加载方式进行模拟[6].对试件的面外位移进行约束,并使柱脚底板固接.此外,对试件BF3,约束加载处柱子顶端截面绕柱子轴线的转动来防止柱子扭转.对BF1和BF2,按试验第一阶段加载的加载制度进行模拟,最大加载位移幅值为100 mm;BF3分析至试验中柱头扭转时停止.将支撑和墙板引入一致初始缺陷,考虑支撑端部通过焊接连接于框架上可能有的初始偏心,适当放大了初弯曲,取为支撑长度的1/750.
3 模拟结果 3.1 滞回曲线分析得到的滞回曲线见图 2.曲线稳定饱满,因试件缺陷尚不能在模拟中完全体现,故结果稍有差别,但总体上吻合较好.在每级位移的两周循环加载中,滞回曲线基本重合,试件未出现明显的承载力和刚度退化,延性和耗能能力良好.
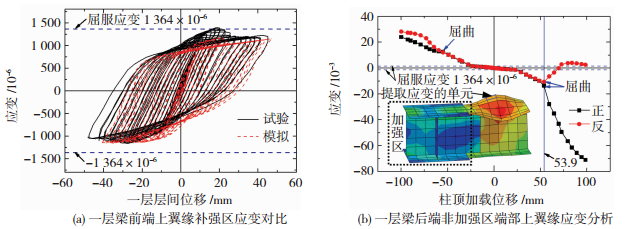
3.2 局部屈曲、屈服和变形试件局部变形见图 5,分析与试验结果基本吻合.可见,在平均侧移角(柱顶位移除以结构高度(3 m))约1/50时,刚接框架钢梁端部的非加强区(即钢梁上没有加强板的区段,见图 1)首先出现局部屈曲,加载位移进一步增大后柱脚出现局部屈曲,梁端盖板加强提高了刚接连接的承载力,同时,塑性区被外移到补强区以外的梁段上,梁柱节点区域基本处于弹性状态.例如,BF1一层梁前端上翼缘加强区域(即钢梁上焊接加强板的区段,见图 1)应变(图 1(a))对比见图 6(a),根据实测屈服应力和弹性模量,得其屈服应变值为1 364×10-6.

|
图 5 试验和模拟中的局部变形 Figure 5 Local deformation in both test and simulation |
|
图 6 BF1中钢梁的应变 Figure 6 Strain of beams in BF1 |
以BF1为例,构件的屈服和屈曲时刻(即柱顶的加载位移)见表 2.可见支撑先屈服,然后梁端屈服,最后柱靠近柱脚部位屈服.且柱和梁端均先屈服再屈曲(表 2).试验中屈服和屈曲判定方法为:支撑骨架曲线的拐点为支撑屈服时刻,据贴于梁端或柱脚翼缘的应变片测值是否超过屈服应变值判定梁、柱的屈服时刻;以目测到的屈曲变形作为梁、柱屈曲时刻.模拟中判定方法为:据各构件Mises应力是否超过屈服应力判定屈服时刻;据梁、柱局部屈曲位置翼缘塑性应变较大单元的正背面的轴向应变值是否反向判定屈曲时刻.如图 6(b)所示,以一层梁后端为例,+53.9 mm时单元正反面应变值开始反向,此时梁端非加强区轻微发展局部屈曲.
| 表 2 BF1中钢构件的屈服和屈曲对应的加载位移 Table 2 Displacements at yielding and buckling of steel members in BF1 |
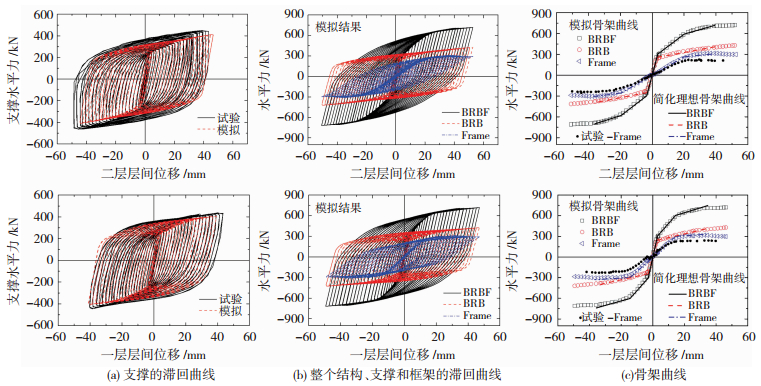
试验和分析均表明,BF1和BF2滞回性能及框架的局部屈曲和塑性发展部位均有类似之处.以BF2为例,因试验中应变片在构件破坏中受到干扰甚至失效,图 7(a)中仅给出支撑可靠的滞回曲线.
|
图 7 BF2滞回曲线和骨架曲线 Figure 7 Hysteretic curves and skeleton curves of BF2 |
因试验测量数据有限,本文研究支撑、框架各自承担的楼层剪力时仅给出模拟结果,支撑剪力由支撑轴力和倾角换算得到.整个结构层间剪力和支撑承担剪力相减便得到框架承担剪力.图 7(b)、7(c)为整个结构(BRBF)、支撑(BRB)和框架(Frame)的滞回曲线和骨架曲线.可见,支撑屈服前结构抗侧刚度几乎由支撑提供,支撑屈服后结构刚度降低,框架分担的剪力逐渐增加.1/50层间侧移角(对应层间侧移30 mm)时,BF2中支撑剪力约为楼层总剪力的55%;BF1中约为45%.
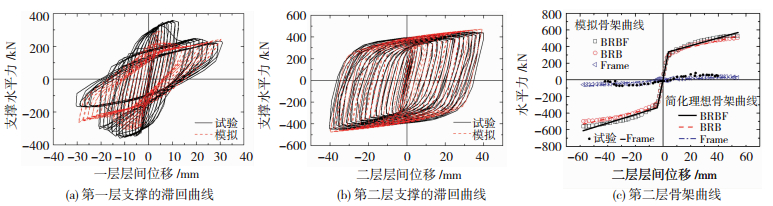
图 8(a)中BF3第一层内前侧(图 4)一根支撑试验中因混凝土浇筑不密实提前局部破坏,模拟中简化为支撑局部无混凝土包裹,因此模拟中支撑较早局部破坏导致承载力降低.但二者整体趋势较一致.且因支撑破坏后框架的抗侧作用增大,整个一层结构抗侧承载力未出现退化(图 2(c)).顶部梁均未局部屈曲,由图 8(b)、8(c)可知,二层支撑可稳定耗能,二层框架基本处于弹性.
|
图 8 BF3滞回曲线和骨架曲线 Figure 8 Hysteretic curves and skeleton curves of BF3 |
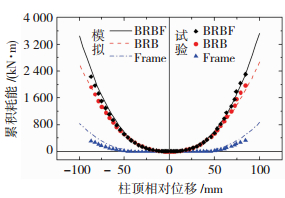
试验和模拟中支撑分别在层间侧移角约1/463~ 1/350和1/416~1/305发生屈服,模拟中钢梁在约1/162~1/129、柱子在靠近柱脚的部位约1/89~1/77中发生屈服.总体上,3个结构中钢框架在约1/50层间侧移角之前塑性发展较少,实现了主要利用支撑集中耗能的设计目的.以BF2为例,整个结构、支撑部分和框架部分的累积耗能见图 9.
|
图 9 BF2的累积耗能 Figure 9 Accumulated energy dissipation of BF2 |
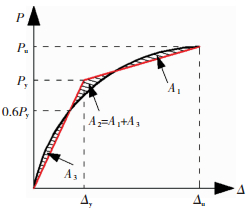
由图 7、8可见,支撑骨架曲线有明显拐点,呈双折线.框架的骨架曲线拐点不明显.借鉴FEMA440[12]推荐的简化理想双折线模型确定方法(图 10),据BF1一层和二层框架分担的层间剪力骨架曲线确定框架的屈服位移分别为-29.2 mm和-29.7 mm,和表 2中梁、柱屈服时刻对比可见用此方法确定的屈服位移介于较早屈服的构件和最晚屈服的构件对应的加载位移之间,可认为是合理的.
|
图 10 框架的理想骨架曲线确定方法 Figure 10 Ways to acquire idealized skeleton curves for frame |
采用该方法,以BF2为例,在框架达到极限承载力前,支撑和框架的骨架曲线均简化为双折线,见图 7(c).整个结构骨架曲线可由支撑和框架的曲线叠加得到.梁柱刚接的结构骨架曲线呈三折线,两个转折点对应支撑和框架屈服.BF1骨架曲线与BF2类似.BF3一层支撑局部破坏并随后导致一层钢梁屈服,二层骨架曲线呈双折线(图 8(c)),支撑屈服出现明显转折点,框架基本保持弹性.
3.5 BF3一根支撑较早发生局部破坏分析BF3第一层层间侧移为正时前侧一根支撑受压(图 4),约1/85层间侧移角后支撑受压承载力可忽略不计(图 11(a)),支撑的受拉承载力也大幅降低.此时一层钢梁靠近跨中位置承受较大的弯矩和剪力,而轴力较小,靠近被撑点处腹板无贴板加强梁段端部截面(图 4)的弯矩图见图 11(b).
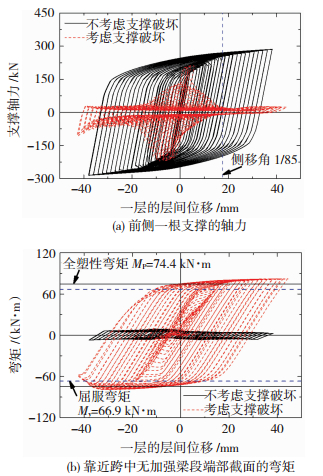
|
图 11 BF3一层内构件的滞回曲线 Figure 11 Hysteretic curves of members in the first story of BF3 |
若近似认为破坏的支撑完全退出工作,则一层钢梁与偏心支撑钢框架中耗能梁段受力类似,在被撑点处支撑大的竖向力作用下,前侧和后侧无加强梁段形成了耗能梁段.分析发现,与破坏支撑同侧的前侧梁段弯曲屈服较严重,梁翼缘在靠近跨中无贴板加强梁段端部先受弯屈服,随着加载位移的增大梁全截面屈服形成塑性铰且翼缘出现局部屈曲.前侧梁段中耗能梁段的净长度a取为铰接梁端至靠近跨中梁腹板无贴板加强处截面间的距离(图 4),根据构造约有a=1.0 m.与常用的两端均刚接的耗能梁段认为反弯点在梁段中部[3]不同,因BF3中梁端为铰接(图 4),弯矩很小,则耗能梁段内反弯点可认为在梁端,且满足如下关系式:
| $ a = 1.0\;{\rm{m > 1}}{\rm{.3}}{\mathit{M}_{\rm{p}}}/{V_1} = 0.58\;{\rm{m, }} $ |
式中:Mp为耗能梁段截面的全塑性弯矩,Vl为梁段的剪切屈服承载力.Mp=Wp×fy=74.4 kNm;Vl=0.58 Aw×fy=166.9 kN.另外,屈服弯矩My=We×fy =66.9 kNm.当a>1.3Mp/Vl时,相当于净长度为2a的两端均刚接的耗能梁段满足2a>2.6Mp/Vl(为弯曲屈服型[3]).因此,此梁段为弯曲屈服型耗能梁段.分析还发现,若不考虑BF3第一层支撑破坏(即两根支撑都不破坏),支撑耗能能力和延性均较好(图 11(a)),且被撑梁保持弹性(图 11(b)).
4 采用梁杆单元的简化模拟分析考虑杆件数量多的结构采用梁、杆单元进行分析会更高效.本节探讨采用梁、杆单元的结构简化模拟方法.钢梁和柱子用梁单元模拟,支撑用杆单元模拟,各构件钢材本构模型均与前述壳元模拟一样.
建模中不考虑框架上的贴板和加劲肋.但试算发现,因柱脚加劲肋较多,对抗侧承载力影响较明显,故将原钢柱在柱脚部分的截面按抗弯、抗剪、轴向刚度近似等效的原则,等效为322.6 mm× 223.5 mm×22 mm×33.3 mm的工字钢截面.考虑每根支撑两端弹性段截面较大而中间屈服段截面较小,用杆单元模拟时只能采用同一截面.故根据支撑弹性阶段抗侧刚度相等的原则确定等效截面面积Aeq,根据屈服承载力相等的原则确定等效屈服点fyeq,具体表达式为:
| $ \begin{array}{l} {A_{{\rm{eq}}}} = \left( {{l_{\rm{p}}} + {l_{\rm{e}}}} \right)/\left( {{l_{\rm{p}}}/{A_{\rm{p}}} + {l_{\rm{e}}}/{\mathit{A}_{\rm{e}}}} \right), \\ \;\;\;\;\;\;\;\;\;\;\;\;{f_{{\rm{yeq}}}} = {A_{\rm{p}}}{f_{\rm{y}}}/{\mathit{A}_{{\rm{eq}}}}. \end{array} $ |
式中:le、lp分别为一根支撑弹性段总长度和屈服段长度;Ae、Ap分别为弹性段和屈服段截面面积.
以BF1和BF2为例,结构滞回曲线对比见图 2.在加载达最大侧移时,分析的承载力在BF1中均略低而在BF2中均略高于试验结果.此外,模拟得到的支撑滞回曲线对比见图 3(a),可见简化的杆元也能近似模拟出支撑的滞回特性.由图 2还可见,相同侧移时,采用梁、杆单元得出的承载力略低于壳元分析结果,这主要是因钢梁和柱子采用梁单元模拟时未能像壳元那样来细致考虑加强区段的补强钢板等导致的.而无论梁、杆单元还是壳元模拟,都会因试件的缺陷和试验中钢材累积损伤等因素尚不能在模拟中完全体现,故分析与试验结果稍有差别.总体上,采用梁、杆单元的简化模型能够合理体现结构的滞回性能,分析得出的承载-变形特点和试验较一致,可参考应用.
5 结论1) 混合强化模型能较切实地反应内置支撑构件的滞回性能.钢梁和柱子采用随动强化模型也能较好地再现框架的滞回性能.除采用壳单元进行分析,对于实际应用中杆件数量较多的结构,可采用梁、杆单元的杆系模型简化结构的建模和分析.
2) 当墙板构造合理无局部破坏时,本文对支撑与墙板间的相互作用通过简化的耦合方式建立,可合理考虑墙板内置支撑整体受力机制,特别是墙板为支撑提供的抗弯能力.
3) 试验和模拟均表明,对梁柱刚接的框架节点区进行补强,可有效提高梁柱节点的承载力,且将钢梁端部的塑性区成功地转移到补强区(也是支撑连于框架的区域)以外的梁端,实现了1/50层间侧移角内梁柱节点区基本处于弹性,且可确保支撑具有稳定的受力性能以及良好的延性和耗能能力.
4) 总体上,三个结构均实现了主要利用支撑进行耗能的设计意图,抗震性能较好.梁柱刚接的结构骨架曲线呈三折线,梁柱铰接的结构呈双折线,均可由支撑和框架的骨架曲线叠加得到.
5) 当人字形支撑中一根支撑受压发生局部破坏后,其承载力将迅速退化,两支撑的竖向不平衡力将使被撑梁在较大的弯剪作用下大幅发展塑性.这使结构实际受力与预期的状况不符,因此,应注意墙板内置支撑的制作质量,避免局部破坏.
| [1] |
XIE Qiang. State the art of buckling-restrained braces in Asia[J]. Journal of Constructional Steel Research, 2005, 61: 727. DOI:10.1016/j.jcsr.2004.11.005 |
| [2] |
CHEN C C, LU L W. Development and experimental investigation of a ductile CBF system[C]// Proceedings of the 4th National Conference on Earthquake Engineering. Palm Springs: Earthquake Engineering Research Institute (EERI), 1990: 575
|
| [3] |
高层民用建筑钢结构技术规程: JGJ 99—2015[S].北京: 中国建筑工业出版社, 2015 Technical specification for steel structure of tall building: JGJ 99—2015[S]. Beijing: China Architecture and building Press, 2015 |
| [4] |
DING Yukun. Cyclic tests for unbonded steel plate brace encased in reinforced concrete panel or light-weight assembled steel panel[J]. Journal of Constructional Steel Research, 2014, 94: 91. DOI:10.1016/j.jcsr.2013.11.009 |
| [5] |
DING Yukun. Cyclic tests of unbonded steel plate brace encased in steel-concrete composite panel[J]. Journal of constructional steel research, 2014, 102: 233. DOI:10.1016/j.jcsr.2014.07.017 |
| [6] |
郑睿.新型墙板内置无黏结支撑钢框架体系抗震性能研究[D].哈尔滨: 哈尔滨工业大学, 2014 ZHENG Rui. Seismic behavior of steel frames with novel types of unbonded steel brace encased in panel[D]. Harbin: Harbin Institute of Technology, 2014 |
| [7] |
李文文.两种墙板内置无黏结钢板支撑的滞回性能与设计方法研究[D].哈尔滨: 哈尔滨工业大学, 2015 LI Wenwen. Hysteretic behavior and design method on two types of wall panel encasing unbonded steel plate brace[D]. Harbin: Harbin Institute of Technology, 2015 |
| [8] |
WIGLE V R, FAHNESTOCK L A. Buckling-restrained braced frame connection performance[J]. Journal of Constructional Steel Research, 2010, 66(1): 65. DOI:10.1016/j.jcsr.2009.07.014 |
| [9] |
PALMER K D. Seismic behavior, performance and design of steel concentrically braced frame systems[D]. Washington : University of Washington, 2012
|
| [10] |
LIN P C, TSAI K C, WU A C, et al. Seismic design and experiment of single and coupled corner gusset connections in a full-scale two-story buckling-restrained braced frame[J]. Earthquake Engineering & Structural Dynamics, 2015, 44(13): 2177. |
| [11] |
丁玉坤, 张耀春. 无粘结内藏钢板支撑剪力墙滞回性能分析[J]. 哈尔滨工业大学学报, 2008, 40(4): 521. DING Yukun, ZHANG Yaochun. Numerical analysis on hysteretic behavior of unbonded steel plate brace encased in reinforced concrete panel[J]. Journal of Harbin Institute of Technology, 2008, 40(4): 521. DOI:10.3321/j.issn:0367-6234.2008.04.003 |
| [12] |
Federal Emergency Management Agency. Improvement of nonlinear static seismic analysis procedures: FEMA-440[S]. Washington, D.C.: Federal Emergency Management Agency, 2005
|
 2018, Vol. 50
2018, Vol. 50


