2. 浙江财经大学 公共管理学院,杭州 310018
2. College of Public Administration, Zhejiang University of Finance & Economics, Hangzhou 310018, China
随着计算机辅助设计技术的突破和建造工艺的提升,越来越多的自由曲面建筑出现在世界各地.该类建筑通常具有独特的造型需求,常规的网格结构难以表达,而已有的自由曲面网格设计方法,要么耗时耗力,要么适用范围有限.为复杂曲面生成符合建筑要求的网格,是现代空间结构研究的难点与热点. Owen[1]总结了经典的网格划分算法,如Delaunay三角法[2]、波前法[3]、映射法[4]及其组合[5-6]等.但这些方法在自由曲面应用中有局限性,无法满足建筑上对网格规整性、流畅性等方面的要求.近些年,在空间结构领域,自由曲面网格生成的研究,取得了一定进展. Su等[7]在波前法中引入主应力线来控制网格走向,生成均匀的三角形网格,但网格的流畅性较差.危大结等[8]和潘炜等[9]将曲面近似展开并结合平面网格生成方法,实现自由曲面的网格划分,但网格质量依赖于曲面近似展开的效果,易产生映射畸变.Zheleznyakova等[10]和Wang等[11]在曲面参数域内利用物理类比和运动模拟优化节点分布,再结合Delaunay法和映射法生成空间网格.但这两种方法只适用于参数化曲面,且难以保证网格的流畅性.Gao等[12]提出了基于引导线偏移的网格划分方法,但只保证了网格在一个方向上的流畅性.针对以上算法存在网格流畅性欠佳、样式单一、适用范围小等问题,本文提出一种自由曲面的自适应网格划分方法,并通过多个复杂曲面的网格生成算例,说明了方法的有效性.
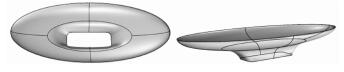
1 几何基础 1.1 曲面表示非均匀有理B样条(non-uniform rational B-splines,简称NURBS)[13],是建筑上常用来表达自由曲面的技术.NURBS曲面是由节点矢量、控制点、权值确定的双参数曲面,能表达任意造型的曲面.但对于复杂的造型,单个NURBS曲面(称为单重曲面)难以表达或不易建模,需要由多个NURBS曲面联合表示,称为多重曲面,见图 1.
|
图 1 由6个曲面组成的多重曲面 Figure 1 A multiple NURBS surface including six surfaces |
1) 等长划分
等长划分是将曲线按给定段数分成相同长度的分段.长度的取值可分为弧长(曲线段长度)和弦长(空间距离).
2) 按长度占比划分
已知各个分段的长度占总长度的比例ei.由式(1)可求得第i段曲线的长度li.已知各段的长度,可求得各个分段点的实际位置,实现曲线的按长度占比划分.
| $ {l_i} = L{e_i}, $ | (1) |
式中L为曲线总长度.
3) 等比划分
等比划分是将曲线按给定段数划分成长度呈比例变化的分段.根据等比公式(2)~(3),可知各分段的长度占比ei,再按长度占比划分曲线,进而实现曲线的等比划分.
| $ L = \frac{{{a_1}\left( {1-{r^n}} \right)}}{{1-r}}, $ | (2) |
| $ {e_i} = \frac{{{a_i}}}{L} = \frac{{\left( {1-r} \right){r^{i-1}}}}{{1-{r^n}}}. $ | (3) |
式中ai是第i段长度,r是比例系数.
2 网格评价针对建筑上常用的四边形网格和三角形网格,采用网格单元形状质量系数评价其规整性,采用节点流畅度指标评价其流畅性.
2.1 规整性评价三角形或四边形的网格单元的形状质量系数为
| $ {q_s} = \left\{ \begin{array}{l} 4\sqrt 3 \frac{S}{{l_{\rm{A}}^2 + l_{\rm{B}}^2 + l_{\rm{C}}^2}}, \;\;\;\;\;\;\;\;\;\;\;\;\;三角形;\\ 4\sqrt[4]{{\frac{{{S_{\Delta {\rm{ABC}}}} \cdot {S_{\Delta {\rm{BCD}}}}}}{{\left( {l_{{\rm{AB}}}^2 + l_{{\rm{AD}}}^2} \right) \cdot \left( {l_{{\rm{AB}}}^2 + l_{{\rm{BC}}}^2} \right)}}}} \times \\ \sqrt[4]{{\frac{{{S_{\Delta {\rm{CDA}}}} \cdot {S_{\Delta {\rm{ABD}}}}}}{{\left( {l_{{\rm{BC}}}^2 + l_{{\rm{CD}}}^2} \right) \cdot \left( {l_{{\rm{CD}}}^2 + l_{{\rm{AD}}}^2} \right)}}}}, 四边形. \end{array} \right. $ | (4) |
式中qs∈(0, 1],且qs越大,单元的形状质量越好[14].
网格整体的规整度由所有网格单元的形状质量系数的平均值qs和标准差σs评定.qs越大,说明网格的形状质量越高;σs越小,说明网格的形状差异越小.当qs越大且σs越小时,网格的规整性越好.
2.2 流畅性评价对于由三角形或四边形组成的结构化网格,所有的内部节点连接着相同数量的杆件,其节点流畅度定义为
| $ {q_{\rm{v}}} = \sqrt {\frac{{\sum\limits_{j = 1}^g {{{\left( {{\beta _{jk}}-\pi } \right)}^2}} }}{g} + \frac{{\sum\limits_{j = 1}^g {{{\left( {{\beta _j}-{\beta _{j + g}}} \right)}^2}} }}{g}} . $ | (5) |
式中:对于三角形网格g=3,四边形网格g=2;βjk是第j边和第k边的夹角, 且k=j+g,而βj是第j边和第j+1(当j+1>2g时,j+1改为1)边的夹角,如图 2所示.qv越小,说明节点的相对边弯折和相对角差异越小,即节点越流畅.当qv=0时,节点最流畅,如图 3所示的4种节点.

|
图 2 夹角示意 Figure 2 Angles diagram |
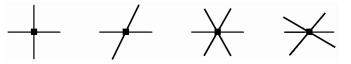
|
图 3 qv=0的节点 Figure 3 Nodes with qv=0 |
网格整体的流畅度由网格内部节点的流畅度平均值qv评定.qv越小,网格流畅性越好.
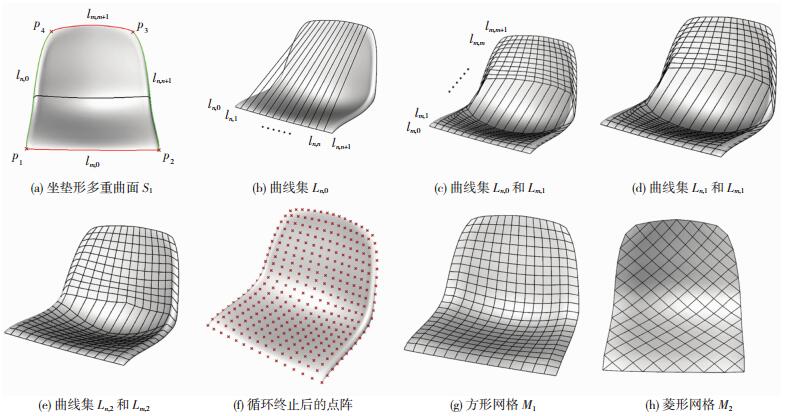
3 网格生成建筑上造型复杂的曲面通常由多个NURBS曲面联合表示,即多重曲面.由于多重曲面的各个子曲面有独立的映射关系,而且子曲面逐个展开后不能保证内部边界的吻合,已有的基于NURBS映射技术或曲面展开技术开发的网格划分方法[9, 10, 15]都难以用于多重曲面的网格划分.为此,提出了与曲面表达方式无关的网格生成方法,可用于单重曲面和多重曲面的网格划分,具体步骤如下(以图 4(a)中的曲面S1为例):
|
图 4 网格生成的各阶段示意 Figure 4 Stages of grid generation |
1) 确定网格划分区域
读入曲面模型,对边界线进行分割或合并,得到4条曲线组成的网格生成区域A.考虑到网格的规整性要求,最好保证这4条曲线中任意两条相连曲线的走势近似垂直.
2) 设置网格生成参数
设定主方向插值曲线数m,次方向插值曲线数n,曲线的分段原则,输出的网格样式等.曲面S1的算例中,设定横向为主方向,m=20,n=13,采用等弧长划分,输出方形网格和菱形网格.
3.2 布置网格点1) 将主方向边界线lm, 0和lm, m+1分别划分为n+1段,连接相同编号的分段点,得到n条曲线.将这n条曲线和两条次方向边界线ln, 0、ln, n+1作为初步的次方向网格曲线,记为Ln, 0,见图 4(b).
2) 将次方向网格曲线Ln, 0划分为m+1段,然后将分段点拉取到曲面上相应的最近点,接着将拉取后编号相同的分段点依次连接成m条曲线.这m条曲线和两条主方向边界线构成了主方向网格曲线,记为Lm, 1,见图 4(c).
3) 类似地,划分主方向网格曲线Lm, 1为n+1段,再拉取分段点到曲面上,并依次连接同一编号的分段点,得到n条曲线.这n条曲线和两条次方向边界线构造成了次方向网格曲线,记为Ln, 1,见图 4(d).
4) 对以上两步进行循环,即利用新得到的主方向曲线Lm, k,生成新的次方向曲线Ln, k(k为循环次数),反之亦然(图 4(e)).根据一次循环前后各网格点的移动距离是否足够小或者循环次数是否到达上限,判断是否结束循环.
5) 循环终止后,曲线Lm, k或Ln, k的分段点组成(m+2)×(n+2)的点阵,即为所求网格点,见图 4(f).
上述分段点和网格线的编号满足以下关系:对于分段点pit, j,上标t, j表示该点所在的曲线为lt, j,下标i为该点的编号,编号相同即指i相同的点;将编号相同的点{pit, j,j=0, 1, …, t+1}按j的大小依次连接,得到曲线ls, i;在第k次循环中,曲线集{ls, i,i=0, 1, …, s+1}构成了Ls, k;t、s =m或n且t≠s.
3.3 后处理将网格点按照特定的规律进行拓扑连接,得到期望的曲面网格样式,如方形网格M1(图 4(g))和菱形网格M2(图 4(h)).再计算网格的杆件长度、单元形状质量系数和节点流畅度,进行规整性和流畅性的评价,如表 1所示.网格M1和M2的qs、qv都在9.7、0.178左右,表明网格的规整性和流畅性较好.
| 表 1 网格评价 Table 1 Grid evaluation |
后续可以在一定的范围内调整m、n的取值,重新按照上述方法生成多组网格,并根据各网格的形状质量系数、节点流畅度和建筑要求,选取最满意的网格作为最终的网格.
4 网格调控通过调整上述算法中的分段原则,实现网格大小的调控,使网格大小与边界条件或曲面形态相适应,从而改善网格的规整性.
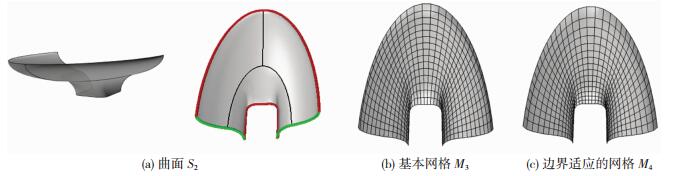
4.1 边界自适应倘若一对边界线的长度相差较大,采用上述方法生成的网格规整性较差.例如,图 5(a)给出的曲面采用上述算法生成的网格M3,如图 5(b)所示,其形状质量系数均值qs仅0.8.为此,调整算法中的曲线分段原则,将等长划分改为等比划分,其他步骤不变,实现网格大小对边界长度的自适应.曲线等比分段的比值r为:
|
图 5 边界适应调整前后的网格对比 Figure 5 Grid comparison before and after adjustment of boundary adaptation |
| $ R = \frac{{{a_n}}}{{{a_1}}} = {r^{n-1}}, $ | (6) |
| $ r = \sqrt[{n-1}]{R}, $ | (7) |
式中:R为相对边界线的长度比,划分曲线Lm, k时,
由此生成的网格M4见图 5(c).由表 1可知,调整后的网格形状质量系数均值较之前提升了6.6%,达到0.853,说明通过在算法中考虑边界线的长度关系,改进了网格的规整性.
4.2 全局自适应对于形态较为复杂的曲面,采用等长原则或等比原则生成的网格,其规整性可能都难以满足要求.为此,调整算法中的曲线分段原则,根据en, ji和em, ij分别对曲线ln, j和lm, i进行按相对位置的曲线划分,而算法中的其他步骤不变,实现网格大小对曲面形态全局的自适应,其中en, ji和em, ij为:
| $ {e_{n, ji}} = \frac{{{l_{m, i}} + {l_{m, i + 1}}}}{{\sum\limits_{i = 0}^m {\left( {{l_{m, i}} + {l_{m, i + 1}}} \right)} }}, \;i \in \left[{0, m} \right], $ | (8) |
| $ {e_{m, ij}} = \frac{{{l_{n, j}} + {l_{n, j + 1}}}}{{\sum\limits_{j = 0}^n {\left( {{l_{n, j}} + {l_{n, j + 1}}} \right)} }}, \;j \in \left[{0, n} \right]. $ | (9) |
式中:en, ji为曲线ln, j上第i段长度占曲线总长的比例;em, ij为曲线lm, i上第j段长度占曲线总长的比例.
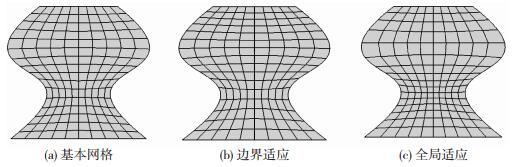
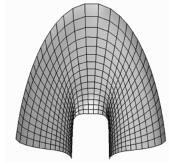
图 6给出了分别采用基本方法、边界自适应调整和全局自适应调整生成的网格.从图中可以明显看出,前两种网格在边界附近较为规整,但在曲面内部“细腰”处较不规整,而第三种网格整体上都较为规整.再对曲面S2进行考虑全局自适应的网格生成,得到的网格M5如图 7所示.结合表 1可知,网格M5的形状质量系数进一步提升到0.885,较网格M3和M4分别提高了10.1%和4.8%.
|
图 6 “细腰”形曲面的网格 Figure 6 Grids for a surface with "a slender waist" |
|
图 7 全局适应的网格M5 Figure 7 Global adaptive grid M5 |
由以上分析可知,经全局适应调整后,网格大小对曲面形态有了更好的适应,网格的规整性有了明显的提高.
5 环形曲面处理以上算法主要针对由4条边界线圈定的曲面区域,而对于仅有两条边界的环形曲面需要做一些局部的调整.以图 8(a)中的曲面为例,先在曲面上画一条连接两条边界线的曲线C(图 8(a)中的竖向绿线),再将曲面看成有两条边界线在C处重合的四边曲面,且以不重合的两条边界线为主方向边界线,其他步骤基本不变,生成由主方向m+2条曲线和次方向n+1条曲线相交而成的(m+2)×(n+1)的点阵,最后按规律将环形点阵连接成网格,如图 8所示.上述过程中,曲线的分段和点阵的连接需要在算法实现上做局部调整,使其适配环形曲面.

|
图 8 环形曲面的网格生成 Figure 8 Grid generation for a toroidal surface |
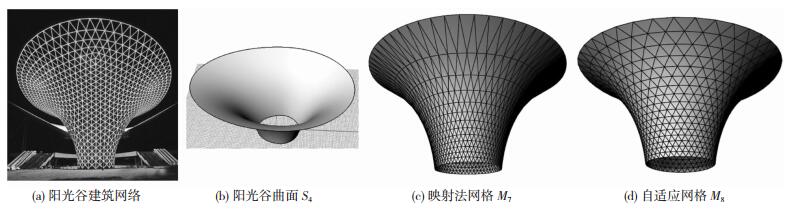
已建成的世博轴阳光谷是比较有代表性的自由曲面建筑,如图 9(a)所示,其网格具有较好的规整性,但网格内存在多个奇异点,即以该点为节点的杆件数目不为6的点.这些奇异点破坏了网格整体的流畅性,降低了建筑美感.基于阳光谷建筑造型,建立相应的曲面模型(图 9(b)),其顶部近似长轴100 m、短轴80 m的椭圆,底部近似长轴30 m、短轴27 m的椭圆,高度40 m,分别采用映射法和本法进行网格划分.由图 9(c)、(d)和表 1可知,映射法划分的网格不存在奇异点,网格流畅性较好(qv=0.092),但网格的规整性明显较差(qs=0.828).而本法生成的网格兼顾了流畅性和规整性,达到了两者的协调统一,更符合建筑审美的要求,其qs=0.988,相较映射法提高了19.3%.
|
图 9 阳光谷曲面的网格生成 Figure 9 Grid generation for the Sun Valley |
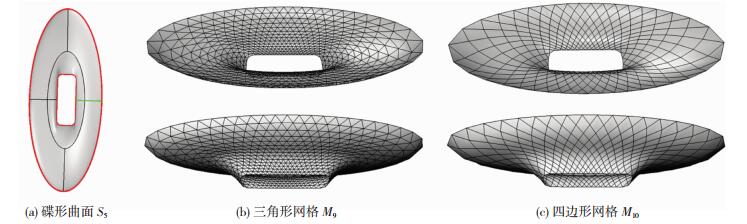
另一个算例是图 1所示的碟形曲面,其最大跨度250 m,宽100 m,高33 m.该曲面由5个子曲面组成,映射法难以适用.在曲面上拟合一条连接两条边界线的曲线,构造适合本法的边界条件,如图 10(a)所示.再采用本法生成网格大小自适应的三角形网格M9和四边形网格M10,如图 10所示.网格M9和M10具有较好的规整性和流畅性,其形状质量系数约8.5,节点流畅度指标约0.21(表 1).
|
图 10 碟形曲面的网格生成 Figure 10 Grid generation for a dish surface |
本文针对多重曲面提出了一种以规整性和流畅性为目标的网格划分方法.通过一系列的几何操作,如曲线分段、分段点连接等,实现了三角形或四边形网格的快速生成;通过调整曲线的分段原则,实现网格大小对曲面形态的自适应;通过调整分段和连线规律,使算法能适用于环形曲面和生成多种样式的网格.算例表明,本法自动化程度高,运算速度快,生成的网格线条流畅、形状规整,无映射变形,符合建筑审美的要求,为网格结构的设计提供了有用的工具.
但需要说明的是,本法的第一步需要以4条曲线构造网格划分区域,并且为了保证网格的规整性,要求这4条曲线中任意两条相连曲线的走势近似垂直.而对于非常复杂的曲面,难以构造合适的网格划分区域,导致生成的网格质量较差,甚至方法失效.
| [1] |
OWEN S.A survey of unstructured mesh generation technology[C]// 7th International Meshing Roundtable. Berlin: Springer-Verlag, 1998: 239
|
| [2] |
WANG B, KHOO B C, XIE Z Q, et al. Fast centroidal Voronoi Delaunay triangulation for unstructured mesh generation[J]. Journal of Computational & Applied Mathematics, 2015, 280(5): 158. DOI:10.1016/j.cam.2014.11.035 |
| [3] |
LO S H. Dynamic grid for mesh generation by the advancing front method[J]. Computers & Structures, 2013, 123(1): 15. DOI:10.1108/02644409810208516 |
| [4] |
CUILLI RE J C. An adaptive method for the automatic triangulation of 3D parametric surfaces[J]. Computer-Aided Design, 1998, 30(2): 139. DOI:10.1016/s0010-4485(97)00085-7 |
| [5] |
熊英, 胡于进, 赵建军. 基于映射法和Delaunay方法的曲面三角网格划分算法[J]. 计算机辅助设计与图形学学报, 2002, 14(1): 56. XIONG Ying, HU Yujin, ZHAO Jianjun. An algorithm of surface triangulation based on mapping and Delaunay method[J]. Journal of Computer-Aided Design & Computer Graphics, 2002, 14(1): 56. DOI:10.3321/j.issn:1003-9775.2002.01.013 |
| [6] |
FREY P J. 3D Delaunay mesh generation coupled with an advancing-front approach[J]. Computer Methods in Applied Mechanics & Engineering, 1998, 157(1): 115. DOI:10.1016/s0045-7825(97)00222-3 |
| [7] |
SU Liang, ZHU Shunlai, XIAO Nan, et al. An automatic grid generation approach over free-form surface for architectural design[J]. Journal of Central South University, 2014, 21(6): 2444. DOI:10.1007/s11771-014-2198-7 |
| [8] |
危大结, 舒赣平. 自由曲面网格的划分与优化方法[J]. 建筑结构, 2013, 43(19): 48. WEI Dajie, SHU Ganping. Mesh generation and optimization method for free-form surface grid[J]. Building Structure, 2013, 43(19): 48. DOI:10.19701/j.jzjg.2013.19.011 |
| [9] |
潘炜, 吴慧, 李铁瑞, 等. 基于曲面展开的自由曲面网格划分[J]. 浙江大学学报(工学版), 2016, 50(10): 1973. PAN Wei, WU Hui, LI Tierui, et al. Grid generation on free-form surface based on surface flattening[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(10): 1973. DOI:10.3785/j.issn.1008-973X.2016.10.018 |
| [10] |
ZHELEZNYAKOVA A L. Molecular dynamics-based triangulation algorithm of free-form parametric surfaces for computer-aided engineering[J]. Computer Physics Communications, 2015, 190: 1. DOI:10.1016/j.cpc.2014.12.018 |
| [11] |
WANG Qisheng, GAO Boqing, LI Tierui, et al. A triangular mesh generator over free-form surfaces for architectural design[J]. Automation in Construction, 2018, 93: 280. DOI:10.1016/j.autcon.2018.05.018 |
| [12] |
GAO Boqing, LI Tierui, MA Teng, et al. A practical grid generation procedure for the design of free-form structures[J]. Computers & Structures, 2017(10): 196. DOI:10.1016/j.compstruc.2017.10.006 |
| [13] |
PIEGL L, TILLER W. 非均匀有理B样条[M]. 2版. 北京: 清华大学出版社, 2010: 86.
|
| [14] |
丁慧, 罗尧治. 自由形态网壳结构网格生成的等参线分割法[J]. 浙江大学学报(工学版), 2014, 48(10): 1795. DING Hui, LUO Yaozhi. Isoparametric line dividing grid generation method for free-form lattice shells[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(10): 1795. DOI:10.3785/j.issn.1008-973X.2014.10.012 |
| [15] |
王奇胜, 李铁瑞, 吴慧, 等. 基于映射技术和双向等分的自由曲面网格生成方法[J]. 建筑结构学报, 2018(7): 18. WANG Qisheng, LI Tierui, WU Hui, et al. Grid generation for free-form surface based on mapping technique and bidirectional equal-division[J]. Journal of Building Structures, 2018(7): 18. DOI:10.14006/j.jzjgxb.2018.07.003 |
 2018, Vol. 50
2018, Vol. 50


