引用本文

池斌, 王凤来, 张志铭, 杨旭. 配筋砌块砌体剪力墙受剪承载力预测方法[J]. 哈尔滨工业大学学报, 2018, 50(12): 156-164. DOI: 10.11918/j.issn.0367-6234.201805144.

CHI Bin, WANG Fenglai, ZHANG Zhiming, YANG Xu. Shear capacity prediction of reinforced concrete block masonry walls[J]. Journal of Harbin Institute of Technology, 2018, 50(12): 156-164. DOI: 10.11918/j.issn.0367-6234.201805144.

基金项目

国家重点研发计划(2016YFC0701502)

作者简介

池斌(1992—)，男，博士研究生;
王凤来(1971—)，男，教授，博士生导师

通信作者

王凤来，wflai@sina.com

文章历史

收稿日期: 2018-05-25

Abstract Full text Figures/Tables PDF

配筋砌块砌体剪力墙受剪承载力预测方法

池斌¹, 王凤来^1,2,3, 张志铭¹, 杨旭¹

1. 哈尔滨工业大学土木工程学院，哈尔滨150090;
2. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学)，哈尔滨 150090;
3. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学)，哈尔滨150090

收稿日期: 2018-05-25

基金项目: 国家重点研发计划(2016YFC0701502)

作者简介: 池斌(1992—)，男，博士研究生;
王凤来(1971—)，男，教授，博士生导师

通信作者: 王凤来，wflai@sina.com

摘要: 为建立配筋砌块砌体剪力墙受剪破坏的力学模型和受剪承载力计算方法，根据配筋砌块砌体剪力墙受剪破坏试验特征，考虑灌芯砌块砌体材料受压过程的软化效应，提出了基于软化拉压杆模型的配筋砌块砌体剪力墙受剪承载力预测方法.通过国内外54片配筋砌块砌体剪力墙受剪试验数据对软化拉压杆模型合理性进行验证，并将其预测结果与国内外相关建议公式计算值进行对比分析.研究结果表明：软化拉压杆模型计算得到的配筋砌块砌体剪力墙受剪承载力与试验结果吻合较好，其预测值相较国内外相关建议公式计算值更接近于试验值，同时变异系数较小；而且此模型具有明确的力学模型，能够较好反映剪跨比不大于2.0的配筋砌块砌体剪力墙的剪切传力机理.

关键词: 配筋砌块砌体剪力墙拉压杆模型受剪承载力软化系数

Shear capacity prediction of reinforced concrete block masonry walls

CHI Bin¹, WANG Fenglai^1,2,3, ZHANG Zhiming¹, YANG Xu¹

1. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China;
2. Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, Harbin 150090, China;
3. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China

Abstract: To establish a mechanical model and shear bearing capacity calculation method for reinforced concrete masonry walls, a prediction method based on the analysis of the shear failure test characteristics of reinforced concrete masonry walls was proposed, in which the softened strut-and-tie model was adopted and the softening effect of concrete block masonry under compression was considered. The rationality of softened strut-and-tie model was verified by the 54 existing tested reinforced concrete block masonry walls failed in shear, and the prediction results were compared with those of relevant formulas at home and abroad. The research results show that good agreement is achieved between the prediction results and tested results, and the prediction results are closer to the tested results than those of relevant formula with a lower coefficient of variation value.Furthermore, this model has a clear and definite mechanical model and it can reasonably reveal the shear failure mechanism of reinforced concrete block masonry walls with span-to-depth ratios no greater than 2.0.

Keywords: reinforced concrete block masonry shear wall strut-and-tie model shear capacity softened coefficient

配筋砌块砌体剪力墙结构体系是由混凝土空心砌块、砂浆、灌芯混凝土和钢筋组成的新型承重结构体系，近年来国内外研究成果和工程实践证明该类结构体系表现出类似于钢筋混凝土剪力墙结构体系的抗震性能，其整体性和受力性能优于传统砌体结构，在世界范围内获得广泛应用^[1].配筋砌块砌体剪力墙作为该类体系中重要的竖向受力构件，其受力性能和破坏特征一直备受国内外学者关注.在实际工程应用和地震灾害过程中发现，剪跨比小于2.0的配筋砌块砌体剪力墙多发生剪切破坏且破坏表征突然性和脆性，目前为止对配筋砌块砌体剪力墙的受剪破坏机理仍没有定论.近年来，为提高配筋砌块砌体剪力墙受剪承载力计算的准确性，国内外学者开展了相关的试验和理论研究.试验方面，国内外学者针对目前常用的290 mm(陈君军^[2]、赵艳等^[3])、190 mm(Seifeidin等^[4]、EI-Dakhakhni等^[5]、姜洪斌等^[6])和140 mm(Voon等^[7]，Shing等^[8]，Sveinsson等^[9])等不同墙体厚度的配筋砌块砌体剪力墙从剪跨比、轴向压力、竖向钢筋配筋率和水平钢筋配筋率等方面进行试验研究，基于试验结果给出了各因素对配筋砌块砌体剪力墙受剪承载力的影响规律.理论研究方面，Shing等^[10]基于灌芯砌块砌体斜向开裂和受剪钢筋利用率给出了半经验公式，周强等^[11]基于智能算法ANFIS和ANN给出了配筋砌块砌体剪力墙受剪承载力预测模型，Banting等^[12]通过开裂砌体单元应力状态分析给出了基于正应变协调的受剪承载力计算方法，潘东辉^[13]考虑配筋砌块砌体剪力墙与钢筋混凝土剪力墙受力状态相似性提出了基于软化桁架模型的承载力计算方法，《砌体结构设计规范》^[14]基于广义剪摩理论和空间变角桁架模型结合试验数据给出了受剪承载力计算公式.但由于不同的理论模型、试验数据和工程习惯导致目前关于配筋砌块砌体剪力墙受剪破坏时承载力计算尚无统一的表达式，缺乏较为合理的理论模型.

试验和理论研究证明^[15-16]配筋砌块砌体剪力墙的力学性能与钢筋混凝土剪力墙类似，因而许多学者将混凝土中应用较为成功的拉压杆模型引入到砌体墙受力分析中，但由于拉压杆模型仅满足平衡条件，目前也仅限于力学模型中传力路径方面分析和承载力下限值设计，并未能够建立合适的计算方法.Hwang等^[20-23]提出的软化拉压杆模型是在桁架模型基础上发展而来的，模型中考虑力平衡条件、材料本构方程和应变协调条件等参数，在分析钢筋混凝土结构中不符合平截面假定区域时获得较好精度，特别是近年来在多材料组合混凝土构件(纤维混凝土梁柱节点^[24]、型钢混凝土剪力墙^[25]等)中也获得较为理想的结果.

鉴于此，本文基于软化拉压杆模型，根据配筋砌块砌体剪力墙受剪过程受力特点和破坏特征，考虑灌芯砌块砌体材料受压过程的软化效应，建立配筋砌块砌体剪力墙受剪承载力计算方法.通过收集整理国内外符合受剪破坏特点的试件试验数据进行模型验证，并与目前国内外配筋砌块砌体剪力墙受剪承载力相关计算公式进行对比分析，对比验证模型的合理性.

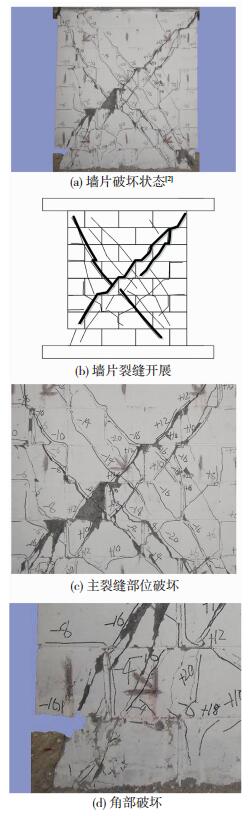
1 配筋砌块砌体剪力墙试验分析

为研究配筋砌块砌体剪力墙受剪破坏试验特征，课题组前期完成10片剪跨比小于2.0的配筋砌块砌体剪力墙在低周往复荷载下的拟静力试验，试验中所有试件均发生剪切破坏^[2-3].试验过程表明，配筋砌块砌体剪力墙的受力破坏过程主要分为4个阶段：1)墙体底部受拉区水平灰缝开裂，墙体进入弹塑性阶段；2)墙体中下部沿砂浆和砌块接触面出现阶梯形裂缝；3)墙体端部砌块壁出现斜裂缝，并伴随着阶梯形裂缝逐渐形成交叉裂缝；4)墙体中部出现贯通斜裂缝，墙体主裂缝交叉处和角部砌块壁脱落，此时墙片发生典型剪切破坏，无法继续承载.如图 1所示，配筋砌块砌体剪力墙受剪破坏特征与钢筋混凝土剪力墙较为相似，墙片表面产生相互交叉的斜裂缝，但是也具有其自身材料的特点，墙体破坏位置集中在墙体的角部和交叉主裂缝部位，同时灌芯砌体中水平灰缝的存在降低了墙体的刚度，保证了墙体具有更好地变形能力.基于此，本文考虑灌芯砌块砌体材料特点和墙体破坏特征，结合软化拉压杆模型进行配筋砌块砌体剪力墙受剪承载力预测.

图 1 配筋砌块砌体剪力墙破坏特征 Figure 1 Failure characteristics of reinforced concrete block masonry wall

2 配筋砌块砌体剪力墙软化拉压杆模型 2.1 配筋砌块砌体剪力墙软化拉压杆模型的建立

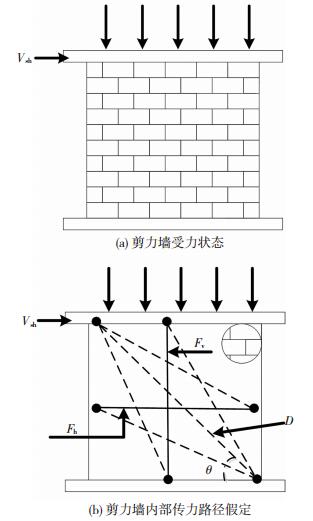
配筋砌块砌体剪力墙作为结构体系中重要的竖向承重构件，其在实际受力过程中承受来自楼屋面传来的竖向荷载和风荷载或地震作用传来的水平荷载.因此，类似于实际状态和试验过程中设定边界条件，假定一较为典型的配筋砌块砌体剪力墙承受竖向荷载和水平荷载，见图 2(a).

图 2 配筋砌块砌体剪力墙软化拉压杆模型 Figure 2 Strut-and-tie model of reinforced concrete block masonry wall

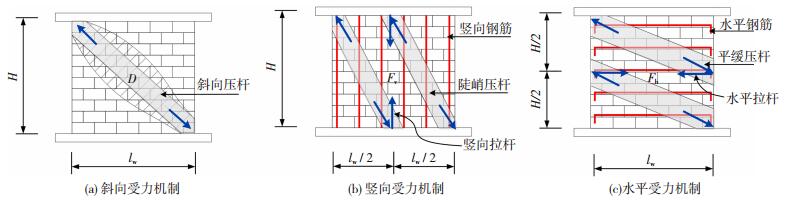
依据软化拉压杆模型分析假定^[20]，配筋砌块砌体剪力墙在受力过程中构成3种传力路径：对角传力路径、水平传力路径和垂直传力路径，各传力路径内部力学平衡见图 2(b).类似于钢筋混凝土剪力墙，假定配筋砌块砌体剪力墙对角受力杆为灌芯砌块砌体压杆，水平传力路径由水平钢筋构成的水平拉杆和灌芯砌块砌体压杆组成，垂直传力路径由竖向钢筋构成的竖向拉杆和灌芯砌块砌体压杆组成.试验中发现，位于墙体中不同位置的水平钢筋最终受力状态不同，靠近主裂缝的水平钢筋已进入塑性阶段，而相对远离主裂缝的水平钢筋可能处于弹性阶段^[2].依据Hwang等^[20]对水平拉杆和竖向拉杆的假定，当水平钢筋均匀布置时，水平拉杆中水平钢筋取全部水平钢筋量的75%参与计算，竖向拉杆中竖向钢筋取墙中央0.8l_w范围内的竖向钢筋量参与计算，各传力路径具体构建见图 3.

图 3 配筋砌块砌体剪力墙各传力路径示意 Figure 3 Schematic of the force path of reinforced concrete block masonry wall

软化拉压杆模型主要通过力平衡方程、材料本构方程和应变协调方程3组条件来实现对非连续区域应力流的描述，下面介绍各方程参数计算方法.

2.1.1 力平衡方程

配筋砌块砌体剪力墙对角压杆可定义为单一受压斜杆，通常假定受压斜杆与墙体水平主轴夹角与灌芯砌块砌体实际受力主应力方向一致，故该倾斜角可定义为^[20]

$ \theta = {\tan ^{-1}}\left( {H/d} \right), $

(1)

式中:H为墙体水平力作用点距离墙体底面高度，d为墙体受剪截面的有效高度.

同时，定义配筋砌块砌体剪力墙受压斜杆为D，水平拉杆拉力为F_h，竖向拉杆拉力为F_v，则墙体所受水平剪力V_sh^[20]为

$ {V_{{\rm{sh}}}} =-D\cos \theta + {F_{\rm{h}}} + {F_{\rm{v}}}\cot \theta . $

(2)

根据Hwang等^[20]的研究，墙体可承担剪力按以下比例分配到3种传力路径中:

$ -D\cos \theta :{F_{\rm{h}}}:{F_{\rm{v}}}\cot \theta = {R_{\rm{d}}}:{R_{\rm{h}}}:{R_{\rm{v}}}, $

(3)

式中：R_d、R_h、R_v分别为斜向、水平向和竖向传力路径剪力分配系数，可按下式计算：

$ {R_{\rm{d}}} = \frac{{\left( {1-{\gamma _{\rm{h}}}} \right)\left( {1-{\gamma _{\rm{v}}}} \right)}}{{1-{\gamma _{\rm{h}}}{\gamma _{\rm{v}}}}}, $

(4a)

$ {R_{\rm{h}}} = \frac{{{\gamma _{\rm{h}}}\left( {1-{\gamma _{\rm{v}}}} \right)}}{{1-{\gamma _{\rm{h}}}{\gamma _{\rm{v}}}}}, $

(4b)

$ {R_{\rm{v}}} = \frac{{{\gamma _{\rm{v}}}\left( {1-{\gamma _{\rm{h}}}} \right)}}{{1-{\gamma _{\rm{h}}}{\gamma _{\rm{v}}}}}. $

(4c)

式中：γ_h为不计算竖向传力时水平拉杆的剪力分配系数，γ_v为不计算水平传力时竖向拉杆的剪力分配系数，可按下式计算：

$ {\gamma _{\rm{h}}} = \frac{{2\tan \theta-1}}{3}, $

(5a)

$ {\gamma _{\rm{v}}} = \frac{{2\cot \theta-1}}{3}. $

(5b)

因此，节点区域中的最大压应力σ_dmax可通过斜向压杆、平缓压杆和陡峭压杆受力计算共同推导得出，其值可按下式计算^[20]:

$ \begin{array}{l} {\sigma _{{\rm{dmax}}}} = \frac{1}{{{A_{{\rm{str}}}}}}\left\{ {D- \frac{{\cos \left[{\theta-{{\tan }^{-1}}\left( {\frac{H}{{2{l_{\rm{w}}}}}} \right)} \right]}}{{\cos \left[{{{\tan }^{-1}}\left( {\frac{H}{{2{l_{\rm{w}}}}}} \right)} \right]}}F - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{{\cos \left[{{{\tan }^{-1}}\left( {\frac{H}{{2{l_{\rm{w}}}}}} \right)-\theta } \right]}}{{\sin \left[{{{\tan }^{-1}}\left( {\frac{H}{{2{l_{\rm{w}}}}}} \right)} \right]}}{F_{\rm{v}}}} \right\}, \end{array} $

(6)

式中：A_str为受压斜杆的有效截面面积，A_str=a_wb，a_w为墙体受压区高度，可近似按Priestley建议的近似公式^[20]计算:

$ {a_{\rm{w}}} = \left( {0.25 + 0.85\frac{N}{{{A_{\rm{w}}}{{f'}_{\rm{m}}}}}} \right)h, $

(7)

式中：N为墙体所受竖向压力，f_m^′为灌芯砌块砌体抗压强度标准值，h为墙体长度.

2.1.2 材料本构方程

软化拉压杆模型假定当节点区域的最大压应力σ_dmax达到受压材料的最大主应力ζf_m^′，构件达到峰值承载力.实际试验中发现，混凝土材料处于三轴受力状态时抗压强度与单轴抗压强度存在差异，Hsu提出混凝土软化系数ζ来定义这种差异并指出软化系数ζ与混凝土材料的抗压强度及单轴拉应变有关^[21].结合试验中破坏特征和考虑灌芯砌块砌体材料复杂性，本文假定灌芯砌块砌体材料的软化系数与3个影响因素相关：1)主应力与材料主轴夹角；2)受拉应变的影响；3)砌体角部弱化.即ζ=ζ_aζ_bζ_c，下面将介绍各影响因素如何确定.

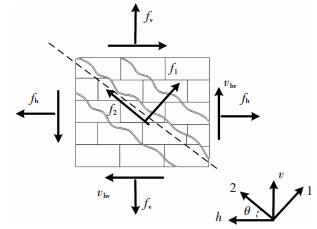
1) 灌芯砌块砌体是由混凝土空心砌块、砂浆和混凝土组成的复杂材料，其实际受力状态抗压强度和材料主应力与材料主轴夹角相关，并不能单独通过灌芯砌块砌体标准件抗压强度表征，其材料实际应力状态见图 4.Banting等^[12]结合已有试验数据给出了灌芯砌块砌体随主应力与材料主轴夹角变化强度的计算公式：

图 4 灌芯砌块砌体材料应力状态 Figure 4 Stress state of grouted concrete block masonry

$ \begin{array}{l} \frac{{{{f'}_{{\rm{m}}\left( \theta \right)}}}}{{{{f'}_{{\rm{m}}\left( {{{90}^ \circ }} \right)}}}} = \left( {4.74 \times {{10}^{-4}}} \right){\theta ^2} + \left( {-2.43 \times {{10}^{-2}}} \right)\theta + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;0.883 \le 1.0, \;\;\;\;\theta \le {45^ \circ }; \end{array} $

(8a)

$ \begin{array}{l} \frac{{{{f'}_{{\rm{m}}\left( \theta \right)}}}}{{{{f'}_{{\rm{m}}\left( {{{90}^ \circ }} \right)}}}} = \left( {2.66 \times {{10}^{-4}}} \right){\theta ^2} + \left( {-3.04 \times {{10}^{-2}}} \right)\theta + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;1.58 \le 1.0, \;\;\;\;\theta > {45^ \circ }. \end{array} $

(8b)

式中:f_m(θ)^′为主应力与材料主轴夹角为θ时灌芯砌块砌体受压强度，f_m(90°)^′为灌芯砌块砌体单轴受压强度.故由上式可得ζ_a=f_m(θ)^′/f_m(90°)^′，其中θ可按上节对角压杆与墙体水平主轴夹角定义.

2) Drysdale等^[28]参照Hognestad应力应变曲线给出了灌芯砌块砌体的应力应变关系，定义砌体峰值应变ε₀为-0.001 8，故压应力f_m2和受压应变ε₂关系式为

$ {f_{{\rm{m}}2}} = {f_{{\rm{m2, max}}}}\left[{2\frac{{{\varepsilon _2}}}{{-{\varepsilon _0}}}-{{\left( {\frac{{{\varepsilon _2}}}{{-{\varepsilon _0}}}} \right)}^2}} \right]. $

(9)

式中f_{m2, max}除与第一项主应力与材料主轴夹角相关外，其与灌芯砌块砌体材料主拉应变ε₁相关，Banting等^[12]结合试验给出拟合曲线及其表达式：

$ {f_{{\rm{m2, max}}}} = \frac{{{{f'}_{{\rm{m}}\left( \theta \right)}}}}{{0.41 + 0.33\frac{{{\varepsilon _1}}}{{{\varepsilon _0}}}}} \le {f'_{{\rm{m}}\left( \theta \right)}}, $

(10)

故由该项可确定ζ_b=1/(0.41+0.33(ε₁/ε₀)).

3) 试验中发现配筋砌块砌体剪力墙在最终破坏时其角部的砌块出现压溃现象，砌块壁脱落分离，弱化了剪力墙端部的约束.Fonseca等^[16]参考ACI 318规范结合考虑砌体的各项异性给出了节点区域有效强度计算公式：

$ {f'_{\rm{n}}} = 0.8{\beta _{\rm{n}}}{f'_{\rm{m}}}, $

(11)

式中β_n为节点有效系数，当节点区域存在有多于两个锚固时，β_n=0.6.

参照以上定义，可确定ζ_c=0.48.

软化拉压杆模型中假定钢筋为理想弹塑性，其应力应变关系式可表示为：

$ {f_{\rm{s}}} = {E_{\rm{s}}}{\varepsilon _{\rm{s}}}, {\varepsilon _{\rm{s}}} \le {\varepsilon _{\rm{y}}}; $

(12a)

$ {f_{\rm{s}}} = {f_{\rm{y}}}, {\varepsilon _{\rm{s}}} > {\varepsilon _{\rm{y}}}. $

(12b)

式中E_s为钢筋弹性模量，ε_y和f_y分别为钢筋受拉屈服应变和屈服应力.

2.1.3 应变协调方程

在软化拉压杆模型计算中各材料应满足应变协调方程^[20]:

$ {\varepsilon _1} + {\varepsilon _2} = {\varepsilon _{\rm{h}}} + {\varepsilon _{\rm{v}}}, $

(13)

式中墙体水平应变ε_h、竖向应变ε_v可按下式确定：

$ {F_{\rm{h}}} = {A_{{\rm{sh}}}}{E_{\rm{s}}}{\varepsilon _{\rm{h}}} \le {F_{{\rm{yh}}}}, $

(14a)

$ {F_{\rm{v}}} = {A_{{\rm{sv}}}}{E_{\rm{s}}}{\varepsilon _{\rm{v}}} \le {F_{{\rm{yv}}}}. $

(14b)

2.2 程序计算流程

2.1节通过结合试验破坏特征和灌芯砌块砌体材料特性建立了软化拉压杆模型中的力平衡方程、材料本构方程和应变协调方程，因此本文采用Matlab程序对软化拉压杆模型进行编程实现，其主要计算流程：

1) 通过试验样本中已有试验数据设计计算初始承载力V₀，利用力平衡方程(1)~(5)确定初始D₀、F_{h, 0}、F_{v, 0}值；

2) 如图 5(b)所示基于软化拉压杆中拉杆屈服判断流程^[20]对3种受力机制中D₀、F_{h, 0}、F_{v, 0}进行重新分配，确定新的D₁、F_{h, 1}、F_{v, 1}值；

图 5 软化拉压杆模型计算流程 Figure 5 Flow chart for softened strut-and-tie model

3) 利用式(6)确定节点区域压应力σ_{d, max}，根据软化拉压杆模型破坏准则，确定初始软化系数ζ₁；

4) 利用应变协调方程(13)~(14)确定初始ε₁，利用材料本构方程(8)~(12)确定由应变对应的软化系数ζ₂；

5) 进行步骤3)软化系数和步骤4)软化系数的比较，若ζ₁＜ζ₂，则更新承载力初始值V₂=V₁+ΔV，若ζ₁＞ζ₂，则更新承载力初始值V₂=V₁-ΔV，返回步骤1)继续计算，直到ζ₁和ζ₂的误差在允许范围内时，计算停止输出结果.

3 软化拉压杆模型试验验证

为验证本文提出的配筋砌块砌体剪力墙受剪承载力计算模型有效性，搜集整理国内外配筋砌块砌体剪力墙受剪试验数据54片，所搜集的试件在试验过程中均发生剪切破坏.为确保所应用的试件能够具有代表性和普适性，故所引用的试件中试验参数取值覆盖范围较广，且同时需满足以下分析条件：1)试件设计类型为一字型矩形截面；2)试件无洞口和无端部约束设置；3)在试验过程中试件均发生平面内剪切破坏；4)试件试验参数完备，能够满足模型验证需要.试验参数分布见图 6.将整理的配筋砌块砌体剪力墙受剪试验数据代入本文提出的软化拉压杆模型进行计算，并将预测值结果与试验结果对比，具体计算结果对比见表 1和图 7.

图 6 配筋砌块砌体剪力墙受剪试验参数分布 Figure 6 Distribution of experimental parameters for reinforced block masonry wall

表 1 软化拉压杆模型预测值与试验值结果对比 Table 1 Comparison between prediction values by softened strut-and-tie model and experimental values

No.	H/mm	L/mm	B/mm	ρ_v/%	f_yv/MPa	ρ_h/%	f_yh/MPa	f_m^′/MPa	σ/MPa	λ	V_exp/kN	V_st/kN	V_st/V_exp	数据来源
1	2200	1400	290	0.77	472	0.17	274	24.40	1.50	1.85	530	545	1.027	[2]
2	2200	1400	290	0.77	472	0.17	274	24.40	2.00	1.85	578	576	0.997	[2]
3	1600	1400	290	0.77	472	0.17	274	24.40	1.50	1.38	683	621	0.909	[2]
4	1600	1400	290	0.77	472	0.17	274	24.40	2.00	1.38	735	651	0.885	[2]
5	1000	1400	290	0.77	472	0.17	274	24.40	1.50	0.92	700	835	1.193	[2]
6	1000	1400	290	0.77	472	0.17	274	24.40	2.00	0.92	883	875	0.991	[2]
7	2200	1400	290	0.77	397	0.17	300	19.26	1.50	1.85	406	473	1.164	[3]
8	2200	1400	290	0.77	397	0.17	300	19.26	2.00	1.85	430	504	1.173	[3]
9	2200	1400	290	0.77	397	0.14	300	19.26	2.00	1.85	426	482	1.131	[3]
10	2200	1400	290	0.77	397	0.14	300	19.26	1.50	1.85	388	460	1.116	[3]
11	1600	1800	190	0.79	430	0.13	430	13.10	1.00	1.20	418	387	0.926	[4]
12	1600	1800	190	0.79	430	0.13	430	13.10	0.00	1.20	345	303	0.878	[4]
13	1600	1800	190	0.79	430	0.13	430	13.10	1.50	1.20	458	424	0.926	[4]
14	1600	1800	190	0.79	430	0.13	430	13.10	1.00	1.80	315	319	1.014	[4]
15	2000	2000	190	0.79	425	0.08	425	15.40	1.00	1.00	408	457	1.128	[5]
16	2000	2000	190	0.79	425	0.13	425	12.70	0.00	1.00	443	336	0.856	[5]
17	3000	2000	190	1.32	425	0.12	425	15.40	0.00	1.50	450	354	0.914	[5]
18	2000	3000	190	1.32	425	0.13	425	12.70	1.00	0.67	974	709	0.827	[5]
19	3000	2000	190	1.32	425	0.07	425	12.70	1.00	1.50	390	309	0.907	[5]
20	3000	3000	190	0.79	425	0.12	425	15.40	1.00	1.00	774	758	1.076	[5]
21	2000	3000	190	1.32	425	0.08	425	15.40	0.00	0.67	851	643	0.887	[5]
22	3000	3000	190	0.79	425	0.07	425	12.70	0.00	1.00	569	485	1.021	[5]
23	1000	1200	190	0.55	406	0.13	358	15.30	1.10	0.91	300	308	1.025	[6]
24	1000	1200	190	0.55	406	0.21	388	15.30	1.10	0.91	305	316	0.904	[6]
25	1000	1200	190	0.55	406	0.30	406	15.30	1.10	0.91	366	321	0.879	[6]
26	1000	1200	190	0.55	406	0.30	406	15.30	2.19	0.91	476	383	0.804	[6]
27	1000	1200	190	0.55	406	0.30	406	15.30	3.29	0.91	545	444	0.816	[6]
28	1000	1200	190	0.55	406	0.30	406	15.30	3.95	0.91	606	481	0.795	[6]
29	1000	1200	190	0.55	406	0.18	406	15.30	1.10	0.91	350	315	0.900	[6]
30	1000	1200	190	0.55	406	0.18	406	15.30	1.75	0.91	410	351	0.857	[6]
31	1800	1800	140	0.62	318	0.05	325	17.60	0.00	1.00	215	282	1.311	[7]
32	1800	1800	140	0.62	318	0.01	325	17.60	0.00	1.00	195	271	1.392	[7]
33	1800	1800	140	0.62	318	0.06	320	17.00	0.00	1.00	223	274	1.227	[7]
34	1800	1800	140	0.62	318	0.05	325	18.80	0.50	1.00	263	328	1.246	[7]
35	1800	1800	140	0.62	318	0.05	325	18.80	0.25	1.00	244	312	1.279	[7]
36	1800	3000	140	0.60	318	0.05	325	24.30	0.25	0.60	598	819	1.369	[7]
37	1830	1830	143	0.78	496	0.12	386	20.70	1.86	1.06	456	450	0.987	[8]
38	1830	1830	143	0.78	496	0.12	386	17.90	0.00	1.06	354	309	0.873	[8]
39	1830	1830	143	0.78	496	0.12	386	17.90	0.69	1.06	385	344	0.892	[8]
40	1830	1830	143	0.78	496	0.12	386	20.70	0.69	1.06	431	395	0.914	[8]
41	1830	1830	143	0.40	441	0.12	386	20.70	1.86	1.06	427	450	1.054	[8]
42	1830	1830	143	0.57	448	0.22	462	22.80	1.86	1.06	500	520	1.039	[8]
43	1830	1830	143	0.57	448	0.12	386	22.80	1.86	1.06	467	488	1.045	[8]
44	1830	1830	143	0.78	496	0.22	462	17.20	1.86	1.06	536	418	0.780	[8]
45	1422	1219	194	0.18	407	0.29	356	23.20	1.88	1.17	461	485	1.052	[9]
46	1422	1219	194	0.18	407	0.29	356	23.20	3.01	1.17	561	544	0.967	[9]
47	1422	1219	143	0.47	438	0.39	391	15.80	2.76	1.17	429	374	0.871	[9]
48	1422	1219	143	0.47	438	0.39	391	15.80	2.76	1.17	428	374	0.871	[9]
49	1422	1219	143	0.47	438	0.20	391	15.10	2.76	1.17	410	364	0.884	[9]
50	1422	1219	143	0.47	438	0.20	391	15.10	2.76	1.17	389	364	0.936	[9]
51	1422	1219	143	0.47	438	0.08	391	15.10	2.76	1.17	334	299	0.892	[9]
52	1422	1219	143	0.47	438	0.27	391	15.10	2.76	1.17	423	366	0.864	[9]
53	1422	1219	143	0.47	438	0.20	391	15.10	1.74	1.17	342	325	0.950	[9]
54	1422	1219	143	0.47	438	0.20	391	15.10	2.76	1.17	419	364	0.869	[9]
											平均值		0.991
											变异系数		0.151
注：H、L、B分别为试件高、长、宽；ρ_v和f_yv分别为竖向钢筋配筋率和受拉屈服强度；ρ_h和f_yh分别为水平钢筋配筋率和受拉屈服强度；f_m^′为试件灌芯砌块砌体抗压强度；σ为试件试验中加载的竖向应力值；λ为试件剪跨比.

表 1 软化拉压杆模型预测值与试验值结果对比 Table 1 Comparison between prediction values by softened strut-and-tie model and experimental values

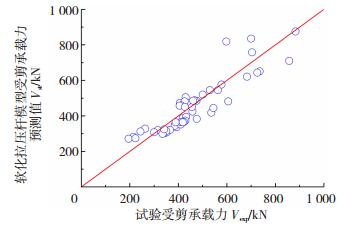
图 7 软化拉压杆模型受剪承载力预测值 Figure 7 Prediction values for shear capacity by softened strut-and-tie model

由图 7结果可知，本文提出软化拉压杆模型计算值与配筋砌块砌体剪力墙受剪试验值比值的平均值为0.991，变异系数为0.151，数据沿45°斜直线分布较均匀，表明软化拉压杆模型能够较为准确地预测评估配筋砌块砌体剪力墙的受剪承载力，验证了模型的合理性.

4 与已有计算公式结果对比

鉴于目前国内外规范中关于配筋砌块砌体剪力墙受剪承载力计算模型普遍采用灌芯砌体贡献项、轴压力贡献项和抗剪钢筋贡献项3项相加的形式，为对比分析本文提出的软化拉压杆模型的适用性，本节总结整理国内外目前较为经典的配筋砌块砌体剪力墙受剪承载力计算公式，对GB 50003—2011《砌体结构设计规范》^[14](简称“GB 50003”)、美国规范TMS 402-13/ACI 530-13^[17](简称“ACI”)、加拿大规范CSA-S304^[18](简称“CSA”)、新西兰规范NZS 4230.2004^[19](简称“NZS”)和Shing等^[10]建议计算公式(简称“Shing”)的受剪承载力计算模型进行试验数据验算，公式形式见表 2，各公式具体参数取值参考所引文献.

表 2 配筋砌块砌体剪力墙受剪承载力计算公式 Table 2 Calculation formula for shear capacity of reinforced concrete block masonry wall

将文中统计54组试验数据代入各计算公式进行受剪承载力计算，各计算式中材料强度指标均取试验值.为分析对比各模型适用性，将各模型计算值与试验结果比值进行比较，并与本文提出的软化拉压杆模型(简称“ST”)进行对比分析，具体见表 3.

表 3 不同模型计算值与试验结果对比 Table 3 Comparison between calculation values by different model and experimental values

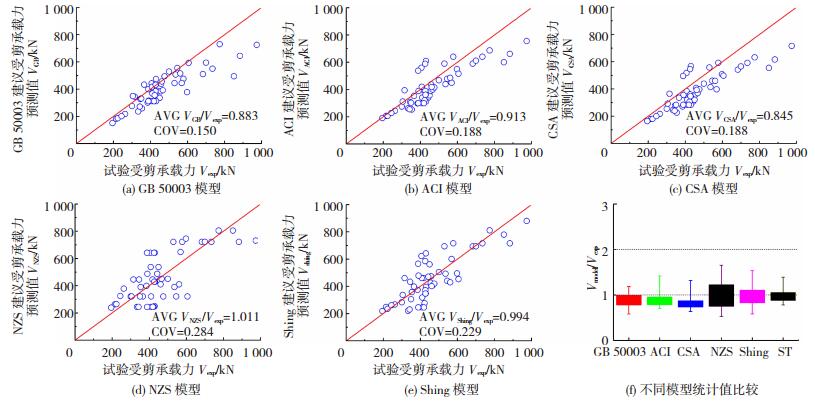
图 8(a)~(e)为表 3中不同模型承载力预测值与试验受剪承载力对比，位于图中左上区域点的预测值大于试验值，计算结果偏于不安全，而位于图中右下区域点的预测值小于试验值，计算结果偏于安全.图 8(f)为不同计算模型统计值箱形对比图，从图 8(f)可看出本文提出的ST模型相对于其他模型均值更接近于1，离散程度相对较小.

图 8 不同模型计算值与试验结果对比 Figure 8 Comparison between calculation values by different model and experimental values

表 3和图 8结果表明，本文提出的ST模型预测值较各国规范和Shing等^[10]的建议公式计算值更接近于试验值，变异系数相对较小.除NZS规范外，其余各模型计算值与试验值比值平均值小于1，表明各模型计算结果为试验值的偏下限值，且平均值越小表明模型计算结果越偏于保守.NZS规范模型计算值与试验值比值大于1，偏于不安全，且其变异系数为0.284，离散性较大.Shing等^[10]建议公式并未考虑剪跨比的影响，因此其计算值与试验值比值变异系数相对较高.

5 结论

1) 在结合配筋砌块砌体剪力墙受剪试验中破坏特征的基础上，考虑灌芯砌块砌体材料受压过程中的软化效应，基于软化拉压杆模型建立了适合于剪跨比小于2.0的配筋砌块砌体剪力墙受剪承载力计算方法，具有明确的力学模型，能够较好地反映配筋砌块砌体剪力墙的剪切传力机理和最终破坏模式，并通过与国内外54片配筋砌块砌体剪力墙受剪试验结果对比，验证了模型的合理性.

2) 本文提出软化拉压杆模型计算值比国内外相关建议公式计算结果更接近于试验值，同时变异系数较小，表明软化拉压杆模型可较为准确地预测配筋砌块砌体剪力墙的受剪承载力，为后期完善配筋砌块砌体剪力墙受剪理论设计提供了理论基础.

参考文献

[1]	El-DAKHAKHNI W, ASHOUR A. Seismic response of reinforced-concrete masonry shear-wall components and systems: State of the art[J]. Journal of Structural Engineering, 2017, 143(9): 03117001. DOI:10.1061/(ASCE)ST.1943-541X.0001840
[2]	陈君军.低周往复荷载下290配筋砌块砌体剪切破坏模式试验研究[D].哈尔滨: 哈尔滨工业大学, 2013 CHEN Junjun. Experimental study on shear behavior of 290 reinforced masonry shear walls under quas-static cyclic test[D]. Harbin: Harbin Institute of Technology, 2013
[3]	ZHAO Yan, WANG Fenglai. Experimental studies on behavior of fully grouted reinforced-concrete masonry shear walls[J]. Earthquake Engineering and Engineering Vibration, 2015, 14(4): 743. DOI:10.1007/s11803-015-0030-5
[4]	SEIFElDIN H M, GALAL K. In-plane seismic performance of fully grouted reinforced masonry shear walls[J]. Journal of Structural Engineering, 2017, 143(7): 04017054. DOI:10.1061/(ASCE)ST.1943-541X.0001758
[5]	El-DAKHAKHNI W W, BANTING B R, MILLER S C. Seismic performance parameter quantification of shear-critical reinforced concrete masonry squat walls[J]. Journal of Structural Engineering, 2013, 139(6): 957. DOI:10.1061/(ASCE)ST.1943-541X.0000713
[6]	姜洪斌, 唐岱新, 张洪涛. 配筋混凝土小砌块剪力墙承载力试验研究[J]. 哈尔滨建筑大学学报, 2001, 34(3): 30. JIANG Hongbin, TANG Daixin, ZHANG Hongtao. Test on mechanics behavior of reinforced concrete block shear wall[J]. Journal of Harbin University of C.E. & Architecture, 2001, 34(3): 30.
[7]	VOON K C, INGHAM J M. Experimental in-plane shear strength investigation of reinforced concrete masonry walls[J]. Journal of Structural Engineering, 2006, 132: 400. DOI:10.1061/(ASCE)0733-9445(2006)132:3(400)
[8]	SHING P B, NOLAND J L, KLAMERUS E, et al. Inelastic behavior of concrete masonry shear walls[J]. Journal of Structural Engineering, 1989, 115(9): 2204. DOI:10.1061/(ASCE)0733-9445(1989)115:9(2204)
[9]	SVEINSSON B I, MCNIVEN H D, SUCUOGLU H.Cyclic loading tests of masonry single piers[C]// Vol. 4- Additional tests with height to width ratio of 1 (UCB/EERC-85/15).Berkeley, CA: University of California, 1985
[10]	SHING P B, SCHULLER M, HOSKEREV S. In-plane resistance of reinforced masonry shear walls[J]. Journal of Structural Engineering, 1990, 116(3): 619. DOI:10.1061/(ASCE)0733-9445(1990)116:3(619)
[11]	ZHOU Qiang, ZHU Fei, YANG Xu, et al. Shear capacity estimation of fully grouted reinforced concrete masonry walls using neural network and adaptive neuro-fuzzy inference system models[J]. Construction and Building Materials, 2017, 153: 947. DOI:10.1016/j.conbuildmat.2017.07.171
[12]	BANTING B R, El-DAKHAKHNI W. Normal strain-adjusted shear strength expression for fully grouted reinforced masonry structural walls[J]. Journal of Structural Engineering, 2014, 140(3): 04013075. DOI:10.1061/(ASCE)ST.1943-541X.0000842
[13]	潘东辉. 灌孔配筋砌体剪力墙受剪承载力软化剪压强度模型[J]. 建筑结构学报, 2011, 32(6): 135. PAN Donghui. Softened shear-compression model of shear capacity of grouted reinforced-block-masonry shear walls[J]. Journal of Building Structures, 2011, 32(6): 135. DOI:10.14006/j.jzjgxb.2011.06.006
[14]	Code for design of masonry structure: GB 50003—2011[S]. Beijing: Chinese Standards Association, 2011
[15]	GHAISAS K V, BASU D, BRZEV S, et al. Strut-and-Tie model for seismic design of confined masonry buildings[J]. Construction and Building Materials, 2017, 147: 677. DOI:10.1016/j.conbuildmat.2017.04.200
[16]	FONSECA F S, DILLON P B. Analysis of masonry shear walls using strut-and-ties models[C]//13th Canadian Masonry Symposium.Canada.Halifax: Canada Masonry Design Centre, 2017
[17]	Building code requirements for masonry structures: TMS 402-08/ACI 530-08/ASCE 5-08[S]. Farmington Hills: Masonry Standards Joint Committee, 2008
[18]	Design of masonry structures: S304.1-04[S]. Mississauga: Canadian Standards Association, 2004
[19]	Design of reinforced concrete masonry structures: NZS 4230: 2004[S]. Wellington: Standards Association of New Zealand, 2004
[20]	HWANG S J, LEE H J. Analytical model for predicting shear strengths of interior reinforced concrete beam-column joints for seismic resistance[J]. ACI Structural Journal, 2000, 97(1): 35.
[21]	HWANG S J, FANG W H, LEE H J, et al. Analytical model for predicting shear strength of squat walls[J]. Journal of Structural Engineering, 2001, 127: 43. DOI:10.1061/(ASCE)0733-9445(2001)127:1(43)
[22]	HWANG S J, LEE H J. Analytical model for predicting shear strengths of exterior reinforced concrete beam-column joints for seismic resistance[J]. ACI Structural Journal, 1999, 96(5): 846.
[23]	HWANG S J, LEE H J. Strength prediction for discontinuity regions by softened strut-and-tie model[J]. Journal of Structural Engineering, ASCE, 2002, 128(12): 1519. DOI:10.1061/(ASCE)0733-9445(2002)128:12(1519)
[24]	高丹盈, 史科, 赵顺波. 基于软化拉压杆模型的钢筋钢纤维混凝土梁柱节点受剪承载力计算方法[J]. 土木工程学报, 2014, 47(9): 101. GAO Danying, SHI Ke, ZHAO Shunbo. Calculation method for shear capacity of steel fiber reinforced concrete beam-column joints based on softened strut-and-tie model[J]. China Civil Engineering Journal, 2014, 47(9): 101. DOI:10.15951/j.tmgcxb.2014.09.038
[25]	初明进, 冯鹏, 叶列平. 冷弯薄壁型钢混凝土剪力墙受剪承载力计算模型[J]. 建筑结构学报, 2011, 32(9): 107. CHU Mingjin, FENG Peng, YE Lieping. Analytical model for predicting shear strength of cold-formed thin-walled steel reinforced concrete shear walls[J]. Journal of Building Structures, 2011, 32(9): 107. DOI:10.14006/j.jzjgxb.2011.09.014
[26]	PAULAY T, PRIESTLEY M N J. Seismic design of reinforcedconcrete and masonry buildings[M]. New York: John Wiley & Sons, 1992.
[27]	刘立鹏, 唐岱新, 田玉斌. 注芯混凝土砌块砌体各向异性强度变化规律试验研究[J]. 建筑结构学报, 2005, 26(5): 91. LIU Liupeng, TANG Daixin, TIAN Yubin. Experimental study of anisotropic strength characteristics of grouted concrete block masonry[J]. Journal of Building Structures, 2005, 26(5): 91. DOI:10.14006/j.jzjgxb.2005.05.013
[28]	DRYSDALE R G, KHATTABM M. In-plane behavior of grouted concrete masonry under biaxial tension-compression[J]. ACI Structure Journal, 1995, 92(6): 1.