2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
近年来,全球范围内针对重要建筑物的恐怖袭击活动呈上升趋势,国内外众多学者做了大量研究来减少建筑物所受的爆炸和冲击荷载以及降低结构内的人员伤亡.耗能材料是人们研究的主要方向之一,耗能材料遭受冲击时能把冲击能量完全或部分转换成其他形式的能量.
过去,人们常用金属材料作为耗能材料,其中,金属管因其易于制造和较高的能量吸收性能而引起极大关注.Gupta等[1]针对金属管进行侧向压缩试验研究,研究表明在金属管受到侧向压缩时其变形对能量吸收起到了很大作用,此外,还从此研究获得了用来评估材料耗能性能的力-位移曲线.Chirwa[2]通过试验和数值分析对一系列厚度不均的薄壁管进行了研究,通过研究证明这些厚度不均管的耗能能力约比厚度恒定的金属管要高50%.Sedghi等[3]针对在圆柱管不同部位开槽,对其破坏和耗能性能的影响进行了试验研究,研究表明,这些圆柱管的破坏位移几乎相同,但是因为开槽影响,其最大承受荷载会有所减小.此后,Niknejad等[4]开发出另一种带有纵向凹槽的嵌套管式耗能系统,和单圆管相比,这种嵌套管系统的耗能性能有了明显改善.
近年来,金属泡沫因其轻质和高效的耗能能力[5],越来越多地被用来吸收爆炸冲击能量,并且在金属管中填充金属泡沫也明显表现出了耗能性能的改善,其中泡沫铝是研究重点之一.Deshpande等[6]在不同应变率下对开孔泡沫铝的受压变形进行了试验研究,得出其平台应力(plateau stress)对应变率变化并不敏感的结论.Mukai等[7]发现闭孔泡沫铝在高应变率下的受压和应变硬化有着明显的相关性,进一步研究证明,闭孔泡沫铝平台应力的应变率敏感性随着泡沫铝相对密度的减小而增加.另一方面,Hanssen等[8]对泡沫铝填充的薄壁柱进行了静力轴压试验,试验结果表明泡沫铝的直接抗压强度以及泡沫铝与壁柱之间的相互作用会导致薄壁柱破坏荷载有明显的增大.Seitzberger等[9]针对泡沫铝填充的钢管进行了类似的轴压实验,也得到了类似的结果,并且试验得到的泡沫铝的压缩模式与文献[10-12]提出的低密度聚氨酯泡沫的压缩模式相吻合.
上述对耗能材料的研究均在静力荷载作用下,而爆炸冲击属于动力作用,目前国内外针对耗能材料的动力特性研究相对较少.Fan等[13]对夹心管在动力冲击作用下的受压状态进行了试验研究,试验证明通过增加压缩速度可以改善夹心管的耗能性能.Shrive等[14]通过试验研究了一个包括两个同心环及一层较小的夹心管的嵌套系统,从冲击试验发现,在试验中嵌套管系统并未出现极限变形,但却从试验得到了类似于静力试验的极限承载力.Smith等[15]对泡沫铝填充不锈钢管在横向冲击作用下进行了试验研究,给出了总能量吸收(total energy absorption)、比能量吸收(specific energy absorption)和吸能效率(crush force efficiency)等指标参数.Liu等[16]通过研究不同密度的泡沫铝在冲击作用下的变形模式和力学特性,发现铝合金的耗能能力会优于纯泡沫铝.贾斌等[17]通过对填充泡沫铝防护结构进行高速冲击数值模拟,发现泡沫铝的填充位置对防护结构能量吸收特性会有影响.
基于上述研究,本文提出一种新型的内嵌泡沫铝耗能节点,在已经进行静载压缩试验的基础上[18]进行冲击试验来进一步研究其在冲击作用下的耗能性能,并研究了有无泡沫铝填充、折板厚度对这种耗能节点的耗能性能的影响.
1 试验设计通过冲击试验对本文提出的耗能节点耗能性能进行研究,并进一步探究有无泡沫铝填充以及折板厚度两个参数对这种耗能节点的耗能性能的影响.
1.1 试件设计本文研究中,泡沫铝被用来作为耗能节点主要的能量吸收部分.从泡沫铝在单轴压缩荷载作用下得到的应力-应变曲线[19]看,可以明显看到有3个阶段:线弹性变形阶段、塑性变形阶段和致密化阶段(densification stage).塑性变形阶段应力几乎没有变化,这决定其可以作为能量吸收区,而压力急剧增加的致密化阶段可视为安全后备区,这些功能都决定泡沫铝是一种理想的能量吸收材料.
如图 1所示,此类耗能节点由上下钢板及两侧折板用螺栓连接,并在中间嵌入泡沫铝,试件上下钢板的尺寸均为620 mm×200 mm×8 mm.试验设计并制作了4个试件,各试件的具体参数见表 1.试验使用钢材为厂家提供Q235钢,使用泡沫铝为闭孔泡沫铝,孔径5~10 mm,孔隙率68%~91%,分别通过拉伸试验和轴压试验来获取节点试件所用钢板和泡沫铝的其他材料性能,见表 2.

|
图 1 节点试件 Figure 1 Photographs of energy absorption connectors |
| 表 1 各试件参数统计 Table 1 Geometry of energy absorption connectors |
| 表 2 钢材和泡沫铝力学性能数据 Table 2 Material properties of mild steel and aluminum foam |
本次冲击试验利用哈尔滨工业大学国防抗爆与防护工程实验室落锤式冲击试验台进行.试验平台见图 2,试验时耗能节点试件放置于锤头和底座之间,重400 kg的落锤从预定高度落下,对耗能节点试件进行冲击,预先通过分析来确定下落高度从而保证试件所受的最大冲击力一致.为了避免上下钢板在冲击作用下产生弯曲变形,将两块20 mm厚的钢垫板分别用螺栓与顶部和底部的钢板相连接.在试验中,利用落锤配套软件来控制落锤冲击的高度,在试件下方放置力传感器并连接到数据采集仪器,用以测量施加在耗能节点上的冲击力,并通过磁栅来测量试验过程中冲击锤头的位移.

|
图 2 试验设备 Figure 2 Photographs of test loading device |
在本试验中所有试件的失效模式均类似,因此仅从图 3、4给出45-5.70-no和45-7.36两个典型试件的破坏过程.此外,图 3、4同时也给出了无泡沫铝填充和有泡沫铝填充的试件的破坏过程对比.如图 3所示,无泡沫铝填充的耗能节点仅依靠折板塑性变形耗能,而图 4则显示有泡沫铝填充的耗能节点既有折板塑性变形耗能也有泡沫铝不断被压密实耗能.

|
图 3 45-5.70-no破坏过程 Figure 3 Collapse process of the 45-5.70-no specimen |

|
图 4 45-7.36破坏过程 Figure 4 Collapse process of the 45-7.36 specimen |
从图 4也可以看出,在试件受到冲击作用产生压缩位移的同时,泡沫铝在不断地压实,并且由于泡沫铝的多孔性结构,在泡沫铝压实过程中一直伴随着泡沫铝的破碎,产生“掉渣”现象.在试验中,所有试件均未观察到钢板的断裂,表现出了良好的延性.
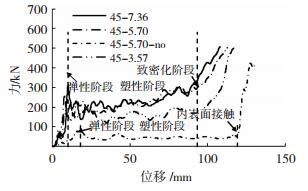
2.2 力-位移曲线如图 5所示,通过这一系列冲击试验同时也获得了此种耗能节点的压力-位移曲线.从此类耗能节点试件的力-位移曲线均可以明显观察到3个变形阶段,对于有泡沫铝填充节点试件来说,包括弹性阶段、塑性阶段和致密化阶段;无泡沫铝填充节点试件则包括弹性阶段、塑性阶段和内表面接触阶段.对于有泡沫铝填充的试件,在弹性阶段力随位移增长速度较快.从试验结果还可以看出,随着节点试件所用折板厚度的增加,力在弹性阶段的极限值也在不断增大.当达到弹性阶段峰值力后,试件开始进入塑性阶段,一开始试件均表现出力的急剧下降,随着泡沫铝不断的被压密实,力又开始不断波动,在很长一段位移内压缩力仅是稍有增加,基本保持不变.当泡沫铝基本被压到密实,试件进入致密化阶段,力又开始急剧上升,这也意味着试件已经基本失去耗能作用,达到其极限耗能能力.
|
图 5 压力-位移曲线对比 Figure 5 Comparison of compressive force-displacement curves of all specimens |
对于无泡沫铝填充的试件,也能明显的观察到3个变形阶段,但是由于仅靠折板塑性变形耗能,线弹性阶段力的上升并不明显,且极限值远小于有泡沫铝填充试件的弹性阶段力的极限值,在力达到弹性阶段极限值时的位移也明显大于其他3个试件.随后,试件进入塑性阶段,在塑性阶段力基本保持不变,且持续位移较长.对于无泡沫铝填充的试件来说,塑性阶段力的变化是由于折板受压产生形变以及钢材的硬化而产生的.最后,无泡沫铝填充的节点试件在折板内表面相接触后表现出急剧的压缩力的增加,同时这也表明节点已经达到了其最大的耗能能力.从位移来看,无泡沫铝填充的试件受到冲击产生的位移最大,达到130 mm,其他3个试件按折板厚度递增冲击位移分别为118、111、110 mm,均有明显的减小.
总的来说,在一开始的弹塑性变形阶段,试件在达到屈服位移后,压缩力都表现出了逐渐的增加.在试件进入致密化阶段和内表面接触阶段后,压缩力也都表现出了急剧的增加,这意味着试件基本达到极限耗能能力.一般来说,此类耗能节点的耗能能力都是通过图 5所示的力-位移曲线来进行对比.
3 耗能性能分析 3.1 耗能指标一般来说,此类耗能节点的耗能性能可以通过如下几个耗能指标来进行评价,包括平均承载力(mean force)、致密化位移(densification displacement)、能量吸收效率(energy absorption efficiency)、能量吸收值(energy absorption capacity)和吸能效率(crush force efficiency).其中,平均承载力和致密化位移是两个最重要的指标,其他的几个耗能指标也都是通过这两个指标计算得来的.由于试验获得的力-位移曲线和泡沫铝受压时的应力-应变曲线在形状上大致相似,所以本文采用了计算泡沫铝平台应力和致密化起始应变相同的方法来计算试件的平均承载力和致密化位移.目前,有几种方法可以用来确定泡沫铝致密化的起始应变,包括寻找应力平台区域和致密化区域的交点、在应力急剧上升之前的最后局部应变最小值等.为了降低上述方法的不确定性,Li等[20]提出了基于能量吸收率的方法来确定泡沫铝致密化的起始应变.本文基于Li等[20]提出的能量吸收率的方法,并考虑力-位移曲线特征,提出更合理的计算确定耗能节点的致密化位移的方法.通过用力和位移代替应力和应变,能量吸收效率可以按下式计算:
| $ \eta \left( x \right) = \frac{1}{{F\left( x \right)H}}\int_{{x_{\rm{y}}}}^x {F\left( {\bar x} \right){\rm{d}}\bar x}, $ | (1) |
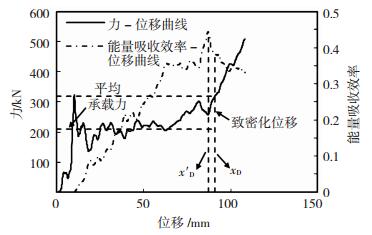
式中:F(x)为试件所受到的冲击力,H为所用的泡沫铝的高度,xy为试件的屈服位移.试件的致密化位移xD可按如下方式确定:先确定能量吸收效率达到最大值时所对应的位移x′D,即
| $ \frac{{{\rm{d}}\eta \left( x \right)}}{{{\rm{d}}x}}\left| {_{x = {{x'}_{\rm{D}}}}} \right. = 0. $ | (2) |
并找出此位移(x′D)之前力的最大值(Fmax),接下来找出该力所对应的大于x′D的位移,此位移即为节点试件的致密化位移xD.
图 6给出了通过给定的力-位移曲线来确定致密化位移的方法.那么,平均力的确定可以按照下式来计算,即
|
图 6 致密化位移的测定 Figure 6 Determination of densification displacement |
| $ {F_{\rm{m}}} = \frac{{\int_0^{{x_{\rm{D}}}} {F\left( {\bar x} \right){\rm{d}}\bar x} }}{{{x_{\rm{D}}}}}, $ | (3) |
能量吸收值Ea是对应于节点试件力-位移曲线所包围的面积,即
| $ {E_{\rm{a}}} = \int_0^{{x_{\rm{D}}}} {F\left( {\bar x} \right){\rm{d}}\bar x} . $ | (4) |
显然,对于耗能材料并不能完全用能量吸收率或者能量吸收值Ea来评价其是否适合作为耗能材料,峰值应力也是一个非常重要的参数.为了避免冲击过程中对建筑物和内部人员的伤害,抗瞬时冲击承载力不宜过高.在节点试件耗能能力一定的前提下,具有塑性变形阶段的泡沫铝材料,避免了抗瞬时冲击承载力过大产生的破坏,所以另外定义一个耗能指标—吸能效率(平均承载力与平均最大力的比值)来进行评价,吸能效率越大说明节点试件在塑性阶段瞬时冲击力波动越小,则耗能性能相应的也会更优, 即
| $ {e_{\rm{f}}} = \frac{{{F_{\rm{m}}}}}{{{F_{\max }}}}. $ | (5) |
节点试件耗能指标参数见表 3,有无泡沫铝、折板厚度对耗能性能的影响将在下面讨论.
| 表 3 耗能节点耗能指标总结 Table 3 Summary of energy absorption performance of all specimens |
有无泡沫铝填充对45-5.70-no和45-5.70试件耗能性能影响对比见图 7.可看出:1)当试件有泡沫铝填充时,和无泡沫铝填充的试件相比,平均承载力和能量吸收值这两个耗能指标有明显增大,分别增大了391.4%和273.1%.相比之下,可以看出有泡沫铝填充的试件耗能性能得到显著改善;2)对于有泡沫铝填充的试件来说,能量吸收值的提高程度要比平均承载力的提高程度低,这是因为在节点试件中填充泡沫铝之后,试件的致密化位移减小所导致的.和无填充相比,填充泡沫铝之后节点试件的致密化位移减少了23.0%;3)吸能效率ef可以描述塑性耗能阶段试件所受瞬时力的波动程度,和未填充泡沫铝的试件相比,填充泡沫铝的试件吸能效率也有明显的增加,由50.38%增加到70.86%,增加了40.7%,即有泡沫铝填充的试件平均承载力更接近于平均最大力,塑性耗能阶段更为平缓,耗能效率更高.

|
图 7 有无泡沫铝对耗能性能影响对比 Figure 7 Effect of aluminum foam on energy absorption performance |
试验还探究了折板厚度变化对耗能节点试件的耗能性能的影响,见图 8.可以看出,折板厚度从3.57 mm增大到7.36 mm,耗能节点的致密化位移和吸能效率变化均不大,分别从99.72 mm下降到90.85 mm和从74.84%下降到65.77%,这说明厚度变化对耗能节点试件的致密化位移和吸能效率影响并不大.

|
图 8 折板厚度对耗能性能的影响对比 Figure 8 Effect of plate thickness on energy absorption performance |
当折板厚度从3.57 mm增大到5.70 mm,耗能节点试件的平均承载力、能量吸收值均有明显的增长,和45-3.57节点试件相比,45-5.70试件平均承载力和能量吸收值分别增加了37.9%、28.1%.当节点试件折板厚度增加到7.36 mm时,节点试件平均承载力和能量吸收值分别增长了34.7%和22.7%.这说明增大折板厚度会改善节点试件的耗能性能.
和45-5.70试件相比,45-7.36试件平均承载力和能量吸收值反而有所下降,这是因为泡沫铝特有的多孔结构导致其密度分布并不均匀.本次试验过程中45-7.36试件所用泡沫铝质量轻于45-5.70试件,试验完成后测量所得45-7.36试件泡沫铝质量为1.56kg,而45-5.70试件泡沫铝质量为1.62 kg,这也证明下降的原因正是泡沫铝密度分布不均.
总的来说,有泡沫铝填充的试件耗能性能要明显优于无泡沫铝填充的节点试件,且折板厚度越大,节点试件的耗能性能会越好.
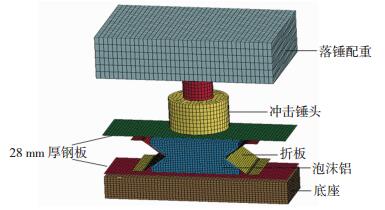
4 有限元分析 4.1 有限元模型采用有限元仿真软件LS-DYNA对此耗能节点试件进行有限元模拟.模拟所用构件尺寸均为实际值,并将有限元模拟结果和试验结果对比,以验证建立的有限元模型的精确性.根据结构的实际几何尺寸、所受载荷和边界条件,建立结构模型如图 9所示.耗能节点Q235钢面板选用S/R Hughes-Liu壳体单元模拟,泡沫铝选用8节点SOLID单元模拟.网格划分时,在折板的拐角处使用更密的网格划分来模拟塑性铰处的塑性变形.试验过程中,8 mm厚钢板和20 mm厚垫板通过螺栓连接在一起且在试验中并未出现分离.因此,在模拟中选择一整块28 mm厚钢板来模拟这两块钢板.
|
图 9 耗能节点有限元模型 Figure 9 FE model of energy absorption connectors |
面板Q235钢选用LS-DYNA中的分段线性塑性模型(the piecewise linear plasticity material model).在此材料模型中,采用Cowper-Symonds模型来考虑材料的应变率效应,即
| $ {\sigma _{\rm{y}}}\left( {\xi _{{\rm{eff}}}^{\rm{p}}, \dot \xi _{{\rm{eff}}}^{\rm{p}}} \right) = {\sigma _{\rm{y}}}\left( {\xi _{{\rm{eff}}}^{\rm{p}}} \right)\left[{1 + {{\left( {\frac{{\dot \xi _{{\rm{eff}}}^{\rm{p}}}}{C}} \right)}^{1/P}}} \right], $ | (6) |
式中:σy(ξeffp)为未考虑应变率的屈服应力,
在LS-DYNA中,有几种材料模型可以用来模拟泡沫铝,比如MAT26,63,75,126,154.Hanssen等[21]对比有限元结果和试验结果发现, MAT63在这些材料模型中表现出了较好的模拟性能和较高的计算效率.因此,本文泡沫铝选用LS-DYNA中的MAT63材料模型,输入的泡沫铝应力-应变曲线见图 10.

|
图 10 泡沫铝应力-应变曲线 Figure 10 Stress-strain curve for aluminum foam in FE model |
冲击试验结果和有限元数值仿真结果对比见图 11(test表示试验结果,FE表示数值仿真结果).耗能节点的数值仿真结果与试验结果吻合较好,有限元模拟真实地再现了从锤头接触到最终停止的冲击全过程,耗能节点试件的变形和损伤变化过程也被完整记录下来,说明本文所建立的有限元模型是可靠的,可以用于分析此类耗能节点的抗冲击性能.

|
图 11 试验和有限元力-位移曲线对比 Figure 11 Comparison of force-displacement curves between tests and FE models |
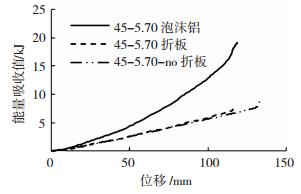
通过分析有限元结果,可得到45-5.70和45-5.70-no两个耗能节点试件能量吸收值对比,见图 12.无泡沫铝填充节点试件折板最终能量吸收值为8.717 kJ,而有泡沫铝填充折板最终能量吸收值为7.662 kJ,变化并不大,这说明泡沫铝填充对折板能量吸收值影响不大.
|
图 12 能量吸收值对比 Figure 12 Comparison of energy absorption capacities |
对于有泡沫铝填充的节点试件来说,试件吸收的总能量为26.848 kJ, 其中泡沫铝吸收的能量值为19.186 kJ, 占节点试件总能量吸收值的71.5%,折板能量吸收值仅为7.662 kJ,占节点试件总能量吸收值的29.5%.结果表明,填充泡沫铝可以显著提高节点试件的总能量吸收值,和无泡沫铝填充时相比,增大了208.0%;且在有泡沫铝填充的节点试件中,泡沫铝对于能量吸收的增长起到了主要作用,这也进一步说明泡沫铝这种材料耗能性能优良.
4.5 冲击速度对耗能节点耗能性能影响为比较冲击速度对耗能节点试件耗能性能的影响,对初始冲击质量为400 kg,冲击速度分别为10、20、30、50、100 m/s,45-5.70耗能节点试件总能量吸收值,以及耗能节点试件的压缩位移进行考察,得到不同冲击速度下总能量吸收值-位移关系曲线,见图 13.在冲击质量一定的条件下,试件达到致密化位移时,和冲击速度为10 m/s时耗能节点试件总能量吸收值相比,当冲击速度分别为20、30、50、100 m/s时,耗能节点试件总能量吸收值分别提高了8.5%、18.1%、44.8%、180.3%.结果表明,随着冲击速度增大,耗能节点试件总能量吸收值也在不断增大.耗能节点在高速冲击下耗能能力的提升是由材料的应变率效应和结构惯性引进结构变形模式改变引起的.

|
图 13 不同冲击速度下总能量吸收值-位移曲线 Figure 13 Total energy absorption capacity-displacement curves under different impact velocities |
1) 冲击试验结果表明,无泡沫铝填充的耗能节点仅依靠折板塑性变形耗能,而有泡沫铝填充的耗能节点既有折板塑性变形耗能又有泡沫铝受压密实耗能,且在受压过程中伴随着泡沫铝的破碎“掉渣”现象.
2) 在受压过程中,此种耗能节点均有3个明显的变形阶段.对于无泡沫铝填充的耗能节点来说,包括弹性阶段、塑性阶段和内表面接触阶段;对于有泡沫铝填充的耗能节点,则包括弹性阶段、塑性阶段和致密化阶段.
3) 填充泡沫铝可以明显改善此种耗能节点的平均承载力、能量吸收值和吸能效率指标,但会明显减小试件节点的致密化位移;增大折板厚度对耗能节点的致密化位移指标和吸能效率指标影响不大,但增大折板厚度可以增大平均承载力指标和能量吸收值指标.
4) 冲击速度会对此类耗能节点的耗能性能有一定影响.冲击速度越大,耗能节点的能量吸收值越大.
| [1] |
GUPTA N K, SEKHON G S, GUPTA P K. Study of lateral compression of round metallic tubes[J]. Thin-Walled Structures, 2005, 43(6): 895. DOI:10.1016/j.tws.2004.12.002 |
| [2] |
CHIRWA E C. Theoretical analysis of tapered thin-walled metal inverbucktube[J]. International Journal of Mechanical Sciences, 1993, 35(3): 325. |
| [3] |
SEDGHI M, ALAVI N A, LABBAFI H, et al. Effect of circumferential grooves geometries on crashworthiness of axially loaded cylindrical tubes[C]// Proc 16th Annu 12th Int Conf Mech Eng Bahonar University. Kerman, Iran: [s.n.], 2008
|
| [4] |
NIKNEJAD A, OROJLOO P H. A novel nested system of tubes with special cross-section as the energy absorber[J]. Thin-Walled Structures, 2016, 100: 113. DOI:10.1016/j.tws.2015.12.009 |
| [5] |
刘志芳, 王军, 秦庆华. 横向冲击载荷下泡沫铝夹芯双圆管的吸能研究[J]. 兵工学报, 2017, 38(11): 2259. LIU Zhifang, WANG Jun, QIN Qinghua. Research on energy absorption of aluminum foam-filled double circular tubes under lateral impact loadings[J]. Acta Armamentarii, 2017, 38(11): 2259. DOI:10.3969/j.issn.1000-1093.2017.11.024 |
| [6] |
DESHPANDE V S, FLECK N A. High strain rate compressive behavior of aluminum alloy foams[J]. International Journal of Impact Engineering, 2000, 24(3): 277. DOI:10.1016/S0734-743X(99)00153-0 |
| [7] |
MUKAI T, MIYOSHI T, NAKANO S, et al. Compressive response of a closed-cell aluminum foam at high strain rate[J]. Scripta Materialia, 2006, 54(4): 535. |
| [8] |
HANSSEN A G, LANGSETH M. Development in aluminum based crash absorption components[C]// Norwegian-French Industry Conference.Paris: [s.n.], 1996
|
| [9] |
SEITZBERGER M, RAMMERSTORFER F G, DEGISCHER H P, et al. Crushing of axially compressed steel tubes filled with aluminum foam[J]. Acta Mechanica, 1997, 125(1/2/3/4): 101. |
| [10] |
THORNTON P H. Energy absorption by foam filled structures[J]. SAE Technical, 1980, 529. |
| [11] |
SHAHBEYK S, PETRINIC N, VAFAI A. Numerical modelling of dynamically loaded metal foam-filled square columns[J]. International Journal of Impact Engineering, 2007, 34(3): 573. DOI:10.1016/j.ijimpeng.2005.11.005 |
| [12] |
REID S R, REDDY T Y, GRAY M D. Static and dynamic axial crushing of foam-filled sheet metal tubes[J]. International Journal of Mechanical Sciences, 1986, 28(5): 295. DOI:10.1016/0020-7403(86)90043-3 |
| [13] |
FAN Zhihua, SHEN Jianhu, LU Guoxing, et al. Dynamic lateral crushing of empty and sandwich tubes[J]. International Journal of Impact Engineering, 2013, 53(3): 12. |
| [14] |
SHRIVE N, ANDREWS K, ENGLAND G. The impact energy dissipation of cylindrical systems[J]. Structural impact and crashworthiness, 1984, 2: 544. |
| [15] |
SMITH R, ALTENHOF W, LAPAIN M. Transverse impact loading of aluminum foam filled braided stainless steel tubes[J]. International Journal of Impact Engineering, 2016, 88: 214. DOI:10.1016/j.ijimpeng.2015.10.008 |
| [16] |
LIU Huan, CAO Zhuokun, LUO Hongjie, et al. Performance of closed-cell aluminum foams subjected to impact loading[J]. Materials Science & Engineering A, 2013, 570: 29. |
| [17] |
贾斌, 马志涛, 庞宝君. 填充泡沫铝防护结构的超高速撞击数值模拟[J]. 哈尔滨工业大学学报, 2011, 43(1): 18. JIA Bin, MA Zhitao, PANG Baojun. Numerical simulation investigation in hypervelocity impact on Al-foam stuffed shields[J]. Journal of Harbin Institute of Technology, 2011, 43(1): 18. |
| [18] |
WANG Yonghui, ZHAI Ximei, WANG Wei. Numerical studies of aluminum foam filled energy absorption connectors under quasi-static compression loading[J]. Thin-Walled Structures, 2017, 116: 228. |
| [19] |
兰凤崇, 曾繁波, 周云郊, 等. 闭孔泡沫铝力学特性及其在汽车碰撞吸能中的应用研究进展[J]. 机械工程学报, 2014, 50(22): 97. LAN Fengchong, ZENG Fanbo, ZHOU Yunjiao, et al. Progress on research of mechanical properties of closed-cell aluminum foams and its applications in automobile crashworthiness[J]. Journal of Mechanical Engineering, 2014, 50(22): 97. |
| [20] |
LI Qingming, MAGKIRIADIS I, HARRIGAN J J. Compressive strain at the onset of densification of cellular solids[J]. Journal of Cellular Plastics, 2006, 42(5): 371. DOI:10.1177/0021955X06063519 |
| [21] |
HANSSEN A G, HOPPERSTAD O S, LANGSETH M, et al. Validation of constitutive models applicable to aluminum foams[J]. International Journal of Mechanical Sciences, 2002, 44(2): 359. DOI:10.1016/S0020-7403(01)00091-1 |
 2018, Vol. 50
2018, Vol. 50


