2. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),哈尔滨150090;
3. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨150090
2. Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, Harbin 150090, China;
3. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
消声室以及竖向振动敏感型设施常需按多点矩阵式布置弹簧隔振支座,隔振支座的选择与布置考虑的主要因素为竖向振动条件下的动刚度,阻尼及幅值等基本参数.关于弹簧隔振支座竖向输入下的受力性能的研究已较成熟,主要针对弹簧隔振支座的竖向动刚度、受激励幅值及激励频率影响等开展了较系统的试验和分析.何庆烈等[1-2]针对地铁浮置板用隔振器的刚度与阻尼进行了试验研究,测试了疲劳试验前后的作用力与位移曲线,发现了疲劳试验前后隔振器刚度与阻尼参数值变化很小,其最大参数值变化不超过5%,隔振性能较稳定.王建伟等[3]通过对隔振器刚度与阻尼的频率与幅值的依赖性进行研究,发现隔振器的动刚度随着激振频率的增加总体趋势是增大的,但在共振频率附近,动刚度有减小趋势;等效黏性阻尼系数随激振频率增加而减小,在共振频率附近,变化幅度不大;能量耗散比则随着激振频率的增加而增大;随着激振幅值的增加,动刚度、等效黏性阻尼系数与能量耗散比变化幅度均不大.弹簧隔振支座的竖向刚度与水平刚度均对结构外界环境扰动和地震动下的响应有重要影响.然而,当前进行这种设备隔振设计时,更多关注隔振支座竖向刚度,较少考虑水平荷载下以竖向弹簧为基本元件的隔振支座的水平刚度、黏滞阻尼、吸能与耗能等.
事实上,风洞等大型基础设施所需的隔振装置常支承着数百吨甚至上千吨的相关设施,其巨大的体量,使其与土木工程结构类似面临着地震灾害风险,若措施不当则可能造成其在强地震动下损伤甚至破坏.近期,针对弹簧隔振器应用于建筑结构隔振有了少量报道.如任莹等[4]针对正在施工中的地铁某双线隧道沿线一栋地上6层,地下2层的特殊住宅楼,通过设置弹簧隔振器,完成了隔振试验;通过非线性分析表明,弹簧隔振层安装后的预期减振效果良好.
隔振支座可实现其各弹簧单元在竖向荷载下的同步变形,以往常认为同一隔振支座的各弹簧及多个隔振支座点阵均是并联的,其刚度及阻尼等特性主要由弹簧的伸缩特性所控制[5].然而,隔振支座下端固定在基础上,其上表面通过盖板与隔振对象连为整体,在水平荷载下将因隔振支座支承的隔振对象发生侧移,而产生近似水平剪切变形,同时将在隔振对象较大自重P-Δ效应下,表现出一定的倾斜趋势.恒定竖向荷载作用下的弹簧隔振支座水平变形能力、荷载侧移关系,特别是在反复荷载作用下的滞回曲线、水平刚度、黏滞阻尼等动力特性,本质上决定了弹簧隔振支座抵抗水平地震的能力,也控制着地震作用下隔振对象的动力响应.因此,有必要针对这种以竖向弹簧为基本单元的隔振支座的水平荷载与水平位移关系开展试验研究,确定刚度、变形能力等抗震性能,从而为消声室等大型基础设施隔振设计提供依据.
1 试验参数与加载方案 1.1 弹簧隔振支座构造与试验参数以某公司生产的额定竖向荷载为100 kN和300 kN的弹簧隔振支座为研究对象,支座均由3×4布置的竖向弹簧单元、底板、盖板与挡板及固定螺栓等组成,每个弹簧内空腔均布置1根固定螺栓并使其与上下板连为一体.其中,100 kN隔振支座的钢底板平面尺寸b×h×t=400 mm×450 mm×15 mm,钢盖板平面尺寸b×h×t=400 mm×500 mm×15 mm,盖板周边焊接厚度为4 mm、高度为90 mm的钢裙板;其内布置的弹簧采用直径为18 mm的高强弹簧钢制作,弹簧高度为155 mm、螺距为32 mm、内径为65 mm、外径为101 mm.300 kN隔振支座的钢底板平面尺寸b×h×t=500 mm×550 mm×15 mm,钢盖板平面尺寸b×h×t=500 mm×600 mm×15 mm,盖板周边焊接厚度为4 mm、高度为120 mm的钢裙板;其内布置的弹簧采用直径为25 mm的高强弹簧钢制作,弹簧高度为220 mm、螺距为45 mm、内径为75 mm、外径为125 mm.底板、底挡板、盖板及裙板均采用Q235B钢,弹簧隔振支座构造见图 1.
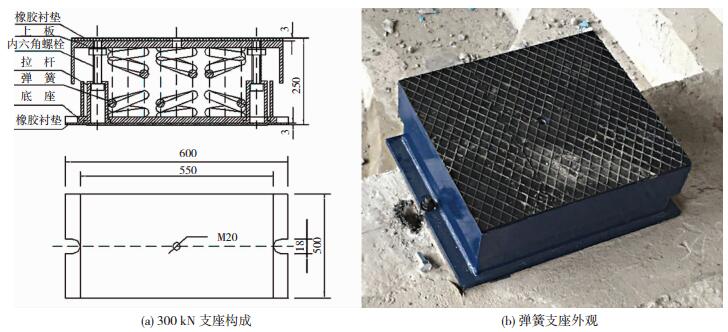
|
图 1 弹簧隔振支座构造 Figure 1 Spring vibration isolation bearing structure |
针对10个弹簧隔振支座,以钢裙板及固定螺栓连接是否拆除为参数,每类隔振支座处于原始封装状态即带侧向挡板与固定螺栓的试件各3个,为避免上盖板受到限制而拆除侧向挡板与固定螺栓的隔振支座各2个.考虑到弹簧隔振支座最不利工况,试验时应使弹簧隔振支座分别承担着其额定竖向荷载,试验试件见表 1.
| 表 1 试验试件 Table 1 Test specimen |
由于需恒定竖向荷载的条件下同步施加反复水平荷载,获得相应的水平变形和竖向变形,宜采用自平衡加载体系完成弹簧隔振支座试验,试验中以立放的钢筋混凝土环梁同时提供两个方向的反向平衡体系.由于试验要求同步施加竖向荷载和水平荷载,且支座盖板能水平自由滑动,应使支座盖板上方的加载梁在承担恒定竖向荷载同时,保证水平荷载和水平位移.综合考虑后,以环梁为支撑,水平和竖向各布置一个千斤顶和力传感器.由于水平方向需要反复加载,故水平为拉压千斤顶和拉压传感器.为保证隔振支座盖板自由平动位移,在竖向千斤顶与加载分配钢箱梁间布置了滚轴支座(滚轴表面涂刷润滑脂,使摩擦系数降低至最小).加载钢箱梁下表面直接覆盖到弹簧隔振支座盖板上,以向其传递竖向荷载;其端面则与拉压传感器相连后再连接拉压千斤顶,拉压千斤顶通过高强螺杆及相应前后刚性端板固定在钢筋混凝土环梁上.试验用自平衡加载系统见图 2.
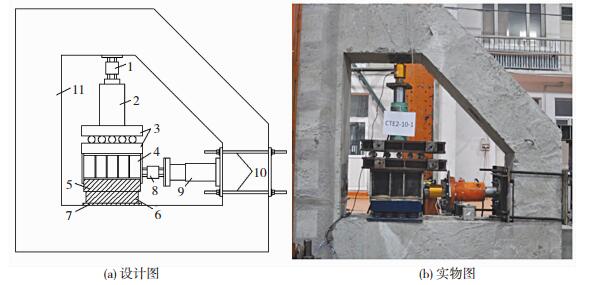
|
1-压力传感器; 2-液压千斤顶; 3-滚轴加载座; 4-加载分配钢箱梁; 5-弹簧隔振支座盖板; 6-弹簧隔振支座钢裙板; 7-弹簧隔振支座底板; 8-拉压传感器; 9-拉压千斤顶; 10-高强螺杆; 11-环梁 图 2 自平衡加载系统 Figure 2 Self-balancing loading system |
试验采用水平位移控制加载,以弹簧隔振支座的发生明显的倾覆迹象或钢裙板严重撕裂分别为盖板有无位移限制的支座破坏标志.为量测隔振支座盖板水平位移与竖向压缩变形,分别在隔振支座的盖板两侧、底板相应位置布置了LVDT.由于采用对盖板施加水平位移控制整体加载过程,支座的位移实测值由盖板水平位移与底板水平滑动实测差值确定.按4mm倍数施加水平位移,每级位移循环3次.对于SWGZ-30T-3、SWGZ-30T-4和SWGZ-30T-5支座,由于其上下端板间缝隙较小,且水平刚度较大,加载时一级为2 mm,每级循环3次.相应的LVDT布置见图 2(b).
2 试验现象 2.1 位移无限制弹簧隔振支座因盖板无限制,CTE1-10-1和CTE1-10-2两个隔振支座,水平位移直接反应了发生竖向压缩的3×4弹簧单元平动大小.当水平位移达到一定值时,内部弹簧两端与盖板和底板间产生错动声音,负向加载(水平力传感器受拉)过程中支座倾斜较严重,弹簧水平变形过大而卸载.加载结束后移除支座上板后,隔振支座试件的相邻两侧边弹簧有较明显未恢复受压残余变形,且相交处角部弹簧变形最严重.
CTE1-30-1和CTE1-30-2虽然同为盖板无位移限制的隔振支座试件,但加载全过程中试件未发出错动声音,也未发生较明显倾斜,卸载后其弹簧单元高度也与初始弹簧高度一致.即这两个隔振支座试件总体上表现为弹性,其非弹性不显著,这也与后文中滞回曲线相一致.
2.2 位移受限制弹簧隔振支座对于CTE2-10-1、CTE2-10-2和CTE2-10-3,盖板水平位移受到钢裙板及弹簧单元内置连接螺栓的限制.CTE2-10-1与CTE2-10-2两个试件,在加载全过程中均无明显的损伤现象且未出现错动声音,而试件CTE2-10-3在16 mm正向第一次循环过程中到达13.55 mm时隔振支座试件发出响声,到达16 mm时发出第二次响声,此时复位时残余变形已达4.58 mm,隔振支座试件已发生较明显损伤.3个试件均随着位移增大超过钢裙板与下侧板的间隙,远加载端一侧钢裙板两角部焊缝撕裂,见图 3(a),且随着撕裂程度随荷载增大而扩大.CTE2-10-3在加载过程中还出现近加载端一侧钢裙板鼓起现象,弹簧支座有明显倾斜现象,见图 3(b).

|
图 3 试件的变形及破坏 Figure 3 Deformation and damage of the test piece |
对于CTE2-30-1、CTE2-30-2和CTE2-30-3均发现水平位移超过钢裙板与下侧板的间隙后,远加载端一侧钢裙板角部焊缝撕裂,同时伴有较大断裂声响.
3 试验结果分析依据试验结果,可获得两类弹簧支座试件的滞回曲线、骨架曲线、割线刚度、耗能能力和等效黏滞阻尼系数等静力滞回性能[9].
3.1 滞回曲线两类弹簧隔振支座的水平荷载P与弹簧支座顶盖水平位移Δ的关系,即滞回曲线分别见图 4、5.
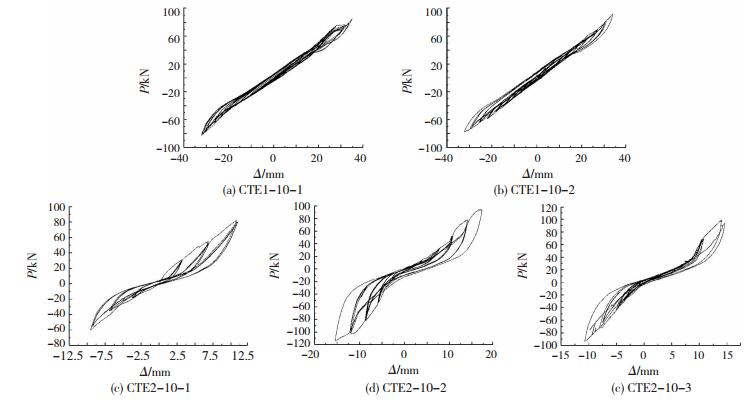
|
图 4 100 kN型隔振支座滞回曲线 Figure 4 Hysteresis curve of 100 kN vibration isolation bearing test piece |
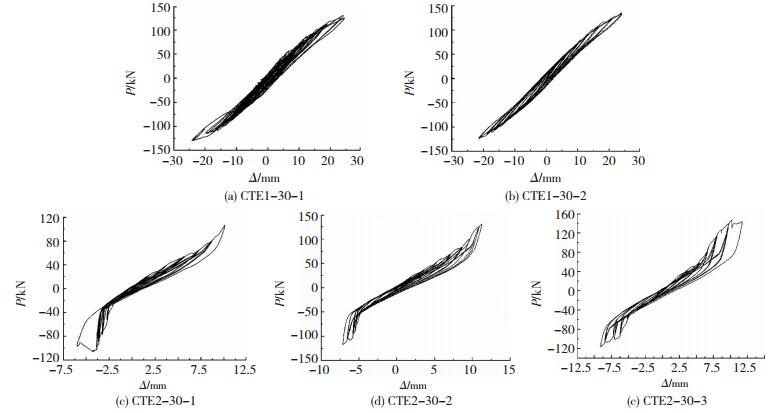
|
图 5 300 kN型隔振支座滞回曲线 Figure 5 Hysteresis curve of 300 kN vibration isolation bearing test piece |
结合图 4、5可知,若顶盖位移无限制,两类弹簧隔振支座的滞回曲线均呈中部等宽度、近端部捏拢尖锐的“扁梭形”,中部带宽较小;在恒定为额定值的竖向荷载和一定压缩变形的条件下,隔振支座试件的位移基本线性发展,直至停止加载,水平加卸载刚度变化有限,滞回曲线欠饱满.虽然,一定级别位移下,两类隔振支座试件也表现为一定的非弹性,但总体上其滞回曲线斜率变化不大,这集中体现了弹簧单元的弹性性能以及试件的少量边界弹簧(边部和角部)在恒定的竖向荷载下和过大的水平位移下,边界弹簧的压缩量超过了其弹性极限,导致了一定程度的损伤及刚度和承载力退化[11].
若顶盖位移受限制,两类弹簧隔振支座试件也承担着恒定为额定值的竖向荷载和一定压缩变形,两类隔振支座的滞回曲线相对于有位移限制时饱满.总体上,在不大的水平位移的表现与顶盖位移无限制时相同,即滞回环表现为中部带宽较小的“梭形”,而超过一定位移后,即单圈极限位移大于顶盖的钢裙板与底板的挡板间缝隙后,顶盖水平位移受到了弹簧内置连接螺栓和钢裙板限制,水平荷载的贡献者除了隔振支座试件弹簧单元,钢裙板与下挡板及连接螺栓共同承担,且后者的作用更为明显,这可由滞回环的“扁梭形”变为近两端部翘起“叶片状”体现.极限位移荷载循环时,两类隔振支座试件的“近端部翘起区域”滞回环范围均不同程度大于中部等带宽区域;每级荷载下,“近端部翘起区域”的卸载程度不同,反应了钢裙板与下挡板间挤压作用导致的钢裙板的弹塑性,这可由试验中发现的钢裙板逐步鼓起、角部焊缝撕裂等现象予以说明.实际上,由于钢裙板存在,超过一定位移下,隔振支座试件的水平刚度有明显增大,当然不同试件在不同加卸载循环时增幅程度不同.
隔振支座的峰值、极限荷载与水平位移见表 2.
| 表 2 隔振支座的峰值、荷载与位移 Table 2 Peaks, loads, and displacements of vibration isolation bearings |
将试验支座的滞回曲线各级第一次循环的峰值点相连后可得各支座试件的骨架曲线,见图 6.
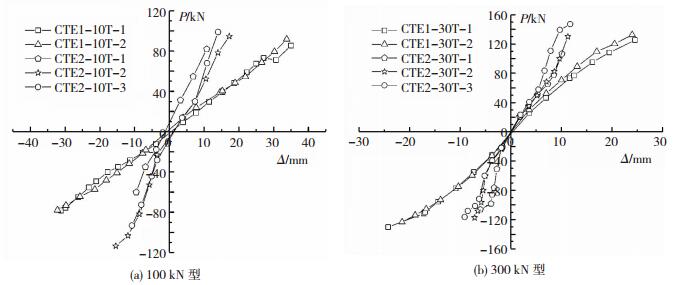
|
图 6 隔振支座的骨架曲线 Figure 6 Skeleton curve of vibration isolation bearing |
由图 5可知,顶盖位移无限制时,100 kN型支座试件的骨架曲线总体为线性,且两个试件的曲线斜率相近;而300 kN型支座试件,两个试件的骨架曲线负向近似重合,正向形状相同、斜率存在一定差异,在超过一定位移后骨架曲线的正、负向均有明显的非弹性.顶盖位移有限制时,100 kN型支座3个试件骨架曲线总体上均呈线性,但各试件的斜率不相同;300 kN型支座3个试件的骨架曲线呈现一定的非弹性.
3.3 刚度退化两类弹簧隔振支座中总体呈现出随着加载位移的增大割线刚度呈现出不同程度的变化趋势,当然,隔振支座顶盖水平位移受限时,其刚度随着钢裙板参与工作的程度不同而有一定的变化.割线刚度可表达为
| $ {K_i} = \frac{{\left| { + {P_i}} \right| + \left| {-{P_i}} \right|}}{{\left| { + {\Delta _i}} \right| + \left| {-{\Delta _i}} \right|}}, $ | (1) |
式中:Pi为第i级控制位移下第一次循环的峰值荷载,Δi为与峰值荷载相对应的位移值.两类隔振支座的割线刚度随水平位移变化关系见图 7.
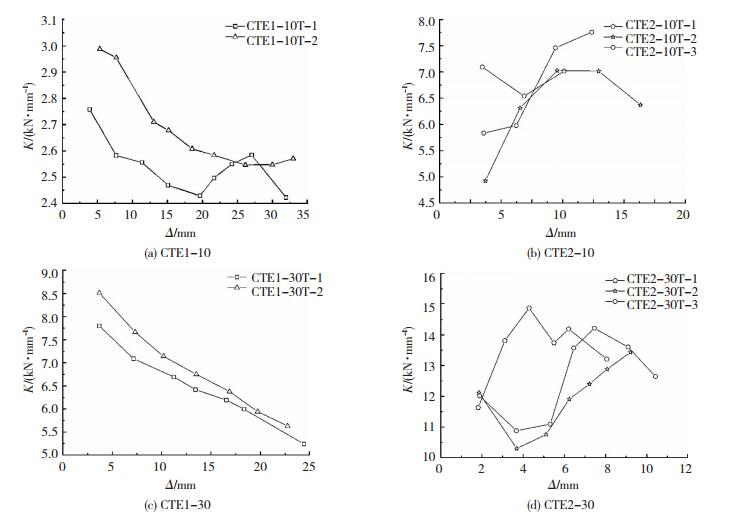
|
图 7 两类隔振支座割线刚度 Figure 7 Tangent stiffness of two types of vibration isolation bearings |
顶盖位移无限制时,两类隔振支座的割线刚度均随水平位移的增大基本呈现下降趋势,其中,100 kN型支座试件的刚度降低程度低于300 kN型.顶盖位移受限制时,两类隔振支座试件的割线刚度未能表现为明显的退化规律,且随着不同的水平位移表现为一定跳跃,100 kN型支座的2个试件割线刚度先增大后减小,1个试件割线刚度先退化后有一定程度的增大;而300 kN型支座的2个试件割线刚度先退化后再有较为明显的增大,1个试件表现为先增大后有一定程度的减小.割线刚度与位移的变化趋势揭示出,顶盖位移无限制时,由于弹簧单元的不可逆的非弹性性能导致的割线刚度退化,这种退化趋势随着位移荷载的增大而持续增大;而盖板受限后,除了弹簧单元对支座水平刚度有贡献外,受限的盖板及其限制部件对割线刚度有增大作用,且当超过一定侧移后,受限盖板对割线刚度增大作用的贡献可能大于因非弹性变形损伤造成的割线刚度降低,可判断该侧移点即是转折点,造成割线刚度随位移增大的规律性总体上呈现出先增大后减小的趋势.
3.4 耗能能力每级加载位移构成滞回曲线所围成的面积,即该级位移下支座试件的消耗能量,以每级位移下的第一圈循环消耗的能量作为研究对象,可得支座的单圈耗能和位移的关系,见图 8.

|
图 8 两类隔振支座单圈耗能 Figure 8 Two types of vibration isolation bearing single-loop energy consumption |
各支座的单圈耗能能力基本都随着位移增大而提高,且随着位移增大,变化速率也在提高.相比之下,300 kN型支座试件的耗能能力优于100 kN型支座试件;同一类型支座试件中,顶盖位移有约束的试件单圈耗能能力明显高于无约束的支座试件.单圈耗能累加后获得的试验过程中试件消耗总能量,即累积耗能见图 9.两类隔振支座试件的累积耗能随位移发展及各试件间的差异与单圈耗能的变化规律相同.
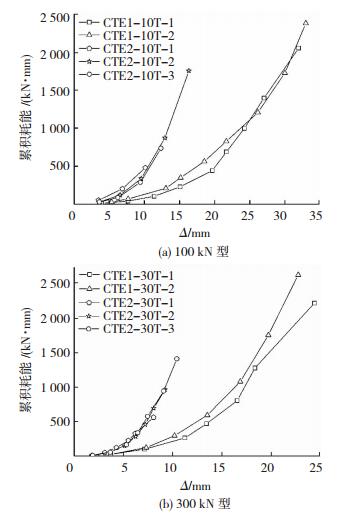
|
图 9 两类隔振支座累积耗能 Figure 9 Cumulative energy consumption of two types of vibration isolation bearings |
按图 10可进行两类支座的等效黏滞阻尼系数确定[8],ABCD四点构成的曲线即试验支座的滞回曲线,滞回曲线的面积即支座在该次滞回循环中消耗的能量;两个三角形OBE和ODF的面积之和表示理想弹性材料在相同滞回循环中消耗的能量.等效黏滞阻尼系数用式(2)和式(3)确定,其大小表征了滞回曲线的饱满程度,也就是耗能能力.
| $ E = \frac{{{S_{\left( {ABC + CDA} \right)}}}}{{{S_{\left( {OBE + ODF} \right)}}}}, $ | (2) |
| $ {h_{\rm{e}}} = \frac{E}{{2\pi }}. $ | (3) |
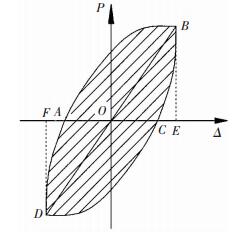
|
图 10 能量耗散系数 Figure 10 Energy dissipation coefficient |
两类隔振支座的等效黏滞阻尼系数见图 11.
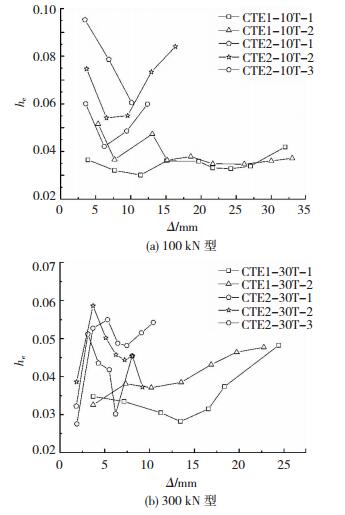
|
图 11 两类隔振支座等效黏滞阻尼系数 Figure 11 Equivalent viscous damping coefficient of two types of vibration isolation bearings |
由图 11可知,顶盖位无限制时,100 kN型两个试件的各级位移下的等效黏滞阻尼系数最小值为0.03,最大值为0.051,两个试件在加载前期有一定差异,在15 mm水平位移后二者随位移发展幅度相近,且均近似在0.03~0.04;300 kN型两个试件等效黏滞阻尼系数随位移的发展规律存在一定差异,其大小近似在0.03~0.05.顶盖位移受限制时,在相近位移区段,两类隔振支座的等效黏滞阻尼系数高于顶盖位移无限制情况;100 kN型3个试件间存在明显差异,各试件大小范围分别为0.04~0.06、0.055~0.085及0.06~0.095;300 kN型3个试件间在相应位移下也存在一定偏差,各试件的大小范围分别为0.03~0.052、0.028~0.055及0.038~0.058.
3.6 地震动下弹簧隔振支座侧移限值对于顶盖位移无限制隔振支座,根据单圈滞回曲线斜率的变化,通过做不同斜率段的切线可找到隔振支座弹簧损伤时的荷载及位移,见图 12.虽然水平位移过大可能导致弹簧单元中边角部弹簧压缩变形增大,且可能发生同一弹簧部分压缩、部分拉伸的情况,使隔振支座的刚度有增大的趋势,但这种局部的拉压复合作用也可能导致弹簧的损伤.
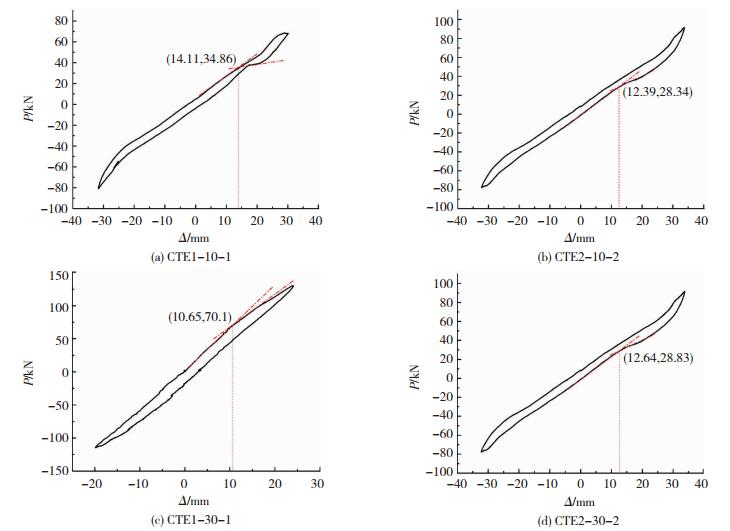
|
图 12 弹簧单元损伤点 Figure 12 Spring unit damage point |
CTE1-10-1加载至第6级荷载(13.9 mm位移)时弹簧单元出现损伤,CTE1-10-2,CTE1-30-1及CTE1-30-2均加载至第7级荷载(分别为12.6、10.7、12.4 mm位移)时弹簧单元出现损伤,可将初始损伤时的水平位移与支座高度之比作为相对位移限值,则为避免地震动下隔振支座的损伤,100 kN型隔振支座的水平弹性相对位移限值为1/2.68,300 kN型隔振支座的水平弹性相对位移限值为1/2.72;实际上这两个位移限值下,若隔振支座顶盖位移受限制,钢裙板已发生了一定损伤,虽然震后可将钢裙板更换,并不影响隔振支座的继续服役,但这种损伤的存在同时改变了隔振支座的刚度和耗能,为此,建议将上述限值作为弹簧隔振支座在罕遇地震下的侧移限值.
在多遇地震应保证布置隔振支座的上部设施处于良好的工作状态,地震后隔振支座及其上部设施应复位到静载下平衡位置,即应使弹簧隔振支座处于弹性工作阶段,建议支座弹性水平位移角限值,分别取为顶盖位移受限制支座的试件位移的弹性与非弹性阶段的交点位置,100 kN型隔振支座的水平弹性位移角限值为1/3.20,300 kN型隔振支座的水平弹性位移角限值为1/3.26.由于这两个值较为接近,且考虑到误差等不可避免因素,建议100 kN型和300 kN型隔振支座的水平弹性位移角限值均取两者中的较小值, 即1/3.26.
4 结论1) 完成了两类共计10个试件的弹簧隔振支座水平反复荷载与水平位移关系的拟静力试验,获得了考虑竖向荷载影响的滞回关系曲线,发现超过一定水平位移后盖板有位移限制的弹簧隔振支座,其水平位移表现为明显的非线性,其滞回曲线呈现一定的耗能特征;盖板位移无限制的弹簧隔振支座,竖向变形与较大水平变形的累加效应导致的局部弹簧出现不可逆的塑性变形.
2) 相近的极限位移条件下,顶盖位移无限制试件可加载的位移循环次数明显大于位移有限制试件.顶盖位移无限制时,支座滞回曲线均呈中部等宽度、近端部捏拢尖锐的“扁梭形”,位移基本线性发展,滞回曲线欠饱满.顶盖位移受限制的试件,滞回环为近两端部翘起“叶片状”.超过一定位移下,钢裙板对于隔振支座试件骨架曲线、割线刚度、耗能能力及黏滞阻尼系数影响显著.
3) 提出了两类弹簧隔振支座分别在多遇地震下的弹性刚度建议值及弹性变形限值,罕遇地震作用时可能发生弹簧隔振支座的弹塑性耗能行为,将造成局部弹簧永久位移,降低其竖向承载能力并使其产生明显的倾斜变形.建议不同设防烈度下考虑罕遇地震影响下弹簧隔振支座的位移弹性变形应组合竖向压缩.
| [1] |
何庆烈, 朱胜阳, 蔡成标, 等. 地铁浮置板用弹簧隔振器力学特性试验研究[J]. 铁道科学与工程学报, 2016, 13(8): 1492. HE Qinglie, ZHU Shengyang, CAI Chengbiao, et al. Experimental study on mechanical characteristics of the subway-using steel spring vibration isolator[J]. Journal of Railway Science and Engineering, 2016, 13(8): 1492. DOI:10.3969/j.issn.1672-7029.2016.08.007 |
| [2] |
何庆烈, 王建伟, 陈再刚. 地铁浮置板用隔振器刚度与阻尼试验[J]. 西南科技大学学报, 2015, 30(4): 41. HE Qinglie, WANG Jianwei, CHEN Zaigang. Stiffness and damping measurement of vibration isolator used for the metro floating slab[J]. Journal of Southwest University of Science and Technology, 2015, 30(4): 41. DOI:10.3969/j.issn.51-1660/C.2015.04.008 |
| [3] |
王建伟, 蔡成标, 朱胜阳. 浮置板轨道钢弹簧隔振器动态特性参数的频率与幅值依赖性试验研究[J]. 中国科学:技术科学, 2016, 46(8): 808. WANG Jianwei, CAI Chengbiao, ZHU Shengyang. Experimental study on frequency and amplitude dependent behavior of dynamic parameters of steel-spring vibration isolator used in floating slab track[J]. Scientia Sinica(Technologica), 2016, 46(8): 808. |
| [4] |
任莹, 管立加, 刘骞, 等. 弹簧隔振层在民用工程整体隔振中的减振分析[J]. 工程抗震与加固改造, 2015, 37(1): 77. REN Ying, GUAN Lijia, LIU Qian, et al. Analysis of spring vibration isolation layer of a residential engineering[J]. Earthquake resistant Engineering and Retrofitting, 2015, 37(1): 77. |
| [5] |
朱振江, 严雄. 隔振器横向刚度的测定[J]. 噪声与振动控制, 1994(2): 46. ZHU Zhenjiang, YAN Xiong. Determination of lateral stiffness of vibration isolator[J]. Noise and Vibration Control, 1994(2): 46. |
| [6] |
梁上燕, 肖安鑫, 耿传智. 阻尼钢弹簧浮置板轨道结构隔振性能分析[J]. 噪声与振动控制, 2013(1): 137. LIANG Shangyan, XIAO Anxin, GENG Chuanzhi. Analysis of vibration isolation performance of floating slab track structure with damping steel springs[J]. Noise and Vibration Control, 2013(1): 137. |
| [7] |
严济宽, 柴敏, 陈小琳. 振动隔振效果的评定[J]. 噪声与振动控制, 1997(6): 23. YAN Jikuan, CHAI Min, CHEN Xiaolin. Evaluation of vibration isolation effect[J]. Noise and Vibration Control, 1997(6): 23. |
| [8] |
姜袁, 朱乔森, 彭刚. SMA耗能弹簧的阻尼性能研究[J]. 三峡大学学报(自然科学版), 2003, 25(3): 213. JIANG Yuan, ZHU Qiaosen, PENG Gang. Investigation on damp capability of energy dissipation spring made of shape memory alloy[J]. Journal of China Three Gorges University(Natural Sciences), 2003, 25(3): 213. |
| [9] |
徐龙河, 樊晓伟, 逯登成, 等. 预压弹簧自恢复耗能支撑恢复力模型与滞回特性研究[J]. 工程力学, 2016, 33(10): 116. XU Longhe, FAN Xiaowei, LU Dengcheng, et al. Study on restoring force model and hysteretic behaviors of pre-pressed spring self-centering energy dissipation brace[J]. Engineering Mechanics, 2016, 33(10): 116. |
| [10] |
韦凯, 豆银玲, 杨麒陆, 等. 钢弹簧浮置板轨道的随机振动分析及参数优化[J]. 华中科技大学学报(自然科学版), 2017, 45(8): 115. WEI Kai, DOU Yinling, YANG Qilu, et al. Random vibration analysis and parameter optimization of steel spring floating-slab track[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2017, 45(8): 115. |
| [11] |
周颖, 龚顺明, 吕西林. 粘弹性阻尼器滞回曲线及特征参数的相似准则[J]. 中南大学学报(自然科学版), 2014, 45(12): 4317. ZHOU Ying, GONG Shunming, LU Xilin. Similarity of hysteretic loops and characteristic parameters of viscoelastic dampers[J]. Journal of Central South University (Science and Technology), 2014, 45(12): 4317. |
| [12] |
段忠东, 闫桂荣, 欧进萍. 土木工程结构振动损伤识别面临的挑战[J]. 哈尔滨工业大学学报, 2008, 40(4): 505. DUAN Zhongdong, YAN Guirong, OU Jinping. Challenges in applying the vibration-based damage detection to civil structures[J]. Journal of Harbin Institute of Technology, 2008, 40(4): 505. DOI:10.3321/j.issn:0367-6234.2008.04.001 |
 2018, Vol. 50
2018, Vol. 50


