随着结构设计技术的创新和新型结构形式的不断涌现,现代结构向着轻质、大体量和多样化的方向发展,出现了许多大跨度空间结构,其中铰接杆系结构运用最为广泛.由于杆系结构构件数量众多,局部构件的破坏有可能引起结构的连续性倒塌,造成不可估量的经济财产和人员安全损失,因此铰接杆系结构的鲁棒性显得尤为重要.各国规范[1-4]中鲁棒性很少有量化规定,但都要求对重要部位的构件进行加强来保证结构鲁棒性[5-6].由此可见,构件重要性是结构鲁棒性的一个重要指标.
现有结构构件重要性评价的研究中,根据是否考虑荷载作用的影响,可以分为两类评价方法.与荷载作用相关的评价方法,除了考虑结构体系的几何拓扑和刚度分布外,还考虑荷载的作用.文献[7-8]基于刚度、强度、能量等多种方法,探讨了结构构件重要性的评价方法及结构鲁棒性的评价指标.文献[9]根据结构体系传力路径中传递荷载比例大的构件重要性大的思路, 定义了考虑荷载作用的广义结构刚度.文献[10]基于H∞鲁棒控制理论,采用系统传递函数的H∞范数作为桁架结构鲁棒性定量评价指标,并基于破坏场景确定构件的重要性系数.文献[11]提出了基于节点主刚度系数的节点构形度的概念,并通过凝聚过程建立结构拓扑关系层级模型,来识别得到结构具有易损性的破坏模式.文献[12]总结了平均应力比法、稳定退化系数法和刚度退化系数3种关键构件评估方法,并引入客观赋权法综合考虑3种方法,得到一个综合的构件重要性评价指标.文献[13]提出了初选范围的多重响应分析法,并将其应用于世界大学生运动会主体育场结构中.文献[14]提出了基于系统可靠度理论的评价方法,其构件重要性评价指标定义为该构件对结构整体可靠度的影响.但该方法仅具有理论意义,难以应用于一般的工程结构.文献[15]将可靠度退化作为鲁棒性评价指标,以结构位移和应力响应作为性能标准,提出了基于概率易损性的杆件重要性分析方法.另一类与荷载无关的评价方法,主要从结构体系的几何拓扑和刚度分布来分析结构构件的重要性.文献[16]提出用标准化后的结构刚度矩阵行列式来衡量结构的安全性,并将重要性评价指标定义为原结构的刚度矩阵行列式与拆除构件后结构的刚度矩阵行列式的比值.文献[17]从图论的角度寻找结构中可能因为很小的损伤引起不成比例破坏的潜在损伤源,在研究结构易损性过程中基于刚度矩阵行列式的概念提出了整体性指标,并基于该指标定义了损伤程度指标.
许多研究通过易损性、可靠度[18-19]、敏感性等角度研究结构鲁棒性,本文拟从冗余度入手,不考虑特定荷载的作用,研究构件在杆系结构体系构成中的重要性.对于超静定结构,结构冗余度是指“由于杆件过多,其内力、反力等无法由平衡条件确定”[20]的特性.文献[21]基于变形形式的能量方程,提出了杆、梁和板的冗余度理论.文献[22-23]在此基础上提出了索杆柔性体系的冗余度理论,并引入了预应力的作用.文献[24]对梁系结构冗余度及其特性进行研究,将整体冗余度的概念扩展到单元层面.该冗余度理论将结构刚度,几何拓扑以及材料特性等物理信息集成于冗余度矩阵中,能够综合反映结构自身的物理特性.本文以铰接杆系结构为研究对象,基于单元层面的冗余度,提出一种定量评价铰接杆系结构构件重要性的方法,综合考虑结构物理特性对构件重要性进行评价.根据单元冗余度分布的均衡性,定义杆系结构单元冗余度标准差和单元冗余度平均值的商为结构冗余度分布系数.通过考察拆除不同构件的情况下,剩余结构单元冗余度分布系数的大小来定量分析杆系结构构件重要性,并定义剩余结构单元冗余度分布系数为构件重要性评价系数.通过3个算例分析,验证结构冗余度分布系数反映结构冗余度分布的均衡性,可作为评价结构鲁棒性的一个指标;验证剩余结构单元冗余度分布系数可作为构件重要性的定量评价指标.
1 杆系结构单元冗余度理论为探索杆系结构冗余度分布与结构本身物理特性之间的关系,本文通过对变形形式的势能方程进行推导,将冗余度的概念扩展到单元层面.杆系结构的势能方程可表示为更一般的形式[21]:
| $ \begin{array}{l} \boldsymbol{\prod} \left( {\mathit{\boldsymbol{X}}, \mathit{\boldsymbol{V}}, \mathit{\boldsymbol{S}}} \right) = \frac{1}{2}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{CV}}-{\mathit{\boldsymbol{S}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{D}}_0} + \mathit{\boldsymbol{V}}-\mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{X}} \right)} \right)-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{P}}^{\rm{T}}}\left( {\mathit{\boldsymbol{X}} - {\mathit{\boldsymbol{X}}_0}} \right), \end{array} $ | (1) |
式中:X为变形后的节点坐标向量,X0为变形前的节点坐标向量,V为变形向量,S为单元内力向量,C为变形向量对应的权系数矩阵,D0为变形前的形状参数向量,F(X)为变形后的形状参数向量,与D0对应,P为节点外荷载向量.
通过势能方程分别对未知量X、V、S求偏导,可得到三大基本方程:
| $ 平衡方程:\frac{{\partial \mathit{\Pi} }}{{\partial \mathit{\boldsymbol{X}}}} = {\left( {\frac{{\partial \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{X}} \right)}}{{\partial \mathit{\boldsymbol{X}}}}} \right)^{\rm{T}}}\mathit{\boldsymbol{S}}-\mathit{\boldsymbol{P}} = 0, $ | (2) |
| $ 物理方程:\frac{{\partial \mathit{\Pi} }}{{\partial \mathit{\boldsymbol{V}}}} = \mathit{\boldsymbol{CV}}-\mathit{\boldsymbol{S}} = 0, $ | (3) |
| $ 几何方程:\frac{{\partial \mathit{\Pi} }}{{\partial \mathit{\boldsymbol{S}}}} =-\left( {{\mathit{\boldsymbol{D}}_0} + \mathit{\boldsymbol{V}}-\mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{X}} \right)} \right) = 0. $ | (4) |
根据小位移假定,变形后形状参数向量F(X)为
| $ \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{X}} \right) \approx \mathit{\boldsymbol{BX}}, $ | (5) |
式中B为初始状态下杆系结构的协调矩阵.则雅克比矩阵J的表达式为
| $ \mathit{\boldsymbol{J}} = \frac{{\partial \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{X}} \right)}}{{\partial \mathit{\boldsymbol{X}}}} \approx \mathit{\boldsymbol{B}}. $ | (6) |
由式(4)移项并对F(X)泰勒展开可得:
| $ \begin{array}{l} \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{X}} \right)-{\mathit{\boldsymbol{D}}_0} \approx \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{\tilde X}}} \right) + \frac{{\partial \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{X}} \right)}}{{\partial \mathit{\boldsymbol{X}}}}\left( {\mathit{\boldsymbol{X}}-\mathit{\boldsymbol{\tilde X}}} \right)-{\mathit{\boldsymbol{D}}_0} = \\ \;\;\;\;\;\;\mathit{\boldsymbol{J}}\Delta \mathit{\boldsymbol{X}} - \left( {{\mathit{\boldsymbol{D}}_0} - \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{\tilde X}}} \right)} \right) - \mathit{\boldsymbol{J}}\Delta \mathit{\boldsymbol{X}} - \mathit{\boldsymbol{\tilde D}}. \end{array} $ | (7) |
式中:ΔX为坐标增量,
将式(7)代入式(2)、(3),可得坐标增量ΔX和内力S表达式:
| $ \Delta \mathit{\boldsymbol{X}} = {\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{CJ}}} \right)^{-1}}\left( {\mathit{\boldsymbol{P}} + {\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{C\tilde D}}} \right), $ | (8) |
| $ \begin{array}{l} \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{CV}} = \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{J}}\Delta \mathit{\boldsymbol{X}}- \mathit{\boldsymbol{\tilde D}}} \right) = \\ \;\;\;\;\;\;\mathit{\boldsymbol{C}}\left[{\mathit{\boldsymbol{J}}{{\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{CJ}}} \right)}^{-1}}\mathit{\boldsymbol{P}}-\left( {\mathit{\boldsymbol{E}}-{\mathit{\boldsymbol{J}}_0}} \right)\mathit{\boldsymbol{\tilde D}}} \right] = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{S}}_{\rm{F}}} + {\mathit{\boldsymbol{S}}_{\rm{E}}}. \end{array} $ | (9) |
式中:J0=J(JTCJ)-1JTC,E表示和J0维数相同的单位矩阵,SF表示由外力荷载引起的内力分量,SE表示由已知变形引起的内力分量.为分离出只与结构自身特性相关的部分,只需考虑
根据文献[21-22],容易证明矩阵R为幂等矩阵.结合幂等矩阵的性质,由矩阵分析理论[25]可推导得到杆系结构对应的矩阵R的秩和迹分别为:
| $ {\rm{rank}}\left( {{\mathit{\boldsymbol{J}}_0}} \right) = {\rm{tr}}\left( {{\mathit{\boldsymbol{J}}_0}} \right) = {\rm{tr}}\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{CJ}}{{\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{CJ}}} \right)}^{-1}}} \right) = m, $ | (10) |
| $ \begin{array}{l} {\rm{tr}}\left( \mathit{\boldsymbol{R}} \right) = {\rm{rank}}\left( \mathit{\boldsymbol{R}} \right) = {\rm{rank}}\left( \mathit{\boldsymbol{E}} \right)-{\rm{rank}}\left( {{\mathit{\boldsymbol{J}}_0}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;b-m-n. \end{array} $ | (11) |
式中:m是节点自由度数,b为杆件数,n为杆系结构超静定数.
平面杆系结构:m=2k-a, n=b-(2k-a),
空间杆系结构:m=3k-a, n=b-(3k-a),
式中k为节点总数,a为约束自由度数.
式(11)从数学角度证明了矩阵R的秩等于结构的超静定数,反映结构整体的冗余度,用RT表示.并且冗余度矩阵的迹也等于结构超静定数,即其对角线元素之和等于结构超静定数.用ri表示矩阵R中第i个对角元素,对于杆系结构,ri表示i号构件对结构冗余度的贡献,将ri定义为i号杆件的单元冗余度.则结构整体冗余度RT和i号构件单元冗余度ri的关系式为
| $ {R_{\rm{T}}} = {\rm{rank}}\left( \mathit{\boldsymbol{R}} \right) = {\rm{tr}}\left( \mathit{\boldsymbol{R}} \right) = \sum\limits_{i = 1}^b {{r_i}} . $ | (12) |
铰接杆系结构的冗余度矩阵R为内力强制重分布矩阵,与刚度、几何拓扑等结构本身物理特性相关,矩阵的秩等于结构超静定数,反映结构整体冗余度.该矩阵的对角线元素对应结构整体冗余度在各单元上的分量,反映结构冗余分布特性.本节基于冗余度矩阵,分别提出反映结构冗余度分布均衡性的杆系结构冗余度分布系数和基于剩余结构冗余度分布系数的构件重要性评价方法.该构件重要性评价方法仅讨论构件在结构体系构成中的重要性,不考虑外荷载的作用.
2.1 冗余度分布系数当结构中不存在个别突出构件时,即当结构单元冗余度分布相对均匀时,结构具有较好的鲁棒性.因此,结构冗余度分布的均衡性可作为结构鲁棒性的一个评价标准.
由式(12)中所示的结构整体冗余度和单元冗余度之间的关系,可得铰接杆系结构单元冗余度平均值r为
| $ \bar r = \frac{{{R_{\rm{T}}}}}{b}. $ | (13) |
为考察整体结构冗余分布的均衡性,通过标准差计算公式可得单元冗余度标准差σ为
| $ \sigma = \sqrt {\frac{1}{b}\sum\limits_i^b {{{\left( {{r_i}-\bar r} \right)}^2}} }, $ | (14) |
式中ri为i号杆件对应的单元冗余度.
为定量评价结构冗余度分布的均衡性,定义杆系结构单元冗余度标准差σ和单元冗余度平均值r的商为杆系结构冗余度分布系数λ,其表达式为
| $ \lambda = \frac{\sigma }{{\bar r}}. $ | (15) |
因此,冗余度分布系数λ为杆系结构冗余度分布均衡性的评价指标.冗余度分布系数λ越小,则结构冗余度分布越均匀,结构鲁棒性越好;反之,则结构冗余度分布越不均匀,结构鲁棒性越差.
2.2 构件重要性系数结构中一个构件的破坏对结构造成的影响越大,则该构件的重要性越大.本文基于结构冗余度分布的均衡性,即冗余度分布系数,提出一种定量评价杆系结构构件重要性的方法:定义拆除不同构件为不同的破坏模式,通过对比不同破坏模式下剩余结构单元冗余度分布的均衡性来评价构件重要性.
拆除杆件j后,杆系结构剩余结构的单元冗余度平均值rj为
| $ {\bar r_j} = \frac{{{R_{\rm{T}}}-1}}{{b-1}}, $ | (16) |
式中j为拆除杆件对应的编号,并对应破坏模式编号.
拆除杆件j后,空间铰接杆系结构剩余结构的单元冗余度标准差σj为
| $ {\sigma _j} = \sqrt {\frac{1}{{b-1}}\sum\limits_i^{b-1} {{{\left( {r_i^j-{{\bar r}_j}} \right)}^2}} }, $ | (17) |
式中rij为拆除杆件j后剩余结构中i号杆件的单元冗余度.
基于冗余度分布系数指数λ,定义拆除杆件j后的剩余结构单元冗余度分布指数λj为杆件j的构件重要性系数,其表达式为
| $ {\lambda _j} = \frac{{{\sigma _j}}}{{{{\bar r}_j}}}. $ | (18) |
因此,杆件j的构件重要性系数λj越大,则拆除该杆件对结构的影响越大,该杆件在结构中越重要;反之,拆除该杆件对结构的影响越小,该杆件在结构中越次要.基于每根杆件的构件重要性系数,对结构构件的重要性进行排序,操作步骤如下:
1) 根据结构对称性对杆件进行分组(共t组),每组中选择一根杆件作为该组的代表杆件并编号j(j=1, 2, …, t).
2) 分别拆除每组的代表杆件,并为对应的破坏形式编号.拆除代表杆件j,并将对应的破坏形式记为破坏形式j.
3) 通过杆系结构冗余度理论计算各个破坏形式下剩余结构的冗余度矩阵和单元冗余度.破坏形式j下剩余结构的冗余度矩阵为Rj,此时剩余结构中i号杆件的单元冗余度为rij=Riij.
4) 根据式(15)~(17)计算各根代表杆件的构件重要性系数.代表杆件j的构件重要性系数为λj.
5) 根据各根代表杆件的重要性系数为杆件重要性进行排序.
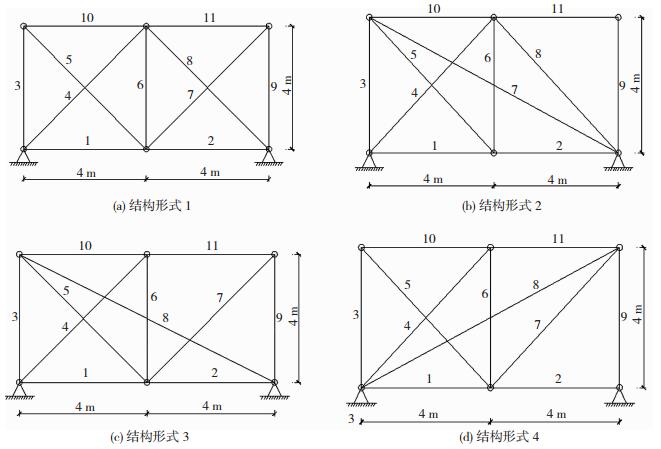
3 算例 3.1 平面桁架的冗余度分布均衡性如图 1所示4种形式的平面桁架结构,所有杆件截面面积均为A=0.000 5 m2,弹性模量均为E=2×105 MPa.根据杆系结构冗余度分布系数计算方法,可分别得到4种结构的单元冗余度和冗余度分布系数,结果见表 1.
|
图 1 4种形式的平面桁架 Figure 1 Four forms of plane truss |
| 表 1 4种平面桁架的单元冗余度和冗余度分布系数 Table 1 Element-redundancy and redundancy distribution indexes of four plane trusses |
由表 1可得,结构形式1的冗余度分布系数最小,结构冗余均衡性最好; 结构形式4的冗余分布系数最大,结构冗余度均衡性最差.4种结构冗余度分布均衡性的排序依次为:结构形式1>结构形式3>结构形式2>结构形式4,结果符合直观判断.
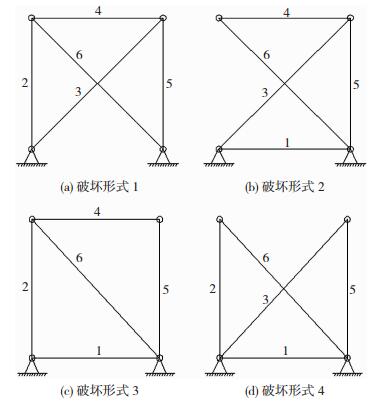
3.2 平面桁架的构件重要性如图 2所示平面桁架结构,A=0.000 5 m2,E=2×105 MPa.根据结构对称性对杆件进行分组,分别拆除各组中的代表杆件可得4种破坏形式见图 3.分别计算原结构和4种破坏形式下剩余结构的单元冗余度值,根据本文提出的构件重要性评价方法计算原结构的冗余度分布系数和4根代表杆件的构件重要性系数,结果见表 2.由表 2可得,原始结构的总冗余度为2,4种破坏形式下结构的总冗余为1,说明任意一根杆件破坏都会造成总冗余的下降.原始结构中杆件1为完全冗余杆件,可以拆除,因此破坏形式1(拆除杆件1)对剩余杆件的单元冗余度没有影响.破坏形式2、3、4(拆除杆件2、3、4)对杆件1的单元冗余度没有影响,而剩余结构中其余杆件的单元冗余度均为0,不能再拆除.杆件1的构件重要性系数为λ1=0.515,其余杆件的构件重要性系数为λ2, 3, 4=1.790,因此对于该平面桁架,杆件1重要性最低,其余杆件的重要性相当.其中,4单元和5单元截面面积和长度均相等,从图 2可知,4单元和5单元关于单元3对称,且拓扑连接关系相似,因此采用本文提出的基于冗余度的构件重要性评价方法可得出4和5单元的构件重要性相同.该结论仅讨论构件在结构体系构成中的重要性,不考虑特定荷载作用.

|
图 2 简单平面桁架 Figure 2 Simple plane truss |
|
图 3 平面桁架的4种破坏形式 Figure 3 Four damaged forms of plane truss |
| 表 2 平面桁架的单元冗余度和构件重要性系数 Table 2 Element-redundancy and the component importance indexes of plane truss |
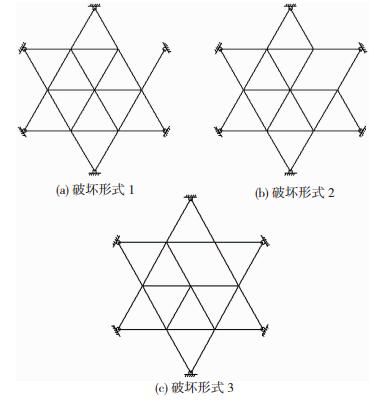
以图 4六角星形穹顶为例,该空间杆系结构由24根铰接杆件组成,所有杆件A=313 cm2,E=3.030×105 MPa,结构内圈半径R1=25 cm,结构外圈半径R2=43.3 cm,结构内外圈矢高分别为h1=2.0 cm, h2=6.66 cm.根据结构对称性对杆件进行分组,所有外层纵杆为①组,所有环杆为②组,所有内层纵杆为③组,分组见图 5.选择各组中的任意一根杆件作为该组的代表杆件,分别拆除这3根代表杆件,可得到对应的3种破坏形式,见图 6.

|
图 4 六角星形穹顶及其几何参数 Figure 4 Hexagonal space dome and its geometric parameters |

|
图 5 六角星形穹顶杆件分组 Figure 5 Grouping of hexagonal space dome |
|
图 6 六角星形穹顶破坏形式 Figure 6 Damage forms of hexagonal space dome |
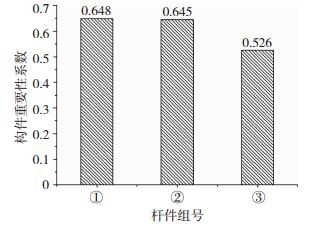
分别计算3种破坏形式下单元冗余度标准差σj(j=1, 2, 3)与单元冗余度平均值rj(j=1, 2, 3),进而计算剩余结构冗余度分布指数λ1、λ2、λ3,计算结果见图 7.
|
图 7 六角星形穹顶构件重要性系数 Figure 7 Component importance indexes of hexagonal space dome |
原始结构的冗余度为RT=3,三种破坏形式下结构的冗余度均为RT1, 2, 3=2,说明拆除任意一根杆件都会对结构鲁棒性造成削弱.根据2.1节的计算方法可得原始结构冗余度分布系数为λ=0.379,由图 7计算结果可得,三组代表杆件的构件重要性系数分别为λ1=0.648, λ2=0.645, λ3=0.526,破坏形式1对结构鲁棒性的削弱最大,破坏形式3最小,因此该六角星形穹顶的构件重要性排序为:①组杆件>②组杆件>③组杆件.
4 结论1) 单元冗余度分布系数λ能够定量反映结构冗余分布的均衡性,本文通过单元冗余度分布系数来定量评价结构鲁棒性.通过算例1表明,λ越小则结构冗余分布越均匀,结构鲁棒性越好;反之,则结构冗余分布越不均匀,结构鲁棒性越差.
2) 本文通过考察构件拆除后,剩余结构单元冗余度分布系数的大小来定量评价铰接杆系结构构件重要性,并定义其为构件重要性系数.通过算例2、3表明,构件j对应的单元冗余度分布系数λj越大,说明拆除杆件j对结构冗余度分布的影响越大,构件重要性越高;反之,则构件重要性越小.
3) 荷载作用具有不确定性,不同荷载作用下结构响应及每根杆的作用不同,考虑荷载情况下很难统一定义杆件的作用或重要性.因此,本文仅讨论杆件在结构体系构成中的重要性,将剩余结构的单元冗余度分布系数λj作为构件重要性评价指标.该指标从构件刚度和几何拓扑等物理特性出发,不考虑外荷载的作用来对构件的重要性作出评价.该评价方法简洁明了,避免了复杂的力学分析和繁冗的数值迭代计算,其优势在复杂铰接杆系结构中更为突出.
| [1] |
CEN. Eurocode: Basis of structural design: EN 1990: 2002[S]. Brussels: CEN/TC 250, 2002
|
| [2] |
CEN. Eurocode 1: Actions on structures part 1-7: general actions-accidental actions: EN 1991-1-7: 2006[S]. Brussels: CEN/TC 250, 2002
|
| [3] |
ASCE. Minimum design loads for buildings and other structures: SEI/ASCE7-05[S]. Reston: American Society of Civil Engineers, 2005
|
| [4] |
Design of buildings to resist progressive collapse: UFC4-023-03[S]. Washington D.C: Unified Facilities Criteria, 2009
|
| [5] |
高层建筑混凝土结构技术规程: JGJ 3—2010[S].北京: 中国建筑工业出版社, 2010
|
| [6] |
建筑结构荷载规范: GB 5009—2012[J].北京: 中国建筑工业出版社, 2012
|
| [7] |
柳承茂, 刘西拉. 基于刚度的构件重要性评估及其与冗余度的关系[J]. 上海交通大学学报, 2005, 39(5): 746. DOI:10.3321/j.issn:1006-2467.2005.05.019 |
| [8] |
高扬, 刘西拉. 结构鲁棒性评价中的构件重要性系数[J]. 岩石力学与工程学报, 2008, 27(12): 2575. DOI:10.3321/j.issn:1000-6915.2008.12.027 |
| [9] |
叶列平, 林旭川, 曲哲, 等. 基于广义结构刚度的构件重要性评价方法研究[J]. 建筑科学与工程学报, 2010, 27(1): 1. |
| [10] |
何江飞, 高博青. 桁架结构的易损性评价及破坏场景识别研究[J]. 浙江大学学报(工学版), 2012, 46(9): 1634. |
| [11] |
刘文政, 叶继红. 杆系结构的拓扑易损性分析[J]. 振动与冲击, 2012, 31(17): 67. DOI:10.3969/j.issn.1000-3835.2012.17.012 |
| [12] |
朱丽华, 王宁娟, 戴军. 基于客观赋权法的构件重要性评估[J]. 建筑科学与工程学报, 2015, 32(4): 46. DOI:10.3969/j.issn.1673-2049.2015.04.007 |
| [13] |
田黎敏, 魏建鹏, 郝际平, 等. 基于多重响应的大跨度空间网格结构重要构件评估方法[J]. 湖南大学学报(自然科学版), 2016, 43(11): 39. DOI:10.3969/j.issn.1674-2974.2016.11.007 |
| [14] |
GHARAIBEH E S, FRANGOPOL D M, ONOUFRIOU T. Reliability-based importance assessment of structural members with applications to complex structures[J]. Computers & Structures, 2002, 80(12): 1113. DOI:10.1016/S0045-7949(02)00070-6 |
| [15] |
杨逢春.基于结构体系可靠度的空间结构杆件重要性分析[D].杭州: 浙江大学, 2015
|
| [16] |
NAFDAY A M. System safety performance metrics for skeletal structures[J]. Journal of Structural Engineering, 2008, 134(3): 499. DOI:10.1061/(ASCE)0733-9445(2008)134:3(499) |
| [17] |
AGARWAL J, BLOCKLEY D I. Vulnerability of structural systems[J]. Structural Safety, 2003, 25: 263. DOI:10.1016/S0167-4730(02)00068-1 |
| [18] |
樊学平, 吕大刚. 基于BDNM的桥梁结构可靠度预测[J]. 哈尔滨工业大学学报, 2014, 46(2): 1. FAN Xueping, LV Dagang. Reliability prediction of bridge structures based on BDNM[J]. Journal of Harbin Institute of Technology, 2014, 46(2): 1. DOI:10.11918/j.issn.0367-6234.2014.02.001 |
| [19] |
吕大刚, 宋鹏彦, 王光远. 考虑统计不确定性的结构可靠度分析方法[J]. 哈尔滨工业大学学报, 2011, 43(8): 11. LV Dagang, SONG Pengyan, WANG Guangyuan. Reliability analysis methods of structures considering statistical uncertainty[J]. Journal of Harbin Institute of Technology, 2011, 43(8): 11. DOI:10.11918/j.issn.0367-6234.2011.08.003 |
| [20] |
陈以一, 赵宪忠. 高冗余度钢结构倒塌设计控制设计指南[M]. 上海: 同济大学出版社, 2007: 77.
|
| [21] |
STRÖBEL D. Die anwendung der ausgleichungsrechnung auf elastomechanische systeme[D]. Munchen: Universität Stuttgart, 1995
|
| [22] |
朱红飞.索杆体系的冗余度及其特性分析[D].上海: 上海交通大学, 2012
|
| [23] |
ZHOU Jinyu, CHEN Wujun, ZHAO Bin, et al. Distributed indeterminacy evaluation of cable-strut structures: formulations and applications[J]. Journal of Zhejiang University, 2015, 16(9): 737. DOI:10.1631/jzus.A1500081 |
| [24] |
袁行飞, 蒋淑慧, 丁锐. 梁系结构冗余度及其特性分析[J]. 建筑结构学报, 2016, 37(11): 167. |
| [25] |
史荣昌, 魏丰. 矩阵分析[M]. 北京: 北京理工大学出版社, 1996: 16.
|
 2018, Vol. 50
2018, Vol. 50


