2. 计算智能与智能系统北京市重点实验室(北京工业大学),北京 100124;
3. 数字社区教育部工程研究中心(北京工业大学),北京 100124
2. Beijing Key Laboratory of Computational Intelligence and Intelligent Systems (Beijing University of Technology), Beijing 100124, China;
3. Engineering Research Center of Digital Community (Beijing University of Technology), Ministry of Education, Beijing 100124, China
随着中国水环境问题的日益突出,污水处理作为保护环境的重要措施,受到全社会越来越多的关注.生化需氧量(BOD)反映污水中生物可降解有机物含量.是评价水质的重要指标,也是污水处理过程中直接控制的参数,能否对BOD进行实时监测已成为提高治污质量的关键.由于仪器水平或成本方面的原因,目前,污水处理厂多采用离线人工化验的方法:BOD5离线分析测定周期为5 d,检测存在滞后,直接影响污水处理过程的实时控制和优化操作.实现BOD的高品质在线实时监测是个难题.软测量技术具有成本低、时效性好和准确度高等优点,被引入到污水处理过程中,为出水BOD高品质实时监测提供一个有效途径[1].
污水处理过程具有机理复杂、强非线性和高度不确定性等特点,因而基于生化反应机理建立软测量模型的传统方法效果欠佳.而神经网络凭借其优良的逼近能力被广泛应用于污水处理出水BOD软测量建模中.祁国强等[2]提出基于径向基函数(RBF)神经网络的软测量方法,运用大量实测数据对RBF神经网络进行训练和仿真,通过实验证明基于RBF神经网络的软测量模型的有效性.Huang等[3]建立基于粒子群的改进最小二乘支持向量机回归模型,实现出水BOD、化学需氧量(COD)、总氮(TN)、氨氮(NH4-N)、总固体悬浮物(TSS)等浓度的预测,取得较精确的结果.王树东等[4]提出基于混合递阶遗传算法优化RBF神经网络的BOD软测量方法,并通过实验证明此方法具有较好的实时性、稳定性和较高的预测精度.许玉格等[5]提出一种基于快速相关向量机(Fast-RVM)的在线软测量回归模型来实时预测出水BOD,并对比支持向量机和相关向量机在离线和在线情况下的预测效果,通过实验证明基于Fast-RVM的在线软测量回归模型能取得更好的预测效果.Qiao等[6]将COD、固体悬浮物(SS)、pH、溶解氧(DO)作为输入变量,利用改进的T-S模糊神经网络模型实现出水BOD的预测,取得较好的结果.当前工作多是获得一个单一值预测出水BOD浓度,而未曾给出评估真实值和预测值之间偏差(即预测误差)的有效方法.即使已采用均方根误差(RMSE)来评估神经网络建模精度,但通过此指标不易直接导出各时刻预测误差的计算公式.目前,围绕污水处理区间预测模型开展研究的工作尚不多见[7-8].
系统辨识理论中的区间预测方法有很多[9-16],基本上可以分为两大类.一类方法基于随机误差假设,如最小二乘法或极大似然法,要求误差的统计特性已知或部分已知,然后通过概率论给出被估计量的置信区间[9-10].另一类方法基于有界误差假设,如集员辨识,只要求误差有界而不需要知道其统计特性,然后通过集理论给出被估计量的置信区间[11-16].文献[7-8]提出的污水处理软测量方法即属于第一类.而在实际应用中误差的统计特性可能难以获得,此时第一类方法给出的置信区间不一定可靠.为此,给出一种新的BOD软测量方法,可以实现其保证估计.利用径向基函数神经网络的逼近能力,将其用于污水处理出水BOD软测量建模.径向基函数神经网络的中心被确定之后,考虑到建模误差有界,使用参数线性集员辨识算法得到网络输出权值的集合描述.在污水处理系统运行过程中,所建立好的软测量模型可以预测出水BOD的上下界.此外,本文建立多个软测量模型,并将多模型测量结果进行融合以降低单一模型所给结果的保守性.
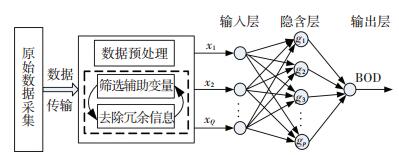
1 BOD软测量模型 1.1 软测量模型整体结构神经网络软测量模型的一般设计步骤为:辅助变量的初选、现场(原始)数据采集、数据预处理、软测量模型搭建.辅助变量的初选是在可测变量集中初步选择与被估计变量有关的原始辅助变量,这些变量中部分可能是相关变量.数据预处理利用现场的历史数据作统计分析计算,将原始辅助变量化成少数几个互不相关的变量作为神经网络模型的输入.这里现场数据指某污水处理厂记录的历史数据及实际运行数据.本文设计污水处理出水BOD软测量模型整体结构如图 1所示.
|
图 1 BOD软测量模型整体结构 Figure 1 Structure of the soft sensor for BOD |
数据预处理主要是去除冗余信息,选取BOD预测的主要辅助变量.由于取自污水处理现场的参数不是全部有助于出水水质参数BOD的预测,在预测前首先需要确定选择哪些变量作为软测量模型的输入.筛选辅助变量的主要目的是:简化神经网络模型的输入,提高网络的预测精度与计算效率.主元分析(PCA)是最常见的方法[17],该方法通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分.限于篇幅和突出重点,PCA的具体计算公式参考文献[17].
1.3 RBF神经网络模型RBF神经网络因为其简单的拓扑结构和强大的逼近能力,在软测量建模中得到广泛的应用.RBF神经网络是典型的三层前馈网络,包括输入层、非线性隐含层和线性输出层,可以表示为
| $ y = \sum\limits_{i = 1}^p {{w_i}{g_i}\left( {x, \sigma, {c_i}} \right).} $ | (1) |
式中:y∈R和x∈RQ分别为网络的输出和输入,在软测量模型中分别代表出水BOD和辅助变量,Q表示辅助变量的个数;gi(x, σ, ci)为神经网络第i个隐含层节点的输出,ci∈RQ和σ∈R分别为中心和宽度;wi∈R为线性输出权值; p为隐含层节点个数.RBF神经网络的隐单元基函数
| $ {g_i}\left( {x, \sigma, {c_i}} \right) = \exp \left( {-\frac{{{{\left\| {x-{c_i}} \right\|}^2}}}{{{\sigma ^2}}}} \right), $ | (2) |
式中
将降维后的数据分成两部分.一份用于神经网络模型建立,表示为D1={xk, yk}k=1N;另一份用于模型预测,表示为D2={xk, yk}k=N+1L.软测量模型建立好后,预测出水BOD的过程可以表示为
| $ {\hat y_k} = \sum\limits_{i = 1}^p {{{\hat w}_i}{g_i}\left( {{x_k}, \sigma, {c_i}} \right)}, N + 1 \le k \le L. $ | (3) |
式中:
如果采用集员辨识算法估计RBF神经网络输出权值wi,则可以预测出水BOD的上下界.
2 BOD置信区间计算 2.1 置信区间的基本计算采用聚类算法[18]确定RBF神经网络的中心ci和宽度σ.此算法的优点在于不需要知道数据集的任何先验知识,一旦神经网络隐含层中心和宽度被确定,就可以得到关于输出权值wi的线性方程
| $ {y_k} = \mathit{\boldsymbol{\phi}} _k^{\rm{T}}\mathit{\boldsymbol{\theta }} + {e_k} = \sum\limits_{i = 1}^p {{w_i}{g_i}\left( {{x_k}, \sigma, {c_i}} \right)} + {e_k}. $ | (4) |
式中
| $ {\mathit{\boldsymbol{\phi}} _k} = {\left[{{g_1}\left( {{x_k}, \sigma, {c_1}} \right), {g_2}\left( {{x_k}, \sigma, {c_2}} \right), \cdots, {g_p}\left( {{x_k}, \sigma, {c_p}} \right)} \right]^{\rm{T}}}, $ | (5) |
| $ \boldsymbol{\theta} = {\left[{{w_1}, {w_2}, \cdots, {w_p}} \right]^{\rm{T}}}. $ | (6) |
ek包含RBF神经网络中心、宽度和输出权值的选择带来的建模误差,而建模误差是与神经网络逼近能力有关的有界量,则可认为ek为有界误差,即|ek|≤ε.
集员辨识是一种有效的可以替代随机参数估计(如最小二乘和极大似然估计)的方法,因为其在应用时只需要知道误差的上下界.这里采用集员辨识方法估计神经网络的输出权值.一方面是因为这里的估计问题符合集员辨识的应用条件,另一方面以集员辨识的估计结果为基础可以给出BOD的置信区间.
由样本数据D1={xk, yk}k=1N、误差的有界假设|ek|≤ε以及式(4)可以得到
| $ {S_k} = \left\{ {\theta \in {{\bf{R}}^p}:\left| {{y_k}-\mathit{\boldsymbol{\phi}} _k^{\rm{T}}\mathit{\boldsymbol{\theta }}} \right| \le \varepsilon } \right\}, k = 1, 2, \cdots, N. $ | (7) |
N个Sk的交集可得到一个凸多面体ΘN⊂Rp,即
| $ \hat y_k^{\rm{m}} = \mathop {\min }\limits_{\theta \in {\mathit{\Theta} _N}} \mathit{\boldsymbol{\phi}} _k^{\rm{T}}\mathit{\boldsymbol{\theta }}, \hat y_k^{\rm{M}} = \mathop {\max }\limits_{\mathit{\boldsymbol{\theta }} \in {\mathit{\Theta} _N}} \phi _k^{\rm{T}}\mathit{\boldsymbol{\theta }}. $ | (8) |
这个区间表示出神经网络模型输出
| $ {y_k} \in \left[{\hat y_k^{\rm{m}}-\varepsilon, \hat y_k^{\rm{M}} + \varepsilon } \right], k \ge N + 1. $ | (9) |
出水BOD的置信区间式(8)和(9)可通过线性规划的方法得到,但是当隐含层节点数太多和/或样本数据量很大时,该方法计算成本过重.为了降低计算成本,采用集员辨识中的椭球外界算法给出一个包含权值不确定性集ΘN的椭球
| $ {E_N} = \left\{ {\theta \in {{\bf{R}}^p}:{{\left( {\theta-{{\hat \theta }_N}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}_N^{-1}\left( {\theta-{{\hat \theta }_N}} \right) \le 1} \right\}. $ | (10) |
式中:
算法1
初始化.置
递推:对k=1, 2, …, N.
步骤1(a) 计算
| $ {\beta _k} = \boldsymbol{\phi} _k^{\rm{T}}{P_{k-1}}{\boldsymbol{\phi} _k}, $ | (11) |
| $ {v_k} = {y_k}-\boldsymbol{\phi} _k^{\rm{T}}{\mathit{\boldsymbol{\hat \theta }}_{k-1}}. $ | (12) |
步骤1(b) 如果
步骤1(c) 如果
| $ \varepsilon ' = \frac{{{v_k} + \varepsilon + \sqrt {{\beta _k}} }}{2}, $ | (13) |
| $ {v'_k} = \frac{{{v_k} + \varepsilon-\sqrt {{\beta _k}} }}{2}, $ | (14) |
| $ {q_k} = \left\{ \begin{array}{l} \frac{{\varepsilon '\left( {\sqrt {{\beta _k}}-p\left( {\varepsilon + {v_k}} \right)} \right)}}{{\left( {p-1} \right){\beta _k}}}, 当\sqrt {{\beta _k}} > p\left( {\varepsilon + {v_k}} \right);\\ \;\;\;\;\;\;\;\;\;\;\;\;0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他. \end{array} \right. $ | (15) |
如果
步骤1(d) 如果
| $ \varepsilon ' = \frac{{-{v_k} + \varepsilon + \sqrt {{\beta _k}} }}{2}, $ | (16) |
| $ {v'_k} = \frac{{{v_k}-\varepsilon + \sqrt {{\beta _k}} }}{2}, $ | (17) |
| $ {q_k} = \left\{ {\begin{array}{*{20}{l}} {\frac{{\varepsilon '\left( {\sqrt {{\beta _k}}-p\left( {\varepsilon - {v_k}} \right)} \right)}}{{\left( {p-1} \right){\beta _k}}}, 当\sqrt {{\beta _k}} > p\left( {\varepsilon - {v_k}} \right);}\\ {\;\;\;\;\;\;\;\;\;\;\;\;0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他.} \end{array}} \right. $ | (18) |
如果
步骤1(e) 如果βk≤p(ε2-vk2),则置
| $ \begin{array}{l} \left( {p-1} \right)\beta _k^2q_k^2 + \left( {\left( {2p-1} \right){\varepsilon ^2}-{\beta _k} + v_k^2} \right){\beta _k}{q_k} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\varepsilon ^2}\left( {p\left( {{\varepsilon ^2} - v_k^2} \right) - {\beta _k}} \right) = 0. \end{array} $ | (19) |
步骤2 将qk代入式(20)~(22)中,计算
| $ {P_k} = \left( {1 + {q_k}-\frac{{{q_k}v_k^2}}{{{\varepsilon ^2} + {q_k}{\beta _k}}}} \right){P'_{k-1}}, $ | (20) |
| $ {\hat \theta _k} = {\hat \theta _{k-1}} + \frac{{{q_k}{v_k}}}{{{\varepsilon ^2} + {q_k}{\beta _k}}}{P_{k-1}}{\phi _k}, $ | (21) |
式中
| $ {P'_{k-1}} = {P_{k-1}}-\frac{{{q_k}}}{{{\varepsilon ^2} + {q_k}{\beta _k}}}{P_{k - 1}}{\boldsymbol{\phi} _k}\boldsymbol{\phi} _k^{\rm{T}}{P_{k - 1}}. $ | (22) |
步骤3 如果k < N,则k增1并返回步骤1.
由于有ΘN⊆EN,所以得
| $ {\bar {\hat y}}_k^{\rm{m}} = \mathop {\min }\limits_{\theta \in {E_N}} \boldsymbol{\phi} _k^{\rm{T}}\mathit{\boldsymbol{\theta }}, \bar {\hat y}_k^{\rm{M}} = \mathop {\max }\limits_{\theta \in {E_N}} \boldsymbol{\phi} _k^{\rm{T}}\mathit{\boldsymbol{\theta }}. $ | (23) |
可以推导出
| $ \bar {\hat y}_k^{\rm{m}} = \boldsymbol{\phi} _k^{\rm{T}}{{\mathit{\boldsymbol{\hat \theta }}}_N}-\sqrt {\boldsymbol{\phi} _k^{\rm{T}}{P_N}{\boldsymbol{\phi} _k}}, $ | (24) |
| $ \bar {\hat y}_k^{\rm{M}} = \boldsymbol{\phi} _k^{\rm{T}}{{\mathit{\boldsymbol{\hat \theta }}}_N} + \sqrt {\boldsymbol{\phi} _k^{\rm{T}}{P_N}{\boldsymbol{\phi} _k}} . $ | (25) |
替换式(9),出水BOD的置信区间可以表示为
| $ {y_k} \in \left[{{\bar {\hat y}}_k^{\rm{m}}-\varepsilon, \bar {\hat y}_k^{\rm{M}} + \varepsilon } \right], k \ge N + 1. $ | (26) |
借鉴集员估计文献[21]的思想,设计多个BOD神经网络软测量模型(对于这些神经网络模型,隐含层节点个数、中心、宽度以及建模误差界设不同值),并将多模型测量结果进行融合以降低单一模型所给结果的保守性.设软测量模型个数为M,第i个软测量模型的输出为置信区间I(i).可以得到关于实际出水BOD yk的如下关系式
| $ {y_k} \in I_k^{\left( i \right)}, i = 1, \cdots, M. $ | (27) |
因而有
| $ \forall i, \;\;\bigcap\nolimits_{i = 1}^M {I_k^{\left( i \right)}} \subseteq I_k^{\left( i \right)}. $ | (28) |
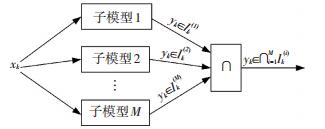
即将各模型输出的交集作为最终结果,并且最终结果比任意单一模型的输出具有更低的保守性.该方法如图 2所示.另外,有
|
图 2 置信区间的保守性降低方案 Figure 2 Scheme for reducing the conservatism of the confidence interval |
| $ \forall \Sigma \subseteq \left\{ {1, 2, \cdots, M} \right\}, \bigcap\nolimits_{i = 1}^M {I_k^{\left( i \right)}} \subseteq \bigcap\nolimits_{i \in \Sigma } {I_k^{\left( i \right)}} . $ | (29) |
由上式可以看出:子模型个数越多,所得结果的保守性越低.因此,在时间允许的前提下,可建立更多的模型以进一步降低保守性.
3 BOD置信区间的使用所计算出的置信区间描述了出水BOD真实值yk的存在范围,即yk∈[ykm, ykM].式中:ykM和ykm分别表示置信区间的上下界.通过此置信区间可给出一个点估计[22]
| $ y_k^{\rm{e}} = \arg, \mathop {\min }\limits_{y \in {\bf{R}}} \mathop {\max }\limits_{{y_k} \in \left[{y_k^{\rm{m}}, y_k^{\rm{M}}} \right]} \left| {{y_k} -y} \right| = \left( {y_k^{\rm{M}} + y_k^{\rm{m}}} \right)/2. $ | (30) |
可以作为BOD真实值yk的一个预测.而且,不难推导出|yk-yke|≤(ykM-ykm)/2.即BOD真实值yk与预测值yke之间的偏差小于置信区间的半径.因此,置信区间的保守性越低,预测误差的最大值就越小.可以看出,通过出水BOD置信区间不仅可给出BOD真实值的一个预测, 还可以评估预测误差.现有工作多是获得一个BOD预测值,而未曾给出评估各时刻预测误差的有效方法.关于水质参数BOD是否达标或满足运行调控要求,直接使用预测值而不参考预测误差(预测精度没有保证)可能会导致错误的分析和判断.
4 实验实验数据共200组,即L=200,来源于北京市某污水处理厂.使用PCA方法选取辅助变量.在累计方差贡献率大于90%的前提下,出水BOD软测量模型的辅助变量选取为COD、SS、pH和DO.将降维后的数据分成两部分,一份用于神经网络模型建立,共150组,即N=150;另一份用于模型预测,共50组.
实验建立3个软测量模型,然后将各模型输出的交集作为最终结果.在神经网络建模之前,先对数据进行归一化处理,即式(4)中的xk和yk都是归一化后的数据.试凑隐节点数使建模误差界尽可能小.对于模型1,神经网络隐节点数p、宽度σ以及建模误差界ε分别为50、0.9和0.477 5;对于模型2,3个参数分别为55、1和0.442 5;对于模型3,3个参数分别为60、0.7和0.395 3.在权值估计过程中,集员辨识重复处理所有数据200次以进一步降低椭球描述的保守性.
图 3~5分别为已建立好的模型1~3给出的出水BOD置信区间.图 6是模型1、2以及3所给结果的交集.图中实线为测量值yk,虚线和点线分别为反归一化后的区间上下界ykM和ykm.可以看出,出水BOD实测值完全落入3个模型所给出的置信区间中,以及其进一步完全落入3个模型所给结果的交集中,并且融合后的结果比单一结果保守性更低.不难看出,在时间允许的前提下,可建立更多的模型以进一步降低保守性.第3节已指出,置信区间的保守性越低,预测误差的最大值就越小,从而结果就越能反映真实值.

|
图 3 模型1给出的出水BOD置信区间 Figure 3 Confidence interval of the effluent BOD given by Model 1 |

|
图 4 模型2给出的出水BOD置信区间 Figure 4 Confidence interval of the effluent BOD given by Model 2 |

|
图 5 模型3给出的出水BOD置信区间 Figure 5 Confidence interval of the effluent BOD given by Model 3 |
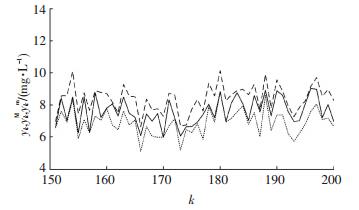
|
图 6 3个模型给出结果的交集 Figure 6 Intersection of the results given by the three models |
此外,本实验还与传统的神经网络软测量建模方法进行对比.该方法采用最小二乘法确定RBF神经网络输出权值,并且试凑中心和宽度使建模误差尽可能小.神经网络隐节点数p和宽度σ分别为60和0.7.针对归一化后的数据,最终RSME为0.227 5.置信区间计算公式见文献[16].图 7给出该方法的结果.图中实线为测量值yk,点划线为单点估计yke,虚线和点线分别为反归一化后的区间上下界ykM和ykm.可以看出,点估计不能保证预测效果始终可靠,尽管建模误差已被降低,比如在时刻165出现较大预测误差.并且,该方法基于随机误差假设计算置信区间,而这里误差的统计特性难以获得,因而所计算出的置信区间并不理想,其保守性大于本文方法所得结果.

|
图 7 采用最小二乘法所建模型给出的结果 Figure 7 Results given by the model built by the least squares |
污水处理过程要求实时监测出水水质指标,以防止超标造成环境污染.本文给出一种新的软测量方法,可以计算出水BOD的置信区间,从而实现水质指标的可靠监测.该方法通过PCA选取辅助变量;采用RBF神经网络建立软测量模型;使用参数线性集员辨识算法给出网络输出权值的不确定集合描述.此外,本文借鉴集员估计文献[21]的思想,设计多个BOD神经网络软测量模型,并将多模型测量结果进行融合以降低单一模型所给结果的保守性.
| [1] |
HAIMI H, MULAS M, CORONA F, et al. Data-derived soft-sensors for biological wastewater treatment plants: An overview[J].
Environmental Modelling & Software, 2013, 47: 88-107.
DOI: 10.1016/j.envsoft.2013.05.009 |
| [2] |
祁国强, 刘载文, 崔莉凤. 基于RBF人工神经网络的生活污水处理软测量方法[J].
北京工商大学学报(自然科学版), 2004, 22(3): 36-38.
QI Guoqiang, LIU Zaiwen, CUI Lifeng. The soft measuring method based on RBF neural network for municipal wastewater treatment[J]. Journal of Beijing Technology and Business University (Natural Science Edition), 2004, 22(3): 36-38. DOI: 10.3969/j.issn.1671-1513.2004.03.010 |
| [3] |
HUANG Zhiqing, LUO Jianxu, LI Xiongjun, et al. Prediction of effluent parameters of wastewater treatment plant based on improved least square support vector machine with PSO[C]//Proceedings of the 1st International Conference on Information Science and Engineering. Piscataway, NJ: IEEE Press, 2009: 4058-4061. DOI: 10.1109/ICISE.2009.846.
|
| [4] |
王树东, 葛珉昊, 陈明明. 基于混合递阶遗传算法优化RBF神经网络的BOD5软测量方法[J].
给水排水, 2014, 40(3): 149-153.
WANG Shudong, GE Minhao, CHEN Mingming. Soft measuring method for BOD5 based on RBF neural network optimized by hybrid hierarchy genetic algorithm[J]. Water Supply and Drainage, 2014, 40(3): 149-153. DOI: 10.3969/j.issn.1002-8471.2014.03.036 |
| [5] |
许玉格, 刘莉, 曹涛. 基于Fast-RVM的在线软测量预测模型[J].
化工学报, 2015, 66(11): 4540-4545.
XU Yuge, LIU Li, CAO Tao. On-line soft measuring model based on Fast-RVM[J]. CIESC Jorunal, 2015, 66(11): 4540-4545. DOI: 10.11949/j.issn.0438-1157.20150566 |
| [6] |
QIAO Junfei, LI Wei, HAN Honggui. Soft computing of biochemical oxygen demand using an improved T-S fuzzy neural network[J].
Chinese Journal of Chemical Engineering, 2014, 22(11/12): 1254-1259.
DOI: 10.1016/j.cjche.2014.09.023 |
| [7] |
LIU Yiqi, HUANG Daoping, LI Yan. Development of interval soft sensors using enhanced just-in-time learning and inductive confidence predictor[J].
Industrial and Engineering Chemistry, 2012, 51(8): 3356-3367.
DOI: 10.1021/ie201053j |
| [8] |
ŠKRJANCI. Confidence interval of fuzzy models: An example using a waste-water treatment plant[J].
Chemometrics and Intelligent Laboratory Systems, 2009, 96(2): 182-187.
DOI: 10.1016/j.chemolab.2009.01.009 |
| [9] |
LJUNG L.
System identification-theory for the user[M]. 2nd ed. Englewood-Cliffs, NJ: Prentice-Hall, 1999.
|
| [10] |
NINNESS B, GOODWIN G. Estimation of model quality[J].
Automatica, 1995, 31(12): 1771-1797.
DOI: 10.1016/0005-1098(95)00108-7 |
| [11] |
MRUGALSKI M, WITCZAK M, KORBICZ J. Confidence estimation of the multi-layer perceptron and its application in fault detection systems[J].
Engineering Applications of Artificial Intelligence, 2008, 21(6): 895-906.
DOI: 10.1016/j.engappai.2007.09.008 |
| [12] |
FÁBREGA A J S, CARO J M B, HERRERA P J A, et al. Data-driven bounded-error fault detection[J].
International Journal of Adaptive Control and Signal Processing, 2014, 28(12): 1299-1324.
DOI: 10.1002/acs.2443 |
| [13] |
FÁBREGA A J S, CARO J M B, HERRERA P J A, et al. Fault detection method based on bounded error and dynamic threshold techniques[J].
International Journal of Adaptive Control and Signal Processing, 2016, 30(2): 256-270.
DOI: 10.1002/acs.2558 |
| [14] |
柴伟, 孙先仿. 一种非线性系统集员辨识算法[J].
北京航空航天大学学报, 2005, 31(11): 1237-1241.
CHAI Wei, SUN Xianfang. Set membership identification algorithm of nonlinear systems[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(11): 1237-1241. DOI: 10.3969/j.issn.1001-5965.2005.11.018 |
| [15] |
CHAI Wei, QIAO Junfei. Non-linear system identification and fault detection method using RBF neural networks with set membership estimation[J].
International Journal of Modelling, Identification and Control, 2013, 20(2): 114-120.
DOI: 10.1504/IJMIC.2013.056183 |
| [16] |
CHAI Wei, QIAO Junfei. Passive robust fault detection using RBF neural modeling based on set membership identification[J].
Engineering Applications of Artificial Intelligence, 2014, 28: 1-12.
DOI: 10.1016/j.engappai.2013.10.005 |
| [17] |
杨斌, 田永青, 朱仲英. 智能建模方法中的数据预处理[J].
信息与控制, 2002, 31(4): 380-384.
YANG Bin, TIAN Yongqing, ZHU Zhongying. Data pretreatment in intelligent modeling methods[J]. Information and Control, 2002, 31(4): 380-384. DOI: 10.3969/j.issn.1002-0411.2002.04.019 |
| [18] |
BEZDEK J C.
Pattern recognition with fuzzy objective function algorithms[M]. New York: Plenum Press, 1981.
|
| [19] |
FOGEL E, HUANG Y F. On the value of information in system identification-bounded noise case[J].
Automatica, 1982, 18(2): 229-238.
DOI: 10.1016/0005-1098(82)90110-8 |
| [20] |
BELFORTE G, BONA B. An improved parameter identification algorithm for signals with unknown but bounded errors[C]//Proceedings of the 7th IFAC/IFORS Symposium on Identification and System Parameter Estimation. Oxford: Pergamon Press, 1985: 1507-1511.
|
| [21] |
MOISAN M, BERNARD O, GOUZE J L. Near optimal interval observers bundle for uncertain bioreactors[J].
Automatica, 2009, 45(1): 291-295.
DOI: 10.1016/j.automatica.2008.07.006 |
| [22] |
MILANESE M, VICINO A. Optimal estimation theory for dynamic systems with set membership uncertainty: An overview[J].
Automatica, 1991, 27(6): 997-1009.
DOI: 10.1016/0005-1098(91)90134-N |
 2018, Vol. 50
2018, Vol. 50


