2. 哈尔滨工业大学 数学系,哈尔滨 150001
2. Department of Mathematics, Harbin Institute of Technology, Harbin 150001, China
管道气液两相流动存在于石油、化工、能源、输配水等多个行业,研究气液两相瞬变流对管道安全运行十分重要.传统瞬变流模型只考虑暂态过程中的稳定摩阻[1],而研究表明,与稳定摩阻相比,与流速变化率相关的非稳定摩阻对瞬变流压力衰减的作用更为重要[2-4].另外,越来越多的黏弹性管材在工程中使用,一方面给管道建设维护带来方便,另一方面可抑制瞬变流过程中产生的升压[5].在单相水瞬变流过程中,管材黏弹性对瞬变流压力衰减的影响比非稳定摩阻大得多[6-7],因此,针对黏弹性管道的瞬变流模型必须考虑管壁的黏弹性效应.对瞬变流模型的研究从简单到复杂经历了很长的过程,其中最简单的是只考虑流体轴向速度的一维模型[1];而同时考虑到流体轴向速度和径向速度的准二维模型在模拟结果上要比一维模型更加精准[6];复杂的是基于湍流模型的二维模型和三维模型,其考虑的因素更多,更符合实际情况,但计算复杂[8-9].前两种模型通常用特征线法就可以求解,而后两种模型由于计算流体力学的发展,已有成型的商业软件可供求解,但对于工程应用来讲仍不现实.气液两相流模型的研究大多集中在稳定流方面[10],主要分为:1)均相流模型:将气液两相混合物看成均匀介质,其物性参数取两相加权平均值;2)分相流模型:将气液两相流动看成各自分开流动,每相介质都有其平均流速和独立的物性参数;3)漂移流模型:既考虑气液两相之间相对运动,又考虑空隙率和流速沿过流断面分布规律.现今对气液两相瞬变流模型的研究比较少,一般以均相流为基础,将气体存在对瞬变流的影响考虑在波速计算中[1, 11].
本文首先介绍了在黏弹性管道中进行的气液两相快关阀瞬变流实验.其次,基于均相流模型,建立了两个将非稳定摩阻和管材黏弹性影响考虑在内气液两相一维瞬变流模型.再次,通过实验结果与模型结果的对比,得到对管道设计来讲更安全的气液两相瞬变流模型.最后,用气液两相瞬变流模型分析了非稳定摩阻和管壁黏弹性对压力衰减的影响.
1 实验 1.1 实验装置如图 1所示,实验装置是一个循环供水系统,水流依靠重力从高位水箱流到低位水箱,再通过水泵回流到高位水箱.实验管道采用有机玻璃管材,管道内径90 mm,壁厚10 mm,由材料力学实验确定该管材的弹性模量为2.684 GPa,泊松比为0.358.高位水箱的平面尺寸为1.0×1.5 m2,其面积远大于管道截面积,因此,在瞬变流过程中,高位水箱水位几乎不变.重力管线的末端是自由出流,高位水箱水位与末端出口之间位差约5.3 m,整个管线通过铁架与地面之间形成固定约束.从高位水箱出口到气动蝶阀的管道长度约36 m,在离水箱出口10.5、20.5、27.5、35.5 m(序号:1, 2, 3, 4)的位置分别安装了精度0.2%、频响10 kHz、量程-10~60 m的压力传感器,并使用研华USB-4711A数据采集卡采集压力信号.

|
图 1 实验装置示意 Figure 1 Sketch map of experimental set-up |
瞬变流实验是在重力管线中进行的,实验中由电动球阀调节水速,由空压机出口压力控制注入到管道前部的气量,水速和进气量分别通过超声波流量计和气体浮子流量计来计量.当水速和进气量稳定以后,通过气动蝶阀快关在管道中实现瞬变流,并且在气动蝶阀关阀的同时停止进气.气动蝶阀的工作压力为0.3 MPa(远高于初始流动下的管道内压),可保证在每一次实验的关阀时间大致相同.实验中通过15帧/s的高速相机记录关阀过程,根据记录可知每次关阀时间约为0.9 s.压力信号采样率为1 000 Hz,采集到的压力信号后期经过小波滤波得到更为可靠的实验值,在实验中由压力传感器精度和信号干扰引起的误差可忽略不计.
2 气液两相瞬变流模型 2.1 一维瞬变流模型考虑管材黏弹性效应后,一维瞬变流模型的动量方程和质量方程为[12]
| $ \frac{{\partial H}}{{\partial x}} + \frac{1}{g}\left( {V\frac{{\partial V}}{{\partial x}} + \frac{{\partial V}}{{\partial t}}} \right) + {h_{\rm{f}}} = 0, $ | (1) |
| $ \frac{{\partial H}}{{\partial t}} + V\left( {\frac{{\partial H}}{{\partial x}} + \sin \theta } \right) + \frac{{{a^2}}}{g}\frac{{\partial V}}{{\partial x}} + \frac{{2{a^2}}}{g}\frac{{\partial {\varepsilon _{\rm{r}}}}}{{\partial t}} = 0. $ | (2) |
式中:H为管道内压,V为流速,x为空间长度,t为时间,g为重力加速度,hf为暂态摩阻,θ为管道与水平方向的角度,a为波速,εr为管壁的滞后应变.由于气体存在,需对式(2)中的波速进行修正.对波速修正有两种不同的方法,分别对应两个不同的气液两相瞬变流模型.
1) 方法一:以DVCM为基础,波速在整个暂态过程中不变,当压力降到汽化压强以下时,出现断流空腔[1].此时波速表达式为
| $ a = \frac{1}{{\sqrt {{\rho _1}\left( {1-\alpha } \right)\left( {1/{K_1} + \alpha /{K_{\rm{g}}} + {C_1}D/Ee} \right)} }}. $ | (3) |
式中:ρl为液体密度,α为体积含气率,其在任何位置任何时间都不变,Kl为液体体积模量,Kg为气体体积模量,D为管道内径,e为管道壁厚,E为管材弹性模量,C1是与管道约束有关的参数,当管道两端完全固定时
| $ {C_1} = \frac{{2e}}{D}\left( {1 + \mu } \right) + \frac{D}{{D + e}}\left( {1-{\mu ^2}} \right), $ | (4) |
式中μ为实验装置管材泊松比.
2) 方法二:以DGCM为基础,波速与体积含气率相关,而管道中气体体积变化满足理想气体定律,因此,瞬变流过程中波速在不断变化[13].此时波速表达式为
| $ a = \frac{1}{{\sqrt {{\rho _1}\left( {1-{\alpha _0}} \right)\left( {1/{K_1} + \alpha /p + {C_1}D/Ee} \right)} }}, $ | (5) |
式中:α0为初始体积含气率,p为管道内绝对压力.管道某节点某时刻体积含气率为
| $ \alpha = \frac{{{\alpha _0}{h_{\rm{a}}}}}{{H-Z-{H_{\rm{v}}}}}. $ | (6) |
式中:ha为大气压,Z为某节点位置高程,Hv为真空压力.
2.2 非稳定摩阻考虑非稳定摩阻时,瞬变流的暂态摩阻可表示为
| $ {h_{\rm{f}}} = {h_{{\rm{fs}}}} + {h_{{\rm{fu}}}}, $ | (7) |
式中:hfs为稳定摩阻,hfu为非稳定摩阻,均与雷诺数(Re)相关.
| $ {h_{{\rm{fs}}}} = \left\{ \begin{array}{l} \frac{{fV\left| V \right|}}{{2gD}}, {\mathop{\mathit Re}\nolimits} > 2000;\\ \frac{{32\nu V}}{{g{D^2}}}, {\mathop{\mathit Re}\nolimits} \le 2000. \end{array} \right. $ | (8) |
式中:f为稳定摩阻对应的摩阻系数(由初始状态下的实验数据求得),ν为气液两相混合介质的运动黏滞系数.非稳定摩阻跟速度变化率相关,其数值计算的格式如下[4]:
| $ {h_{{\rm{fu}}}} = \frac{{16\nu }}{{g{D^2}}}\sum\limits_{k = 1}^N {{y_k}\left( t \right)}, $ | (9) |
| $ \begin{array}{l} {y_k}\left( {t + \Delta t} \right) = {{\rm{e}}^{- {n_k}\frac{{\Delta \tau }}{2}}}{m_k}\left[{V\left( {t + \Delta t} \right)-V\left( t \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\rm{e}}^{ -{n_k}\Delta \tau }}{y_k}\left( t \right). \end{array} $ | (10) |
式中:Δt为迭代计算的时间步长,Δτ=KΔt,K=4ν/D2,mk和nk是根据实验数据拟合得到的与流态相关的系数.
2.3 管壁黏弹性管壁黏弹性对瞬变流过程的影响可通过管壁的形变过程来描述,而管壁在受到加载下的形变过程一般用Kelvin-Voigt模型来表示.式(2)中第4项黏弹性项的数值计算方法如下[14]:
| $ \frac{{\partial {\varepsilon _{\rm{r}}}\left( {x, t} \right)}}{{\partial t}} = \sum\limits_{k = 1}^N {\frac{{\partial {\varepsilon _{{\rm{r}}k}}\left( {x, t} \right)}}{{\partial t}}, } $ | (11) |
| $ F\left( {x, t} \right) = \frac{{{C_1}D}}{{2{\rm{e}}}}{\gamma _1}\left[{H\left( {x, t} \right)-{H_0}\left( x \right)} \right], $ | (12) |
| $ \frac{{\partial {\varepsilon _{{\rm{r}}k}}\left( {x, t} \right)}}{{\partial t}} = \frac{{{J_k}}}{{{\tau _k}}}F\left( {x, t} \right)-\frac{{{\varepsilon _{{\rm{r}}k}}\left( {x, t} \right)}}{{{\tau _k}}}, $ | (13) |
| $ \begin{array}{l} {\varepsilon _{{\rm{r}}k}}\left( {x, t} \right) = {J_k}F\left( {x, t} \right)-{J_k}{{\rm{e}}^{-\Delta t/{\tau _k}}}F\left( {x, t-\Delta t} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{J_k}{\tau _k}\left( {1 - {{\rm{e}}^{ - \Delta t/{\tau _k}}}} \right)\frac{{F\left( {x, t} \right) - F\left( {x, t - \Delta t} \right)}}{{\Delta t}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\rm{e}}^{ - \Delta t/{\tau _k}}}{\varepsilon _{{\rm{r}}k}}\left( {x, t - \Delta t} \right). \end{array} $ | (14) |
式中:N代表用来描述管壁黏弹性行为的Kelvin-Voigt元件的组数,γl为水的容重,Jk、τk为对应的第k组元件的黏弹性参数.
由于气体存在会使得瞬变流波速大为降低,为了保证求解精度,模型中的对流项不可忽略,因此,采用带内插的矩形网格法,并通过Matlab编程来求解模型.
3 模型校核为了验证本文模型及程序的可靠性,首先以文献[14]中图 4的实验数据与本文程序的求解结果进行对比.由图 2可见,由于本文程序中非稳定摩阻计算所用参数与文献[14]的实验条件有所差别,在瞬变流后期模拟结果与实验数据之间存在一些误差,但模拟结果与实验数据大体吻合较好,且DVCM和DGCM的模拟结果几乎重合,因此,本文所用模型及其程序是可靠的.
|
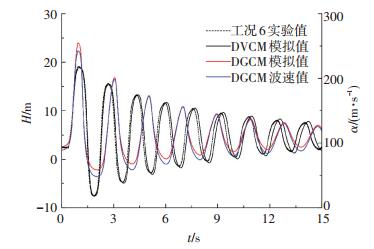
图 4 工况6实验与模拟结果对比 Figure 4 Comparison between model results and experimental data of case 6 |

|
图 2 模型结果与文献实验数据对比 Figure 2 Comparison between model results and experimental data in reference |
管道的黏弹性参数受管材分子结构、温度、管道轴向及环向约束、管壁应力加载过程、波速等因素影响[14],虽然不同波速下管道的黏弹性参数有所区别,在此以单相水瞬变流实验数据(初始流速为0.9 m/s)校核本实验装置的黏弹性参数.选取3组黏弹性参数描述管壁在瞬变流过程中的黏弹性行为,校核过程如下:首先,从实验数据中找到前5个峰值和谷值;其次,固定τ1、τ2、τ3为0.05、0.5、1.5 s,让J1、J2、J3在0.01×10-9与1.01×10-9 Pa-1之间变化,采用枚举法计算不同J1、J2、J3组合下的模拟结果,并找出其中前5个峰值和谷值;最后,将模拟结果的前5个峰值和谷值与实验数据的前5个峰值和谷值,做相关性分析和最小二乘法,找到最佳黏弹性参数.
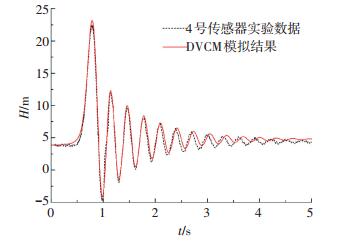
由图 2可知,DVCM和DGCM对单相水瞬变流的模拟结果几乎一样,为计算简便,以DVCM模拟结果与实验数据对比来校核黏弹性参数.图 3实验和模拟结果总体吻合得很好,但由于程序中非稳定摩阻计算所用参数与实验管道真实情况有所差别,且只使用了前5个峰值和谷值来校核黏弹性参数,实验和模拟结果在4个周期后在压力衰减相位上存在着微小差别.通过校核得到黏弹性参数如下:J1=0.008 39×10-9 Pa-1,J2 = 0.350 4×10-9 Pa-1,J3 = 0.355 2×10-9 Pa-1.
|
图 3 黏弹性参数校核 Figure 3 Calibration of viscoelastic parameters |
气液两相瞬变流的实验波速可通过2L/T求得,其中L为高位水箱出口到气动蝶阀的管道长度,T为瞬变流压力的平均周期.DVCM波速可由式(3)求得.而DGCM波速是不断变化的,为了便于比较,将管道某位置波速在整个瞬变流过程中的平均值作为DGCM波速.以4号传感器位置处的波速为例,实验波速与理论波速的对比见表 1.
| 表 1 实验波速与理论波速对比 Table 1 Comparison between experimental and theoretical wave speeds |
用DGCM模拟单相水瞬变流时,通常将体积含气率设为10-7,此时波速在瞬变流过程中变化非常微小,其计算结果与恒定波速计算结果几乎一样[13],这在表 1的工况1中得到了很好的印证.由表 1中的其他工况可知,气液两相瞬变实验波速与DVCM波速非常接近,而这两者均小于DGCM平均波速.这是因为在计算DVCM波速时,将式(3)中空气体积模量取值为1.013×105 Pa(即为大气压ha).式(3)和(4)的不同之处在于α/Kg和α/P,由前文描述可得
| $ \frac{\alpha }{{{K_{\rm{g}}}}} = \frac{{{\alpha _0}}}{{{\rho _1}g{h_{\rm{a}}}}}, $ | (15) |
| $ \frac{\alpha }{P} = \frac{{{\alpha _0}}}{{{\rho _1}g{{\left( {H-Z-{H_{\rm{v}}}} \right)}^2}/{h_{\rm{a}}}}}. $ | (16) |
在整个瞬变流过程中,出现负压的时长一般短于正压存在的时长,因此,很容易得到
| $ {\rho _1}g{\left( {H-Z-{H_{\rm{v}}}} \right)^2}/{h_{\rm{a}}} > {\rho _1}g{h_{\rm{a}}}. $ | (17) |
从而最终使DVCM波速小于DGCM波速.空气体积模量随着大气压而变化,在低压系统中可认为其值等于1个标准大气压.从实验中瞬变流的平均压力来看,实验系统可认为是低压系统,所以,在计算DVCM波速时假设空气体积模量为1个标准大气压是合理的.表 1中气液两相瞬变流工况中的最大体积含气率为2.37%,且通过对实验中初始流动的观察得知,5个工况的初始流态都属于泡状流流型.由上述分析可知,在初始流型为泡状流的低压系统中,DVCM波速与实际波速吻合得很好,但两者均小于DGCM波速.
4.2 气液两相瞬变流实验与模型结果对比将校核所得黏弹性参数代入到程序中模拟气液两相瞬变流.图 4为表 1中工况6在4号传感器位置的实验数据与模拟结果的对比.可以看出,DVCM模拟结果与实验数据非常接近,只在压力衰减相位上稍有差异,这可能由3个原因造成:程序中非稳定摩阻计算所用参数与实际管道情况有微小区别;黏弹性参数校核只用了实验数据和模拟结果的前5个峰值和谷值,且气液两相瞬变流波速与单相水瞬变流波速不同会引起黏弹性参数发生变化;从表 1可知,工况6中DVCM波速比实验波速略小,刚好导致DVCM模拟结果在周期上稍大于实验数据.
从图 4看出,DGCM模拟结果与DGCM瞬时波速的变化趋势一致,且其最大峰值大于DVCM模拟值和实验值.用DGCM计算时,正压波波形陡峭,而稀疏波波形平缓[13],因此,模拟结果中波速值大的部分持续时间较短,而波速值小的部分持续时间较长,DGCM的这一特点导致虽然DGCM的平均波速大于DVCM,但其在衰减相位上却滞后于DVCM.由于DGCM升压幅度较高,其最低谷值也高于DVCM模拟值和实验值的最低谷值,这说明当用DGCM模拟气液两相瞬变流时不易出现液柱分离现象.
在单相水瞬变流模拟中,DVCM的最大峰值通常都大于DGCM的最大峰值,一般推荐用DVCM来模拟单相水瞬变流更为安全[15].而由上述分析可知,在气液两相瞬变流模拟中,DGCM的最大峰值大于DVCM的最大峰值,出于安全考虑,使用DGCM模拟气液两相瞬变流更好.但是,DVCM模拟结果在峰值、谷值及相位上都更接近实验结果.
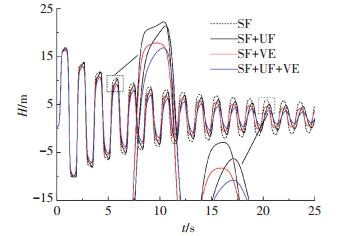
4.3 非稳定摩阻和黏弹性对气液两相瞬变流的影响由前文可知,DVCM的模拟结果与实验值非常接近,在此以DVCM为基础,将稳定摩阻(SF)、非稳定摩阻(UF)、管材黏弹性(VE)这3个影响压力衰减的因素互相组合,建立不同的瞬变流模型,用来研究非稳定摩阻和管材黏弹性对气液两相瞬变流压力衰减的影响.以表 1中工况6为例,将关阀时间设为0.5 s,忽略管道初始压力,将4号传感器位置不同模型计算结果的对比绘于图 5.可以看出,只考虑稳定摩阻的模型其模拟结果衰减最慢,而同时考虑稳定摩阻、非稳定摩阻及管材黏弹性的模型其模拟结果衰减最快.在瞬变流初期,非稳定摩阻对压力衰减的影响不如管材黏弹性重要,而随着时间进展,非稳定摩阻的影响变得越来越重要,在瞬变流后期,其对压力的衰减作用与管材黏弹性的作用相当.这一现象与单相水瞬变流过程中的压力衰减有所区别,在单相水瞬变流中,管材黏弹性对压力衰减起主导作用,以至于非稳定摩阻的作用可忽略不计[6, 14].气液两相瞬变流中管材黏弹性对压力衰减作用不再显著可从两个角度解释:从数学角度来看,气体存在使波速大为降低,同时瞬变流升压也随之减小,两者共同作用导致式(2)中黏弹性项(第4项)的值变小;从物理角度来看,当有气体存在,瞬变流过程中液体膨胀时首先压缩气体,使得原本该由管壁产生的应变量被气体压缩抵消了一部分,则管壁膨胀收缩的过程中消耗的能量减小.由此可知,在气液两相瞬变流中,管材黏弹性对压力衰减作用变小,致使非稳定摩阻作用不可忽略,且由于黏弹性效应的削弱,即使同时考虑非稳定摩阻和管材黏弹性,压力衰减速度依然很慢.
|
图 5 非稳定摩阻和黏弹性对气液两相瞬变流的影响 Figure 5 Effects of unsteady friction and viscoelasticity on gas-liquid two-phase transient flow |
1) 在初始流型为泡状流的低压系统中,DVCM波速与实际波速非常接近,而DGCM的平均波速大于前两者.
2) 在模拟泡状流瞬变流时,DVCM模拟结果与实验值吻合得很好,而从安全角度,使用DGCM模拟泡状流瞬变流更好,因为DGCM模拟结果的最大峰值更高.
3) 在气液两相瞬变流中,管材黏弹性效应对压力的衰减作用大为削弱,使得非稳定摩阻的影响不可忽略,同时导致整个瞬变流过程中压力衰减变慢.
4) 虽然DGCM在模拟泡状流下气液两相瞬变流时衰减相位与实际情况相差较大,但其是否适合模拟更高含气率(段塞流等)的瞬变流还有待验证.
| [1] |
怀利EB, 斯特里特VL.
瞬变流[M]. 北京: 水利电力出版社, 1983: 14-16.
WYLIE E B, STREETER V L. Fluid transients[M]. Beijing: Water Resources and Electric Power Press, 1983: 14-16. |
| [2] |
ZIELKE W. Frequency-dependent friction in transient pipe flow[J].
Journal of Basic Engineering, 1968, 90(1): 109-115.
DOI: 10.1115/1.3605049 |
| [3] |
TRIKHA A K. An efficient method for simulating frequency-dependent friction in transient liquid flow[J].
Journal of Fluids Engineering, 1975, 97(1): 97-105.
DOI: 10.1115/1.3447224 |
| [4] |
VTKOVSK J P, STEPHENS M, BERGANT A, et al. Efficient and accurate calculation of Zielke and Vardy-Brown unsteady friction in pipe transients[C]//Proceedings of the 9th International Conference on Pressure Surges. Chester, United Kingdom, 2004: 405-419.
|
| [5] |
DUAN Huanfeng, GHIDAOUI M S, TUNG Y K. Energy analysis of viscoelasticity effect in pipe fluid transients[J].
Journal of Applied Mechanics, 2010, 77(4): 044503.
DOI: 10.1115/1.4000915 |
| [6] |
DUAN Huanfeng, GHIDAOUI M, LEE P J, et al. Unsteady friction and visco-elasticity in pipe fluid transients[J].
Journal of Hydraulic Research, 2010, 48(3): 354-362.
DOI: 10.1080/00221681003726247 |
| [7] |
MENICONI S, BRUNONE B, FERRANTE M, et al. Energy dissipation and pressure decay during transients in viscoelastic pipes with an in-line valve[J].
Journal of Fluids and Structures, 2014, 45: 235-249.
DOI: 10.1016/j.jfluidstructs.2013.12.013 |
| [8] |
ZHAO Ming, GHIDAOUI M S. Efficient quasi-two-dimensional model for water hammer problems[J].
Journal of Hydraulic Engineering, 2003, 129(12): 1007-1013.
DOI: 10.1061/(ASCE)0733-9429(2003)129:12(1007) |
| [9] |
MARTINS N M C, SOARES A K, RAMOS H M, et al. CFD modeling of transient flow in pressurized pipes[J].
Computers & Fluids, 2016, 126: 129-140.
DOI: 10.1016/j.compfluid.2015.12.002 |
| [10] |
郭烈锦.
两相与多相流动力学[M]. 西安: 西安交通大学出版社, 2002: 575-583.
GUO Liejin. Dynamics of two-phase and multiphase[M]. Xi'an: Xi'an Jiaotong University Press Co., Ltd., 2002: 575-583. |
| [11] |
福克斯J A.
管网中不稳定流动的水力分析[M]. 北京: 石油工业出版杜, 1983: 99-101.
FOX J A. Hydraulic analysis of unsteady flow in pipelines[M]. Beijing: Petroleum Industry Press, 1983: 99-101. |
| [12] |
BERGANT A, TIJSSELING A S, VTKOVSK J P, et al. Parameters affecting water-hammer wave attenuation, shape and timing-Part 1: Mathematical tools[J].
Journal of Hydraulic Research, 2008, 46(3): 373-381.
DOI: 10.1080/00221686.2004.9641221 |
| [13] |
WYLIE E B. Simulation of vaporous and gaseous cavitation[J].
Journal of Fluids Engineering, 1984, 106(3): 307-311.
DOI: 10.1115/1.3243120 |
| [14] |
COVAS D, STOIANOV I N, MANO J F, et al. The dynamic effect of pipe-wall viscoelasticity in hydraulic transients. Part Ⅱ-Model development, calibration and verification[J].
Journal of Hydraulic Research, 2005, 43(1): 56-70.
DOI: 10.1080/00221680509500111 |
| [15] |
SOARES A K, COVAS D I C, RAMOS H M, et al. Unsteady flow with cavitation in viscoelastic pipes[J].
International Journal of Fluid Machinery and Systems, 2009, 2(4): 269-277.
DOI: 10.5293/IJFMS.2009.2.4.269 |
 2018, Vol. 50
2018, Vol. 50


