供水管网是城市重要的基础设施和生命线.管道阀门是保障供水管网安全运行、增强管网可靠性的关键设备.目前，中国多数城市供水管网已步入事故高发期，“爆管”事故频发^[1].为了提高事故工况下管网快速反应能力，降低管网事故影响，科学制定关阀预案(方案)成为管网安全管理重点工作.同时，要求隔离阀门具有较高的可靠性.基于深度搜索和广度搜索的关阀算法是制定关阀方案主要算法^[2-4]，但是搜索算法与事故地点紧密耦合，对阀门失灵和多事故并发工况适应能力弱，并且因计算效率问题，全网关阀预案生成困难.

在管网可靠性研究领域，Walski^[5]将关闭阀门隔离事故管线形成的管网最小隔离区域称为“管网子区”(segment).Giustolisi和Savic^[6]将管网子区隔离后引起的下游停水子区称为“关联子区”(unintended segment).管网子区支持关阀方案与事故地点松散耦合，为全网关阀预案制定及阀门失灵后扩展关阀分析奠定了技术基础.

近年来，管网学者对管网子区识别进行了深入研究.Li和Kao^[2]基于拓扑矩阵应用深度搜索算法逐个遍历识别管网子区.Giustolisi和Savic^[6]将阀门虚拟化为管线，重构管点-管线拓扑矩阵，通过矩阵高幂次运算计算管线传递闭包，一次性识别全部管网子区.Creaco等^[7]通过移动虚拟水源点，解算水力方程逐个识别管网子区.Alvisi等^[8]构建阀门附属矩阵，通过矩阵运算识别管网子区，并考虑了单向控制阀门对管网子区识别影响.上述研究成果涉及复杂矩阵运算或非线性方程解算，管网子区识别效率低下，主要用于简化管网管网子区识别.近年，Gao^[9]基于图论传递闭包理论研究提出非简化管网管网子区高效识别算法，支持大型管网管网子区一次性高效识别.

管网子区深刻揭示了事故工况下管网拓扑结构变化，广泛用于管网优化和管网可靠性研究^{[6-7, 10-14]}.文献[6-7]应用管网子区评估阀门系统可靠性，指导阀门优化选址.Giustolisi等^[12]基于管网子区优化管径设计，增强事故工况下管网可靠性.Gheisi等^[13-14]认为管网可靠性研究应考虑多事故并发工况.为此，曾文等^[4]构建阀门-环节(管网子区)模型图，设计了面向多事故点的关阀算法.但算法涉及大量搜索运算，效率不高.Jun等^[15]以管网子区为单元统计事故工况下停水用户数量，指示阀门和管线重要性.由于停水用户数量未能顾及用户用水性质，影响了评估分析结果质量.Rajan^[16]集成管网地理信息系统GIS与水力模型，计算事故工况下用户缺水量百分比，评估管网子区重要性.该方法要求拥有管网GIS和水力模型系统，并且需要关联用户数据与管网数据，数据准备工作繁重.

本文应用图论传递闭包理论计算识别管网子区和多余阀门(对隔离事故管线不起作用的阀门，如因阀门分布不合理而位于管网环上的唯一阀门)，建立阀门-管网子区拓扑模型，分析非必关阀门(下游阀门)并提出适用单事故点和多事故点工况的供水管网全网关阀预案一次性生成算法；按用户性质分组统计事故工况下用户缺水量，评估管网子区(管线)重要性，分析关键子区；同时，基于阀门—管网子区模型分析阀门失灵后扩展关阀方案，评估阀门重要性，识别关键阀门.为了保证分析效率，在阀门重要性评估中只考虑单个阀门失灵工况.

管点传递闭包是直接或间接连通的管点集合.阀门关闭后形成的管点传递闭包代表管网子区.首先，应用Warshall算法^[17]计算全网阀门统一关闭后形成的管点传递闭包(详见文献[9])，一次性识别全部管网子区.

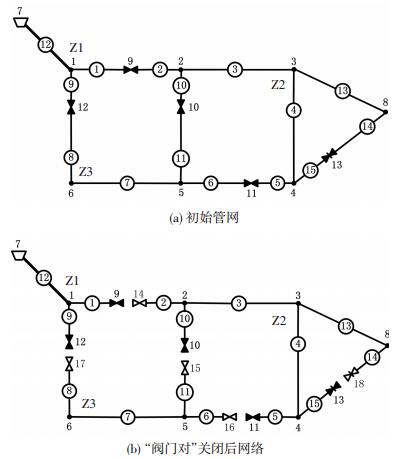
图 1(a)是一个简单供水管网系统，包含13个管点(含1个水源、5个阀门)和15条管线.克隆真实阀门生成虚拟阀门，真实阀门与虚拟阀门构成“阀门对”(表 1)，指示阀门开闭状态(真实阀门与虚拟阀门直接连接代表阀门开启.否则，关闭).阀门关闭后(图 1(b))形成Z1、Z2和Z3 3个管网子区，其管点连接矩阵为B_nn(表 2).其中，当节点i与节点j通过1条管线直接相连或i = j时，B_ij=1；否则，B_ij=0.

Figure 1

N7为水源点；N13为多余阀门 图 1 简单管网 Figure 1 A simple network

表 1

表 1 “阀门对”对照 Table 1 Valve pairs 阀门对 真实阀门 虚拟阀门 1 N9 N14 2 N10 N15 3 N11 N16 4 N12 N17 5 N13 N18

表 1 “阀门对”对照 Table 1 Valve pairs

表 2

表 2 图 1(b)管点连接矩阵Bnn Table 2 Node topological incidence matrix Bnn of Fig. 1(b) 点号 N1 N2 N3 N4 N5 N6 N7 N8 N9 N10 N11 N12 N13 N14 N15 N16 N17 N18 N1 1 0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 0 N2 0 1 1 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 N3 0 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 N4 0 0 1 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 N5 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0 N6 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 N7 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 N8 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 N9 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 N10 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 N11 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 N12 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 N13 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 N14 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 N15 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 N16 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 N17 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 N18 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1  注：下划线点号代表阀门(下同)

表 2 图 1(b)管点连接矩阵Bnn Table 2 Node topological incidence matrix Bnn of Fig. 1(b)

Warshall算法^[17]计算连接矩阵(B_nn)传递闭包步骤包括：1)初始化传递闭包集合E为空集；2)第1行与第2行求交，若存在交集取二者并集作为运算结果.否则，以第1行元素为运算结果.运算结果再与第3行求交，类同运算直到第n行，得到与第1行管点相连通的管点集合A.A作为第1个传递闭包保存到传递闭包集合E中；3)第2行(若未归并到E中)与第3行到第n行未归并到E中的剩余各行分别求交，计算与第2行管点相连通的管点集合B，B再与E中的传递闭包元素E_i依次求交，若存在交集则将E_i归并到B中，并从E中删除E_i，将B追加到传递闭包集合E中.若不存在交集，则将B直接加入到E中；4)依此类推，完成第3行到第n行传递闭包计算与合并.最后，传递闭包集合E每一行中非零元素组成的集合是一个相互连通的管点传递闭包.

首先，关闭管网中全部“阀门对”，应用Warshall算法计算管点连接矩阵B_nn(表 2)中的管点传递闭包E_zn(表 3).参照表 1将E_zn中的虚拟阀门还原为真实阀门.若还原后，行管点集合中出现重复管点编号，其为不能截断水流的多余阀门.如表 3(E_zn)第2行中真实阀门N13与其虚拟阀门N18所在列的值均为1.虚拟阀门还原为真实阀门后，N13在第2行管点集合中出现两次，判定其为不能截断水流的多余阀门.当管网闭合环上仅有一个阀门时会产生多余阀门.虚拟阀门还原为真实阀门并唯一化处理后得到管点传递闭包，指示管网子区.管网子区包含管点(非零元素)拓扑矩阵F_zn见表 4.

表 3

表 3 图 1(b)计算后的管点传递闭包矩阵Ezn Table 3 Node transitive closure sets (Ezn) in Fig. 1(b) 点号 N1 N2 N3 N4 N5 N6 N7 N8 N9 N10 N11 N12 N13 N14 N15 N16 N17 N18 Z1 1 0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 0 Z2 0 1 1 1 0 0 0 1 0 1 1 0 1 1 0 0 0 1 Z3 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 1 0

表 3 图 1(b)计算后的管点传递闭包矩阵Ezn Table 3 Node transitive closure sets (Ezn) in Fig. 1(b)

表 4

表 4 图 1(a)子区-管点(阀门)连接矩阵Fzn Table 4 Segment-node (valve) matrix Fzn of Fig. 1(a) 点号 N1 N2 N3 N4 N5 N6 N7 N8 N9 N10 N11 N12 N13 Z1 1 0 0 0 0 0 1 0 1 0 0 1 0 Z2 0 1 1 1 0 0 0 1 1 1 1 0 1 Z3 0 0 0 0 1 1 0 0 0 1 1 1 0

表 4 图 1(a)子区-管点(阀门)连接矩阵Fzn Table 4 Segment-node (valve) matrix Fzn of Fig. 1(a)

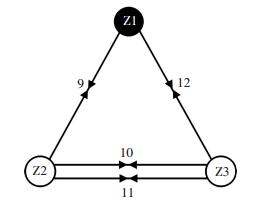
将管网子区虚拟化为点对象，阀门(不含多余阀门N13)虚拟化为线对象，建立阀门-管网子区模型(图 2).依次指定事故隔离子区即断开管网子区周围边界阀门(将表 4中隔离子区对应行的阀门列置0)，应用Warshall算法计算子区传递闭包.分析管网子区连通性，与水源子区(包含水源点的子区)不连通的子区是隔离子区的关联子区.事故隔离子区管点集合与其关联子区管点集合的交集是隔离子区的下游阀门，下游阀门是事故隔离时的非必关阀门.在隔离子区边界阀门集合中排除下游阀门后生成关阀方案.识别全部管网子区的下游阀门则可生成全网关阀方案.当管网中同时出现多个事故点时，将事故关阀方案中的边界阀门取和，和集中出现的重复阀门是位于关阀方案(管网子区)交界线上的阀门，它们包含在多事故隔离区域内部，不能截断上游来水.从关阀方案和集中排除重复阀门，即可生成面向多事故点的关阀方案.例如，若图 1(a)中管线3和7同时发生事故，隔离事故管线3需要关闭Z2的边界阀门N9、N10和N11.隔离事故管线7需要关闭Z3的边界阀门N12、N10和N11.阀门N10和N11位于两个事故隔离子区Z2和Z3交界线上，它们是关阀方案和集中的重复阀门，排除阀门N10和N11后，隔离事故管线3和7需要关闭的阀门为N9和N12.

Figure 2

图 2 阀门-管网子区模型图(Z1水源子区) Figure 2 Valve-segment model (Z1 source segment)

阀门失灵造成管网子区合并，关阀范围扩展到失灵阀门相邻子区.在子区管点连接矩阵F_zn(表 4)上查找与失灵阀门连接的两个子区所在行Row1和Row2.Row1与Row2并集Vor是合并新子区管点集合(含阀门)，Row1与Row2交集Vand是这两个子区分界线上的阀门集合(含失灵阀门)，Vor与Vand的异或差集Xor中包含的阀门是合并新子区边界阀门(不含多余阀门)，过滤去除与失灵阀门相邻的两个子区的下游阀门后，即可生成阀门失灵后扩展关阀方案.合并新子区的关联子区是与失灵阀门相连的两个子区的关联子区并集.

关闭阀门隔离事故管线造成部分用户(位于隔离子区及其关联子区)停水.本文以停水用户(不含压力下降用户)的缺水量为指标评价隔离子区的重要性.当管网图形系统与收费系统存在接口时，使用用户正常工况下实际水量计算用户缺水量.否则，根据用户用水性质对用户进行分组，以采样用户归算人口数量为权重，计算各组单用户平均小时水量，然后根据子区内分组用户数量汇总计算管网子区用水量.隔离子区及其关联子区用水量之和代表事故隔离后用户缺水量，指示隔离子区重要性

式中：D_i(m³/h)为停水区域(含隔离子区及其关联子区)内第i个用户组的单用户加权平均用水量，g_i为该组内的用户数量，n为停水区域内用户组数量.统计分析管网子区重要性，重要性大于平均值与3倍中误差之和的管网子区是管网中的关键子区，其中管线为重要管线.

阀门失灵后扩展关阀造成的缺水量代表失灵阀门的重要性.失灵阀门的重要性V等于与失灵阀门相连接的两个子区的重要性之和，即

式中：S₁，S₂为与失灵阀门相连接的两个子区的重要性指标.逐个假定阀门失灵，统计分析阀门重要性，重要性大于平均值与3倍中误差之和的阀门是管网中的关键阀门.

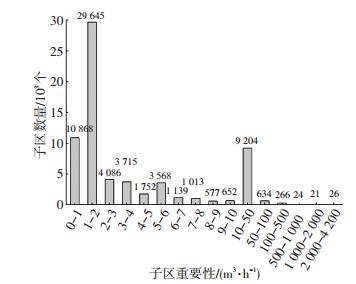
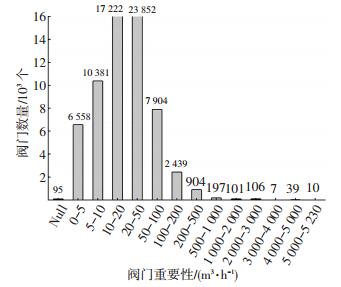
天津市主城区供水管网地理数据库包含722 428个管点(其中包含16个水源点、69 815个阀门)和725 758条管线，管线长度为6 031.9 km.用户共分为28个组，包含居民、餐饮、学校、度假村、医院、机关、工业等.生成全网关阀预案(管网子区)67 189个(表 5)，识别多余阀门95个.管网子区和阀门重要性分级统计结果见图 3、4(多余阀门的重要性为Null值).关键阀门和多余阀门地理分布见图 5、6.在CPU 2.93 GHz、8G内存电脑环境下，主城区全网关阀预案制定用时26 h 54 min，管网子区和阀门重要性评估用时8 h 23 min.通过与天津市供水管网地理信息系统82条管线模拟爆管关阀结果及17个人工关阀方案对比分析，验证了本文关阀方案正确可靠.另外，2016年4月9日天津市河西区福建路与温州道交口600 mm水管发生爆裂，调取本文关阀预案成功实现了快速关阀止水，有效减少了管网事故损失.

表 5

表 5 天津市供水管网全网关阀方案 Table 5 Valve closing schemes for Tianjin water networks 方案(子区)编号 关阀数量 上游必关阀门数量 上游阀门列表 下游非必关阀门数量 下游阀门列表 1 1 1 2 0 2 6 1 23 5 2;8;9;16;18 3 7 1 549 6 23;25;137;147;515;538       67189 7 2 99990;100543 5 100148;100299;100352;100375;100511

表 5 天津市供水管网全网关阀方案 Table 5 Valve closing schemes for Tianjin water networks

Figure 3

图 3 管网子区重要性统计 Figure 3 Segment importance

Figure 4

图 4 阀门重要性统计 Figure 4 Valve importance

Figure 5

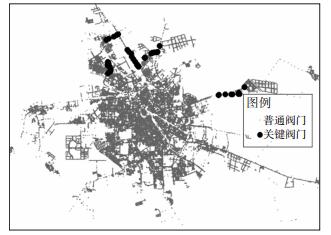
图 5 关键阀门地理分布 Figure 5 Distribution of key valves

Figure 6

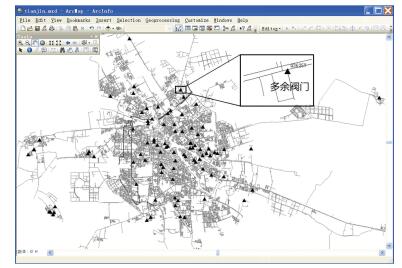
图 6 多余阀门地理分布 Figure 6 Distribution of redundant valves

分析认为：1)管网结构具有相对稳定性，全网关阀预案仅需定期生成(如一个季度生成一次).但当管网结构变化较大时，应及时重新生成全网关阀预案.当用水量变化较大时，应重新评估管网子区(管线)和阀门重要性；2)单向控制阀门是否需要关闭，需要根据实际水流方向决定；3)天津市供水管网中重要性指标较大的管网子区和阀门较多，并有95个多余阀门，说明存在阀门分布不合理现象；4)管网中管网子区数量(67 189)与阀门数量(69 815)相当；5)新增阀门和管线可以有效改善管网拓扑关系，降低关联子区数量，进而降低管网子区重要性；6)关键子区和关键阀门是管网改造、管网巡检和设备保养重点地区和对象；7)多余阀门不仅浪费资源，而且会误导关阀，应重视管网中多余阀门的识别与改造.

1) 引入“阀门对”概念指示阀门开闭状态，应用Warshall算法计算管点传递闭包，支持大型非简化供水管网管网子区高效识别以及多余阀门与下游阀门快速分析.

2) 管网子区支持关阀方案与事故地点松散耦合，为全网关阀预案一次性生成奠定了技术基础.基于阀门—管网子区模型制定的全网关阀预案适用于单事故或多事故并发工况.

3) 管网子区为管线和阀门重要性评估提供了捷径.以用户统计缺水量为指标评估管网子区(管线)和阀门重要性时，应对用户进行科学分组，并正确估算分组内单用户用水量.