2. 农业部环境保护科研监测所, 天津 300191;
3. 城市水资源与水环境国家重点实验室(哈尔滨工业大学), 哈尔滨 150090
2. Agro-Environmental Protection Institute, Ministry of Agriculture, Tianjin 300191, China;
3. State Key Laboratory of Urban Water Resource and Environment (Harbin Institute of Technology), Harbin 150090, China
近年来, 随着中国经济粗放式的快速增长, 环境风险大量积累, 迄今为止, 河流中已发生了数百起突发性污染事件.当突发水污染事件时, 决策者需要立即启动应急响应[1], 做出科学、有效的应急决策, 进行快速、高效的应急处置, 以期最大限度地减小污染程度和影响范围[2].但在现实中, 经常由于相关责任人对污染危害程度及其发展趋势认识严重不足, 致使应急物资准备缺失和处置响应迟滞[3], 造成了严重的环境污染、重大的经济损失和恶劣的社会影响.虽然目前在应急响应与决策领域的理论与应用研究已有很多[4-6], 并取得了一些较为显著的成果, 如开发了基于化学品理化性质和毒性等或GIS(地理信息系统)的应急决策系统等[5-6], 但多数研究是通过水质模拟来预测污染物的扩散情况支持应急决策, 而从响应时间对污染控制费用的影响角度进行分析, 通过相关的量化评估, 使相关责任人在最短时间内对突发污染可能产生的灾害损失做出估算, 以便高效地进行应急决策, 到目前为止还未见相关报道.
在环境污染控制工程中, 天然水体中污染物的去除费用存在着处理规模经济效应和处理效率的经济效应[7], 如以吸附法去除水中污染物, 单位时间内单位质量的吸附材料在高浓度污水中吸附的污染物一般要显著高于低浓度污水; 当污染物浓度随着扩散降低时, 吸附材料的利用率会因水中其他物质的附着而对污染物的吸附效率显著下降, 若要达到同样的去除率, 就要消耗更多的吸附材料和相应的装置及人工.因此, 当污染物进入天然水体中后, 应急处置的响应时间会对所要消耗的费用产生显著的影响.另外, 由于突发水污染事件时空分布的不确定性及其应急处置工程的难盈利性, 相关技术装备的研发和生产缺乏经济动力, 致使应急处置预案的可选择范围和实施效果都非常有限[8-9].在已实施过的天然水体突发污染应急处置工程中, 主要以混凝沉淀法[9]和吸附法[8]为主, 实施方式多以向水体中进行简单的投放为主, 处置材料亦为聚合氯化铝和活性炭等传统的水处理药剂和材料.存在的问题是:处置技术体系不完善、专业配套装备缺乏、准备时间长、实施效率低、施工人员粉尘暴露量大、处置材料利用率低、处置效果有限、流失材料的二次污染风险大等; 亟需具有现场适用度高、次生污染风险低的应急处置装置与材料的充分供给, 而关于响应时间对污染控制费用的量化评估会使应急处置预案的选择更加客观高效, 也有助于应急处置新技术、新装置和新材料的涌现.
综上, 从污染物在河流中的扩散规律及其环境经济危害与污染控制费用的动态发展趋势的角度出发, 构建了以响应时间为决策变量、以处置费用(装置费用、材料费用、人员费用和运输费用)为目标函数、以水质达标和物资准备时间为约束条件的突发水污染应急处置决策分析模型, 并采用情景分析的方法, 对物资获取、运输、装卸与装配等的时间因素对目标函数的影响进行了量化分析, 揭示了应急处置准备工作中各个环节的实施时间、以及污染现场条件对应急处置费用的影响程度, 以期能为应急决策提供量化的信息支持, 同时为突发水污染应急处置技术的发展指明方向.
1 模型构建 1.1 问题描述与模型说明构建的基于响应时间效应的应急处置决策模型基于以下问题描述:在实际应对突发水污染时, 应急响应时间越短, 则应急处置的实施越及时, 越容易快速限制污染物的扩散, 主要表现为减缓污染带面积(宽度和长度)的增加.根据污染物在水中的扩散规律, 污染物迅速完成竖向混合后, 受近河床剪切离散的影响, 纵向弥散加强, 逐渐被拉伸成污染带; 污染带的宽度(污染物在横向的扩散距离)在横向继续不断地延伸, 直到横向混合完成(断面任意一点处污染物的浓度在断面平均浓度的95%~105%); 与此同时, 在水流速度的推动下, 污染带的长度(污染物在纵向的扩散距离)沿水流方向一直延伸[10], 污染范围持续扩大, 从而引发更大的污染灾害损失.
吸附法因其可将污染物直接从水体中去除且具有原理简单、处理效率高和适用范围广等优点[11], 是目前突发污染应急处置的首选方法, 因此, 针对频繁发生的突发有机化学品污染, 以吸附法为例进行应急处置决策分析, 但相关分析方法也适用于其他应急处置技术.
1.2 模型目标函数的建立突发水污染的灾害损失评估是进行应急处置决策的依据[12-13], 根据国家环保部发布的《环境污染损害数额计算推荐方法》, 突发水污染的灾害损失包括人身损失、财产损失、应急处置费用、调查评估费用和污染修复费用.人身损失是指因突发水污染事故而支出的医疗费、误工费、护理费、住宿费、交通费、住院伙食补助费等一般性医疗支出费用及造成人身伤残、死亡的特别损害等费用[14]; 财产损失是指因突发水污染事故直接造成的资产性财产损失损毁、减少的实际价值, 按照财产的所有权分为为集体财产损失(如国家和单位的固定资产损失等)和个人财产损失(如居民财产损失、渔业损失和农作物减产绝收损失等)[14]; 应急处置费用是指突发水污染事故发生后现场抢救和应急处置所发生的合理费用, 具体包括应急监测及行政费用、污染控制和现场抢救费用、事故现场清理费用、人员转移安置费用等[14]; 调查评估费用是指对突发水污染事故评估所支出的费用, 包括现场调查、勘察监测、风险评估、损害评估等过程中产生的费用[14]; 污染修复费用是指突发水污染事故应急处置结束后, 为恢复被损害的生态环境资源所支出的费用[14].当突发水污染发生时, 应急响应时间越长, 应急处置的实施就越滞后, 则污染物在水中的扩散范围越大, 突发水污染所引发的上述各项灾害损失也就越大.因此, 突发水污染的灾害损失与污染物在水中的扩散范围呈正相关, 直接反映了应急响应时间效应的影响.
突发污染的灾害损失评估涉及面广、情况复杂, 为便于研究, 暂时只考虑应急响应时间效应对污染损失中应急处置费用这一最直接部分的影响.结合突发水污染自身的特点, 对突发水污染事故的应急处置费用从应急装置、应急材料、应急人员和应急物资运输4个方面进行定量化分析.已知应急处置费用为Z(t), 应急装置费用为Z1(t), 应急材料费用为Z2(t), 应急人员费用为Z3(t), 应急物资运输费用为Z4(t), 有如下的关系式[14]:
| $ \min Z\left( t \right) = {Z_1}\left( t \right) + {Z_2}\left( t \right) + {Z_3}\left( t \right) + {Z_4}\left( t \right). $ | (1) |
应急装置费用取决于应急装置的需求量, 而应急装置的用量与污染物在水中的扩散面积有关.理论上当应急装置的水力作用面积与整个污染物的扩散面积相等时, 处置效果最好.为便于分析, 假定应急装置的水力作用范围等于该装置在水面上的覆盖面积, 实际上随着装置覆盖区域内污染物浓度的减小, 在浓度差的传质推动力作用下, 周围区域的污染物浓度会进行‘补给’, 这就使得应急装置的水力作用范围要大于此覆盖面积.
定义污染物在水中的扩散面积为在排污口附近及下游, 水中污染物浓度高于该水体环境功能类别标准的区域(同一断面上边缘点的浓度为最大浓度5%的范围).该区域随扩散时间不断地发生变化, 在水面上的扩散范围(称为污染带)可近似为椭圆[10].要计算出污染带的扩散面积, 首先需要确定污染带的长度和宽度.
突发水污染没有固定的排放口, 属于非稳定源排放, 且为瞬时排放; 污染物在水中存在弥散.根据一维流场瞬时点源排放模型, 污染物的浓度在纵向服从正态分布, 在最大浓度发生点附近±2σx的范围内, 包含了大约95%的污染物总量.定义纵向距离4σx为污染带的长度Lc(t), 计算公式为[7]
| $ {L_{\rm{c}}}\left( t \right) = 4{\sigma _x} = 4\sqrt {2{D_x}t} . $ | (2) |
式中:σx为污染物在纵向的扩散长度, m; Dx为纵向弥散系数, m2/s.
实际中河流宽度是一定的, 有边界, 河流水深相对于其宽度与长度要小得多, 因此, 水溶性污染物的竖向弥散很快就会完成, 只需要考虑其在水中横向和纵向的扩散.根据二维流场有边界约束的瞬时点源排放模型, 污染物的浓度在横向上服从正态分布, 当横向宽度为±2σy的正态分布曲线下的面积占污染物总量的95%, 定义纵向距离4σy为污染带的宽度Wc(t), 计算公式为[7]
| $ {W_{\rm{c}}}\left( t \right) = 4{\sigma _y} = 4\sqrt {2{D_y}t} . $ | (3) |
由Elder和Fisher的研究结果可知[7], 竖向、横向和纵向弥散系数的计算公式如下:
| $ {D_z} = 0.067h{u^ * }. $ | (4) |
| $ {D_y} = 0.15h{u^ * }. $ | (5) |
| $ {D_x} = 5.93h{u^ * }. $ | (6) |
式中Dz为竖向扩散系数, m2/s.
河流剪切速度u*的计算公式如下[7]:
| $ {u^ * } = \sqrt {ghi} . $ | (7) |
式中:g为重力加速度, m2/s; i为河流平均坡度.
根据椭圆的计算公式, 可求得污染带的扩散面积Sc(t), 即
| $ {S_{\rm{c}}}\left( t \right) = {\rm{ \mathit{ π} }}\frac{{{L_{\rm{c}}}{W_{\rm{c}}}}}{4} = 8{\rm{ \mathit{ π} }}\sqrt {{D_x}{D_y}} t. $ | (8) |
已知每个应急装置单元的水力作用面积为Sa, 则所需装置单元的用量Na(t)为
| $ {N_{\rm{a}}}\left( t \right) = \frac{{{S_{\rm{c}}}\left( t \right)}}{{{S_{\rm{a}}}}} = \frac{{8{\rm{ \mathit{ π} }}\sqrt {{D_x}{D_y}} }}{{{S_{\rm{a}}}}}t. $ | (9) |
已知应急装置单元的价格为Pa, 则应急装置费用模型公式为
| $ {Z_1}\left( t \right) = {N_{\rm{a}}}\left( t \right) \times {P_{\rm{a}}} = \frac{{8{\rm{ \mathit{ π} }}\sqrt {{D_x}{D_y}} }}{{{S_{\rm{a}}}}}t{P_{\rm{a}}}. $ | (10) |
当突发污染时, 污染物在水中的扩散面积会急剧增加, 受限于应急装置的水力作用范围, 需要不断地增加应急装置.考虑到每个装置中的材料用量是一定的, 能根据应急装置的用量大致估算出应急材料用量.已知每个装置中吸附材料的质量为γ, 结合式(9), 则应急材料用量M(t)的计算公式为
| $ M\left( t \right) = \gamma \times {N_{\rm{a}}}\left( t \right) = \gamma \frac{{{S_{\rm{c}}}\left( t \right)}}{{{S_{\rm{a}}}}} = \gamma \frac{{8{\rm{ \mathit{ π} }}\sqrt {{D_x}{D_y}} }}{{{S_{\rm{a}}}}}t. $ | (11) |
已知应急材料的价格为Pb, 则应急材料费用模型公式为
| $ {Z_2}\left( t \right) = M\left( t \right) \times {P_{\rm{b}}} = \gamma \frac{{8{\rm{ \mathit{ π} }}\sqrt {{D_x}{D_y}} }}{{{S_{\rm{a}}}}}t{P_{\rm{b}}}. $ | (12) |
定义应急人员是能对应急装置进行装配和操作的工作人员, 因此, 应急人员的数目与装置的用量有关.已知每个装置需要的人员数量为Np, 人员工资标准为Pp, 应急人员费用模型公式为
| $ {Z_3}\left( t \right) = {N_{\rm{a}}}\left( t \right) \times {N_{\rm{P}}} \times {P_{\rm{p}}} = \frac{{8{\rm{ \mathit{ π} }}\sqrt {{D_x}{D_y}} }}{{{S_{\rm{a}}}}}t{N_{\rm{P}}}{N_{\rm{p}}}. $ | (13) |
定义应急物资运输是对应急装置和材料的运输, 因此, 应急物资运输费用与材料和装置的用量有关.已知单位数量装置单元和单位质量材料的运输费用分别为Ta和Tb, 应急物资运输费用模型公式为
| $ \begin{array}{*{20}{c}} {{Z_4}\left( t \right) = {N_{\rm{a}}}\left( t \right) \times {T_{\rm{a}}} + M\left( t \right) \times {T_{\rm{b}}} = }\\ {\frac{{8{\rm{ \mathit{ π} }}\sqrt {{D_x}{D_y}} }}{{{S_{\rm{a}}}}}t{T_{\rm{a}}} + \gamma \frac{{8{\rm{ \mathit{ π} }}\sqrt {{D_x}{D_y}} }}{{{S_{\rm{a}}}}}t{T_{\rm{b}}}.} \end{array} $ | (14) |
则基于响应时间效应的应急处置决策模型的目标函数为
| $ \begin{array}{l} \min Z\left( t \right) = {N_{\rm{a}}}\left( t \right) \times {P_{\rm{a}}} + M\left( t \right) \times {P_{\rm{b}}} + {N_{\rm{a}}}\left( t \right) \times {N_{\rm{P}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{P_{\rm{p}}} + \left[{{N_{\rm{a}}}\left( t \right) \times {T_{\rm{a}}} + M\left( t \right) \times {T_{\rm{b}}}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{8{\rm{ \mathit{ π} }}\sqrt {{D_x}{D_y}} }}{{{S_{\rm{a}}}}}t \times \left( {{P_{\rm{a}}} + \gamma {P_{\rm{b}}} + {N_{\rm{P}}}{P_{\rm{p}}} + {T_{\rm{a}}} + \gamma {T_{\rm{b}}}} \right). \end{array} $ | (15) |
应急处置的首要目标就是让水质达标即水中污染物的浓度达到水质标准质量浓度ρe, 因此, 存在水质约束, 约束条件如下:
| $ {10^6}{M_{\rm{c}}} - {10^3}M\left( t \right) \times {q_{\rm{d}}} \le {\rho _{\rm{e}}}{V_{\rm{e}}}\left( t \right). $ | (16) |
式中:Mc为污染物的瞬时排放量, kg; qd为吸附材料的实际吸附容量, mg/g; ρe为水质标准中污染物的质量浓度, mg/L; Ve(t)为扩散时间t对应的污染带体积, L.
在考察水质约束时, 为简化计算, 实际吸附容量qd取动态吸附量的实验测定值.
假定当对污染物进行应急处置时, 污染物便不再扩散, 即污染物达到平衡浓度时的扩散范围仍是扩散时间t对应的污染带体积Ve(t), 计算公式如下:
| $ {V_{\rm{e}}}\left( t \right) = 1000h \times {S_{\rm{c}}} = 8000h{\rm{ \mathit{ π} }}\sqrt {{D_x}{D_y}} t. $ | (17) |
根据水质约束, 可以得到污染物扩散时间的范围, 能大致估算满足水质约束条件至少所需要应急材料和装置的用量.
1.3.2 应急物资准备时间的约束假定前期应急准备如应急预案的制定、应急组织体系的建立和应急队伍的建设均能在第一时间完成[15], 暂时忽略了上述因素对应急响应时间的影响, 即认为应急响应时间只由应急物资的准备时间决定.
应急物资的准备时间包括应急装置和材料的准备时间.具体来说, 应急装置准备时间包括装置获取时间ta1、装车时间ta2、运输时间ta3和卸车时间ta4; 应急材料准备时间包括材料获取时间tb1、装车时间tb2、运输时间tb3、卸车时间tb4, 以及应急物资的装配时间tab5.污染物的扩散时间需要满足如下约束关系式:
| $ t \ge {t_{{\rm{a1}}}} + {t_{{\rm{a2}}}} + {t_{{\rm{a3}}}} + {t_{{\rm{a4}}}} + {t_{{\rm{ab5}}}}. $ | (18) |
| $ t \ge {t_{{\rm{b1}}}} + {t_{{\rm{b2}}}} + {t_{{\rm{b3}}}} + {t_{{\rm{b4}}}} + {t_{{\rm{ab5}}}}. $ | (19) |
上述约束条件公式(16)、(18)和(19)中的参数均符合非负约束.
为简化分析, 假定污染物在岸边排放, 已知排放点与水源地取水口之间的距离为xj.根据污染物在水中的扩散规律, 从应急处置的现场实施难度对应急物资准备时间进行分级, 结果如表 1所示.表 1中, tz为污染物完成竖向混合的时间, tf为污染物到达岸边的时间, ty为污染物完成横向混合的时间, tj为污染物到达水源地取水口的时间.4种时间的计算公式如下[7]:
| 表 1 突发水污染的应急物资准备时间分级 Table 1 Gradation of emergency supplies preparation time for sudden water pollution |
| $ {t_z} = \frac{{0.4 \times {h^2}}}{{{D_z}}}. $ | (20) |
| $ {t_f} = \frac{{0.055 \times {B^2}}}{{{D_y}}}. $ | (21) |
| $ {t_x} = \frac{{0.4 \times {B^2}}}{{{D_y}}}. $ | (22) |
| $ {t_j} = \frac{{{x_j}}}{{{u_x}}}. $ | (23) |
结合表 1, 由约束方程(18)和(19)可知, 应急物资准备时间越长, 则应急响应时间越长, 导致污染物在水中的扩散时间越长, 使得应急处置的实施难度越大, 由式(15)可知, 将污染物从水中移除的成本也会急剧增长.因此, 根据污染物在水中的扩散规律, 在竖向混合完成之前, 限制污染团的进一步扩散并将其移出水体是突发性水污染应急处置的最佳时机, 且由表 1可知, 此时应急处置的实施难度最小.但对于河流, 如前文所述, 污染物的竖向扩散很快就会完成, 在实际突发污染中很难能在竖向扩散之前完成应急物资的准备.而完成竖向扩散后, 污染团被拉长的速度开始增加, 扩散到岸后, 剪切流速分布会更大, 弥散效应加剧, 扩散限制等应急处置措施更难实施, 取水口上游便会成为最后的防线.但是取水口周边环境功能区等级高, 受地形等条件的影响, 可供选择的应急处置技术是很有限的, 导致应急处置实施难度进一步增大.此时, 可以在取水口上游设置软体围隔导流吸附帘, 围隔范围以满足取水流量为估算依据, 然后在各区域内进行应急处置, 这样可在保证城市供水不间断的情况下处置费用最低, 但是沿河流的其他污染损失依然存在.否则, 就只能暂时关闭取水口, 使水厂停水, 直到污染带流过后, 再重新开启取水口, 但这样会引起更大的经济损失, 产生恶劣的社会影响.综上, 基于响应时间效应的突发水污染应急处置模型的目标函数为
| $ \begin{array}{l} \min Z\left( t \right) = {N_{\rm{a}}}\left( t \right) \times {P_{\rm{a}}} + M\left( t \right) \times {P_{\rm{b}}} + {N_{\rm{a}}}\left( t \right) \times {N_{\rm{P}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{P_{\rm{p}}} + \left[{{N_{\rm{a}}}\left( t \right) \times {T_{\rm{a}}} + M\left( t \right) \times {T_{\rm{b}}}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{8{\rm{ \mathit{ π} }}\sqrt {{D_x}{D_y}} }}{{{S_{\rm{a}}}}}t \times \left( {{P_{\rm{a}}} + \gamma {P_{\rm{b}}} + {N_{\rm{P}}}{P_{\rm{p}}} + {T_{\rm{a}}} + \gamma {T_{\rm{b}}}} \right). \end{array} $ |
约束条件为
| $ {\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} {10^6}{M_{\rm{c}}} - {10^3}M\left( t \right) \times {q_{\rm{d}}} \le {C_{\rm{e}}}{V_{\rm{e}}}\left( t \right), \\ t \ge {t_{{\rm{a1}}}} + {t_{{\rm{a2}}}} + {t_{{\rm{a3}}}} + {t_{{\rm{a4}}}} + {t_{{\rm{ab5}}}}, \\ t \ge {t_{{\rm{b1}}}} + {t_{{\rm{b2}}}} + {t_{{\rm{b3}}}} + {t_{{\rm{b4}}}} + {t_{{\rm{ab5}}}}, \\ {M_{\rm{c}}} > 0, {q_{\rm{d}}} > 0, {t_{{\rm{a}}i}} \ge 0, {t_{{\rm{b}}i}} \ge 0, \\ \left( {i = 1, 2, 3, 4} \right), {t_{{\rm{ab5}}}} \ge 0. \end{array} \right. $ |
为更加直观地考察响应时间对应急处置费用的影响, 以曾经发生过突发污染事件、相关文献研究报道多、数据信息丰富的北江韶关—飞来峡水库段作为研究场景河段, 假设在距飞来峡水库水源地取水口160 km处发生苯胺泄漏事件, 有总量为3 t的苯胺瞬时进入水体.研究河段无其他支流的汇入, 平均流量取500 m3/s[16], 平均坡降取0.18‰[17].该段河道顺直, 但河道宽窄、深浅变化较大, 为便于分析, 假定该段的河宽和水深一定, 河道横截面认为是矩形, 河面平均宽度取400 m, 平均水深取6 m; 由流量与平均流速的关系式(式(24)), 计算求得河流的平均流速为0.21 m/s.
| $ {u_x} = \frac{Q}{{h \times B}}. $ | (24) |
式中: ux为平均流速, m/s; Q为平均流量, m3/s; B为平均宽度, m.
在此次典型情景中, 选用了一种大流量、低流阻的适合明渠突发污染应急处置的新技术——移动流化吸附法来去除苯胺[18].在现场施用时, 流化床固定在可组装的浮排上, 跟踪污染物进行移动处置.考虑到操作人员的安全, 建议浮排的设计尺寸为10 m×4 m×0.4 m, 共需160个浮筒[18], 流化床的一端通过进水管与潜水泵相连, 另一端通过出水管与明渠下游相通, 可以推算每个处置单元的水力作用面积为40 m2.
装置所需的组件均为市场上常见的产品, 如果流化床没有储备, 需要进行加工, 根据实验室的加工时间, 假定每个流化床的加工时间为10 h, 每个装置单元的花费为500元; 同时假定有足够的机床能使所需的装置可一次性加工完成, 则流化床的获取时间为10 h; 但若事先储备好所需的应急装置, 则认为装置的获取时间为0 h.
所用的应急材料主要为椰壳活性炭, 根据调研, 其市场价格约为6 000元/t(价格为6元/kg), 该材料为市场上的大宗产品, 可直接获取, 认为物资获取时间为0 h.
假定每个应急装置单元需要2名人员, 且应急人员工资标准为200元/人.
选择广东韶关为物资集结地, 根据以往突发污染事件的处置经验, 往往还需要从多个地方调运物资[19-20], 但为便于讨论运输方式对应急响应时间的影响, 假定A地周边应急物资厂家众多且距离韶关较近, 运输方式有公路运输和航空运输两种, 且有足够的交通工具, 使得所需的应急物资均能一次性完成供应; 相关运输方式情况如表 2所示.
| 表 2 突发水污染的应急物资运输方式与时间 Table 2 Emergency supplies transportation ways and time for sudden water pollution |
对典型情景中的相关信息进行整理, 得到应急处置决策模型中所需要的相关参数, 结果如表 3所示.
| 表 3 典型情景下的应急处置决策模型参数 Table 3 Parameters of emergency disposal decision-making model in the typical situation |
将表 3中相关的参数值代入式(2)、(3)和(8), 得到污染带长度、宽度和扩散面积的计算公式为
| $ {L_{\rm{c}}}\left( t \right) = 10.82\sqrt t, $ | (25) |
| $ {W_{\rm{c}}}\left( t \right) = 1.72\sqrt t, $ | (26) |
| $ {S_{\rm{c}}}\left( t \right) = 14.63t. $ | (27) |
将表 3中相关的参数值代入式(9), 得到所需装置单元个数
| $ {N_{\rm{a}}}\left( t \right) = 0.37t. $ | (28) |
将表 3中相关的参数值代入式(11), 则需要椰壳活性炭总量
| $ M\left( t \right) = 14.63t. $ | (29) |
结合式(28), 将表 3中相关的参数值代入式(10), 可得应急装置费用模型公式为
| $ {Z_1}\left( t \right) = 182.89t. $ | (30) |
结合式(29), 将表 3中相关的参数值代入式(12), 可得应急材料费用模型公式为
| $ {Z_2}\left( t \right) = 87.79t. $ | (31) |
结合式(28), 将表 3中相关的参数值代入式(13), 可得应急人员费用模型公式为
| $ {Z_3}\left( t \right) = 146.32t. $ | (32) |
结合式(28)和(29), 将表 3中相关的参数值代入式(14), 当应急物资均选择公路运输时, 应急物资运输费用模型公式为
| $ {Z_4}\left( t \right) = 36.58t. $ | (33) |
当应急物资采用公路运输时, 根据式(1)可知, 应急处置费用模型公式为
| $ \min Z\left( t \right) = 453.58t. $ | (34) |
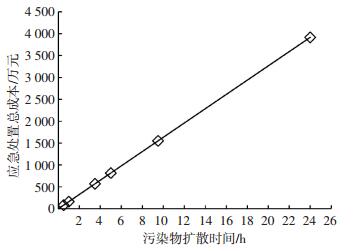
由式(34)可得公路运输方式下应急处置费用在一天内随污染物扩散时间的变化趋势, 结果如图 1所示.可以看出, 应急处置的总费用随污染物扩散时间的延长而急剧增长.当应急物资的准备时间多耽误1 h, 污染物在水中则会多扩散1 h, 此时, 应急处置费用就会增加约163万元, 由此可见, 缩短应急物资的准备时间对于降低应急处置费用至关重要.
|
图 1 应急处置费用随污染物扩散时间的变化 Figure 1 Change of emergency disposal cost with pollutant diffusion time |
同样当应急物资采用航空运输时, 根据式(34)可知, 应急处置费用变为
| $ \min Z = 545.02t. $ | (35) |
实验室研究中流化床去除水中苯胺的动态吸附量约为70 mg/g[18], 由前文假定可知, 实际吸附容量qd为70 mg/g.
由式(17)可计算得到水中污染物扩散体积的计算公式为
| $ {V_{\rm{e}}}\left( t \right) = 87789.03t. $ | (36) |
当应急处置结束时, 苯胺浓度需要达到地表水环境质量标准(GB3838—2002)中集中式生活饮用水地表水源地标准(0.1 mg/L).根据表 3中模型相关参数和α的取值, 最终水质约束关系式变为
| $ t \ge 488\;{\rm{s}}. $ | (37) |
根据式(37)和(28), 可大致估算所需要的应急处置单元个数为180个; 根据式(37)和(29)可大致估算所需要的椰壳活性炭总量约为7 132.7 kg, 上述所求得的应急物资需求量, 是满足水质约束情况下的最小值.当将水质约束放宽10%(即变为0.11 mg/L)和收紧10%(即变为0.09 mg/L)时, 椰壳活性炭的需求量分别约为7 131.7和7 133.7 kg, 目标函数值分别为221 144和221 081元, 即当水质约束变化±10%时, 目标函数值的变化幅度仅为±0.03%, 说明该模型中目标函数对水质约束的灵敏度较低.
2.2.2 应急物资准备时间对应急处置费用的影响在讨论应急物资准备时间约束对处置决策方案的影响时, 应急装置储备和无储备时所用的时间分别为0和5 h, 应急材料认为可直接获取; 在物资运输方面, 根据市场调研, 取每辆货车的材料和装置的运输量分别为20 t和30 m3(折合成应急装置个数为18个), 假定借助装载机能同时装卸10辆车, 10辆车材料和装置的装(卸)车时间分别为30和18 min; 实际上航空运输的单次运输量要大于公路运输的, 但为便于将航空运输与公路运输进行比较, 假定二者的运输量和装(卸)车时间相同; 结合上述水质约束, 则应急材料和装置的装(卸)车总时间分别约为0.5和0.3 h.在物资装配方面, 假定每个应急装置单元和材料的装配时间为30 min, 应急人员可同时对这些物资进行装配, 则认为总的应急物资装配时间为30 min.从而确定了该典型情景下应急材料和应急装置的各项准备时间, 结果如表 4所示.
| 表 4 突发水污染的应急物资各项准备时间 Table 4 Emergency supplies preparation time for sudden water pollution |
在实际应急处置物资准备过程中, 任何一项准备时间的改变都会给应急处置方案的决策带来较大的影响, 所以, 需要应急处置方案具备一定弹性余量和容错性, 结合表 4, 具体分析如下:
1) 装车前物资获取时间与应急物资的储备程度有关.以应急装置为例, 当应急装置事先加工好并作为应急物资进行储备时, 因其可直接获取, 该项时间为0;但如果没有进行储备, 则需要先进行加工才能获取, 在保证其他条件相同的情况下, 则应急响应时间和污染物的扩散时间增加了5 h.当物资运输方式为公路运输时, 由式(34)可知, 应急处置费用增加了约816万元.由此可见, 有针对性地构建应急处置物资库, 可以保证突发污染后的应急处置物资迅速到位, 从而大幅度降低应急处置费用.理论上物资库构建的越多越好, 但这可能会大幅度地增加物资库的维护费用, 还可能引起应急物资的浪费, 这就需要控制物资库的数量.因此, 物资库应当遵循科学、有效的方法进行构建, 建议物资库的构建以风险源为中心, 另外, 对没有常用应急物资生产厂家或距离物资生产厂家较远的地区, 也应当构建物资库.
2) 装(卸)车时间均与应急物资的需求量有关.应急物资需求量越大, 在装(卸)载速率一定的情况下, 装(卸)车时间越多, 应急处置的响应时间越长, 越不利于后期的应急处置.以应急装置为例, 假定装置需求量增加180个, 则装(卸)车时间增加18 min, 在其他条件相同的情况下, 则应急处置的响应时间和污染物的扩散时间会增加18 min.当物资运输方式为公路运输时, 由式(34)可知, 应急处置费用减少了约49万元.由此可见, 减少应急物资的用量, 可以减少应急物资的装(卸)车时间, 从而缩短应急处置的响应时间, 降低应急处置成本.另外, 在实际应急处置时, 为减少应急物资的用量, 可以配合应急吸附技术采取相应的措施, 如在河流的支流汇入处, 用一定量的吸附材料对水中的污染物进行控制释放来实现污染物的高效稀释, 以期减缓干流内污染物的扩散速度, 提高吸附材料的处置效率.
3) 应急物资运输时间与所选择的物资运输方式有关.当应急处置战略点选定时, 即物资的运输距离一定, 应急物资的运输时间主要由运输方式决定.应急物资的运输不同于普通的物流配送, 具有时间约束的紧迫性和弱经济性, 即需要在最短的时间内进行应急物资保障以期能把灾害损失降低到最低程度.在本次典型情景中, 假定需要在2 h内把应急物资送到战略点, 而如果采用航空应急运输, 恰好能完成任务, 在战略点进行高效应急处置.如果采用公路运输, 运输时间会延长10 h, 在其他条件相同的情况下, 则应急响应时间和污染物的扩散时间延长了10 h, 此时原有的应急处置技术方案可能无法应对现有的污染状况, 因而原有选择的战略点变得失去意义.尽管航空运输的价格要高于公路运输的, 但由式(34)和(35)可知, 与公路运输相比, 采用航空运输的应急处置费用能节省约80%.因此, 物资运输方式的选择首先要满足战略点的需求, 同时根据现有的运输能力来恰当地选择应急处置战略点.此外, 为减少应急物资运输时间, 除了选择较快的运输方式, 恰当地选择战略点外, 在构建应急物资库时, 要保证一定的物资储备能力, 还需要考虑运输方式是否便利及附近是否有对应的物资生产厂家等因素.
4) 应急装置的装配时间与其本身的结构有关.当应急装置和材料不易装配和布设时, 则装配时间会增加; 假定增加0.1 h时, 在保证其他条件相同的情况下, 则应急响应时间和污染物的扩散时间增加了0.1 h.当物资运输方式为公路运输时, 由式(34)可知, 应急处置成本增加了约16万元.因此, 在实际应急处置中, 为减少应急响应时间, 需要在短时间内完成大量处置装置与材料的装配与布设.考虑到目前突发水污染应急装置较少, 自动化程度较低, 在应急处置过程中耗费大量的人力而且处置效率低下, 有必要研发可快速组装的应急装置.
将表 3中相关的参数值分别代入式(20)~(23), 可得到污染物完成竖向扩散的时间约为5 min、到岸时间为26 h、完成横向混合的时间约为192 h和到达取水口的时间约为213 h.由表 4可知, 即使是最短的应急响应时间也要大于完成竖向扩散的时间, 这就说明, 在污染物完成竖向扩散之前, 应急物资很难准备到位.根据上述应急物资各单项准备时间对应急处置费用的影响, 在本次典型情景中, 当应急物资有准备, 采用航空运输, 所花费的应急物资准备时间最少, 结合应急物资准备时间的约束条件(式(18)和(19)), 应急响应时间至少为3.5 h, 该时间小于污染物的到岸时间, 这就说明当应急物资准备完成时, 污染物还未到岸, 由表 1可知, 此时实施难度较易.如果应急物资没有准备, 且采用公路运输, 结合应急物资准备时间的约束条件(式(18)和(19)), 可以得知污染物扩散时间至少为23.1 h, 已接近污染物的到岸时间, 此时实施难度加大, 且所需的应急物资进一步增加.
2.2.3 污染现场条件对应急处置费用的影响一般来说, 突发污染风险源多分布在河流的支流附近, 其污染物要经过由径流到支流、再由支流到干流的过程, 而每一段的弥散系数都会因剪切流速的增加而增大, 污染扩散速度会逐级跃升, 处置难度与处置费用也会随之跃升.以曾经发生的硝基苯污染事件为例, 若响应及时, 在条件允许的情况下, 能在100 t苯类物质(如苯和硝基苯等)从下水管道进入江水之前进行处置[14], 如将污染物引入到事故池进行单独处理或对污染区域构筑简单的吸附坝, 即可实现对污染物的拦截, 对于被拦截的污染物应尽快转移到安全地区; 如果条件不允许, 需要立即去除污染物.假定这100 t苯类物质全为较难处理的硝基苯, 采用活性炭吸附法进行应急处置, 根据活性炭对硝基苯的吸附容量约为25 mg/g[21], 估算其用量为4 000 t, 当时市场活性炭价格为5 500元/t, 则应急处置费用约为2 200万元.
硝基苯是难溶于水的有机物, 其熔点为5.7 ℃, 液态时的密度约为1.20 g/cm3, 重于水, 而固态时的密度轻于水.当时的污染事件发生在初冬季节, 泄入点的江水水温已低于硝基苯的凝固点, 进入江中的硝基苯一部分与冷水换热凝固, 其固态部分会漂浮在水面上, 未来得及充分换热的液态部分会沉入排放口水底, 继续完成换热而凝固在江底, 并被流过的江水逐渐溶解、流走.事故责任方期望通过加大上游水库放流量来稀释污染团以实现污染物浓度的减降; 而实际上, 一方面污染物浓度的稀释会降低单位质量吸附材料的利用率, 另一方面, 扩大的污染团的面积会占用更多的处置装置和人力资源, 由式(34)和(35)可知, 应急处置费用会大大增加.如果能在污染物排入江中的第一时间采取扩散限制及移动跟踪处置(如移动吸附流化床等)的方式, 则会快速有效地将大部分硝基苯从江中移除, 剩余的少部分硝基苯随着江水的稀释、挥发, 有望在到达下游重要水体功能区前达到水质标准.为便于分析, 假定只选用前文提及的移动流化吸附床来去除污染物(实际应急处置中一般采用多种方法联合处置), 为满足水质约束, 装置中活性炭用量约为4 000 t, 考虑到每个流化床中可填充40 kg, 则应急装置的用量约为10万个, 考虑到每个装置的价格为500元, 最终的应急处置费用约为7 700万元.但在现实中, 由于错失最佳处置时机, 最终该污染事故造成直接经济损失约为30.95亿元, 其中仅采取开闸放水所损失的实际费用与在控制污染过程中投入的水体防护工程等费用, 共计约为3.65亿元[14].
3 结论1) 以假定发生在广东北江韶关-飞来峡水库段的苯胺泄露事件为典型情景, 采用移动流化吸附法进行应急处置, 当应急物资采用公路运输时, 由基于响应时间效应的应急处置决策模型研究可得, 当突发水污染应急响应延误1 h, 应急处置费用会增加约163万元, 揭示了缩短应急响应时间对降低污染损失的重要性.
2) 在加快应急响应时间的各个环节中, 具有提升空间的环节分别是应急物资获取、运输和装配, 有针对性地进行应急物资储备、优化物资库网络和研发可快装投放的应急装置等, 是有效提高突发水污染应急处置效率的必要措施.
3) 根据污染现场条件对应急处置费用的影响, 为降低应急处置的实施难度和应急处置费用, 建议在污染物汇入干流之前, 及时采取措施来对污染物进行拦截去除.
| [1] |
杜婷婷. 突发性环境污染事件应急管理体系研究[D]. 南京: 南京大学, 2011.
DU Tingting. Study on the emergency management system of environmental pollution accident[D]. Nanjing: Nanjing University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10284-1011127092.htm |
| [2] |
周园园. 突发水污染事件应急响应支持系统研究[D]. 昆明: 昆明理工大学, 2011.
ZHOU Yuanyuan. Environmental emergency response support system for sudden water pollution accidents[D]. Kunming: Kunming University of Science and Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10674-1012263635.htm |
| [3] |
刘伟龙. 论我国环境应急管理的问题和对策——以紫金矿业污染为例[D]. 兰州: 兰州大学, 2011.
LIU Weilong. Analysis on China's environmental issues and emergency management measures-in the case of Zijin mining pollution[D]. Lanzhou: Lanzhou University, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=J0052862 |
| [4] |
PINT R G G. The danube accident emergency warning system[J].
Water Science & Technology, 1999, 40(10): 27-33.
DOI: 10.1016/S0273-1223(99)00669-1 |
| [5] |
SHI S, CAO J, LI F, et al. Construction of a technique plan repository and evaluation system based on AHP groupdecision-making for emergency treatment and disposal in chemical pollution accidents[J].
Journal of Hazardous Materials, 2014, 276C(9): 200-206.
DOI: 10.1016/j.jhazmat.2014.05.034 |
| [6] |
HE Q, PENG S, ZHAI J, et al. Development and application of a water pollution emergency response system for the Three Gorges Reservoir in the Yangtze River, China[J].
Journal of Environmental Sciences, 2011, 23(4): 595-600.
DOI: 10.1016/s1001-0742(10)60424-x |
| [7] |
程声通.
环境系统分析教程[M]. 北京: 化学工业出版社, 2012: 34-242.
CHENG Shengtong. Environmental systems analysis[M]. Beijing: Chemical Industry Press, 2012: 34-242. |
| [8] |
LIMA L S D, ARAUJO M D M, QUIN I S P, et al. Adsorption modeling of Cr, Cd and Cu on activated carbon of different origins by using fractional factorial design[J].
Chemical Engineering Journal, 2011, 166(3): 881-889.
DOI: 10.1016/j.cej.2010.11.062 |
| [9] |
曹福, 童佳. 混凝-吸附联合处理含铬废水的研究[J].
电镀与环保, 2012, 32(4): 46-48.
CAO Fu, TONG Jia. A study of joint treatment of wastewater containing chromium by coagulation and adsorption[J]. Electroplating & Pollution Control, 2012, 32(4): 46-48. |
| [10] |
许劲. 基于传质原理的二维随机水质模型研究与应用[D]. 重庆: 重庆大学, 2007.
XU Jin. Research on mass transfer theory for 2-D stochastic water quality model[D]. Chongqing: Chongqing University, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D456819 |
| [11] |
郑彤, 杜兆林, 贺玉强, 等. 水体重金属污染处理方法现状分析与应急处置策略[J].
中国给水排水, 2013, 29(6): 18-21.
ZHENG Tong, DU Zhaolin, HE Yuqiang, et al. Analysis on current treatment of heavy metal pollution in water bodies and emergency disposal strategy[J]. China Water & Wastewater, 2013, 29(6): 18-21. DOI: 10.3969/j.issn.1000-4602.2013.06.005 |
| [12] |
MCINTOSH B S, II J C A, TWERY M, et al. Environmental decision support systems (EDSS) development: Challenges and best practices[J].
Environmental Modelling & Software, 2011, 26(12): 1389-402.
DOI: 10.1016/j.envsoft.2011.09.009 |
| [13] |
王彦贺, 匡正. 基于蚁群算法的突发性水污染应急物资调配[J].
智能计算机与应用, 2014(4): 75-77.
WANG Yanhe, KUANG Zheng. Emergency supplies distribution of sudden water pollution based on ant colony algorithm[J]. Intelligent Computer and Applications, 2014(4): 75-77. DOI: 10.3969/j.issn.2095-2163.2014.04.021 |
| [14] |
张佩. 基于经济损益分析的突发水污染风险评估及应对策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.
ZHANG Pei. Study on risk assessment and copingstrategy of accidental water contamination based on economic cost-benefit analysis[D]. Harbin: Harbin Institute of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10213-1015981577.htm |
| [15] |
李湖生. 非常规突发事件应急准备体系的构成及其评估理论与方法研究[J].
中国应急管理, 2013(8): 13-21.
LI Husheng. Unconventional emergency preparedness system and its assessment theory and method of study[J]. Emergency Management in China, 2013(8): 13-21. |
| [16] |
李媛. 北江白石窑坝下河段水流特性研究[D]. 长沙: 长沙理工大学, 2013. DOI: 10.7666/d.Y2306221.
LI Yuan. Study on flow characteristics of downstream of Baishiyao complex[D]. Changsha: Changsha Univeristy of Science and Technology, 2013. DOI: 10.7666/d.Y2306221. |
| [17] |
张绪进, 程小龙, 王云莉. 北江白石窑水利枢纽下游引航道通航水力学试验研究[J].
水运工程, 2014(3): 119-124.
ZHANG Xujin, CHENG Xiaolong, WANG Yunli. Experimental research on navigation hydraulics of downstream access channel on Beijiang Baishiyao hydro-junction[J]. Port & Waterway Engineering, 2014(3): 119-124. DOI: 10.3969/j.issn.1002-4972.2014.03.024 |
| [18] |
ZHENG T, DU Z, CAO H, et al. Development of a novel mobile industrial-scale fluidized adsorption process for emergency treatment of water polluted by aniline: CFD simulation and experiments[J].
Advanced Powder Technology, 2016, 27(4): 1576-1587.
DOI: 10.1016/j.apt.2016.05.021 |
| [19] |
陈善荣, 陈明. 广东省北江韶关段镉污染事件案例分析[J].
环境教育, 2008(1): 49-53.
CHEN Shanrong, CHEN Ming. Case analysis of Guangdong shaoguan section of Beijiang River cadmium pollution incidents[J]. Environmental Education, 2008(1): 49-53. DOI: 10.3969/j.issn.1007-1679.2008.01.020 |
| [20] |
杨悦林. 铁路建设物资汽车运输单价探讨[J].
铁路工程造价管理, 2014, 29(4): 10-14.
YANG Yuelin. Discussion of railway construction supplies automotive transport unit price[J]. Railway Engineering Cost Management, 2014, 29(4): 10-14. DOI: 10.3969/j.issn.1007-9890.2014.04.004 |
| [21] |
张岩, 薛健, 褚宏举. 活性炭改性处理硝基苯废水的研究[J].
广东化工, 2012, 39(4): 83-84.
ZHANG Yan, XUE Jian, CHU Hongju. The research of modified activated carbon to remove Nitrobenzene wastewater[J]. Guangdong Chemical Industry, 2012, 39(4): 83-84. DOI: 10.3969/j.issn.1007-1865.2012.04.043 |
 2018, Vol. 50
2018, Vol. 50


